期末综合评价(含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 期末综合评价(含答案) 2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 90.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-19 21:16:18 | ||
图片预览



文档简介
期末综合评价
时间:90分钟 满分:120分]
题号 一 二 三 总分
得分
一、选择题(每小题3分,共30分)
1.下列各式是最简二次根式的是 ( )
B.
2.三角形的三边长a,b,c满足 则此三角形是
( )
A.钝角三角形 B.锐角三角形
C.直角三角形 D.等边三角形
3.下列函数中,y是x的一次函数的是 ( )
①y=x-6;②y= ;③y=π/8;④y=7-x.
A.①②③ B.①③④ C.①②③④ D.②③④
4.测试五位学生“一分钟跳绳”成绩,得到五个各不相同的数据,统计时,出现了一处错误:将最高成绩写得更高了.计算结果不受影响的是 ( )
A.方差 B.标准差 C.中位数 D.平均数
5.若四边形ABCD的四边相等,且面积为120cm ,对角线AC=24 cm,则四边形ABCD的周长为 ( )
A.52cm B.40cm C.39 cm D.26 cm
6.已知下列命题:①若a>b,则 ②若a>1,则( ③两个全等的三角形的面积相等;④四条边相等的四边形是菱形.
其中原命题与逆命题均为真命题的个数是 ( )
A.4个 B.3个 C.2个 D.1个
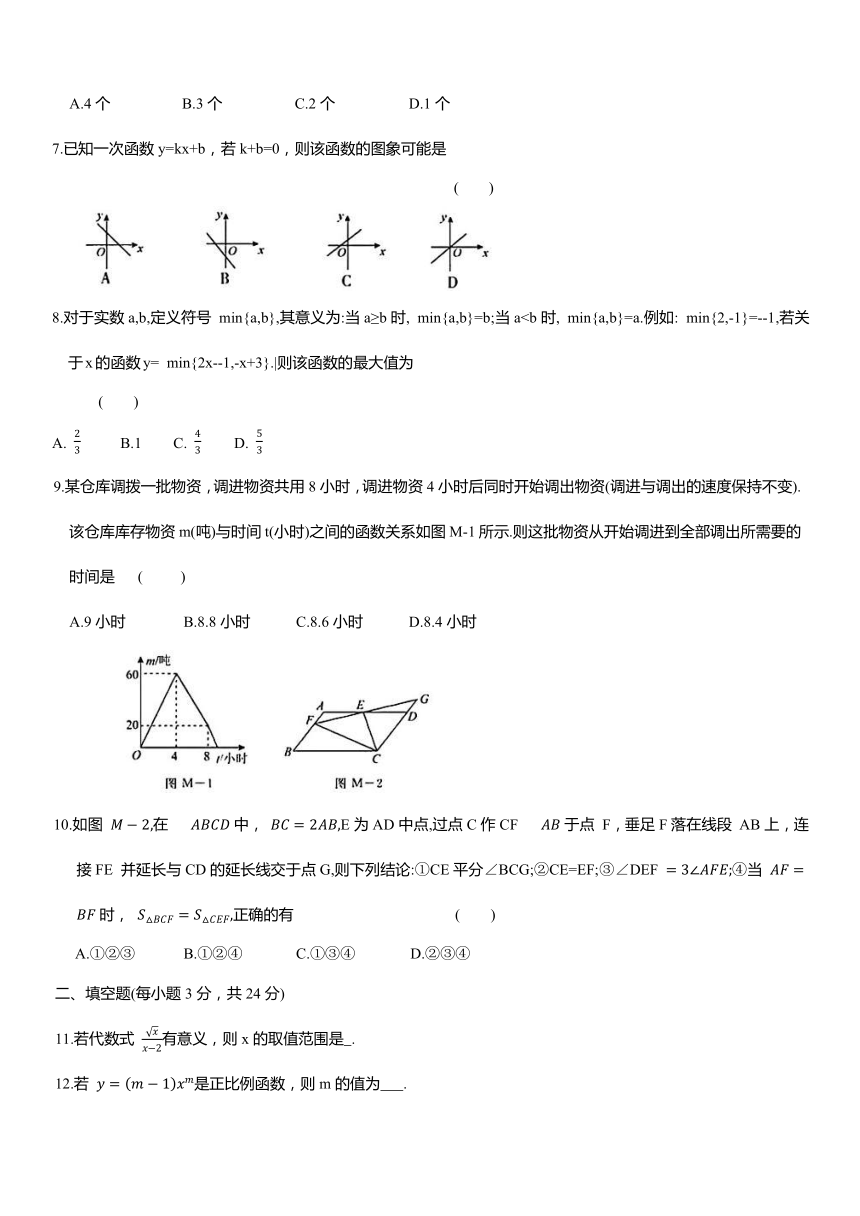
7.已知一次函数y=kx+b,若k+b=0,则该函数的图象可能是
( )
8.对于实数a,b,定义符号 min{a,b},其意义为:当a≥b时, min{a,b}=b;当aA. B.1 C. D.
9.某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资m(吨)与时间t(小时)之间的函数关系如图M-1所示.则这批物资从开始调进到全部调出所需要的时间是 ( )
A.9小时 B.8.8小时 C.8.6小时 D.8.4小时
10.如图 在 中, E为AD中点,过点C作CF 于点 F,垂足F落在线段 AB上,连接FE 并延长与CD的延长线交于点G,则下列结论:①CE平分∠BCG;②CE=EF;③∠DEF ④当 时, 正确的有 ( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题(每小题3分,共24分)
11.若代数式 有意义,则x的取值范围是 .
12.若 是正比例函数,则m的值为 .
13.小明参加了某电视台招聘记者的三项素质测试,成绩如下:采访写作70分,计算机操作60分,创意设计88分,若采访写作、计算机操作和创意设计的成绩按4:1:3计算,则他的素质测试平均成绩为 分.
14.若一次函数 的图象经过第二、三、四象限,则k的取值范围是 .
15.如图M--3是一段楼梯,高 BC是3米,斜边AC是5 米,若在楼梯上铺地毯,则至少需要地毯 米.
16.如图 在 中, M是BC 边上的动点, ,垂足分别是D、E,线段 DE 的最小值是 cm.
17.在菱形ABCD中,AE为BC边上的高,若 则线段CE 的长为 .
18.如图 点 O(0,0),A(0,1)是正方形 的两个顶点,以对角线 为边作正方形 再以正方形的对角线 作正方形 依此规律,则点 的坐标是 .
三、解答题(共66分)
19.(8分)计算:
20.(8分)在由6个大小相同的小正方形组成的方格中,如图 M--6,A,B,C是三个格点(即小正方形的顶点).判断AB与BC的关系,并说明理由.
21.(8分)如图 在 中, D为BC的中点,四边形ABDE是平行四边形,AC,DE相交于点O.
(1)求证:四边形ADCE是矩形;
(2)若 求矩形ADCE的对角线 AC的长.
22.(10 分)如图 M-8,已知直线 经过点A(5,0).B(1,4).
(1)求直线AB的解析式;
(2)若直线 与直线AB相交于点C.求点C的坐标;
(3)根据图象,写出关于x的不等式2x--4> kx+b的解集.
23.(10分)八年级一班和二班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如下表,请根据表中数据回答下列问题.
进球数/个 10 9 8 7 6 5
一班人数/人 1 1 1 4 。 3
二班人数人 0 1 2 5 0 2
(1)分别求一班和二班选手进球数的平均数、众数、中位数.
(2)如果要从这两个班中选出一个班代表本年级参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班 如果要争取个人进球数进入学校前三名,你认为应该选择哪个班
24.(10分)为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
人均住房面积 单价/万元
不超过30 0.3
超过30不超过a部分( 0.5
超过a部分 0.7
根据这个购房方案:
(1)若某三口之家欲购买 的商品房,求其应缴纳的房款:
(2)设该家庭购买商品房的人均面积为 缴纳房款 y万元,请求出 y关于x的函数解析式;
(3)若该家庭购买商品房的人均面积为 缴纳房款为y万元,且 时,求a的取值范围.
25.(12分)已知:如图 在正方形 CD中,点E为边AB的中点,连接DE,点F在DE上, 过点 F作 交AD 于点G.
(1)求证:
(2)连接AF,求证:
期末综合评价
1. B 2. C 3. B 4. C 5. A 6. D 7. A 8. D 9. B 10. A11. x≥0且x≠2 12.-1 13.75.5 14. k>3 15.7 16.4.817.2或8 18.(0.16)
19.解:(1)原式
(2)原式
20.解:相等且垂直.
理由:假设小正方形的边长为1.连接AC.
山勾股定理可得:/
∴△ABC是以∠B为直角的直角三角形.
即AB⊥BC.
∴AB 和BC 的关系是相等且垂直.
21.(1)证明:∵四边形ABDE是平行四边形.
∴BD=AE,BD∥AE.
∵AB=AC,D为BC中点,∴∠ADC=90°.('D=BD.
∴CD∥AE,CD=AE.∴四边形AECD 是平行四边形.
∵∠ADC=90°,∴四边形ADCE是矩形.
(2)解:∵四边形AIXE是矩形.∴AO=E().又∠AOE=60°.
∴△AOE为等边三角形,∴AO=4.故AC=8.
22.解:(1)∵直线y= kx+b经过点A(5.0). B(1.4).
解得
∴直线AB的解析式为. y=-x+5.
(2)由直线y=2x-4与直线AB相交于点C.
得 解得 点C的坐标为(3.2).
(3)根据图象可得不等式的解集为x>3.
23.解:(1)一班选手进球数的平均数为 7×4÷6×0-5×3)-7(个)。
二班选手进球数的平均数为 6×0+5×2)=7(个):
一班投中7个球的有4人。人数最多,故众数为7个。
二班投中7个球的有5人.人数最多.故众数为7个:
一班选手进球数按由小到大排第五、第六名同学进7个球。故中位数为7个.二班选手进球数按由小到大排第五、第六名同学进7个球,故中位数为7个.
(2)一班选手进球数的方差
二班选手进球数的方差
二班选手水平发挥更稳定,如果争取夺得总进球数团体第·名.应该选择二班:
一班前三名选手的成绩突出,分别进10个、9个、8个球,如果要争取个人进球数进入学校前三名,应该选择一班。
21.解:(1)由题意,得三口之家应缴购房款为0.3×90÷0.5×30=12(万元).
(2)由题意.得
①当0≤x≤30时,y=0.3×3x=0.9x:
②当30y=0.3×3×30-0.5×3×(. r-30)=1.5x--18;
③当x>u时. y=0.3×3×30+0.5×3(a-30)+0.7×3×(. r-(1)-2.1. r-0.6u-18.
(3)由题意.得
①当50<,a<60时,人均面积为50m'没有超过a.所以应缴纳的房款y=1.5x-18=1.5×50-18=57(舍去);
②当45≤u<50时,人均面积为50m 超过u。
则y-2.1. r-0.6u-18-2.1×50-0.6a-18-87-0.6a.
∵57综上所述.45≤a<'50.
25.证明:证法一:(1)∵四边形 ABCD 是正方形。∴∠ADC-90°.∵FG⊥FC∴∴∠GFC=90°.∵(F=('D.
∴∠CDF=∠CFD.
∴∠CFG-∠CFD-∠CDG-∠CDF.即∠GFD-∠GDF.
∴GF=GD.
(2)如答图M-1所示.连接(G.∵CF=CD. GF=GD.
∴点G、C在线段FD的垂直平分线上.∴GC⊥DE.∴∠CDF-∠IX'G= 90°.∵∠CDF+∠ADE=90°.∴∠I)(G=∠ADE.∵四边形ABCD是正方形,∴AD=DC,∠DAE=∠CDG≌90'.∴△DAE≌△CDG.∴AE=DG.∵点 E 是边AB 的中点,∴点G是边AD 的中点,∴AG=GD=GF.
∴∠DAF=∠AF(;.∠GDF=∠GFD.
∵∠DAF+∠AFG+∠GFD+∠GDF=180°.
∴2∠AFG+2∠GFD=180°.
∴∠AFD=90°,即AF⊥DE.
证法二:(1)如答图 M-1所示,连接(Y;交 ED于点 H.∵四边形ABCD 是正方形.∴∠ADC=90°.∵FG FC.∴∠GF(°=90°,在Rt△CFG与Rt△CIXi中.
∴Rt△(TGG≌Rt△CTX;.∴(;F=(;1).
(2)∵GF=GD,CF=(D,∴点G,C在线段FD 的中垂线上,∴FH=11D. GC⊥DE.∴∠EDC+∠DCH=90∵∠ADE+∠EIX'=90'∴∠ADE=∠IXCH.∵四边形ABCD是正方形。∴AD=DC°= AB.∠DAE=∠C'IX;=90°.∵∠ADE=∠IX' ll. AD=DC.∠EAD=∠GDC.∴△ADE≌△DC(;.∴AE=IX;.∵点E是边AB的中点,∴点G是边AD的中点.∵点H 是边 FD的中点,∴GH 是△AFD的中位线,∴(GH∥AF.∴∠AFD=∠GHD.∵GH FD.∴∠GHD=90°.
时间:90分钟 满分:120分]
题号 一 二 三 总分
得分
一、选择题(每小题3分,共30分)
1.下列各式是最简二次根式的是 ( )
B.
2.三角形的三边长a,b,c满足 则此三角形是
( )
A.钝角三角形 B.锐角三角形
C.直角三角形 D.等边三角形
3.下列函数中,y是x的一次函数的是 ( )
①y=x-6;②y= ;③y=π/8;④y=7-x.
A.①②③ B.①③④ C.①②③④ D.②③④
4.测试五位学生“一分钟跳绳”成绩,得到五个各不相同的数据,统计时,出现了一处错误:将最高成绩写得更高了.计算结果不受影响的是 ( )
A.方差 B.标准差 C.中位数 D.平均数
5.若四边形ABCD的四边相等,且面积为120cm ,对角线AC=24 cm,则四边形ABCD的周长为 ( )
A.52cm B.40cm C.39 cm D.26 cm
6.已知下列命题:①若a>b,则 ②若a>1,则( ③两个全等的三角形的面积相等;④四条边相等的四边形是菱形.
其中原命题与逆命题均为真命题的个数是 ( )
A.4个 B.3个 C.2个 D.1个
7.已知一次函数y=kx+b,若k+b=0,则该函数的图象可能是
( )
8.对于实数a,b,定义符号 min{a,b},其意义为:当a≥b时, min{a,b}=b;当a
9.某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资m(吨)与时间t(小时)之间的函数关系如图M-1所示.则这批物资从开始调进到全部调出所需要的时间是 ( )
A.9小时 B.8.8小时 C.8.6小时 D.8.4小时
10.如图 在 中, E为AD中点,过点C作CF 于点 F,垂足F落在线段 AB上,连接FE 并延长与CD的延长线交于点G,则下列结论:①CE平分∠BCG;②CE=EF;③∠DEF ④当 时, 正确的有 ( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题(每小题3分,共24分)
11.若代数式 有意义,则x的取值范围是 .
12.若 是正比例函数,则m的值为 .
13.小明参加了某电视台招聘记者的三项素质测试,成绩如下:采访写作70分,计算机操作60分,创意设计88分,若采访写作、计算机操作和创意设计的成绩按4:1:3计算,则他的素质测试平均成绩为 分.
14.若一次函数 的图象经过第二、三、四象限,则k的取值范围是 .
15.如图M--3是一段楼梯,高 BC是3米,斜边AC是5 米,若在楼梯上铺地毯,则至少需要地毯 米.
16.如图 在 中, M是BC 边上的动点, ,垂足分别是D、E,线段 DE 的最小值是 cm.
17.在菱形ABCD中,AE为BC边上的高,若 则线段CE 的长为 .
18.如图 点 O(0,0),A(0,1)是正方形 的两个顶点,以对角线 为边作正方形 再以正方形的对角线 作正方形 依此规律,则点 的坐标是 .
三、解答题(共66分)
19.(8分)计算:
20.(8分)在由6个大小相同的小正方形组成的方格中,如图 M--6,A,B,C是三个格点(即小正方形的顶点).判断AB与BC的关系,并说明理由.
21.(8分)如图 在 中, D为BC的中点,四边形ABDE是平行四边形,AC,DE相交于点O.
(1)求证:四边形ADCE是矩形;
(2)若 求矩形ADCE的对角线 AC的长.
22.(10 分)如图 M-8,已知直线 经过点A(5,0).B(1,4).
(1)求直线AB的解析式;
(2)若直线 与直线AB相交于点C.求点C的坐标;
(3)根据图象,写出关于x的不等式2x--4> kx+b的解集.
23.(10分)八年级一班和二班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如下表,请根据表中数据回答下列问题.
进球数/个 10 9 8 7 6 5
一班人数/人 1 1 1 4 。 3
二班人数人 0 1 2 5 0 2
(1)分别求一班和二班选手进球数的平均数、众数、中位数.
(2)如果要从这两个班中选出一个班代表本年级参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班 如果要争取个人进球数进入学校前三名,你认为应该选择哪个班
24.(10分)为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
人均住房面积 单价/万元
不超过30 0.3
超过30不超过a部分( 0.5
超过a部分 0.7
根据这个购房方案:
(1)若某三口之家欲购买 的商品房,求其应缴纳的房款:
(2)设该家庭购买商品房的人均面积为 缴纳房款 y万元,请求出 y关于x的函数解析式;
(3)若该家庭购买商品房的人均面积为 缴纳房款为y万元,且 时,求a的取值范围.
25.(12分)已知:如图 在正方形 CD中,点E为边AB的中点,连接DE,点F在DE上, 过点 F作 交AD 于点G.
(1)求证:
(2)连接AF,求证:
期末综合评价
1. B 2. C 3. B 4. C 5. A 6. D 7. A 8. D 9. B 10. A11. x≥0且x≠2 12.-1 13.75.5 14. k>3 15.7 16.4.817.2或8 18.(0.16)
19.解:(1)原式
(2)原式
20.解:相等且垂直.
理由:假设小正方形的边长为1.连接AC.
山勾股定理可得:/
∴△ABC是以∠B为直角的直角三角形.
即AB⊥BC.
∴AB 和BC 的关系是相等且垂直.
21.(1)证明:∵四边形ABDE是平行四边形.
∴BD=AE,BD∥AE.
∵AB=AC,D为BC中点,∴∠ADC=90°.('D=BD.
∴CD∥AE,CD=AE.∴四边形AECD 是平行四边形.
∵∠ADC=90°,∴四边形ADCE是矩形.
(2)解:∵四边形AIXE是矩形.∴AO=E().又∠AOE=60°.
∴△AOE为等边三角形,∴AO=4.故AC=8.
22.解:(1)∵直线y= kx+b经过点A(5.0). B(1.4).
解得
∴直线AB的解析式为. y=-x+5.
(2)由直线y=2x-4与直线AB相交于点C.
得 解得 点C的坐标为(3.2).
(3)根据图象可得不等式的解集为x>3.
23.解:(1)一班选手进球数的平均数为 7×4÷6×0-5×3)-7(个)。
二班选手进球数的平均数为 6×0+5×2)=7(个):
一班投中7个球的有4人。人数最多,故众数为7个。
二班投中7个球的有5人.人数最多.故众数为7个:
一班选手进球数按由小到大排第五、第六名同学进7个球。故中位数为7个.二班选手进球数按由小到大排第五、第六名同学进7个球,故中位数为7个.
(2)一班选手进球数的方差
二班选手进球数的方差
二班选手水平发挥更稳定,如果争取夺得总进球数团体第·名.应该选择二班:
一班前三名选手的成绩突出,分别进10个、9个、8个球,如果要争取个人进球数进入学校前三名,应该选择一班。
21.解:(1)由题意,得三口之家应缴购房款为0.3×90÷0.5×30=12(万元).
(2)由题意.得
①当0≤x≤30时,y=0.3×3x=0.9x:
②当30
③当x>u时. y=0.3×3×30+0.5×3(a-30)+0.7×3×(. r-(1)-2.1. r-0.6u-18.
(3)由题意.得
①当50<,a<60时,人均面积为50m'没有超过a.所以应缴纳的房款y=1.5x-18=1.5×50-18=57(舍去);
②当45≤u<50时,人均面积为50m 超过u。
则y-2.1. r-0.6u-18-2.1×50-0.6a-18-87-0.6a.
∵57
25.证明:证法一:(1)∵四边形 ABCD 是正方形。∴∠ADC-90°.∵FG⊥FC∴∴∠GFC=90°.∵(F=('D.
∴∠CDF=∠CFD.
∴∠CFG-∠CFD-∠CDG-∠CDF.即∠GFD-∠GDF.
∴GF=GD.
(2)如答图M-1所示.连接(G.∵CF=CD. GF=GD.
∴点G、C在线段FD的垂直平分线上.∴GC⊥DE.∴∠CDF-∠IX'G= 90°.∵∠CDF+∠ADE=90°.∴∠I)(G=∠ADE.∵四边形ABCD是正方形,∴AD=DC,∠DAE=∠CDG≌90'.∴△DAE≌△CDG.∴AE=DG.∵点 E 是边AB 的中点,∴点G是边AD 的中点,∴AG=GD=GF.
∴∠DAF=∠AF(;.∠GDF=∠GFD.
∵∠DAF+∠AFG+∠GFD+∠GDF=180°.
∴2∠AFG+2∠GFD=180°.
∴∠AFD=90°,即AF⊥DE.
证法二:(1)如答图 M-1所示,连接(Y;交 ED于点 H.∵四边形ABCD 是正方形.∴∠ADC=90°.∵FG FC.∴∠GF(°=90°,在Rt△CFG与Rt△CIXi中.
∴Rt△(TGG≌Rt△CTX;.∴(;F=(;1).
(2)∵GF=GD,CF=(D,∴点G,C在线段FD 的中垂线上,∴FH=11D. GC⊥DE.∴∠EDC+∠DCH=90∵∠ADE+∠EIX'=90'∴∠ADE=∠IXCH.∵四边形ABCD是正方形。∴AD=DC°= AB.∠DAE=∠C'IX;=90°.∵∠ADE=∠IX' ll. AD=DC.∠EAD=∠GDC.∴△ADE≌△DC(;.∴AE=IX;.∵点E是边AB的中点,∴点G是边AD的中点.∵点H 是边 FD的中点,∴GH 是△AFD的中位线,∴(GH∥AF.∴∠AFD=∠GHD.∵GH FD.∴∠GHD=90°.
同课章节目录
