【期末押题卷】湖南省长沙市2024-2025学年六年级下学期期末素养评价数学预测卷人教版(含解析)
文档属性
| 名称 | 【期末押题卷】湖南省长沙市2024-2025学年六年级下学期期末素养评价数学预测卷人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-19 20:22:58 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024-2025学年六年级下学期期末素养评价数学预测卷
一.选择题(共7小题)
1.如图,从梯形里剪去一个最大的平行四边形后,剩下的面积是( )平方厘米。
A.64 B.48 C.12 D.24
2.为了更直观地表示新蒲新区2022上半年月平均降雨量的多少及其变化趋势,绘制( )最合适。
A.统计表 B.条形统计图
C.折线统计图 D.扇形统计图
3.两个人轮流报数,每次只能报1或2,把两个人报的所有数加起来,谁报数后和是100谁就获胜。如果让你先报数,为了确保获胜,你第一次应该报( )
A.1 B.2 C.都可以 D.无法确定
4.把圆柱的侧面展开不可能得到一个( )
A.长方形 B.正方形
C.三角形 D.平行四边形
5.把14个棱长是1cm的正方体放在地面上,堆成如图所示的组合体,然后将露出的表面部分涂成红色(底面不涂)。那么红色部分的面积是( )
A.33 B.38 C.42
6.在一张图纸上量得一个零件的长度是6厘米,已知这张图纸的比例尺是1:100,求这个零件的实际长度是( )米。
A.6 B.0.6 C.60 D.600
7.立体图形从上面看到的形状是( )
A. B. C. D.
二.填空题(共10小题)
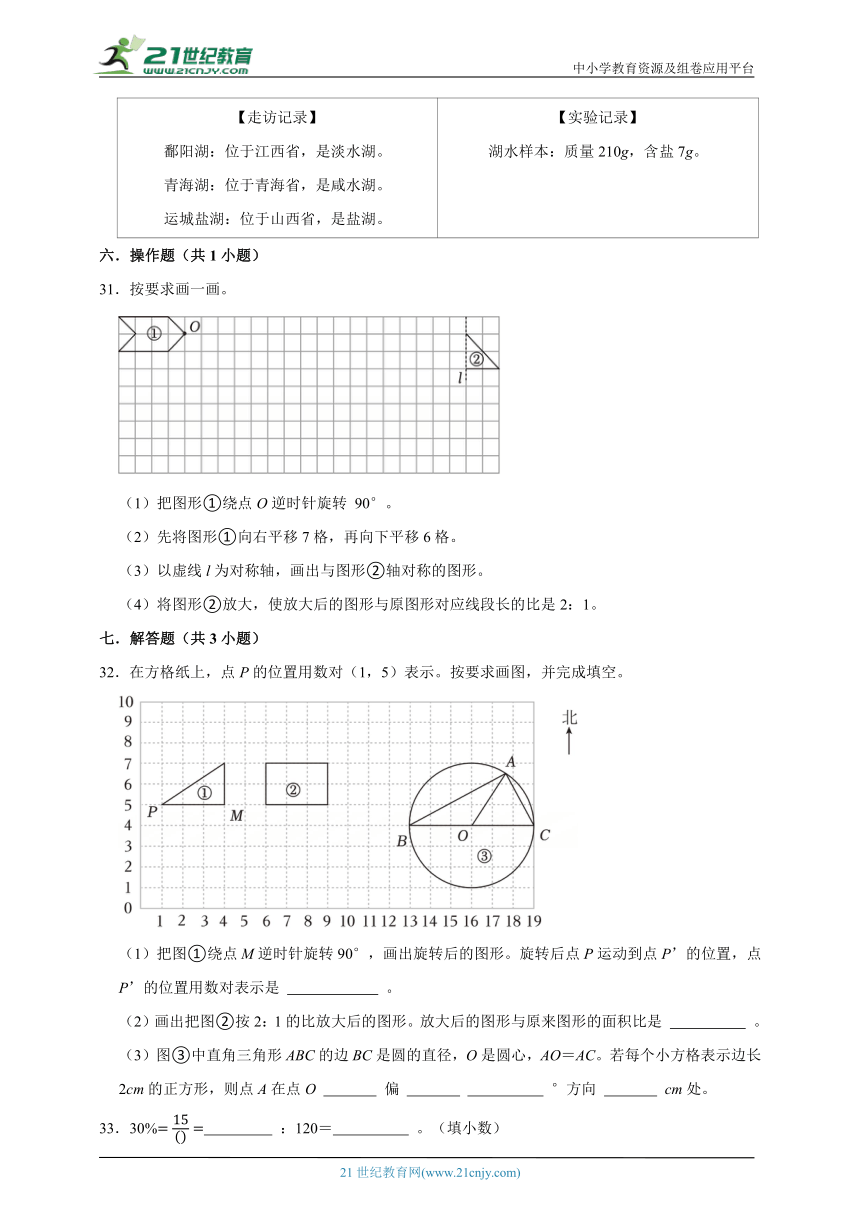
8.在一幅比例尺是40:1的地图上,量得一个零件的长是5cm,这个零件的实际长是 。
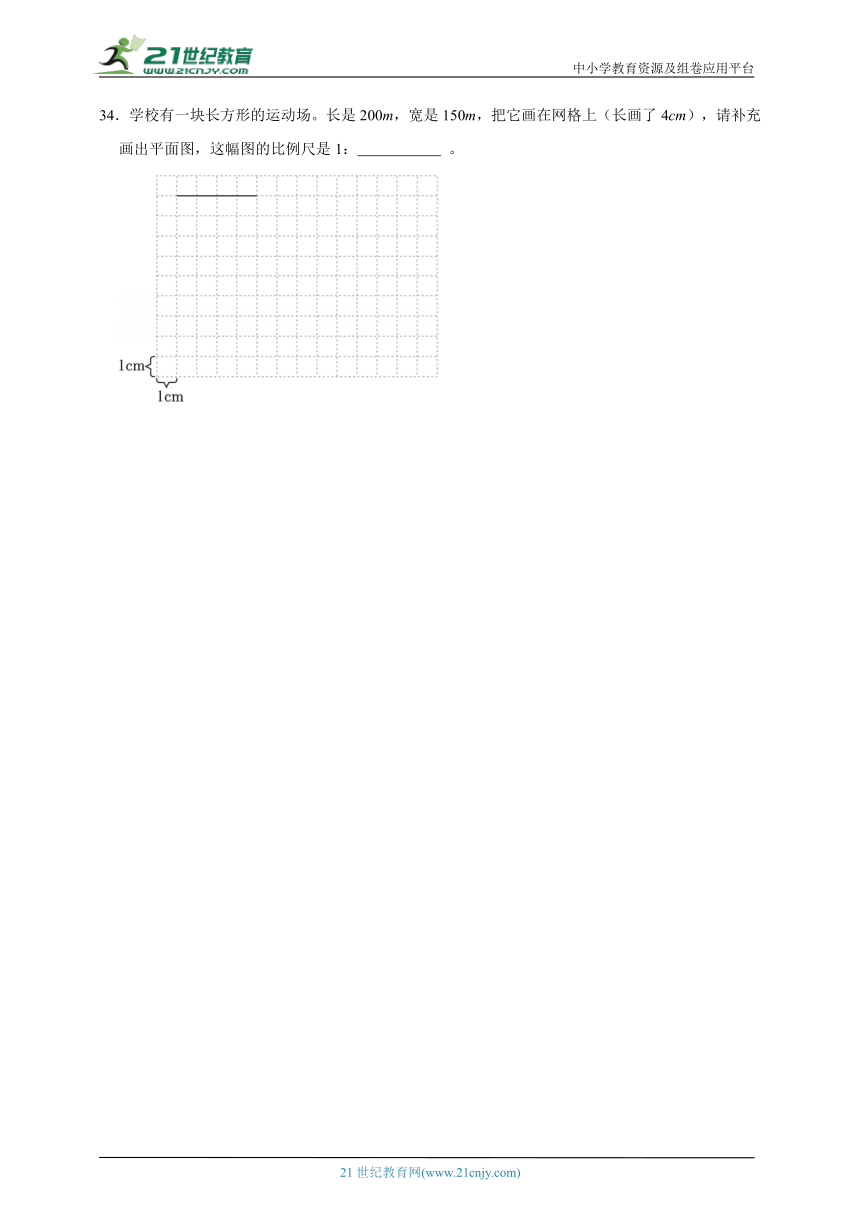
9.如果m(m、n均不为0),那么m与n成 比例关系。如果3m=7n(m、n均不为0),那么m:n= 。
10.一根长5m的铁丝平均分成8段,每段的长度是这根铁丝的 ,每段长是
m。
11.哥哥得到一笔4800元的劳务报酬,其中800元是免税的,超过800元的部分要按20%的税率缴税。这笔劳务报酬一共要缴税 元。
12.明年的第一季度有 天。
13.今年“五一”假期,成都假日文旅市场呈现安全平稳、繁荣有序的良好发展态势。数据显示,成都接待游客一千四百六十一万三千人次,横线上的数写作 ,改为以“万”为单位的数是 万。
14.有一个底面直径是3cm的圆柱形玩具,高8cm,滚动一周后前进了 cm,压过的面积是 cm2。
15.如图:1张桌子可以坐下8人,2张桌子拼起来可以坐下 人,5张这样的桌子拼起来能够坐下 人。
16.李明家的挂钟的分针长8厘米,经过15分钟分针的尖端所走的路程是 厘米;经过30分钟扫过的面积是 平方厘米。
17.如图,将图形D绕点O 时针旋转 °得到图形C。
三.判断题(共5小题)
18.六(1)班人数的40%是女生,六(2)班人数的45%是女生,两班女生人数相等。那么六(1)班比六(2)班人数少。
19.小华在晓东家东偏南30°方向上,晓东就在小华家南偏东30°方向上。
20.学校一共植树102棵,其中2棵没有成活,这批树的成活率是100%。
21.一张方桌可以坐8人,两张这样的方桌并起来,可以坐16人。
22.学校买来9个足球,每个a元,又买来b个篮球,每个58元,一共用了多少钱?用式子表示应是9a+58。
四.计算题(共3小题)
23.解方程。
30% xx=42
24.直接写出得数。
0.25×0.4= 0.77+0.32= 32÷0.4= 0×0.24=
7.2÷0.1=
25.怎样简便怎样算。
() ()
()×72 (25%)
五.应用题(共5小题)
26.水果店新进一批苹果,第一天卖出了全部的,第二天卖出了余下的,第三天比第一天少卖了,这时还剩下350千克。水果店共运进了多少千克苹果?
27.某工地有一个近似圆锥形沙堆,量得它的底面周长是18.84m,高是1.5m。如果每立方米沙约重1.6吨,这堆沙约有多少吨?
28.一堆圆锥形小麦堆,高1.2米,占地面积是16平方米,如果每立方米小麦重700千克,那么这堆小麦重多少千克?
29.叔叔买一套家具,按原价的八五折购买可以便宜2250元,这套家具的原价是多少元?
30.阅读下面的材料,回答问题。
中国湖泊众多,共有湖泊24800多个,其中面积在1平方千米以上的天然湖泊就有2800多个。按照湖水含盐率分类,这些湖泊可分为淡水湖(含盐率<0.1%)、微咸水湖(0.1%≤含盐率<1%)、咸水湖(1%≤含盐率<3.5%)和盐湖(含盐率≥3.5%)。
淘气在假期中游玩了三个湖泊,并在其中一个湖泊中采集了湖水样本,请你根据他的实验记录计算并判断所采样本来自哪个湖泊?(百分号前保留两位小数)
【走访记录】 鄱阳湖:位于江西省,是淡水湖。 青海湖:位于青海省,是咸水湖。 运城盐湖:位于山西省,是盐湖。 【实验记录】 湖水样本:质量210g,含盐7g。
六.操作题(共1小题)
31.按要求画一画。
(1)把图形①绕点O逆时针旋转 90°。
(2)先将图形①向右平移7格,再向下平移6格。
(3)以虚线l为对称轴,画出与图形②轴对称的图形。
(4)将图形②放大,使放大后的图形与原图形对应线段长的比是2:1。
七.解答题(共3小题)
32.在方格纸上,点P的位置用数对(1,5)表示。按要求画图,并完成填空。
(1)把图①绕点M逆时针旋转90°,画出旋转后的图形。旋转后点P运动到点P’的位置,点P’的位置用数对表示是 。
(2)画出把图②按2:1的比放大后的图形。放大后的图形与原来图形的面积比是 。
(3)图③中直角三角形ABC的边BC是圆的直径,O是圆心,AO=AC。若每个小方格表示边长2cm的正方形,则点A在点O 偏 °方向 cm处。
33.30% :120= 。(填小数)
34.学校有一块长方形的运动场。长是200m,宽是150m,把它画在网格上(长画了4cm),请补充画出平面图,这幅图的比例尺是1: 。
2024-2025学年六年级下学期期末素养评价数学预测卷
参考答案与试题解析
一.选择题(共7小题)
1.如图,从梯形里剪去一个最大的平行四边形后,剩下的面积是( )平方厘米。
A.64 B.48 C.12 D.24
【答案】C
【分析】要想在这个梯形中剪去一个最大的平行四边形,必须把梯形的上底8厘米作为平行四边形的底进行剪切,剩下的部分是一个底为(12﹣8)厘米、高即为梯形的高6厘米的三角形,求剩下的面积利用三角形的面积公式:S=ah÷2,代入数值求解即可。
【解答】解:(12﹣8)×6÷2
=4×6÷2
=12(平方厘米)
答:剩下的面积是12平方厘米。
故选:C。
【点评】此题考查组合图形的面积,解决此题关键是弄明白怎么剪才能使平行四边形的面积最大,并明确剩下的三角形的底和高,进而得出剩下的三角形的面积。
2.为了更直观地表示新蒲新区2022上半年月平均降雨量的多少及其变化趋势,绘制( )最合适。
A.统计表 B.条形统计图
C.折线统计图 D.扇形统计图
【答案】C
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【解答】解:为了更直观地表示新蒲新区2022上半年月平均降雨量的多少及其变化趋势,绘制折线统计图最合适。
故选:C。
【点评】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
3.两个人轮流报数,每次只能报1或2,把两个人报的所有数加起来,谁报数后和是100谁就获胜。如果让你先报数,为了确保获胜,你第一次应该报( )
A.1 B.2 C.都可以 D.无法确定
【答案】A
【分析】因为100÷(1+2)=33……1,所以,先报的一定要报1,然后每次报的数始终都与另一人的和是3,一定会赢。
【解答】解:先报数的人第1次一定要报1,和还剩100﹣1=99,99是3的倍数,
所以,以后每次报的数始终都与另一人报的数的和是3,
最后一次总是先报数的人,
所以只要这样做先报数的人一定会赢。
答:为了确保获胜,我第一次应该报1。
故选:A。
【点评】本题关键根据余数确定先报的数,以后每次报的数始终都与另一人报的数的和是3,一定会赢。
4.把圆柱的侧面展开不可能得到一个( )
A.长方形 B.正方形
C.三角形 D.平行四边形
【答案】C
【分析】根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形(或正方形),如果圆柱的侧面斜着展开是一个平行四边形。据此解答即可。
【解答】解:由分析得:圆柱的侧面沿高展开是一个长方形(或正方形),如果圆柱的侧面斜着展开是一个平行四边形。
所以把一个圆柱的侧面展开不可能得到一个三角形。
故选:C。
【点评】此题考查的目的是理解掌握圆柱侧面展开图的特征及应用。
5.把14个棱长是1cm的正方体放在地面上,堆成如图所示的组合体,然后将露出的表面部分涂成红色(底面不涂)。那么红色部分的面积是( )
A.33 B.38 C.42
【答案】A
【分析】画出立体图形的三视图,染色的总面积=正视图面积×2+左视图面积×2+俯视图面积,计算即可。
【解答】解:画出此立体图形的三视图:
每个小正方形的面积为:1×1=1
俯视图的面积为:3×3×1=9
正视图的面积为:(3+2+1)×1=6
左视图的面积为:(3+2+1)×1=6
所以,染色的总面积为:
9+6×2+6×2
=9+12+12
=33
故选:A。
【点评】本题主要考查了染色问题,理解露出的表面部分也就是能看到的部分,并画出三视图求解,是本题解题的关键。
6.在一张图纸上量得一个零件的长度是6厘米,已知这张图纸的比例尺是1:100,求这个零件的实际长度是( )米。
A.6 B.0.6 C.60 D.600
【答案】A
【分析】要求零件的实际长度是多少毫米,根据“图上距离÷比例尺=实际距离”,代入数值,计算即可。
【解答】解:6600(厘米)
600厘米=6米
答:这个零件的实际长度是6米。
故选:A。
【点评】此题考查了实际距离、图上距离和比例尺之间的关系,注意统一单位。
7.立体图形从上面看到的形状是( )
A. B. C. D.
【答案】C
【分析】根据观察,可知的正面图形为;左面图形为;上面图形为;右面图形为。
【解答】解:立体图形从上面看到的形状是。
故选:C。
【点评】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
二.填空题(共10小题)
8.在一幅比例尺是40:1的地图上,量得一个零件的长是5cm,这个零件的实际长是 0.125厘米 。
【答案】0.125厘米。
【分析】要求这个零件的实际长度是多少,根据“图上距离÷比例尺=实际距离”,代入数值,计算即可.
【解答】解:50.125(厘米)
答:这个零件的实际长度是0.125厘米。
故答案为:0.125厘米。
【点评】此题由计算公式可用,根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论。
9.如果m(m、n均不为0),那么m与n成 反 比例关系。如果3m=7n(m、n均不为0),那么m:n= 。
【答案】反,。
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此判断;在比例中,两个外项的积等于两个内项的积,这叫作比例的基本性质。据此解答。
【解答】解:根据分母×分数值=分子,将m改写成mn=2024(一定),因为mn的积一定,所以mn成反比例。
如果3m=7n(m、n均不为0),那么m:n=7:3。
如果m(m、n均不为0),那么m与n成反比例关系。如果3m=7n(m、n均不为0),那么m:n。
故答案为:反,。
【点评】此题考查了辨识成正比例的量与成反比例的量,要求学生掌握。
10.一根长5m的铁丝平均分成8段,每段的长度是这根铁丝的 ,每段长是 m。
【答案】,。
【分析】把这根铁丝的长度看作单位“1”,把它平均分成8段,求每段的长度是这根铁丝的几分之几,用1除以8;求每段长,用这根铁丝的长度除以8。
【解答】解:1÷8
5÷8(m)
答:每段的长度是这根铁丝的,每段长是m。
故答案为:,。
【点评】解决此题关键是弄清求的是“分率”还是“具体的数量”,求分率:平均分的是单位“1”;求具体的数量:平均分的是具体的数量。注意:分率不能带单位名称,而具体的数量要带单位名称。
11.哥哥得到一笔4800元的劳务报酬,其中800元是免税的,超过800元的部分要按20%的税率缴税。这笔劳务报酬一共要缴税 800 元。
【答案】800。
【分析】用劳务报酬的总数减去800元,再乘税率,即可求出这笔劳务报酬一共要缴税多少钱。
【解答】解:(4800﹣800)×20%
=4000×20%
=800(元)
答:这笔劳务报酬一共要缴税800元。
故答案为:800。
【点评】本题考查百分数的计算及应用。理解题意,找出数量关系,列式计算即可。
12.明年的第一季度有 91 天。
【答案】91。
【分析】今年是2023年,明年是2024年;先判断2024年是平年还是闰年,平年二月份有28天,闰年二月份有29天;无论平年还是闰年一月份和三月份都是31天,由此求出第一季度的天数。
【解答】解:明年是2024年
2024÷4=506
2024年是闰年,二月份有29天;
31+29+31=91(天)
答:明年的第一季度有91天。
故答案为:91。
【点评】本题关键是考查了对闰年和平年的判断,用年份除以4(或400),看是否能整除即可;还要记住一年中各个月份的天数。
13.今年“五一”假期,成都假日文旅市场呈现安全平稳、繁荣有序的良好发展态势。数据显示,成都接待游客一千四百六十一万三千人次,横线上的数写作 14613000 ,改为以“万”为单位的数是 1461.3 万。
【答案】14613000,1461.3。
【分析】(1)整数的写法,从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0,据此写出此数;
(2)改写时在万位的后边,点上小数点,去掉小数点末尾的0,并加上一个“万”字即可。
【解答】解:根据题意可知:
一千四百六十一万三千写作:14613000
14613000改为“万”为单位的数是1461.3万。
故答案为:14613000,1461.3。
【点评】此题考查了亿以内数的读写与改写,要求学生掌握。
14.有一个底面直径是3cm的圆柱形玩具,高8cm,滚动一周后前进了 9.42 cm,压过的面积是 75.36 cm2。
【答案】9.42,75.36。
【分析】根据圆的周长公式:C=πd,圆柱的侧面积公式:S=Ch,把数据代入公式解答。
【解答】解:3.14×3=9.42(厘米)
9.42×8=75.36(平方厘米)
答:滚动一周前进了9.42厘米,压过的面积是75.36平方厘米。
故答案为:9.42,75.36。
【点评】此题主要考查圆的周长公式、圆柱的侧面积公式的灵活运用,关键是熟记公式。
15.如图:1张桌子可以坐下8人,2张桌子拼起来可以坐下 12 人,5张这样的桌子拼起来能够坐下 24 人。
【答案】12,24。
【分析】观察图形发现,第1张桌子可以坐8人,每多1张桌子可以多做4人,那么第n张桌子能做(4n+4)人,据此解答。
【解答】解:由分析可得,
1张桌子可以坐下8人,2张桌子拼起来可以坐下12人,5张这样的桌子拼起来能够坐下24人。
故答案为:12,24。
【点评】此题考查数与形结合的规律,找到规律是解题的关键。
16.李明家的挂钟的分针长8厘米,经过15分钟分针的尖端所走的路程是 12.56 厘米;经过30分钟扫过的面积是 100.48 平方厘米。
【答案】12.56,100.48。
【分析】钟面上,分针15分钟分针尖端所走的路程是以分针为半径的圆周长的,根据圆周长计算公式“C=2πr”及分数乘法的意义即可解答;经过30分钟扫过的面积是以分针为半径的圆面积的,根据圆面积计算公式“C=πr2”及分数乘法的意义即可解答。
【解答】解:3.14×2×8
=6.28×8
=50.24
=12.56(厘米)
3.14×82
=3.14×64
=100.48(平方厘米)
答:经过15分钟分针的尖端所走的路程是12.56厘米;经过30分钟扫过的面积是100.48平方厘米。
故答案为:12.56,100.48。
【点评】解答此题的关键是圆周长计算公式、圆面积计算公式的灵活运用。
17.如图,将图形D绕点O 逆 时针旋转 90 °得到图形C。
【答案】逆,90。
【分析】根据旋转的特征,图形的旋转是图形上的每一点在平面上绕着某个固定点旋转固定角度的位置移动,其中对应点到旋转中心的距离相等,对应线段的长度、对应角的大小相等,旋转前后图形的大小和形状没有改变,据此解答即可。
【解答】解:如图,将图形D绕点O逆时针旋转90°得到图形C。
故答案为:逆,90。
【点评】本题考查了旋转知识,结合旋转的方向和角度解答即可。
三.判断题(共5小题)
18.六(1)班人数的40%是女生,六(2)班人数的45%是女生,两班女生人数相等。那么六(1)班比六(2)班人数少。 ×
【答案】×。
【分析】根据题意,比较两个百分数的大小,再根据两个班女生的关系判断即可。
【解答】解:40%<45%
因为两班女生人数相等,
即六(1)班人数的40%与六(2)班人数的45%相等,
所以六(1)班总人数比六(2)班总人数多。
所以原题说法错误。
故答案为:×。
【点评】本题主要考查百分数的实际应用。
19.小华在晓东家东偏南30°方向上,晓东就在小华家南偏东30°方向上。 ×
【答案】×
【分析】根据方向的相对性:方向相反,角度不变;据此判断即可。
【解答】解:根据方向的相对性可得:小华在晓东家东偏南30°方向上,晓东就在小华家西偏北30°方向上。所以原题说法错误。
故答案为:×。
【点评】本题主要考查了方向,注意方向的相对性。
20.学校一共植树102棵,其中2棵没有成活,这批树的成活率是100%。 ×
【答案】×
【分析】成活率=成活棵数÷总棵数×100%,据此计算并判断即可。
【解答】解:(102﹣2)÷102×100%≠100%
所以原题说法错误。
故答案为:×。
【点评】本题主要考查百分率的实际应用,关键是注意成活率的计算方法的应用。
21.一张方桌可以坐8人,两张这样的方桌并起来,可以坐16人。 ×
【答案】×
【分析】如图,两张这样的方桌并起来,可以坐12人。据此判断。
【解答】解:一张方桌可以坐8人,两张这样的方桌并起来,可以坐12人。所以原题说法错误。
故答案为:×。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
22.学校买来9个足球,每个a元,又买来b个篮球,每个58元,一共用了多少钱?用式子表示应是9a+58。 ×
【答案】×
【分析】根据单价×数量=总价,解答此题即可。
【解答】解:学校买来9个足球,每个a元,又买来b个篮球,每个58元,一共用了多少钱?用式子表示应是9a+58b。
所以题干说法是错误的。
故答案为:×。
【点评】熟练掌握单价、数量、总价的关系,是解答此题的关键。
四.计算题(共3小题)
23.解方程。
30% xx=42
【答案】x=1.2,x=36。
【分析】根据等式的基本性质,方程两边同时乘4。
根据等式的基本性质,先计算出左边的结果为x,方程两边再同时除以,据此即可解答。
【解答】解:30%
4=30%×4
x=1.2
xx=42
x=42
x42
x=36
【点评】熟练掌握等式的基本性质是解题的关键。
24.直接写出得数。
0.25×0.4= 0.77+0.32= 32÷0.4= 0×0.24=
7.2÷0.1=
【答案】0.1;1.09;80;0;;;;72。
【分析】根据小数、分数加、减、乘、除的计算方法,依次口算结果。
【解答】解:
0.25×0.4=0.1 0.77+0.32=1.09 32÷0.4=80 0×0.24=0
7.2÷0.1=72
【点评】本题解题的关键是熟练掌握小数、分数加、减、乘、除的计算方法。
25.怎样简便怎样算。
() ()
()×72 (25%)
【答案】,,38,。
【分析】(1)先算小括号里的减法,再算括号外的乘法,最后算括号外的加法;
(2)先算小括号里面的乘法,再算小括号里面的减法,最后算括号外的除法;
(3)运用乘法分配律简算;
(4)先算小括号里面的减法,再算括号外的除法,最后算乘法。
【解答】解:(1)()
(2)()
()
(3)()×72
727272
=40+42﹣44
=82﹣44
=38
(4)(25%)
【点评】考查了运算定律与简便运算,四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算律简便计算。
五.应用题(共5小题)
26.水果店新进一批苹果,第一天卖出了全部的,第二天卖出了余下的,第三天比第一天少卖了,这时还剩下350千克。水果店共运进了多少千克苹果?
【答案】10500千克。
【分析】把这批苹果的总质量看作单位“1”,第一天卖出,则余下(1),根据分数乘法的意义,用(1)就是第二天卖出部分所占的分率,再把第一天卖出部分看作单位“1”,第三天卖出部分是(1)。根据分数除法的意义,用最后还剩下的质量除以所占的分率就是这批苹果的质量。
【解答】解:350÷[1(1)(1)]
=350÷[1]
=350÷[1]
=350
=10500(千克)
答:水果店共运进了10500千克苹果。
【点评】此题考查了分数复合应用题。弄清最后剩下的350千克占这批苹果质量的几分之几是关键,也是难点。
27.某工地有一个近似圆锥形沙堆,量得它的底面周长是18.84m,高是1.5m。如果每立方米沙约重1.6吨,这堆沙约有多少吨?
【答案】22.608吨。
【分析】要求这堆沙子的重量,先求得沙堆的体积,沙堆的形状是圆锥形的,利用圆锥的体积计算公式Vπr2h求得体积,进一步再求沙堆的重量,问题得解。
【解答】解:3.14×(18.84÷3.14÷2)2×1.5
3.14×32×1.5
=3.14×3×1.5
=14.13(立方米)
14.13×1.6=22.608(吨)
答:这堆沙约有22.608吨。
【点评】此题主要考查圆锥的体积计算公式Vπr2h,运用公式计算时不要漏乘。
28.一堆圆锥形小麦堆,高1.2米,占地面积是16平方米,如果每立方米小麦重700千克,那么这堆小麦重多少千克?
【答案】4480千克。
【分析】根据圆锥的高与底面积(占地面积),运用公式可求体积,然后再乘单位体积小麦的重量,即可得这堆小麦重多少。
【解答】解:16×1.2700
=6.4×700
=4480(千克).
答:这堆小麦重4480千克。
【点评】此题主要考查学生运用圆锥的体积计算公式Vπr2h解决实际问题的能力。
29.叔叔买一套家具,按原价的八五折购买可以便宜2250元,这套家具的原价是多少元?
【答案】15000元。
【分析】将原价看作单位“1”,由题意可知,原价的(1﹣85%)等于2250元。据此解答。
【解答】解:八五折=85%
2250÷(1﹣85%)
=2250÷15%
=15000(元)
答:这套家具的原价是15000元。
【点评】本题考查了利用整数与百分数除减混合运算解决问题,需明确折扣的意义。
30.阅读下面的材料,回答问题。
中国湖泊众多,共有湖泊24800多个,其中面积在1平方千米以上的天然湖泊就有2800多个。按照湖水含盐率分类,这些湖泊可分为淡水湖(含盐率<0.1%)、微咸水湖(0.1%≤含盐率<1%)、咸水湖(1%≤含盐率<3.5%)和盐湖(含盐率≥3.5%)。
淘气在假期中游玩了三个湖泊,并在其中一个湖泊中采集了湖水样本,请你根据他的实验记录计算并判断所采样本来自哪个湖泊?(百分号前保留两位小数)
【走访记录】 鄱阳湖:位于江西省,是淡水湖。 青海湖:位于青海省,是咸水湖。 运城盐湖:位于山西省,是盐湖。 【实验记录】 湖水样本:质量210g,含盐7g。
【答案】青海湖。
【分析】含盐率=盐的质量÷盐水的总质量×100%,由此求出样本的含盐率;再根据湖水含盐率分类,判断样本是哪个湖水的即可。
【解答】解:7÷210×100%
≈0.0333×100%
=3.33%
1%<3.33%<3.5%,属于咸水湖,是青海湖。
答:所采样本来自青海湖。
【点评】解答本题的关键是熟练掌握含盐率的意义及计算方法。
六.操作题(共1小题)
31.按要求画一画。
(1)把图形①绕点O逆时针旋转 90°。
(2)先将图形①向右平移7格,再向下平移6格。
(3)以虚线l为对称轴,画出与图形②轴对称的图形。
(4)将图形②放大,使放大后的图形与原图形对应线段长的比是2:1。
【答案】(1)(2)(3)(4)如图:
【分析】(1)把图形①的每条边都绕点O逆时针旋转 90°。
(2)先将图形①的每个顶点向右平移7格,顺次连接,再将每个顶点向下平移6格,顺次连接。
(3)在对称轴的左侧画出图②的对称图形。
(4)将图形②放大,使放大后的图形与原图形对应线段长的比是2:1。
【解答】解:(1)(2)(3)(4)如图:
【点评】熟悉图形运动后的画法及放大后的作法是解决本题的关键。
七.解答题(共3小题)
32.在方格纸上,点P的位置用数对(1,5)表示。按要求画图,并完成填空。
(1)把图①绕点M逆时针旋转90°,画出旋转后的图形。旋转后点P运动到点P’的位置,点P’的位置用数对表示是 (4,2) 。
(2)画出把图②按2:1的比放大后的图形。放大后的图形与原来图形的面积比是 4:1 。
(3)图③中直角三角形ABC的边BC是圆的直径,O是圆心,AO=AC。若每个小方格表示边长2cm的正方形,则点A在点O 东 偏 北 60° °方向 6 cm处。
【答案】(1)(4,2);(2)4:1;(3)东,北60°,6;(1)、(2)、(3)。
【分析】(1)先把相交于点M的两条边绕点M逆时针旋转90°,再连线,再根据数对中,前面的数表示列,后面的数表示行,即可解答;
(2)先把长方形的长和宽按2:1的比放大,再根据长方形面积=长×宽,分别求出放大前后的长方形面积,再写出北并化简,即可解答;
(3)根据图③中直角三角形ABC的边BC是圆的直径,O是圆心,AO=AC。若每个小方格表示边长2cm的正方形,那么三角形AOC是等边三角形,OA=AC=OC=2×3=6(cm),再根据上北下南左西右东的方向,以及角度和距离,即可解答。
【解答】解:(1)点P’的位置用数对表示是(4,2)。
(2)3×2=6(cm)
2×2=4(cm)
(6×4):(3×2)
=24:6
=4:1
答:放大后的图形与原来图形的面积比是4:1。
(3)OA=AC=OC=2×3=6(cm),所以∠AOC=60°
答:点A在点O北东60°°方向6cm处。
(1)、(2)、(3)作图如下:
故答案为:(4,2);4:1;东,北60°,6。
【点评】本题是考查图形的放大与缩小、旋转等变化。使学生在观察、比较、思考和交流等活动中,感受图形放大、缩小,初步体会图形的相似,进一步发展空间观念。
33.30% 36 :120= 0.3 。(填小数)
【答案】50,36,0.3。
【分析】把30%化成分母是100的分数再化简,根据分数的基本性质,分子、分母都乘5就是;根据比与分数的关系,3:10,再根据比的性质比的前、后项都乘12就是36:120;把30%的小数点向左移动两位同时去掉百分号就是0.3。
【解答】解:30%36:120=0.3。
故答案为:50,36,0.3。
【点评】此题主要是考查小数、分数、百分数、比之间的关系及转化。利用它们之间的关系和性质进行转化即可。
34.学校有一块长方形的运动场。长是200m,宽是150m,把它画在网格上(长画了4cm),请补充画出平面图,这幅图的比例尺是1: 5000 。
【答案】,5000。
【分析】先把米数化成厘米数,根据实际的长和图上的长,求出比例尺,再根据实际的宽和比例尺求出图上的宽,画出平面图,解决问题。
【解答】解:200m=20000cm,150m=15000cm
4:20000=1:5000
150003(厘米)
平面图如下:
故答案为:5000。
【点评】此题主要考查比例尺的意义及已知比例尺和实际距离求图上距离,注意单位的换算。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024-2025学年六年级下学期期末素养评价数学预测卷
一.选择题(共7小题)
1.如图,从梯形里剪去一个最大的平行四边形后,剩下的面积是( )平方厘米。
A.64 B.48 C.12 D.24
2.为了更直观地表示新蒲新区2022上半年月平均降雨量的多少及其变化趋势,绘制( )最合适。
A.统计表 B.条形统计图
C.折线统计图 D.扇形统计图
3.两个人轮流报数,每次只能报1或2,把两个人报的所有数加起来,谁报数后和是100谁就获胜。如果让你先报数,为了确保获胜,你第一次应该报( )
A.1 B.2 C.都可以 D.无法确定
4.把圆柱的侧面展开不可能得到一个( )
A.长方形 B.正方形
C.三角形 D.平行四边形
5.把14个棱长是1cm的正方体放在地面上,堆成如图所示的组合体,然后将露出的表面部分涂成红色(底面不涂)。那么红色部分的面积是( )
A.33 B.38 C.42
6.在一张图纸上量得一个零件的长度是6厘米,已知这张图纸的比例尺是1:100,求这个零件的实际长度是( )米。
A.6 B.0.6 C.60 D.600
7.立体图形从上面看到的形状是( )
A. B. C. D.
二.填空题(共10小题)
8.在一幅比例尺是40:1的地图上,量得一个零件的长是5cm,这个零件的实际长是 。
9.如果m(m、n均不为0),那么m与n成 比例关系。如果3m=7n(m、n均不为0),那么m:n= 。
10.一根长5m的铁丝平均分成8段,每段的长度是这根铁丝的 ,每段长是
m。
11.哥哥得到一笔4800元的劳务报酬,其中800元是免税的,超过800元的部分要按20%的税率缴税。这笔劳务报酬一共要缴税 元。
12.明年的第一季度有 天。
13.今年“五一”假期,成都假日文旅市场呈现安全平稳、繁荣有序的良好发展态势。数据显示,成都接待游客一千四百六十一万三千人次,横线上的数写作 ,改为以“万”为单位的数是 万。
14.有一个底面直径是3cm的圆柱形玩具,高8cm,滚动一周后前进了 cm,压过的面积是 cm2。
15.如图:1张桌子可以坐下8人,2张桌子拼起来可以坐下 人,5张这样的桌子拼起来能够坐下 人。
16.李明家的挂钟的分针长8厘米,经过15分钟分针的尖端所走的路程是 厘米;经过30分钟扫过的面积是 平方厘米。
17.如图,将图形D绕点O 时针旋转 °得到图形C。
三.判断题(共5小题)
18.六(1)班人数的40%是女生,六(2)班人数的45%是女生,两班女生人数相等。那么六(1)班比六(2)班人数少。
19.小华在晓东家东偏南30°方向上,晓东就在小华家南偏东30°方向上。
20.学校一共植树102棵,其中2棵没有成活,这批树的成活率是100%。
21.一张方桌可以坐8人,两张这样的方桌并起来,可以坐16人。
22.学校买来9个足球,每个a元,又买来b个篮球,每个58元,一共用了多少钱?用式子表示应是9a+58。
四.计算题(共3小题)
23.解方程。
30% xx=42
24.直接写出得数。
0.25×0.4= 0.77+0.32= 32÷0.4= 0×0.24=
7.2÷0.1=
25.怎样简便怎样算。
() ()
()×72 (25%)
五.应用题(共5小题)
26.水果店新进一批苹果,第一天卖出了全部的,第二天卖出了余下的,第三天比第一天少卖了,这时还剩下350千克。水果店共运进了多少千克苹果?
27.某工地有一个近似圆锥形沙堆,量得它的底面周长是18.84m,高是1.5m。如果每立方米沙约重1.6吨,这堆沙约有多少吨?
28.一堆圆锥形小麦堆,高1.2米,占地面积是16平方米,如果每立方米小麦重700千克,那么这堆小麦重多少千克?
29.叔叔买一套家具,按原价的八五折购买可以便宜2250元,这套家具的原价是多少元?
30.阅读下面的材料,回答问题。
中国湖泊众多,共有湖泊24800多个,其中面积在1平方千米以上的天然湖泊就有2800多个。按照湖水含盐率分类,这些湖泊可分为淡水湖(含盐率<0.1%)、微咸水湖(0.1%≤含盐率<1%)、咸水湖(1%≤含盐率<3.5%)和盐湖(含盐率≥3.5%)。
淘气在假期中游玩了三个湖泊,并在其中一个湖泊中采集了湖水样本,请你根据他的实验记录计算并判断所采样本来自哪个湖泊?(百分号前保留两位小数)
【走访记录】 鄱阳湖:位于江西省,是淡水湖。 青海湖:位于青海省,是咸水湖。 运城盐湖:位于山西省,是盐湖。 【实验记录】 湖水样本:质量210g,含盐7g。
六.操作题(共1小题)
31.按要求画一画。
(1)把图形①绕点O逆时针旋转 90°。
(2)先将图形①向右平移7格,再向下平移6格。
(3)以虚线l为对称轴,画出与图形②轴对称的图形。
(4)将图形②放大,使放大后的图形与原图形对应线段长的比是2:1。
七.解答题(共3小题)
32.在方格纸上,点P的位置用数对(1,5)表示。按要求画图,并完成填空。
(1)把图①绕点M逆时针旋转90°,画出旋转后的图形。旋转后点P运动到点P’的位置,点P’的位置用数对表示是 。
(2)画出把图②按2:1的比放大后的图形。放大后的图形与原来图形的面积比是 。
(3)图③中直角三角形ABC的边BC是圆的直径,O是圆心,AO=AC。若每个小方格表示边长2cm的正方形,则点A在点O 偏 °方向 cm处。
33.30% :120= 。(填小数)
34.学校有一块长方形的运动场。长是200m,宽是150m,把它画在网格上(长画了4cm),请补充画出平面图,这幅图的比例尺是1: 。
2024-2025学年六年级下学期期末素养评价数学预测卷
参考答案与试题解析
一.选择题(共7小题)
1.如图,从梯形里剪去一个最大的平行四边形后,剩下的面积是( )平方厘米。
A.64 B.48 C.12 D.24
【答案】C
【分析】要想在这个梯形中剪去一个最大的平行四边形,必须把梯形的上底8厘米作为平行四边形的底进行剪切,剩下的部分是一个底为(12﹣8)厘米、高即为梯形的高6厘米的三角形,求剩下的面积利用三角形的面积公式:S=ah÷2,代入数值求解即可。
【解答】解:(12﹣8)×6÷2
=4×6÷2
=12(平方厘米)
答:剩下的面积是12平方厘米。
故选:C。
【点评】此题考查组合图形的面积,解决此题关键是弄明白怎么剪才能使平行四边形的面积最大,并明确剩下的三角形的底和高,进而得出剩下的三角形的面积。
2.为了更直观地表示新蒲新区2022上半年月平均降雨量的多少及其变化趋势,绘制( )最合适。
A.统计表 B.条形统计图
C.折线统计图 D.扇形统计图
【答案】C
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【解答】解:为了更直观地表示新蒲新区2022上半年月平均降雨量的多少及其变化趋势,绘制折线统计图最合适。
故选:C。
【点评】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
3.两个人轮流报数,每次只能报1或2,把两个人报的所有数加起来,谁报数后和是100谁就获胜。如果让你先报数,为了确保获胜,你第一次应该报( )
A.1 B.2 C.都可以 D.无法确定
【答案】A
【分析】因为100÷(1+2)=33……1,所以,先报的一定要报1,然后每次报的数始终都与另一人的和是3,一定会赢。
【解答】解:先报数的人第1次一定要报1,和还剩100﹣1=99,99是3的倍数,
所以,以后每次报的数始终都与另一人报的数的和是3,
最后一次总是先报数的人,
所以只要这样做先报数的人一定会赢。
答:为了确保获胜,我第一次应该报1。
故选:A。
【点评】本题关键根据余数确定先报的数,以后每次报的数始终都与另一人报的数的和是3,一定会赢。
4.把圆柱的侧面展开不可能得到一个( )
A.长方形 B.正方形
C.三角形 D.平行四边形
【答案】C
【分析】根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形(或正方形),如果圆柱的侧面斜着展开是一个平行四边形。据此解答即可。
【解答】解:由分析得:圆柱的侧面沿高展开是一个长方形(或正方形),如果圆柱的侧面斜着展开是一个平行四边形。
所以把一个圆柱的侧面展开不可能得到一个三角形。
故选:C。
【点评】此题考查的目的是理解掌握圆柱侧面展开图的特征及应用。
5.把14个棱长是1cm的正方体放在地面上,堆成如图所示的组合体,然后将露出的表面部分涂成红色(底面不涂)。那么红色部分的面积是( )
A.33 B.38 C.42
【答案】A
【分析】画出立体图形的三视图,染色的总面积=正视图面积×2+左视图面积×2+俯视图面积,计算即可。
【解答】解:画出此立体图形的三视图:
每个小正方形的面积为:1×1=1
俯视图的面积为:3×3×1=9
正视图的面积为:(3+2+1)×1=6
左视图的面积为:(3+2+1)×1=6
所以,染色的总面积为:
9+6×2+6×2
=9+12+12
=33
故选:A。
【点评】本题主要考查了染色问题,理解露出的表面部分也就是能看到的部分,并画出三视图求解,是本题解题的关键。
6.在一张图纸上量得一个零件的长度是6厘米,已知这张图纸的比例尺是1:100,求这个零件的实际长度是( )米。
A.6 B.0.6 C.60 D.600
【答案】A
【分析】要求零件的实际长度是多少毫米,根据“图上距离÷比例尺=实际距离”,代入数值,计算即可。
【解答】解:6600(厘米)
600厘米=6米
答:这个零件的实际长度是6米。
故选:A。
【点评】此题考查了实际距离、图上距离和比例尺之间的关系,注意统一单位。
7.立体图形从上面看到的形状是( )
A. B. C. D.
【答案】C
【分析】根据观察,可知的正面图形为;左面图形为;上面图形为;右面图形为。
【解答】解:立体图形从上面看到的形状是。
故选:C。
【点评】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
二.填空题(共10小题)
8.在一幅比例尺是40:1的地图上,量得一个零件的长是5cm,这个零件的实际长是 0.125厘米 。
【答案】0.125厘米。
【分析】要求这个零件的实际长度是多少,根据“图上距离÷比例尺=实际距离”,代入数值,计算即可.
【解答】解:50.125(厘米)
答:这个零件的实际长度是0.125厘米。
故答案为:0.125厘米。
【点评】此题由计算公式可用,根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论。
9.如果m(m、n均不为0),那么m与n成 反 比例关系。如果3m=7n(m、n均不为0),那么m:n= 。
【答案】反,。
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此判断;在比例中,两个外项的积等于两个内项的积,这叫作比例的基本性质。据此解答。
【解答】解:根据分母×分数值=分子,将m改写成mn=2024(一定),因为mn的积一定,所以mn成反比例。
如果3m=7n(m、n均不为0),那么m:n=7:3。
如果m(m、n均不为0),那么m与n成反比例关系。如果3m=7n(m、n均不为0),那么m:n。
故答案为:反,。
【点评】此题考查了辨识成正比例的量与成反比例的量,要求学生掌握。
10.一根长5m的铁丝平均分成8段,每段的长度是这根铁丝的 ,每段长是 m。
【答案】,。
【分析】把这根铁丝的长度看作单位“1”,把它平均分成8段,求每段的长度是这根铁丝的几分之几,用1除以8;求每段长,用这根铁丝的长度除以8。
【解答】解:1÷8
5÷8(m)
答:每段的长度是这根铁丝的,每段长是m。
故答案为:,。
【点评】解决此题关键是弄清求的是“分率”还是“具体的数量”,求分率:平均分的是单位“1”;求具体的数量:平均分的是具体的数量。注意:分率不能带单位名称,而具体的数量要带单位名称。
11.哥哥得到一笔4800元的劳务报酬,其中800元是免税的,超过800元的部分要按20%的税率缴税。这笔劳务报酬一共要缴税 800 元。
【答案】800。
【分析】用劳务报酬的总数减去800元,再乘税率,即可求出这笔劳务报酬一共要缴税多少钱。
【解答】解:(4800﹣800)×20%
=4000×20%
=800(元)
答:这笔劳务报酬一共要缴税800元。
故答案为:800。
【点评】本题考查百分数的计算及应用。理解题意,找出数量关系,列式计算即可。
12.明年的第一季度有 91 天。
【答案】91。
【分析】今年是2023年,明年是2024年;先判断2024年是平年还是闰年,平年二月份有28天,闰年二月份有29天;无论平年还是闰年一月份和三月份都是31天,由此求出第一季度的天数。
【解答】解:明年是2024年
2024÷4=506
2024年是闰年,二月份有29天;
31+29+31=91(天)
答:明年的第一季度有91天。
故答案为:91。
【点评】本题关键是考查了对闰年和平年的判断,用年份除以4(或400),看是否能整除即可;还要记住一年中各个月份的天数。
13.今年“五一”假期,成都假日文旅市场呈现安全平稳、繁荣有序的良好发展态势。数据显示,成都接待游客一千四百六十一万三千人次,横线上的数写作 14613000 ,改为以“万”为单位的数是 1461.3 万。
【答案】14613000,1461.3。
【分析】(1)整数的写法,从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0,据此写出此数;
(2)改写时在万位的后边,点上小数点,去掉小数点末尾的0,并加上一个“万”字即可。
【解答】解:根据题意可知:
一千四百六十一万三千写作:14613000
14613000改为“万”为单位的数是1461.3万。
故答案为:14613000,1461.3。
【点评】此题考查了亿以内数的读写与改写,要求学生掌握。
14.有一个底面直径是3cm的圆柱形玩具,高8cm,滚动一周后前进了 9.42 cm,压过的面积是 75.36 cm2。
【答案】9.42,75.36。
【分析】根据圆的周长公式:C=πd,圆柱的侧面积公式:S=Ch,把数据代入公式解答。
【解答】解:3.14×3=9.42(厘米)
9.42×8=75.36(平方厘米)
答:滚动一周前进了9.42厘米,压过的面积是75.36平方厘米。
故答案为:9.42,75.36。
【点评】此题主要考查圆的周长公式、圆柱的侧面积公式的灵活运用,关键是熟记公式。
15.如图:1张桌子可以坐下8人,2张桌子拼起来可以坐下 12 人,5张这样的桌子拼起来能够坐下 24 人。
【答案】12,24。
【分析】观察图形发现,第1张桌子可以坐8人,每多1张桌子可以多做4人,那么第n张桌子能做(4n+4)人,据此解答。
【解答】解:由分析可得,
1张桌子可以坐下8人,2张桌子拼起来可以坐下12人,5张这样的桌子拼起来能够坐下24人。
故答案为:12,24。
【点评】此题考查数与形结合的规律,找到规律是解题的关键。
16.李明家的挂钟的分针长8厘米,经过15分钟分针的尖端所走的路程是 12.56 厘米;经过30分钟扫过的面积是 100.48 平方厘米。
【答案】12.56,100.48。
【分析】钟面上,分针15分钟分针尖端所走的路程是以分针为半径的圆周长的,根据圆周长计算公式“C=2πr”及分数乘法的意义即可解答;经过30分钟扫过的面积是以分针为半径的圆面积的,根据圆面积计算公式“C=πr2”及分数乘法的意义即可解答。
【解答】解:3.14×2×8
=6.28×8
=50.24
=12.56(厘米)
3.14×82
=3.14×64
=100.48(平方厘米)
答:经过15分钟分针的尖端所走的路程是12.56厘米;经过30分钟扫过的面积是100.48平方厘米。
故答案为:12.56,100.48。
【点评】解答此题的关键是圆周长计算公式、圆面积计算公式的灵活运用。
17.如图,将图形D绕点O 逆 时针旋转 90 °得到图形C。
【答案】逆,90。
【分析】根据旋转的特征,图形的旋转是图形上的每一点在平面上绕着某个固定点旋转固定角度的位置移动,其中对应点到旋转中心的距离相等,对应线段的长度、对应角的大小相等,旋转前后图形的大小和形状没有改变,据此解答即可。
【解答】解:如图,将图形D绕点O逆时针旋转90°得到图形C。
故答案为:逆,90。
【点评】本题考查了旋转知识,结合旋转的方向和角度解答即可。
三.判断题(共5小题)
18.六(1)班人数的40%是女生,六(2)班人数的45%是女生,两班女生人数相等。那么六(1)班比六(2)班人数少。 ×
【答案】×。
【分析】根据题意,比较两个百分数的大小,再根据两个班女生的关系判断即可。
【解答】解:40%<45%
因为两班女生人数相等,
即六(1)班人数的40%与六(2)班人数的45%相等,
所以六(1)班总人数比六(2)班总人数多。
所以原题说法错误。
故答案为:×。
【点评】本题主要考查百分数的实际应用。
19.小华在晓东家东偏南30°方向上,晓东就在小华家南偏东30°方向上。 ×
【答案】×
【分析】根据方向的相对性:方向相反,角度不变;据此判断即可。
【解答】解:根据方向的相对性可得:小华在晓东家东偏南30°方向上,晓东就在小华家西偏北30°方向上。所以原题说法错误。
故答案为:×。
【点评】本题主要考查了方向,注意方向的相对性。
20.学校一共植树102棵,其中2棵没有成活,这批树的成活率是100%。 ×
【答案】×
【分析】成活率=成活棵数÷总棵数×100%,据此计算并判断即可。
【解答】解:(102﹣2)÷102×100%≠100%
所以原题说法错误。
故答案为:×。
【点评】本题主要考查百分率的实际应用,关键是注意成活率的计算方法的应用。
21.一张方桌可以坐8人,两张这样的方桌并起来,可以坐16人。 ×
【答案】×
【分析】如图,两张这样的方桌并起来,可以坐12人。据此判断。
【解答】解:一张方桌可以坐8人,两张这样的方桌并起来,可以坐12人。所以原题说法错误。
故答案为:×。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
22.学校买来9个足球,每个a元,又买来b个篮球,每个58元,一共用了多少钱?用式子表示应是9a+58。 ×
【答案】×
【分析】根据单价×数量=总价,解答此题即可。
【解答】解:学校买来9个足球,每个a元,又买来b个篮球,每个58元,一共用了多少钱?用式子表示应是9a+58b。
所以题干说法是错误的。
故答案为:×。
【点评】熟练掌握单价、数量、总价的关系,是解答此题的关键。
四.计算题(共3小题)
23.解方程。
30% xx=42
【答案】x=1.2,x=36。
【分析】根据等式的基本性质,方程两边同时乘4。
根据等式的基本性质,先计算出左边的结果为x,方程两边再同时除以,据此即可解答。
【解答】解:30%
4=30%×4
x=1.2
xx=42
x=42
x42
x=36
【点评】熟练掌握等式的基本性质是解题的关键。
24.直接写出得数。
0.25×0.4= 0.77+0.32= 32÷0.4= 0×0.24=
7.2÷0.1=
【答案】0.1;1.09;80;0;;;;72。
【分析】根据小数、分数加、减、乘、除的计算方法,依次口算结果。
【解答】解:
0.25×0.4=0.1 0.77+0.32=1.09 32÷0.4=80 0×0.24=0
7.2÷0.1=72
【点评】本题解题的关键是熟练掌握小数、分数加、减、乘、除的计算方法。
25.怎样简便怎样算。
() ()
()×72 (25%)
【答案】,,38,。
【分析】(1)先算小括号里的减法,再算括号外的乘法,最后算括号外的加法;
(2)先算小括号里面的乘法,再算小括号里面的减法,最后算括号外的除法;
(3)运用乘法分配律简算;
(4)先算小括号里面的减法,再算括号外的除法,最后算乘法。
【解答】解:(1)()
(2)()
()
(3)()×72
727272
=40+42﹣44
=82﹣44
=38
(4)(25%)
【点评】考查了运算定律与简便运算,四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算律简便计算。
五.应用题(共5小题)
26.水果店新进一批苹果,第一天卖出了全部的,第二天卖出了余下的,第三天比第一天少卖了,这时还剩下350千克。水果店共运进了多少千克苹果?
【答案】10500千克。
【分析】把这批苹果的总质量看作单位“1”,第一天卖出,则余下(1),根据分数乘法的意义,用(1)就是第二天卖出部分所占的分率,再把第一天卖出部分看作单位“1”,第三天卖出部分是(1)。根据分数除法的意义,用最后还剩下的质量除以所占的分率就是这批苹果的质量。
【解答】解:350÷[1(1)(1)]
=350÷[1]
=350÷[1]
=350
=10500(千克)
答:水果店共运进了10500千克苹果。
【点评】此题考查了分数复合应用题。弄清最后剩下的350千克占这批苹果质量的几分之几是关键,也是难点。
27.某工地有一个近似圆锥形沙堆,量得它的底面周长是18.84m,高是1.5m。如果每立方米沙约重1.6吨,这堆沙约有多少吨?
【答案】22.608吨。
【分析】要求这堆沙子的重量,先求得沙堆的体积,沙堆的形状是圆锥形的,利用圆锥的体积计算公式Vπr2h求得体积,进一步再求沙堆的重量,问题得解。
【解答】解:3.14×(18.84÷3.14÷2)2×1.5
3.14×32×1.5
=3.14×3×1.5
=14.13(立方米)
14.13×1.6=22.608(吨)
答:这堆沙约有22.608吨。
【点评】此题主要考查圆锥的体积计算公式Vπr2h,运用公式计算时不要漏乘。
28.一堆圆锥形小麦堆,高1.2米,占地面积是16平方米,如果每立方米小麦重700千克,那么这堆小麦重多少千克?
【答案】4480千克。
【分析】根据圆锥的高与底面积(占地面积),运用公式可求体积,然后再乘单位体积小麦的重量,即可得这堆小麦重多少。
【解答】解:16×1.2700
=6.4×700
=4480(千克).
答:这堆小麦重4480千克。
【点评】此题主要考查学生运用圆锥的体积计算公式Vπr2h解决实际问题的能力。
29.叔叔买一套家具,按原价的八五折购买可以便宜2250元,这套家具的原价是多少元?
【答案】15000元。
【分析】将原价看作单位“1”,由题意可知,原价的(1﹣85%)等于2250元。据此解答。
【解答】解:八五折=85%
2250÷(1﹣85%)
=2250÷15%
=15000(元)
答:这套家具的原价是15000元。
【点评】本题考查了利用整数与百分数除减混合运算解决问题,需明确折扣的意义。
30.阅读下面的材料,回答问题。
中国湖泊众多,共有湖泊24800多个,其中面积在1平方千米以上的天然湖泊就有2800多个。按照湖水含盐率分类,这些湖泊可分为淡水湖(含盐率<0.1%)、微咸水湖(0.1%≤含盐率<1%)、咸水湖(1%≤含盐率<3.5%)和盐湖(含盐率≥3.5%)。
淘气在假期中游玩了三个湖泊,并在其中一个湖泊中采集了湖水样本,请你根据他的实验记录计算并判断所采样本来自哪个湖泊?(百分号前保留两位小数)
【走访记录】 鄱阳湖:位于江西省,是淡水湖。 青海湖:位于青海省,是咸水湖。 运城盐湖:位于山西省,是盐湖。 【实验记录】 湖水样本:质量210g,含盐7g。
【答案】青海湖。
【分析】含盐率=盐的质量÷盐水的总质量×100%,由此求出样本的含盐率;再根据湖水含盐率分类,判断样本是哪个湖水的即可。
【解答】解:7÷210×100%
≈0.0333×100%
=3.33%
1%<3.33%<3.5%,属于咸水湖,是青海湖。
答:所采样本来自青海湖。
【点评】解答本题的关键是熟练掌握含盐率的意义及计算方法。
六.操作题(共1小题)
31.按要求画一画。
(1)把图形①绕点O逆时针旋转 90°。
(2)先将图形①向右平移7格,再向下平移6格。
(3)以虚线l为对称轴,画出与图形②轴对称的图形。
(4)将图形②放大,使放大后的图形与原图形对应线段长的比是2:1。
【答案】(1)(2)(3)(4)如图:
【分析】(1)把图形①的每条边都绕点O逆时针旋转 90°。
(2)先将图形①的每个顶点向右平移7格,顺次连接,再将每个顶点向下平移6格,顺次连接。
(3)在对称轴的左侧画出图②的对称图形。
(4)将图形②放大,使放大后的图形与原图形对应线段长的比是2:1。
【解答】解:(1)(2)(3)(4)如图:
【点评】熟悉图形运动后的画法及放大后的作法是解决本题的关键。
七.解答题(共3小题)
32.在方格纸上,点P的位置用数对(1,5)表示。按要求画图,并完成填空。
(1)把图①绕点M逆时针旋转90°,画出旋转后的图形。旋转后点P运动到点P’的位置,点P’的位置用数对表示是 (4,2) 。
(2)画出把图②按2:1的比放大后的图形。放大后的图形与原来图形的面积比是 4:1 。
(3)图③中直角三角形ABC的边BC是圆的直径,O是圆心,AO=AC。若每个小方格表示边长2cm的正方形,则点A在点O 东 偏 北 60° °方向 6 cm处。
【答案】(1)(4,2);(2)4:1;(3)东,北60°,6;(1)、(2)、(3)。
【分析】(1)先把相交于点M的两条边绕点M逆时针旋转90°,再连线,再根据数对中,前面的数表示列,后面的数表示行,即可解答;
(2)先把长方形的长和宽按2:1的比放大,再根据长方形面积=长×宽,分别求出放大前后的长方形面积,再写出北并化简,即可解答;
(3)根据图③中直角三角形ABC的边BC是圆的直径,O是圆心,AO=AC。若每个小方格表示边长2cm的正方形,那么三角形AOC是等边三角形,OA=AC=OC=2×3=6(cm),再根据上北下南左西右东的方向,以及角度和距离,即可解答。
【解答】解:(1)点P’的位置用数对表示是(4,2)。
(2)3×2=6(cm)
2×2=4(cm)
(6×4):(3×2)
=24:6
=4:1
答:放大后的图形与原来图形的面积比是4:1。
(3)OA=AC=OC=2×3=6(cm),所以∠AOC=60°
答:点A在点O北东60°°方向6cm处。
(1)、(2)、(3)作图如下:
故答案为:(4,2);4:1;东,北60°,6。
【点评】本题是考查图形的放大与缩小、旋转等变化。使学生在观察、比较、思考和交流等活动中,感受图形放大、缩小,初步体会图形的相似,进一步发展空间观念。
33.30% 36 :120= 0.3 。(填小数)
【答案】50,36,0.3。
【分析】把30%化成分母是100的分数再化简,根据分数的基本性质,分子、分母都乘5就是;根据比与分数的关系,3:10,再根据比的性质比的前、后项都乘12就是36:120;把30%的小数点向左移动两位同时去掉百分号就是0.3。
【解答】解:30%36:120=0.3。
故答案为:50,36,0.3。
【点评】此题主要是考查小数、分数、百分数、比之间的关系及转化。利用它们之间的关系和性质进行转化即可。
34.学校有一块长方形的运动场。长是200m,宽是150m,把它画在网格上(长画了4cm),请补充画出平面图,这幅图的比例尺是1: 5000 。
【答案】,5000。
【分析】先把米数化成厘米数,根据实际的长和图上的长,求出比例尺,再根据实际的宽和比例尺求出图上的宽,画出平面图,解决问题。
【解答】解:200m=20000cm,150m=15000cm
4:20000=1:5000
150003(厘米)
平面图如下:
故答案为:5000。
【点评】此题主要考查比例尺的意义及已知比例尺和实际距离求图上距离,注意单位的换算。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
