【期末押题卷】湖南省长沙市2024-2025学年五年级下学期期末素养评价数学预测卷人教版(含解析)
文档属性
| 名称 | 【期末押题卷】湖南省长沙市2024-2025学年五年级下学期期末素养评价数学预测卷人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 777.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 09:50:48 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
湖南省长沙市2024-2025学年五年级下学期期末素养评价数学预测卷
一.选择题(共7小题)
1.图,从左面看到的是( )
A.B.C.
2.要使2□40既是2的倍数,又是3的倍数,还是5的倍数,□中最小填( )
A.3 B.0 C.6 D.9
3.有一个长方体,它有一组相对的面是正方形,其余4个面的面积( )
A.不一定相等 B.一定不相等
C.一定相等 D.无法确定
4.一个正六边形被分成了6个相同的小三角形(如图). 如果用红、黄两种颜色分别涂满小三角形,那么有( )种不同的涂法.(旋转后图案相同的认为是同一种涂法.)
A.13 B.14 C.15
5.要使是假分数,是真分数,则X是( )
A.6 B.7 C.8
6.在分数加法中,要把异分母分数变成同分母才能进行计算。把异分母分数变成同分母分数,这一过程运用了( )的思想方法。
A.计算 B.转化 C.类比 D.假设
7.有20个乒乓球,其中有一个是次品,比正品略轻。用一架天平去称,至少称( )次才能保证找到这个次品。
A.2 B.3 C.4 D.5
二.填空题(共8小题)
8.下面的三个图形分别是从什么方向看到的?填一填。
面 面 面
9.一个四位数□47□同时是2、3、5的倍数,这个数最小是 ,最大是 .
10.把一个大正方体切割成27个同样大小的小正方体后,3面涂色的有 个.1面涂色的有 个.
11.两个数 的因数,叫做它们的公因数.其中最大的公因数,叫做它们的最大公因数.
12.长方形有 条对称轴,正方形有 条对称轴,圆有 条对称轴.
13.分数单位是的最小假分数与分数单位是的最大真分数的差是 。
14.有83个玻璃球,其中有一个球比其他的球重一些,如果用天平来测量,至少要称 次,才能保证找出来.
15.从正面看到的是 图形,从上面看到的是 图形,从左侧面看到的是 ,从右侧面看到的是 图形.
三.判断题(共7小题)
16.一个数既是12的因数,又是12的倍数,那么这个数一定是12.
17.一个长方体的底面积减少,高增加,则体积不变。
18.一个表面涂色的正方体,先把棱平均分成5份,再切成同样大的小正方体,两面涂色的小正方体有24个。
19.一根绳子,截去它的后,再接上m,绳子和原来一样长.
20.折线统计图是用点的高低表示数量的多少,线的起伏表示数量的增减变化.
21.有14瓶口香糖,其中13瓶质量相同,另有1瓶质量不足,如果用天平称,至少称2次才能保证找出这瓶口香糖。
22.三个连续自然数的和必定是3的倍数。
四.计算题(共2小题)
23.计算
1
1
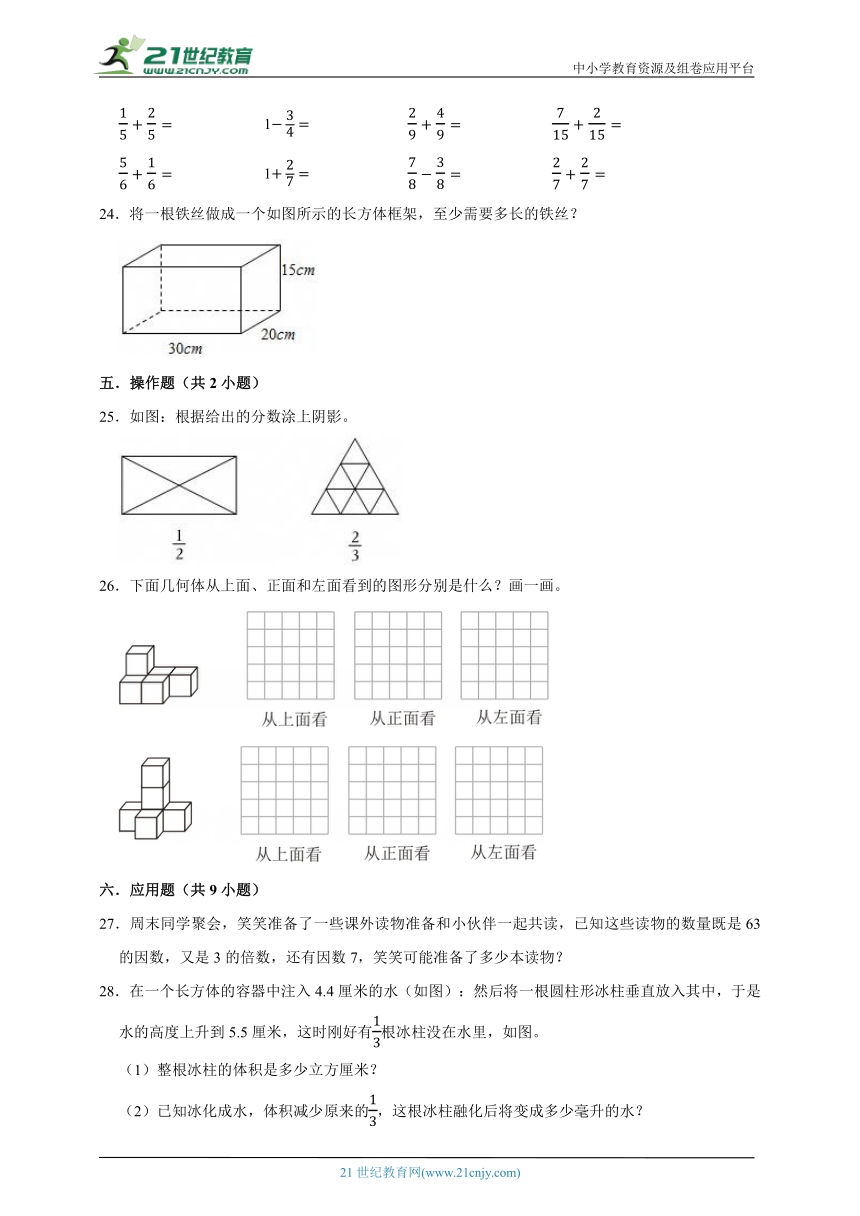
24.将一根铁丝做成一个如图所示的长方体框架,至少需要多长的铁丝?
五.操作题(共2小题)
25.如图:根据给出的分数涂上阴影。
26.下面几何体从上面、正面和左面看到的图形分别是什么?画一画。
六.应用题(共9小题)
27.周末同学聚会,笑笑准备了一些课外读物准备和小伙伴一起共读,已知这些读物的数量既是63的因数,又是3的倍数,还有因数7,笑笑可能准备了多少本读物?
28.在一个长方体的容器中注入4.4厘米的水(如图):然后将一根圆柱形冰柱垂直放入其中,于是水的高度上升到5.5厘米,这时刚好有根冰柱没在水里,如图。
(1)整根冰柱的体积是多少立方厘米?
(2)已知冰化成水,体积减少原来的,这根冰柱融化后将变成多少毫升的水?
(3)当冰柱完全融化时,容器内水深一共是多少厘米?
29.体积问题:一个长方体水池,从里面量长12m、宽5m、深2m。如果每小时注水60立方米,几小时能注满?
30.有一个横2000格,竖1000格的矩形方格纸。现从它的左上角开始向右沿着边框逐格涂色到右边框,再从上到下逐格涂色到底边框,再沿底边框从右到左逐格涂色到左边框,再从下到上逐格涂色到上面涂色过的方格,如此一直螺旋式地涂下去……,直到将所有的方格都涂满,那么最后被涂的那格是从上到下的第 行,从左到右的第 列。
31.一根2米长绳子从起点开始.每隔4cm标记一个红点,每隔5cm标记一个黄点,最后用剪刀在每个标记点处剪一刀,问一个可以将绳子剪成多少段?
32.王阿姨买来两条丝带,第一条长为m,第二条比第一条短m,两条丝带一共长多少m?
33.有几瓶糖果,其中1瓶被吃了几颗,其余的质量相等.如果用天平称4次就能保证找到那瓶被吃了几颗的,那么这些糖果最多有几瓶?
34.有一个长方体,从上面截下一个高是2厘米的长方体后正好得到一个正方体(如图),正方体的表面积比原来长方体的表面积减少了32平方厘米,求原来长方体的体积。
35.小明和妈妈到商店买了3箱同样的牛奶,售货员阿姨说应付130元,小明马上认为不对。你同意小明的看法吗?说说你的理由。
湖南省长沙市2024-2025学年五年级下学期期末素养评价数学预测卷
参考答案与试题解析
一.选择题(共7小题)
题号 1 2 3 4 5 6 7
答案 A B C B B B B
一.选择题(共7小题)
1.图,从左面看到的是( )
A. B.
C.
【答案】A
【分析】这个立体图形由5个相同的小正方体构成。从左面能看到一列2个相同的正方形。
【解答】解:如图:
从左面看到的是
故选:A。
【点评】本题是考查作简单图形的三视图。能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形。
2.要使2□40既是2的倍数,又是3的倍数,还是5的倍数,□中最小填( )
A.3 B.0 C.6 D.9
【答案】B
【分析】2的倍数的特征:个位上是 0、2、4、6、8 的数,都是2的倍数。
3的倍数的特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
5的倍数的特征:个位上是0或5的数,都是5的倍数。
如果一个数同时是2和5的倍数,那它的个位上的数字一定是0。
【解答】解:2+4=6,6是3的倍数。
要使2□40既是2的倍数,又是3的倍数,还是5的倍数,□中最小填0。
故选:B。
【点评】本题考查了2、3、5倍数的特征。
3.有一个长方体,它有一组相对的面是正方形,其余4个面的面积( )
A.不一定相等 B.一定不相等
C.一定相等 D.无法确定
【答案】C
【分析】根据长方体的特征,长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等;有一组相对的面是正方形的长方体,它的长和宽相等,其余四个面的面积相等;由此解答.
【解答】解:根据分析,有一个长方体,它有一组相对的面是正方形,其余四个面的面积一定相等.
故选:C.
【点评】此题主要根据长方体的特征解决问题.
4.一个正六边形被分成了6个相同的小三角形(如图). 如果用红、黄两种颜色分别涂满小三角形,那么有( )种不同的涂法.(旋转后图案相同的认为是同一种涂法.)
A.13 B.14 C.15
【答案】B
【分析】分别按含有红色0、1、2、3、4、5、6块,7种情况讨论即可得出结论.
【解答】解:可按分类来求解:
(1)无红全黄:1种涂法;
(2)1红5黄:1种涂法;
(3)2红4黄:3种涂法;
(4)3红3黄:4种涂法;
(5)4红2黄:3种涂法;
(6)5红1黄:1种涂法;
(7)全红无黄:1种涂法.
1+1+3+4+3+1+1=14(种);
一共七种情况14种不同的涂法.
故选:B.
【点评】本题解题的关键是注意条件中所给的相同的区域不能用相同的颜色,可利用加法原理进行解答.
5.要使是假分数,是真分数,则X是( )
A.6 B.7 C.8
【答案】B
【分析】要使是假分数,则x为等于或大于7的任意一个整数;要使是真分数,x只能是1、2、3、4、5、6、7共7个整数,由此根据题意解答问题.
【解答】解:要使是假分数,x大于或等于7;
要使是真分数,x小于或等于7;
所以x只能等于7.
故选:B。
【点评】此题主要利用真分数与假分数的意义进行解答即可.
6.在分数加法中,要把异分母分数变成同分母才能进行计算。把异分母分数变成同分母分数,这一过程运用了( )的思想方法。
A.计算 B.转化 C.类比 D.假设
【答案】B
【分析】异分母分数相加减,一般先通分,化成同分母分数,然后按照同分母分数的加减法则进行计算。据此解答。
【解答】解:在分数加法中,要把异分母分数变成同分母才能进行计算。把异分母分数变成同分母分数,这一过程运用了转化的思想方法。
故选:B。
【点评】解答本题需熟练掌握转化思想在异分母分数加减计算过程中的应用。
7.有20个乒乓球,其中有一个是次品,比正品略轻。用一架天平去称,至少称( )次才能保证找到这个次品。
A.2 B.3 C.4 D.5
【答案】B
【分析】根据题意,第一次,把20给乒乓球分成3份:7个、7个、6个,取7个的两份分别放在天平两侧,若天平平衡,则次品在未取的一份中,若天平不平衡,取较轻的一份继续;第二次,取含有较轻的一份(7个或6个),分成3份:2个、2个、2个(或3个)取2个的两份分别放在天平两侧,若天平平衡,则次品在未取的一份,若天平不平衡,取较轻的一份继续;第三次,取含有较轻的一份(2个或3个),取其中2个放在天平两侧,即可找到较轻的一个。由此解答即可。
【解答】解:第一次,把20给乒乓球分成3份:7个、7个、6个,取7个的两份分别放在天平两侧,若天平平衡,则次品在未取的一份中,若天平不平衡,取较轻的一份继续;
第二次,取含有较轻的一份(7个或6个),分成3份:2个、2个、2个(或3个)取2个的两份分别放在天平两侧,若天平平衡,则次品在未取的一份,若天平不平衡,取较轻的一份继续;
第三次,取含有较轻的一份(2个或3个),取其中2个放在天平两侧,即可找到较轻的一个。
答:至少称3次才能保证找到这个次品。
故选:B。
【点评】此题考查找次品的应用。
二.填空题(共8小题)
8.下面的三个图形分别是从什么方向看到的?填一填。
面 面 面
【答案】上,正(或左),右。
【分析】左面的立体图形由4个相同的小正方体组成。从正面能看到3个相同的正方形,分两层,上层1个,下层2个,左齐;从上面能看到3个相同的正方形,分两层,上层2个,下层1个,左齐;从左面看到的图形与从正面看到的相同;从右面能看到3个相同的正方形,分两层,上层1个,下层2个,右齐。
【解答】答案为:上,正(或左),右。
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形。
9.一个四位数□47□同时是2、3、5的倍数,这个数最小是 1470 ,最大是 7470 .
【答案】见试题解答内容
【分析】根据能同时被2、3、5整除的数的特征:该数的个位数0,并且该数各个数位上数的和能被3整除,进行分析、解答即可.
【解答】解:能同时被0、5整除,则个位数字是0,
4+7+0=11,
11+7=18=3×6,7是能被3整除的千位数字最大的数,即7470;
11+1=12=3×4,1是能被3整除的千位数字最小的数,即1470;
故答案为:1470,7470.
【点评】解答此题应根据能被2、3、5整除的数的特征进行解答.
10.把一个大正方体切割成27个同样大小的小正方体后,3面涂色的有 8 个.1面涂色的有 6 个.
【答案】见试题解答内容
【分析】根据只有一面涂色的小正方体在每个正方体的面上,只有2面涂色的小正方体在长方体的棱长上(不包括8个顶点处的小正方体)3面三面涂色的小正方体都在顶点处,即可解答问题.
【解答】解:3×3×3=27,
一个大正方体切割成27个同样大小的小正方体,则每条棱上有3个小正方体,
大正方体8个顶点上各有1个3面涂色的小正方体,因此三面涂色的小正方体一共有8个;
每个面的正中间的一个只有一面涂色,故只有一面涂色的正方体有6个;
故答案为:8,6.
【点评】抓住表面涂色的正方体切割小正方体的特点:1面涂色的在面上,2面涂色的在棱长上,3面涂色的在顶点处,没有涂色的在内部,由此即可解决此类问题.
11.两个数 公有 的因数,叫做它们的公因数.其中最大的公因数,叫做它们的最大公因数.
【答案】见试题解答内容
【分析】根据公因数的意义,几个数公有的因数叫作这几个数的公因数,其中最大的一个数叫作它们的最大公因数作答即可.
【解答】解:几个数公有的因数叫做这几个数的公因数,其中最大的一个数叫作它们的最大公因数.
故答案为:公因.
【点评】此题考查了公因数和最大公因数的含义,属于基础题,比较简单.
12.长方形有 2 条对称轴,正方形有 4 条对称轴,圆有 无数 条对称轴.
【答案】见试题解答内容
【分析】根据轴对称图形的意义:一个图形沿一条直线对折,直线两旁的部分能够完全重合,那么这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,由此分析各图形的对称轴条数即可求解.
【解答】解:长方形有2条对称轴,正方形有4条对称轴,圆有无数条对称轴.
故答案为:2,4,无数.
【点评】此题考查轴对称图形的知识,关键是掌握轴对称图形的意义及对称轴的描述.
13.分数单位是的最小假分数与分数单位是的最大真分数的差是 。
【答案】。
【分析】根据真分数、假分数的意义,分子小于分母的分数叫做真分数,分子等于或大于分母的分数叫做假分数,分数单位是的最小假分数是,分数单位是的最大真分数是,根据分数减法的计算法则计算。
【解答】解:分数单位是的最小假分数是,分数单位是的最大真分数是
答:分数单位是 的最小假分数与分数单位是 的最大真分数的差是。
故答案为:。
【点评】此题考查的目的是理解掌握真分数、假分数的意义,分数减法的计算法则及应用。
14.有83个玻璃球,其中有一个球比其他的球重一些,如果用天平来测量,至少要称 5 次,才能保证找出来.
【答案】见试题解答内容
【分析】把83个分成四组(27、27、27、2),在天平两端各放一组27个的,不平衡即可找到有次品的一组,平衡,次品在未称的27个的一组或在2的个一组;再称一次即可确定在未称的27个一组还是在2个的一组,若在2个一组,再称一次即可找出次品(这样称3次即可找出次品,这种概率不是100%),若不在2个的一组,不论在那组,都是个27个,再把27个分成三组(9,9,9),在天平两端各放一组,平衡,在未称的一组,不平衡在轻的一组,不论那组,都是9个,再把9个分成三组(3,3,3),天平两端各放一组,称1次即可找出次品在哪组,不论那组都是3个,再3个分成(1,1,1),再称一次即可找到次品.即83个时称2次找到次品在哪组,27个、9个、3个再各称1次,一共需要称5次即可保证找到重的次品.
【解答】解:83(27、27、27、2)
称2次即可确定次品是否在27个组的里还是在2个组里
若在2个组里,再称1次即可找到次品(这样称3次即可找出次品,这种概率不是100%),
若在27组里
27(9、9、9)
称1次即可确定次品在哪组
9(3、3、3)
再称1次即可确定次品在哪组
3(1、1,1)
再称1次即可确定次品.
2+1+1=5(次)
答:至少称5次才能把次品保证找出来.
故答案为:5.
【点评】用天平找次品时,所测物品的数目与测试的次数有以下关系(只含一个次品,并且知道比正品重或轻):物品数目2~3,称1次;4~9称2次;10~27称3次;28~31称4次;82~243称5次…记住这一规律,能快速解答此类题目.
15.从正面看到的是 图形,从上面看到的是 图形,从左侧面看到的是 ,从右侧面看到的是 图形.
【答案】见试题解答内容
【分析】观察图形可知,从正面看到的图形是3层:最下层是3个小正方形,上两层都是1个小正方形居中;从上面看到的图形是两行,上面1行3个正方形,下面1行1个小正方形居中;从左侧面看到的图形是3层:最下层是2个小正方形,上两层都是1个小正方形靠左;右侧面看到的图形是3层:最下层是2个小正方形,上两层都是1个小正方形靠右,据此即可解答问题.
【解答】解:从正面看到的是图形,从上面看到的是图形,从左侧面看到的是,从右侧面看到的是图形.
故答案为:,,,.
【点评】此题主要考查从不同方向观察物体的能力,意在培养学生的观察能力和空间思维能力.
三.判断题(共7小题)
16.一个数既是12的因数,又是12的倍数,那么这个数一定是12. √
【答案】见试题解答内容
【分析】根据因数与倍数的意义,一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身;一个数的倍数的个数是无限的,最小的倍数是它本身,没有最大倍数.据此解答.
【解答】解:因为一个数的最大因数是它本身.一个数的最小倍数是它本身.
所以,一个数既是12的因数,又是12的倍数,那么这个数一定是12.这种说法是正确的.
故答案为:√.
【点评】此题考查的目的是理解掌握因数、倍数的意义,明确:一个数的最大因数是它本身.一个数的最小倍数是它本身.
17.一个长方体的底面积减少,高增加,则体积不变。 ×
【答案】×
【分析】根据长方体的体积=底面积×高;可以假设底面积为15平方米,高为12米,分别代入数据求出数值,再进行比较即可。
【解答】解:假设长方体的底面积为15平方米,高为12米,
原来长方体的体积为:15×12=180(立方米)
变化后的长方体体积:(1515)×(1212)
=(15﹣5)×(12+4)
=10×16
=160(立方米)
180>160
所以一个长方体的底面积减少,高增加,则体积变小,原题说法错误。
故答案为:×。
【点评】解答本题依据的公式为:长方体体积=底面积×高。
18.一个表面涂色的正方体,先把棱平均分成5份,再切成同样大的小正方体,两面涂色的小正方体有24个。 ×
【答案】×
【分析】一个表面涂色的正方体,先把棱平均分成5份,切成同样大的小正方体,共切成了53个,即125个。位于每条棱非两端的都两面涂色,一个正方体有12条棱,每条棱上有(5﹣2)个小正方体,据此解答即可。
【解答】解:如图
(5﹣2)×12
=3×12
=36(个)
所以两面涂色的小正方体有36个;故原题说法错误。
故答案为:×。
【点评】解答此题的关键是弄清位于什么位置的小正方体两面涂色。
19.一根绳子,截去它的后,再接上m,绳子和原来一样长. ×
【答案】见试题解答内容
【分析】如果一根绳子长1米,1米的等于米,截去它的,再接上米,和原来一样长;如果这根绳子长不到1米,它的也不到米,截去它的后,再接上米,比原来长;如果这根绳子长大于1米,它的也大于米,截去它的后,再接上米,比原来短.
【解答】解:如果这根绳子长1米,1米的等于米,截去它的,再接上米,和原来一样长;
如果这根绳子长小于1米,它的也小于米,截去它的后,再接上米,比原来长;
如果这根绳子长大于1米,它的也大于米,截去它的后,再接上米,比原来短.
由于这根绳子的长度未知,因此不能判定截去它的后,再接上m,绳子和原来一样长,原题的说法是错误的.
故答案为:×
【点评】这根绳子的的长度受这根绳子长度的制约,而米是一个固定的长度,因此,在不知绳子长度的情况下,不能确定截去它的后,再接上m,绳子和原来一样长.
20.折线统计图是用点的高低表示数量的多少,线的起伏表示数量的增减变化. √
【答案】见试题解答内容
【分析】条形统计图能很容易看出数量的多少;折线统计图用折线的起伏表示数量的增减变化,不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.
【解答】解:折线统计图是用点的高低表示数量的多少,线的起伏表示数量的增减变化,说法正确.
故答案为:√.
【点评】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答.
21.有14瓶口香糖,其中13瓶质量相同,另有1瓶质量不足,如果用天平称,至少称2次才能保证找出这瓶口香糖。 ×
【答案】×
【分析】根据“n次可以找出3的n次幂个零件中一个较轻次品”判断。
【解答】解:2次可以找出32=9(个)待测物品的一个较轻次品;
3次可以找出33=27(个)待测物品的一个较轻次品;
因此3次可以找出10~27个待测物品中的一个较轻次品;
14在10~27范围之内,所以需要3次才能保证找出这瓶口香糖。
故答案为:×。
【点评】运用找次品问题总结的规律是解答本题的捷径。
22.三个连续自然数的和必定是3的倍数。 √
【答案】√
【分析】设三个连续自然数中的第一个为a,由这三个连续的自然数可表示为a、a+1,a+2.其和为:a+(a+1)+(a+2)=3×(a+1),所以三个连续自然数的和一定是3的倍数;据此判断即可。
【解答】解:设三个连续自然数中的第一个为a,则三个连续自然数的和为:
a+(a+1)+(a+2)=3×(a+1),所以三个连续自然数的和一定是3的倍数。
故答案为:√。
【点评】本题是根据相邻的两个自然数相差1的特点从而求出个连续自然数的和是3的倍数的。
四.计算题(共2小题)
23.计算
1
1
【答案】见试题解答内容
【分析】根据分数加减法的计算方法进行计算.
【解答】解:
1
1 11
【点评】口算时,注意运算符号和数据,然后再进一步计算.
24.将一根铁丝做成一个如图所示的长方体框架,至少需要多长的铁丝?
【答案】见试题解答内容
【分析】根据长方体的棱长和=(长+宽+高)×4,长宽高已知,代入解答即可求出至少需要多长的铁丝.
【解答】解:(30+20+15)×4
=65×4
=260(厘米)
答:至少需要260厘米长的铁丝.
【点评】此题主要考查长方体的棱长总和的计算方法.
五.操作题(共2小题)
25.如图:根据给出的分数涂上阴影。
【答案】
【分析】一个物体、一个计量单位或一些物体都可以看成不同的一个整体。这些不同的一个整体都可以用自然数1来表示,通常把它叫作单位“1”;把一个长方形平均分成2份,其中的1份就是这个长方形的,涂色即可。把9个小三角形组成的大三角形看作一个整体,平均分成3份,其中的2份就是这个大三角形的,即将6个小三角形,涂色即可。据此解答。
【解答】解:根据分析,涂色如下图:
【点评】本题考查的是分数的意义,理解和应用分数的意义是解答关键。
26.下面几何体从上面、正面和左面看到的图形分别是什么?画一画。
【答案】
【分析】1图.这个立体图形由6个相同的小正方体构成,从正面能看到4个正方形,分两行,上行1个,下行3个,左齐;从左面能看到3个正方形,分两行,上行1个,下行2个,左齐;从上面能看到5个正方形,分两行,上行3个,下行2个,左齐;
2图.这个立体图形由6个相同的小正方体构成,从正面能看到5个正方形,分3行,1、2行都是1个,3行3个,后面对齐;从左面能看到4个正方形,分3行,1、2行都是1个,3行2个,左齐;从上面能看到4个正方形,分两行,上行3个,下行1个,中间对齐。
【解答】解:根据分析,画图如下:
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形。
六.应用题(共9小题)
27.周末同学聚会,笑笑准备了一些课外读物准备和小伙伴一起共读,已知这些读物的数量既是63的因数,又是3的倍数,还有因数7,笑笑可能准备了多少本读物?
【答案】21或63本读物。
【分析】先根据找一个数因数的方法找出63的所有因数,然后根据:这些读物的数量既是63的因数,又是3的倍数,还有因数7,确定出读物的数量。
【解答】解:63的因数有1、3、7、9、21、63;
既是63的因数,又是3的倍数,还有因数7,所以可能是21或63倍。
答:笑笑可能准备了21或63本读物。
【点评】灵活找一个数因数和倍数的方法,是解答此题的关键。
28.在一个长方体的容器中注入4.4厘米的水(如图):然后将一根圆柱形冰柱垂直放入其中,于是水的高度上升到5.5厘米,这时刚好有根冰柱没在水里,如图。
(1)整根冰柱的体积是多少立方厘米?
(2)已知冰化成水,体积减少原来的,这根冰柱融化后将变成多少毫升的水?
(3)当冰柱完全融化时,容器内水深一共是多少厘米?
【答案】(1)330立方厘米;
(2)220毫升;
(3)6.6厘米。
【分析】(1)长方体的容器中上升水面的体积冰柱的体积。整根冰柱的体积=长方体的容器中上升水面的体积。根据长方体的体积计算公式V=abh代入数值计算出得数,即可解答。
(2)冰化成水,体积减少原来的,用冰柱的体积×(1)=冰化成水后的体积。
(3)根据冰化成水后的体积÷长方体的长×宽=长方体内水面上升的高。用4.4+冰化成水后的水面上升的高=容器内水深一共是多少厘米。
【解答】解:(1)10×10×(5.5﹣4.4)
=100×1.1
=110×3
=330(立方厘米)
答:整根冰柱的体积是330立方厘米。
(2)330×(1)
=330
=220(立方厘米)
220立方厘米=220毫升
答:这根冰柱融化后将变成220毫升的水。
(3)220÷(10×10)+4.4
=220÷100+4.4
=2.2+4.4
=6.6(厘米)
答:容器内水深一共是6.6厘米。
【点评】此题主要考查长方体体积公式的灵活运用,关键是熟记公式。
29.体积问题:一个长方体水池,从里面量长12m、宽5m、深2m。如果每小时注水60立方米,几小时能注满?
【答案】2小时。
【分析】利用长方体的体积公式计算需要注水的体积,然后计算需要注水的时间。
【解答】解:12×5×2÷60
=120÷60
=2(小时)
答:2小时能注满。
【点评】本题考查的是长方体的体积公式的应用。
30.有一个横2000格,竖1000格的矩形方格纸。现从它的左上角开始向右沿着边框逐格涂色到右边框,再从上到下逐格涂色到底边框,再沿底边框从右到左逐格涂色到左边框,再从下到上逐格涂色到上面涂色过的方格,如此一直螺旋式地涂下去……,直到将所有的方格都涂满,那么最后被涂的那格是从上到下的第 501 行,从左到右的第 500 列。
【答案】501,500。
【分析】第1圈涂完,止于2行1列,即(2,1 );第2圈涂完,止于3行2列,即(3,2);……第k圈涂完,止于k+1行k列,即( k+1,k)。横2000格,竖1000格,需要1000:2=500(圈),涂完。所以,止于501行500列。
【解答】解:顺时针涂完第1圈后,有两行两列被涂了色,下一个要涂色的是第2行第2列的方格。涂完第499圈后,有998行998列被涂了色,剩下2行1002列未被涂色。最后一圈从500行500列开始,到501行500列结束.那么最后被涂色的就是第501行,第500列。
故答案为:501,500。
【点评】一圈涂上下两行,所以最后涂色的方格位于第501行。当涂到这一行时,左边已经涂完499列,所以最后涂色的方格位于第500列。
31.一根2米长绳子从起点开始.每隔4cm标记一个红点,每隔5cm标记一个黄点,最后用剪刀在每个标记点处剪一刀,问一个可以将绳子剪成多少段?
【答案】见试题解答内容
【分析】首先求出每4厘米作一个记号,可以作几个记号;再求出每5厘米作一个记号,可以作几个记号;因为4和5的最小公倍数是20,所以每20厘米处的记号重合,由此即可求出绳子被剪出的段数.
【解答】解:2米=200厘米
200÷4﹣1=49(个)
200÷5﹣1=39(个)
4和5互质,所以4和5的最小公倍数是4×5=20;
200÷20﹣1=9(个)
49+39﹣9=79(个)
79+1=80(段)
答:可以将绳子剪成80段.
【点评】解答此题的关键是分析出每20厘米处的记号重合,并求出重合的记号的个数.
32.王阿姨买来两条丝带,第一条长为m,第二条比第一条短m,两条丝带一共长多少m?
【答案】m。
【分析】根据题意,用m减去m,求出第二条丝带的长度,然后再加上第一条的长度即可。
【解答】解:
(m)
答:两条丝带一共长m。
【点评】本题关键是根据减法的意义,求出第二条丝带的长度,然后再根据加法的意义进行解答。
33.有几瓶糖果,其中1瓶被吃了几颗,其余的质量相等.如果用天平称4次就能保证找到那瓶被吃了几颗的,那么这些糖果最多有几瓶?
【答案】见试题解答内容
【分析】根据题意,先把这几瓶分成三份,如果瓶子数量是三的倍数的话,则三分瓶子数量相同,如果不是三的倍数,则分成两份相同和一份不同的情况,拿两份相同放到天平上,若两份质量不相同,则那瓶再较轻的一份,若质量相同,则在另外没称的一份.接下来步骤同上.
【解答】解:先把这几瓶分成三份,如果瓶子数量是三的倍数的话,则三分瓶子数量相同,如果不是三的倍数,则分成两份相同和一份不同的情况,拿两份相同放到天平上,若两份质量不相同,则那瓶再较轻的一份,若质量相同,则在另外没称的一份.接下来步骤同上.所以要看糖果的瓶数是多少瓶,这个数在3n﹣1和3n之间,则需要称的最少次数是n次.所以如果瓶数小于81瓶则可4次称出,如果大于81瓶,则4次不能称出.
答:这些糖果最多有81瓶.
【点评】本题的关键是把瓶子要分三份来称,然后找出规律进行解答.
34.有一个长方体,从上面截下一个高是2厘米的长方体后正好得到一个正方体(如图),正方体的表面积比原来长方体的表面积减少了32平方厘米,求原来长方体的体积。
【答案】96立方厘米。
【分析】根据高截短2厘米,就剩下一个正方体可知,则长方体的长和宽相等,这个正方体比原长方体表面积减少的4个面是相同的,根据已知表面积减少32平方厘米,则减少一个面的面积是32÷4=8(平方厘米),再根据长方形的面积=长×宽,用一个面的面积除以2,求出原长方体的长和宽,原长方体的高等于原长方体的长加上2就是长方体的高,再根据长方体的体积=长×宽×高,即可计算原长方体的体积。
【解答】解:减少的面的长(剩下正方体的棱长)32÷4÷2=4(厘米)
原来长方体的高:4+2=6(厘米)
原来的体积:4×4×6=96(立方厘米)
答:原来长方体的体积是96立方厘米。
【点评】此题主要考查长方体的体积公式的灵活运用,关键是求出原来长方体的高。
35.小明和妈妈到商店买了3箱同样的牛奶,售货员阿姨说应付130元,小明马上认为不对。你同意小明的看法吗?说说你的理由。
【答案】同意小明的看法。因为130不是3的倍数。
【分析】买了3箱同样的牛奶,总价应是3的倍数,根据3的倍数特征,一个数各个数位上数的和是3的倍数,这个数就是3的倍数;先把130各个数位上的数字加起来,再判断和是不是3的倍数,据此解答。
【解答】解:1+3+0=4
答:因为4不是3的倍数,即130不是3的倍数,所以小明的看法正确。
【点评】此题主要是考查3的倍数特征的应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
湖南省长沙市2024-2025学年五年级下学期期末素养评价数学预测卷
一.选择题(共7小题)
1.图,从左面看到的是( )
A.B.C.
2.要使2□40既是2的倍数,又是3的倍数,还是5的倍数,□中最小填( )
A.3 B.0 C.6 D.9
3.有一个长方体,它有一组相对的面是正方形,其余4个面的面积( )
A.不一定相等 B.一定不相等
C.一定相等 D.无法确定
4.一个正六边形被分成了6个相同的小三角形(如图). 如果用红、黄两种颜色分别涂满小三角形,那么有( )种不同的涂法.(旋转后图案相同的认为是同一种涂法.)
A.13 B.14 C.15
5.要使是假分数,是真分数,则X是( )
A.6 B.7 C.8
6.在分数加法中,要把异分母分数变成同分母才能进行计算。把异分母分数变成同分母分数,这一过程运用了( )的思想方法。
A.计算 B.转化 C.类比 D.假设
7.有20个乒乓球,其中有一个是次品,比正品略轻。用一架天平去称,至少称( )次才能保证找到这个次品。
A.2 B.3 C.4 D.5
二.填空题(共8小题)
8.下面的三个图形分别是从什么方向看到的?填一填。
面 面 面
9.一个四位数□47□同时是2、3、5的倍数,这个数最小是 ,最大是 .
10.把一个大正方体切割成27个同样大小的小正方体后,3面涂色的有 个.1面涂色的有 个.
11.两个数 的因数,叫做它们的公因数.其中最大的公因数,叫做它们的最大公因数.
12.长方形有 条对称轴,正方形有 条对称轴,圆有 条对称轴.
13.分数单位是的最小假分数与分数单位是的最大真分数的差是 。
14.有83个玻璃球,其中有一个球比其他的球重一些,如果用天平来测量,至少要称 次,才能保证找出来.
15.从正面看到的是 图形,从上面看到的是 图形,从左侧面看到的是 ,从右侧面看到的是 图形.
三.判断题(共7小题)
16.一个数既是12的因数,又是12的倍数,那么这个数一定是12.
17.一个长方体的底面积减少,高增加,则体积不变。
18.一个表面涂色的正方体,先把棱平均分成5份,再切成同样大的小正方体,两面涂色的小正方体有24个。
19.一根绳子,截去它的后,再接上m,绳子和原来一样长.
20.折线统计图是用点的高低表示数量的多少,线的起伏表示数量的增减变化.
21.有14瓶口香糖,其中13瓶质量相同,另有1瓶质量不足,如果用天平称,至少称2次才能保证找出这瓶口香糖。
22.三个连续自然数的和必定是3的倍数。
四.计算题(共2小题)
23.计算
1
1
24.将一根铁丝做成一个如图所示的长方体框架,至少需要多长的铁丝?
五.操作题(共2小题)
25.如图:根据给出的分数涂上阴影。
26.下面几何体从上面、正面和左面看到的图形分别是什么?画一画。
六.应用题(共9小题)
27.周末同学聚会,笑笑准备了一些课外读物准备和小伙伴一起共读,已知这些读物的数量既是63的因数,又是3的倍数,还有因数7,笑笑可能准备了多少本读物?
28.在一个长方体的容器中注入4.4厘米的水(如图):然后将一根圆柱形冰柱垂直放入其中,于是水的高度上升到5.5厘米,这时刚好有根冰柱没在水里,如图。
(1)整根冰柱的体积是多少立方厘米?
(2)已知冰化成水,体积减少原来的,这根冰柱融化后将变成多少毫升的水?
(3)当冰柱完全融化时,容器内水深一共是多少厘米?
29.体积问题:一个长方体水池,从里面量长12m、宽5m、深2m。如果每小时注水60立方米,几小时能注满?
30.有一个横2000格,竖1000格的矩形方格纸。现从它的左上角开始向右沿着边框逐格涂色到右边框,再从上到下逐格涂色到底边框,再沿底边框从右到左逐格涂色到左边框,再从下到上逐格涂色到上面涂色过的方格,如此一直螺旋式地涂下去……,直到将所有的方格都涂满,那么最后被涂的那格是从上到下的第 行,从左到右的第 列。
31.一根2米长绳子从起点开始.每隔4cm标记一个红点,每隔5cm标记一个黄点,最后用剪刀在每个标记点处剪一刀,问一个可以将绳子剪成多少段?
32.王阿姨买来两条丝带,第一条长为m,第二条比第一条短m,两条丝带一共长多少m?
33.有几瓶糖果,其中1瓶被吃了几颗,其余的质量相等.如果用天平称4次就能保证找到那瓶被吃了几颗的,那么这些糖果最多有几瓶?
34.有一个长方体,从上面截下一个高是2厘米的长方体后正好得到一个正方体(如图),正方体的表面积比原来长方体的表面积减少了32平方厘米,求原来长方体的体积。
35.小明和妈妈到商店买了3箱同样的牛奶,售货员阿姨说应付130元,小明马上认为不对。你同意小明的看法吗?说说你的理由。
湖南省长沙市2024-2025学年五年级下学期期末素养评价数学预测卷
参考答案与试题解析
一.选择题(共7小题)
题号 1 2 3 4 5 6 7
答案 A B C B B B B
一.选择题(共7小题)
1.图,从左面看到的是( )
A. B.
C.
【答案】A
【分析】这个立体图形由5个相同的小正方体构成。从左面能看到一列2个相同的正方形。
【解答】解:如图:
从左面看到的是
故选:A。
【点评】本题是考查作简单图形的三视图。能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形。
2.要使2□40既是2的倍数,又是3的倍数,还是5的倍数,□中最小填( )
A.3 B.0 C.6 D.9
【答案】B
【分析】2的倍数的特征:个位上是 0、2、4、6、8 的数,都是2的倍数。
3的倍数的特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
5的倍数的特征:个位上是0或5的数,都是5的倍数。
如果一个数同时是2和5的倍数,那它的个位上的数字一定是0。
【解答】解:2+4=6,6是3的倍数。
要使2□40既是2的倍数,又是3的倍数,还是5的倍数,□中最小填0。
故选:B。
【点评】本题考查了2、3、5倍数的特征。
3.有一个长方体,它有一组相对的面是正方形,其余4个面的面积( )
A.不一定相等 B.一定不相等
C.一定相等 D.无法确定
【答案】C
【分析】根据长方体的特征,长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等;有一组相对的面是正方形的长方体,它的长和宽相等,其余四个面的面积相等;由此解答.
【解答】解:根据分析,有一个长方体,它有一组相对的面是正方形,其余四个面的面积一定相等.
故选:C.
【点评】此题主要根据长方体的特征解决问题.
4.一个正六边形被分成了6个相同的小三角形(如图). 如果用红、黄两种颜色分别涂满小三角形,那么有( )种不同的涂法.(旋转后图案相同的认为是同一种涂法.)
A.13 B.14 C.15
【答案】B
【分析】分别按含有红色0、1、2、3、4、5、6块,7种情况讨论即可得出结论.
【解答】解:可按分类来求解:
(1)无红全黄:1种涂法;
(2)1红5黄:1种涂法;
(3)2红4黄:3种涂法;
(4)3红3黄:4种涂法;
(5)4红2黄:3种涂法;
(6)5红1黄:1种涂法;
(7)全红无黄:1种涂法.
1+1+3+4+3+1+1=14(种);
一共七种情况14种不同的涂法.
故选:B.
【点评】本题解题的关键是注意条件中所给的相同的区域不能用相同的颜色,可利用加法原理进行解答.
5.要使是假分数,是真分数,则X是( )
A.6 B.7 C.8
【答案】B
【分析】要使是假分数,则x为等于或大于7的任意一个整数;要使是真分数,x只能是1、2、3、4、5、6、7共7个整数,由此根据题意解答问题.
【解答】解:要使是假分数,x大于或等于7;
要使是真分数,x小于或等于7;
所以x只能等于7.
故选:B。
【点评】此题主要利用真分数与假分数的意义进行解答即可.
6.在分数加法中,要把异分母分数变成同分母才能进行计算。把异分母分数变成同分母分数,这一过程运用了( )的思想方法。
A.计算 B.转化 C.类比 D.假设
【答案】B
【分析】异分母分数相加减,一般先通分,化成同分母分数,然后按照同分母分数的加减法则进行计算。据此解答。
【解答】解:在分数加法中,要把异分母分数变成同分母才能进行计算。把异分母分数变成同分母分数,这一过程运用了转化的思想方法。
故选:B。
【点评】解答本题需熟练掌握转化思想在异分母分数加减计算过程中的应用。
7.有20个乒乓球,其中有一个是次品,比正品略轻。用一架天平去称,至少称( )次才能保证找到这个次品。
A.2 B.3 C.4 D.5
【答案】B
【分析】根据题意,第一次,把20给乒乓球分成3份:7个、7个、6个,取7个的两份分别放在天平两侧,若天平平衡,则次品在未取的一份中,若天平不平衡,取较轻的一份继续;第二次,取含有较轻的一份(7个或6个),分成3份:2个、2个、2个(或3个)取2个的两份分别放在天平两侧,若天平平衡,则次品在未取的一份,若天平不平衡,取较轻的一份继续;第三次,取含有较轻的一份(2个或3个),取其中2个放在天平两侧,即可找到较轻的一个。由此解答即可。
【解答】解:第一次,把20给乒乓球分成3份:7个、7个、6个,取7个的两份分别放在天平两侧,若天平平衡,则次品在未取的一份中,若天平不平衡,取较轻的一份继续;
第二次,取含有较轻的一份(7个或6个),分成3份:2个、2个、2个(或3个)取2个的两份分别放在天平两侧,若天平平衡,则次品在未取的一份,若天平不平衡,取较轻的一份继续;
第三次,取含有较轻的一份(2个或3个),取其中2个放在天平两侧,即可找到较轻的一个。
答:至少称3次才能保证找到这个次品。
故选:B。
【点评】此题考查找次品的应用。
二.填空题(共8小题)
8.下面的三个图形分别是从什么方向看到的?填一填。
面 面 面
【答案】上,正(或左),右。
【分析】左面的立体图形由4个相同的小正方体组成。从正面能看到3个相同的正方形,分两层,上层1个,下层2个,左齐;从上面能看到3个相同的正方形,分两层,上层2个,下层1个,左齐;从左面看到的图形与从正面看到的相同;从右面能看到3个相同的正方形,分两层,上层1个,下层2个,右齐。
【解答】答案为:上,正(或左),右。
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形。
9.一个四位数□47□同时是2、3、5的倍数,这个数最小是 1470 ,最大是 7470 .
【答案】见试题解答内容
【分析】根据能同时被2、3、5整除的数的特征:该数的个位数0,并且该数各个数位上数的和能被3整除,进行分析、解答即可.
【解答】解:能同时被0、5整除,则个位数字是0,
4+7+0=11,
11+7=18=3×6,7是能被3整除的千位数字最大的数,即7470;
11+1=12=3×4,1是能被3整除的千位数字最小的数,即1470;
故答案为:1470,7470.
【点评】解答此题应根据能被2、3、5整除的数的特征进行解答.
10.把一个大正方体切割成27个同样大小的小正方体后,3面涂色的有 8 个.1面涂色的有 6 个.
【答案】见试题解答内容
【分析】根据只有一面涂色的小正方体在每个正方体的面上,只有2面涂色的小正方体在长方体的棱长上(不包括8个顶点处的小正方体)3面三面涂色的小正方体都在顶点处,即可解答问题.
【解答】解:3×3×3=27,
一个大正方体切割成27个同样大小的小正方体,则每条棱上有3个小正方体,
大正方体8个顶点上各有1个3面涂色的小正方体,因此三面涂色的小正方体一共有8个;
每个面的正中间的一个只有一面涂色,故只有一面涂色的正方体有6个;
故答案为:8,6.
【点评】抓住表面涂色的正方体切割小正方体的特点:1面涂色的在面上,2面涂色的在棱长上,3面涂色的在顶点处,没有涂色的在内部,由此即可解决此类问题.
11.两个数 公有 的因数,叫做它们的公因数.其中最大的公因数,叫做它们的最大公因数.
【答案】见试题解答内容
【分析】根据公因数的意义,几个数公有的因数叫作这几个数的公因数,其中最大的一个数叫作它们的最大公因数作答即可.
【解答】解:几个数公有的因数叫做这几个数的公因数,其中最大的一个数叫作它们的最大公因数.
故答案为:公因.
【点评】此题考查了公因数和最大公因数的含义,属于基础题,比较简单.
12.长方形有 2 条对称轴,正方形有 4 条对称轴,圆有 无数 条对称轴.
【答案】见试题解答内容
【分析】根据轴对称图形的意义:一个图形沿一条直线对折,直线两旁的部分能够完全重合,那么这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,由此分析各图形的对称轴条数即可求解.
【解答】解:长方形有2条对称轴,正方形有4条对称轴,圆有无数条对称轴.
故答案为:2,4,无数.
【点评】此题考查轴对称图形的知识,关键是掌握轴对称图形的意义及对称轴的描述.
13.分数单位是的最小假分数与分数单位是的最大真分数的差是 。
【答案】。
【分析】根据真分数、假分数的意义,分子小于分母的分数叫做真分数,分子等于或大于分母的分数叫做假分数,分数单位是的最小假分数是,分数单位是的最大真分数是,根据分数减法的计算法则计算。
【解答】解:分数单位是的最小假分数是,分数单位是的最大真分数是
答:分数单位是 的最小假分数与分数单位是 的最大真分数的差是。
故答案为:。
【点评】此题考查的目的是理解掌握真分数、假分数的意义,分数减法的计算法则及应用。
14.有83个玻璃球,其中有一个球比其他的球重一些,如果用天平来测量,至少要称 5 次,才能保证找出来.
【答案】见试题解答内容
【分析】把83个分成四组(27、27、27、2),在天平两端各放一组27个的,不平衡即可找到有次品的一组,平衡,次品在未称的27个的一组或在2的个一组;再称一次即可确定在未称的27个一组还是在2个的一组,若在2个一组,再称一次即可找出次品(这样称3次即可找出次品,这种概率不是100%),若不在2个的一组,不论在那组,都是个27个,再把27个分成三组(9,9,9),在天平两端各放一组,平衡,在未称的一组,不平衡在轻的一组,不论那组,都是9个,再把9个分成三组(3,3,3),天平两端各放一组,称1次即可找出次品在哪组,不论那组都是3个,再3个分成(1,1,1),再称一次即可找到次品.即83个时称2次找到次品在哪组,27个、9个、3个再各称1次,一共需要称5次即可保证找到重的次品.
【解答】解:83(27、27、27、2)
称2次即可确定次品是否在27个组的里还是在2个组里
若在2个组里,再称1次即可找到次品(这样称3次即可找出次品,这种概率不是100%),
若在27组里
27(9、9、9)
称1次即可确定次品在哪组
9(3、3、3)
再称1次即可确定次品在哪组
3(1、1,1)
再称1次即可确定次品.
2+1+1=5(次)
答:至少称5次才能把次品保证找出来.
故答案为:5.
【点评】用天平找次品时,所测物品的数目与测试的次数有以下关系(只含一个次品,并且知道比正品重或轻):物品数目2~3,称1次;4~9称2次;10~27称3次;28~31称4次;82~243称5次…记住这一规律,能快速解答此类题目.
15.从正面看到的是 图形,从上面看到的是 图形,从左侧面看到的是 ,从右侧面看到的是 图形.
【答案】见试题解答内容
【分析】观察图形可知,从正面看到的图形是3层:最下层是3个小正方形,上两层都是1个小正方形居中;从上面看到的图形是两行,上面1行3个正方形,下面1行1个小正方形居中;从左侧面看到的图形是3层:最下层是2个小正方形,上两层都是1个小正方形靠左;右侧面看到的图形是3层:最下层是2个小正方形,上两层都是1个小正方形靠右,据此即可解答问题.
【解答】解:从正面看到的是图形,从上面看到的是图形,从左侧面看到的是,从右侧面看到的是图形.
故答案为:,,,.
【点评】此题主要考查从不同方向观察物体的能力,意在培养学生的观察能力和空间思维能力.
三.判断题(共7小题)
16.一个数既是12的因数,又是12的倍数,那么这个数一定是12. √
【答案】见试题解答内容
【分析】根据因数与倍数的意义,一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身;一个数的倍数的个数是无限的,最小的倍数是它本身,没有最大倍数.据此解答.
【解答】解:因为一个数的最大因数是它本身.一个数的最小倍数是它本身.
所以,一个数既是12的因数,又是12的倍数,那么这个数一定是12.这种说法是正确的.
故答案为:√.
【点评】此题考查的目的是理解掌握因数、倍数的意义,明确:一个数的最大因数是它本身.一个数的最小倍数是它本身.
17.一个长方体的底面积减少,高增加,则体积不变。 ×
【答案】×
【分析】根据长方体的体积=底面积×高;可以假设底面积为15平方米,高为12米,分别代入数据求出数值,再进行比较即可。
【解答】解:假设长方体的底面积为15平方米,高为12米,
原来长方体的体积为:15×12=180(立方米)
变化后的长方体体积:(1515)×(1212)
=(15﹣5)×(12+4)
=10×16
=160(立方米)
180>160
所以一个长方体的底面积减少,高增加,则体积变小,原题说法错误。
故答案为:×。
【点评】解答本题依据的公式为:长方体体积=底面积×高。
18.一个表面涂色的正方体,先把棱平均分成5份,再切成同样大的小正方体,两面涂色的小正方体有24个。 ×
【答案】×
【分析】一个表面涂色的正方体,先把棱平均分成5份,切成同样大的小正方体,共切成了53个,即125个。位于每条棱非两端的都两面涂色,一个正方体有12条棱,每条棱上有(5﹣2)个小正方体,据此解答即可。
【解答】解:如图
(5﹣2)×12
=3×12
=36(个)
所以两面涂色的小正方体有36个;故原题说法错误。
故答案为:×。
【点评】解答此题的关键是弄清位于什么位置的小正方体两面涂色。
19.一根绳子,截去它的后,再接上m,绳子和原来一样长. ×
【答案】见试题解答内容
【分析】如果一根绳子长1米,1米的等于米,截去它的,再接上米,和原来一样长;如果这根绳子长不到1米,它的也不到米,截去它的后,再接上米,比原来长;如果这根绳子长大于1米,它的也大于米,截去它的后,再接上米,比原来短.
【解答】解:如果这根绳子长1米,1米的等于米,截去它的,再接上米,和原来一样长;
如果这根绳子长小于1米,它的也小于米,截去它的后,再接上米,比原来长;
如果这根绳子长大于1米,它的也大于米,截去它的后,再接上米,比原来短.
由于这根绳子的长度未知,因此不能判定截去它的后,再接上m,绳子和原来一样长,原题的说法是错误的.
故答案为:×
【点评】这根绳子的的长度受这根绳子长度的制约,而米是一个固定的长度,因此,在不知绳子长度的情况下,不能确定截去它的后,再接上m,绳子和原来一样长.
20.折线统计图是用点的高低表示数量的多少,线的起伏表示数量的增减变化. √
【答案】见试题解答内容
【分析】条形统计图能很容易看出数量的多少;折线统计图用折线的起伏表示数量的增减变化,不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.
【解答】解:折线统计图是用点的高低表示数量的多少,线的起伏表示数量的增减变化,说法正确.
故答案为:√.
【点评】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答.
21.有14瓶口香糖,其中13瓶质量相同,另有1瓶质量不足,如果用天平称,至少称2次才能保证找出这瓶口香糖。 ×
【答案】×
【分析】根据“n次可以找出3的n次幂个零件中一个较轻次品”判断。
【解答】解:2次可以找出32=9(个)待测物品的一个较轻次品;
3次可以找出33=27(个)待测物品的一个较轻次品;
因此3次可以找出10~27个待测物品中的一个较轻次品;
14在10~27范围之内,所以需要3次才能保证找出这瓶口香糖。
故答案为:×。
【点评】运用找次品问题总结的规律是解答本题的捷径。
22.三个连续自然数的和必定是3的倍数。 √
【答案】√
【分析】设三个连续自然数中的第一个为a,由这三个连续的自然数可表示为a、a+1,a+2.其和为:a+(a+1)+(a+2)=3×(a+1),所以三个连续自然数的和一定是3的倍数;据此判断即可。
【解答】解:设三个连续自然数中的第一个为a,则三个连续自然数的和为:
a+(a+1)+(a+2)=3×(a+1),所以三个连续自然数的和一定是3的倍数。
故答案为:√。
【点评】本题是根据相邻的两个自然数相差1的特点从而求出个连续自然数的和是3的倍数的。
四.计算题(共2小题)
23.计算
1
1
【答案】见试题解答内容
【分析】根据分数加减法的计算方法进行计算.
【解答】解:
1
1 11
【点评】口算时,注意运算符号和数据,然后再进一步计算.
24.将一根铁丝做成一个如图所示的长方体框架,至少需要多长的铁丝?
【答案】见试题解答内容
【分析】根据长方体的棱长和=(长+宽+高)×4,长宽高已知,代入解答即可求出至少需要多长的铁丝.
【解答】解:(30+20+15)×4
=65×4
=260(厘米)
答:至少需要260厘米长的铁丝.
【点评】此题主要考查长方体的棱长总和的计算方法.
五.操作题(共2小题)
25.如图:根据给出的分数涂上阴影。
【答案】
【分析】一个物体、一个计量单位或一些物体都可以看成不同的一个整体。这些不同的一个整体都可以用自然数1来表示,通常把它叫作单位“1”;把一个长方形平均分成2份,其中的1份就是这个长方形的,涂色即可。把9个小三角形组成的大三角形看作一个整体,平均分成3份,其中的2份就是这个大三角形的,即将6个小三角形,涂色即可。据此解答。
【解答】解:根据分析,涂色如下图:
【点评】本题考查的是分数的意义,理解和应用分数的意义是解答关键。
26.下面几何体从上面、正面和左面看到的图形分别是什么?画一画。
【答案】
【分析】1图.这个立体图形由6个相同的小正方体构成,从正面能看到4个正方形,分两行,上行1个,下行3个,左齐;从左面能看到3个正方形,分两行,上行1个,下行2个,左齐;从上面能看到5个正方形,分两行,上行3个,下行2个,左齐;
2图.这个立体图形由6个相同的小正方体构成,从正面能看到5个正方形,分3行,1、2行都是1个,3行3个,后面对齐;从左面能看到4个正方形,分3行,1、2行都是1个,3行2个,左齐;从上面能看到4个正方形,分两行,上行3个,下行1个,中间对齐。
【解答】解:根据分析,画图如下:
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形。
六.应用题(共9小题)
27.周末同学聚会,笑笑准备了一些课外读物准备和小伙伴一起共读,已知这些读物的数量既是63的因数,又是3的倍数,还有因数7,笑笑可能准备了多少本读物?
【答案】21或63本读物。
【分析】先根据找一个数因数的方法找出63的所有因数,然后根据:这些读物的数量既是63的因数,又是3的倍数,还有因数7,确定出读物的数量。
【解答】解:63的因数有1、3、7、9、21、63;
既是63的因数,又是3的倍数,还有因数7,所以可能是21或63倍。
答:笑笑可能准备了21或63本读物。
【点评】灵活找一个数因数和倍数的方法,是解答此题的关键。
28.在一个长方体的容器中注入4.4厘米的水(如图):然后将一根圆柱形冰柱垂直放入其中,于是水的高度上升到5.5厘米,这时刚好有根冰柱没在水里,如图。
(1)整根冰柱的体积是多少立方厘米?
(2)已知冰化成水,体积减少原来的,这根冰柱融化后将变成多少毫升的水?
(3)当冰柱完全融化时,容器内水深一共是多少厘米?
【答案】(1)330立方厘米;
(2)220毫升;
(3)6.6厘米。
【分析】(1)长方体的容器中上升水面的体积冰柱的体积。整根冰柱的体积=长方体的容器中上升水面的体积。根据长方体的体积计算公式V=abh代入数值计算出得数,即可解答。
(2)冰化成水,体积减少原来的,用冰柱的体积×(1)=冰化成水后的体积。
(3)根据冰化成水后的体积÷长方体的长×宽=长方体内水面上升的高。用4.4+冰化成水后的水面上升的高=容器内水深一共是多少厘米。
【解答】解:(1)10×10×(5.5﹣4.4)
=100×1.1
=110×3
=330(立方厘米)
答:整根冰柱的体积是330立方厘米。
(2)330×(1)
=330
=220(立方厘米)
220立方厘米=220毫升
答:这根冰柱融化后将变成220毫升的水。
(3)220÷(10×10)+4.4
=220÷100+4.4
=2.2+4.4
=6.6(厘米)
答:容器内水深一共是6.6厘米。
【点评】此题主要考查长方体体积公式的灵活运用,关键是熟记公式。
29.体积问题:一个长方体水池,从里面量长12m、宽5m、深2m。如果每小时注水60立方米,几小时能注满?
【答案】2小时。
【分析】利用长方体的体积公式计算需要注水的体积,然后计算需要注水的时间。
【解答】解:12×5×2÷60
=120÷60
=2(小时)
答:2小时能注满。
【点评】本题考查的是长方体的体积公式的应用。
30.有一个横2000格,竖1000格的矩形方格纸。现从它的左上角开始向右沿着边框逐格涂色到右边框,再从上到下逐格涂色到底边框,再沿底边框从右到左逐格涂色到左边框,再从下到上逐格涂色到上面涂色过的方格,如此一直螺旋式地涂下去……,直到将所有的方格都涂满,那么最后被涂的那格是从上到下的第 501 行,从左到右的第 500 列。
【答案】501,500。
【分析】第1圈涂完,止于2行1列,即(2,1 );第2圈涂完,止于3行2列,即(3,2);……第k圈涂完,止于k+1行k列,即( k+1,k)。横2000格,竖1000格,需要1000:2=500(圈),涂完。所以,止于501行500列。
【解答】解:顺时针涂完第1圈后,有两行两列被涂了色,下一个要涂色的是第2行第2列的方格。涂完第499圈后,有998行998列被涂了色,剩下2行1002列未被涂色。最后一圈从500行500列开始,到501行500列结束.那么最后被涂色的就是第501行,第500列。
故答案为:501,500。
【点评】一圈涂上下两行,所以最后涂色的方格位于第501行。当涂到这一行时,左边已经涂完499列,所以最后涂色的方格位于第500列。
31.一根2米长绳子从起点开始.每隔4cm标记一个红点,每隔5cm标记一个黄点,最后用剪刀在每个标记点处剪一刀,问一个可以将绳子剪成多少段?
【答案】见试题解答内容
【分析】首先求出每4厘米作一个记号,可以作几个记号;再求出每5厘米作一个记号,可以作几个记号;因为4和5的最小公倍数是20,所以每20厘米处的记号重合,由此即可求出绳子被剪出的段数.
【解答】解:2米=200厘米
200÷4﹣1=49(个)
200÷5﹣1=39(个)
4和5互质,所以4和5的最小公倍数是4×5=20;
200÷20﹣1=9(个)
49+39﹣9=79(个)
79+1=80(段)
答:可以将绳子剪成80段.
【点评】解答此题的关键是分析出每20厘米处的记号重合,并求出重合的记号的个数.
32.王阿姨买来两条丝带,第一条长为m,第二条比第一条短m,两条丝带一共长多少m?
【答案】m。
【分析】根据题意,用m减去m,求出第二条丝带的长度,然后再加上第一条的长度即可。
【解答】解:
(m)
答:两条丝带一共长m。
【点评】本题关键是根据减法的意义,求出第二条丝带的长度,然后再根据加法的意义进行解答。
33.有几瓶糖果,其中1瓶被吃了几颗,其余的质量相等.如果用天平称4次就能保证找到那瓶被吃了几颗的,那么这些糖果最多有几瓶?
【答案】见试题解答内容
【分析】根据题意,先把这几瓶分成三份,如果瓶子数量是三的倍数的话,则三分瓶子数量相同,如果不是三的倍数,则分成两份相同和一份不同的情况,拿两份相同放到天平上,若两份质量不相同,则那瓶再较轻的一份,若质量相同,则在另外没称的一份.接下来步骤同上.
【解答】解:先把这几瓶分成三份,如果瓶子数量是三的倍数的话,则三分瓶子数量相同,如果不是三的倍数,则分成两份相同和一份不同的情况,拿两份相同放到天平上,若两份质量不相同,则那瓶再较轻的一份,若质量相同,则在另外没称的一份.接下来步骤同上.所以要看糖果的瓶数是多少瓶,这个数在3n﹣1和3n之间,则需要称的最少次数是n次.所以如果瓶数小于81瓶则可4次称出,如果大于81瓶,则4次不能称出.
答:这些糖果最多有81瓶.
【点评】本题的关键是把瓶子要分三份来称,然后找出规律进行解答.
34.有一个长方体,从上面截下一个高是2厘米的长方体后正好得到一个正方体(如图),正方体的表面积比原来长方体的表面积减少了32平方厘米,求原来长方体的体积。
【答案】96立方厘米。
【分析】根据高截短2厘米,就剩下一个正方体可知,则长方体的长和宽相等,这个正方体比原长方体表面积减少的4个面是相同的,根据已知表面积减少32平方厘米,则减少一个面的面积是32÷4=8(平方厘米),再根据长方形的面积=长×宽,用一个面的面积除以2,求出原长方体的长和宽,原长方体的高等于原长方体的长加上2就是长方体的高,再根据长方体的体积=长×宽×高,即可计算原长方体的体积。
【解答】解:减少的面的长(剩下正方体的棱长)32÷4÷2=4(厘米)
原来长方体的高:4+2=6(厘米)
原来的体积:4×4×6=96(立方厘米)
答:原来长方体的体积是96立方厘米。
【点评】此题主要考查长方体的体积公式的灵活运用,关键是求出原来长方体的高。
35.小明和妈妈到商店买了3箱同样的牛奶,售货员阿姨说应付130元,小明马上认为不对。你同意小明的看法吗?说说你的理由。
【答案】同意小明的看法。因为130不是3的倍数。
【分析】买了3箱同样的牛奶,总价应是3的倍数,根据3的倍数特征,一个数各个数位上数的和是3的倍数,这个数就是3的倍数;先把130各个数位上的数字加起来,再判断和是不是3的倍数,据此解答。
【解答】解:1+3+0=4
答:因为4不是3的倍数,即130不是3的倍数,所以小明的看法正确。
【点评】此题主要是考查3的倍数特征的应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
