2024-2025学年七年级下学期数学期末模拟(杭州市、萧山、余杭、富阳、临平等专用)(含解析)
文档属性
| 名称 | 2024-2025学年七年级下学期数学期末模拟(杭州市、萧山、余杭、富阳、临平等专用)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 998.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 06:13:40 | ||
图片预览




文档简介
保密★启用前
2024-2025学年七年级下册期末模拟卷
(杭州市、萧山、余杭、富阳、临平等专用)
数 学
(考试范围:浙江版七下全册 考试时间:120分钟 分值:120分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.甲骨文主要流行于商周时期,是迄今为止中国发现的年代最早的成熟文字系统,是汉字的源头和中华优秀传统文化的根脉,下列甲骨文中,能用其中一部分平移得到的是( )
A.杯 B.立 C.比 D.曲
2.下列方程中,属于二元一次方程的是( )
A. B. C. D.
3.“春江潮水连海平,海上明月共潮生”,水是诗人钟爱的意象,经测算,一个水分子的直径约为,数据用科学记数法表示为( )
A. B. C. D.
4.下列各式从左到右,属于因式分解的是( )
A. B.
C. D.
5.如果将分式中的字母,的值分别扩大为原来的3倍,那么分式的值()
A.不改变 B.扩大为原来的3倍
C.缩小为原来的6倍 D.缩小为原来的3倍
6.每年的4月23日为“世界读书日”.阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快.昆明某中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A.科普,B.文学,C.体育,D.其他)数据后,绘制出两幅不完整的统计图.下列说法正确的是( )
A.本次抽样喜欢文学类书籍的人数是30人
B.本次抽样的样本容量为180
C.本次抽样喜欢科普类书籍的人数是70人
D.若该校有2600名学生,则该校学生中喜欢科普类书籍的人数约为520人
7.下列多项式因式分解的结果中不含因式的是( )
A. B. C. D.
8.下列各式从左向右的变形中,是因式分解的为( )
A. B.
C. D.
9.如图所示,将两个正方形并列放置,其中B、C、E三点在一条直线上,C、G、D三点在一条直线上,已知,,则阴影部分的面积是( )
A.10 B.20 C.30 D.40
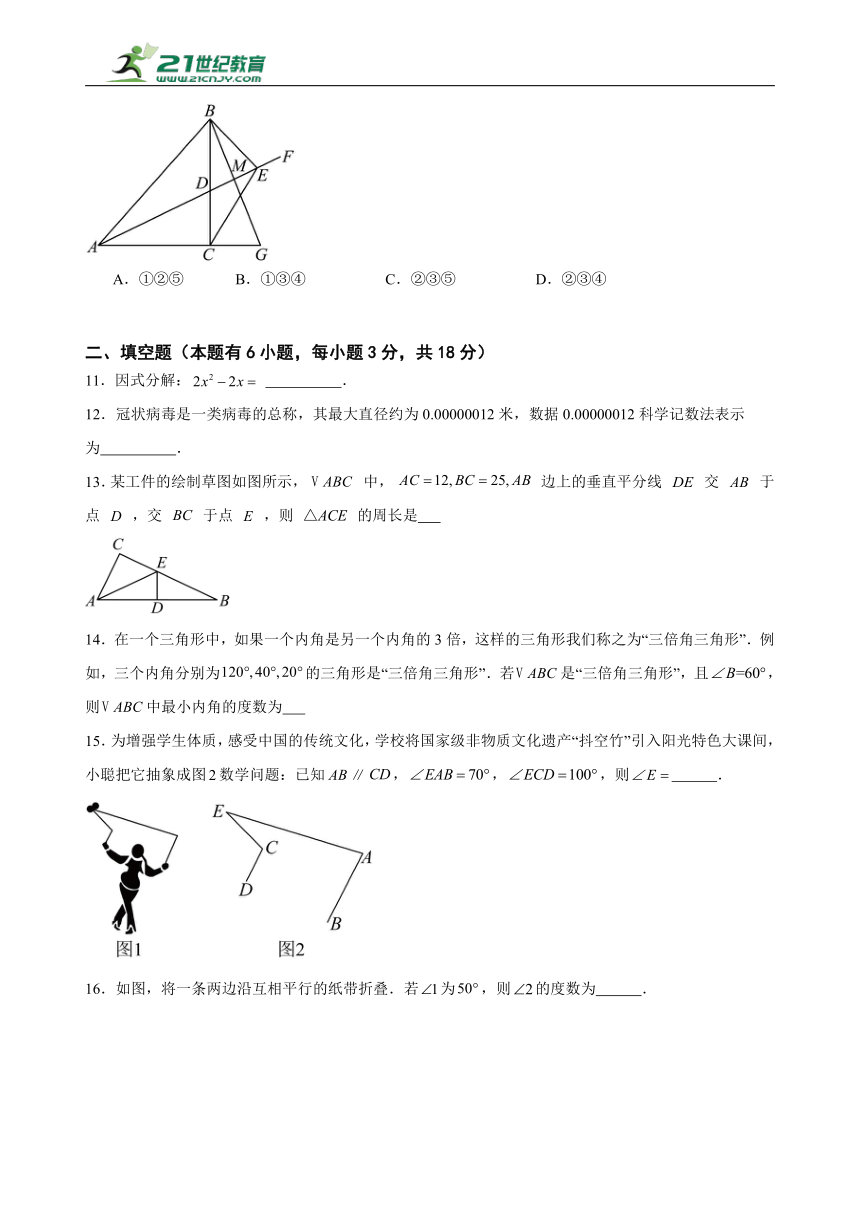
10.如图,在中,,,射线是的角平分线,交于点D,过点B作的垂线与射线交于点E,连接,M是的中点,连接并延长与的延长线交于点G.则下列结论中:①;②垂直平分;③;④;⑤.正确的有( )
A.①②⑤ B.①③④ C.②③⑤ D.②③④
二、填空题(本题有6小题,每小题3分,共18分)
11.因式分解: .
12.冠状病毒是一类病毒的总称,其最大直径约为0.00000012米,数据0.00000012科学记数法表示为 .
13.某工件的绘制草图如图所示, 中, 边上的垂直平分线 交 于点 ,交 于点 ,则 的周长是
14.在一个三角形中,如果一个内角是另一个内角的3倍,这样的三角形我们称之为“三倍角三角形”.例如,三个内角分别为的三角形是“三倍角三角形”.若是“三倍角三角形”,且,则中最小内角的度数为
15.为增强学生体质,感受中国的传统文化,学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间,小聪把它抽象成图数学问题:已知,,,则 .
16.如图,将一条两边沿互相平行的纸带折叠.若为,则的度数为 .
三、解答题 (本题有 7 小题, 第17-21题每题 10 分, 第 22,23 题每题 11 分, 共 72 分)
17.(1)计算:
(2)化简:.
18.解下列方程组:
(1)
(2)
19.学校团委开展了消防知识普及活动,并对全校名学生进行了消防知识检测,随机抽取部分学生的答题情况,绘制成如图的统计图(部分).请根据调查的信息,解答下列问题:
(1)共抽查了多少名学生;
(2)请补全条形统计图;
(3)请估计该校学生答对道(含道)以上的人数.
20.如图,分别是射线上的点,连接平分,平分,.
(1)判定与的位置关系,并说明理由;
(2)若,求的度数.
21.观察下列各等式:
①;②;③;……
(1)按照以上等式规律,写出第4个等式是: ;
(2)写出第个等式(用含的代数式表示),并说明等式成立的理由;
(3)计算: .
22.杨梅是我市特产水果之一,素有“初疑一颗值千金”之美誉!某杨梅园的杨梅除了直接销售到市区外,还可以让市民去园区采摘.已知杨梅在市区和园区的销售价格分别是15元/千克和10元/千克,该杨梅园今年六月第一周一共销售了1000千克,销售收入12000元.
(1)该杨梅园今年六月第一周市区和园区分别销售了多少千克杨梅?
(2)为了促销,该杨梅园决定六月第二周将市区和园区销售价格均以相同折扣进行销售,小方发现用3240元购买市区的重量比用2430元购买园区的重量少30千克,求本次活动对市区和园区进行几折销售?
(3)在(2)的促销条件下,杨梅园想第二周市区和园区杨梅的平均售价和第一周的市区和园区平均售价相等.若第二周杨梅在市区的销量为a千克,园区的销量为b千克,请直接写出a与b的数量关系.
23.【问题情境】:在综合实践课上,老师组织班上的同学开展了探究两角之间数量关系的数学活动,如图1,已知直线,点E、G分别为直线、上的点,点F是平面内任意一点,连接、.
【探索发现】:
(1)如图1,当时,求证:;
【深入探究】:
(2)如图2点P、Q分别是直线上的点,且,直线,交于点K,“智胜小组”探究与之间的数量关系.请写出它们的关系,并说明理由;
(3)如图3,在(2)的探究基础上,,“科创小组”探究与之间的数量关系.请直接写出它们的关系,不需要说明理由.
《2024-2025学年七年级下学期数学期末模拟( 杭州市、萧山、余杭、富阳、临平等专用)》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B D A D D C C A
1.C
本题考查了图形的平移,根据图形的平移的定义逐一判断即可求解,熟记:“某一基本的平面图形沿着一定的方向移动,这种图形的平行移动,简称为平移”是解题的关键.
解:由平移的性质知,只有C是利用图形的平移得到的,
故选:C.
2.D
本题考查二元一次方程的定义,根据含有两个未知数,未知数的次数都是1的整式方程是二元一次方程进行判断即可.
解:A.该方程的次数是2,不是二元一次方程,故该选项不符合题意;
B.该方程的次数是2,不是二元一次方程,故该选项不符合题意;
C.不是整式方程,故该选项不符合题意;
D.是二元一次方程,故该选项符合题意;
故选:D.
3.B
用科学记数法表示绝对值小于1的数,一般形式为,其中,由原数左边起第一个不为零的数字前面的0的个数所决定,据此即可得到答案.
解:,
故选B.
本题考查了用科学记数法表示绝对值小于1的数,熟练掌握表示方法是解题关键.
4.D
本题考查了因式分解,熟练掌握因式分解的定义是解题关键.把一个多项式化成几个整式积的形式,像这样的式子变形叫做这个多项式的因式分解.根据因式分解的定义逐一判断,即可得到答案.
A、,结果不是整式乘积的性质,不属于因式分解,是多项式乘多项式,不符合题意;
B、,结果不是整式乘积的性质,不属于因式分解,不符合题意;
C、,原等式不成立,不符合题意;
D、,属于因式分解,符合题意;
故选:D.
5.A
本题主要考查了分式的基本性质,掌握分式的基本性质是解题的关键,分式的基本性质是分式的分子分母同时乘或除以同一个不为0的整式,分式的值不变.根据分式的基本性质即可求解.
解:分式中的字母的值分别扩大为原来的3倍,
,
分式的值不改变,
故选:A.
6.D
根据条形统计图,即可判断A,由喜欢文学的人数除以占比,即可判断B,由扇形统计图得到喜欢科普类书籍的人数占比,乘以样本容量,即可判断C,用该校人数乘以样本中喜欢科普类书籍的人数占比,即可判断D,
本题考查了,条形统计图和扇形统计图的信息关联,由样本估计总体,解题的关键是:从统计图中获得信息.
解:A、由条形统计图可知:喜欢文学类书籍的人数为60人,故该选项错误,不符合题意,
B、,本次抽样的样本容量为200,故该选项错误,不符合题意,
C、由扇形统计图可知,科普与文学共占,喜欢科普类书籍的人数占比,人数为:(人),故该选项错误,不符合题意,
D、该校学生中喜欢科普类书籍的人数约为:(人),故该选项正确,符合题意,
故选:.
7.D
分别利用公式法以及提取公因式分解因式进而判断得出答案.
解:A、,含有因式,本选项不符合题意;
B、,含有因式,本选项不符合题意;
C、,含有因式,本选项不符合题意;
D、,不含有因式,本选项符合题意;
故选:D.
本题主要考查了公式法以及提取公因式法分解因式,正确运用公式是解题关键.
8.C
本题考查因式分解的定义以及利用公式法进行因式分解,掌握完全平方公式的形式是解决此题的关键.把一个多项式化成几个整式的积的形式,这种变形叫做因式分解.
解:A、,是整式乘法,不符合题意;
B、,错误,不符合题意;
C、,正确,符合题意;
D、,不是几个整式的积的形式,故错误,不符合题意;
故选:C.
9.C
本题考查整式乘法的几何应用,完全平方公式的应用,设小正方形的边长为x,大正方形的边长为y,则,,根据几何图形得到阴影部分的面积等于,列出式子,利用完全平方公式变形,计算即可.
解:设小正方形的边长为x,大正方形的边长为y,
,,
,,
则阴影部分的面积等于,
即,
,
故选:C.
10.A
先由题意得到,再由角平分线的定义得到,从而推出,再由三线合一定理即可证明,即可判断②;得到,再由,可得,则,从而可证明,即可判断①;则,再由,可得到,即可判断③;由,即可判断④.延长交延长线于G,若,证明即可;
解:∵,
∴,
∴,
∵平分,
∴,
∴,
又∵,
∴,
又∵M是的中点,
∴,
∴垂直平分,,故②正确,
∴,
∵,
∴,
∴,
∴,
又∵,
∴,故①正确;
∴,
∵,
∴,故⑤正确;
∵,
∴,故④错误;
如图所示,延长交延长线于G,
∵,,
∴是等腰直角三角形,
若,
∴,
∴,
∴,
∵,
∴C为的中点,
∴,
∴,
∴与矛盾;
∴与不垂直,故③错误;
故选A.
本题主要考查了全等三角形的性质与判定,等腰三角形的性质与判定,三角形内角和定理,熟知等腰三角形的性质与判定条件是解题的关键.
11.
根据提公因式法可进行求解.
解:原式;
故答案为:.
本题主要考查因式分解,熟练掌握因式分解的方法是解题的关键.
12.1.2×10-7
将0.00000012写成a×10n(1<|a |<10,n为负整数)的形式即可.
解: 0.00000012=1.2×10-7.
故填1.2×10-7.
本题主要考查运用科学记数法, 将原数写成a×10n(1<|a |<10,n为负整数),确定a和n的值成为解答本题的关键.
13.37
本题主要考查垂直平分线的性质,掌握垂直平分线的性质是解题的关键.根据垂直平分线的性质,可得,根据三角形的周长公式即可求解.
解:∵边上的垂直平分线交于点,
∴,
∵的周长为,
∴,
故答案为:37.
14.或
本题考查的是三角形的内角和定理的应用,分类思想的应用,掌握以上知识是解题的关键.
由是“三倍角三角形”,且,不妨设,再分三种情况讨论,当时,当时,当时,再结合三角形的内角和定理可得答案.
解:∵是“三倍角三角形”,且,不妨设,
当时,则,
,
当时,
,
,
,
当时,则,不合题意舍去,
综上:是“三倍角三角形”,中最小内角的度数为或.
故答案为:或.
15./30度
过点作,先根据平行线的性质可得,再根据平行公理推论、平行线的性质可得,然后根据角的和差即可得.
解:如图,过点作,
,,
,
,,
,
,
,
,
,
故答案为.
本题考查了平行线的判定与性质,熟练掌握平行线的性质是解题关键.
16.
本题考查了平行线的性质、翻折变换问题,找着重合的角,利用平角定义求出的度数是解题的关键.
如图,由折叠可得重合的角相等,利用平角可求得的度数,由于纸片的两边平行,可得,即可求解.
解:如图所示:
由折叠的性质得:,
则
又∵
∴
纸片两边平行,
,
故答案为::.
17.(1);(2)
此题考查了实数及整式的混合运算能力,关键是能准确确定运算顺序和方法,并能进行正确地计算.
(1)先计算零次幂、负整数指数幂和绝对值,再计算减法;
(2)先运用平方差公式和完全平方公式计算多项式乘多项式,再合并同类项.
解:(1)
;
(2)
.
18.(1)
(2)
本题考查了解二元一次方程组,熟练掌握加减消元法解方程组是解题的关键.
(1)利用加减消元法解二元一次方程组即可;
(2)先将方程组化简,然后利用加减消元法解二元一次方程组即可.
(1)解:,
①②,得,
解得,
把代入②,得,
所以方程组的解是;
(2)解:,
方程组可化为,
②,得③,
①③,得,
解得,
把代入②,得,
所以原方程组的解是.
19.(1)共抽查了名学生;
(2)补全条形统计图见解析;
(3)估计该校学生答对道(含道)以上的人数为名.
()用答对道题的人数除以所占的百分比可得本次调查共抽取的学生人数;
()用总人数乘以答对道题的人数除以所占的百分比求出答对道题的人数,再补全条形统计图即可;
()用乘以答对道 (含道) 以上的人数所占的百分比即可得出答案;
本题考查了条形统计图,扇形统计图,用样本估计总体,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
(1)解: (名),
答:共抽查了名学生;
(2)答对道题的人数为(名),补全条形统计图如图所示:
(3)(名),
答:估计该校学生答对道(含道)以上的人数为名.
20.(1);理由见解析
(2)
本题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解题的关键.
(1)利用角平分线的定义可得,从而利用等量代换可得,然后利用内错角相等,两直线平行可得,即可解答;
(2)根据已知可得,然后利用平行线的性质可得,从而利用角平分线的定义可得,再利用平角定义可得,最后进行计算可求出,从而得出的度数,即可解答.
(1)解:;理由如下:
平分,
,
,
,
∴;
(2)解:,
,
∵,
∴,
,
,
平分,
,
,
,
,
.
21.(1)
(2),理由见解析
(3)
本题主要考查了实数混合运算的规律题。根据题意准确找出相应规律是解题关键.
(1)按照①②③的规律写出第4个等式即可.
(2)总结规律并证明等式左边等于右边即可.
(3)按照规律,将原式变形,然后简便运算即可.
(1)解:根据①②③可得出第4个等式:,
故答案为:.
(2)根据①②③,可得出:
理由如下:
等式左边为: ,
等式右边为:.
∴.
(3)
22.(1)该杨梅园今年六月第一周市区销售了400千克杨梅,园区销售了600千克杨梅
(2)本次活动对市区和园区进行9折销售
(3)a与b的数量关系为
(1)设该杨梅园今年六月第一周市区销售了x千克杨梅,园区销售了y千克杨梅,利用总价=单价数量,结合“该杨梅园今年六月第一周一共销售了1000千克,销售收入12000元”,可列出关于x,y的二元一次方程组,解之即可得出结论;
(2)设本次活动对市区和园区进行m折销售,利用数量=总价单价,结合用3240元购买市区的重量比用2430元购买园区的重量少30千克,可列出关于m的分式方程,解之经检验后,即可得出结论;
(3)根据该杨梅园想第二周市区和园区杨梅的平均售价和第一周的市区和园区平均售价相等,可列出关于a,b的二元一次方程,变形后,即可得出结论.
(1)解:设该杨梅园今年六月第一周市区销售了x千克杨梅,园区销售了y千克杨梅,
根据题意得:,
解得:
答:该杨梅园今年六月第一周市区销售了400千克杨梅,园区销售了600千克杨梅;
(2)设本次活动对市区和园区进行m折销售,
根据题意得:,
解得:,
经检验,是所列方程的解,且符合题意.
答:本次活动对市区和园区进行9折销售;
(3)根据题意得:,
答:a与b的数量关系为
本题考查了二元一次方程组的应用、分式方程的应用以及二元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出分式方程;(3)找准等量关系,正确列出分式方程.
23.(1)见解析;(2);理由见解析;(3)
本题主要考查了利用平行线的性质探求角的度数及关系,根据图准确作出辅助线是解题关键.
(1)过F作,可得,再根据两直线平行内错角相等,可推出,从而得出结果;
(2)与之间的数量关系为,利用平行线的性质即可求证;
(3)过点M作,设,利用平行线的性质即可求证.
证明:(1)如图所示,过F作,
,
,
∴,,
∴,
∵,
∴;
(2)与之间的数量关系为,理由如下:
设,
∴,
∵,
∴,
又∵,
∴,
∴,
∴;
(3)∵,
∴设,
过点M作,
,
,
∴,
根据解析(2)可知,,
∴,
∴,
又∵,
∴.
2024-2025学年七年级下册期末模拟卷
(杭州市、萧山、余杭、富阳、临平等专用)
数 学
(考试范围:浙江版七下全册 考试时间:120分钟 分值:120分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.甲骨文主要流行于商周时期,是迄今为止中国发现的年代最早的成熟文字系统,是汉字的源头和中华优秀传统文化的根脉,下列甲骨文中,能用其中一部分平移得到的是( )
A.杯 B.立 C.比 D.曲
2.下列方程中,属于二元一次方程的是( )
A. B. C. D.
3.“春江潮水连海平,海上明月共潮生”,水是诗人钟爱的意象,经测算,一个水分子的直径约为,数据用科学记数法表示为( )
A. B. C. D.
4.下列各式从左到右,属于因式分解的是( )
A. B.
C. D.
5.如果将分式中的字母,的值分别扩大为原来的3倍,那么分式的值()
A.不改变 B.扩大为原来的3倍
C.缩小为原来的6倍 D.缩小为原来的3倍
6.每年的4月23日为“世界读书日”.阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快.昆明某中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A.科普,B.文学,C.体育,D.其他)数据后,绘制出两幅不完整的统计图.下列说法正确的是( )
A.本次抽样喜欢文学类书籍的人数是30人
B.本次抽样的样本容量为180
C.本次抽样喜欢科普类书籍的人数是70人
D.若该校有2600名学生,则该校学生中喜欢科普类书籍的人数约为520人
7.下列多项式因式分解的结果中不含因式的是( )
A. B. C. D.
8.下列各式从左向右的变形中,是因式分解的为( )
A. B.
C. D.
9.如图所示,将两个正方形并列放置,其中B、C、E三点在一条直线上,C、G、D三点在一条直线上,已知,,则阴影部分的面积是( )
A.10 B.20 C.30 D.40
10.如图,在中,,,射线是的角平分线,交于点D,过点B作的垂线与射线交于点E,连接,M是的中点,连接并延长与的延长线交于点G.则下列结论中:①;②垂直平分;③;④;⑤.正确的有( )
A.①②⑤ B.①③④ C.②③⑤ D.②③④
二、填空题(本题有6小题,每小题3分,共18分)
11.因式分解: .
12.冠状病毒是一类病毒的总称,其最大直径约为0.00000012米,数据0.00000012科学记数法表示为 .
13.某工件的绘制草图如图所示, 中, 边上的垂直平分线 交 于点 ,交 于点 ,则 的周长是
14.在一个三角形中,如果一个内角是另一个内角的3倍,这样的三角形我们称之为“三倍角三角形”.例如,三个内角分别为的三角形是“三倍角三角形”.若是“三倍角三角形”,且,则中最小内角的度数为
15.为增强学生体质,感受中国的传统文化,学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间,小聪把它抽象成图数学问题:已知,,,则 .
16.如图,将一条两边沿互相平行的纸带折叠.若为,则的度数为 .
三、解答题 (本题有 7 小题, 第17-21题每题 10 分, 第 22,23 题每题 11 分, 共 72 分)
17.(1)计算:
(2)化简:.
18.解下列方程组:
(1)
(2)
19.学校团委开展了消防知识普及活动,并对全校名学生进行了消防知识检测,随机抽取部分学生的答题情况,绘制成如图的统计图(部分).请根据调查的信息,解答下列问题:
(1)共抽查了多少名学生;
(2)请补全条形统计图;
(3)请估计该校学生答对道(含道)以上的人数.
20.如图,分别是射线上的点,连接平分,平分,.
(1)判定与的位置关系,并说明理由;
(2)若,求的度数.
21.观察下列各等式:
①;②;③;……
(1)按照以上等式规律,写出第4个等式是: ;
(2)写出第个等式(用含的代数式表示),并说明等式成立的理由;
(3)计算: .
22.杨梅是我市特产水果之一,素有“初疑一颗值千金”之美誉!某杨梅园的杨梅除了直接销售到市区外,还可以让市民去园区采摘.已知杨梅在市区和园区的销售价格分别是15元/千克和10元/千克,该杨梅园今年六月第一周一共销售了1000千克,销售收入12000元.
(1)该杨梅园今年六月第一周市区和园区分别销售了多少千克杨梅?
(2)为了促销,该杨梅园决定六月第二周将市区和园区销售价格均以相同折扣进行销售,小方发现用3240元购买市区的重量比用2430元购买园区的重量少30千克,求本次活动对市区和园区进行几折销售?
(3)在(2)的促销条件下,杨梅园想第二周市区和园区杨梅的平均售价和第一周的市区和园区平均售价相等.若第二周杨梅在市区的销量为a千克,园区的销量为b千克,请直接写出a与b的数量关系.
23.【问题情境】:在综合实践课上,老师组织班上的同学开展了探究两角之间数量关系的数学活动,如图1,已知直线,点E、G分别为直线、上的点,点F是平面内任意一点,连接、.
【探索发现】:
(1)如图1,当时,求证:;
【深入探究】:
(2)如图2点P、Q分别是直线上的点,且,直线,交于点K,“智胜小组”探究与之间的数量关系.请写出它们的关系,并说明理由;
(3)如图3,在(2)的探究基础上,,“科创小组”探究与之间的数量关系.请直接写出它们的关系,不需要说明理由.
《2024-2025学年七年级下学期数学期末模拟( 杭州市、萧山、余杭、富阳、临平等专用)》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B D A D D C C A
1.C
本题考查了图形的平移,根据图形的平移的定义逐一判断即可求解,熟记:“某一基本的平面图形沿着一定的方向移动,这种图形的平行移动,简称为平移”是解题的关键.
解:由平移的性质知,只有C是利用图形的平移得到的,
故选:C.
2.D
本题考查二元一次方程的定义,根据含有两个未知数,未知数的次数都是1的整式方程是二元一次方程进行判断即可.
解:A.该方程的次数是2,不是二元一次方程,故该选项不符合题意;
B.该方程的次数是2,不是二元一次方程,故该选项不符合题意;
C.不是整式方程,故该选项不符合题意;
D.是二元一次方程,故该选项符合题意;
故选:D.
3.B
用科学记数法表示绝对值小于1的数,一般形式为,其中,由原数左边起第一个不为零的数字前面的0的个数所决定,据此即可得到答案.
解:,
故选B.
本题考查了用科学记数法表示绝对值小于1的数,熟练掌握表示方法是解题关键.
4.D
本题考查了因式分解,熟练掌握因式分解的定义是解题关键.把一个多项式化成几个整式积的形式,像这样的式子变形叫做这个多项式的因式分解.根据因式分解的定义逐一判断,即可得到答案.
A、,结果不是整式乘积的性质,不属于因式分解,是多项式乘多项式,不符合题意;
B、,结果不是整式乘积的性质,不属于因式分解,不符合题意;
C、,原等式不成立,不符合题意;
D、,属于因式分解,符合题意;
故选:D.
5.A
本题主要考查了分式的基本性质,掌握分式的基本性质是解题的关键,分式的基本性质是分式的分子分母同时乘或除以同一个不为0的整式,分式的值不变.根据分式的基本性质即可求解.
解:分式中的字母的值分别扩大为原来的3倍,
,
分式的值不改变,
故选:A.
6.D
根据条形统计图,即可判断A,由喜欢文学的人数除以占比,即可判断B,由扇形统计图得到喜欢科普类书籍的人数占比,乘以样本容量,即可判断C,用该校人数乘以样本中喜欢科普类书籍的人数占比,即可判断D,
本题考查了,条形统计图和扇形统计图的信息关联,由样本估计总体,解题的关键是:从统计图中获得信息.
解:A、由条形统计图可知:喜欢文学类书籍的人数为60人,故该选项错误,不符合题意,
B、,本次抽样的样本容量为200,故该选项错误,不符合题意,
C、由扇形统计图可知,科普与文学共占,喜欢科普类书籍的人数占比,人数为:(人),故该选项错误,不符合题意,
D、该校学生中喜欢科普类书籍的人数约为:(人),故该选项正确,符合题意,
故选:.
7.D
分别利用公式法以及提取公因式分解因式进而判断得出答案.
解:A、,含有因式,本选项不符合题意;
B、,含有因式,本选项不符合题意;
C、,含有因式,本选项不符合题意;
D、,不含有因式,本选项符合题意;
故选:D.
本题主要考查了公式法以及提取公因式法分解因式,正确运用公式是解题关键.
8.C
本题考查因式分解的定义以及利用公式法进行因式分解,掌握完全平方公式的形式是解决此题的关键.把一个多项式化成几个整式的积的形式,这种变形叫做因式分解.
解:A、,是整式乘法,不符合题意;
B、,错误,不符合题意;
C、,正确,符合题意;
D、,不是几个整式的积的形式,故错误,不符合题意;
故选:C.
9.C
本题考查整式乘法的几何应用,完全平方公式的应用,设小正方形的边长为x,大正方形的边长为y,则,,根据几何图形得到阴影部分的面积等于,列出式子,利用完全平方公式变形,计算即可.
解:设小正方形的边长为x,大正方形的边长为y,
,,
,,
则阴影部分的面积等于,
即,
,
故选:C.
10.A
先由题意得到,再由角平分线的定义得到,从而推出,再由三线合一定理即可证明,即可判断②;得到,再由,可得,则,从而可证明,即可判断①;则,再由,可得到,即可判断③;由,即可判断④.延长交延长线于G,若,证明即可;
解:∵,
∴,
∴,
∵平分,
∴,
∴,
又∵,
∴,
又∵M是的中点,
∴,
∴垂直平分,,故②正确,
∴,
∵,
∴,
∴,
∴,
又∵,
∴,故①正确;
∴,
∵,
∴,故⑤正确;
∵,
∴,故④错误;
如图所示,延长交延长线于G,
∵,,
∴是等腰直角三角形,
若,
∴,
∴,
∴,
∵,
∴C为的中点,
∴,
∴,
∴与矛盾;
∴与不垂直,故③错误;
故选A.
本题主要考查了全等三角形的性质与判定,等腰三角形的性质与判定,三角形内角和定理,熟知等腰三角形的性质与判定条件是解题的关键.
11.
根据提公因式法可进行求解.
解:原式;
故答案为:.
本题主要考查因式分解,熟练掌握因式分解的方法是解题的关键.
12.1.2×10-7
将0.00000012写成a×10n(1<|a |<10,n为负整数)的形式即可.
解: 0.00000012=1.2×10-7.
故填1.2×10-7.
本题主要考查运用科学记数法, 将原数写成a×10n(1<|a |<10,n为负整数),确定a和n的值成为解答本题的关键.
13.37
本题主要考查垂直平分线的性质,掌握垂直平分线的性质是解题的关键.根据垂直平分线的性质,可得,根据三角形的周长公式即可求解.
解:∵边上的垂直平分线交于点,
∴,
∵的周长为,
∴,
故答案为:37.
14.或
本题考查的是三角形的内角和定理的应用,分类思想的应用,掌握以上知识是解题的关键.
由是“三倍角三角形”,且,不妨设,再分三种情况讨论,当时,当时,当时,再结合三角形的内角和定理可得答案.
解:∵是“三倍角三角形”,且,不妨设,
当时,则,
,
当时,
,
,
,
当时,则,不合题意舍去,
综上:是“三倍角三角形”,中最小内角的度数为或.
故答案为:或.
15./30度
过点作,先根据平行线的性质可得,再根据平行公理推论、平行线的性质可得,然后根据角的和差即可得.
解:如图,过点作,
,,
,
,,
,
,
,
,
,
故答案为.
本题考查了平行线的判定与性质,熟练掌握平行线的性质是解题关键.
16.
本题考查了平行线的性质、翻折变换问题,找着重合的角,利用平角定义求出的度数是解题的关键.
如图,由折叠可得重合的角相等,利用平角可求得的度数,由于纸片的两边平行,可得,即可求解.
解:如图所示:
由折叠的性质得:,
则
又∵
∴
纸片两边平行,
,
故答案为::.
17.(1);(2)
此题考查了实数及整式的混合运算能力,关键是能准确确定运算顺序和方法,并能进行正确地计算.
(1)先计算零次幂、负整数指数幂和绝对值,再计算减法;
(2)先运用平方差公式和完全平方公式计算多项式乘多项式,再合并同类项.
解:(1)
;
(2)
.
18.(1)
(2)
本题考查了解二元一次方程组,熟练掌握加减消元法解方程组是解题的关键.
(1)利用加减消元法解二元一次方程组即可;
(2)先将方程组化简,然后利用加减消元法解二元一次方程组即可.
(1)解:,
①②,得,
解得,
把代入②,得,
所以方程组的解是;
(2)解:,
方程组可化为,
②,得③,
①③,得,
解得,
把代入②,得,
所以原方程组的解是.
19.(1)共抽查了名学生;
(2)补全条形统计图见解析;
(3)估计该校学生答对道(含道)以上的人数为名.
()用答对道题的人数除以所占的百分比可得本次调查共抽取的学生人数;
()用总人数乘以答对道题的人数除以所占的百分比求出答对道题的人数,再补全条形统计图即可;
()用乘以答对道 (含道) 以上的人数所占的百分比即可得出答案;
本题考查了条形统计图,扇形统计图,用样本估计总体,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
(1)解: (名),
答:共抽查了名学生;
(2)答对道题的人数为(名),补全条形统计图如图所示:
(3)(名),
答:估计该校学生答对道(含道)以上的人数为名.
20.(1);理由见解析
(2)
本题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解题的关键.
(1)利用角平分线的定义可得,从而利用等量代换可得,然后利用内错角相等,两直线平行可得,即可解答;
(2)根据已知可得,然后利用平行线的性质可得,从而利用角平分线的定义可得,再利用平角定义可得,最后进行计算可求出,从而得出的度数,即可解答.
(1)解:;理由如下:
平分,
,
,
,
∴;
(2)解:,
,
∵,
∴,
,
,
平分,
,
,
,
,
.
21.(1)
(2),理由见解析
(3)
本题主要考查了实数混合运算的规律题。根据题意准确找出相应规律是解题关键.
(1)按照①②③的规律写出第4个等式即可.
(2)总结规律并证明等式左边等于右边即可.
(3)按照规律,将原式变形,然后简便运算即可.
(1)解:根据①②③可得出第4个等式:,
故答案为:.
(2)根据①②③,可得出:
理由如下:
等式左边为: ,
等式右边为:.
∴.
(3)
22.(1)该杨梅园今年六月第一周市区销售了400千克杨梅,园区销售了600千克杨梅
(2)本次活动对市区和园区进行9折销售
(3)a与b的数量关系为
(1)设该杨梅园今年六月第一周市区销售了x千克杨梅,园区销售了y千克杨梅,利用总价=单价数量,结合“该杨梅园今年六月第一周一共销售了1000千克,销售收入12000元”,可列出关于x,y的二元一次方程组,解之即可得出结论;
(2)设本次活动对市区和园区进行m折销售,利用数量=总价单价,结合用3240元购买市区的重量比用2430元购买园区的重量少30千克,可列出关于m的分式方程,解之经检验后,即可得出结论;
(3)根据该杨梅园想第二周市区和园区杨梅的平均售价和第一周的市区和园区平均售价相等,可列出关于a,b的二元一次方程,变形后,即可得出结论.
(1)解:设该杨梅园今年六月第一周市区销售了x千克杨梅,园区销售了y千克杨梅,
根据题意得:,
解得:
答:该杨梅园今年六月第一周市区销售了400千克杨梅,园区销售了600千克杨梅;
(2)设本次活动对市区和园区进行m折销售,
根据题意得:,
解得:,
经检验,是所列方程的解,且符合题意.
答:本次活动对市区和园区进行9折销售;
(3)根据题意得:,
答:a与b的数量关系为
本题考查了二元一次方程组的应用、分式方程的应用以及二元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出分式方程;(3)找准等量关系,正确列出分式方程.
23.(1)见解析;(2);理由见解析;(3)
本题主要考查了利用平行线的性质探求角的度数及关系,根据图准确作出辅助线是解题关键.
(1)过F作,可得,再根据两直线平行内错角相等,可推出,从而得出结果;
(2)与之间的数量关系为,利用平行线的性质即可求证;
(3)过点M作,设,利用平行线的性质即可求证.
证明:(1)如图所示,过F作,
,
,
∴,,
∴,
∵,
∴;
(2)与之间的数量关系为,理由如下:
设,
∴,
∵,
∴,
又∵,
∴,
∴,
∴;
(3)∵,
∴设,
过点M作,
,
,
∴,
根据解析(2)可知,,
∴,
∴,
又∵,
∴.
同课章节目录
