内蒙古巴彦淖尔市多校2025年初中学业水平考试模拟(二)数学试卷(含答案)
文档属性
| 名称 | 内蒙古巴彦淖尔市多校2025年初中学业水平考试模拟(二)数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 985.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 11:32:59 | ||
图片预览




文档简介
2025年中考模拟测试题数学(二)
一、单选题:(每小题3分,共24分)
1.下列为正数的是( )
A. B. C.0 D.
2.下图中,经过折叠能围成如图所示的几何体的是( )
A. B.C. D.
3.估计的值应在( )
A.和之间 B.和之间 C.和之间 D.和之间
4.如图为甲、乙两地2024年12月1日日这5天每天最高气温的折线图,下列说法正确的是( )
A.甲地5天最高气温的中位数是8 B.甲地5天最高气温的众数是6
C.乙地5天最高气温的平均数是6 D.乙地5天最高气温的方差比较小
5.点是正五边形边的中点,连接并延长与延长线交于点,则的度数为( )
A. B. C. D.
6.小孔成像是光在均匀介质中沿直线传播形成的一种物理现象.两千四百多年前,我国学者墨子就在《墨经》中记载了小孔成像实验的做法与成因.如图是小孔成像原理的示意图,长的蜡烛在暗盒中所成的像的长是,蜡烛到小孔O的距离为,则像到小孔O的距离为( )
A. B. C. D.
7.若点,,在反比例函数(m为常数)的图象上,则a,b,c的大小关系是( )
A. B. C. D.
8.如图,在菱形中,,,、分别是、上的动点,连接、,、分别为、的中点,则的最小值是( )
A. B. C.1 D.2
二、填空题:(每小题3分,共12分)
9.的平方根是 .
10.观察下列图形:它们是按一定规律排列的,依此规律,第10个图形共有 个★.
11.如图,在平面直角坐标系中,函数与反比例函数交于、两点,点在轴上,且,若,则 .
12.某校“综合与实践”活动小组的同学要测量两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在两楼之间上方的点O处,点O距地面的高度为,此时观测到楼底部点A处的俯角为,楼上点E处的俯角为.沿水平方向由点O飞行到达点F,此时测得点E处俯角为,其中点A,B,C,D,E,F,O均在同一竖直平面内,则楼与之间的距离的长约为 .(结果精确到.参考数据:,)
三、解答题:(共64分)
13(10分).(1)计算:;
(2) 先化简,再求值:,其中.
14(10分).寒假期间,数学实践活动小组对九年级班全体同学进行了主题为“你最喜欢的电影”的线上调查,每位同学在《哪吒》《唐探》《》《封神》《美国队长》这5部电影中选择部,将调查结果绘制成如下两幅不完整的统计图表.
电影 人数 百分数
(哪吒)
《唐探》
《》
《封神》
《美国队长》
(1)九年级班共有学生________名:________;
(2)若该年级有学生名,请估计最喜欢的电影为《哪吒》的学生人数;
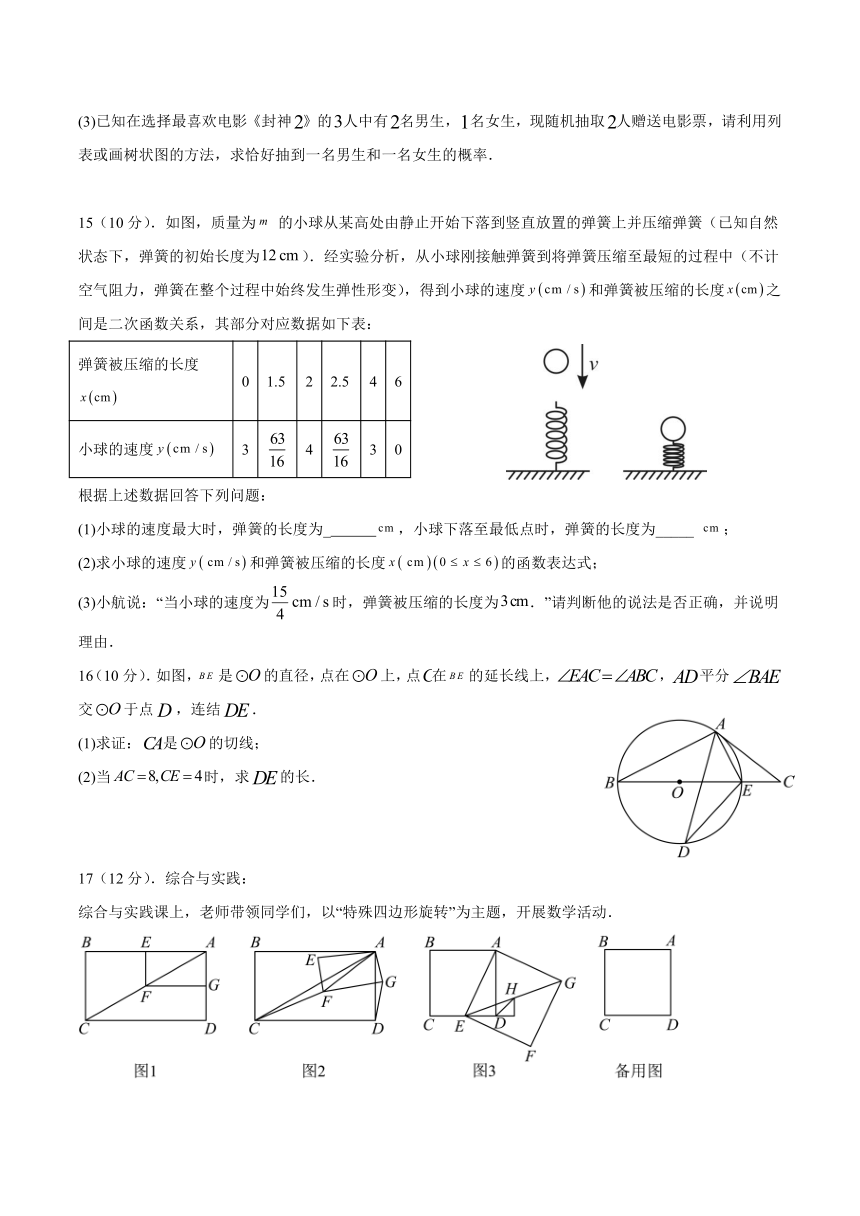
(3)已知在选择最喜欢电影《封神》的人中有名男生,名女生,现随机抽取人赠送电影票,请利用列表或画树状图的方法,求恰好抽到一名男生和一名女生的概率.
15(10分).如图,质量为的小球从某高处由静止开始下落到竖直放置的弹簧上并压缩弹簧(已知自然状态下,弹簧的初始长度为).经实验分析,从小球刚接触弹簧到将弹簧压缩至最短的过程中(不计空气阻力,弹簧在整个过程中始终发生弹性形变),得到小球的速度和弹簧被压缩的长度之间是二次函数关系,其部分对应数据如下表:
弹簧被压缩的长度 0 1.5 2 2.5 4 6
小球的速度 3 4 3 0
根据上述数据回答下列问题:
(1)小球的速度最大时,弹簧的长度为_ ,小球下落至最低点时,弹簧的长度为_____ ;
(2)求小球的速度和弹簧被压缩的长度的函数表达式;
(3)小航说:“当小球的速度为时,弹簧被压缩的长度为.”请判断他的说法是否正确,并说明理由.
16(10分).如图,是的直径,点在上,点在的延长线上,,平分交于点,连结.
(1)求证:是的切线;
(2)当时,求的长.
17(12分).综合与实践:
综合与实践课上,老师带领同学们,以“特殊四边形旋转”为主题,开展数学活动.
【问题发现】
如图,在矩形中,,点在对角线上,过点分别作和的垂线,垂足为,,则四边形为矩形.请问线段与的数量关系为 .
【拓展探究】
如图,将图中的矩形绕点逆时针旋转,记旋转角为,当时,连接,,在旋转的过程中,与的数量关系是否仍然成立?请利用图进行证明.
【解决问题】
如图3,当矩形的边时,点为直线上异于,的一点,以为边作正方形,点为正方形的中心,连接,若,,直接写出的长.
18(12分)0.如图所示,直线与轴交于点,与轴交于点,抛物线经过、两点,与轴的另一个交点为点.
(1)求抛物线的解析式;
(2)点是轴正半轴上一动点,过点作轴于点,交直线于点,交抛物线于点,连结.
①当点在线段上时,若与△ABC相似,求点的坐标;
②若,求出的值.
2025年中学模拟测试题(数学)(二)
参考答案及评分细则
一.选择题(共8小题,每小题3分,共24分)
题号 1 2 3 4 5 6 7 8
答案 D C A C A B B A
二.填空题(共4小题,每小题3分,共12分)
9.+2和-2.10. 24 . 11. . 12. .
三.解答题(共64分)
13.(10分)计算:
解:(1)解:
. ————————4分
. ————————5分
解:(2)
, ————————4分
当时,原式=+3. ————————5分
14(10分)(1),; ————————2分
(2)解:由统计表可知:九年级班喜欢《唐探》的有名,喜欢《》的有名,喜欢《封神》的有名,喜欢《美国队长》的有名,
喜欢《哪吒》的人数是名,
喜欢《哪吒》的人数占全班人数的,
可知该年级有学生名,估计最喜欢的电影为《哪吒》的学生人数为名;
————————6分
(3)解:画树状图如下,
从图中可知共有种等可能的情况,其中恰好抽到一名男生和一名女生的有种,
恰好抽到一名男生和一名女生的概率为. ————————10分
15(10分)(1)10,6; ————————4分
(2)解:由(1)得这个抛物线的对称轴为直线,所对应的,
即函数的顶点坐标为,
∴设函数的表达式为,
∴把代入,
得,
解得,
∴函数的表达式为. ————————7分
(3)解:小航的说法不正确,理由如下:
由(2)得,
由题意得:令,
则,
解得,,
∴当小球的速度为时,弹簧被压缩的长度为或.
小航的说法不正确 ————————10分
16(10分)(1)证明:连接,
是的直径,
,
,
,
,
,
,
,
,
是的半径,
是的切线; ————————5分
(2)解:,,
,
,
,
,
,
连接,
平分,
,
,
,
是的直径,
,
. ————————10分
17(12分); ————————3分
解:仍然成立,
理由如下,
由图可知,,,
,,
由图可知,由旋转可得:,
,,
,,
,; ————————8分
的长为或. ————————12分
18(12分).(1)解:把代入得:,
故,
则的坐标为,
把代入中
得,
解得:,
∴抛物线的解析式的为:. ————————3分
(2)解:①∵,
令,则,解得:或3,
∴,
又∵,
∴,,,
又轴,
,
,
,
∵,
∴,,
,
当,即时,,
解得:(舍去)或,
故;
当,即时,,
解得:(舍去)或,
故,
综上,或. ————————8分
②∵点,,
设直线的解析式为:,
则,解得:,
∴直线的解析式为:,
当点P在x轴上方时,如图,连接,延长交x轴于N,
,
,
,
,
,
,
,
设直线的解析式为:,则,解得:,
∴直线的解析式为:,
,
解得:(舍去);
当点P在x轴下方时,如下图所示:
,
,
,
,
,
,
设直线的解析式为:,则,解得:,
∴直线的解析式为:,
,
解得:(舍去);
综上所述,的值为:或5. ————————12分
一、单选题:(每小题3分,共24分)
1.下列为正数的是( )
A. B. C.0 D.
2.下图中,经过折叠能围成如图所示的几何体的是( )
A. B.C. D.
3.估计的值应在( )
A.和之间 B.和之间 C.和之间 D.和之间
4.如图为甲、乙两地2024年12月1日日这5天每天最高气温的折线图,下列说法正确的是( )
A.甲地5天最高气温的中位数是8 B.甲地5天最高气温的众数是6
C.乙地5天最高气温的平均数是6 D.乙地5天最高气温的方差比较小
5.点是正五边形边的中点,连接并延长与延长线交于点,则的度数为( )
A. B. C. D.
6.小孔成像是光在均匀介质中沿直线传播形成的一种物理现象.两千四百多年前,我国学者墨子就在《墨经》中记载了小孔成像实验的做法与成因.如图是小孔成像原理的示意图,长的蜡烛在暗盒中所成的像的长是,蜡烛到小孔O的距离为,则像到小孔O的距离为( )
A. B. C. D.
7.若点,,在反比例函数(m为常数)的图象上,则a,b,c的大小关系是( )
A. B. C. D.
8.如图,在菱形中,,,、分别是、上的动点,连接、,、分别为、的中点,则的最小值是( )
A. B. C.1 D.2
二、填空题:(每小题3分,共12分)
9.的平方根是 .
10.观察下列图形:它们是按一定规律排列的,依此规律,第10个图形共有 个★.
11.如图,在平面直角坐标系中,函数与反比例函数交于、两点,点在轴上,且,若,则 .
12.某校“综合与实践”活动小组的同学要测量两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在两楼之间上方的点O处,点O距地面的高度为,此时观测到楼底部点A处的俯角为,楼上点E处的俯角为.沿水平方向由点O飞行到达点F,此时测得点E处俯角为,其中点A,B,C,D,E,F,O均在同一竖直平面内,则楼与之间的距离的长约为 .(结果精确到.参考数据:,)
三、解答题:(共64分)
13(10分).(1)计算:;
(2) 先化简,再求值:,其中.
14(10分).寒假期间,数学实践活动小组对九年级班全体同学进行了主题为“你最喜欢的电影”的线上调查,每位同学在《哪吒》《唐探》《》《封神》《美国队长》这5部电影中选择部,将调查结果绘制成如下两幅不完整的统计图表.
电影 人数 百分数
(哪吒)
《唐探》
《》
《封神》
《美国队长》
(1)九年级班共有学生________名:________;
(2)若该年级有学生名,请估计最喜欢的电影为《哪吒》的学生人数;
(3)已知在选择最喜欢电影《封神》的人中有名男生,名女生,现随机抽取人赠送电影票,请利用列表或画树状图的方法,求恰好抽到一名男生和一名女生的概率.
15(10分).如图,质量为的小球从某高处由静止开始下落到竖直放置的弹簧上并压缩弹簧(已知自然状态下,弹簧的初始长度为).经实验分析,从小球刚接触弹簧到将弹簧压缩至最短的过程中(不计空气阻力,弹簧在整个过程中始终发生弹性形变),得到小球的速度和弹簧被压缩的长度之间是二次函数关系,其部分对应数据如下表:
弹簧被压缩的长度 0 1.5 2 2.5 4 6
小球的速度 3 4 3 0
根据上述数据回答下列问题:
(1)小球的速度最大时,弹簧的长度为_ ,小球下落至最低点时,弹簧的长度为_____ ;
(2)求小球的速度和弹簧被压缩的长度的函数表达式;
(3)小航说:“当小球的速度为时,弹簧被压缩的长度为.”请判断他的说法是否正确,并说明理由.
16(10分).如图,是的直径,点在上,点在的延长线上,,平分交于点,连结.
(1)求证:是的切线;
(2)当时,求的长.
17(12分).综合与实践:
综合与实践课上,老师带领同学们,以“特殊四边形旋转”为主题,开展数学活动.
【问题发现】
如图,在矩形中,,点在对角线上,过点分别作和的垂线,垂足为,,则四边形为矩形.请问线段与的数量关系为 .
【拓展探究】
如图,将图中的矩形绕点逆时针旋转,记旋转角为,当时,连接,,在旋转的过程中,与的数量关系是否仍然成立?请利用图进行证明.
【解决问题】
如图3,当矩形的边时,点为直线上异于,的一点,以为边作正方形,点为正方形的中心,连接,若,,直接写出的长.
18(12分)0.如图所示,直线与轴交于点,与轴交于点,抛物线经过、两点,与轴的另一个交点为点.
(1)求抛物线的解析式;
(2)点是轴正半轴上一动点,过点作轴于点,交直线于点,交抛物线于点,连结.
①当点在线段上时,若与△ABC相似,求点的坐标;
②若,求出的值.
2025年中学模拟测试题(数学)(二)
参考答案及评分细则
一.选择题(共8小题,每小题3分,共24分)
题号 1 2 3 4 5 6 7 8
答案 D C A C A B B A
二.填空题(共4小题,每小题3分,共12分)
9.+2和-2.10. 24 . 11. . 12. .
三.解答题(共64分)
13.(10分)计算:
解:(1)解:
. ————————4分
. ————————5分
解:(2)
, ————————4分
当时,原式=+3. ————————5分
14(10分)(1),; ————————2分
(2)解:由统计表可知:九年级班喜欢《唐探》的有名,喜欢《》的有名,喜欢《封神》的有名,喜欢《美国队长》的有名,
喜欢《哪吒》的人数是名,
喜欢《哪吒》的人数占全班人数的,
可知该年级有学生名,估计最喜欢的电影为《哪吒》的学生人数为名;
————————6分
(3)解:画树状图如下,
从图中可知共有种等可能的情况,其中恰好抽到一名男生和一名女生的有种,
恰好抽到一名男生和一名女生的概率为. ————————10分
15(10分)(1)10,6; ————————4分
(2)解:由(1)得这个抛物线的对称轴为直线,所对应的,
即函数的顶点坐标为,
∴设函数的表达式为,
∴把代入,
得,
解得,
∴函数的表达式为. ————————7分
(3)解:小航的说法不正确,理由如下:
由(2)得,
由题意得:令,
则,
解得,,
∴当小球的速度为时,弹簧被压缩的长度为或.
小航的说法不正确 ————————10分
16(10分)(1)证明:连接,
是的直径,
,
,
,
,
,
,
,
,
是的半径,
是的切线; ————————5分
(2)解:,,
,
,
,
,
,
连接,
平分,
,
,
,
是的直径,
,
. ————————10分
17(12分); ————————3分
解:仍然成立,
理由如下,
由图可知,,,
,,
由图可知,由旋转可得:,
,,
,,
,; ————————8分
的长为或. ————————12分
18(12分).(1)解:把代入得:,
故,
则的坐标为,
把代入中
得,
解得:,
∴抛物线的解析式的为:. ————————3分
(2)解:①∵,
令,则,解得:或3,
∴,
又∵,
∴,,,
又轴,
,
,
,
∵,
∴,,
,
当,即时,,
解得:(舍去)或,
故;
当,即时,,
解得:(舍去)或,
故,
综上,或. ————————8分
②∵点,,
设直线的解析式为:,
则,解得:,
∴直线的解析式为:,
当点P在x轴上方时,如图,连接,延长交x轴于N,
,
,
,
,
,
,
,
设直线的解析式为:,则,解得:,
∴直线的解析式为:,
,
解得:(舍去);
当点P在x轴下方时,如下图所示:
,
,
,
,
,
,
设直线的解析式为:,则,解得:,
∴直线的解析式为:,
,
解得:(舍去);
综上所述,的值为:或5. ————————12分
同课章节目录
