第五单元解决问题期末复习练 (含解析) 北京版数学四年级下册
文档属性
| 名称 | 第五单元解决问题期末复习练 (含解析) 北京版数学四年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 155.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 16:12:32 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
第五单元解决问题
学校:___________姓名:___________班级:___________考号:___________
一、选择题
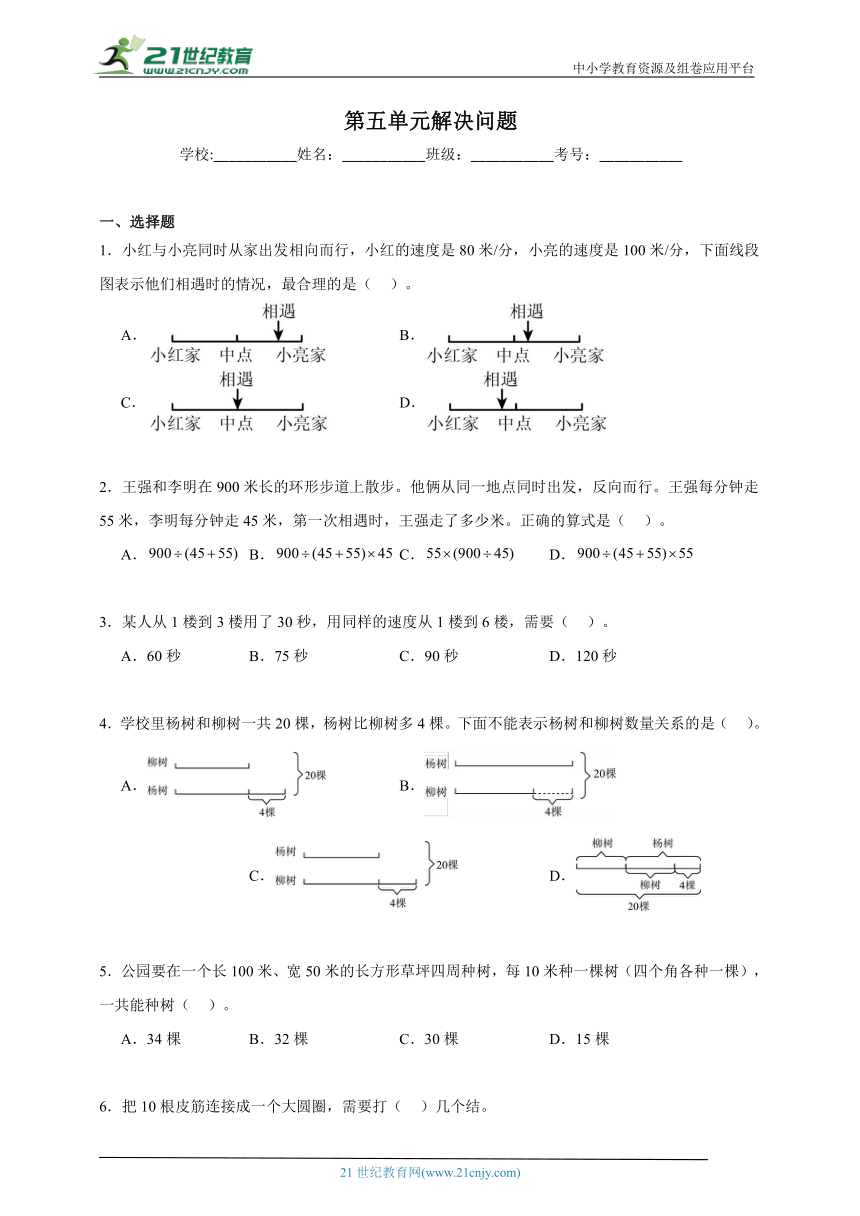
1.小红与小亮同时从家出发相向而行,小红的速度是80米/分,小亮的速度是100米/分,下面线段图表示他们相遇时的情况,最合理的是( )。
A. B.
C. D.
2.王强和李明在900米长的环形步道上散步。他俩从同一地点同时出发,反向而行。王强每分钟走55米,李明每分钟走45米,第一次相遇时,王强走了多少米。正确的算式是( )。
A. B. C. D.
3.某人从1楼到3楼用了30秒,用同样的速度从1楼到6楼,需要( )。
A.60秒 B.75秒 C.90秒 D.120秒
4.学校里杨树和柳树一共20棵,杨树比柳树多4棵。下面不能表示杨树和柳树数量关系的是( )。
A. B. C. D.
5.公园要在一个长100米、宽50米的长方形草坪四周种树,每10米种一棵树(四个角各种一棵),一共能种树( )。
A.34棵 B.32棵 C.30棵 D.15棵
6.把10根皮筋连接成一个大圆圈,需要打( )几个结。
A.9 B.10 C.11 D.12
7.用a表示工作效率,t表示工作时间,c表示工作总量,写出已知工效和工作总量,求工作时间的公式是( )
A.t=c÷a B.a=c÷t C.c=at D.a=ct
8.下列选项中,不能用算式(50+60)×5解答的是( )。
A.亮亮和芳芳从一条道路的两端同时出发,相向而行,经过5分钟相遇。亮亮每分钟走50米,芳芳每分钟走60米,这条道路长多少米?
B.王强和李明在一条环形跑道上从同一地点同时出发,反向而行,王强每分钟走50米,李明每分钟走60米,经过5分钟两人第一次相遇。这条环形跑道长多少米?
C.小刚和小丽同时出发从甲地到乙地。小刚每分钟走60米,小丽每分钟走50米。经过5分钟小刚到达乙地,这时小丽离乙地还有多远?
9.王强和李明在900米长的环形步道上散步。他俩从同一地点同时出发,反向而行。王强每分钟走55米,李明每分钟走45米,第一次相遇时,王强走了多少米。正确的算式是( )。
A. B. C.
10.甲、乙两个人骑电动自行车同时从相距99千米的两地相向而行。甲每小时行20千米,乙每小时行15千米,3小时后两人相距( )千米。
A.105 B.204 C.6 D.84
二、填空题
11.修路队为了测量一条路的长度,先立了一根标杆,然后每隔50米立一根标杆。现在测的长度是500米,所以立了( )根标杆。
12.一列客车和一列货车同时从甲、乙两个城市相对开出,客车每小时行55千米,货车每小时行45千米,经过6.3小时两车相遇。甲、乙两个城市相距 千米。
13.10个同学围成一圈做游戏,每相邻两个同学之间有1个间隔,共有( )个间隔;如果是16个同学这样围成一圈,有( )个间隔。
14.在一条小路的一边安装路灯(两端都要安装),每隔10米安装一盏,一共安装了29盏。这条小路长( )米。
15.伏羲山景区有一棵古树,园林管理处要为它做一个周长为30m的圆形防护栏。如果给这个圆形防护栏每隔2m打一个桩,一共需要打( )个桩。
三、解答题
16.两辆汽车从甲、乙两地同时出发相向而行,一辆每小时行65千米,另一辆每小时行70千米。3小时后两车仍未相遇且相距55千米,甲、乙两地相距多少千米?
17.一条环湖步道全长3000米,小明和小亮同时从环湖步道的某地点出发,沿相反方向步行。
①10分钟后两人能相遇吗?用你喜欢的方式解答。
②请你自己提出一个数学问题并解答。
18.李大爷以相同的速度在乡间布满电话线杆的小路上散步.他从第1根电话线杆走到第12根电话线杆用了22分钟.他如果走36分钟,应走到第几根电话线杆?
19.把一根木料锯成7段需要36分钟,如果将它锯成9段需要多少分钟?
20.学校开展文创作品设计活动,李红设计一个面积为81平方厘米的正方形杯子垫,每条边上要贴4张小贴画(间隔相等,每个角上都贴)。
①共需要多少张小贴画?
②每隔几厘米贴一张小贴画?
《第五单元解决问题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B C C B A C C C
1.D
【分析】因为小红的速度是80米/分,小亮的速度是100米/分,相遇时用的时间相同,根据“路程=速度×时间“,可知小亮走的路程多,小红走的路程少;据此解答。
【详解】根据分析:因为小红与小亮同时从家出发相向而行,到相遇时用的时间相同,而小红的速度是80米/分,小亮的速度是100米/分,100>80,小亮的速度比小红的速度快,根据“路程=速度×时间“,可知小亮走的路程多,小红走的路程少,最合理的是。
故答案为:D
【点睛】本题要注意相遇时两人走的时间是相同的,所以只需要比较速度。
2.D
【分析】王强走的路程等于速度乘时间,故应先算出相遇时走了多少时间,再乘速度即可得到答案。
【详解】相遇时走到时间为:900÷(45+55)
王强走的路程为:900÷(45+55)×55
故答案为:D
【点睛】记住路程等于速度乘时间是解题的关键。
3.B
【分析】分析题意可知从一楼爬到三楼用了30秒,一楼到三楼有2个楼层,所以每个楼层花了30÷2=15秒走完。从六楼到一楼有5个楼层,需要15×5=75秒。据此解答。
【详解】3-1=2(层)
6-1=5(层)
30÷2=15(秒)
15×5=75(秒)
某人从1楼到3楼用了30秒,用同样的速度从1楼到6楼,需要75秒。
故答案为:B
4.C
【分析】根据题干“学校里杨树和柳树一共20棵,杨树比柳树多4棵”,可知柳树的棵数+杨树的棵数=20(棵),杨树的棵数-柳树的棵数=4(棵),根据二者之间的数量关系,来判断哪一种图示不能表示二者的数量关系即可。
【详解】A.根据该图列出的二者的数量关系式为:柳树的棵数+杨树的棵数=20(棵),杨树的棵数-柳树的棵数=4(棵),所以A选项的图可以正确表示杨树和柳树数量关系。
B.根据该图列出的二者的数量关系式为:柳树的棵数+杨树的棵数=20(棵),杨树的棵数-柳树的棵数=4(棵),所以B选项的图可以正确表示杨树和柳树数量关系。
C.根据该图列出的二者的数量关系式为:柳树的棵数+杨树的棵数=20(棵),柳树的棵数-杨树的棵数=4(棵),所以C选项的图不能表示杨树和柳树数量关系。
D. 根据该图列出的二者的数量关系式为:柳树的棵数+杨树的棵数=20(棵),杨树的棵数-柳树的棵数=4(棵),所以D选项的图可以正确表示杨树和柳树数量关系。
故答案为:C
5.C
【分析】根据长方形的长和宽计算长方形的周长,在封闭图形上面植树,间隔数=棵数,根据“间隔数=全长÷间距”即可求出棵数。
【详解】(100+50)×2÷10
=150×2÷10
=300÷10
=30(棵)
一共能种树30棵。
故答案为:C
6.B
【分析】此问题属于封闭图形里植树问题,结的个数=皮筋根数,据此分析。
【详解】根据分析,把10根皮筋连接成一个大圆圈,需要打10个结。
故答案为:B
【点睛】关键是掌握植树问题解题方法,理解棵数和段数之间的关系。
7.A
【分析】数量关系:工作时间=工作总量÷工作效率,用字母表示出这个公式即可。
【详解】根据分析可得:
t=c÷a
故答案为:A
8.C
【分析】先根据每个选项中的问题和条件列出综合算式,然后再选择即可。
速度之和×相遇时间=总路程,(小刚的速度-小丽的速度)×小刚到达乙地用的时间=这时小丽到乙地的距离,依此列式并选择即可。
【详解】A.这条道路长:(50+60)×5=110×5=550(米)。
B.这条环形跑道长:(50+60)×5=110×5=550(米)。
C.这时小丽离乙地还有:(60-50)×5=10×5=50(米)。
故答案为:C
【点睛】熟练掌握普通行程问题和相遇问题的计算方法,是解答此题的关键。
9.C
【分析】根据相遇时间=路程÷速度和,先求出相遇时间,再根据路程=速度×时间,进行解答即可。
【详解】900÷(55+45)×55
=900÷100×55
=9×55
=495(米)
王强走了495米。正确的算式是900÷(55+45)×55。
故答案为:C
【点睛】此题考查了相遇时间、速度和与路程之间的数量关系。
10.C
【分析】
路程=速度×时间,甲骑车速度乘骑行时间,可以算出甲骑行了(20×3)千米;乙骑车速度乘骑行时间,可以算出乙骑行了(15×3)千米;3小时后两人骑行路程和大于两地的距离,则甲、乙的位置关系如图:。两地距离减去甲、乙两人骑行的路程和,可算出3小时后两人相距多少千米。
【详解】20×3=60(千米)
15×3=45(千米)
60+45=105(千米)
105-99=6(千米)
3小时后两人相距6千米。
故答案为:C
11.11
【分析】棵树=段数+1,即用500÷50+1即可解答。
【详解】500÷50+1
=10+1
=11(根)
【点睛】此题主要考查学生对植树问题的理解与应用。
12.630
【分析】客车每小时行55千米,货车每小时行45千米,则两车每小时共行(55+45)千米,又经过6.3小时两车相遇,根据乘法的意义,全程为:(55+45)×6.3千米。
【详解】(55+45)×6.3
=100×6.3
=630(千米)
答:甲、乙两个城市相距630千米。
【点睛】根据相遇问题的数量关系“速度和×时间=路程”列式计算即可。
13. 10 16
【分析】如果小朋友手拉手围成一个圆做游戏,则属于在封闭图形上植树,根据间隔数=植树棵数解答即可。
【详解】把同学的数量看作植树的棵数,依据间隔数=植树棵数可知:
10个同学围成一圈做游戏,每相邻两个同学之间有1个间隔,共有10个间隔;如果是16个同学这样围成一圈,有16个间隔。
【点睛】此题可以归属在植树问题中的封闭图形上植树的情况,只要求出间隔数问题即可解决。
14.280
【分析】由于是两端都要安装路灯,并且植树棵数=间隔数+1,所以用29减去1求出间隔数,然后用间隔数乘间距10米即可求解。
【详解】(29-1)×10
=28×10
=280(米)
所以这条小路长280米。
15.15
【分析】封闭图形的植树问题,打桩数目等于30米中有多少个2米,据此解答即可。
【详解】30÷2=15(个),因此一共需要打15个桩。
【点睛】本题考查植树问题,解答本题的关键是掌握植树问题中的数量关系,注意本题是封闭图形,与一般的植树问题有所区别。
16.460千米
【详解】首先,先求出两辆汽车的速度和:65+70=135(千米);它们行驶了3小时,可以求出一共行驶了多少路程:135×3=405(千米);现在两车依然相距55千米,甲乙两地相距405+55=460(千米)。
(65+70)×3+55=460(千米)
答:甲、乙两地相距460千米。
17.①不能
②小明和小亮需要多少分钟才能相遇?20分钟;(答案不唯一)
【分析】①路程=速度之和×相遇时间,依此计算出10分钟两人走的路程之和,再与3000米比较即可。
②根据题意提出数学问题并解答,符合题意即可,例如我的问题是:小明和小亮需要多少分钟才能相遇?计算时用环湖步道的全长除以两人的速度之和即可。
【详解】①(74+76)×10
=150×10
=1500(米)
1500米<3000米,不能
答:10分钟后两人不能相遇。
②小明和小亮需要多少分钟才能相遇?
3000÷(74+76)
=3000÷150
=20(分钟)
答:小明和小亮需要20分钟才能相遇。
【点睛】熟练掌握相遇问题的计算是解答此题的关键。
18.第19根
【分析】根据“从第1根电话线杆走到第12根电话线杆用了22分钟,”知道走了(12﹣1)个间隔用了22分钟,由此求出走一个间隔的时间;再用36除以走一个间隔的时间即可求出36分钟走的间隔数,再加1就是应走到第几根电话线杆.
【详解】走一个间隔的时间:22÷(12﹣1)=2(分钟),
36分钟走的间隔数:36÷2=18(个),
应走到的电话线杆:18+1=19(根),
答:应走到第19根电话线杆.
19.x=48分钟
【详解】略
20.①12张
②3厘米
【分析】本题考查了正方形的周长和面积。正方形的周长=边长×4,正方形的面积=边长×边长。
①根据题意,先用4乘4,再减去4个角上的4张小贴画,即可求出需要多少张小贴画。
②根据题意,用正方形的周长除以小贴画的张数,即可求出每隔几厘米贴一张小贴画。
【详解】①4×4-4
=16-4
=12(张)
答:共需要12张小贴画。
②9×9=81(平方厘米)
9×4=36(厘米)
36÷12=3(厘米)
答:每隔3厘米贴一张小贴画。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五单元解决问题
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.小红与小亮同时从家出发相向而行,小红的速度是80米/分,小亮的速度是100米/分,下面线段图表示他们相遇时的情况,最合理的是( )。
A. B.
C. D.
2.王强和李明在900米长的环形步道上散步。他俩从同一地点同时出发,反向而行。王强每分钟走55米,李明每分钟走45米,第一次相遇时,王强走了多少米。正确的算式是( )。
A. B. C. D.
3.某人从1楼到3楼用了30秒,用同样的速度从1楼到6楼,需要( )。
A.60秒 B.75秒 C.90秒 D.120秒
4.学校里杨树和柳树一共20棵,杨树比柳树多4棵。下面不能表示杨树和柳树数量关系的是( )。
A. B. C. D.
5.公园要在一个长100米、宽50米的长方形草坪四周种树,每10米种一棵树(四个角各种一棵),一共能种树( )。
A.34棵 B.32棵 C.30棵 D.15棵
6.把10根皮筋连接成一个大圆圈,需要打( )几个结。
A.9 B.10 C.11 D.12
7.用a表示工作效率,t表示工作时间,c表示工作总量,写出已知工效和工作总量,求工作时间的公式是( )
A.t=c÷a B.a=c÷t C.c=at D.a=ct
8.下列选项中,不能用算式(50+60)×5解答的是( )。
A.亮亮和芳芳从一条道路的两端同时出发,相向而行,经过5分钟相遇。亮亮每分钟走50米,芳芳每分钟走60米,这条道路长多少米?
B.王强和李明在一条环形跑道上从同一地点同时出发,反向而行,王强每分钟走50米,李明每分钟走60米,经过5分钟两人第一次相遇。这条环形跑道长多少米?
C.小刚和小丽同时出发从甲地到乙地。小刚每分钟走60米,小丽每分钟走50米。经过5分钟小刚到达乙地,这时小丽离乙地还有多远?
9.王强和李明在900米长的环形步道上散步。他俩从同一地点同时出发,反向而行。王强每分钟走55米,李明每分钟走45米,第一次相遇时,王强走了多少米。正确的算式是( )。
A. B. C.
10.甲、乙两个人骑电动自行车同时从相距99千米的两地相向而行。甲每小时行20千米,乙每小时行15千米,3小时后两人相距( )千米。
A.105 B.204 C.6 D.84
二、填空题
11.修路队为了测量一条路的长度,先立了一根标杆,然后每隔50米立一根标杆。现在测的长度是500米,所以立了( )根标杆。
12.一列客车和一列货车同时从甲、乙两个城市相对开出,客车每小时行55千米,货车每小时行45千米,经过6.3小时两车相遇。甲、乙两个城市相距 千米。
13.10个同学围成一圈做游戏,每相邻两个同学之间有1个间隔,共有( )个间隔;如果是16个同学这样围成一圈,有( )个间隔。
14.在一条小路的一边安装路灯(两端都要安装),每隔10米安装一盏,一共安装了29盏。这条小路长( )米。
15.伏羲山景区有一棵古树,园林管理处要为它做一个周长为30m的圆形防护栏。如果给这个圆形防护栏每隔2m打一个桩,一共需要打( )个桩。
三、解答题
16.两辆汽车从甲、乙两地同时出发相向而行,一辆每小时行65千米,另一辆每小时行70千米。3小时后两车仍未相遇且相距55千米,甲、乙两地相距多少千米?
17.一条环湖步道全长3000米,小明和小亮同时从环湖步道的某地点出发,沿相反方向步行。
①10分钟后两人能相遇吗?用你喜欢的方式解答。
②请你自己提出一个数学问题并解答。
18.李大爷以相同的速度在乡间布满电话线杆的小路上散步.他从第1根电话线杆走到第12根电话线杆用了22分钟.他如果走36分钟,应走到第几根电话线杆?
19.把一根木料锯成7段需要36分钟,如果将它锯成9段需要多少分钟?
20.学校开展文创作品设计活动,李红设计一个面积为81平方厘米的正方形杯子垫,每条边上要贴4张小贴画(间隔相等,每个角上都贴)。
①共需要多少张小贴画?
②每隔几厘米贴一张小贴画?
《第五单元解决问题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B C C B A C C C
1.D
【分析】因为小红的速度是80米/分,小亮的速度是100米/分,相遇时用的时间相同,根据“路程=速度×时间“,可知小亮走的路程多,小红走的路程少;据此解答。
【详解】根据分析:因为小红与小亮同时从家出发相向而行,到相遇时用的时间相同,而小红的速度是80米/分,小亮的速度是100米/分,100>80,小亮的速度比小红的速度快,根据“路程=速度×时间“,可知小亮走的路程多,小红走的路程少,最合理的是。
故答案为:D
【点睛】本题要注意相遇时两人走的时间是相同的,所以只需要比较速度。
2.D
【分析】王强走的路程等于速度乘时间,故应先算出相遇时走了多少时间,再乘速度即可得到答案。
【详解】相遇时走到时间为:900÷(45+55)
王强走的路程为:900÷(45+55)×55
故答案为:D
【点睛】记住路程等于速度乘时间是解题的关键。
3.B
【分析】分析题意可知从一楼爬到三楼用了30秒,一楼到三楼有2个楼层,所以每个楼层花了30÷2=15秒走完。从六楼到一楼有5个楼层,需要15×5=75秒。据此解答。
【详解】3-1=2(层)
6-1=5(层)
30÷2=15(秒)
15×5=75(秒)
某人从1楼到3楼用了30秒,用同样的速度从1楼到6楼,需要75秒。
故答案为:B
4.C
【分析】根据题干“学校里杨树和柳树一共20棵,杨树比柳树多4棵”,可知柳树的棵数+杨树的棵数=20(棵),杨树的棵数-柳树的棵数=4(棵),根据二者之间的数量关系,来判断哪一种图示不能表示二者的数量关系即可。
【详解】A.根据该图列出的二者的数量关系式为:柳树的棵数+杨树的棵数=20(棵),杨树的棵数-柳树的棵数=4(棵),所以A选项的图可以正确表示杨树和柳树数量关系。
B.根据该图列出的二者的数量关系式为:柳树的棵数+杨树的棵数=20(棵),杨树的棵数-柳树的棵数=4(棵),所以B选项的图可以正确表示杨树和柳树数量关系。
C.根据该图列出的二者的数量关系式为:柳树的棵数+杨树的棵数=20(棵),柳树的棵数-杨树的棵数=4(棵),所以C选项的图不能表示杨树和柳树数量关系。
D. 根据该图列出的二者的数量关系式为:柳树的棵数+杨树的棵数=20(棵),杨树的棵数-柳树的棵数=4(棵),所以D选项的图可以正确表示杨树和柳树数量关系。
故答案为:C
5.C
【分析】根据长方形的长和宽计算长方形的周长,在封闭图形上面植树,间隔数=棵数,根据“间隔数=全长÷间距”即可求出棵数。
【详解】(100+50)×2÷10
=150×2÷10
=300÷10
=30(棵)
一共能种树30棵。
故答案为:C
6.B
【分析】此问题属于封闭图形里植树问题,结的个数=皮筋根数,据此分析。
【详解】根据分析,把10根皮筋连接成一个大圆圈,需要打10个结。
故答案为:B
【点睛】关键是掌握植树问题解题方法,理解棵数和段数之间的关系。
7.A
【分析】数量关系:工作时间=工作总量÷工作效率,用字母表示出这个公式即可。
【详解】根据分析可得:
t=c÷a
故答案为:A
8.C
【分析】先根据每个选项中的问题和条件列出综合算式,然后再选择即可。
速度之和×相遇时间=总路程,(小刚的速度-小丽的速度)×小刚到达乙地用的时间=这时小丽到乙地的距离,依此列式并选择即可。
【详解】A.这条道路长:(50+60)×5=110×5=550(米)。
B.这条环形跑道长:(50+60)×5=110×5=550(米)。
C.这时小丽离乙地还有:(60-50)×5=10×5=50(米)。
故答案为:C
【点睛】熟练掌握普通行程问题和相遇问题的计算方法,是解答此题的关键。
9.C
【分析】根据相遇时间=路程÷速度和,先求出相遇时间,再根据路程=速度×时间,进行解答即可。
【详解】900÷(55+45)×55
=900÷100×55
=9×55
=495(米)
王强走了495米。正确的算式是900÷(55+45)×55。
故答案为:C
【点睛】此题考查了相遇时间、速度和与路程之间的数量关系。
10.C
【分析】
路程=速度×时间,甲骑车速度乘骑行时间,可以算出甲骑行了(20×3)千米;乙骑车速度乘骑行时间,可以算出乙骑行了(15×3)千米;3小时后两人骑行路程和大于两地的距离,则甲、乙的位置关系如图:。两地距离减去甲、乙两人骑行的路程和,可算出3小时后两人相距多少千米。
【详解】20×3=60(千米)
15×3=45(千米)
60+45=105(千米)
105-99=6(千米)
3小时后两人相距6千米。
故答案为:C
11.11
【分析】棵树=段数+1,即用500÷50+1即可解答。
【详解】500÷50+1
=10+1
=11(根)
【点睛】此题主要考查学生对植树问题的理解与应用。
12.630
【分析】客车每小时行55千米,货车每小时行45千米,则两车每小时共行(55+45)千米,又经过6.3小时两车相遇,根据乘法的意义,全程为:(55+45)×6.3千米。
【详解】(55+45)×6.3
=100×6.3
=630(千米)
答:甲、乙两个城市相距630千米。
【点睛】根据相遇问题的数量关系“速度和×时间=路程”列式计算即可。
13. 10 16
【分析】如果小朋友手拉手围成一个圆做游戏,则属于在封闭图形上植树,根据间隔数=植树棵数解答即可。
【详解】把同学的数量看作植树的棵数,依据间隔数=植树棵数可知:
10个同学围成一圈做游戏,每相邻两个同学之间有1个间隔,共有10个间隔;如果是16个同学这样围成一圈,有16个间隔。
【点睛】此题可以归属在植树问题中的封闭图形上植树的情况,只要求出间隔数问题即可解决。
14.280
【分析】由于是两端都要安装路灯,并且植树棵数=间隔数+1,所以用29减去1求出间隔数,然后用间隔数乘间距10米即可求解。
【详解】(29-1)×10
=28×10
=280(米)
所以这条小路长280米。
15.15
【分析】封闭图形的植树问题,打桩数目等于30米中有多少个2米,据此解答即可。
【详解】30÷2=15(个),因此一共需要打15个桩。
【点睛】本题考查植树问题,解答本题的关键是掌握植树问题中的数量关系,注意本题是封闭图形,与一般的植树问题有所区别。
16.460千米
【详解】首先,先求出两辆汽车的速度和:65+70=135(千米);它们行驶了3小时,可以求出一共行驶了多少路程:135×3=405(千米);现在两车依然相距55千米,甲乙两地相距405+55=460(千米)。
(65+70)×3+55=460(千米)
答:甲、乙两地相距460千米。
17.①不能
②小明和小亮需要多少分钟才能相遇?20分钟;(答案不唯一)
【分析】①路程=速度之和×相遇时间,依此计算出10分钟两人走的路程之和,再与3000米比较即可。
②根据题意提出数学问题并解答,符合题意即可,例如我的问题是:小明和小亮需要多少分钟才能相遇?计算时用环湖步道的全长除以两人的速度之和即可。
【详解】①(74+76)×10
=150×10
=1500(米)
1500米<3000米,不能
答:10分钟后两人不能相遇。
②小明和小亮需要多少分钟才能相遇?
3000÷(74+76)
=3000÷150
=20(分钟)
答:小明和小亮需要20分钟才能相遇。
【点睛】熟练掌握相遇问题的计算是解答此题的关键。
18.第19根
【分析】根据“从第1根电话线杆走到第12根电话线杆用了22分钟,”知道走了(12﹣1)个间隔用了22分钟,由此求出走一个间隔的时间;再用36除以走一个间隔的时间即可求出36分钟走的间隔数,再加1就是应走到第几根电话线杆.
【详解】走一个间隔的时间:22÷(12﹣1)=2(分钟),
36分钟走的间隔数:36÷2=18(个),
应走到的电话线杆:18+1=19(根),
答:应走到第19根电话线杆.
19.x=48分钟
【详解】略
20.①12张
②3厘米
【分析】本题考查了正方形的周长和面积。正方形的周长=边长×4,正方形的面积=边长×边长。
①根据题意,先用4乘4,再减去4个角上的4张小贴画,即可求出需要多少张小贴画。
②根据题意,用正方形的周长除以小贴画的张数,即可求出每隔几厘米贴一张小贴画。
【详解】①4×4-4
=16-4
=12(张)
答:共需要12张小贴画。
②9×9=81(平方厘米)
9×4=36(厘米)
36÷12=3(厘米)
答:每隔3厘米贴一张小贴画。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
