第六单元数学百花园期末复习练(含解析) 北京版数学五年级下册
文档属性
| 名称 | 第六单元数学百花园期末复习练(含解析) 北京版数学五年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 372.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 16:26:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第六单元数学百花园
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.立体图形是由棱长为1厘米的4个小正方体搭拼成的,它的表面积是( )。
A.18平方厘米 B.15平方厘米 C.9平方厘米
2.++++的结果是( )。
A. B. C.
3.将小正方体按如图方式摆放在地上,6个小正方体有( )个面露在外面。
A.21 B.23 C.27
4.小芳像下图那样计算一组有规律的算式,下一个算式应该是( )。
1×8+1=9 12×8+2=98 123×8+3=987 …
A.123×8+4=988 B.123×9+3=1110
C.1234×8+3=9875 D.1234×8+4=9876
5.把5个相同的正方体纸箱摆放在墙角,下面选项中露在外面的面最多的摆法是( )。
A. B.
C. D.
6.把棱长3cm的正方体表面涂色后,再锯成棱长为1cm的小正方体,那么至少有一个面涂色的有( )块。
A.24 B.25 C.26 D.27
7.观察1×1=1,11×11=121,111×111=12321,那么1111×1111=( )。
A.1234321 B.123454321 C.12345654321
8.剪纸是中国的民间艺术,剪纸的方法很多,下面是一种剪纸方法的图示(如图1,先将纸折叠,然后再剪,展开即得到图案):选项中的四个图案,不能用上述方法剪出的是( )。
A. B. C. D.
9.把5个棱长为1dm的正方体摆在桌面上(如下图4种摆法),露在外面的面积最大的是( )。
A.① B.② C.③ D.④
10.小胖有15颗草莓,吃掉了其中的,小亮有16颗草莓,吃掉了其中的,小丫有20颗草莓,吃掉了其中的,( )剩下的草莓最少。
A.小胖 B.小亮 C.小丫
二、填空题
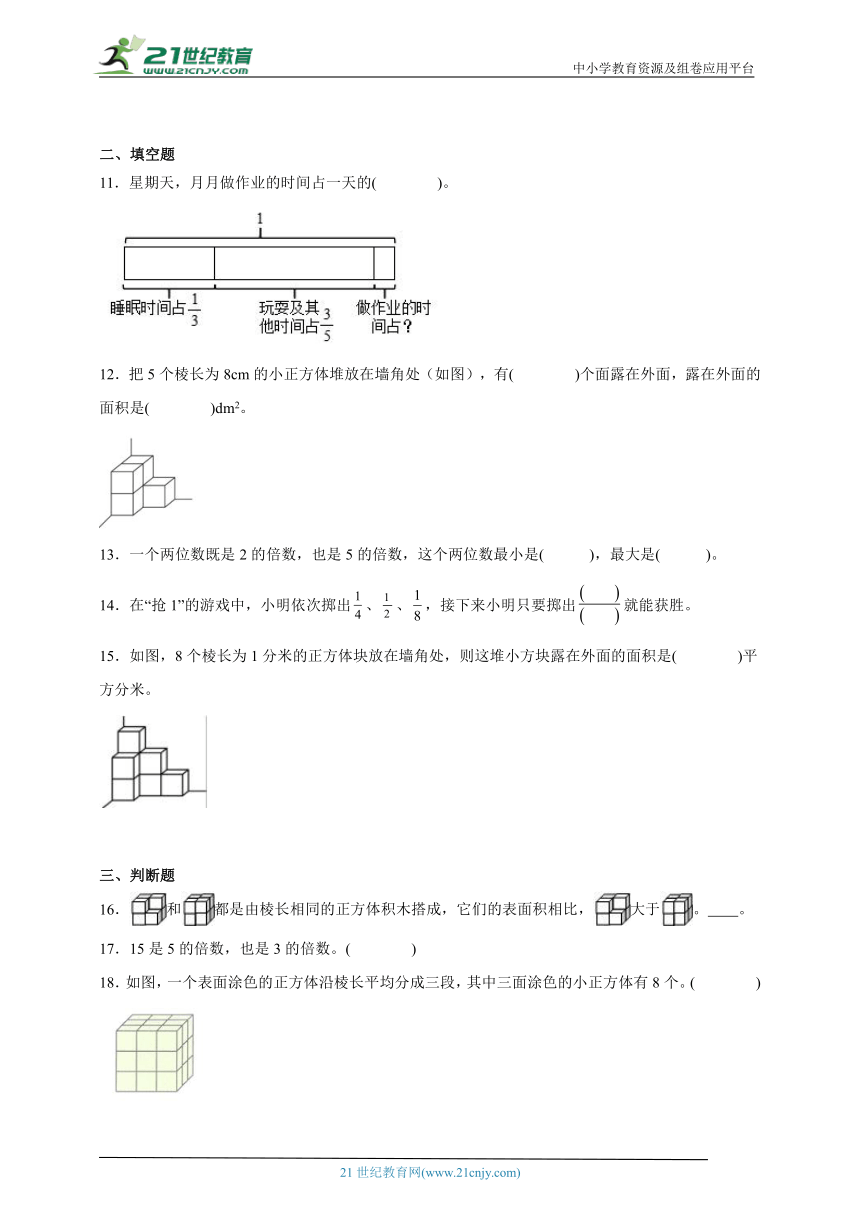
11.星期天,月月做作业的时间占一天的( )。
12.把5个棱长为8cm的小正方体堆放在墙角处(如图),有( )个面露在外面,露在外面的面积是( )dm2。
13.一个两位数既是2的倍数,也是5的倍数,这个两位数最小是( ),最大是( )。
14.在“抢1”的游戏中,小明依次掷出、、,接下来小明只要掷出就能获胜。
15.如图,8个棱长为1分米的正方体块放在墙角处,则这堆小方块露在外面的面积是( )平方分米。
三、判断题
16.和都是由棱长相同的正方体积木搭成,它们的表面积相比,大于。 。
17.15是5的倍数,也是3的倍数。( )
18.如图,一个表面涂色的正方体沿棱长平均分成三段,其中三面涂色的小正方体有8个。( )
四、计算题
19.找规律计算。
20.想一想,算一算。
五、解答题
21.淘气将正方体按下面的方式摆放在桌面上。
(1)填一填。
小正方体的个数 1 2 3 4
露在外面的面/个
(2)你发现了什么规律?
(3)根据你发现的规律,10个这样的小正方体这样摆放,有( )个露在外面的面。
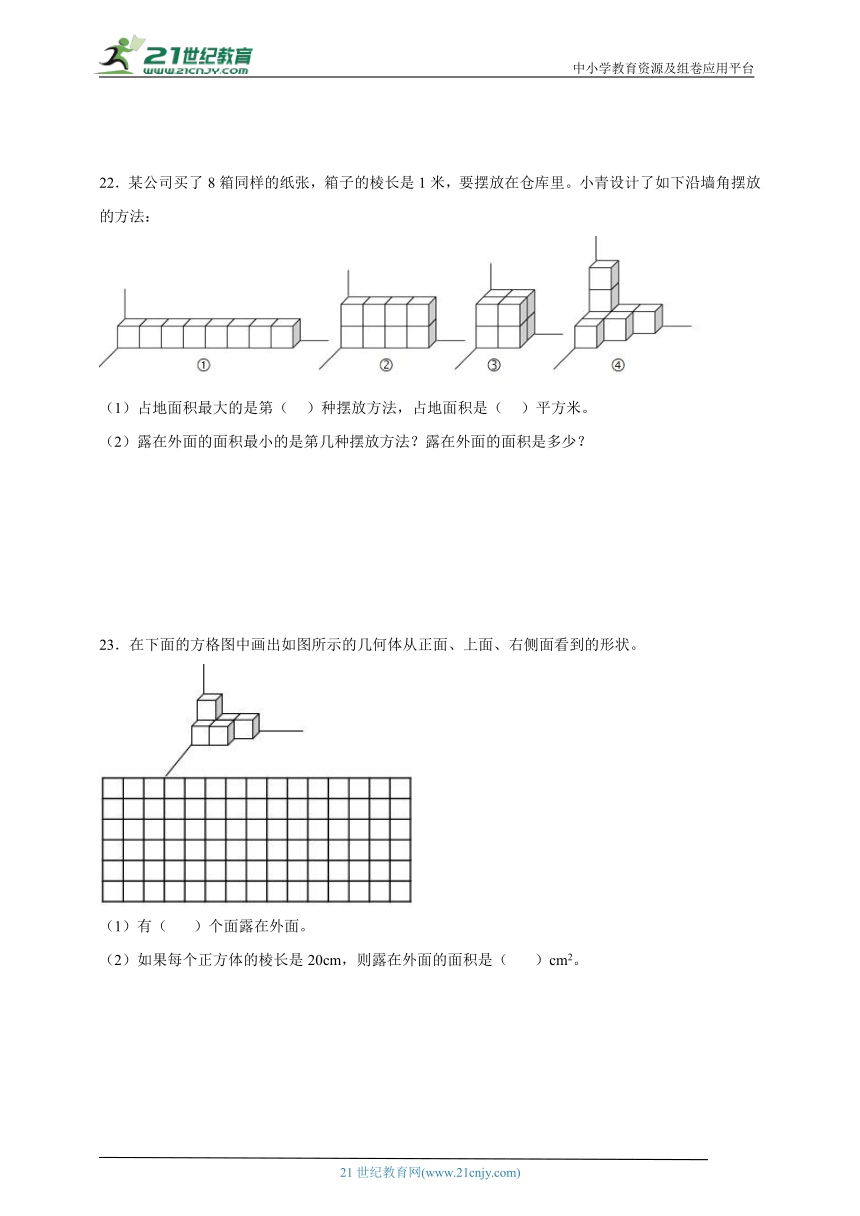
22.某公司买了8箱同样的纸张,箱子的棱长是1米,要摆放在仓库里。小青设计了如下沿墙角摆放的方法:
(1)占地面积最大的是第( )种摆放方法,占地面积是( )平方米。
(2)露在外面的面积最小的是第几种摆放方法?露在外面的面积是多少?
23.在下面的方格图中画出如图所示的几何体从正面、上面、右侧面看到的形状。
(1)有( )个面露在外面。
(2)如果每个正方体的棱长是20cm,则露在外面的面积是( )cm2。
24.如图,是由27个棱长为1cm的小正方体摆成的大正方体.将它放在墙角.
(1)露在外面的面积是多少平方厘米?
(2)如果拿掉涂色的小正方体,露出的面的面积会发生变化吗?变化了多少?
25.将3个棱长为5cm的正方体拼成一个长方体,长方体的表面积与原来的3个正方体的表面积之和相比,会发生变化吗?变化了多少?
《第六单元数学百花园》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C D D C A D C A
1.A
【分析】这个图形左右面、前后面、上下面都是3个正方形的面组成的,因此共有18个正方形的面,每个正方形的面积是1平方厘米,这样就能计算图形的表面积。
【详解】1×1=1(平方厘米)
1×3×6=18(平方厘米)
所以它的表面积是18平方厘米。
故答案为:A
【点睛】本题考查了组合体的表面积,要有一定的空间想象能力。
2.C
【分析】根据=-,=-,以此类推,再计算出++++的和,据此选择。
【详解】++++
=+-+-+-+-
=+-
=-
=-
=
故答案为:C
【点睛】本题考查了加法交换律和结合律,有一定观察和运算能力是解题的关键。
3.C
【分析】第一个立方体由一个小正方体组成,露在外面有5个面,第二个立方体由两个小正方体组成露在外面有(4+5)个面,第三个立方体由三个小正方体组成露在外面有(4+4+5)个面,将它们相加即可。
【详解】5+(4+5)+(4+4+5)
=5+9+13
=14+13
=27(个)
6个小正方体有27个面露在外面。
故答案为:C
【点睛】本题主要考查了正方体的特征。正方体和长方体都有6个面,正方体的6个面都是完全相同的正方形,长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等。
4.D
【分析】观察前面三个式子可知,第一个因数最高位上是1,从左往右,后面数位上的数比相邻的前面数位上的数大1,第二个因数是8,再加上第一个因数个位上的数,算式的结果的位数与第一个因数的位数相同,最高位上是9,从左往右,后面数位上的数比相邻的前面数位上的数小1,后面一个算式第一个因数比前面一个算式第一个因数的位数多1,据此即可解答。
【详解】1×8+1=9
12×8+2=98
123×8+3=987
1234×8+4=9876
故答案为:D
【点睛】找规律,本题主要考查学生的分析推理能力。
5.D
【分析】先计算出每个选项露在外面的面个数,再比较即可。
【详解】A.5+5+1=11(个)
B.3+5+2=10(个)
C.5+4+2=11(个)
D.5+4+2+1=12(个)
12>11>10
选项中露在外面的面最多的摆法是D。
故答案为:D
【点睛】解答本题要注意分类计数,用前面的面、上面的面、左右面的面相加,不要遗漏。
6.C
【详解】3×3×3=27(块)
所以,一共分成27块,没有涂色的在正中心,只有1块,至少有一个面涂色的有26块。
故答案为:C
7.A
【分析】观察这组算式,两个因数相同,均由若干个1组成。积的位数比两个因数的位数和少1。积中间的数字等于一个因数的位数,并向两边分别依次递减1,积的最高位和个位都是1。
【详解】1111×1111=1234321。
故答案为:A
【点睛】根据已知的算式得出前后算式之间的变化关系和规律,然后利用这个变化规律解决问题。
8.D
【详解】略
9.C
【分析】先数清各选项露在外面的面的个数,再根据正方形面积公式:边长×边长,代入数据,求出一个面的面积,再乘露在外面的面的个数,求出露在外面的面的面积,进行比较,即可解答。
【详解】
A. 一共有17个面露在外面;面积:1×1×17=17(dm2);
B. 一共有18个面露在外面;面积:1×1×18=18(dm2);
C.一共有19个面露在外面;面积:1×1×19=19(dm2);
D.一共有17个面露在外面,面积:1×1×17=17(dm2)。
故答案为:C
【点睛】解答本题的关键是数清楚露在外面的面积的个数,进行解答。
10.A
【分析】小胖有15颗草莓,吃掉了其中的,表示把小胖的15颗草莓平均分成3份,吃掉了1份,剩余(3-1)份没吃。
小亮有16颗草莓,吃掉了其中的,表示把小亮的16颗草莓平均分成4份,吃掉了1份,剩余(4-1)份没吃。
小丫有20颗草莓,吃掉了其中的,表示把小丫的20颗草莓平均分成5份,吃掉了2份,剩余(5-2)份没吃。
先用除法分别求出小胖、小亮和小丫每份草莓的颗数,再乘各自剩余草莓的份数,求出剩余草莓的颗数,再进行比较即可。
【详解】根据分析可得:
小胖剩余的草莓数量是:
15÷3×(3-1)
=15÷3×2
=5×2
=10(颗)
小亮剩余的草莓数量是:
16÷4×(4-1)
=16÷4×3
=4×3
=12(颗)
小丫剩余的草莓数量是:
20÷5×(5-2)
=20÷5×3
=4×3
=12(颗)
小胖剩余10颗,小亮剩余12颗,小丫也剩余12颗,所以小胖剩余的最少。
故答案为:A。
【点睛】本题考查的是对分数意义的应用,关键是先求出每份的数量。
11.
【分析】把一天的时间(24小时)看作单位“1”,首先根据减法的意义,用一天的时间“1”减去睡眠时间、玩耍及其他时间所占一天时间的分率,即可求出做作业的时间占一天时间的几分之几。
【详解】1
=
=
=
即做作业的时间占一天的。
【点睛】此题考查的目的是理解分数减法的意义,掌握分数减法的计算法则及应用。
12. 10 6.4
【分析】正面看有3个面露在外面,从上面看有3个面露在外面,从右面看有4个面露在外面,一共有3+3+4个面露在外面;再根据正方形面积公式:面积=边长×边长,代入数据,求出正方体一个面的面积,再乘露在外面面的个数,即可求出露在外面的面的面积。
【详解】3+3+4
=6+4
=10(个)
8×8×10
=64×10
=640(cm2)
640cm2=6.4dm2
把5个棱长为8cm的小正方体堆放在墙角处(如图),有10个面露在外面,露在外面的面积是6.4dm2。
【点睛】解答本题的关键是数清楚露在外面的面的个数,注意单位名数的换算。
13. 10 90
【分析】既是2的倍数,也是5的倍数,说明这个两位数的个位上只能是0。
【详解】个位上是0的最小的两位数是10,最大的两位数是90。
【点睛】掌握2和5倍数的特征是解决此题的关键,5的倍数:个位上是0或5;2的倍数:个位上是0、2、4、6、8;2和5共同的倍数:个位上是0。
14.
【分析】首先根据加法的意义,用加法求出小明已经掷出的三个分数的和,然后根据减法的意义,用1减去已经掷出的三个分数的和即可。
【详解】+
=+
=+
=
1=
接下来小明只要掷出就能获胜。
【点睛】此题考查的目的是理解掌握异分母分数加减法的计算法则,并且能够正确熟练地进行计算。
15.15
【分析】看图,数一数露在外面的有几个面。根据正方形的面积公式,求出1个面的面积,再利用乘法求出露在外面的面的面积和。
【详解】1×1×15=15(平方分米)
则这堆小方块露在外面的面积是15平方分米。
【点睛】本题考查了露在外面的面,数时需细心,避免犯错。
16.×
【详解】根据题干分析可得:
正方体木块,从顶点上挖去一个小正方体后,其实剩下的图形的表面积与原正方体的面表积是相等的,也就是说这两个立体图形的表面积是相等的。
故答案为×。
17.√
【分析】据因数和倍数的意义:如果整数a能被整数b整除(b≠0),a就叫作b的倍数,b就叫作a的因数。
【详解】因为15÷5=3
所以15是5的倍数,也是3的倍数。
故答案为:√
【点睛】此题应根据因数和倍数的意义进行解答。
18.√
【分析】根据题意,三个面均为涂色的是各顶点处的小正方体,正方体有8个顶点,所以一共有8块三面涂色的小正方体。
【详解】由分析可知:
一个表面涂色的正方体沿棱长平均分成三段,其中三面涂色的小正方体有8个。原题干说法正确。
故答案为:√
19.;
;
【分析】根据异分母分数加减法计算前3题,再找出规律,解答最后1题。
【详解】
规律为:分子是1,分母2倍扩大的几个分数相加,和的分母与最后一个分数的分母相同,分子为分母减1。
【点睛】考查了学生分析问题的能力,根据前3题找出规律是解答此题的关键。
20.
【详解】
思路引导
通过观察可以发现这个算式中的每个加数都为单位分数(分子为1),且分母从2开始依次乘2。
画正方形图理解算法如下:
从图中可以看出:如果先借来一个就得到“1”,然后从1中把借来的减去即为所求结果。
正确解答:
=1-
=
(1)画图有助于找到转化的方法。
(2)对于一些复杂的算式,可以根据算式中各数的特点,把原算式转化成简单的算式。
21.(1)5;8;11;14;(2)见详解;(3)32
【分析】(1)观察图形,小正方体的个数为1时,露在外面的面有5个面,小正方体的个数为2时,露在外面的面有(5+3)个面,小正方体的个数为3时,露在外面的面有(5+3×2)个面,小正方体的个数为4时,露在外面的面有(5+3×3)个面,据此完成填空。
(2)通过前面计算出来的数据,我们可以看出随着小正方体的个数的增多,露在外面的面的个数也在增加,具体的变化规律是当前图形露在外面的面的个数比前一个露在外面的面的个数要多3个。
(3)依次类推,小正方体的个数为n时,露在外面的面有个面,当n=10时,把数据代入,即可求出有多少个露在外面的面。
【详解】(1)5+3=8(个)
5+3×2
=5+6
=11(个)
5+3×3
=5+9
=14(个)
填表如下:
小正方体的个数 1 2 3 4
露在外面的面/个 5 8 11 14
(2)答:我发现当前图形露在外面的面的个数比前一个露在外面的面的个数要多3个。
(3)小正方体的个数为n时,露在外面的面有个面,
当n=10时,
=
=
=5+27
=32(个)
【点睛】此题的解题关键是利用数与形的结合,通过观察图形,把图形中变化的规律转化成数字,多多练习,培养数感。
22.(1)①;8;
(2)第③种;12平方米
【分析】(1)从上面看,小正方形数量最多的占地面积最大;根据棱长1米的正方形面积是1平方米,1个正方形的面积×从上面看到的小正方形个数=占地面积。
(2)分别从上面、前面和右面观察这四种摆放方法,观察出从上面、前面和右面看到的小正方形的个数,再确定这四种摆放方法分别有几个小正方形露在外面,比较,再求出面积即可。
【详解】(1)①从上面看有8个小正方形;②从上面看有4个小正方形;③从上面看有4个小正方形;④从上面看有6个小正方形。
1×8=8(平方米)
占地面积最大的是第①种摆放方法,占地面积是8平方米。
(2)①从上面看有8个小正方形,从前面看有8个小正方形,从右面看有1个小正方形,露在外面的共17个小正方形;②从上面看有4个小正方形,从前面看有8个小正方形,从右面看有2个小正方形,露在外面的共14个小正方形;③从上面、前面和右面看都是4个小正方形,露在外面的共12个小正方形;④从上面看有6个小正方形,从前面看有5个小正方形,从右面看有5个小正方形,露在外面的共16个小正方形。
12<14<16<17
1×12=12(平方米)
答:露在外面的面积最小的是第③种摆放方法,露在外面的面积是12平方米。
【点睛】关键是具有一定的空间想象能力,能想象出从不同方向观察到不同摆法的样子。
23.图见详解;
(1)12;(2)4800
【分析】分别从正面、上面、右面观察几何体,画出三视图。
(1)根据所画图形,数出各个方向看到的小正方形个数,相加即可;
(2)小正方形的面积×露在外面的个数,即可。
【详解】画图如下:
(1)从上面看5个,从正面看4个,从右面看3个,则一共有5+4+3=12(个)面露在外面。
(2)20×20×12
=400×12
=4800(平方厘米)
则露在外面的面积是4800cm2。
【点睛】此题主要考查露在外面的面,数面的时候要按一定的顺序来数。
24.(1)27平方厘米 (2)露出的面的面积会变大,增加了2平方厘米
【详解】(1)3×3×3=27(平方厘米)
答:露在外面的面是27平方厘米.
(2)如果拿掉涂色的小正方体,露出的面的面积会变大,增加了1×1×2=2(平方厘米)
答:如果拿掉涂色的小正方体,露出的面的面积会变大,增加了2平方厘米.
25.面积减少了,减少了100cm2
【分析】观察可知,将3个棱长为5cm的正方体拼成一个长方体,长方体的表面积与原来的3个正方体的表面积之和相比,减少了4个接触面的面积,用一个面的面积×4=减少的面积,据此解答。
【详解】5×5×4
=25×4
=100(cm2)
答:长方体的表面积与原来的3个正方体的表面积之和相比,面积减少了,减少了100cm2。
【点睛】本题考查了立体图形的切拼,每拼一次减少两个面。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六单元数学百花园
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.立体图形是由棱长为1厘米的4个小正方体搭拼成的,它的表面积是( )。
A.18平方厘米 B.15平方厘米 C.9平方厘米
2.++++的结果是( )。
A. B. C.
3.将小正方体按如图方式摆放在地上,6个小正方体有( )个面露在外面。
A.21 B.23 C.27
4.小芳像下图那样计算一组有规律的算式,下一个算式应该是( )。
1×8+1=9 12×8+2=98 123×8+3=987 …
A.123×8+4=988 B.123×9+3=1110
C.1234×8+3=9875 D.1234×8+4=9876
5.把5个相同的正方体纸箱摆放在墙角,下面选项中露在外面的面最多的摆法是( )。
A. B.
C. D.
6.把棱长3cm的正方体表面涂色后,再锯成棱长为1cm的小正方体,那么至少有一个面涂色的有( )块。
A.24 B.25 C.26 D.27
7.观察1×1=1,11×11=121,111×111=12321,那么1111×1111=( )。
A.1234321 B.123454321 C.12345654321
8.剪纸是中国的民间艺术,剪纸的方法很多,下面是一种剪纸方法的图示(如图1,先将纸折叠,然后再剪,展开即得到图案):选项中的四个图案,不能用上述方法剪出的是( )。
A. B. C. D.
9.把5个棱长为1dm的正方体摆在桌面上(如下图4种摆法),露在外面的面积最大的是( )。
A.① B.② C.③ D.④
10.小胖有15颗草莓,吃掉了其中的,小亮有16颗草莓,吃掉了其中的,小丫有20颗草莓,吃掉了其中的,( )剩下的草莓最少。
A.小胖 B.小亮 C.小丫
二、填空题
11.星期天,月月做作业的时间占一天的( )。
12.把5个棱长为8cm的小正方体堆放在墙角处(如图),有( )个面露在外面,露在外面的面积是( )dm2。
13.一个两位数既是2的倍数,也是5的倍数,这个两位数最小是( ),最大是( )。
14.在“抢1”的游戏中,小明依次掷出、、,接下来小明只要掷出就能获胜。
15.如图,8个棱长为1分米的正方体块放在墙角处,则这堆小方块露在外面的面积是( )平方分米。
三、判断题
16.和都是由棱长相同的正方体积木搭成,它们的表面积相比,大于。 。
17.15是5的倍数,也是3的倍数。( )
18.如图,一个表面涂色的正方体沿棱长平均分成三段,其中三面涂色的小正方体有8个。( )
四、计算题
19.找规律计算。
20.想一想,算一算。
五、解答题
21.淘气将正方体按下面的方式摆放在桌面上。
(1)填一填。
小正方体的个数 1 2 3 4
露在外面的面/个
(2)你发现了什么规律?
(3)根据你发现的规律,10个这样的小正方体这样摆放,有( )个露在外面的面。
22.某公司买了8箱同样的纸张,箱子的棱长是1米,要摆放在仓库里。小青设计了如下沿墙角摆放的方法:
(1)占地面积最大的是第( )种摆放方法,占地面积是( )平方米。
(2)露在外面的面积最小的是第几种摆放方法?露在外面的面积是多少?
23.在下面的方格图中画出如图所示的几何体从正面、上面、右侧面看到的形状。
(1)有( )个面露在外面。
(2)如果每个正方体的棱长是20cm,则露在外面的面积是( )cm2。
24.如图,是由27个棱长为1cm的小正方体摆成的大正方体.将它放在墙角.
(1)露在外面的面积是多少平方厘米?
(2)如果拿掉涂色的小正方体,露出的面的面积会发生变化吗?变化了多少?
25.将3个棱长为5cm的正方体拼成一个长方体,长方体的表面积与原来的3个正方体的表面积之和相比,会发生变化吗?变化了多少?
《第六单元数学百花园》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C D D C A D C A
1.A
【分析】这个图形左右面、前后面、上下面都是3个正方形的面组成的,因此共有18个正方形的面,每个正方形的面积是1平方厘米,这样就能计算图形的表面积。
【详解】1×1=1(平方厘米)
1×3×6=18(平方厘米)
所以它的表面积是18平方厘米。
故答案为:A
【点睛】本题考查了组合体的表面积,要有一定的空间想象能力。
2.C
【分析】根据=-,=-,以此类推,再计算出++++的和,据此选择。
【详解】++++
=+-+-+-+-
=+-
=-
=-
=
故答案为:C
【点睛】本题考查了加法交换律和结合律,有一定观察和运算能力是解题的关键。
3.C
【分析】第一个立方体由一个小正方体组成,露在外面有5个面,第二个立方体由两个小正方体组成露在外面有(4+5)个面,第三个立方体由三个小正方体组成露在外面有(4+4+5)个面,将它们相加即可。
【详解】5+(4+5)+(4+4+5)
=5+9+13
=14+13
=27(个)
6个小正方体有27个面露在外面。
故答案为:C
【点睛】本题主要考查了正方体的特征。正方体和长方体都有6个面,正方体的6个面都是完全相同的正方形,长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等。
4.D
【分析】观察前面三个式子可知,第一个因数最高位上是1,从左往右,后面数位上的数比相邻的前面数位上的数大1,第二个因数是8,再加上第一个因数个位上的数,算式的结果的位数与第一个因数的位数相同,最高位上是9,从左往右,后面数位上的数比相邻的前面数位上的数小1,后面一个算式第一个因数比前面一个算式第一个因数的位数多1,据此即可解答。
【详解】1×8+1=9
12×8+2=98
123×8+3=987
1234×8+4=9876
故答案为:D
【点睛】找规律,本题主要考查学生的分析推理能力。
5.D
【分析】先计算出每个选项露在外面的面个数,再比较即可。
【详解】A.5+5+1=11(个)
B.3+5+2=10(个)
C.5+4+2=11(个)
D.5+4+2+1=12(个)
12>11>10
选项中露在外面的面最多的摆法是D。
故答案为:D
【点睛】解答本题要注意分类计数,用前面的面、上面的面、左右面的面相加,不要遗漏。
6.C
【详解】3×3×3=27(块)
所以,一共分成27块,没有涂色的在正中心,只有1块,至少有一个面涂色的有26块。
故答案为:C
7.A
【分析】观察这组算式,两个因数相同,均由若干个1组成。积的位数比两个因数的位数和少1。积中间的数字等于一个因数的位数,并向两边分别依次递减1,积的最高位和个位都是1。
【详解】1111×1111=1234321。
故答案为:A
【点睛】根据已知的算式得出前后算式之间的变化关系和规律,然后利用这个变化规律解决问题。
8.D
【详解】略
9.C
【分析】先数清各选项露在外面的面的个数,再根据正方形面积公式:边长×边长,代入数据,求出一个面的面积,再乘露在外面的面的个数,求出露在外面的面的面积,进行比较,即可解答。
【详解】
A. 一共有17个面露在外面;面积:1×1×17=17(dm2);
B. 一共有18个面露在外面;面积:1×1×18=18(dm2);
C.一共有19个面露在外面;面积:1×1×19=19(dm2);
D.一共有17个面露在外面,面积:1×1×17=17(dm2)。
故答案为:C
【点睛】解答本题的关键是数清楚露在外面的面积的个数,进行解答。
10.A
【分析】小胖有15颗草莓,吃掉了其中的,表示把小胖的15颗草莓平均分成3份,吃掉了1份,剩余(3-1)份没吃。
小亮有16颗草莓,吃掉了其中的,表示把小亮的16颗草莓平均分成4份,吃掉了1份,剩余(4-1)份没吃。
小丫有20颗草莓,吃掉了其中的,表示把小丫的20颗草莓平均分成5份,吃掉了2份,剩余(5-2)份没吃。
先用除法分别求出小胖、小亮和小丫每份草莓的颗数,再乘各自剩余草莓的份数,求出剩余草莓的颗数,再进行比较即可。
【详解】根据分析可得:
小胖剩余的草莓数量是:
15÷3×(3-1)
=15÷3×2
=5×2
=10(颗)
小亮剩余的草莓数量是:
16÷4×(4-1)
=16÷4×3
=4×3
=12(颗)
小丫剩余的草莓数量是:
20÷5×(5-2)
=20÷5×3
=4×3
=12(颗)
小胖剩余10颗,小亮剩余12颗,小丫也剩余12颗,所以小胖剩余的最少。
故答案为:A。
【点睛】本题考查的是对分数意义的应用,关键是先求出每份的数量。
11.
【分析】把一天的时间(24小时)看作单位“1”,首先根据减法的意义,用一天的时间“1”减去睡眠时间、玩耍及其他时间所占一天时间的分率,即可求出做作业的时间占一天时间的几分之几。
【详解】1
=
=
=
即做作业的时间占一天的。
【点睛】此题考查的目的是理解分数减法的意义,掌握分数减法的计算法则及应用。
12. 10 6.4
【分析】正面看有3个面露在外面,从上面看有3个面露在外面,从右面看有4个面露在外面,一共有3+3+4个面露在外面;再根据正方形面积公式:面积=边长×边长,代入数据,求出正方体一个面的面积,再乘露在外面面的个数,即可求出露在外面的面的面积。
【详解】3+3+4
=6+4
=10(个)
8×8×10
=64×10
=640(cm2)
640cm2=6.4dm2
把5个棱长为8cm的小正方体堆放在墙角处(如图),有10个面露在外面,露在外面的面积是6.4dm2。
【点睛】解答本题的关键是数清楚露在外面的面的个数,注意单位名数的换算。
13. 10 90
【分析】既是2的倍数,也是5的倍数,说明这个两位数的个位上只能是0。
【详解】个位上是0的最小的两位数是10,最大的两位数是90。
【点睛】掌握2和5倍数的特征是解决此题的关键,5的倍数:个位上是0或5;2的倍数:个位上是0、2、4、6、8;2和5共同的倍数:个位上是0。
14.
【分析】首先根据加法的意义,用加法求出小明已经掷出的三个分数的和,然后根据减法的意义,用1减去已经掷出的三个分数的和即可。
【详解】+
=+
=+
=
1=
接下来小明只要掷出就能获胜。
【点睛】此题考查的目的是理解掌握异分母分数加减法的计算法则,并且能够正确熟练地进行计算。
15.15
【分析】看图,数一数露在外面的有几个面。根据正方形的面积公式,求出1个面的面积,再利用乘法求出露在外面的面的面积和。
【详解】1×1×15=15(平方分米)
则这堆小方块露在外面的面积是15平方分米。
【点睛】本题考查了露在外面的面,数时需细心,避免犯错。
16.×
【详解】根据题干分析可得:
正方体木块,从顶点上挖去一个小正方体后,其实剩下的图形的表面积与原正方体的面表积是相等的,也就是说这两个立体图形的表面积是相等的。
故答案为×。
17.√
【分析】据因数和倍数的意义:如果整数a能被整数b整除(b≠0),a就叫作b的倍数,b就叫作a的因数。
【详解】因为15÷5=3
所以15是5的倍数,也是3的倍数。
故答案为:√
【点睛】此题应根据因数和倍数的意义进行解答。
18.√
【分析】根据题意,三个面均为涂色的是各顶点处的小正方体,正方体有8个顶点,所以一共有8块三面涂色的小正方体。
【详解】由分析可知:
一个表面涂色的正方体沿棱长平均分成三段,其中三面涂色的小正方体有8个。原题干说法正确。
故答案为:√
19.;
;
【分析】根据异分母分数加减法计算前3题,再找出规律,解答最后1题。
【详解】
规律为:分子是1,分母2倍扩大的几个分数相加,和的分母与最后一个分数的分母相同,分子为分母减1。
【点睛】考查了学生分析问题的能力,根据前3题找出规律是解答此题的关键。
20.
【详解】
思路引导
通过观察可以发现这个算式中的每个加数都为单位分数(分子为1),且分母从2开始依次乘2。
画正方形图理解算法如下:
从图中可以看出:如果先借来一个就得到“1”,然后从1中把借来的减去即为所求结果。
正确解答:
=1-
=
(1)画图有助于找到转化的方法。
(2)对于一些复杂的算式,可以根据算式中各数的特点,把原算式转化成简单的算式。
21.(1)5;8;11;14;(2)见详解;(3)32
【分析】(1)观察图形,小正方体的个数为1时,露在外面的面有5个面,小正方体的个数为2时,露在外面的面有(5+3)个面,小正方体的个数为3时,露在外面的面有(5+3×2)个面,小正方体的个数为4时,露在外面的面有(5+3×3)个面,据此完成填空。
(2)通过前面计算出来的数据,我们可以看出随着小正方体的个数的增多,露在外面的面的个数也在增加,具体的变化规律是当前图形露在外面的面的个数比前一个露在外面的面的个数要多3个。
(3)依次类推,小正方体的个数为n时,露在外面的面有个面,当n=10时,把数据代入,即可求出有多少个露在外面的面。
【详解】(1)5+3=8(个)
5+3×2
=5+6
=11(个)
5+3×3
=5+9
=14(个)
填表如下:
小正方体的个数 1 2 3 4
露在外面的面/个 5 8 11 14
(2)答:我发现当前图形露在外面的面的个数比前一个露在外面的面的个数要多3个。
(3)小正方体的个数为n时,露在外面的面有个面,
当n=10时,
=
=
=5+27
=32(个)
【点睛】此题的解题关键是利用数与形的结合,通过观察图形,把图形中变化的规律转化成数字,多多练习,培养数感。
22.(1)①;8;
(2)第③种;12平方米
【分析】(1)从上面看,小正方形数量最多的占地面积最大;根据棱长1米的正方形面积是1平方米,1个正方形的面积×从上面看到的小正方形个数=占地面积。
(2)分别从上面、前面和右面观察这四种摆放方法,观察出从上面、前面和右面看到的小正方形的个数,再确定这四种摆放方法分别有几个小正方形露在外面,比较,再求出面积即可。
【详解】(1)①从上面看有8个小正方形;②从上面看有4个小正方形;③从上面看有4个小正方形;④从上面看有6个小正方形。
1×8=8(平方米)
占地面积最大的是第①种摆放方法,占地面积是8平方米。
(2)①从上面看有8个小正方形,从前面看有8个小正方形,从右面看有1个小正方形,露在外面的共17个小正方形;②从上面看有4个小正方形,从前面看有8个小正方形,从右面看有2个小正方形,露在外面的共14个小正方形;③从上面、前面和右面看都是4个小正方形,露在外面的共12个小正方形;④从上面看有6个小正方形,从前面看有5个小正方形,从右面看有5个小正方形,露在外面的共16个小正方形。
12<14<16<17
1×12=12(平方米)
答:露在外面的面积最小的是第③种摆放方法,露在外面的面积是12平方米。
【点睛】关键是具有一定的空间想象能力,能想象出从不同方向观察到不同摆法的样子。
23.图见详解;
(1)12;(2)4800
【分析】分别从正面、上面、右面观察几何体,画出三视图。
(1)根据所画图形,数出各个方向看到的小正方形个数,相加即可;
(2)小正方形的面积×露在外面的个数,即可。
【详解】画图如下:
(1)从上面看5个,从正面看4个,从右面看3个,则一共有5+4+3=12(个)面露在外面。
(2)20×20×12
=400×12
=4800(平方厘米)
则露在外面的面积是4800cm2。
【点睛】此题主要考查露在外面的面,数面的时候要按一定的顺序来数。
24.(1)27平方厘米 (2)露出的面的面积会变大,增加了2平方厘米
【详解】(1)3×3×3=27(平方厘米)
答:露在外面的面是27平方厘米.
(2)如果拿掉涂色的小正方体,露出的面的面积会变大,增加了1×1×2=2(平方厘米)
答:如果拿掉涂色的小正方体,露出的面的面积会变大,增加了2平方厘米.
25.面积减少了,减少了100cm2
【分析】观察可知,将3个棱长为5cm的正方体拼成一个长方体,长方体的表面积与原来的3个正方体的表面积之和相比,减少了4个接触面的面积,用一个面的面积×4=减少的面积,据此解答。
【详解】5×5×4
=25×4
=100(cm2)
答:长方体的表面积与原来的3个正方体的表面积之和相比,面积减少了,减少了100cm2。
【点睛】本题考查了立体图形的切拼,每拼一次减少两个面。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
