第二十四章勾股定理期末单元复习题(含解析)
文档属性
| 名称 | 第二十四章勾股定理期末单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1009.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 22:38:26 | ||
图片预览

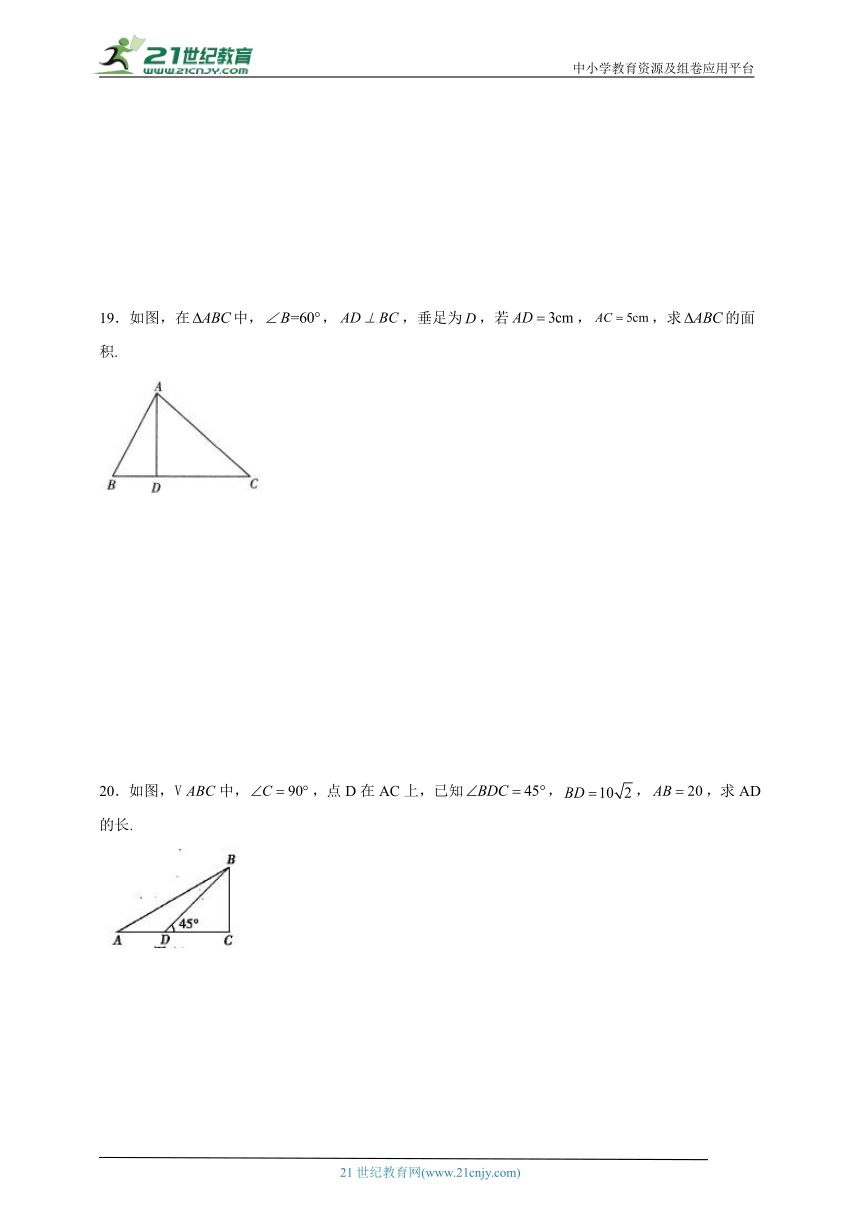
文档简介
中小学教育资源及组卷应用平台
第二十四章勾股定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,我国古代的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形的面积为1,大正方形的面积为13,则直角三角形较短的直角边a与较长的直角边b的比的值是( )
A. B. C. D.
2.如图,长方形中,,,将此长方形折叠,使点D与点B重合,折痕为,则的面积为( )
A. B. C. D.
3.若一个三角形的三边长的平方分别为:32,42,x2则此三角形是直角三角形的x2的值是( )
A.4 B.52 C.7 D.52或7
4.一个三角形的三条边长分别为:5,12,13,把这个三角形的三条边长同时扩大到原来的2倍,那么这个三角形的形状为( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定形状
5.已知直角三角形的两条直角边的长分别是1,,则斜边长为( )
A.1 B. C.2 D.3
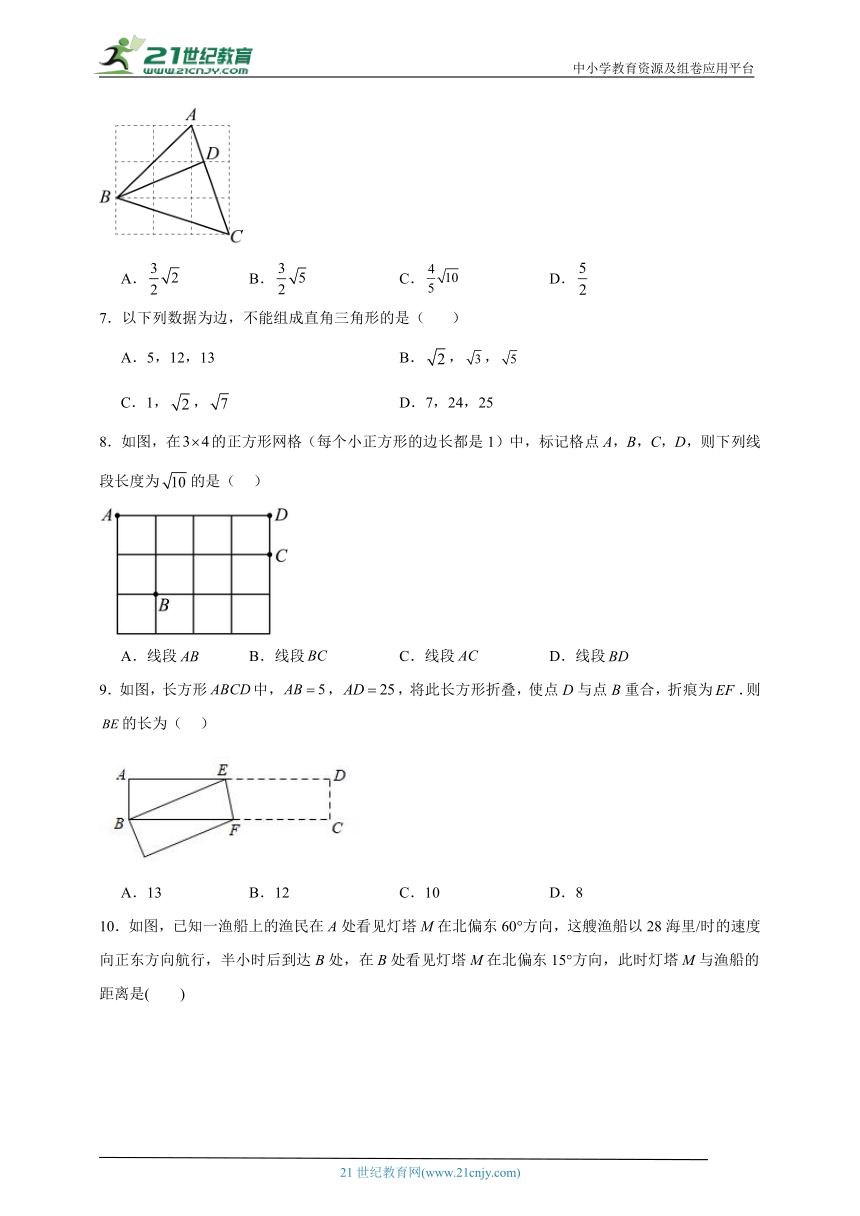
6.如图,在的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若是的高,则的长为()
A. B. C. D.
7.以下列数据为边,不能组成直角三角形的是( )
A.5,12,13 B.,,
C.1,, D.7,24,25
8.如图,在的正方形网格(每个小正方形的边长都是1)中,标记格点A,B,C,D,则下列线段长度为的是( )
A.线段 B.线段 C.线段 D.线段
9.如图,长方形中,,,将此长方形折叠,使点D与点B重合,折痕为.则的长为( )
A.13 B.12 C.10 D.8
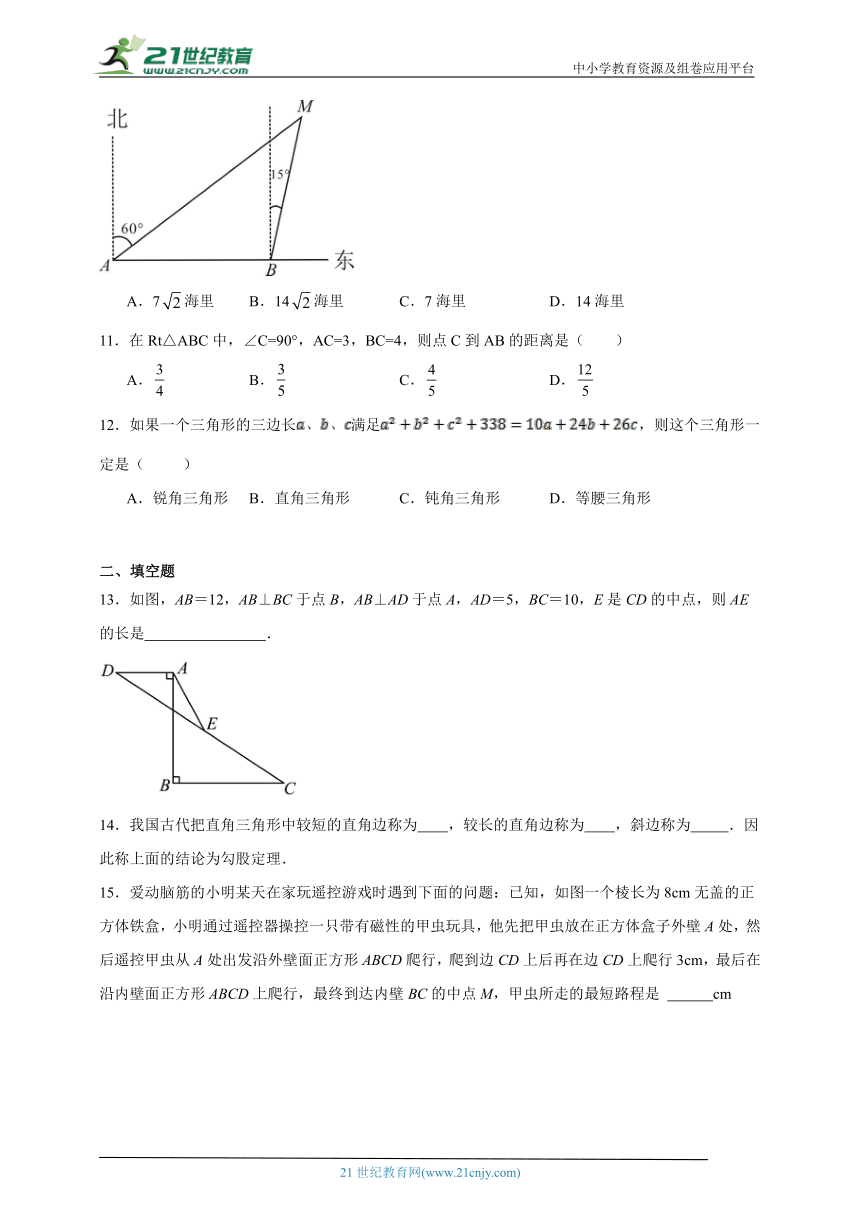
10.如图,已知一渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28海里/时的速度向正东方向航行,半小时后到达B处,在B处看见灯塔M在北偏东15°方向,此时灯塔M与渔船的距离是( )
A.7海里 B.14海里 C.7海里 D.14海里
11.在Rt△ABC中,∠C=90°,AC=3,BC=4,则点C到AB的距离是( )
A. B. C. D.
12.如果一个三角形的三边长满足,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
二、填空题
13.如图,AB=12,AB⊥BC于点B,AB⊥AD于点A,AD=5,BC=10,E是CD的中点,则AE的长是 .
14.我国古代把直角三角形中较短的直角边称为 ,较长的直角边称为 ,斜边称为 .因此称上面的结论为勾股定理.
15.爱动脑筋的小明某天在家玩遥控游戏时遇到下面的问题:已知,如图一个棱长为8cm无盖的正方体铁盒,小明通过遥控器操控一只带有磁性的甲虫玩具,他先把甲虫放在正方体盒子外壁A处,然后遥控甲虫从A处出发沿外壁面正方形ABCD爬行,爬到边CD上后再在边CD上爬行3cm,最后在沿内壁面正方形ABCD上爬行,最终到达内壁BC的中点M,甲虫所走的最短路程是 cm
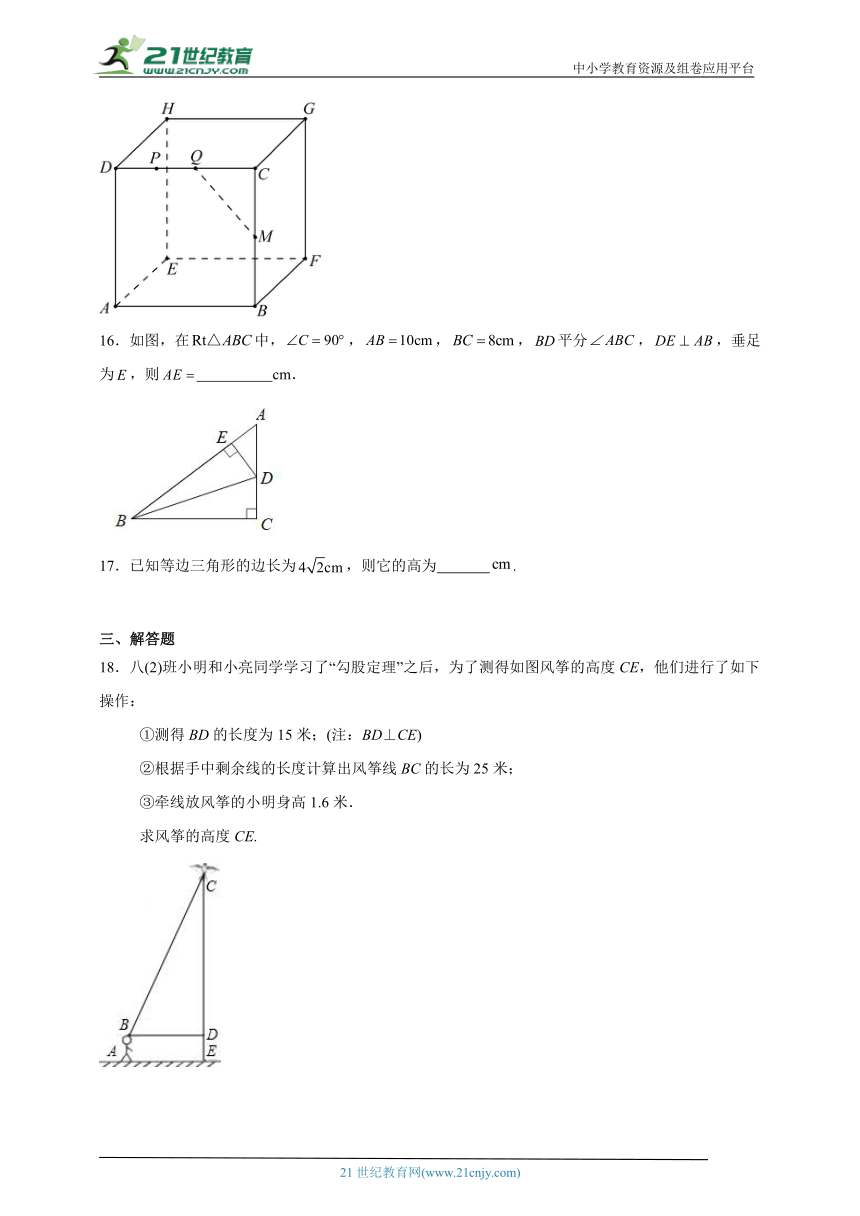
16.如图,在中,,,,平分,,垂足为,则 cm.
17.已知等边三角形的边长为,则它的高为 .
三、解答题
18.八(2)班小明和小亮同学学习了“勾股定理”之后,为了测得如图风筝的高度CE,他们进行了如下操作:
①测得BD的长度为15米;(注:BD⊥CE)
②根据手中剩余线的长度计算出风筝线BC的长为25米;
③牵线放风筝的小明身高1.6米.
求风筝的高度CE.
19.如图,在中,,,垂足为,若,,求的面积.
20.如图,中,,点D在AC上,已知,,,求AD的长.
21.如图,一高层住宅发生火灾,消防车立即赶到距大厦8米(AC的长)处,升起云梯到火灾窗口,云梯AB长17米,云梯底部距地面3米(AE的长),问:发生火灾的住户窗口距离地面有多高(BD的长)?
22.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=CD,求证:∠AEF=90°.
23.如图,点E在梯形ABCD的边BC上,∠B=∠C=90°,CD=CE=1,AE=2,AD=.
(1)求∠AEC的度数.
(2)求梯形ABCD的面积.
24.我们知道每一个无理数都可以用数轴上的一个点表示出来.请在如图所示的数轴上画出表示的点A(要求保留作图痕迹).若数轴上表示数3的点是点B,点A是线段的中点,求数轴上点C表示的数.
《第二十四章勾股定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D A C C C B A A
题号 11 12
答案 D B
1.B
【分析】根据勾股定理可以求得等于大正方形的面积,然后求四个直角三角形的面积,即可得到2ab的值,然后根据即可求得(a+b)的值;根据小正方形的面积为即可求得,进而联立方程组求得a与b的值,则可求出答案.
【详解】解:∵大正方形的面积是13,设边长为c,
∴,
∴,
∵直角三角形的面积是,
又∵直角三角形的面积是,
∴,
∴,
∴.
∵小正方形的面积为,
又∵,
∴,
联立可得 ,解得 ,
∴.
故选:B.
【点睛】本题考查了勾股定理以及完全平方公式的知识,解题关键是熟记完全平方公式,还要注意图形的面积和a、b之间的关系.
2.C
【分析】本题主要考查了勾股定理与折叠问题,由折叠的性质可得,设,则,利用勾股定理可得方程,解方程求出,再利用三角形面积计算公式求解即可.
【详解】解:由折叠的性质可得,
设,则,
由长方形的性质可得,
在中,由勾股定理得,
∴,
解得,
∴,
∴,
故选:C.
3.D
【分析】分两种情况:4是斜边或者x是斜边,再根据勾股定理列出方程解即可.
【详解】当42是斜边的平方时,32+x2=42,x2=42-32=7;
当x2是斜边的平方时,x2=32+42=52.
所以此三角形是直角三角形的x2的值是52或7
故选:D
【点睛】本题主要考查了勾股定理,利用分类讨论思想解答是解题的关键.
4.A
【分析】直接利用勾股定理的逆定理分析得出答案.
【详解】∵一个三角形的三条边长分别为:5,12,13,把这个三角形的三条边长同时扩大到原来的2倍,
∴扩大后三角形三边长分别为:10,24,26,
∵102+242=676,
262=676,
∴102+242=262,
∴这个三角形的形状为直角三角形.
故选A.
【点睛】本题考查了勾股定理的逆定理,正确把握勾股定理的逆定理是解题关键.
5.C
【分析】根据勾股定理进行计算,即可求得结果.
【详解】解:直角三角形的两条直角边的长分别为1,,
则斜边长==2;
故选C.
【点睛】本题考查了勾股定理;熟练运用勾股定理进行求解是解决问题的关键.
6.C
【分析】本题考查了勾股定理,三角形的面积的计算,掌握勾股定理是解题的关键.根据勾股定理计算的长,利用面积差可得三角形的面积,由三角形的面积公式即可得到结论.
【详解】解:由勾股定理得:,
,
,
,
;
故选:C.
7.C
【分析】本题考查勾股定理逆定理.掌握如果三角形两条短边的平方和等于第三边的平方,那么这个三角形就是直角三角形是解题关键.根据勾股定理逆定理逐项判断即可.
【详解】解:∵,
∴A选项可以组成直角三角形,不符合题意;
∵,
∴B选项可以组成直角三角形,不符合题意;
∵,
∴C选项不可以组成直角三角形,符合题意;
∵,
∴D选项可以组成直角三角形,不符合题意.
故选:C.
8.B
【分析】根据勾股定理分别求解,,,,从而可得答案.
【详解】解:由勾股定理可得:
,
,
,
,
故选:B.
【点睛】本题考查的是勾股定理的应用,熟记勾股定理的解本题的关键.
9.A
【分析】设为x,则为,在由勾股定理有,即可求得.
【详解】解:由折叠的性质可知,
设为x,则为,
∵四边形为长方形
∴,
∴在中由勾股定理有
即
化简得
解得,
故选:A.
【点睛】本题考查了折叠问题求折痕或其他边长,主要可根据折叠前后两图形的全等条件,把某个直角三角形的三边都用同一未知量表示出来,并根据勾股定理建立方程,进而可以求解.
10.A
【分析】过点B作BN⊥AM于点N,由已知可求得BN的长,再根据勾股定理求BM的长.
【详解】解:由已知得,AB=×28=14km,∠MAB=30°,∠ABM=105°.
过点B作BN⊥AM于点N.
∵在直角△ABN中,∠BAN=30°
∴BN=AB=7km.
在直角△BNM中,∠MBN=45°,
则直角△BNM是等腰直角三角形,
即BN=MN=7km,
∴BM===km.
故选:A.
【点睛】本题考查了解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线构造直角三角形,再用直角三角形的性质和勾股定理进行求解.
11.D
【详解】在Rt△ABC中 ∠C=90°,AC=3,BC=4,根据勾股定理求得AB=5,设点C到AB的距离为h,即可得h×AB=AC×BC,即h×5=×3×4,解得h= ,故选D.
12.B
【详解】由,整理,
得,
即,所以,符合,所以这个三角形一定是直角三角形.
13.6.5/
【详解】解:如图,延长AE交BC于点F,
∵点E是CD的中点,
∴DE=CE,
∵AB⊥BC,AB⊥AD,
∴AD∥BC,
∴∠ADE=∠BCE且DE=CE,∠AED=∠CEF,
∴△AED≌△FEC(ASA),
∴AD=FC=5,AE=EF,
∴BF=BC-FC=5,
∴在Rt△ABF中,,
,
故答案为:6.5.
14. 勾, 股, 弦
【解析】略
15.16
【分析】将正方形沿着翻折得到正方形 ,过点在正方形内部作,使,连接,过作于点,此时最小,运用勾股定理求解即可.
【详解】
如图,将正方形沿着翻折得到正方形 ,过点在正方形内部作,使,连接,过作于点,则四边形是矩形,四边形是平行四边形,
∴,,,,
此时最小,
∵点是中点,
∴cm,
∴cm,cm,
在中,cm,
∴cm,
故答案为:16.
【点睛】本题考查最短路径问题,考查了正方形的性质,矩形的性质,平行四边形的性质和判定,勾股定理,轴对称性质等,解题的关键是将立体图形中的最短距离转换为平面图形的两点之间线段长度进行计算.
16.
【分析】根据已知条件得到,再根据角平分线的性质得到,,设,在中,得到,代入求解即可;
【详解】根据已知条件可知,在中,,,,则由勾股定理可得:,
∵平分,,,
∴,,
设,
在中,,即,
解得:,即;
∴,
在中,,
∴;
故答案是:.
【点睛】本题主要考查了勾股定理和角平分线的性质,准确理解题意,找准直角三角形利用勾股定理计算是解题的关键.
17.2
【分析】先画出图形,再根据等腰三角形的三线合一的性质及勾股定理求得结果.
【详解】解:如图:
∵△ABC是等边三角形,
∴
∴.
故答案为:.
【点睛】本题考查的是等腰三角形的性质,勾股定理,解答本题的关键是熟练掌握等腰三角形的三线合一的性质:等腰三角形顶角平分线,底边上的高,底边上的中线重合.
18.风筝的高度CE为21.6米.
【分析】利用勾股定理求出CD的长,再加上DE的长度,即可求出CE的高度.
【详解】解:在Rt△CDB中,由勾股定理,得CD===20(米).
∴CE=CD+DE=20+1.6=21.6(米).
答:风筝的高度CE为21.6米.
【点睛】本题考查了勾股定理的应用,熟悉勾股定理,能从实际问题中抽象出勾股定理是解题的关键.
19..
【分析】求出∠ADC=∠ADB=90°,根据三角形内角和定理求出∠BAD=30°,求出AB=2BD,根据勾股定理求出CD和BD,根据面积公式求出即可.
【详解】∵AD⊥BC,垂足为D,
∴∠ADC=∠ADB=90°,
∵∠B=60°,
∴∠BAD=30°,
∴AB=2BD,
∵由勾股定理得:AC2=AD2+DC2,AB2=AD2+BD2,
∴52=32+CD2,(2BD)2=32+BD2,
∴CD=4,BD=,
∴△ABC的面积是BC×AD=×(+4)×3=()cm2.
【点睛】此题考查勾股定理,含30°角的直角三角形性质,三角形的面积的应用,能求出CD、BD的长是解题的关键.
20.
【分析】根据等腰直角三角形的性质求出BC,再利用勾股定理列式计算即可得解.
【详解】在中,,
所以,
因为,
所以,
所以,在中,
因为,即,
所以,
所以.
【点睛】此题考查勾股定理,等腰直角三角形,解题关键在于得出.
21.18米
【分析】根据AB和AC的长度,构造直角三角形,根据勾股定理就可求出直角边BC的长,即可由BD=BC+CD求解.
【详解】解:由题意可知:,米,米,米;
在中,根据勾股定理,得,
即,,
∴(米)
∴(米);
答:发生火灾的住户窗口距离地面18米.
【点睛】本题考查勾股定理的应用.熟练掌握勾股定理是解题的关键.
22.证明见解析.
【分析】利用正方形的性质得出AB=BC=CD=DA,∠B=∠C=∠D=90°,设出边长为a,进一步利用勾股定理求得AE、EF、AF的长,再利用勾股定理逆定理判定即可.
【详解】证明:∵ABCD为正方形,
∴AB=BC=CD=DA,∠B=∠C=∠D=90°.
设AB=BC=CD=DA=a.
∵E是BC的中点,且CF=CD,
∴BE=EC=a,CF=a.
在Rt△ABE中,由勾股定理可得:AE2=AB2+BE2=a2,
同理可得:EF2=EC2+FC2=a2,AF2=AD2+DF2=a2.
∵AE2+EF2=AF2,
∴△AEF为直角三角形,
∴∠AEF=90°.
【点睛】本题考查了正方形的性质,勾股定理、勾股定理逆定理的运用,注意在正方形中的直角三角形的应用.
23.(1)135°
(2)4.5
【分析】(1)连接DE,根据等腰直角三角形的性质求出∠DEC=45°,根据勾股定理求出DE,根据勾股定理的逆定理求出∠AED=90°,计算即可;
(2)根据等腰直角三角形的性质求出AB、BE,根据梯形的面积公式计算,得到答案.
【详解】(1)解:如图,连接,
,,
是等腰直角三角形,
,
由勾股定理,得.
,,
,,
,
是直角三角形,
,
.
(2)由(1)得,
.
,
,
.
在中,,
,
,
.
【点睛】本题考查的是等腰直角三角形的判定和性质、勾股定理的逆定理,根据勾股定理的逆定理求出∠AED=90°是解题的关键.
24.画图见解析,
【分析】先利用勾股定理在数轴上确定的点,设点C表示的数为x,再利用中点的含义建立方程解题即可.
【详解】解:如图,点表示,
∴,
∵点A为的中点,
∴,设点C表示的数为x,
∵点A表示的数为,点B表示的数为3,
∴,
解得,则点C表示的数.
【点睛】本题考查的是勾股定理的应用,实数与数轴,数轴上两点之间的距离,中点的含义,利用方程解题是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章勾股定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,我国古代的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形的面积为1,大正方形的面积为13,则直角三角形较短的直角边a与较长的直角边b的比的值是( )
A. B. C. D.
2.如图,长方形中,,,将此长方形折叠,使点D与点B重合,折痕为,则的面积为( )
A. B. C. D.
3.若一个三角形的三边长的平方分别为:32,42,x2则此三角形是直角三角形的x2的值是( )
A.4 B.52 C.7 D.52或7
4.一个三角形的三条边长分别为:5,12,13,把这个三角形的三条边长同时扩大到原来的2倍,那么这个三角形的形状为( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定形状
5.已知直角三角形的两条直角边的长分别是1,,则斜边长为( )
A.1 B. C.2 D.3
6.如图,在的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若是的高,则的长为()
A. B. C. D.
7.以下列数据为边,不能组成直角三角形的是( )
A.5,12,13 B.,,
C.1,, D.7,24,25
8.如图,在的正方形网格(每个小正方形的边长都是1)中,标记格点A,B,C,D,则下列线段长度为的是( )
A.线段 B.线段 C.线段 D.线段
9.如图,长方形中,,,将此长方形折叠,使点D与点B重合,折痕为.则的长为( )
A.13 B.12 C.10 D.8
10.如图,已知一渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28海里/时的速度向正东方向航行,半小时后到达B处,在B处看见灯塔M在北偏东15°方向,此时灯塔M与渔船的距离是( )
A.7海里 B.14海里 C.7海里 D.14海里
11.在Rt△ABC中,∠C=90°,AC=3,BC=4,则点C到AB的距离是( )
A. B. C. D.
12.如果一个三角形的三边长满足,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
二、填空题
13.如图,AB=12,AB⊥BC于点B,AB⊥AD于点A,AD=5,BC=10,E是CD的中点,则AE的长是 .
14.我国古代把直角三角形中较短的直角边称为 ,较长的直角边称为 ,斜边称为 .因此称上面的结论为勾股定理.
15.爱动脑筋的小明某天在家玩遥控游戏时遇到下面的问题:已知,如图一个棱长为8cm无盖的正方体铁盒,小明通过遥控器操控一只带有磁性的甲虫玩具,他先把甲虫放在正方体盒子外壁A处,然后遥控甲虫从A处出发沿外壁面正方形ABCD爬行,爬到边CD上后再在边CD上爬行3cm,最后在沿内壁面正方形ABCD上爬行,最终到达内壁BC的中点M,甲虫所走的最短路程是 cm
16.如图,在中,,,,平分,,垂足为,则 cm.
17.已知等边三角形的边长为,则它的高为 .
三、解答题
18.八(2)班小明和小亮同学学习了“勾股定理”之后,为了测得如图风筝的高度CE,他们进行了如下操作:
①测得BD的长度为15米;(注:BD⊥CE)
②根据手中剩余线的长度计算出风筝线BC的长为25米;
③牵线放风筝的小明身高1.6米.
求风筝的高度CE.
19.如图,在中,,,垂足为,若,,求的面积.
20.如图,中,,点D在AC上,已知,,,求AD的长.
21.如图,一高层住宅发生火灾,消防车立即赶到距大厦8米(AC的长)处,升起云梯到火灾窗口,云梯AB长17米,云梯底部距地面3米(AE的长),问:发生火灾的住户窗口距离地面有多高(BD的长)?
22.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=CD,求证:∠AEF=90°.
23.如图,点E在梯形ABCD的边BC上,∠B=∠C=90°,CD=CE=1,AE=2,AD=.
(1)求∠AEC的度数.
(2)求梯形ABCD的面积.
24.我们知道每一个无理数都可以用数轴上的一个点表示出来.请在如图所示的数轴上画出表示的点A(要求保留作图痕迹).若数轴上表示数3的点是点B,点A是线段的中点,求数轴上点C表示的数.
《第二十四章勾股定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D A C C C B A A
题号 11 12
答案 D B
1.B
【分析】根据勾股定理可以求得等于大正方形的面积,然后求四个直角三角形的面积,即可得到2ab的值,然后根据即可求得(a+b)的值;根据小正方形的面积为即可求得,进而联立方程组求得a与b的值,则可求出答案.
【详解】解:∵大正方形的面积是13,设边长为c,
∴,
∴,
∵直角三角形的面积是,
又∵直角三角形的面积是,
∴,
∴,
∴.
∵小正方形的面积为,
又∵,
∴,
联立可得 ,解得 ,
∴.
故选:B.
【点睛】本题考查了勾股定理以及完全平方公式的知识,解题关键是熟记完全平方公式,还要注意图形的面积和a、b之间的关系.
2.C
【分析】本题主要考查了勾股定理与折叠问题,由折叠的性质可得,设,则,利用勾股定理可得方程,解方程求出,再利用三角形面积计算公式求解即可.
【详解】解:由折叠的性质可得,
设,则,
由长方形的性质可得,
在中,由勾股定理得,
∴,
解得,
∴,
∴,
故选:C.
3.D
【分析】分两种情况:4是斜边或者x是斜边,再根据勾股定理列出方程解即可.
【详解】当42是斜边的平方时,32+x2=42,x2=42-32=7;
当x2是斜边的平方时,x2=32+42=52.
所以此三角形是直角三角形的x2的值是52或7
故选:D
【点睛】本题主要考查了勾股定理,利用分类讨论思想解答是解题的关键.
4.A
【分析】直接利用勾股定理的逆定理分析得出答案.
【详解】∵一个三角形的三条边长分别为:5,12,13,把这个三角形的三条边长同时扩大到原来的2倍,
∴扩大后三角形三边长分别为:10,24,26,
∵102+242=676,
262=676,
∴102+242=262,
∴这个三角形的形状为直角三角形.
故选A.
【点睛】本题考查了勾股定理的逆定理,正确把握勾股定理的逆定理是解题关键.
5.C
【分析】根据勾股定理进行计算,即可求得结果.
【详解】解:直角三角形的两条直角边的长分别为1,,
则斜边长==2;
故选C.
【点睛】本题考查了勾股定理;熟练运用勾股定理进行求解是解决问题的关键.
6.C
【分析】本题考查了勾股定理,三角形的面积的计算,掌握勾股定理是解题的关键.根据勾股定理计算的长,利用面积差可得三角形的面积,由三角形的面积公式即可得到结论.
【详解】解:由勾股定理得:,
,
,
,
;
故选:C.
7.C
【分析】本题考查勾股定理逆定理.掌握如果三角形两条短边的平方和等于第三边的平方,那么这个三角形就是直角三角形是解题关键.根据勾股定理逆定理逐项判断即可.
【详解】解:∵,
∴A选项可以组成直角三角形,不符合题意;
∵,
∴B选项可以组成直角三角形,不符合题意;
∵,
∴C选项不可以组成直角三角形,符合题意;
∵,
∴D选项可以组成直角三角形,不符合题意.
故选:C.
8.B
【分析】根据勾股定理分别求解,,,,从而可得答案.
【详解】解:由勾股定理可得:
,
,
,
,
故选:B.
【点睛】本题考查的是勾股定理的应用,熟记勾股定理的解本题的关键.
9.A
【分析】设为x,则为,在由勾股定理有,即可求得.
【详解】解:由折叠的性质可知,
设为x,则为,
∵四边形为长方形
∴,
∴在中由勾股定理有
即
化简得
解得,
故选:A.
【点睛】本题考查了折叠问题求折痕或其他边长,主要可根据折叠前后两图形的全等条件,把某个直角三角形的三边都用同一未知量表示出来,并根据勾股定理建立方程,进而可以求解.
10.A
【分析】过点B作BN⊥AM于点N,由已知可求得BN的长,再根据勾股定理求BM的长.
【详解】解:由已知得,AB=×28=14km,∠MAB=30°,∠ABM=105°.
过点B作BN⊥AM于点N.
∵在直角△ABN中,∠BAN=30°
∴BN=AB=7km.
在直角△BNM中,∠MBN=45°,
则直角△BNM是等腰直角三角形,
即BN=MN=7km,
∴BM===km.
故选:A.
【点睛】本题考查了解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线构造直角三角形,再用直角三角形的性质和勾股定理进行求解.
11.D
【详解】在Rt△ABC中 ∠C=90°,AC=3,BC=4,根据勾股定理求得AB=5,设点C到AB的距离为h,即可得h×AB=AC×BC,即h×5=×3×4,解得h= ,故选D.
12.B
【详解】由,整理,
得,
即,所以,符合,所以这个三角形一定是直角三角形.
13.6.5/
【详解】解:如图,延长AE交BC于点F,
∵点E是CD的中点,
∴DE=CE,
∵AB⊥BC,AB⊥AD,
∴AD∥BC,
∴∠ADE=∠BCE且DE=CE,∠AED=∠CEF,
∴△AED≌△FEC(ASA),
∴AD=FC=5,AE=EF,
∴BF=BC-FC=5,
∴在Rt△ABF中,,
,
故答案为:6.5.
14. 勾, 股, 弦
【解析】略
15.16
【分析】将正方形沿着翻折得到正方形 ,过点在正方形内部作,使,连接,过作于点,此时最小,运用勾股定理求解即可.
【详解】
如图,将正方形沿着翻折得到正方形 ,过点在正方形内部作,使,连接,过作于点,则四边形是矩形,四边形是平行四边形,
∴,,,,
此时最小,
∵点是中点,
∴cm,
∴cm,cm,
在中,cm,
∴cm,
故答案为:16.
【点睛】本题考查最短路径问题,考查了正方形的性质,矩形的性质,平行四边形的性质和判定,勾股定理,轴对称性质等,解题的关键是将立体图形中的最短距离转换为平面图形的两点之间线段长度进行计算.
16.
【分析】根据已知条件得到,再根据角平分线的性质得到,,设,在中,得到,代入求解即可;
【详解】根据已知条件可知,在中,,,,则由勾股定理可得:,
∵平分,,,
∴,,
设,
在中,,即,
解得:,即;
∴,
在中,,
∴;
故答案是:.
【点睛】本题主要考查了勾股定理和角平分线的性质,准确理解题意,找准直角三角形利用勾股定理计算是解题的关键.
17.2
【分析】先画出图形,再根据等腰三角形的三线合一的性质及勾股定理求得结果.
【详解】解:如图:
∵△ABC是等边三角形,
∴
∴.
故答案为:.
【点睛】本题考查的是等腰三角形的性质,勾股定理,解答本题的关键是熟练掌握等腰三角形的三线合一的性质:等腰三角形顶角平分线,底边上的高,底边上的中线重合.
18.风筝的高度CE为21.6米.
【分析】利用勾股定理求出CD的长,再加上DE的长度,即可求出CE的高度.
【详解】解:在Rt△CDB中,由勾股定理,得CD===20(米).
∴CE=CD+DE=20+1.6=21.6(米).
答:风筝的高度CE为21.6米.
【点睛】本题考查了勾股定理的应用,熟悉勾股定理,能从实际问题中抽象出勾股定理是解题的关键.
19..
【分析】求出∠ADC=∠ADB=90°,根据三角形内角和定理求出∠BAD=30°,求出AB=2BD,根据勾股定理求出CD和BD,根据面积公式求出即可.
【详解】∵AD⊥BC,垂足为D,
∴∠ADC=∠ADB=90°,
∵∠B=60°,
∴∠BAD=30°,
∴AB=2BD,
∵由勾股定理得:AC2=AD2+DC2,AB2=AD2+BD2,
∴52=32+CD2,(2BD)2=32+BD2,
∴CD=4,BD=,
∴△ABC的面积是BC×AD=×(+4)×3=()cm2.
【点睛】此题考查勾股定理,含30°角的直角三角形性质,三角形的面积的应用,能求出CD、BD的长是解题的关键.
20.
【分析】根据等腰直角三角形的性质求出BC,再利用勾股定理列式计算即可得解.
【详解】在中,,
所以,
因为,
所以,
所以,在中,
因为,即,
所以,
所以.
【点睛】此题考查勾股定理,等腰直角三角形,解题关键在于得出.
21.18米
【分析】根据AB和AC的长度,构造直角三角形,根据勾股定理就可求出直角边BC的长,即可由BD=BC+CD求解.
【详解】解:由题意可知:,米,米,米;
在中,根据勾股定理,得,
即,,
∴(米)
∴(米);
答:发生火灾的住户窗口距离地面18米.
【点睛】本题考查勾股定理的应用.熟练掌握勾股定理是解题的关键.
22.证明见解析.
【分析】利用正方形的性质得出AB=BC=CD=DA,∠B=∠C=∠D=90°,设出边长为a,进一步利用勾股定理求得AE、EF、AF的长,再利用勾股定理逆定理判定即可.
【详解】证明:∵ABCD为正方形,
∴AB=BC=CD=DA,∠B=∠C=∠D=90°.
设AB=BC=CD=DA=a.
∵E是BC的中点,且CF=CD,
∴BE=EC=a,CF=a.
在Rt△ABE中,由勾股定理可得:AE2=AB2+BE2=a2,
同理可得:EF2=EC2+FC2=a2,AF2=AD2+DF2=a2.
∵AE2+EF2=AF2,
∴△AEF为直角三角形,
∴∠AEF=90°.
【点睛】本题考查了正方形的性质,勾股定理、勾股定理逆定理的运用,注意在正方形中的直角三角形的应用.
23.(1)135°
(2)4.5
【分析】(1)连接DE,根据等腰直角三角形的性质求出∠DEC=45°,根据勾股定理求出DE,根据勾股定理的逆定理求出∠AED=90°,计算即可;
(2)根据等腰直角三角形的性质求出AB、BE,根据梯形的面积公式计算,得到答案.
【详解】(1)解:如图,连接,
,,
是等腰直角三角形,
,
由勾股定理,得.
,,
,,
,
是直角三角形,
,
.
(2)由(1)得,
.
,
,
.
在中,,
,
,
.
【点睛】本题考查的是等腰直角三角形的判定和性质、勾股定理的逆定理,根据勾股定理的逆定理求出∠AED=90°是解题的关键.
24.画图见解析,
【分析】先利用勾股定理在数轴上确定的点,设点C表示的数为x,再利用中点的含义建立方程解题即可.
【详解】解:如图,点表示,
∴,
∵点A为的中点,
∴,设点C表示的数为x,
∵点A表示的数为,点B表示的数为3,
∴,
解得,则点C表示的数.
【点睛】本题考查的是勾股定理的应用,实数与数轴,数轴上两点之间的距离,中点的含义,利用方程解题是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
