第二十六章一次函数期末单元复习题(含解析)
文档属性
| 名称 | 第二十六章一次函数期末单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 737.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 22:35:26 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十六章一次函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列四个点中,在函数y=3x+1的图像上的是( )
A.(-1,2) B.(0,-1) C.(1,4) D.(2,-7)
2.下列各曲线中,不能表示y是x的函数的是( )
A. B.
C. D.
3.在某一阶段,某商品的销售量与销售价之间存在如下关系:
销售价/元 90 100 110 120 130 140
销售量/件 90 80 70 60 50 40
设该商品的销售价为x元,销售量为y件,估计当x=127时,y的值为( )
A.63 B.59 C.53 D.43
4.下面关于函数的三种表示方法叙述错误的是( )
A.用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化
B.用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值
C.用公式法表示函数关系,可以方便地计算函数值
D.任何函数关系都可以用上述三种方法来表示
5.在雨地里放置一个无盖的容器,如果雨水均匀地落入容器,容器内水面高度与时间的函数图象如图所示,那么这个容器的形状可能是( )
A. B. C. D.
6.关于正比例函数,下列结论中正确的是( ).
A.函数图象经过点 B.y随x的增大而减小
C.函数图象经过第一、三象限 D.不论x取何值,总有
7.在某一阶段,某商品的销售量与销售价之间存在如下关系:设该商品的销售价为x元,售量为y件,估计当x=137时,y的值可能为( )
销售价/元 90 100 110 120 130 140
销售量/件 90 80 70 60 50 40
A.63 B.59 C.53 D.43
8.早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:
①打电话时,小刚和妈妈的距离为1250米;
②打完电话后,经过23分钟小刚到达学校;
③小刚和妈妈相遇后,妈妈回家的速度为150米/分;
④小刚家与学校的距离为2550米.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
9.已知一次函数的图象经过点,,下列关于m和n的关系正确的是( )
A. B. C. D.
10.已知直线的交点横坐标为3,若,则的值为( )
A.3 B. C.9 D.
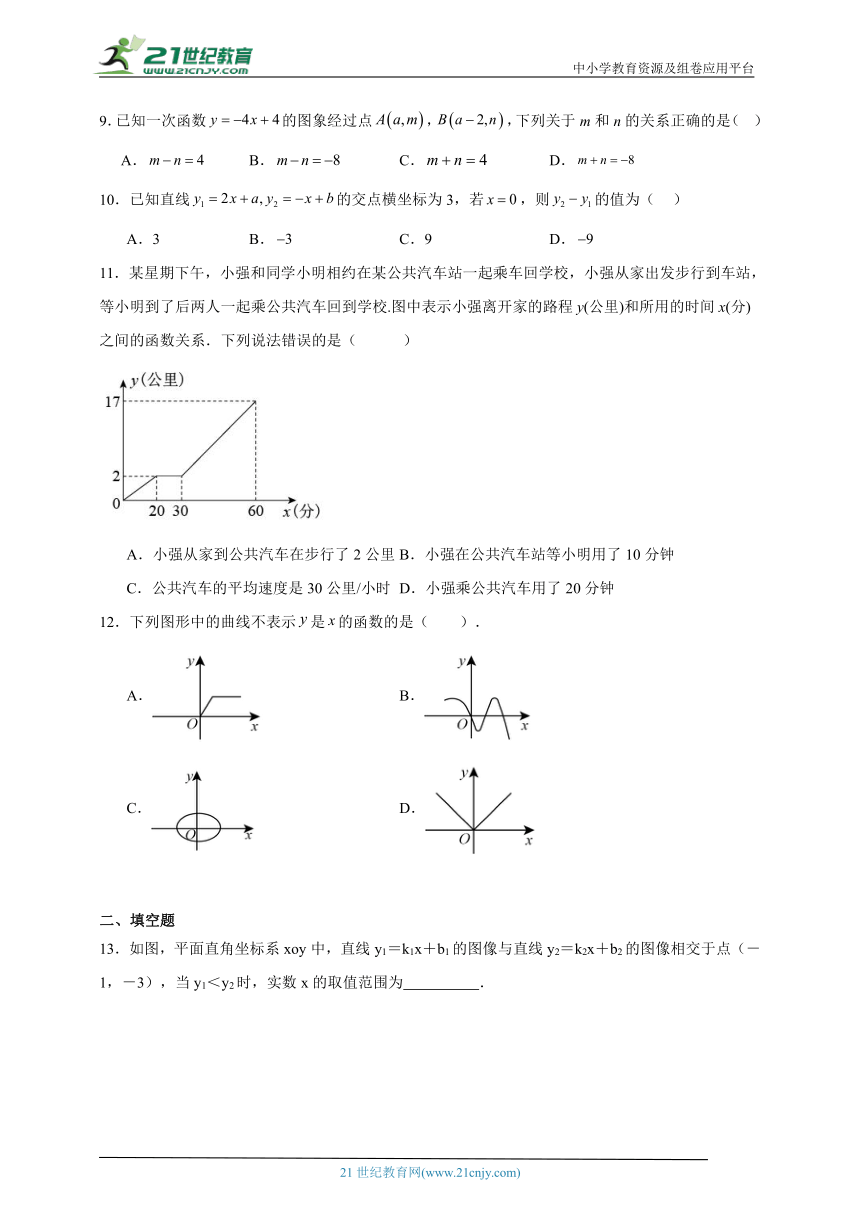
11.某星期下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
A.小强从家到公共汽车在步行了2公里 B.小强在公共汽车站等小明用了10分钟
C.公共汽车的平均速度是30公里/小时 D.小强乘公共汽车用了20分钟
12.下列图形中的曲线不表示是的函数的是( ).
A. B.
C. D.
二、填空题
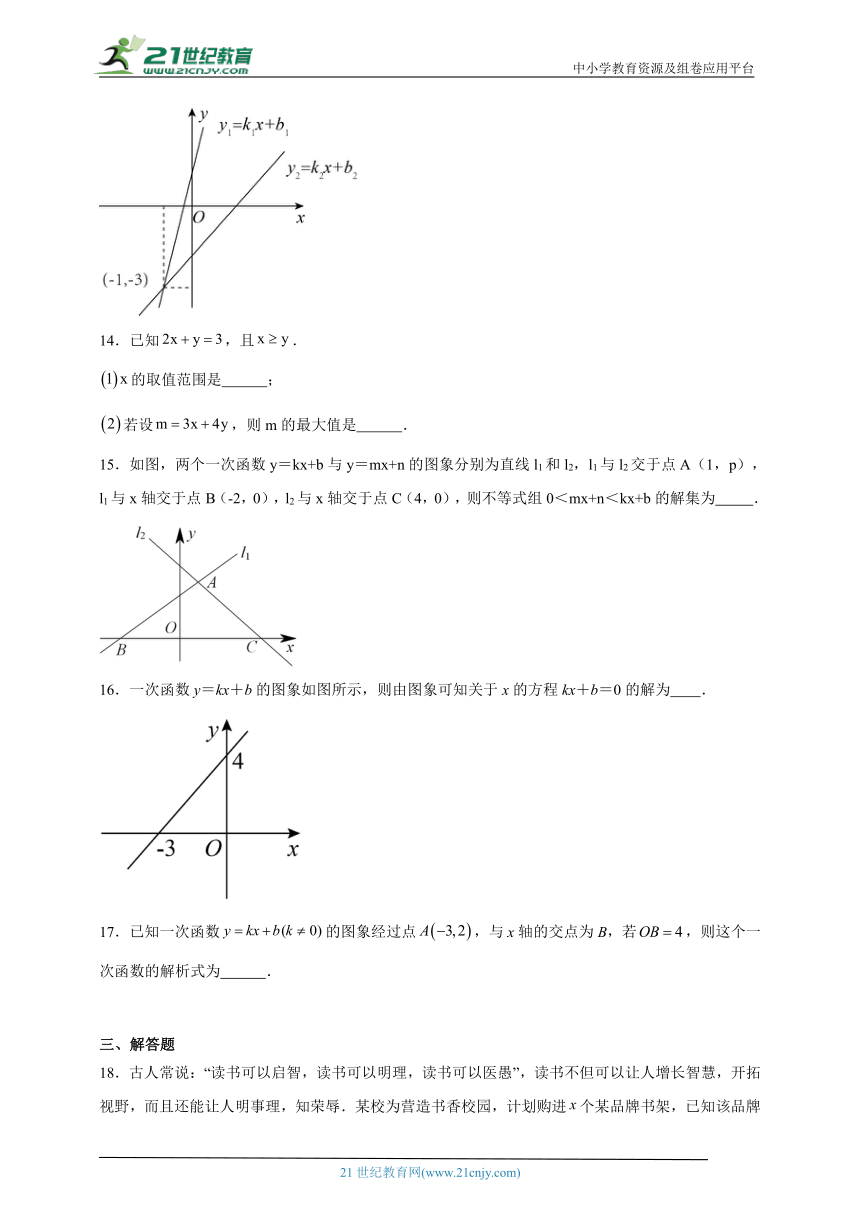
13.如图,平面直角坐标系xoy中,直线y1=k1x+b1的图像与直线y2=k2x+b2的图像相交于点(-1,-3),当y1<y2时,实数x的取值范围为 .
14.已知,且.
的取值范围是 ;
若设,则m的最大值是 .
15.如图,两个一次函数y=kx+b与y=mx+n的图象分别为直线l1和l2,l1与l2交于点A(1,p),l1与x轴交于点B(-2,0),l2与x轴交于点C(4,0),则不等式组0<mx+n<kx+b的解集为 .
16.一次函数y=kx+b的图象如图所示,则由图象可知关于x的方程kx+b=0的解为 .
17.已知一次函数的图象经过点,与x轴的交点为B,若,则这个一次函数的解析式为 .
三、解答题
18.古人常说:“读书可以启智,读书可以明理,读书可以医愚”,读书不但可以让人增长智慧,开拓视野,而且还能让人明事理,知荣辱.某校为营造书香校园,计划购进个某品牌书架,已知该品牌书架的单价为200元/个,经过与厂家协商,厂家给出两种优惠方案:
方案一:所有书架均按原价的八折销售;
方案二:若一次购买不超过10个,则每个书架按原价的九折销售;若一次购买超过10个,则前10个打九折,超过的部分每个书架的价格在九折的基础上再降低30元.
(1)分别求方案一实际付款金额(元)和方案二实际付款金额(元)与之间的函数关系式;
(2)当时,请分别求出两种方案的实际付款金额,并判断选择哪种方案对学校来说更省钱.
19.通过实验获得u,v两个变量的各对应值如下表.
u 0 0.5 1 1.5 2 2.5 3 4
v 50 100 155 207 260 290 365 470
判断变量u,v是否满足或近似地满足一次函数关系式.如果是,求v关于u的函数式,并利用函数式求出当时函数v的值.
20.某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
21.“绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向A,B两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥;A,B两个果园分别需用110吨和70吨有机化肥.两个仓库到A,B两个果园的路程如表所示:
路程(千米)
甲仓库 乙仓库
A果园 15 25
B果园 20 20
设甲仓库运往A果园x吨有机化肥,若汽车每吨每千米的运费为2元,
(1)根据题意,填写下表.(温馨提示:请填写在答题卷相对应的表格内)
运量(吨) 运费(元)
甲仓库 乙仓库 甲仓库 乙仓库
A果园 x 110﹣x 2×15x 2×25(110﹣x)
B果园
(2)设总运费为y元,求y关于x的函数表达式,并求当甲仓库运往A果园多少吨有机化肥时,总运费最省?最省的总运费是多少元?
22.某市为鼓励居民节约用水,规定如下用水收费标准:每户每月的用水量不超过12吨(含12吨)时,水费按a元/吨收费;超过时,不超过12吨(含12吨)时,水费按a元/吨收费;超过时,不超过12吨的部分仍按a元/吨收费,超过的部分按b元/吨收费,已知该市小明家今年3月份和4月份的用水量、水费如表所示:
月份 用水量(立方米) 水费(元)
3 28 56
4 20 35.2
(1)求a,b的值;
(2)设某户1个月的用水量为x(吨),应交水费y(元),求出y与x之间的函数关系式;
(3)已知某户5月份的用水量为18吨,求该户5月份的水费.
23.如图:已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式:
(2)若直线y=2x-4与直线AB相交于点C,求点C的坐标;
(3)根据图象,直接写出关于x的不等式2x-4<kx+b的解集.
24.端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程米与时间分钟之间的函数关系图象如图所示,请你根据图象,回答下列问题:
这次龙舟赛的全程是______ 米,______ 队先到达终点;
求乙与甲相遇时乙的速度;
求出在乙队与甲相遇之前,他们何时相距100米?
《第二十六章一次函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C D C B D C B C
题号 11 12
答案 D C
1.C
【分析】只要把点的坐标代入一次函数的解析式,若左边=右边,则点在函数的图象上,反之就不在函数的图象上,代入检验即可.
【详解】解:A、把(-1,2)代入y=3x+1得:左边=2,右边=3×(-1)+1= -2,左边≠右边,故A选项错误;
B、把(0,-1)代入y=3x+1得:左边= -1,右边=3×0+1=1,左边≠右边,故B选项错误;
C、把(1,4)代入y=3x+1得:左边=4,右边=3×1+1=4,左边=右边,故C选项正确;
D、把(2,-7)代入y=3x+1得:左边= -7,右边=3×2+1=7,左边≠右边,故D选项错误.
故选C.
【点睛】本题考查对一次函数图象上点的坐标特征的理解和掌握,能根据点的坐标判断是否在函数的图象上是解题关键.
2.D
【分析】根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此即可确定函数的个数.
【详解】解:A,B,C的图象都满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故A、B、C的图象是函数,
D的图象不满足满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故D错误;
故选D.
【点睛】主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
3.C
【分析】分析表格得到销售价格每上涨10元,销售量就少10件,据此求解即可.
【详解】解:由表格可知,销售价格每上涨10元,销售量就少10件,
而当售价为120元时,销售量为60件,
所以当售价x=127时,y的值为53件,
故选:C.
【点睛】本题考查了利用表格表示函数关系,也可通过求函数解析式来解题.
4.D
【分析】根据函数的表示方法的优缺点分析解答即可.
【详解】A.用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化,此选项正确;
B.用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值,此选项正确;
C.用公式法表示函数关系,可以方便地计算函数值,此选项正确;
D.并不是任何函数关系都可以用上述三种方法来表示,此选项错误.
故选:D.
【点睛】本题考查函数的表示方法,明确三种表示方法的特点是解题的关键.
5.C
【分析】根据图象得到高度随时间的增大,高度增加的速度,即可判断.
【详解】根据图象可以得到:杯中水的高度随注水时间的增大而增大,而增加的速度越来越小.
则杯子应该是越向上开口越大.
故杯子的形状可能是.
故选:.
【点睛】本题考查了函数的图象,读函数的图象时首先要理解横纵坐标表示的含义,理解问题叙述的过程,能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小.
6.B
【详解】解:A、当x=﹣2时,y=﹣2×(﹣2)=4,即图象经过点(﹣2,4),不经过点(﹣2,1),故本选项错误,不符合题意;
B、由于k=﹣2<0,所以y随x的增大而减小,故本选项正确,符合题意;
C、由于k=﹣2<0,所以图象经过二、四象限,故本选项错误,不符合题意;
D、∵x>0时,y<0,x<0时,y>0,
∴不论x为何值,总有y<0错误,故本选项错误,不符合题意.
故选B.
7.D
【分析】通过待定系数法求出y与x的函数关系式,再将x=137代入求解.
【详解】解:设售量y件与销售价x元之间的关系为y=kx+b,
将x=90,y=90与x=100,y=80分别代入可得:,
解得,
∴y=﹣x+180,
将x=137代入可得y=43,
故选:D.
【点睛】此题主要考查一次函数的实际应用,解题的关键是根据待定系数法求出函数解析式.
8.C
【详解】①由图可知打电话时,小刚和妈妈的距离为1250米是正确的;
②因为打完电话后5分钟两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,经过5+15+3=23分钟小刚到达学校,所以是正确的;
③打完电话后5分钟两人相遇后,妈妈的速度是1250÷5﹣100=150米/分,走的路程为150×5=750米,回家的速度是750÷15=50米/分,所以回家的速度为150米/分是错误的;
④小刚家与学校的距离为750+(15+3)×100=2550米,所以是正确的.
正确的答案有①②④.
故选C.
9.B
【分析】本题考查一次函数图象上点的坐标特征,将点,代入解析式,即可求解.
【详解】解:∵一次函数的图象经过点,,
∴
解得:
∴,
故选:B.
10.C
【分析】根据两直线交点横坐标得到,再将x=0分别代入,可得.
【详解】解:∵,的交点横坐标为3,
∴令,将代入得,
∴,
∴,
∵当时,,,
∴.
故选C.
【点睛】本题考查了一次函数与一元一次方程,解题的关键是掌握两直线的交点坐标同时满足函数表达式.
11.D
【分析】根据函数图象及速度、时间、路程的关系依次判断即可得.
【详解】解:根据图象可得:
小强从家到公共汽车在步行了2公里,A选项正确;
,小强在公共汽车站等小明用了10分钟,B选项正确;
路程为17-2=15,时间为60-30=30,30分钟=0.5小时,
∴速度为:公里/小时,C选项正确;
60-30=30分钟,小强乘公共汽车用了30分钟,选项D错误;
故选:D.
【点睛】题目主要考查根据函数图象获取信息,理解题意,结合图象求解是解题关键.
12.C
【详解】过x轴上一点作x轴的垂线,若与函数图象有且仅有一个交点,则该图象表示函数的图象;若与函数图象有不止一个交点,则该图象不是函数图象,
在C图象中,与y轴平行的直线均与函数图象有两个交点,所以不是函数图象,其余的都只有一个交点,
故选C.
13.x<-1
【分析】直接根据直线y1的图象都在y2的图象下方,解答即可.
【详解】解:当x<-1时,函数y1=k1x+b1的图象都在y2=k2x+b2的图象下方,所以实数x的取值范围为:x<-1,
故答案为:x<-1.
【点睛】本题考查了一次函数与一元一次不等式,观察图象是关键.
14.
【详解】(1)用含x的代数式表示y,并代入中即可求出x的以值范围;
(2)先用含x的代数式表示m,再根据x的取值范围即可求出m的最大值.
解:(1)由可知,
又∵,
∴,
解得,
(2)∵,且,
∴,
即
又,
∴当,有最大值为,
∴最大值为.
15.1<x<4
【分析】先解不等式0<mx+n,结合图像可知上的点在轴的上方,可得< 再解mx+n<kx+b,结合图像可知上的点在的上方,可得> 从而可得0<mx+n<kx+b的解集.
【详解】解: 不等式0<mx+n,
上的点在轴的上方,
<
mx+n<kx+b,
上的点在的上方,
,
>
不等式组0<mx+n<kx+b的解集为1<<4,
故答案为:1<<4,
【点睛】本题考查的是一次函数与不等式组的关系,掌握利用一次函数的图像解不等式组是解题的关键.
16.x=﹣3
【分析】关于x的方程kx + b =0的解其实就是求当函数值为0时x的值,据此可以直接得到答案.
【详解】解:从图象上可知则关于x的方程kx+b=0的解为的解是:x=﹣3.
故答案为:x=﹣3.
【点睛】本题主要考查了一次函数与一元一次方程的关系,关键是知道通过图象怎么求方程的解.
17.或
【分析】由可知:点坐标为或,然后分两种情况利用待定系数法求一次函数的解析式.
【详解】解:由题意:,
∴点坐标为或.
①当一次函数的图象经过和时,
由题意得,
解得:,
∴这个一次函数的解析式为;
②当一次函数的图象经过和时,
由题意得,
解得:,
∴这个一次函数的解析式为.
综上所述,这个一次函数的解析式为或.
故答案为或.
【点睛】本题主要考查的是待定系数法求一次函数的解析式,尤其注意根据线段的长度,点坐标有两种情况,熟练掌握待定系数法是解本题的关键.
18.(1)
(2)3200元,3300元;选择方案一对学校来说更省钱
【详解】解:(1);
当时,,
当时,;
(2)当时,,,
选择方案一对学校来说更省钱.
19.u,v近似地满足一次函数关系式,,当时,v的值为281
【分析】直接利用一次函数的定义进行判定,再利用待定系数法求解即可.
【详解】解:u,v近似地满足一次函数关系式;
理由:由图中数据可知,当u的值依次增加1时,v的值都增加105,当u的值每增加0.5时,大部分的v的值都增加了50左右,因此,u,v近似地满足一次函数关系式.
设,
将、代入解析式可得:
,
解得:,
∴v关于u的函数式为:;
当时,;
∴u,v近似地满足一次函数关系式,;v的值为281.
【点睛】本题考查了一次函数的定义和待定系数法,解题关键是牢记一次函数的特点,并能利用待定系数法求解析式.
20.(1)20,5;(2)购进A种花草的数量为11株、B种20株,费用最省;最省费用是320元.
【分析】(1)设A种花草每棵的价格x元,B种花草每棵的价格y元,根据第一次分别购进A、B两种花草30棵和15棵,共花费940元;第二次分别购进A、B两种花草12棵和5棵,两次共花费675元;列出方程组,即可解答.(2)设A种花草的数量为m株,则B种花草的数量为(31-m)株,根据B种花草的数量少于A种花草的数量的2倍,得出m的范围,设总费用为W元,根据总费用=两种花草的费用之和建立函数关系式,由一次函数的性质就可以求出结论.
【详解】()设,两种花草每棵的价格分别为元和元.
由题意得,
解得:,
答:,两种花草价格分别为元和元.
()设购买种花草棵,则购买种花草为棵,
由题意得,且为整数,
解得:且为整数,
由()可知,的价格为元/棵,的价格为元/棵,
设费用为,
则,
由一次函数的性质可得:随的增大而增大,
∴当取最小整数时,最小值为:,
答:费用最省的方案为购买种花草棵,购买种花草棵,花费最少为元.
21.(1)80﹣x,x﹣10,2×20×(80﹣x),2×20×(x﹣10);(2)当甲仓库运往A果园80吨有机化肥时,总运费最省,最省的总运费是6700元.
【详解】分析:(1)设甲仓库运往A果园x吨有机化肥,根据题意求得甲仓库运往B果园(80-x)吨,乙仓库运往A果园(110-x)吨,乙仓库运往B果园(x-10)吨,然后根据两个仓库到A,B两个果园的路程完成表格;
(2)根据(1)中的表格求得总运费y(元)关于x(吨)的函数关系式,根据一次函数的增减性结合自变量的取值范围,可知当x=80时,总运费y最省,然后代入求解即可求得最省的总运费.
详解:(1)填表如下:
运量(吨) 运费(元)
甲仓库 乙仓库 甲仓库 乙仓库
A果园 x 110﹣x 2×15x 2×25(110﹣x)
B果园 80﹣x x﹣10 2×20×(80﹣x) 2×20×(x﹣10)
故答案为80﹣x,x﹣10,2×20×(80﹣x),2×20×(x﹣10);
(2)y=2×15x+2×25×(110﹣x)+2×20×(80﹣x)+2×20×(x﹣10),
即y关于x的函数表达式为y=﹣20x+8300,
∵﹣20<0,且10≤x≤80,
∴当x=80时,总运费y最省,此时y最小=﹣20×80+8300=6700.
故当甲仓库运往A果园80吨有机化肥时,总运费最省,最省的总运费是6700元.
点睛:此题考查了一次函数的实际应用问题.此题难度较大,解题的关键是理解题意,读懂表格,求得一次函数解析式,然后根据一次函数的性质求解.
22.(1)
(2)
(3)30
【分析】(1)由题意可知,3、4月都超出12吨,所以费用应该由两部分组成,列出方程组即可求出a、b的值;
(2)由于用水量不确定,所以需要分类讨论,第一种情况为当时,第二种情况为;
(3)由题意知,吨,代入(2)中相应的解析式即可求出5月份的水费.
【详解】(1)由题意列出方程为:,
解得:;
(2)当时,,
当时,,
综上所述:;
(3)令,
∴.
【点睛】本题考查了一次函数的应用,二元一次方程组的应用,准确理解题意,找出数量关系是解题的关键.
23.(1)y=-x+5
(2)(3,2)
(3)x<3
【分析】(1)利用待定系数法即可求得函数的解析式;
(2)解两个函数解析式组成方程组即可求解;
(3)关于x的不等式2x-4【详解】(1)解:根据题意得:
,解得:,
则直线AB的解析式是y=-x+5;
(2)根据题意得,
解得:,
则C的坐标是(3,2);
(3)根据图象可得不等式的解集是x<3.
【点睛】本题考查了待定系数法求一次函数的解析式,两直线的交点与二元一次方程组的解,一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
24.(1)1000,乙;(2)375米/分;(3)分或分.
【详解】试题分析:
(1)由图中所给数据信息可知,这次龙舟赛的全程是1000米,乙队先到达终点;
(2)由图中信息可知:乙是在比赛开始后的2.2分钟至3.8分钟之间和甲相遇的,这期间乙共行驶了600米,用时1.6分钟,由此即可求得此时乙的速度;
(3)由图中信息可求出甲的速度和乙在2.2分钟前的速度,这样设甲和乙相遇前x分钟时,两队相距100米,再分2.2分钟前和2.2分钟后两种情况求出答案即可.
试题解析:
(1)由图中信息可知,这次龙舟赛的全程是1000米,乙队先到达终点;
(2)由图中信息可知,乙是在比赛开始后的2.2分钟至3.8分钟之间和甲相遇的,这期间乙共行驶了600米,用时1.6分钟,
∴乙和甲相遇时的速度为:600÷(3.8-2.2)=375(米/分);
(3)由图中信息可知,甲的速度为:1000÷4=250(米/分),乙在2.2分钟前的速度为:400÷2.2=(米/分),
∴在2.2分钟时,甲、乙间的距离为:(米),
∴在2.2分钟之前和之后,各存在一次甲、乙相距100米的时刻,
设甲、乙在相遇之前,x分钟时相距100米,由题意可得:
或,
解得:或,
即甲、乙相遇前,在比赛开始后的第分钟和第2.6分钟时,两队相距100米.
点睛:解本题第3小题时,需先计算出2.2分钟时甲、乙的距离为150米,由此可知在2.2分钟之前和之后各存在一个时刻使两队间的距离为100米,这样即可分两种情况列出对应的方程求解,避免漏掉其中某种情况.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十六章一次函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列四个点中,在函数y=3x+1的图像上的是( )
A.(-1,2) B.(0,-1) C.(1,4) D.(2,-7)
2.下列各曲线中,不能表示y是x的函数的是( )
A. B.
C. D.
3.在某一阶段,某商品的销售量与销售价之间存在如下关系:
销售价/元 90 100 110 120 130 140
销售量/件 90 80 70 60 50 40
设该商品的销售价为x元,销售量为y件,估计当x=127时,y的值为( )
A.63 B.59 C.53 D.43
4.下面关于函数的三种表示方法叙述错误的是( )
A.用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化
B.用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值
C.用公式法表示函数关系,可以方便地计算函数值
D.任何函数关系都可以用上述三种方法来表示
5.在雨地里放置一个无盖的容器,如果雨水均匀地落入容器,容器内水面高度与时间的函数图象如图所示,那么这个容器的形状可能是( )
A. B. C. D.
6.关于正比例函数,下列结论中正确的是( ).
A.函数图象经过点 B.y随x的增大而减小
C.函数图象经过第一、三象限 D.不论x取何值,总有
7.在某一阶段,某商品的销售量与销售价之间存在如下关系:设该商品的销售价为x元,售量为y件,估计当x=137时,y的值可能为( )
销售价/元 90 100 110 120 130 140
销售量/件 90 80 70 60 50 40
A.63 B.59 C.53 D.43
8.早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:
①打电话时,小刚和妈妈的距离为1250米;
②打完电话后,经过23分钟小刚到达学校;
③小刚和妈妈相遇后,妈妈回家的速度为150米/分;
④小刚家与学校的距离为2550米.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
9.已知一次函数的图象经过点,,下列关于m和n的关系正确的是( )
A. B. C. D.
10.已知直线的交点横坐标为3,若,则的值为( )
A.3 B. C.9 D.
11.某星期下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
A.小强从家到公共汽车在步行了2公里 B.小强在公共汽车站等小明用了10分钟
C.公共汽车的平均速度是30公里/小时 D.小强乘公共汽车用了20分钟
12.下列图形中的曲线不表示是的函数的是( ).
A. B.
C. D.
二、填空题
13.如图,平面直角坐标系xoy中,直线y1=k1x+b1的图像与直线y2=k2x+b2的图像相交于点(-1,-3),当y1<y2时,实数x的取值范围为 .
14.已知,且.
的取值范围是 ;
若设,则m的最大值是 .
15.如图,两个一次函数y=kx+b与y=mx+n的图象分别为直线l1和l2,l1与l2交于点A(1,p),l1与x轴交于点B(-2,0),l2与x轴交于点C(4,0),则不等式组0<mx+n<kx+b的解集为 .
16.一次函数y=kx+b的图象如图所示,则由图象可知关于x的方程kx+b=0的解为 .
17.已知一次函数的图象经过点,与x轴的交点为B,若,则这个一次函数的解析式为 .
三、解答题
18.古人常说:“读书可以启智,读书可以明理,读书可以医愚”,读书不但可以让人增长智慧,开拓视野,而且还能让人明事理,知荣辱.某校为营造书香校园,计划购进个某品牌书架,已知该品牌书架的单价为200元/个,经过与厂家协商,厂家给出两种优惠方案:
方案一:所有书架均按原价的八折销售;
方案二:若一次购买不超过10个,则每个书架按原价的九折销售;若一次购买超过10个,则前10个打九折,超过的部分每个书架的价格在九折的基础上再降低30元.
(1)分别求方案一实际付款金额(元)和方案二实际付款金额(元)与之间的函数关系式;
(2)当时,请分别求出两种方案的实际付款金额,并判断选择哪种方案对学校来说更省钱.
19.通过实验获得u,v两个变量的各对应值如下表.
u 0 0.5 1 1.5 2 2.5 3 4
v 50 100 155 207 260 290 365 470
判断变量u,v是否满足或近似地满足一次函数关系式.如果是,求v关于u的函数式,并利用函数式求出当时函数v的值.
20.某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
21.“绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向A,B两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥;A,B两个果园分别需用110吨和70吨有机化肥.两个仓库到A,B两个果园的路程如表所示:
路程(千米)
甲仓库 乙仓库
A果园 15 25
B果园 20 20
设甲仓库运往A果园x吨有机化肥,若汽车每吨每千米的运费为2元,
(1)根据题意,填写下表.(温馨提示:请填写在答题卷相对应的表格内)
运量(吨) 运费(元)
甲仓库 乙仓库 甲仓库 乙仓库
A果园 x 110﹣x 2×15x 2×25(110﹣x)
B果园
(2)设总运费为y元,求y关于x的函数表达式,并求当甲仓库运往A果园多少吨有机化肥时,总运费最省?最省的总运费是多少元?
22.某市为鼓励居民节约用水,规定如下用水收费标准:每户每月的用水量不超过12吨(含12吨)时,水费按a元/吨收费;超过时,不超过12吨(含12吨)时,水费按a元/吨收费;超过时,不超过12吨的部分仍按a元/吨收费,超过的部分按b元/吨收费,已知该市小明家今年3月份和4月份的用水量、水费如表所示:
月份 用水量(立方米) 水费(元)
3 28 56
4 20 35.2
(1)求a,b的值;
(2)设某户1个月的用水量为x(吨),应交水费y(元),求出y与x之间的函数关系式;
(3)已知某户5月份的用水量为18吨,求该户5月份的水费.
23.如图:已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式:
(2)若直线y=2x-4与直线AB相交于点C,求点C的坐标;
(3)根据图象,直接写出关于x的不等式2x-4<kx+b的解集.
24.端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程米与时间分钟之间的函数关系图象如图所示,请你根据图象,回答下列问题:
这次龙舟赛的全程是______ 米,______ 队先到达终点;
求乙与甲相遇时乙的速度;
求出在乙队与甲相遇之前,他们何时相距100米?
《第二十六章一次函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C D C B D C B C
题号 11 12
答案 D C
1.C
【分析】只要把点的坐标代入一次函数的解析式,若左边=右边,则点在函数的图象上,反之就不在函数的图象上,代入检验即可.
【详解】解:A、把(-1,2)代入y=3x+1得:左边=2,右边=3×(-1)+1= -2,左边≠右边,故A选项错误;
B、把(0,-1)代入y=3x+1得:左边= -1,右边=3×0+1=1,左边≠右边,故B选项错误;
C、把(1,4)代入y=3x+1得:左边=4,右边=3×1+1=4,左边=右边,故C选项正确;
D、把(2,-7)代入y=3x+1得:左边= -7,右边=3×2+1=7,左边≠右边,故D选项错误.
故选C.
【点睛】本题考查对一次函数图象上点的坐标特征的理解和掌握,能根据点的坐标判断是否在函数的图象上是解题关键.
2.D
【分析】根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此即可确定函数的个数.
【详解】解:A,B,C的图象都满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故A、B、C的图象是函数,
D的图象不满足满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故D错误;
故选D.
【点睛】主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
3.C
【分析】分析表格得到销售价格每上涨10元,销售量就少10件,据此求解即可.
【详解】解:由表格可知,销售价格每上涨10元,销售量就少10件,
而当售价为120元时,销售量为60件,
所以当售价x=127时,y的值为53件,
故选:C.
【点睛】本题考查了利用表格表示函数关系,也可通过求函数解析式来解题.
4.D
【分析】根据函数的表示方法的优缺点分析解答即可.
【详解】A.用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化,此选项正确;
B.用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值,此选项正确;
C.用公式法表示函数关系,可以方便地计算函数值,此选项正确;
D.并不是任何函数关系都可以用上述三种方法来表示,此选项错误.
故选:D.
【点睛】本题考查函数的表示方法,明确三种表示方法的特点是解题的关键.
5.C
【分析】根据图象得到高度随时间的增大,高度增加的速度,即可判断.
【详解】根据图象可以得到:杯中水的高度随注水时间的增大而增大,而增加的速度越来越小.
则杯子应该是越向上开口越大.
故杯子的形状可能是.
故选:.
【点睛】本题考查了函数的图象,读函数的图象时首先要理解横纵坐标表示的含义,理解问题叙述的过程,能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小.
6.B
【详解】解:A、当x=﹣2时,y=﹣2×(﹣2)=4,即图象经过点(﹣2,4),不经过点(﹣2,1),故本选项错误,不符合题意;
B、由于k=﹣2<0,所以y随x的增大而减小,故本选项正确,符合题意;
C、由于k=﹣2<0,所以图象经过二、四象限,故本选项错误,不符合题意;
D、∵x>0时,y<0,x<0时,y>0,
∴不论x为何值,总有y<0错误,故本选项错误,不符合题意.
故选B.
7.D
【分析】通过待定系数法求出y与x的函数关系式,再将x=137代入求解.
【详解】解:设售量y件与销售价x元之间的关系为y=kx+b,
将x=90,y=90与x=100,y=80分别代入可得:,
解得,
∴y=﹣x+180,
将x=137代入可得y=43,
故选:D.
【点睛】此题主要考查一次函数的实际应用,解题的关键是根据待定系数法求出函数解析式.
8.C
【详解】①由图可知打电话时,小刚和妈妈的距离为1250米是正确的;
②因为打完电话后5分钟两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,经过5+15+3=23分钟小刚到达学校,所以是正确的;
③打完电话后5分钟两人相遇后,妈妈的速度是1250÷5﹣100=150米/分,走的路程为150×5=750米,回家的速度是750÷15=50米/分,所以回家的速度为150米/分是错误的;
④小刚家与学校的距离为750+(15+3)×100=2550米,所以是正确的.
正确的答案有①②④.
故选C.
9.B
【分析】本题考查一次函数图象上点的坐标特征,将点,代入解析式,即可求解.
【详解】解:∵一次函数的图象经过点,,
∴
解得:
∴,
故选:B.
10.C
【分析】根据两直线交点横坐标得到,再将x=0分别代入,可得.
【详解】解:∵,的交点横坐标为3,
∴令,将代入得,
∴,
∴,
∵当时,,,
∴.
故选C.
【点睛】本题考查了一次函数与一元一次方程,解题的关键是掌握两直线的交点坐标同时满足函数表达式.
11.D
【分析】根据函数图象及速度、时间、路程的关系依次判断即可得.
【详解】解:根据图象可得:
小强从家到公共汽车在步行了2公里,A选项正确;
,小强在公共汽车站等小明用了10分钟,B选项正确;
路程为17-2=15,时间为60-30=30,30分钟=0.5小时,
∴速度为:公里/小时,C选项正确;
60-30=30分钟,小强乘公共汽车用了30分钟,选项D错误;
故选:D.
【点睛】题目主要考查根据函数图象获取信息,理解题意,结合图象求解是解题关键.
12.C
【详解】过x轴上一点作x轴的垂线,若与函数图象有且仅有一个交点,则该图象表示函数的图象;若与函数图象有不止一个交点,则该图象不是函数图象,
在C图象中,与y轴平行的直线均与函数图象有两个交点,所以不是函数图象,其余的都只有一个交点,
故选C.
13.x<-1
【分析】直接根据直线y1的图象都在y2的图象下方,解答即可.
【详解】解:当x<-1时,函数y1=k1x+b1的图象都在y2=k2x+b2的图象下方,所以实数x的取值范围为:x<-1,
故答案为:x<-1.
【点睛】本题考查了一次函数与一元一次不等式,观察图象是关键.
14.
【详解】(1)用含x的代数式表示y,并代入中即可求出x的以值范围;
(2)先用含x的代数式表示m,再根据x的取值范围即可求出m的最大值.
解:(1)由可知,
又∵,
∴,
解得,
(2)∵,且,
∴,
即
又,
∴当,有最大值为,
∴最大值为.
15.1<x<4
【分析】先解不等式0<mx+n,结合图像可知上的点在轴的上方,可得< 再解mx+n<kx+b,结合图像可知上的点在的上方,可得> 从而可得0<mx+n<kx+b的解集.
【详解】解: 不等式0<mx+n,
上的点在轴的上方,
<
mx+n<kx+b,
上的点在的上方,
,
>
不等式组0<mx+n<kx+b的解集为1<<4,
故答案为:1<<4,
【点睛】本题考查的是一次函数与不等式组的关系,掌握利用一次函数的图像解不等式组是解题的关键.
16.x=﹣3
【分析】关于x的方程kx + b =0的解其实就是求当函数值为0时x的值,据此可以直接得到答案.
【详解】解:从图象上可知则关于x的方程kx+b=0的解为的解是:x=﹣3.
故答案为:x=﹣3.
【点睛】本题主要考查了一次函数与一元一次方程的关系,关键是知道通过图象怎么求方程的解.
17.或
【分析】由可知:点坐标为或,然后分两种情况利用待定系数法求一次函数的解析式.
【详解】解:由题意:,
∴点坐标为或.
①当一次函数的图象经过和时,
由题意得,
解得:,
∴这个一次函数的解析式为;
②当一次函数的图象经过和时,
由题意得,
解得:,
∴这个一次函数的解析式为.
综上所述,这个一次函数的解析式为或.
故答案为或.
【点睛】本题主要考查的是待定系数法求一次函数的解析式,尤其注意根据线段的长度,点坐标有两种情况,熟练掌握待定系数法是解本题的关键.
18.(1)
(2)3200元,3300元;选择方案一对学校来说更省钱
【详解】解:(1);
当时,,
当时,;
(2)当时,,,
选择方案一对学校来说更省钱.
19.u,v近似地满足一次函数关系式,,当时,v的值为281
【分析】直接利用一次函数的定义进行判定,再利用待定系数法求解即可.
【详解】解:u,v近似地满足一次函数关系式;
理由:由图中数据可知,当u的值依次增加1时,v的值都增加105,当u的值每增加0.5时,大部分的v的值都增加了50左右,因此,u,v近似地满足一次函数关系式.
设,
将、代入解析式可得:
,
解得:,
∴v关于u的函数式为:;
当时,;
∴u,v近似地满足一次函数关系式,;v的值为281.
【点睛】本题考查了一次函数的定义和待定系数法,解题关键是牢记一次函数的特点,并能利用待定系数法求解析式.
20.(1)20,5;(2)购进A种花草的数量为11株、B种20株,费用最省;最省费用是320元.
【分析】(1)设A种花草每棵的价格x元,B种花草每棵的价格y元,根据第一次分别购进A、B两种花草30棵和15棵,共花费940元;第二次分别购进A、B两种花草12棵和5棵,两次共花费675元;列出方程组,即可解答.(2)设A种花草的数量为m株,则B种花草的数量为(31-m)株,根据B种花草的数量少于A种花草的数量的2倍,得出m的范围,设总费用为W元,根据总费用=两种花草的费用之和建立函数关系式,由一次函数的性质就可以求出结论.
【详解】()设,两种花草每棵的价格分别为元和元.
由题意得,
解得:,
答:,两种花草价格分别为元和元.
()设购买种花草棵,则购买种花草为棵,
由题意得,且为整数,
解得:且为整数,
由()可知,的价格为元/棵,的价格为元/棵,
设费用为,
则,
由一次函数的性质可得:随的增大而增大,
∴当取最小整数时,最小值为:,
答:费用最省的方案为购买种花草棵,购买种花草棵,花费最少为元.
21.(1)80﹣x,x﹣10,2×20×(80﹣x),2×20×(x﹣10);(2)当甲仓库运往A果园80吨有机化肥时,总运费最省,最省的总运费是6700元.
【详解】分析:(1)设甲仓库运往A果园x吨有机化肥,根据题意求得甲仓库运往B果园(80-x)吨,乙仓库运往A果园(110-x)吨,乙仓库运往B果园(x-10)吨,然后根据两个仓库到A,B两个果园的路程完成表格;
(2)根据(1)中的表格求得总运费y(元)关于x(吨)的函数关系式,根据一次函数的增减性结合自变量的取值范围,可知当x=80时,总运费y最省,然后代入求解即可求得最省的总运费.
详解:(1)填表如下:
运量(吨) 运费(元)
甲仓库 乙仓库 甲仓库 乙仓库
A果园 x 110﹣x 2×15x 2×25(110﹣x)
B果园 80﹣x x﹣10 2×20×(80﹣x) 2×20×(x﹣10)
故答案为80﹣x,x﹣10,2×20×(80﹣x),2×20×(x﹣10);
(2)y=2×15x+2×25×(110﹣x)+2×20×(80﹣x)+2×20×(x﹣10),
即y关于x的函数表达式为y=﹣20x+8300,
∵﹣20<0,且10≤x≤80,
∴当x=80时,总运费y最省,此时y最小=﹣20×80+8300=6700.
故当甲仓库运往A果园80吨有机化肥时,总运费最省,最省的总运费是6700元.
点睛:此题考查了一次函数的实际应用问题.此题难度较大,解题的关键是理解题意,读懂表格,求得一次函数解析式,然后根据一次函数的性质求解.
22.(1)
(2)
(3)30
【分析】(1)由题意可知,3、4月都超出12吨,所以费用应该由两部分组成,列出方程组即可求出a、b的值;
(2)由于用水量不确定,所以需要分类讨论,第一种情况为当时,第二种情况为;
(3)由题意知,吨,代入(2)中相应的解析式即可求出5月份的水费.
【详解】(1)由题意列出方程为:,
解得:;
(2)当时,,
当时,,
综上所述:;
(3)令,
∴.
【点睛】本题考查了一次函数的应用,二元一次方程组的应用,准确理解题意,找出数量关系是解题的关键.
23.(1)y=-x+5
(2)(3,2)
(3)x<3
【分析】(1)利用待定系数法即可求得函数的解析式;
(2)解两个函数解析式组成方程组即可求解;
(3)关于x的不等式2x-4
,解得:,
则直线AB的解析式是y=-x+5;
(2)根据题意得,
解得:,
则C的坐标是(3,2);
(3)根据图象可得不等式的解集是x<3.
【点睛】本题考查了待定系数法求一次函数的解析式,两直线的交点与二元一次方程组的解,一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
24.(1)1000,乙;(2)375米/分;(3)分或分.
【详解】试题分析:
(1)由图中所给数据信息可知,这次龙舟赛的全程是1000米,乙队先到达终点;
(2)由图中信息可知:乙是在比赛开始后的2.2分钟至3.8分钟之间和甲相遇的,这期间乙共行驶了600米,用时1.6分钟,由此即可求得此时乙的速度;
(3)由图中信息可求出甲的速度和乙在2.2分钟前的速度,这样设甲和乙相遇前x分钟时,两队相距100米,再分2.2分钟前和2.2分钟后两种情况求出答案即可.
试题解析:
(1)由图中信息可知,这次龙舟赛的全程是1000米,乙队先到达终点;
(2)由图中信息可知,乙是在比赛开始后的2.2分钟至3.8分钟之间和甲相遇的,这期间乙共行驶了600米,用时1.6分钟,
∴乙和甲相遇时的速度为:600÷(3.8-2.2)=375(米/分);
(3)由图中信息可知,甲的速度为:1000÷4=250(米/分),乙在2.2分钟前的速度为:400÷2.2=(米/分),
∴在2.2分钟时,甲、乙间的距离为:(米),
∴在2.2分钟之前和之后,各存在一次甲、乙相距100米的时刻,
设甲、乙在相遇之前,x分钟时相距100米,由题意可得:
或,
解得:或,
即甲、乙相遇前,在比赛开始后的第分钟和第2.6分钟时,两队相距100米.
点睛:解本题第3小题时,需先计算出2.2分钟时甲、乙的距离为150米,由此可知在2.2分钟之前和之后各存在一个时刻使两队间的距离为100米,这样即可分两种情况列出对应的方程求解,避免漏掉其中某种情况.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
