2024-2025学年期末全真模拟培优卷(含解析)五年级下册数学(人教版)
文档属性
| 名称 | 2024-2025学年期末全真模拟培优卷(含解析)五年级下册数学(人教版) |  | |
| 格式 | docx | ||
| 文件大小 | 410.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 16:47:53 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024-2025学年五年级下册数学期末全真模拟培优卷(人教版)
一、填空题
1.a是自然数,要使是真分数,则a最大是 ,要使是假分数,则a最小是 。
2.的分数单位是 ,再加 个这样的分数单位就是最小的质数。
3.三个连续的偶数,最小的数是a,这三个数的和是 。
4.甲数是乙数的,则甲数∶乙数=( )∶( );乙数∶甲数=( )∶( ),乙数是甲数的;甲数比乙数少( )%。
5.一个真分数,它的分子、分母同时加上一个相同的非零自然数后,所得到的新分数比原数一定 (用“相等”、“大”、“小”填空)。
6.生产一批齿轮,上半月完成了计划的 ,下半月完成了计划的 ,超额完成计划的 。
7.若m,n为两素数, 且3m+5n=31, 则m+n= 。
8.仓库原有一批货物,运走t后,又运进t,这时共有货物t。仓库原有货物 t。
9.将两个长、宽、高分别为3dm、4dm、5dm的长方体拼成一个大长方体,拼成的长方体的体积是 dm3,表面积最多减少 dm2。
10.在数轴上分别用A、B、C表示出 ,1 , 这三个分数所对应的点 ,并写出数轴上的点D、点E所对应的分数,点D ,点E 。
11.有7个分开摆放的棱长1cm的小正方体,把它们搭成一个几何体(如下图),表面积比原来减少了 cm2。
12. 一个长方体,如果长减少两厘米,宽和高不变,它的体积减少48立方厘米。如果宽增加3厘米,长和高不变都不变,它的体积增加99立方厘米。如果高增加4厘米,长和宽都不变它的体积增加352立方厘米, 那么原长方体的表面积是 。
13.15个零件里有1个是次品(次品重一些)。假如用天平称,至少称 次能保证找出次品。
14.一个立体图形从正面看是 ,从左面看是 。搭成这个立体图形(要求至少有一个面相接),至少需要 个小正方体。
15.有一个长方形(如下图),长80厘米,宽48厘米.如果把它分割成同样大小的正方形,这些正方形的边长最长是 厘米 可以分割成 个这样的正方形
二、判断题
16.一个无盖长方体纸箱的底面是正方形,高6.4cm,将侧面展开后恰好是一个正方形,这个纸箱的体积是40.96cm3。( )
17.长方体是特殊的正方体。( )
18.一个分数的分母不变,分子扩大到原来的3倍,分数值就扩大到原来的3倍。(
)
19.一个正方体的棱长扩大到它的2倍,它的表面积扩大到它的2倍,体积扩大到它的8倍。( )
20.合唱团有男生8人,女生10人,男生人数占合唱团人数的 。( )
21.升和亳升都是常用的容量单位。( )
22.47的因数比10的因数多。( )
23.长方体有时8条棱一样长
( )
三、单选题
24.一块红砖长25厘米,宽15厘米,用这样的红砖拼成一个正方形最少需要多少块?( )
A.15 B.12 C.75 D.8
25.下面4个正方体中,( )可能是用左图的展开图折成的。
A. B. C. D.
26.奇思用几个小正方体搭出了一个几何体,从左面、上面和正面看到的形状如图。这个几何体最少有( )个小立方体搭成的。
A.4 B.5 C.6
27.下列说法正确的是( )。
A.所有的质数都是奇数 B.所有的合数都是偶数
C.所有的奇数都是质数 D.除2以外,所有的偶数都是合数
28.下列各数中,既是15的因数又是12的因数的是( )。
A.7 B.5 C.9 D.3
29.如图,把大长方形的面积看成单位“1”,则斜线部分的面积用算式( )表示。
A. B. C.
30.有一个数,它既是9的约数,又是9的倍数的数是( )
A.3 B.18 C.9 D.81
31.从正面、右面和上面分别观察一个长方体,记录如下。这个长方体的体积是( )立方厘米。
A.45 B.60 C.80 D.100
32.六年级同学计划去探望革命老战士,妙妙准备了一个礼物,包装盒是一个长方体,该长方体上、下两个面是边长为25cm的正方形,棱长总和是320cm,它的高是( ) cm。
A.10 B.20 C.30
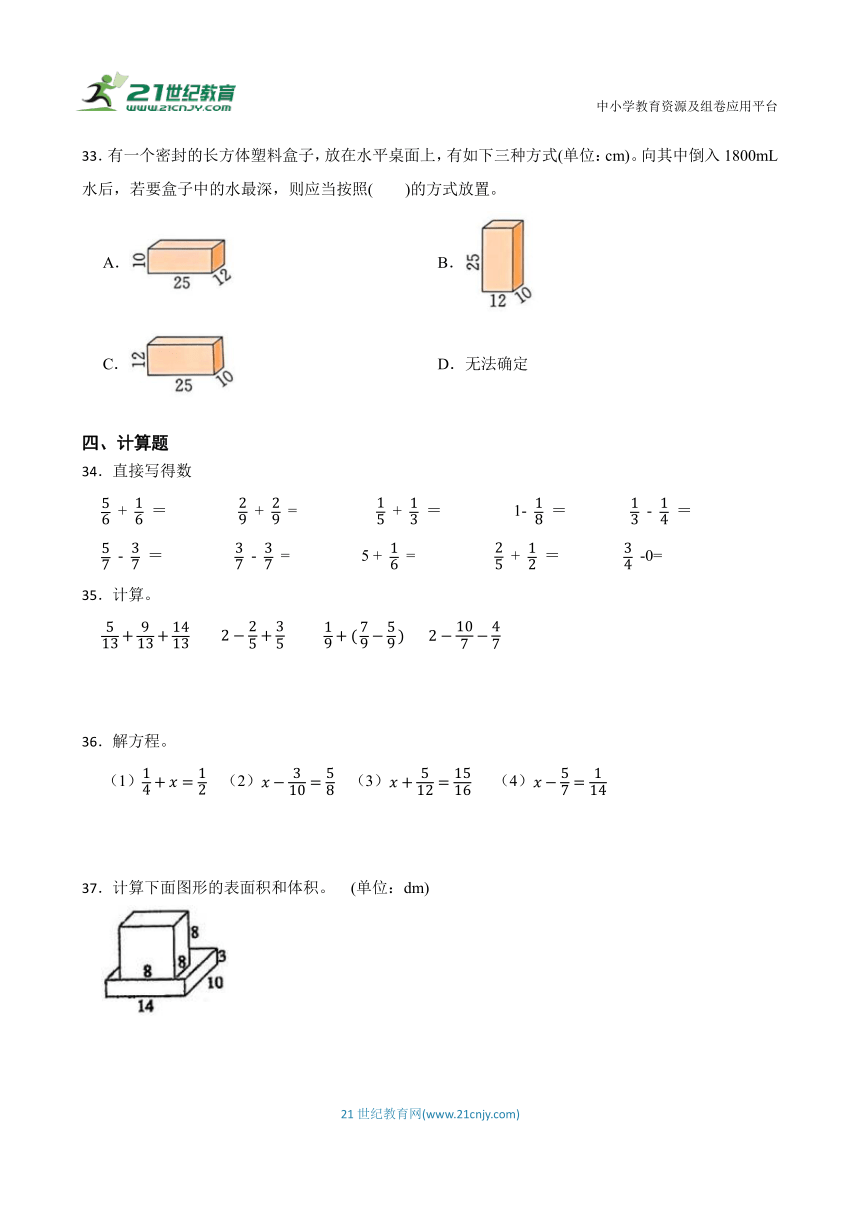
33.有一个密封的长方体塑料盒子,放在水平桌面上,有如下三种方式(单位:cm)。向其中倒入1800mL水后,若要盒子中的水最深,则应当按照( )的方式放置。
A. B.
C. D.无法确定
四、计算题
34.直接写得数
+ = + = + = 1- = - =
- = - = 5 + = + = -0=
35.计算。
36.解方程。
(1) (2) (3) (4)
37.计算下面图形的表面积和体积。 (单位:dm)
38.从一个大长方体上切下一个体积是126立方厘米的小长方体(如图)。剩下长方体的体积是多少立方厘米?
五、作图题
39.
(1)画出把图A向下平移3格后的图形。
(2)把图B绕O点顺时针旋转90°。
(3)画出图C的另一半,使它成为一个轴对称图形。
六、解决问题
40.一个礼盒(如下图),像这样用彩带捆扎起来,至少需要多长的彩带?(打结处需要25厘米)
41.我们从小就要养成保护动物的好习惯,动物园里有8只大象,5只长颈鹿,3只金丝猴。金丝猴是大象的几分之几?
42.一根长方体通风管,长是2.5米, 它的横截面是一个边长为5分米的正方形。要做4根这样的通风管至少需要铁皮多少平方米 (接头处忽略不计)
43.把一个长方体木块截成3个完全相同的正方体,3个正方体的棱长之和比原来正方体的棱长之和增加了160厘米,原来长方体的长是多少厘米?表面积是多少平方厘米?
44.一次考试,参加的学生中有得优,得良,得中,其余的得差,已知参加考试的学生不满50人,那么得差的学生有多少人?
45.在一张9行9列的方格纸上,把每个方格所在的行数和列数加起来,填在这个方格中,例如。问:填入的81个数字中是奇数多还是偶数多?
46.4月2日城北小学开展“党旗飘飘队旗红承古传今文化行”研学活动。五年级有526人,若6人一组,至少需要再来多少人就可以正好6人一组?至少减少多少人也正好6人一组?
47.小田在一个长和宽都是8厘米,高20厘米的长方体水中倒入12厘米高的水,再把5个一样大小的鸡蛋完全浸没在水中,这是测得水面高度是16厘米,算一算,平均每个鸡蛋的体积是多少立方厘米?
48.在学校举办的“书香少年”活动中,六(6)班同学取得了较好成绩,为表扬同学们,秦老师买了作文本112本,铅笔130支,橡皮70块,平均分给六(6)班的同学,结果作文本多出13本,铅笔少了2支,橡皮多出4块。六(6)班最多有多少人?
49.某小学组织五年级学生去春游.五(1)班有36人,五(2)班有42人,为了保证路上安全,老师要把每班分成人数相等的路队.每队最多有多少人?可以分成多少队?
参考答案及试题解析
1.【答案】8;9
【解析】 a是自然数,要使是真分数,则a-1=7,a=8;
要使是假分数,则a-1=8或a-1>8,a最小为9。
故答案为:8;9。
【分析】分子比分母小的分数叫真分数;
当假分数的分子与分母相等时,这个假分数最小,据此解答。
2.【答案】;11
3.【答案】3a+6
4.【答案】3;4;4;3;;25
5.【答案】大
【解析】由题意,得则
则。
故答案为:大。
【分析】利用已知条件和举例的方法,再结合分数的运算和分数的化简,进而由比较法比较出所得到的新分数比原数的大小。
6.【答案】
【解析】解:+-1
=-1
=。
故答案为:。
【分析】超额完成计划的分率=上半月完成计划的分率-下半月完成计划的分率-单位“1”。
7.【答案】7
【解析】解:根据题意,可得
因为3m+5n=31
所以3m与5n必有一个是偶数,一个是奇数
在质数中只有2是偶数,当m是2时,n正好是5
所以,m+n=7
故答案为:7
【分析】因为31是奇数,根据奇数+偶数=奇数,所以3m与5n必有一个是偶数,一个是奇数。3和5都是奇数,奇数乘偶数才能得偶数。所以m与n必有一个是偶数。在质数中只有2是偶数,当m是2时,n正好是5,满足条件,据此即可求解
8.【答案】
【解析】解:-+=+=(吨)
故答案为:
【分析】根据题意,用现有的货物重量减去运进的货物重量,再加上运走的货物重量即可得解。
9.【答案】120;40
【解析】解:3×4×5×2
=12×5×2
=60×2
=120(立方分米)
5×4×2
=20×2
=40(平方分米)。
故答案为:120;40。
【分析】拼成的长方体的体积=原来长方体的体积×2;其中,原来长方体的体积=长×宽×高;表面积最多减少的面积=最大的面的面积×2,其中,最大的面的面积=宽×高。
10.【答案】;4 ;5
【解析】解:;
这三个分数所对应的点A、B、C,点D,点E。
故答案为:;;。
【分析】根据对应的点和数的位置作答即可。
11.【答案】18
【解析】解:原来的表面积:1×1×6×7=42(平方厘米)
几何体的表面积:2×2×6=24(平方厘米)
42-24=18(平方厘米)
故答案为:18。
【分析】棱长×棱长×6=正方体的表面积,正方体的表面积×7=7个小正方体的表面积;棱长×棱长×6=大正方体的表面积,7个小正方体的表面积-大正方体的表面积=减少了面积。
12.【答案】290平方厘米
【解析】解:(48÷2+99÷3+352÷4)×2
=(24+33+88)×2
=145×2
=290(平方厘米)
原长方体的表面积是290平方厘米。
故答案为:290平方厘米。
【分析】首先根据题意,分别求出原长方体的宽×高,长×高,长×宽的面积,然后根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
13.【答案】3
【解析】 15个零件可以平均分成3份,每份是5个,第一次,天平的两边各放5个零件,如果平衡,第二次,把剩下的5个,天平的两边各放2个,如果平衡,剩下的1个即为次品,如果不平衡,第三次,把重的2个,天平两边每边放1个,哪边重,那边就是次品;
15个零件可以平均分成3份,每份是5个,第一次,天平的两边各放5个零件,如果不平衡,哪边重,次品就在那边,第二次,把重的那边的5个,天平的两边各放2个,如果平衡,剩下的1个即为次品,如果不平衡,第三次,把重的2个,天平两边每边放1个,哪边重,那边就是次品;所以,至少称3次能保证找出次品。
故答案为:3。
【分析】此题主要考查了找次品的知识,根据天平的平衡原理对托盘两边的物品进行比较,把待测物品分成三份,要分得尽量平均,能够均分的就平均分成3份,不能平均分的,也应该使多的一份与少的一份只相差1,据此解答。
14.【答案】6
【解析】解:根据分析可得至少需要小正方体的个数=4+1+1=6(个)。
故答案为:6。
【分析】 前一排下面一层有4个小正方体,前一排上面一层最右侧有一个正方体,因为至少有一个面相接,所以后一排有一个小正方体,即可满足从左面看到的图形,所以搭成这样的立体图形最少需要 4+1+1小正方体,据此即可得出答案。
15.【答案】16;15
【解析】解:80和48的最大公因数是16,
80÷16=5
48÷16=3
3×5=15(个)
故答案为:16,15.
【分析】根据求两个数最大公约数也就是这两个数的公有质因数的连乘积求解.
16.【答案】错误
【解析】解:6.4÷4=1.6(厘米)
1.6×1.6×6.4
=2.56×6.4
=16.384(立方厘米)
故答案为:错误。
【分析】这个纸箱的体积=底面积×高;其中,底面积=棱长×棱长;棱长=底面周长÷4=高÷4。
17.【答案】错误
【解析】正方体的概念是:长、宽、高都相等的长方体叫正方体.由此可知正方体是特殊的长方体.
故答案为:错误.
【分析】正方体是特殊的长方体.
18.【答案】正确
【解析】解:一个分数的分母不变,分子扩大到原来的3倍,分数值就扩大到原来的3倍,原题干说法正确。
故答案为:正确。
【分析】 一个分数的分子相等于除法中的被除数,分母相等于除数;一个分数的分母不变,分子扩大到原来的3倍,分数值就扩大到原来的3倍。
19.【答案】错误
【解析】解:2×2=4
2×2×2
=4×2
=8。
故答案为:错误。
【分析】正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,一个正方体的棱长扩大到它的2倍,它的表面积扩大到它的4倍,体积扩大到它的8倍。
20.【答案】正确
【解析】解:8÷(8+10)
=8÷18
=。
故答案为:正确。
【分析】男生人数占合唱团人数的分率=男生人数÷(男生人数+女生人数)。
21.【答案】正确
【解析】解:升和亳升都是常用的容量单位,原题干说法正确。
故答案为:正确。
【分析】常用的液体容积单位有升、毫升;固体容积单位有立方米、立方分米、立方厘米。
22.【答案】错误
【解析】解:47的因数只有1和47,
10的因数有1,2,5,10,
所以47的因数比10的因数少,原题说法错误。
故答案为:错误。
【分析】因数计算方法:如果一个自然数能写成两个自然数的乘积,那么这两个自然数就叫作原来那个数的因数。本题先写出47和10的所有因数,即可得出因数的个数,再比较即可得出答案。
23.【答案】正确
【解析】长方体有时8条棱一样长,说法正确。
【分析】如果在长方体中有两个对面是正方形时,它就有8条棱是一样长的。
24.【答案】A
【解析】解:25和15的最小公倍数是75,所以正方形的边长是75厘米,
(75÷25)×(75÷15)
=3×5
=15(块)
故答案为:A。
【分析】拼成的正方形的边长最少是25和15的最小公倍数,因此先确定正方形最少的边长。用边长分别除以长方形的长和宽,再把两个商相乘就是需要的块数。
25.【答案】C
【解析】解:A.有斜纹的长方形的长(长边)与梅花的对称轴垂直,A错误;
B.黑色长方形的面与有梅花的面相对,B错误;
C.梅花的三个相邻面都是空白面,A符合;
D.有斜纹的长方形的长(长边)与梅花的对称轴垂直,D错误;
故答案为:C。
【分析】根据正方体的展开图知识,此图属于正方体展开图的“1-4-1”型,折成正方体后,有黑色长方形的面与有梅花的面相对,有斜纹长方形的面与空白的相对。然后两个空白的面相对;相邻的面,有斜纹的长方形的长(长边)与梅花的对称轴垂直,据此可排除图形4、图形B、图形D,唯有形C可以由此图折成,据此解答即可。
26.【答案】C
【解析】解:5+1=6(个)。
故答案为:C。
【分析】这个几何体从上面看到5个小正方形,从正方面看到2层,那么第二层至少有1个小正方体,至少共6个。
27.【答案】D
【解析】解:A项:质数2就是偶数,原题干说法错误;
B项:合数9、15等都是奇数,原题干说法错误;
C项:奇数9、15等都是合数,原题干说法错误;
D项:除2以外,所有的偶数都是合数,原题干说法正确。
故答案为:D。
【分析】质数有偶数或奇数;合数有偶数或奇数;除2以外,所有的偶数都是合数。
28.【答案】D
【解析】15的因数有:1、3、5、15;
12的因数有:1、2、3、4、6、12;
既是15的因数又是12的因数的是3。
故答案为:D。
【分析】根据题意可知,先列举出15的因数和12的因数,然后找出它们共同的因数,据此解答。
29.【答案】B
【解析】解:4份涂色,表示,1份涂斜线,表示,所以算式是 。
股答案为:B
【分析】把大长方形的面积看成单位“1”,把它平均分成5份,每份是它的,其中4份涂色,表示;再把涂色部分看作单位“1”,把它平均分成3份,每份是它的,其中1份涂斜线,表示,求斜线部分的面积就是求的是多少,用乘法 计算。
30.【答案】C
【解析】一个数既是9的约数,又是9的倍数,这个数是9.
故答案为:C
【分析】一个数最大的约数是它本身,最小的倍数是它本身,所以一个数既是它最大的约数,又是它最小的倍数;由此选择即可.
31.【答案】B
【解析】解:3×4×5=60立方厘米,所以这个长方体的体积是60立方厘米。
故答案为:B。
【分析】从图中可以看出,一共得到三个数据,每个数据都出现了两次,所以这三个数据分别是长方体的长、宽、高,而长方体的体积=长×宽×高。
32.【答案】C
【解析】解:高是(320-25×8)÷4=30(cm)。
故答案为:C。
【分析】根据题意“ 长方体上、下两个面是边长为25cm的正方形 ”,也就是说这个长方体的长和宽都是25厘米,一共由8条25厘米长的棱,据此得到4条高之和是:320-25×8=120(厘米),然后再求出1条高的长度是120÷4=30(cm)。
33.【答案】B
【解析】解:1800mL=1800cm3
A:1800÷(25×12)
=1800÷300
=6(cm)
B:1800÷(12×10)
=1800÷120
=15(cm)
C:1800÷(25×10)
=1800÷250
=7.2(cm)
15>7.2>6
故答案为:B。
【分析】根据题意可知水的体积不会改变,即三种摆放方式盒子中水的体积是不变的,因此,根据:水的体积÷(长×宽)=水的高,分别计算出三种摆放方式盒子中水的高,再比较大小即可判断;计算前先统一单位:1mL=1cm3。
34.【答案】 + =1 + = + = 1- = - =
- = - =0 5+ =5 + = -0=
【解析】根据分数加法和减法的计算法则即可解答。
同分母分数加减法计算方法:同分母分数相加减,只把分子相加减,分母不变。
异分母分数加减法计算方法:先通分,然后按照同分母分数加减法的的法则进行计算。
35.【答案】解:++
=+
=
2-+
=+
=
+(-)
=+
=
2--
=2-(+)
=2-2
=0
【解析】加减混合运算运算,按从左往右的顺序计算,也可以根据数据特点,调换加减法的顺序;
算式一,同分母分数连加,按从左往右的顺序计算;
算式二,算式中只有加减法,按从左往右的顺序计算;
算式三,算式中有小括号,先算小括号里面的,再算小括号外面的;
算式四,根据减法的性质,一个数连续减去两个数,等于减去这两个数的和。
36.【答案】(1) +x=
解:+x-=-
x=
(2) x-=
解:x-+=+
x=
(3) x+=
解:x+-=-
x=
(4) x-=
解:x-+=+
x=
【解析】根据等式的性质1:等式的两边同时加减相同的数,等式仍然成立,据此解方程.
37.【答案】解:(14×10+10×3+3×14)×2+8×8×4
=(140+30+42)×2+256
=424+256
=680(平方分米)
14×10×3+8×8×8
=420+512
=932(立方分米)
【解析】组合体的表面积=长是14厘米,宽是10厘米,高是3厘米的长方体的表面积+棱长是8厘米的正方体的侧面积;根据长方体的表面积=(长×宽+长×高+宽×高)×2,正方体侧面积=棱长×棱长×4,代入数据,求出组合体的表面积;
组合体的体积=长方体的体积+棱长是8厘米的正方体的体积,根据长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,代入数据,即可解答。
38.【答案】解:126÷6×(20-6)
=21×14
=294(立方厘米)
答:剩下长方体的体积是294立方厘米。
【解析】剩下长方体的体积=切掉的体积÷切掉的高×(原来长方体的长-切掉的长)。
39.【答案】(1)
(2)
(3)
【解析】(1)先把图形中的关键点都按题干要求的方向和格数移动,然后再连接各点;
(2)旋转后图形的位置改变,转动的中心点、形状、大小不变。因此画图时,先弄清楚旋转的方向和角度,找准关键线段旋转后的位置,据此作图即可;
(3)补全轴对称图形方法:根据对称点到对称轴的距离相等,找出各个关键点的对称点,然后再连线。
40.【答案】解:15×2+8×2+10×4+25
=30+16+40+25
=86+25
=111(厘米)
答:至少需要111厘米的彩带。
【解析】根据题意及看图可知彩带由2条长方体礼盒的长、2条宽、4条高和打结处组成,因此,长×2+宽×2+高×4+打结处的长度=彩带的长度。
41.【答案】解:3÷8=
答:金丝猴是大象的。
【解析】金丝猴是大象的几分之几=金丝猴的只数÷大象的只数,据此代入数值作答即可。
42.【答案】解:5分米=0.5米
2.5×0.5×4×4
=1.25×4×4
=5×4
=20(平方米)
答:要做4根这样的通风管至少需要铁皮20平方米。
【解析】要做4根这样的通风管至少需要铁皮的面积=长方体通风管的长×底面边长×4×做的根数。
43.【答案】解: (厘米), (平方厘米)
答:原来长方体的长是30厘米,表面积是1400平方厘米。
【解析】把一个长方体木块截成3个完全相同的正方体,多了4个面,多了16个棱长,一个棱长是160÷16=10厘米,原来长方体的长是10×3=30厘米。长方体的长宽高分别是30厘米、10厘米、10厘米,(长×宽+长×高+宽×高)×2=长方体的表面积。
44.【答案】解:由题意“参加的学生中有 得优, 得良, 得中”,可知参加考试的学生人数是7,3,2的倍数,因为7,2,3的最小公倍数为42, ,所以参加的学生总数为42人,那么得差的学生有: (人)。
答:得差的学生有1人。
【解析】根据分数的意义结合人数的特殊性可知,学生数一定是7、3、2的倍数,先确定7、3、2的最小公倍数,然后根据学生人数的范围确定学生总数。用1减去得优、得良、得中的分率即可求出得差的人数占总人数的几分之几,然后根据分数乘法的意义求出得差的学生人数即可。
45.【答案】解:填入的81个数字中偶数多。
【解析】应该从整体上去比较奇偶数的多少。已知奇数行偶数多一个,偶数行奇数多1个。所以前8行中奇偶数一样,余下第9行奇数行,所以偶数多。
46.【答案】解:526÷6=87(组)······4(人)
6-4=2(人)
答:至少需要再来2人就可以正好6人一组,至少减少4人也正好6人一组。
【解析】可以分的组数=总人数÷平均每组的人数······余下的人数,至少减少的人数=余下的人数,至少再来的人数=平均每组的人数-余下的人数。
47.【答案】解:8×8×(16-12)÷5
=8×8×4÷5
=256÷5
=51.2(立方厘米)
答:平均每个鸡蛋的体积是51.2立方厘米。
【解析】根据题意可知,每个鸡蛋的体积等于上升的水的体积÷鸡蛋的个数=平均每个鸡蛋的体积,据此列式解答。
48.【答案】解:112-13=99(本)
130+2=132(支)
70-4=66(块)
99、132 和66的最大公因数是33
答:六(6)班最多有33人。
【解析】根据条件可得:作业本112本减去13本是99本,余下的99是这个班的同学人数的整数倍,铅笔130支加上2支一共是132支,132是这个班的同学人数的整数倍,橡皮70块减去4块可得66块,66是这个班的同学人数的整数倍,所以这个班最多人数就是99、132和66的最大公因数,据此解答。
49.【答案】解:36=2×2×3×3
42=2×3×7
36和24的最大公因数是=2×3=6,所以每队最多6人.
36÷6+42÷6
=6+7
=13(队)
答:每队最多有6人,可以分成13队。
【解析】根据题意可知,要求每队最多有几人,就是求36和42的最大公因数,据此先把36、42分解质因数,然后求出它们的最大公因数,也就是每队最多的人数,然后用五(1)班的人数÷每队的人数+五(2)班的人数÷每队的人数=一共可以分的队数,据此列式解答.
21世纪教育网(www.21cnjy.com)
2024-2025学年五年级下册数学期末全真模拟培优卷(人教版)
一、填空题
1.a是自然数,要使是真分数,则a最大是 ,要使是假分数,则a最小是 。
2.的分数单位是 ,再加 个这样的分数单位就是最小的质数。
3.三个连续的偶数,最小的数是a,这三个数的和是 。
4.甲数是乙数的,则甲数∶乙数=( )∶( );乙数∶甲数=( )∶( ),乙数是甲数的;甲数比乙数少( )%。
5.一个真分数,它的分子、分母同时加上一个相同的非零自然数后,所得到的新分数比原数一定 (用“相等”、“大”、“小”填空)。
6.生产一批齿轮,上半月完成了计划的 ,下半月完成了计划的 ,超额完成计划的 。
7.若m,n为两素数, 且3m+5n=31, 则m+n= 。
8.仓库原有一批货物,运走t后,又运进t,这时共有货物t。仓库原有货物 t。
9.将两个长、宽、高分别为3dm、4dm、5dm的长方体拼成一个大长方体,拼成的长方体的体积是 dm3,表面积最多减少 dm2。
10.在数轴上分别用A、B、C表示出 ,1 , 这三个分数所对应的点 ,并写出数轴上的点D、点E所对应的分数,点D ,点E 。
11.有7个分开摆放的棱长1cm的小正方体,把它们搭成一个几何体(如下图),表面积比原来减少了 cm2。
12. 一个长方体,如果长减少两厘米,宽和高不变,它的体积减少48立方厘米。如果宽增加3厘米,长和高不变都不变,它的体积增加99立方厘米。如果高增加4厘米,长和宽都不变它的体积增加352立方厘米, 那么原长方体的表面积是 。
13.15个零件里有1个是次品(次品重一些)。假如用天平称,至少称 次能保证找出次品。
14.一个立体图形从正面看是 ,从左面看是 。搭成这个立体图形(要求至少有一个面相接),至少需要 个小正方体。
15.有一个长方形(如下图),长80厘米,宽48厘米.如果把它分割成同样大小的正方形,这些正方形的边长最长是 厘米 可以分割成 个这样的正方形
二、判断题
16.一个无盖长方体纸箱的底面是正方形,高6.4cm,将侧面展开后恰好是一个正方形,这个纸箱的体积是40.96cm3。( )
17.长方体是特殊的正方体。( )
18.一个分数的分母不变,分子扩大到原来的3倍,分数值就扩大到原来的3倍。(
)
19.一个正方体的棱长扩大到它的2倍,它的表面积扩大到它的2倍,体积扩大到它的8倍。( )
20.合唱团有男生8人,女生10人,男生人数占合唱团人数的 。( )
21.升和亳升都是常用的容量单位。( )
22.47的因数比10的因数多。( )
23.长方体有时8条棱一样长
( )
三、单选题
24.一块红砖长25厘米,宽15厘米,用这样的红砖拼成一个正方形最少需要多少块?( )
A.15 B.12 C.75 D.8
25.下面4个正方体中,( )可能是用左图的展开图折成的。
A. B. C. D.
26.奇思用几个小正方体搭出了一个几何体,从左面、上面和正面看到的形状如图。这个几何体最少有( )个小立方体搭成的。
A.4 B.5 C.6
27.下列说法正确的是( )。
A.所有的质数都是奇数 B.所有的合数都是偶数
C.所有的奇数都是质数 D.除2以外,所有的偶数都是合数
28.下列各数中,既是15的因数又是12的因数的是( )。
A.7 B.5 C.9 D.3
29.如图,把大长方形的面积看成单位“1”,则斜线部分的面积用算式( )表示。
A. B. C.
30.有一个数,它既是9的约数,又是9的倍数的数是( )
A.3 B.18 C.9 D.81
31.从正面、右面和上面分别观察一个长方体,记录如下。这个长方体的体积是( )立方厘米。
A.45 B.60 C.80 D.100
32.六年级同学计划去探望革命老战士,妙妙准备了一个礼物,包装盒是一个长方体,该长方体上、下两个面是边长为25cm的正方形,棱长总和是320cm,它的高是( ) cm。
A.10 B.20 C.30
33.有一个密封的长方体塑料盒子,放在水平桌面上,有如下三种方式(单位:cm)。向其中倒入1800mL水后,若要盒子中的水最深,则应当按照( )的方式放置。
A. B.
C. D.无法确定
四、计算题
34.直接写得数
+ = + = + = 1- = - =
- = - = 5 + = + = -0=
35.计算。
36.解方程。
(1) (2) (3) (4)
37.计算下面图形的表面积和体积。 (单位:dm)
38.从一个大长方体上切下一个体积是126立方厘米的小长方体(如图)。剩下长方体的体积是多少立方厘米?
五、作图题
39.
(1)画出把图A向下平移3格后的图形。
(2)把图B绕O点顺时针旋转90°。
(3)画出图C的另一半,使它成为一个轴对称图形。
六、解决问题
40.一个礼盒(如下图),像这样用彩带捆扎起来,至少需要多长的彩带?(打结处需要25厘米)
41.我们从小就要养成保护动物的好习惯,动物园里有8只大象,5只长颈鹿,3只金丝猴。金丝猴是大象的几分之几?
42.一根长方体通风管,长是2.5米, 它的横截面是一个边长为5分米的正方形。要做4根这样的通风管至少需要铁皮多少平方米 (接头处忽略不计)
43.把一个长方体木块截成3个完全相同的正方体,3个正方体的棱长之和比原来正方体的棱长之和增加了160厘米,原来长方体的长是多少厘米?表面积是多少平方厘米?
44.一次考试,参加的学生中有得优,得良,得中,其余的得差,已知参加考试的学生不满50人,那么得差的学生有多少人?
45.在一张9行9列的方格纸上,把每个方格所在的行数和列数加起来,填在这个方格中,例如。问:填入的81个数字中是奇数多还是偶数多?
46.4月2日城北小学开展“党旗飘飘队旗红承古传今文化行”研学活动。五年级有526人,若6人一组,至少需要再来多少人就可以正好6人一组?至少减少多少人也正好6人一组?
47.小田在一个长和宽都是8厘米,高20厘米的长方体水中倒入12厘米高的水,再把5个一样大小的鸡蛋完全浸没在水中,这是测得水面高度是16厘米,算一算,平均每个鸡蛋的体积是多少立方厘米?
48.在学校举办的“书香少年”活动中,六(6)班同学取得了较好成绩,为表扬同学们,秦老师买了作文本112本,铅笔130支,橡皮70块,平均分给六(6)班的同学,结果作文本多出13本,铅笔少了2支,橡皮多出4块。六(6)班最多有多少人?
49.某小学组织五年级学生去春游.五(1)班有36人,五(2)班有42人,为了保证路上安全,老师要把每班分成人数相等的路队.每队最多有多少人?可以分成多少队?
参考答案及试题解析
1.【答案】8;9
【解析】 a是自然数,要使是真分数,则a-1=7,a=8;
要使是假分数,则a-1=8或a-1>8,a最小为9。
故答案为:8;9。
【分析】分子比分母小的分数叫真分数;
当假分数的分子与分母相等时,这个假分数最小,据此解答。
2.【答案】;11
3.【答案】3a+6
4.【答案】3;4;4;3;;25
5.【答案】大
【解析】由题意,得则
则。
故答案为:大。
【分析】利用已知条件和举例的方法,再结合分数的运算和分数的化简,进而由比较法比较出所得到的新分数比原数的大小。
6.【答案】
【解析】解:+-1
=-1
=。
故答案为:。
【分析】超额完成计划的分率=上半月完成计划的分率-下半月完成计划的分率-单位“1”。
7.【答案】7
【解析】解:根据题意,可得
因为3m+5n=31
所以3m与5n必有一个是偶数,一个是奇数
在质数中只有2是偶数,当m是2时,n正好是5
所以,m+n=7
故答案为:7
【分析】因为31是奇数,根据奇数+偶数=奇数,所以3m与5n必有一个是偶数,一个是奇数。3和5都是奇数,奇数乘偶数才能得偶数。所以m与n必有一个是偶数。在质数中只有2是偶数,当m是2时,n正好是5,满足条件,据此即可求解
8.【答案】
【解析】解:-+=+=(吨)
故答案为:
【分析】根据题意,用现有的货物重量减去运进的货物重量,再加上运走的货物重量即可得解。
9.【答案】120;40
【解析】解:3×4×5×2
=12×5×2
=60×2
=120(立方分米)
5×4×2
=20×2
=40(平方分米)。
故答案为:120;40。
【分析】拼成的长方体的体积=原来长方体的体积×2;其中,原来长方体的体积=长×宽×高;表面积最多减少的面积=最大的面的面积×2,其中,最大的面的面积=宽×高。
10.【答案】;4 ;5
【解析】解:;
这三个分数所对应的点A、B、C,点D,点E。
故答案为:;;。
【分析】根据对应的点和数的位置作答即可。
11.【答案】18
【解析】解:原来的表面积:1×1×6×7=42(平方厘米)
几何体的表面积:2×2×6=24(平方厘米)
42-24=18(平方厘米)
故答案为:18。
【分析】棱长×棱长×6=正方体的表面积,正方体的表面积×7=7个小正方体的表面积;棱长×棱长×6=大正方体的表面积,7个小正方体的表面积-大正方体的表面积=减少了面积。
12.【答案】290平方厘米
【解析】解:(48÷2+99÷3+352÷4)×2
=(24+33+88)×2
=145×2
=290(平方厘米)
原长方体的表面积是290平方厘米。
故答案为:290平方厘米。
【分析】首先根据题意,分别求出原长方体的宽×高,长×高,长×宽的面积,然后根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
13.【答案】3
【解析】 15个零件可以平均分成3份,每份是5个,第一次,天平的两边各放5个零件,如果平衡,第二次,把剩下的5个,天平的两边各放2个,如果平衡,剩下的1个即为次品,如果不平衡,第三次,把重的2个,天平两边每边放1个,哪边重,那边就是次品;
15个零件可以平均分成3份,每份是5个,第一次,天平的两边各放5个零件,如果不平衡,哪边重,次品就在那边,第二次,把重的那边的5个,天平的两边各放2个,如果平衡,剩下的1个即为次品,如果不平衡,第三次,把重的2个,天平两边每边放1个,哪边重,那边就是次品;所以,至少称3次能保证找出次品。
故答案为:3。
【分析】此题主要考查了找次品的知识,根据天平的平衡原理对托盘两边的物品进行比较,把待测物品分成三份,要分得尽量平均,能够均分的就平均分成3份,不能平均分的,也应该使多的一份与少的一份只相差1,据此解答。
14.【答案】6
【解析】解:根据分析可得至少需要小正方体的个数=4+1+1=6(个)。
故答案为:6。
【分析】 前一排下面一层有4个小正方体,前一排上面一层最右侧有一个正方体,因为至少有一个面相接,所以后一排有一个小正方体,即可满足从左面看到的图形,所以搭成这样的立体图形最少需要 4+1+1小正方体,据此即可得出答案。
15.【答案】16;15
【解析】解:80和48的最大公因数是16,
80÷16=5
48÷16=3
3×5=15(个)
故答案为:16,15.
【分析】根据求两个数最大公约数也就是这两个数的公有质因数的连乘积求解.
16.【答案】错误
【解析】解:6.4÷4=1.6(厘米)
1.6×1.6×6.4
=2.56×6.4
=16.384(立方厘米)
故答案为:错误。
【分析】这个纸箱的体积=底面积×高;其中,底面积=棱长×棱长;棱长=底面周长÷4=高÷4。
17.【答案】错误
【解析】正方体的概念是:长、宽、高都相等的长方体叫正方体.由此可知正方体是特殊的长方体.
故答案为:错误.
【分析】正方体是特殊的长方体.
18.【答案】正确
【解析】解:一个分数的分母不变,分子扩大到原来的3倍,分数值就扩大到原来的3倍,原题干说法正确。
故答案为:正确。
【分析】 一个分数的分子相等于除法中的被除数,分母相等于除数;一个分数的分母不变,分子扩大到原来的3倍,分数值就扩大到原来的3倍。
19.【答案】错误
【解析】解:2×2=4
2×2×2
=4×2
=8。
故答案为:错误。
【分析】正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,一个正方体的棱长扩大到它的2倍,它的表面积扩大到它的4倍,体积扩大到它的8倍。
20.【答案】正确
【解析】解:8÷(8+10)
=8÷18
=。
故答案为:正确。
【分析】男生人数占合唱团人数的分率=男生人数÷(男生人数+女生人数)。
21.【答案】正确
【解析】解:升和亳升都是常用的容量单位,原题干说法正确。
故答案为:正确。
【分析】常用的液体容积单位有升、毫升;固体容积单位有立方米、立方分米、立方厘米。
22.【答案】错误
【解析】解:47的因数只有1和47,
10的因数有1,2,5,10,
所以47的因数比10的因数少,原题说法错误。
故答案为:错误。
【分析】因数计算方法:如果一个自然数能写成两个自然数的乘积,那么这两个自然数就叫作原来那个数的因数。本题先写出47和10的所有因数,即可得出因数的个数,再比较即可得出答案。
23.【答案】正确
【解析】长方体有时8条棱一样长,说法正确。
【分析】如果在长方体中有两个对面是正方形时,它就有8条棱是一样长的。
24.【答案】A
【解析】解:25和15的最小公倍数是75,所以正方形的边长是75厘米,
(75÷25)×(75÷15)
=3×5
=15(块)
故答案为:A。
【分析】拼成的正方形的边长最少是25和15的最小公倍数,因此先确定正方形最少的边长。用边长分别除以长方形的长和宽,再把两个商相乘就是需要的块数。
25.【答案】C
【解析】解:A.有斜纹的长方形的长(长边)与梅花的对称轴垂直,A错误;
B.黑色长方形的面与有梅花的面相对,B错误;
C.梅花的三个相邻面都是空白面,A符合;
D.有斜纹的长方形的长(长边)与梅花的对称轴垂直,D错误;
故答案为:C。
【分析】根据正方体的展开图知识,此图属于正方体展开图的“1-4-1”型,折成正方体后,有黑色长方形的面与有梅花的面相对,有斜纹长方形的面与空白的相对。然后两个空白的面相对;相邻的面,有斜纹的长方形的长(长边)与梅花的对称轴垂直,据此可排除图形4、图形B、图形D,唯有形C可以由此图折成,据此解答即可。
26.【答案】C
【解析】解:5+1=6(个)。
故答案为:C。
【分析】这个几何体从上面看到5个小正方形,从正方面看到2层,那么第二层至少有1个小正方体,至少共6个。
27.【答案】D
【解析】解:A项:质数2就是偶数,原题干说法错误;
B项:合数9、15等都是奇数,原题干说法错误;
C项:奇数9、15等都是合数,原题干说法错误;
D项:除2以外,所有的偶数都是合数,原题干说法正确。
故答案为:D。
【分析】质数有偶数或奇数;合数有偶数或奇数;除2以外,所有的偶数都是合数。
28.【答案】D
【解析】15的因数有:1、3、5、15;
12的因数有:1、2、3、4、6、12;
既是15的因数又是12的因数的是3。
故答案为:D。
【分析】根据题意可知,先列举出15的因数和12的因数,然后找出它们共同的因数,据此解答。
29.【答案】B
【解析】解:4份涂色,表示,1份涂斜线,表示,所以算式是 。
股答案为:B
【分析】把大长方形的面积看成单位“1”,把它平均分成5份,每份是它的,其中4份涂色,表示;再把涂色部分看作单位“1”,把它平均分成3份,每份是它的,其中1份涂斜线,表示,求斜线部分的面积就是求的是多少,用乘法 计算。
30.【答案】C
【解析】一个数既是9的约数,又是9的倍数,这个数是9.
故答案为:C
【分析】一个数最大的约数是它本身,最小的倍数是它本身,所以一个数既是它最大的约数,又是它最小的倍数;由此选择即可.
31.【答案】B
【解析】解:3×4×5=60立方厘米,所以这个长方体的体积是60立方厘米。
故答案为:B。
【分析】从图中可以看出,一共得到三个数据,每个数据都出现了两次,所以这三个数据分别是长方体的长、宽、高,而长方体的体积=长×宽×高。
32.【答案】C
【解析】解:高是(320-25×8)÷4=30(cm)。
故答案为:C。
【分析】根据题意“ 长方体上、下两个面是边长为25cm的正方形 ”,也就是说这个长方体的长和宽都是25厘米,一共由8条25厘米长的棱,据此得到4条高之和是:320-25×8=120(厘米),然后再求出1条高的长度是120÷4=30(cm)。
33.【答案】B
【解析】解:1800mL=1800cm3
A:1800÷(25×12)
=1800÷300
=6(cm)
B:1800÷(12×10)
=1800÷120
=15(cm)
C:1800÷(25×10)
=1800÷250
=7.2(cm)
15>7.2>6
故答案为:B。
【分析】根据题意可知水的体积不会改变,即三种摆放方式盒子中水的体积是不变的,因此,根据:水的体积÷(长×宽)=水的高,分别计算出三种摆放方式盒子中水的高,再比较大小即可判断;计算前先统一单位:1mL=1cm3。
34.【答案】 + =1 + = + = 1- = - =
- = - =0 5+ =5 + = -0=
【解析】根据分数加法和减法的计算法则即可解答。
同分母分数加减法计算方法:同分母分数相加减,只把分子相加减,分母不变。
异分母分数加减法计算方法:先通分,然后按照同分母分数加减法的的法则进行计算。
35.【答案】解:++
=+
=
2-+
=+
=
+(-)
=+
=
2--
=2-(+)
=2-2
=0
【解析】加减混合运算运算,按从左往右的顺序计算,也可以根据数据特点,调换加减法的顺序;
算式一,同分母分数连加,按从左往右的顺序计算;
算式二,算式中只有加减法,按从左往右的顺序计算;
算式三,算式中有小括号,先算小括号里面的,再算小括号外面的;
算式四,根据减法的性质,一个数连续减去两个数,等于减去这两个数的和。
36.【答案】(1) +x=
解:+x-=-
x=
(2) x-=
解:x-+=+
x=
(3) x+=
解:x+-=-
x=
(4) x-=
解:x-+=+
x=
【解析】根据等式的性质1:等式的两边同时加减相同的数,等式仍然成立,据此解方程.
37.【答案】解:(14×10+10×3+3×14)×2+8×8×4
=(140+30+42)×2+256
=424+256
=680(平方分米)
14×10×3+8×8×8
=420+512
=932(立方分米)
【解析】组合体的表面积=长是14厘米,宽是10厘米,高是3厘米的长方体的表面积+棱长是8厘米的正方体的侧面积;根据长方体的表面积=(长×宽+长×高+宽×高)×2,正方体侧面积=棱长×棱长×4,代入数据,求出组合体的表面积;
组合体的体积=长方体的体积+棱长是8厘米的正方体的体积,根据长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,代入数据,即可解答。
38.【答案】解:126÷6×(20-6)
=21×14
=294(立方厘米)
答:剩下长方体的体积是294立方厘米。
【解析】剩下长方体的体积=切掉的体积÷切掉的高×(原来长方体的长-切掉的长)。
39.【答案】(1)
(2)
(3)
【解析】(1)先把图形中的关键点都按题干要求的方向和格数移动,然后再连接各点;
(2)旋转后图形的位置改变,转动的中心点、形状、大小不变。因此画图时,先弄清楚旋转的方向和角度,找准关键线段旋转后的位置,据此作图即可;
(3)补全轴对称图形方法:根据对称点到对称轴的距离相等,找出各个关键点的对称点,然后再连线。
40.【答案】解:15×2+8×2+10×4+25
=30+16+40+25
=86+25
=111(厘米)
答:至少需要111厘米的彩带。
【解析】根据题意及看图可知彩带由2条长方体礼盒的长、2条宽、4条高和打结处组成,因此,长×2+宽×2+高×4+打结处的长度=彩带的长度。
41.【答案】解:3÷8=
答:金丝猴是大象的。
【解析】金丝猴是大象的几分之几=金丝猴的只数÷大象的只数,据此代入数值作答即可。
42.【答案】解:5分米=0.5米
2.5×0.5×4×4
=1.25×4×4
=5×4
=20(平方米)
答:要做4根这样的通风管至少需要铁皮20平方米。
【解析】要做4根这样的通风管至少需要铁皮的面积=长方体通风管的长×底面边长×4×做的根数。
43.【答案】解: (厘米), (平方厘米)
答:原来长方体的长是30厘米,表面积是1400平方厘米。
【解析】把一个长方体木块截成3个完全相同的正方体,多了4个面,多了16个棱长,一个棱长是160÷16=10厘米,原来长方体的长是10×3=30厘米。长方体的长宽高分别是30厘米、10厘米、10厘米,(长×宽+长×高+宽×高)×2=长方体的表面积。
44.【答案】解:由题意“参加的学生中有 得优, 得良, 得中”,可知参加考试的学生人数是7,3,2的倍数,因为7,2,3的最小公倍数为42, ,所以参加的学生总数为42人,那么得差的学生有: (人)。
答:得差的学生有1人。
【解析】根据分数的意义结合人数的特殊性可知,学生数一定是7、3、2的倍数,先确定7、3、2的最小公倍数,然后根据学生人数的范围确定学生总数。用1减去得优、得良、得中的分率即可求出得差的人数占总人数的几分之几,然后根据分数乘法的意义求出得差的学生人数即可。
45.【答案】解:填入的81个数字中偶数多。
【解析】应该从整体上去比较奇偶数的多少。已知奇数行偶数多一个,偶数行奇数多1个。所以前8行中奇偶数一样,余下第9行奇数行,所以偶数多。
46.【答案】解:526÷6=87(组)······4(人)
6-4=2(人)
答:至少需要再来2人就可以正好6人一组,至少减少4人也正好6人一组。
【解析】可以分的组数=总人数÷平均每组的人数······余下的人数,至少减少的人数=余下的人数,至少再来的人数=平均每组的人数-余下的人数。
47.【答案】解:8×8×(16-12)÷5
=8×8×4÷5
=256÷5
=51.2(立方厘米)
答:平均每个鸡蛋的体积是51.2立方厘米。
【解析】根据题意可知,每个鸡蛋的体积等于上升的水的体积÷鸡蛋的个数=平均每个鸡蛋的体积,据此列式解答。
48.【答案】解:112-13=99(本)
130+2=132(支)
70-4=66(块)
99、132 和66的最大公因数是33
答:六(6)班最多有33人。
【解析】根据条件可得:作业本112本减去13本是99本,余下的99是这个班的同学人数的整数倍,铅笔130支加上2支一共是132支,132是这个班的同学人数的整数倍,橡皮70块减去4块可得66块,66是这个班的同学人数的整数倍,所以这个班最多人数就是99、132和66的最大公因数,据此解答。
49.【答案】解:36=2×2×3×3
42=2×3×7
36和24的最大公因数是=2×3=6,所以每队最多6人.
36÷6+42÷6
=6+7
=13(队)
答:每队最多有6人,可以分成13队。
【解析】根据题意可知,要求每队最多有几人,就是求36和42的最大公因数,据此先把36、42分解质因数,然后求出它们的最大公因数,也就是每队最多的人数,然后用五(1)班的人数÷每队的人数+五(2)班的人数÷每队的人数=一共可以分的队数,据此列式解答.
21世纪教育网(www.21cnjy.com)
同课章节目录
