9.4中心对称 第1课时 课件(共22张PPT) 华东师大版(2024)数学七年级下册
文档属性
| 名称 | 9.4中心对称 第1课时 课件(共22张PPT) 华东师大版(2024)数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 06:59:13 | ||
图片预览




文档简介
(共22张PPT)
9.4 中心对称
【第9章 轴对称、平移与旋转】
第1课时
数学华东师大版(2024)七年级下册
1.理解中心对称概念,区分中心对称图形与成中心对称的图形,运用性质解决图案设计及生活图案分析等问题;
2.借助观察、操作等活动,增强空间观念、直观想象能力,在解决问题中锻炼数学建模与问题解决能力;
3.探究中心对称性质时,体悟从特殊到一般、类比归纳思想,提升逻辑推理与抽象概括能力;
4.借欣赏生活图案激发数学兴趣,培养审美意识,通过小组合作培育团队精神,增强学习自信,养成严谨科学态度.
2.什么是旋转对称图形?
旋转一定角度后能与自身重合的图形叫做旋转对称图形.
1.图形旋转的特征是什么?
图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状和大小不变.
活动一:探究中心对称图形的概念
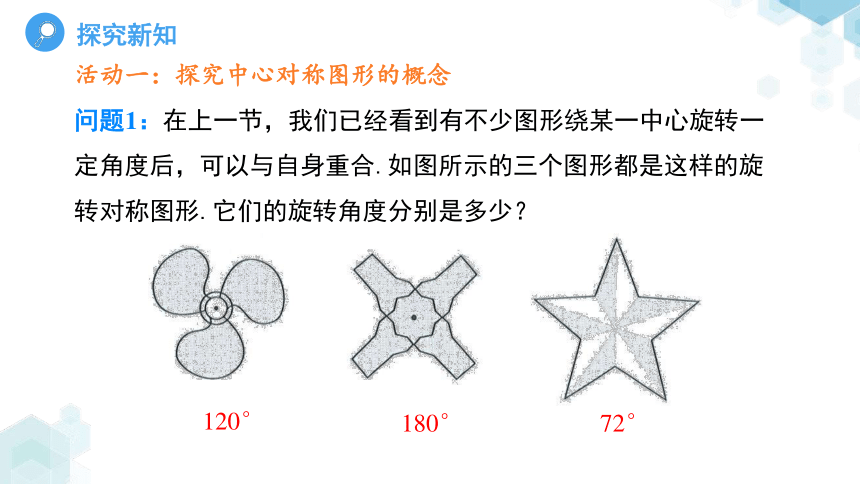
问题1:在上一节,我们已经看到有不少图形绕某一中心旋转一定角度后,可以与自身重合.如图所示的三个图形都是这样的旋转对称图形.它们的旋转角度分别是多少?
120°
180°
72°
活动一:探究中心对称图形的概念
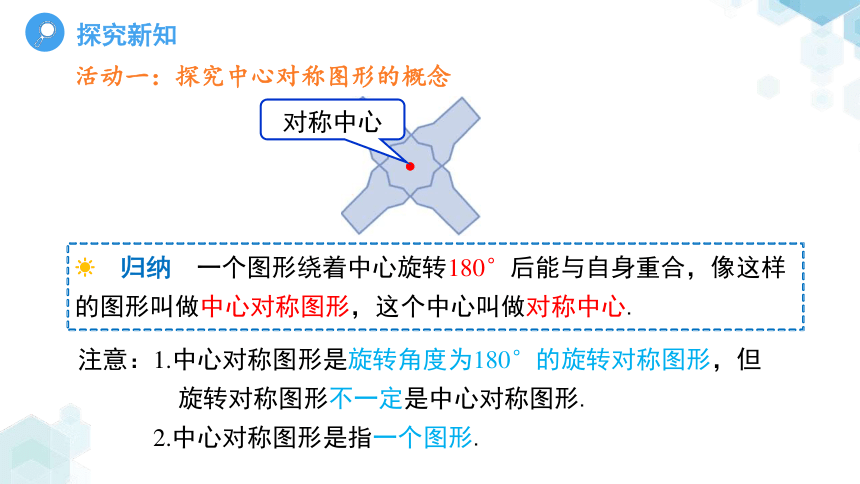
对称中心
注意:1.中心对称图形是旋转角度为180°的旋转对称图形,但
旋转对称图形不一定是中心对称图形.
2.中心对称图形是指一个图形.
归纳 一个图形绕着中心旋转180°后能与自身重合,像这样的图形叫做中心对称图形,这个中心叫做对称中心.
活动二:探究中心对称图形的特征
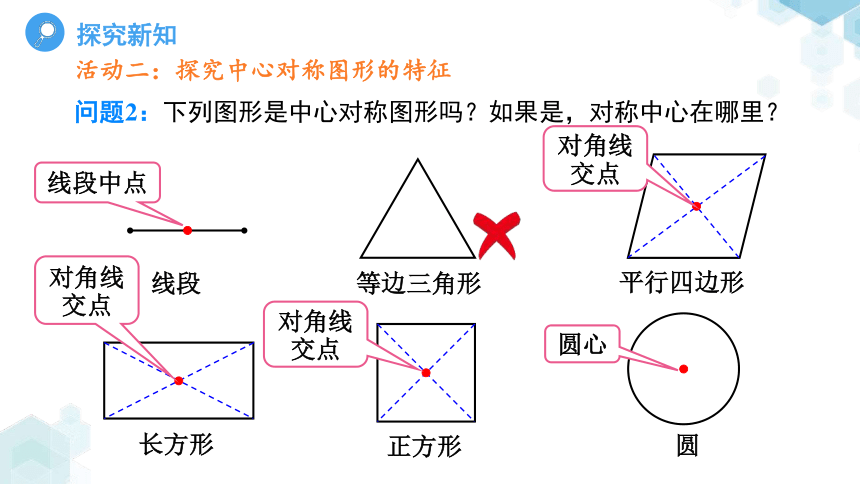
问题2:下列图形是中心对称图形吗?如果是,对称中心在哪里?
线段
等边三角形
平行四边形
长方形
正方形
圆
线段中点
对角线交点
对角线交点
对角线交点
圆心
归纳
(1) 中心对称图形的对称中心一定在图形内;
(2) 中心对称图形是针对一个图形而言的;
(3) 中心对称图形上所有的点关于对称中心的对称点都在这个图形本身上;
(4) 中心对称图形一定是旋转对称图形,但旋转对称图形不一定是中心对称图形.
活动二:探究中心对称图形的特征
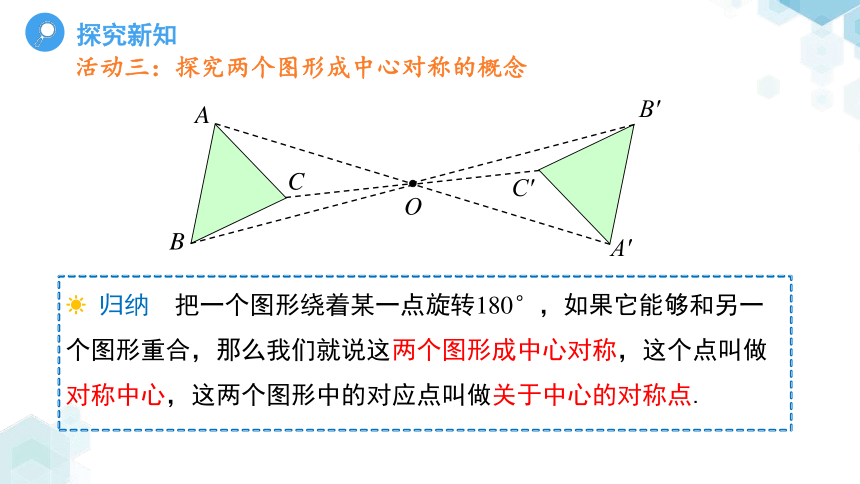
活动三:探究两个图形成中心对称的概念
A
B
C
O
A′
B′
C′
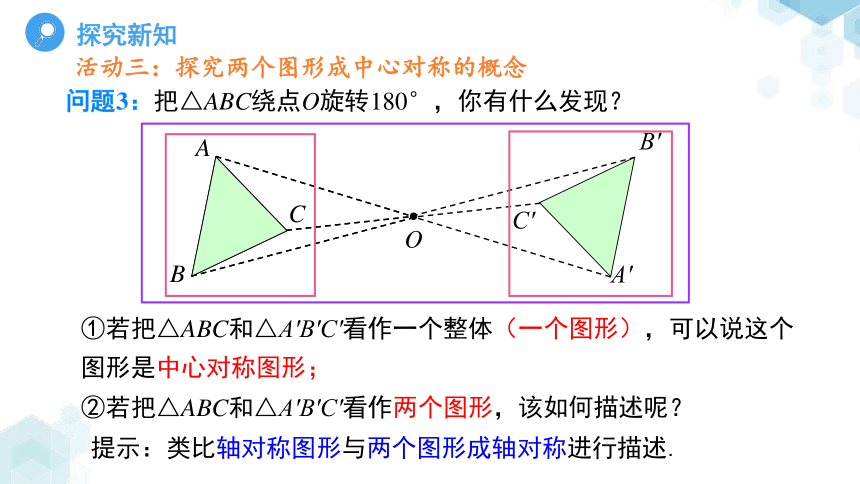
问题3:把△ABC绕点O旋转180°,你有什么发现?
①若把△ABC和△A′B′C′看作一个整体(一个图形),可以说这个图形是中心对称图形;
②若把△ABC和△A′B′C′看作两个图形,该如何描述呢?
提示:类比轴对称图形与两个图形成轴对称进行描述.
活动三:探究两个图形成中心对称的概念
A
B
C
O
A′
B′
C′
归纳 把一个图形绕着某一点旋转180°,如果它能够和另一个图形重合,那么我们就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
活动三:探究两个图形成中心对称的概念
归纳 成中心对称与中心对称图形的区别和联系:
名称 成中心对称 中心对称图形
图形
区别 两个图形的相互位置关系 是一个图形的性质,是指一个图形本身成中心对称
联系 ①将成中心对称的两个图形看成一个整体,则它们是中心对称图形; ②将中心对称图形对称的部分看成两个图形,则它们成中心对称. 问题4:如图,△A′B′C′ 与△ABC 关于O点成中心对称,你能从图中找到哪些等量关系?
活动四:探究两个图形成中心对称的特征
A′
B′
C′
A
B
C
O
点 A 绕中心点O旋转180°后到点A′,于是A、O、A′ 三点在同一条直线上,并且OA=OA′.另外分别在同一条直线的三点还有__________和__________;OB=_____,OC=_____.
B、O、B′
C、O、C′
OB′
OC′
归纳 在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
反之,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
活动四:探究两个图形成中心对称的特征
经典例题
例1 下列图形中,哪些是中心对称图形?如果是,找出它们的对称中心.
答:图形(1)是中心对称图形,中心点O为其对称中心;
图形(2)是中心对称图形,圆心为其对称中心;
图形(3)不是中心对称图形.
例2 如图,已知△ABC和点O,作△DEF,使△DEF和△ABC关于点O成中心对称.
经典例题
解:(1) 连结AO并延长AO到点D,使OD=OA,于是得到
点A关于点O的对称点D;
(2)同样作出点B和点C的对称点E和F;
(3)顺次连结DE、EF、FD.如图,
△DFF即为所求的三角形.
A
B
C
O
D
E
F
教材
例题
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
1.仔细观察如图所示的26个英文字母,将相应的字母填入表中适当的空格内.
轴对称 旋转对称 中心对称
只有一条对称轴 有两条对称轴 英文字母
ABCDEM
TUVWY
HIOX
HINOSXZ
HINOSXZ
教材
练习
解:如图,这个长方形是轴对称图形,有两条对称轴;
是中心对称图形,它的对称中心是两条对角线的交点;
是旋转对称图形,绕对称中心旋转180°后能与自身重合.
A
B
C
D
教材
练习
2.如图,四边形ABCD是长方形,AB>BC.这个长方形是轴对称图形吗?如果是,请作出它的对称轴.它的对称轴有几条?这个长方形是中心对称图形吗?如果是,请作出它的对称中心.这个长方形是旋转对称图形吗?如果是,那么这个长方形绕哪一点旋转多少度后能与自身重合?
3.如图①所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°,魔术师摘除蒙具后,看到4张扑克牌如图②所示,他很快确定了哪一张牌被旋转过.你能确定吗?
解:因为旋转前后牌没有发生任何变化,说明被旋转的牌是中心对称图形,而这几张牌只有方块4是中心对称图形,因此被旋转180°的那张牌是方块4.
教材
练习
1.如下所示的4组图形中,左边数字与右边数字成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
C
2.如图是正三角形、正六边形、正八边形,它们是中心对称图形吗? 如果是,找出它们的对称中心.
答:正三角形不是中心对称图形;
正六边形是中心对称图形,O为其对称中心;
正八边形是中心对称图形,O为其对称中心.
3.如图,作出与△ABC关于点E成中心对称的图形.
(2)同样作出点B、点C的对称点B′、C′;
(3)顺次连结A′B′、B′C′、C′A′如图,四边形A′B′C′即为所求.
定义
中心对称
一个图形绕着中心旋转180°后能与自身重合.
中心对称作图
1.找关键点、对称中心;
2.连结并延长,找对称点;
3.顺次连结对称点得出图形.
成中心对称图形的特征
连结对称点的线段都经过对称中心,并且被对称中心平分.
实践作业
请同学们用旧物改造中心对称摆件,记录制作过程及思路,并将做好的摆件展示,选出最美摆件.
9.4 中心对称
【第9章 轴对称、平移与旋转】
第1课时
数学华东师大版(2024)七年级下册
1.理解中心对称概念,区分中心对称图形与成中心对称的图形,运用性质解决图案设计及生活图案分析等问题;
2.借助观察、操作等活动,增强空间观念、直观想象能力,在解决问题中锻炼数学建模与问题解决能力;
3.探究中心对称性质时,体悟从特殊到一般、类比归纳思想,提升逻辑推理与抽象概括能力;
4.借欣赏生活图案激发数学兴趣,培养审美意识,通过小组合作培育团队精神,增强学习自信,养成严谨科学态度.
2.什么是旋转对称图形?
旋转一定角度后能与自身重合的图形叫做旋转对称图形.
1.图形旋转的特征是什么?
图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状和大小不变.
活动一:探究中心对称图形的概念
问题1:在上一节,我们已经看到有不少图形绕某一中心旋转一定角度后,可以与自身重合.如图所示的三个图形都是这样的旋转对称图形.它们的旋转角度分别是多少?
120°
180°
72°
活动一:探究中心对称图形的概念
对称中心
注意:1.中心对称图形是旋转角度为180°的旋转对称图形,但
旋转对称图形不一定是中心对称图形.
2.中心对称图形是指一个图形.
归纳 一个图形绕着中心旋转180°后能与自身重合,像这样的图形叫做中心对称图形,这个中心叫做对称中心.
活动二:探究中心对称图形的特征
问题2:下列图形是中心对称图形吗?如果是,对称中心在哪里?
线段
等边三角形
平行四边形
长方形
正方形
圆
线段中点
对角线交点
对角线交点
对角线交点
圆心
归纳
(1) 中心对称图形的对称中心一定在图形内;
(2) 中心对称图形是针对一个图形而言的;
(3) 中心对称图形上所有的点关于对称中心的对称点都在这个图形本身上;
(4) 中心对称图形一定是旋转对称图形,但旋转对称图形不一定是中心对称图形.
活动二:探究中心对称图形的特征
活动三:探究两个图形成中心对称的概念
A
B
C
O
A′
B′
C′
问题3:把△ABC绕点O旋转180°,你有什么发现?
①若把△ABC和△A′B′C′看作一个整体(一个图形),可以说这个图形是中心对称图形;
②若把△ABC和△A′B′C′看作两个图形,该如何描述呢?
提示:类比轴对称图形与两个图形成轴对称进行描述.
活动三:探究两个图形成中心对称的概念
A
B
C
O
A′
B′
C′
归纳 把一个图形绕着某一点旋转180°,如果它能够和另一个图形重合,那么我们就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
活动三:探究两个图形成中心对称的概念
归纳 成中心对称与中心对称图形的区别和联系:
名称 成中心对称 中心对称图形
图形
区别 两个图形的相互位置关系 是一个图形的性质,是指一个图形本身成中心对称
联系 ①将成中心对称的两个图形看成一个整体,则它们是中心对称图形; ②将中心对称图形对称的部分看成两个图形,则它们成中心对称. 问题4:如图,△A′B′C′ 与△ABC 关于O点成中心对称,你能从图中找到哪些等量关系?
活动四:探究两个图形成中心对称的特征
A′
B′
C′
A
B
C
O
点 A 绕中心点O旋转180°后到点A′,于是A、O、A′ 三点在同一条直线上,并且OA=OA′.另外分别在同一条直线的三点还有__________和__________;OB=_____,OC=_____.
B、O、B′
C、O、C′
OB′
OC′
归纳 在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
反之,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
活动四:探究两个图形成中心对称的特征
经典例题
例1 下列图形中,哪些是中心对称图形?如果是,找出它们的对称中心.
答:图形(1)是中心对称图形,中心点O为其对称中心;
图形(2)是中心对称图形,圆心为其对称中心;
图形(3)不是中心对称图形.
例2 如图,已知△ABC和点O,作△DEF,使△DEF和△ABC关于点O成中心对称.
经典例题
解:(1) 连结AO并延长AO到点D,使OD=OA,于是得到
点A关于点O的对称点D;
(2)同样作出点B和点C的对称点E和F;
(3)顺次连结DE、EF、FD.如图,
△DFF即为所求的三角形.
A
B
C
O
D
E
F
教材
例题
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
1.仔细观察如图所示的26个英文字母,将相应的字母填入表中适当的空格内.
轴对称 旋转对称 中心对称
只有一条对称轴 有两条对称轴 英文字母
ABCDEM
TUVWY
HIOX
HINOSXZ
HINOSXZ
教材
练习
解:如图,这个长方形是轴对称图形,有两条对称轴;
是中心对称图形,它的对称中心是两条对角线的交点;
是旋转对称图形,绕对称中心旋转180°后能与自身重合.
A
B
C
D
教材
练习
2.如图,四边形ABCD是长方形,AB>BC.这个长方形是轴对称图形吗?如果是,请作出它的对称轴.它的对称轴有几条?这个长方形是中心对称图形吗?如果是,请作出它的对称中心.这个长方形是旋转对称图形吗?如果是,那么这个长方形绕哪一点旋转多少度后能与自身重合?
3.如图①所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°,魔术师摘除蒙具后,看到4张扑克牌如图②所示,他很快确定了哪一张牌被旋转过.你能确定吗?
解:因为旋转前后牌没有发生任何变化,说明被旋转的牌是中心对称图形,而这几张牌只有方块4是中心对称图形,因此被旋转180°的那张牌是方块4.
教材
练习
1.如下所示的4组图形中,左边数字与右边数字成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
C
2.如图是正三角形、正六边形、正八边形,它们是中心对称图形吗? 如果是,找出它们的对称中心.
答:正三角形不是中心对称图形;
正六边形是中心对称图形,O为其对称中心;
正八边形是中心对称图形,O为其对称中心.
3.如图,作出与△ABC关于点E成中心对称的图形.
(2)同样作出点B、点C的对称点B′、C′;
(3)顺次连结A′B′、B′C′、C′A′如图,四边形A′B′C′即为所求.
定义
中心对称
一个图形绕着中心旋转180°后能与自身重合.
中心对称作图
1.找关键点、对称中心;
2.连结并延长,找对称点;
3.顺次连结对称点得出图形.
成中心对称图形的特征
连结对称点的线段都经过对称中心,并且被对称中心平分.
实践作业
请同学们用旧物改造中心对称摆件,记录制作过程及思路,并将做好的摆件展示,选出最美摆件.
