第九章 平面直角坐标系 章末复习课件(共31张PPT) 人教版(2024)数学七年级下册
文档属性
| 名称 | 第九章 平面直角坐标系 章末复习课件(共31张PPT) 人教版(2024)数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 810.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 07:14:02 | ||
图片预览











文档简介
(共31张PPT)
第九章 平面直角坐标系
章末复习
数学人教版新课标(2024)七年级下册
请你带着下面的问题,复习一下全章的内容吧.
1.结合具体实例,谈谈如何建立平面直角坐标系.在平面直角坐标系中描出原点以及其他一些点的位置,并分别指出它们的横坐标、纵坐标及所在的象限.
2.当要用坐标描述一个简单几何图形时,你是如何建立平面直角坐标系的?结合长方形谈谈你的做法.
3.你能结合具体实例,说一说怎样用坐标描述一个区域内的地点分布情况吗?你又是怎样用方向和距离表示两个地点或物体的相对位置的?请结合实例说明.
4.你能结合具体实例,说一说怎样用坐标表示图形的平移吗?
例1 (1)若点 P(m,n)在第二象限,则点 Q(-m,-n)在第_____象限;
(2)若点 A(m+3,m+1)在 y 轴上,则点 A 的坐标为_________.
考点一 平面直角坐标系中点的坐标特征
解析:(1)因为点 P(m,n)在第二象限,所以 m<0,n>0.
所以-m>0,-n<0.
所以点 Q(-m,-n)在第四象限.
四
例1 (1)若点 P(m,n)在第二象限,则点 Q(-m,-n)在第_____象限;
(2)若点 A(m+3,m+1)在 y 轴上,则点 A 的坐标为_________.
解析:(2)因为点 A(m+3,m+1)在 y 轴上,
所以 m+3=0,即 m=-3.
所以 m+1=-2.
所以点 A 的坐标为(0,-2).
(0,-2)
考点一 平面直角坐标系中点的坐标特征
四
根据已知点的横、纵坐标确定某点所在的象限
(1)确定已知点的横、纵坐标的符号;
(2)根据各象限内点的坐标的特征判断点所在的象限.
各象限内点的坐标特征:第一象限(+,+),第二象限(-,+),第三象限(-,-),第四象限(+,-).
考点一 平面直角坐标系中点的坐标特征
根据点的坐标特征求字母的值
(1)明确平面直角坐标系内点的特征;
(2)结合题意列出方程;
(3)解方程,求出字母的值.
考点一 平面直角坐标系中点的坐标特征
1.(1)如果点 A(a,b)在第三象限,那么点 B(-a+1,2b-1)在哪一个象限?
(2)如果点 P(m+2,m-1)在 x 轴上,求点 P 的坐标.
解:(1)因为点 A(a,b)在第三象限,所以 a<0,b<0.
所以-a+1>0,2b-1<0.
所以点 B 在第四象限.
考点一 平面直角坐标系中点的坐标特征
解:(2)因为点 P(m+2,m-1)在 x 轴上,
所以 m-1=0,解得 m=1.
所以 m+2=3.
所以点 P 的坐标为(3,0).
考点一 平面直角坐标系中点的坐标特征
1.(1)如果点 A(a,b)在第三象限,那么点 B(-a+1,2b-1)在哪一个象限?
(2)如果点 P(m+2,m-1)在 x 轴上,求点 P 的坐标.
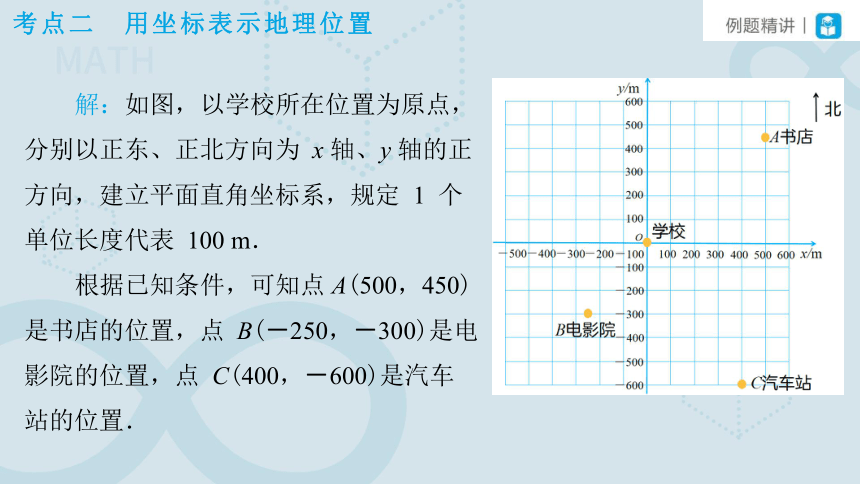
考点二 用坐标表示地理位置
例2 根据下列条件画一幅示意图,标出学校、书店、电影院、汽车站的位置.
书店:从学校向东走 500 m,再向北走 450 m;
电影院:从学校向西走 300 m,再向南走 300 m,最后向东走 50 m;
汽车站:从学校向南走 600 m,再向东走 400 m.
考点二 用坐标表示地理位置
解:如图,以学校所在位置为原点,分别以正东、正北方向为 x 轴、y 轴的正方向,建立平面直角坐标系,规定 1 个单位长度代表 100 m.
根据已知条件,可知点 A(500,450)是书店的位置,点 B(-250,-300)是电影院的位置,点 C(400,-600)是汽车站的位置.
建立平面直角坐标系表示地理位置时的注意事项
(1)选择适当的位置为坐标原点,通常是比较明显的地点或是所要绘制的区域内较居中的位置.
(2)坐标轴的方向通常是以正北为纵轴的正方向,正东为横轴的正方向,这样可以使东西南北的方向与地理位置的方向一致.
考点二 用坐标表示地理位置
考点三 用坐标表示平移
例3 将三角形 ABC 的三个顶点的横坐标都加-6,纵坐标都减5,则三角形ABC平移的方式是( ).
A.向右平移6个单位长度,向上平移5个单位长度
B.向左平移6个单位长度,向上平移5个单位长度
C.向左平移6个单位长度,向下平移5个单位长度
D.向右平移6个单位长度,向下平移5个单位长度
解析:横坐标加-6,就是横坐标减 6,表示向左平移 6 个单位长度;纵坐标减 5,表示向下平移 5 个单位长度.
C
考点三 用坐标表示平移
例4 在平面直角坐标系中,三角形 ABC 的三个顶点的位置如图所示.点 A′ 的坐标为(4,6),现将三角形 ABC 平移,使点 A 平移到点 A′,点 B′,C′分别是点 B,C 的对应点.请画出平移后的三角形 A′B′C′(不写画法),并直接写出点 B′,C′ 的坐标.
(1,2)
考点三 用坐标表示平移
解:由点 A(1,2) 平移到点 A′(4,6),得平移过程是先向右平移 3个单位长度,再向上平移 4 个单位长度.
由平移过程可得出点 B′ 的坐标为(0,4),
点 C′ 的坐标为(3,2).进而可画出平移
后的三角形A′B′C′(如图).
考点三 用坐标表示平移
由点的坐标变化确定点的平移方式
(1)平移后的点与平移前的点的横坐标之差反映了点沿
x轴的平移情况.若差值为正,则表示向右平移;若差值为负,则表示向左平移.
(2)平移后的点与平移前的点的纵坐标之差反映了点沿
y轴的平移情况.若差值为正,则表示向上平移;若差值为负,则表示向下平移.
考点三 用坐标表示平移
坐标平面内的图形平移的步骤
第1步:明确平移的方向和距离;
第2步:找出图形中的关键点;
第3步:利用平移规律确定平移后的各关键点的对应点的坐标,顺次连接各点得到平移后的图形.
考点三 用坐标表示平移
2.在平面直角坐标系中,线段 AB 两个端点的坐标分别是 A(-1,2),B(-2,3),若线段 AB 平移后点 B 的新坐标为(1,4),则点 A 的新坐标是________.
解析:由点 B(-2,3)平移后的新坐标为(1,4),可得坐标的变化规律为横坐标加 3,纵坐标加 1,所以点 A 平移后的横坐标为-1+3=2,纵坐标为 2+1=3,所以平移后点 A 的坐标是(2,3).
(2,3)
考点四 平面直角坐标系中的图形面积问题
H
E
F
例5 如图,四边形 OABC 各个顶点的坐标分别是 O(0,0),A(3,0),B(5,2),C(2,3).求这个四边形的面积.
解:如图,过点 C 作 x 轴的平行线,
交 y 轴于点 F,过点 B 作 y 轴的平行线,
交 x 轴于点 H,且这两条线交于点 E,
则 E(5,3),F(0,3),H(5,0).
考点四 平面直角坐标系中的图形面积问题
=5×3- ×2×2- ×1×3- ×3×2
所以 S四边形OABC=S长方形OHEF-S三角形ABH
-S三角形CBE-S三角形OCF
= .
例5 如图,四边形 OABC 各个顶点的坐标分别是 O(0,0),A(3,0),B(5,2),C(2,3).求这个四边形的面积.
H
E
F
考点四 平面直角坐标系中的图形面积问题
在平面直角坐标系中求图形的面积的两点注意
(1)在平面直角坐标系中求不规则图形的面积时,一般采用割补法,将其割补为规则的图形,求出这些规则图形的面积再相加减即可.
(2)利用点的平移规律,将点的坐标转化为距离是求解图形面积的关键.
考点四 平面直角坐标系中的图形面积问题
3.如图,在三角形 AOB 中,点 A 的坐标为(2,3),点 B 的坐标为(5,2),求三角形 AOB 的面积.
E
D
C
解:如图,过点 B 作 x 轴的垂线,垂足为 C,过点 A 作 y 轴的垂线,垂足为 E,延长 EA,CB 交于点 D.
因为点 A 的坐标为(2,3),点 B 的坐标为(5,2),所以 AE=2,OE=3,AD=3,BD=1,BC=2,OC=5.
考点四 平面直角坐标系中的图形面积问题
所以 S三角形AOB
=S长方形OCDE-S三角形OBC-S三角形ABD-S三角形AEO
=5×3- ×5×2- ×3×1- ×2×3
=15-5- -3
= .
故三角形AOB 的面积为 .
E
D
C
考点五 平面直角坐标系中的点的规律探究
例6 如图,正方形 A1A2A3A4,A5A6A7A8,A9A10A11A12,…(每个正方形的顶点从第三象限开始,按顺时针方向,
依次记为 A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点 O 处,各边均与 x 轴或 y 轴平行,若它们的边长依次是 2,4,6,…,则顶点 A20 的坐标为___________.
考点五 平面直角坐标系中的点的规律探究
解析:因为 =5,所以 A20 在第四象限,是第五个正方形的顶点.
因为第一个正方形的边长是 2,第二个正方形的边长是 4,第三个正方形的边长是 6,…,所以第五个正方形的边长是 10,所以 A20 的坐标为(5,-5).
考点五 平面直角坐标系中的点的规律探究
例6 如图,正方形 A1A2A3A4,A5A6A7A8,A9A10A11A12,…(每个正方形的顶点从第三象限开始,按顺时针方向,
依次记为 A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点 O 处,各边均与 x 轴或 y 轴平行,若它们的边长依次是 2,4,6,…,则顶点 A20 的坐标为___________.
(5,-5)
2
4
-4
-2
y
x
O
A11
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10
考点五 平面直角坐标系中的点的规律探究
4.如图所示,已知点 A1(1,0),
A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点 A2 027 的坐标为________________.
解析:要求 A2 023 的坐标,可先从简单的点的坐标开始探究,发现其中的规律.从各点的位置可以发现:
A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1);
A5(2,-1),A6(2,2),A7(-2,2),A8(-2,-2);
A9(3,-2),A10(3,3),A11(-3,3),A12(-3,-3);
……
观察A3(-1,1),A7(-2,2),A11(-3,3),可知,其横、纵坐标互为相反数.把 A3,A7,A11,…右下角的数字提出来,进行整理.
考点五 平面直角坐标系中的点的规律探究
3=3+4×0,A3(-1,1),
7=3+4×1,A7(-2,2),
11=3+4×2,A11(-3,3),
… …
因为2 027=3+4×506,所以点A2 027的坐标为 (-507,507).
考点五 平面直角坐标系中的点的规律探究
考点五 平面直角坐标系中的点的规律探究
4.如图所示,已知点 A1(1,0),
A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点 A2 027 的坐标为________________.
(-507,507)
2
4
-4
-2
y
x
O
A11
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10
确定平面内点的位置
建立平面直角坐标系
画两条数轴
①互相垂直
②有公共原点
点
坐标
M
(x,y)
表示方向的角,距离
第九章 平面直角坐标系
章末复习
数学人教版新课标(2024)七年级下册
请你带着下面的问题,复习一下全章的内容吧.
1.结合具体实例,谈谈如何建立平面直角坐标系.在平面直角坐标系中描出原点以及其他一些点的位置,并分别指出它们的横坐标、纵坐标及所在的象限.
2.当要用坐标描述一个简单几何图形时,你是如何建立平面直角坐标系的?结合长方形谈谈你的做法.
3.你能结合具体实例,说一说怎样用坐标描述一个区域内的地点分布情况吗?你又是怎样用方向和距离表示两个地点或物体的相对位置的?请结合实例说明.
4.你能结合具体实例,说一说怎样用坐标表示图形的平移吗?
例1 (1)若点 P(m,n)在第二象限,则点 Q(-m,-n)在第_____象限;
(2)若点 A(m+3,m+1)在 y 轴上,则点 A 的坐标为_________.
考点一 平面直角坐标系中点的坐标特征
解析:(1)因为点 P(m,n)在第二象限,所以 m<0,n>0.
所以-m>0,-n<0.
所以点 Q(-m,-n)在第四象限.
四
例1 (1)若点 P(m,n)在第二象限,则点 Q(-m,-n)在第_____象限;
(2)若点 A(m+3,m+1)在 y 轴上,则点 A 的坐标为_________.
解析:(2)因为点 A(m+3,m+1)在 y 轴上,
所以 m+3=0,即 m=-3.
所以 m+1=-2.
所以点 A 的坐标为(0,-2).
(0,-2)
考点一 平面直角坐标系中点的坐标特征
四
根据已知点的横、纵坐标确定某点所在的象限
(1)确定已知点的横、纵坐标的符号;
(2)根据各象限内点的坐标的特征判断点所在的象限.
各象限内点的坐标特征:第一象限(+,+),第二象限(-,+),第三象限(-,-),第四象限(+,-).
考点一 平面直角坐标系中点的坐标特征
根据点的坐标特征求字母的值
(1)明确平面直角坐标系内点的特征;
(2)结合题意列出方程;
(3)解方程,求出字母的值.
考点一 平面直角坐标系中点的坐标特征
1.(1)如果点 A(a,b)在第三象限,那么点 B(-a+1,2b-1)在哪一个象限?
(2)如果点 P(m+2,m-1)在 x 轴上,求点 P 的坐标.
解:(1)因为点 A(a,b)在第三象限,所以 a<0,b<0.
所以-a+1>0,2b-1<0.
所以点 B 在第四象限.
考点一 平面直角坐标系中点的坐标特征
解:(2)因为点 P(m+2,m-1)在 x 轴上,
所以 m-1=0,解得 m=1.
所以 m+2=3.
所以点 P 的坐标为(3,0).
考点一 平面直角坐标系中点的坐标特征
1.(1)如果点 A(a,b)在第三象限,那么点 B(-a+1,2b-1)在哪一个象限?
(2)如果点 P(m+2,m-1)在 x 轴上,求点 P 的坐标.
考点二 用坐标表示地理位置
例2 根据下列条件画一幅示意图,标出学校、书店、电影院、汽车站的位置.
书店:从学校向东走 500 m,再向北走 450 m;
电影院:从学校向西走 300 m,再向南走 300 m,最后向东走 50 m;
汽车站:从学校向南走 600 m,再向东走 400 m.
考点二 用坐标表示地理位置
解:如图,以学校所在位置为原点,分别以正东、正北方向为 x 轴、y 轴的正方向,建立平面直角坐标系,规定 1 个单位长度代表 100 m.
根据已知条件,可知点 A(500,450)是书店的位置,点 B(-250,-300)是电影院的位置,点 C(400,-600)是汽车站的位置.
建立平面直角坐标系表示地理位置时的注意事项
(1)选择适当的位置为坐标原点,通常是比较明显的地点或是所要绘制的区域内较居中的位置.
(2)坐标轴的方向通常是以正北为纵轴的正方向,正东为横轴的正方向,这样可以使东西南北的方向与地理位置的方向一致.
考点二 用坐标表示地理位置
考点三 用坐标表示平移
例3 将三角形 ABC 的三个顶点的横坐标都加-6,纵坐标都减5,则三角形ABC平移的方式是( ).
A.向右平移6个单位长度,向上平移5个单位长度
B.向左平移6个单位长度,向上平移5个单位长度
C.向左平移6个单位长度,向下平移5个单位长度
D.向右平移6个单位长度,向下平移5个单位长度
解析:横坐标加-6,就是横坐标减 6,表示向左平移 6 个单位长度;纵坐标减 5,表示向下平移 5 个单位长度.
C
考点三 用坐标表示平移
例4 在平面直角坐标系中,三角形 ABC 的三个顶点的位置如图所示.点 A′ 的坐标为(4,6),现将三角形 ABC 平移,使点 A 平移到点 A′,点 B′,C′分别是点 B,C 的对应点.请画出平移后的三角形 A′B′C′(不写画法),并直接写出点 B′,C′ 的坐标.
(1,2)
考点三 用坐标表示平移
解:由点 A(1,2) 平移到点 A′(4,6),得平移过程是先向右平移 3个单位长度,再向上平移 4 个单位长度.
由平移过程可得出点 B′ 的坐标为(0,4),
点 C′ 的坐标为(3,2).进而可画出平移
后的三角形A′B′C′(如图).
考点三 用坐标表示平移
由点的坐标变化确定点的平移方式
(1)平移后的点与平移前的点的横坐标之差反映了点沿
x轴的平移情况.若差值为正,则表示向右平移;若差值为负,则表示向左平移.
(2)平移后的点与平移前的点的纵坐标之差反映了点沿
y轴的平移情况.若差值为正,则表示向上平移;若差值为负,则表示向下平移.
考点三 用坐标表示平移
坐标平面内的图形平移的步骤
第1步:明确平移的方向和距离;
第2步:找出图形中的关键点;
第3步:利用平移规律确定平移后的各关键点的对应点的坐标,顺次连接各点得到平移后的图形.
考点三 用坐标表示平移
2.在平面直角坐标系中,线段 AB 两个端点的坐标分别是 A(-1,2),B(-2,3),若线段 AB 平移后点 B 的新坐标为(1,4),则点 A 的新坐标是________.
解析:由点 B(-2,3)平移后的新坐标为(1,4),可得坐标的变化规律为横坐标加 3,纵坐标加 1,所以点 A 平移后的横坐标为-1+3=2,纵坐标为 2+1=3,所以平移后点 A 的坐标是(2,3).
(2,3)
考点四 平面直角坐标系中的图形面积问题
H
E
F
例5 如图,四边形 OABC 各个顶点的坐标分别是 O(0,0),A(3,0),B(5,2),C(2,3).求这个四边形的面积.
解:如图,过点 C 作 x 轴的平行线,
交 y 轴于点 F,过点 B 作 y 轴的平行线,
交 x 轴于点 H,且这两条线交于点 E,
则 E(5,3),F(0,3),H(5,0).
考点四 平面直角坐标系中的图形面积问题
=5×3- ×2×2- ×1×3- ×3×2
所以 S四边形OABC=S长方形OHEF-S三角形ABH
-S三角形CBE-S三角形OCF
= .
例5 如图,四边形 OABC 各个顶点的坐标分别是 O(0,0),A(3,0),B(5,2),C(2,3).求这个四边形的面积.
H
E
F
考点四 平面直角坐标系中的图形面积问题
在平面直角坐标系中求图形的面积的两点注意
(1)在平面直角坐标系中求不规则图形的面积时,一般采用割补法,将其割补为规则的图形,求出这些规则图形的面积再相加减即可.
(2)利用点的平移规律,将点的坐标转化为距离是求解图形面积的关键.
考点四 平面直角坐标系中的图形面积问题
3.如图,在三角形 AOB 中,点 A 的坐标为(2,3),点 B 的坐标为(5,2),求三角形 AOB 的面积.
E
D
C
解:如图,过点 B 作 x 轴的垂线,垂足为 C,过点 A 作 y 轴的垂线,垂足为 E,延长 EA,CB 交于点 D.
因为点 A 的坐标为(2,3),点 B 的坐标为(5,2),所以 AE=2,OE=3,AD=3,BD=1,BC=2,OC=5.
考点四 平面直角坐标系中的图形面积问题
所以 S三角形AOB
=S长方形OCDE-S三角形OBC-S三角形ABD-S三角形AEO
=5×3- ×5×2- ×3×1- ×2×3
=15-5- -3
= .
故三角形AOB 的面积为 .
E
D
C
考点五 平面直角坐标系中的点的规律探究
例6 如图,正方形 A1A2A3A4,A5A6A7A8,A9A10A11A12,…(每个正方形的顶点从第三象限开始,按顺时针方向,
依次记为 A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点 O 处,各边均与 x 轴或 y 轴平行,若它们的边长依次是 2,4,6,…,则顶点 A20 的坐标为___________.
考点五 平面直角坐标系中的点的规律探究
解析:因为 =5,所以 A20 在第四象限,是第五个正方形的顶点.
因为第一个正方形的边长是 2,第二个正方形的边长是 4,第三个正方形的边长是 6,…,所以第五个正方形的边长是 10,所以 A20 的坐标为(5,-5).
考点五 平面直角坐标系中的点的规律探究
例6 如图,正方形 A1A2A3A4,A5A6A7A8,A9A10A11A12,…(每个正方形的顶点从第三象限开始,按顺时针方向,
依次记为 A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点 O 处,各边均与 x 轴或 y 轴平行,若它们的边长依次是 2,4,6,…,则顶点 A20 的坐标为___________.
(5,-5)
2
4
-4
-2
y
x
O
A11
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10
考点五 平面直角坐标系中的点的规律探究
4.如图所示,已知点 A1(1,0),
A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点 A2 027 的坐标为________________.
解析:要求 A2 023 的坐标,可先从简单的点的坐标开始探究,发现其中的规律.从各点的位置可以发现:
A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1);
A5(2,-1),A6(2,2),A7(-2,2),A8(-2,-2);
A9(3,-2),A10(3,3),A11(-3,3),A12(-3,-3);
……
观察A3(-1,1),A7(-2,2),A11(-3,3),可知,其横、纵坐标互为相反数.把 A3,A7,A11,…右下角的数字提出来,进行整理.
考点五 平面直角坐标系中的点的规律探究
3=3+4×0,A3(-1,1),
7=3+4×1,A7(-2,2),
11=3+4×2,A11(-3,3),
… …
因为2 027=3+4×506,所以点A2 027的坐标为 (-507,507).
考点五 平面直角坐标系中的点的规律探究
考点五 平面直角坐标系中的点的规律探究
4.如图所示,已知点 A1(1,0),
A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点 A2 027 的坐标为________________.
(-507,507)
2
4
-4
-2
y
x
O
A11
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10
确定平面内点的位置
建立平面直角坐标系
画两条数轴
①互相垂直
②有公共原点
点
坐标
M
(x,y)
表示方向的角,距离
同课章节目录
