2025人教版八年级(下)期末考试数学试卷(无答案)
文档属性
| 名称 | 2025人教版八年级(下)期末考试数学试卷(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 919.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 00:00:00 | ||
图片预览


文档简介
2025人教版八年级(下)期末考试数学试卷
(全卷共五个大题,满分150分,考试时间120分钟)
一、选择题:(每小题4分,共48分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的代号涂黑。
1.要使分式有意义,x应满足的条件是( )
A. B. C. D.
2.下列因式分解正确的是( )
A. B.
C. D.
3.若两个相似三角形的相似比是1:5,那么它们的周长之比是( )
A. B.1:5 C.1:10 D.1:25
4.如图,过反比例函数上一点A作AB⊥x轴于点B,AC⊥y轴于点C,则四边形OBAC的面积是( )
A.2 B.4 C.6 D.8
5.如图,BE、CD相交于点A,连接BC,DE,下列条件中不能判断 ABC∽ ADE的是( )
A. B. C. D.
6.已知反比例函数的图象经过第一、三象限,则符合条件的m是( )
A.m=-1 B.m = 0 C.m =3 D.m =5
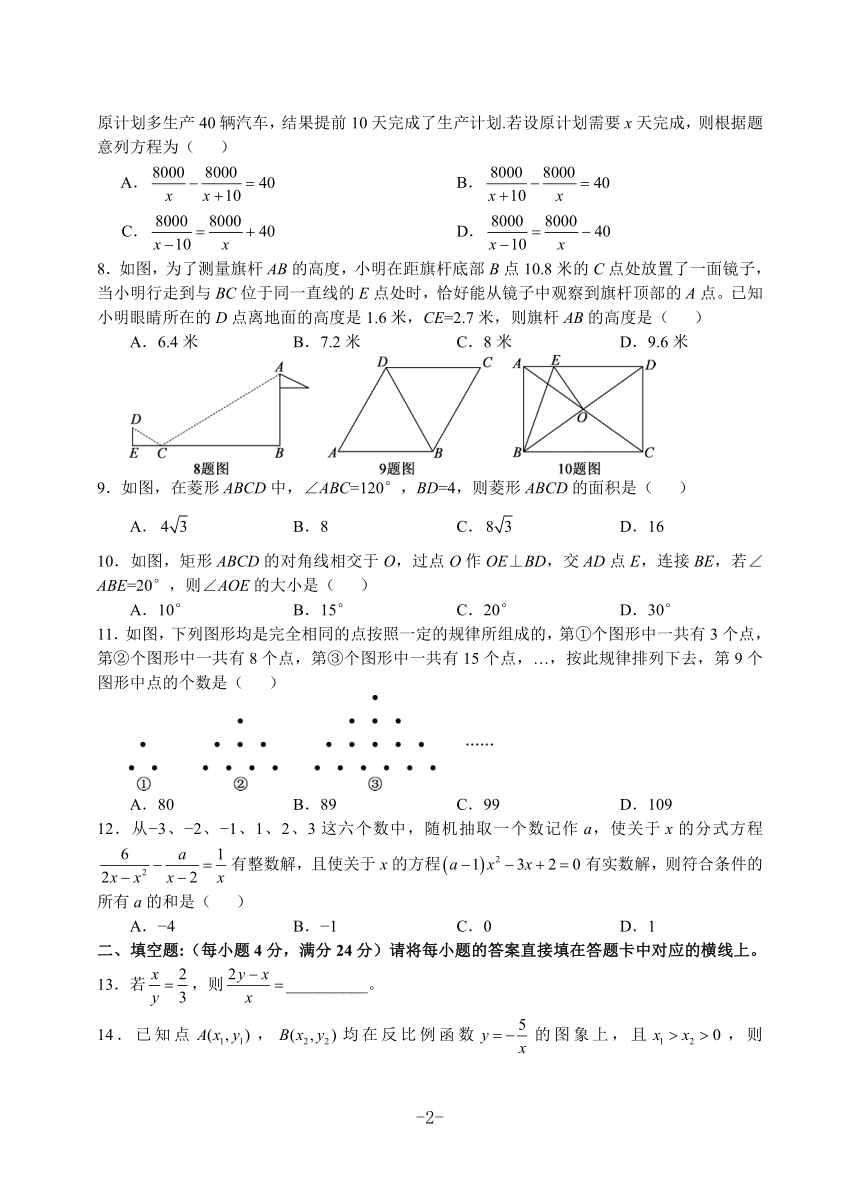
7.某公司原计划生产某一型号的汽车8000辆,为了提高效率,企业改进了技术,现每天可比原计划多生产40辆汽车,结果提前10天完成了生产计划.若设原计划需要x天完成,则根据题意列方程为( )
A. B.
C. D.
8.如图,为了测量旗杆AB的高度,小明在距旗杆底部B点10.8米的C点处放置了一面镜子,当小明行走到与BC位于同一直线的E点处时,恰好能从镜子中观察到旗杆顶部的A点。已知小明眼睛所在的D点离地面的高度是1.6米,CE=2.7米,则旗杆AB的高度是( )
A.6.4米 B.7.2米 C.8米 D.9.6米
9.如图,在菱形ABCD中,∠ABC=120°,BD=4,则菱形ABCD的面积是( )
A. B.8 C. D.16
10.如图,矩形ABCD的对角线相交于O,过点O作OE⊥BD,交AD点E,连接BE,若∠ABE=20°,则∠AOE的大小是( )
A.10° B.15° C.20° D.30°
11.如图,下列图形均是完全相同的点按照一定的规律所组成的,第①个图形中一共有3个点,第②个图形中一共有8个点,第③个图形中一共有15个点,…,按此规律排列下去,第9个图形中点的个数是( )
A.80 B.89 C.99 D.109
12.从 3、 2、 1、1、2、3这六个数中,随机抽取一个数记作a,使关于x的分式方程有整数解,且使关于x的方程有实数解,则符合条件的所有a的和是( )
A. 4 B. 1 C.0 D.1
二、填空题:(每小题4分,满分24分)请将每小题的答案直接填在答题卡中对应的横线上。
13.若,则__________。
14.已知点,均在反比例函数的图象上,且,则________ (填“”或“”)。
15.已知是关于x的一元二次方程的根,则的值为_______.
16.如图,平行四边形ABCD中,E为AB的中点,连接AC,DE相交于点F,若 AEF的面积等于1,则 ACD的面积是_______。
17.已知甲乙两地相距350千米,现有一直达高铁往返于两城市之间,该高铁每次到达甲地、乙地后均需停留1小时再重新出发。暑假期间,乙地铁路局计划在同线路上临时加开一辆慢速直达旅行专列,在试运行期间,该旅行专列与高铁同时从乙地出发,在整个行驶过程中,两车均保持各自速度匀速行驶,经过3.75小时两车第一次相遇。已知两车之间的距离y (千米)与行驶时间x (小时)之间的部分函数关系如图所示,当两车第二次相遇时,该旅行专列共行驶了_______千米。
18.如图,正方形ABCO中,点Q为OC边上的三等分点,连接AQ交对角线OB于点F,将正方形ABCO绕点O按顺时针方向旋转角(),得到正方形A1B1C1O,其中A1B1交对角线OB于点N,边B1C1交OC的延长线于点M,延长B1A1交OA的延长线于点E。若OF=2,AE=MB1,则四边形NOMB1的面积为__________。
三、解答题:(每小题8分,共16分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图(包括辅助线),请将解答过程书写在答题卡中对应的位置上。
19.解下列方程:(1) (2)
20.学校举办生命科学文化节活动。本次活动以“生命 生存 生活 生涯”四生教育为指引,设立了“参观展区”、“体验区”、“名家讲坛”三个活动板块。活动结束以后,为了了解同学们对这次活动的三个板块的参与度,统计小组随机对校园里的同学们进行了问卷调查,并分类整理调查结果:A:参加了三项活动;B:参加了两项活动;C:参加了一项活动;D:一项活动都没有参加,同时根据调查的结果绘制了如图1和图2两幅不完整的统计图。
(1)此次的问卷共调查了________名同学,参与了两项活动的同学所对应的扇形统计图的圆心角是_________度,并请补全折线统计图;
(2)作为本次活动的延续,学校有意组织一个“继续学习小组”,并从学生中选拔负责人。现有小杰和其他三位同样优秀的同学报名参加了负责人的选拔,需要从中任选两位成为负责人,试用画树状图或列表的方法求出小杰被选中的概率。
四、解答题(每小题10分,共40分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线),请将解答过程书写在答题卡中对应的位置上。
21.计算:(1) (2)
22.如图,在平面直角坐标系中,正比例函数与反比例函数相交于A、B两点,已知点A的坐标是,另有一次函数的图象经过点A,交x轴于点C,交y轴于点D,OC=OA。
(1)求该反比例函数和一次函数的解析式;
(2)连接BD,求 ABD的面积。
23.学校原计划向新华书店订购A、B两类图书共5000本,已知A类图书每本单价24元,B类图书每本单价20元。(1)据悉,学校计划购书的总资金不超过11.2万元,那么原计划最多购买A类图书多少本?(2)后来,学校决定就以11.2万元的总资金,按照(1)中A类图书的最大数量进行购买。但图书馆通过调研发现学生们更加青睐B类图书,于是学校接受了图书馆的建议,在原计划的基础上A类图书少订购了 (其中),B类图书多订购了,书店也决定在学校所订购的B类图书的单价上给予的优惠,但保持A类图书的单价不变,最终学校只多花费了500元就完成了订购,求m的值。
24.如图,Rt ABC中,∠C=90°,点D是AC上的一点,过D作DE⊥AB,垂足为点E,连接BD,∠ADE=∠BDE。
(1)如图1,若,AC=4,求AE的长;
(2)如图2,,且AG=CD,点F是线段BC的中点,求证:∠FDC=∠DGA。
五、解答题:(25小题10分,26小题12分,共22分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线),请将解答过程书写在答题卡中对应的位置上。
25.如果任意一个多位数满足其所有的偶数位上的数字之和与所有的奇数位上的数字之和相等,我们就把这样的多位数统称为“奇偶均分数”.例如:对于多位数352,奇数位上的数字是3、2,偶数位上的数字是5,显然3+2=5,所以352是“奇偶均分数”。
(1)三位数中,最大的“奇偶均分数”是 。
求证:任意一个三位“奇偶均分数”都能被11整除;
(2)对于任意一个四位“奇偶均分数”而言,如果前两位数字之和恰好等于后两位数字之和,我们就把这样的四位“奇偶均分数”称为“完美奇偶均分数”。是否存在这样的“完美奇偶均分数”,其本身以及各个数位上的数字之和均能被7整除,如果存在,请求出它的值;如果不存在,请说明理由。
26.如图,在直角坐标系中,直线与x轴交于点C,与y轴交于点A。分别以OC、OA为边作矩形ABCO,直线交线段AB于点E。
(1)求点B、E的坐标;
(2)如图,点F为线段BC的中点,点P为直线l2上一点,点Q为x轴上一点,求四边形BFQP周长的最小值以及周长最小时点P的坐标;
(3)若点D为点A关于x轴的对称点,连接CD,将直线沿着x轴平移,平移后的直线记为l3,直线l3与x轴交于点M,与射线CD交于点N。是否存在这样的点N,使得 OMN为等腰三角形,若存在,请在答题卷上画出满足条件的等腰 OMN并直接写出点N的坐标;若不存在,请说明理由。
-1-
(全卷共五个大题,满分150分,考试时间120分钟)
一、选择题:(每小题4分,共48分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的代号涂黑。
1.要使分式有意义,x应满足的条件是( )
A. B. C. D.
2.下列因式分解正确的是( )
A. B.
C. D.
3.若两个相似三角形的相似比是1:5,那么它们的周长之比是( )
A. B.1:5 C.1:10 D.1:25
4.如图,过反比例函数上一点A作AB⊥x轴于点B,AC⊥y轴于点C,则四边形OBAC的面积是( )
A.2 B.4 C.6 D.8
5.如图,BE、CD相交于点A,连接BC,DE,下列条件中不能判断 ABC∽ ADE的是( )
A. B. C. D.
6.已知反比例函数的图象经过第一、三象限,则符合条件的m是( )
A.m=-1 B.m = 0 C.m =3 D.m =5
7.某公司原计划生产某一型号的汽车8000辆,为了提高效率,企业改进了技术,现每天可比原计划多生产40辆汽车,结果提前10天完成了生产计划.若设原计划需要x天完成,则根据题意列方程为( )
A. B.
C. D.
8.如图,为了测量旗杆AB的高度,小明在距旗杆底部B点10.8米的C点处放置了一面镜子,当小明行走到与BC位于同一直线的E点处时,恰好能从镜子中观察到旗杆顶部的A点。已知小明眼睛所在的D点离地面的高度是1.6米,CE=2.7米,则旗杆AB的高度是( )
A.6.4米 B.7.2米 C.8米 D.9.6米
9.如图,在菱形ABCD中,∠ABC=120°,BD=4,则菱形ABCD的面积是( )
A. B.8 C. D.16
10.如图,矩形ABCD的对角线相交于O,过点O作OE⊥BD,交AD点E,连接BE,若∠ABE=20°,则∠AOE的大小是( )
A.10° B.15° C.20° D.30°
11.如图,下列图形均是完全相同的点按照一定的规律所组成的,第①个图形中一共有3个点,第②个图形中一共有8个点,第③个图形中一共有15个点,…,按此规律排列下去,第9个图形中点的个数是( )
A.80 B.89 C.99 D.109
12.从 3、 2、 1、1、2、3这六个数中,随机抽取一个数记作a,使关于x的分式方程有整数解,且使关于x的方程有实数解,则符合条件的所有a的和是( )
A. 4 B. 1 C.0 D.1
二、填空题:(每小题4分,满分24分)请将每小题的答案直接填在答题卡中对应的横线上。
13.若,则__________。
14.已知点,均在反比例函数的图象上,且,则________ (填“”或“”)。
15.已知是关于x的一元二次方程的根,则的值为_______.
16.如图,平行四边形ABCD中,E为AB的中点,连接AC,DE相交于点F,若 AEF的面积等于1,则 ACD的面积是_______。
17.已知甲乙两地相距350千米,现有一直达高铁往返于两城市之间,该高铁每次到达甲地、乙地后均需停留1小时再重新出发。暑假期间,乙地铁路局计划在同线路上临时加开一辆慢速直达旅行专列,在试运行期间,该旅行专列与高铁同时从乙地出发,在整个行驶过程中,两车均保持各自速度匀速行驶,经过3.75小时两车第一次相遇。已知两车之间的距离y (千米)与行驶时间x (小时)之间的部分函数关系如图所示,当两车第二次相遇时,该旅行专列共行驶了_______千米。
18.如图,正方形ABCO中,点Q为OC边上的三等分点,连接AQ交对角线OB于点F,将正方形ABCO绕点O按顺时针方向旋转角(),得到正方形A1B1C1O,其中A1B1交对角线OB于点N,边B1C1交OC的延长线于点M,延长B1A1交OA的延长线于点E。若OF=2,AE=MB1,则四边形NOMB1的面积为__________。
三、解答题:(每小题8分,共16分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图(包括辅助线),请将解答过程书写在答题卡中对应的位置上。
19.解下列方程:(1) (2)
20.学校举办生命科学文化节活动。本次活动以“生命 生存 生活 生涯”四生教育为指引,设立了“参观展区”、“体验区”、“名家讲坛”三个活动板块。活动结束以后,为了了解同学们对这次活动的三个板块的参与度,统计小组随机对校园里的同学们进行了问卷调查,并分类整理调查结果:A:参加了三项活动;B:参加了两项活动;C:参加了一项活动;D:一项活动都没有参加,同时根据调查的结果绘制了如图1和图2两幅不完整的统计图。
(1)此次的问卷共调查了________名同学,参与了两项活动的同学所对应的扇形统计图的圆心角是_________度,并请补全折线统计图;
(2)作为本次活动的延续,学校有意组织一个“继续学习小组”,并从学生中选拔负责人。现有小杰和其他三位同样优秀的同学报名参加了负责人的选拔,需要从中任选两位成为负责人,试用画树状图或列表的方法求出小杰被选中的概率。
四、解答题(每小题10分,共40分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线),请将解答过程书写在答题卡中对应的位置上。
21.计算:(1) (2)
22.如图,在平面直角坐标系中,正比例函数与反比例函数相交于A、B两点,已知点A的坐标是,另有一次函数的图象经过点A,交x轴于点C,交y轴于点D,OC=OA。
(1)求该反比例函数和一次函数的解析式;
(2)连接BD,求 ABD的面积。
23.学校原计划向新华书店订购A、B两类图书共5000本,已知A类图书每本单价24元,B类图书每本单价20元。(1)据悉,学校计划购书的总资金不超过11.2万元,那么原计划最多购买A类图书多少本?(2)后来,学校决定就以11.2万元的总资金,按照(1)中A类图书的最大数量进行购买。但图书馆通过调研发现学生们更加青睐B类图书,于是学校接受了图书馆的建议,在原计划的基础上A类图书少订购了 (其中),B类图书多订购了,书店也决定在学校所订购的B类图书的单价上给予的优惠,但保持A类图书的单价不变,最终学校只多花费了500元就完成了订购,求m的值。
24.如图,Rt ABC中,∠C=90°,点D是AC上的一点,过D作DE⊥AB,垂足为点E,连接BD,∠ADE=∠BDE。
(1)如图1,若,AC=4,求AE的长;
(2)如图2,,且AG=CD,点F是线段BC的中点,求证:∠FDC=∠DGA。
五、解答题:(25小题10分,26小题12分,共22分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线),请将解答过程书写在答题卡中对应的位置上。
25.如果任意一个多位数满足其所有的偶数位上的数字之和与所有的奇数位上的数字之和相等,我们就把这样的多位数统称为“奇偶均分数”.例如:对于多位数352,奇数位上的数字是3、2,偶数位上的数字是5,显然3+2=5,所以352是“奇偶均分数”。
(1)三位数中,最大的“奇偶均分数”是 。
求证:任意一个三位“奇偶均分数”都能被11整除;
(2)对于任意一个四位“奇偶均分数”而言,如果前两位数字之和恰好等于后两位数字之和,我们就把这样的四位“奇偶均分数”称为“完美奇偶均分数”。是否存在这样的“完美奇偶均分数”,其本身以及各个数位上的数字之和均能被7整除,如果存在,请求出它的值;如果不存在,请说明理由。
26.如图,在直角坐标系中,直线与x轴交于点C,与y轴交于点A。分别以OC、OA为边作矩形ABCO,直线交线段AB于点E。
(1)求点B、E的坐标;
(2)如图,点F为线段BC的中点,点P为直线l2上一点,点Q为x轴上一点,求四边形BFQP周长的最小值以及周长最小时点P的坐标;
(3)若点D为点A关于x轴的对称点,连接CD,将直线沿着x轴平移,平移后的直线记为l3,直线l3与x轴交于点M,与射线CD交于点N。是否存在这样的点N,使得 OMN为等腰三角形,若存在,请在答题卷上画出满足条件的等腰 OMN并直接写出点N的坐标;若不存在,请说明理由。
-1-
同课章节目录
