人教版2024—2025学年七年级下册数学期末复习强化提分训练(含答案)
文档属性
| 名称 | 人教版2024—2025学年七年级下册数学期末复习强化提分训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 536.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 07:31:10 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版2024—2025学年七年级下册数学期末复习强化提分训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列所示的图案分别是奔驰、雪铁龙、大众、三菱汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )
A. B. C. D.
2.下列实数中,无理数是( )
A. B. C.0 D.
3.判断命题“如果n<1,那么n2﹣1<0”是假命题,只需举出一个反例.反例中的n可以为( )
A.﹣2 B.﹣ C.0 D.
4.如表是中国奥运健儿在历届奥运会中获得奖牌的情况.为了能清楚地看出各届获得奖牌的数量,应采用( )
届次 23 24 25 26 27 28 29 30 31 32
奖牌数 32 28 54 50 59 63 100 88 70 89
A.条形统计图 B.扇形统计图
C.折线统计图 D.以上都可以
5.若方程组的解为,则a+b的值为( )
A.1 B.﹣1 C.3 D.﹣3
6.下列命题是真命题的是( )
A.内错角相等 B.同一平面内,过一点有且只有一条直线与已知直线平行
C.相等的角是对顶角 D.同一平面内,过一点有且只有一条直线与已知直线垂直
7.已知点P(a﹣1,a+2)在平面直角坐标系的第三象限内,则a的取值范围是( )
A.1<a<2 B.﹣2<a<1 C.a<﹣2 D.a<1
8.在解关于x,y的方程组时,可以用①×2+②消去未知数x,也可以用①+②×5消去未知数y,则m﹣n=( )
A.4 B. C. D.
9.将一张长方形纸片如图所示折叠后,再展开,如果∠1=54°,则∠2=( )
A.54° B.68°
C.72° D.76°
10.关于x的不等式组的整数解仅有4个,则m的取值范围是( )
A.﹣5≤m<﹣4 B.﹣5<m≤﹣4 C.﹣4≤m<﹣3 D.﹣4<m≤﹣3
二、填空题(6小题,每题3分,共18分)
11.一个样本的数据分别落在5个组内,第1、2、3、4组数据的个数分别是2、8、15、5,且第4组数据的频率为0.1,这个样本的样本容量为 .
12.比较大小 ﹣4.(填“>”,“<”或者“=”)
13.若x,y为实数,且|x﹣2|+(y+1)2=0,则的值是 .
14.如图1,∠DEF=25°,将长方形纸片ABCD沿直线EF折叠成图2,再沿折痕GF折叠成图3,则∠CFE的度数为 .
15.实数x,y,z满足3x+7y+z=1,4x+10y+z=2005.求 .
16.买3本练习本,2支笔,7块橡皮共用了27元,买同样的练习本5本,同样的笔4支,同样的橡皮9块共用了43元,如果买同样的练习本、笔、橡皮各5本、5支、5块,总共需要 元.
第II卷
人教版2024—2025学年七年级下册数学期末复习强化提分训练
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:;
18.解不等式组:,并写出它的所有非负整数解.
19.解二元一次方程组:
(1); (2).
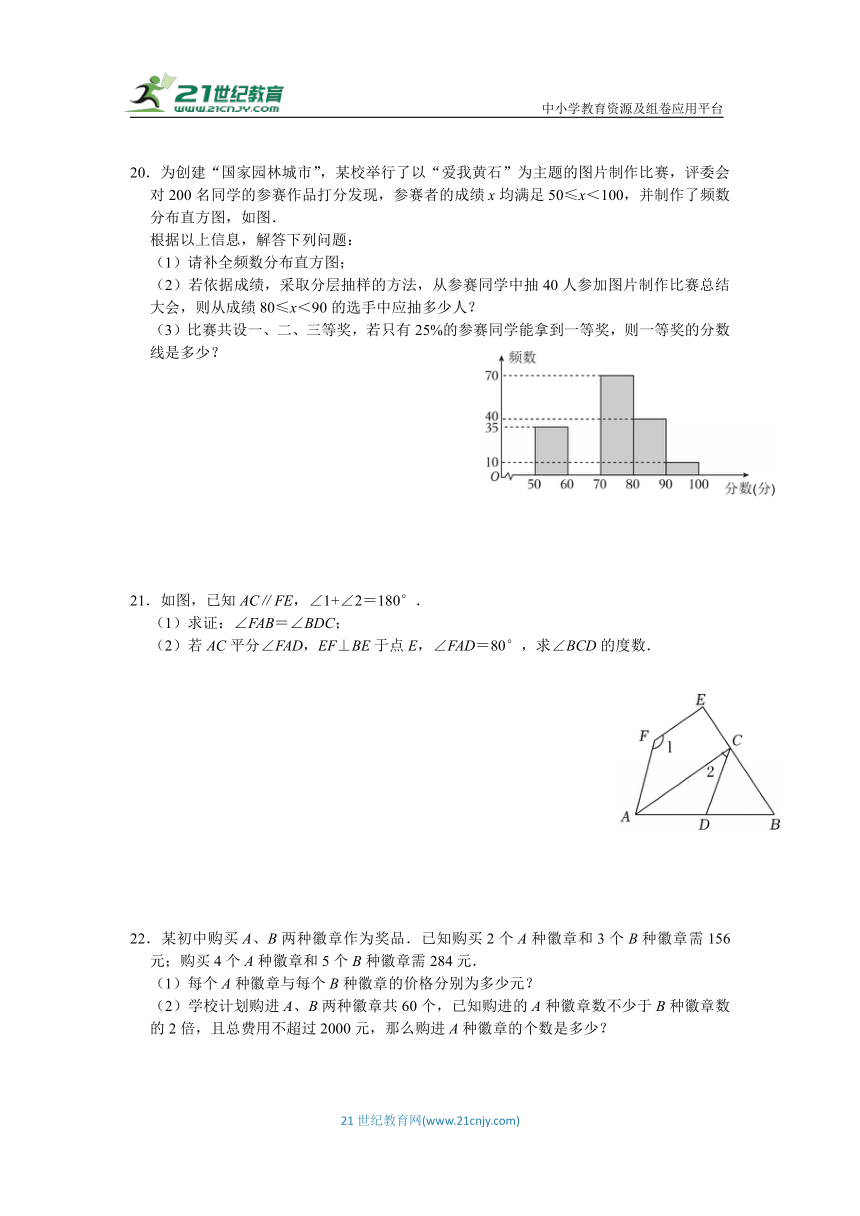
20.为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.
根据以上信息,解答下列问题:
(1)请补全频数分布直方图;
(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?
(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?
21.如图,已知AC∥FE,∠1+∠2=180°.
(1)求证:∠FAB=∠BDC;
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
22.某初中购买A、B两种徽章作为奖品.已知购买2个A种徽章和3个B种徽章需156元;购买4个A种徽章和5个B种徽章需284元.
(1)每个A种徽章与每个B种徽章的价格分别为多少元?
(2)学校计划购进A、B两种徽章共60个,已知购进的A种徽章数不少于B种徽章数的2倍,且总费用不超过2000元,那么购进A种徽章的个数是多少?
23.已知关于x、y的方程组(m、n是常数).
(1)当n=1时,则方程组可化为,
①请直接写出方程x+2y=3的所有非负整数解;
②若该方程组的解也满足方程x+y=2,求m的值;
(2)当m每取一个值时,x﹣2y+mx=﹣5就对应一个方程,而这些方程有一个公共解,你能求出这个公共解吗?
(3)当n=3时,如果方程组有整数解,求整数m的值.
24.我们约定:不等式组,,,的“长度”均为,,不等式组的整数解称为不等式组的“整点”.例如:的“长度”,“整点”为,0,1,2.根据该约定,解答下列问题:
(1)不等式组的“长度”______;“整点”为______;
(2)若不等式组的“长度”,求a的取值范围;
(3)若不等式组的“长度”,此时是否存在实数m使得关于y的不等式组恰有4个“整点”,若存在,求出m的取值范围;若不存在,请说明理由.
25.在综合与实践课上,某班开展了以两条平行线和直角三角尺为主题的数学活动.
【初步感知】
(1)如图1,若三角尺的角的顶点放在上,若,求的度数;
【自主探究】
(2)将一副三角板如图2所示摆放,直线.若三角板不动,而三角板绕点以每秒的速度顺时针旋转,设旋转时间为秒,求当旋转到时,的值是多少?
【探究拓展】
(3)现将三角板绕点以每秒的速度顺时针旋转,同时三角板绕点以每秒的速度顺时针旋转,如图3,设时间为秒,当时,若边与三角板的一条直角边(边)平行,直接写出满足条件的值.
参考答案
选择题
1—10:BAAAA DCCCA
二、填空题
11.【解答】解:∵第4组数据的频数为5,频率为0.1,
∴样本的样本容量为:5÷0.1=50,
故答案为:50.
12.【解答】解:∵,,
,
∴,
故答案为:>.
13.【解答】解:∵|x﹣2|+(y+1)2=0,
∴x﹣2=0,y+1=0,
∴x=2,y=﹣1,
∴,
故答案为:.
14.【解答】解:∵四边形ABCD为长方形,
∴AD∥BC,
∴∠BFE=∠DEF=25°.
由翻折的性质可知:
图2中,∠EFC=180°﹣∠BFE=155°,∠BFC=∠EFC﹣∠BFE=130°,
图3中,∠CFE=∠BFC﹣∠BFE=105°.
故答案为:105°.
15.【解答】解:由题得3x+7y+z=1①,
4x+10y+z=2005②,
②﹣①得x+3y=2004,
∴3x+9y=6012③,
②﹣③得x+y+z=﹣4007,
∴,
∴.
故答案为:.
16.【解答】解:设练习本一本x元,笔 一支y元,橡皮一块z元,
由题意,得,
②﹣①,得2x+2y+2z=16.
∴x+y+z=8.
∴5x+5y+5z
=5(x+y+z)
=5×8
=40(元).
故答案为:40.
三、解答题
17.【解答】解:
.
18.【解答】解:,
解不等式①得,x>﹣6,
解不等式②得,x≤2,
所以,不等式组的解集是﹣6<x≤2,
所以,它的非负整数解是0,1,2.
19.【解答】解:(1),
将①代入②可得2x+2x﹣3=5,
解得:x=2,
将x=2代入①可得y=1,
故方程组的解为:;
(2)原方程组整理可得,
①+②得,6x=30,
解得x=5,
将x=5代入①得,15﹣2y=20,
解得y,
故原方程组的解为.
20.【解答】解:(1)200﹣(35+40+70+10)=45,如图:
(2)设抽了x人,则,解得x=8;
(3)依题意知获一等奖的人数为200×25%=50(人).
则一等奖的分数线是80分.
21.【解答】(1)证明:∵AC∥EF,
∴∠1+∠FAC=180°,
又∵∠1+∠2=180°,
∴∠FAC=∠2,
∴FA∥CD,
∴∠FAB=∠BDC;
(2)解:∵AC平分∠FAD,
∴∠FAC=∠CAD,∠FAD=2∠FAC,
由(1)知∠FAC=∠2,
∴∠FAD=2∠2,
∴∠2∠FAD,
∵∠FAD=80°,
∴∠280°=40°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠2=50°.
22.【解答】解:(1)设每个A种徽章的价格为x元,每个B种徽章的价格为y元,
由题意得:,
解得:,
答:每个A种价格为36元,每个B种价格分别为28元;
(2)设购进m个A种徽章,则:
,
∴,
∴m=40,
答:购进A种徽章的个数是40.
23.【解答】解:(1)①当y=0时,x=3;
当y=1时,x=1;
∴x+2y=3的所有非负整数解为或;
②由题意可得,
①﹣②得,y=1,
将y=1代入②,得x=1,
∴方程组的解为,
将代入x﹣2y+mx=﹣5中,
∴1﹣2+m=﹣5,
解得m=﹣4;
(2)x﹣2y+mx=﹣5变形为(m+1)x﹣2y=﹣5,
∵当m每取一个值时,方程有一个公共解,
∴当x=0时,y,
∴是方程的公共解;
(3)当n=3时,,
②×2得,2x﹣4y+2mx=﹣10③,
①+③得,5x+2mx=﹣5,
整理得(5+2m)x=﹣5,
∵方程组有整数解,且m是整数,
∴5+2m=±1,5+2m=±5,
当5+2m=1时,m=﹣2,此时方程组的解为;
当5+2m=﹣1时,m=﹣3,此时方程组的解为;
当5+2m=5时,m=0,此时方程组的解为;
当5+2m=﹣5时,m=﹣5,此时方程组的解为;
综上所述:m=﹣2或m=0.
24.(1)解:
解不等式①得:,
解不等式②得:,
∴不等式组的解集为,
∴,整点为,
故答案为:;,;
(2)解:
解不等式得:,
当时,即时,,
∵,,,
∴,
解得:,
∴,
当时,即时,,
∵,,,
∴,
解得,,
∴
当时,方程组解为:,
满足题意,
综上所述:的取值范围.
(3)解:存在,理由如下:
当时,不等式的解集为,
∴,不符合,
当时,不等式的解集为,
∵,
∴,
解得:,
当时,不等式的解集为,
∴,
解得:,
当,不等式的解集为,
∴,
解得:,当时,,不符合,
当或,方程组无解,
综上所述:,
∴为,
解不等式组得:,
∵关于y的不等式组恰有4个“整点”,
∴,
解得:.
25.解:(1),
.
,
,
(2)①如图所示,当在上方时,延长交于,
,
,
,
,
;
②当在下方时,只需要在旋转40秒的基础上再旋转180度即有,;
综上所述,当旋转到时,的值是40或100;
(3)①如图,当时,
设直线与分别交于,
此时,
,
,
,
,
,即,解得:;
②如图,当时,延长,分别与交于,
此时,,
,
,
,即,
,
,
解得:;
③如图所示,当时,
设直线分别交、于、,
此时,,
,
,
,,
,
.
解得.
综上:所有满足条件的的值为15或60或105.
21世纪教育网(www.21cnjy.com)
人教版2024—2025学年七年级下册数学期末复习强化提分训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列所示的图案分别是奔驰、雪铁龙、大众、三菱汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )
A. B. C. D.
2.下列实数中,无理数是( )
A. B. C.0 D.
3.判断命题“如果n<1,那么n2﹣1<0”是假命题,只需举出一个反例.反例中的n可以为( )
A.﹣2 B.﹣ C.0 D.
4.如表是中国奥运健儿在历届奥运会中获得奖牌的情况.为了能清楚地看出各届获得奖牌的数量,应采用( )
届次 23 24 25 26 27 28 29 30 31 32
奖牌数 32 28 54 50 59 63 100 88 70 89
A.条形统计图 B.扇形统计图
C.折线统计图 D.以上都可以
5.若方程组的解为,则a+b的值为( )
A.1 B.﹣1 C.3 D.﹣3
6.下列命题是真命题的是( )
A.内错角相等 B.同一平面内,过一点有且只有一条直线与已知直线平行
C.相等的角是对顶角 D.同一平面内,过一点有且只有一条直线与已知直线垂直
7.已知点P(a﹣1,a+2)在平面直角坐标系的第三象限内,则a的取值范围是( )
A.1<a<2 B.﹣2<a<1 C.a<﹣2 D.a<1
8.在解关于x,y的方程组时,可以用①×2+②消去未知数x,也可以用①+②×5消去未知数y,则m﹣n=( )
A.4 B. C. D.
9.将一张长方形纸片如图所示折叠后,再展开,如果∠1=54°,则∠2=( )
A.54° B.68°
C.72° D.76°
10.关于x的不等式组的整数解仅有4个,则m的取值范围是( )
A.﹣5≤m<﹣4 B.﹣5<m≤﹣4 C.﹣4≤m<﹣3 D.﹣4<m≤﹣3
二、填空题(6小题,每题3分,共18分)
11.一个样本的数据分别落在5个组内,第1、2、3、4组数据的个数分别是2、8、15、5,且第4组数据的频率为0.1,这个样本的样本容量为 .
12.比较大小 ﹣4.(填“>”,“<”或者“=”)
13.若x,y为实数,且|x﹣2|+(y+1)2=0,则的值是 .
14.如图1,∠DEF=25°,将长方形纸片ABCD沿直线EF折叠成图2,再沿折痕GF折叠成图3,则∠CFE的度数为 .
15.实数x,y,z满足3x+7y+z=1,4x+10y+z=2005.求 .
16.买3本练习本,2支笔,7块橡皮共用了27元,买同样的练习本5本,同样的笔4支,同样的橡皮9块共用了43元,如果买同样的练习本、笔、橡皮各5本、5支、5块,总共需要 元.
第II卷
人教版2024—2025学年七年级下册数学期末复习强化提分训练
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:;
18.解不等式组:,并写出它的所有非负整数解.
19.解二元一次方程组:
(1); (2).
20.为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.
根据以上信息,解答下列问题:
(1)请补全频数分布直方图;
(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?
(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?
21.如图,已知AC∥FE,∠1+∠2=180°.
(1)求证:∠FAB=∠BDC;
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
22.某初中购买A、B两种徽章作为奖品.已知购买2个A种徽章和3个B种徽章需156元;购买4个A种徽章和5个B种徽章需284元.
(1)每个A种徽章与每个B种徽章的价格分别为多少元?
(2)学校计划购进A、B两种徽章共60个,已知购进的A种徽章数不少于B种徽章数的2倍,且总费用不超过2000元,那么购进A种徽章的个数是多少?
23.已知关于x、y的方程组(m、n是常数).
(1)当n=1时,则方程组可化为,
①请直接写出方程x+2y=3的所有非负整数解;
②若该方程组的解也满足方程x+y=2,求m的值;
(2)当m每取一个值时,x﹣2y+mx=﹣5就对应一个方程,而这些方程有一个公共解,你能求出这个公共解吗?
(3)当n=3时,如果方程组有整数解,求整数m的值.
24.我们约定:不等式组,,,的“长度”均为,,不等式组的整数解称为不等式组的“整点”.例如:的“长度”,“整点”为,0,1,2.根据该约定,解答下列问题:
(1)不等式组的“长度”______;“整点”为______;
(2)若不等式组的“长度”,求a的取值范围;
(3)若不等式组的“长度”,此时是否存在实数m使得关于y的不等式组恰有4个“整点”,若存在,求出m的取值范围;若不存在,请说明理由.
25.在综合与实践课上,某班开展了以两条平行线和直角三角尺为主题的数学活动.
【初步感知】
(1)如图1,若三角尺的角的顶点放在上,若,求的度数;
【自主探究】
(2)将一副三角板如图2所示摆放,直线.若三角板不动,而三角板绕点以每秒的速度顺时针旋转,设旋转时间为秒,求当旋转到时,的值是多少?
【探究拓展】
(3)现将三角板绕点以每秒的速度顺时针旋转,同时三角板绕点以每秒的速度顺时针旋转,如图3,设时间为秒,当时,若边与三角板的一条直角边(边)平行,直接写出满足条件的值.
参考答案
选择题
1—10:BAAAA DCCCA
二、填空题
11.【解答】解:∵第4组数据的频数为5,频率为0.1,
∴样本的样本容量为:5÷0.1=50,
故答案为:50.
12.【解答】解:∵,,
,
∴,
故答案为:>.
13.【解答】解:∵|x﹣2|+(y+1)2=0,
∴x﹣2=0,y+1=0,
∴x=2,y=﹣1,
∴,
故答案为:.
14.【解答】解:∵四边形ABCD为长方形,
∴AD∥BC,
∴∠BFE=∠DEF=25°.
由翻折的性质可知:
图2中,∠EFC=180°﹣∠BFE=155°,∠BFC=∠EFC﹣∠BFE=130°,
图3中,∠CFE=∠BFC﹣∠BFE=105°.
故答案为:105°.
15.【解答】解:由题得3x+7y+z=1①,
4x+10y+z=2005②,
②﹣①得x+3y=2004,
∴3x+9y=6012③,
②﹣③得x+y+z=﹣4007,
∴,
∴.
故答案为:.
16.【解答】解:设练习本一本x元,笔 一支y元,橡皮一块z元,
由题意,得,
②﹣①,得2x+2y+2z=16.
∴x+y+z=8.
∴5x+5y+5z
=5(x+y+z)
=5×8
=40(元).
故答案为:40.
三、解答题
17.【解答】解:
.
18.【解答】解:,
解不等式①得,x>﹣6,
解不等式②得,x≤2,
所以,不等式组的解集是﹣6<x≤2,
所以,它的非负整数解是0,1,2.
19.【解答】解:(1),
将①代入②可得2x+2x﹣3=5,
解得:x=2,
将x=2代入①可得y=1,
故方程组的解为:;
(2)原方程组整理可得,
①+②得,6x=30,
解得x=5,
将x=5代入①得,15﹣2y=20,
解得y,
故原方程组的解为.
20.【解答】解:(1)200﹣(35+40+70+10)=45,如图:
(2)设抽了x人,则,解得x=8;
(3)依题意知获一等奖的人数为200×25%=50(人).
则一等奖的分数线是80分.
21.【解答】(1)证明:∵AC∥EF,
∴∠1+∠FAC=180°,
又∵∠1+∠2=180°,
∴∠FAC=∠2,
∴FA∥CD,
∴∠FAB=∠BDC;
(2)解:∵AC平分∠FAD,
∴∠FAC=∠CAD,∠FAD=2∠FAC,
由(1)知∠FAC=∠2,
∴∠FAD=2∠2,
∴∠2∠FAD,
∵∠FAD=80°,
∴∠280°=40°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠2=50°.
22.【解答】解:(1)设每个A种徽章的价格为x元,每个B种徽章的价格为y元,
由题意得:,
解得:,
答:每个A种价格为36元,每个B种价格分别为28元;
(2)设购进m个A种徽章,则:
,
∴,
∴m=40,
答:购进A种徽章的个数是40.
23.【解答】解:(1)①当y=0时,x=3;
当y=1时,x=1;
∴x+2y=3的所有非负整数解为或;
②由题意可得,
①﹣②得,y=1,
将y=1代入②,得x=1,
∴方程组的解为,
将代入x﹣2y+mx=﹣5中,
∴1﹣2+m=﹣5,
解得m=﹣4;
(2)x﹣2y+mx=﹣5变形为(m+1)x﹣2y=﹣5,
∵当m每取一个值时,方程有一个公共解,
∴当x=0时,y,
∴是方程的公共解;
(3)当n=3时,,
②×2得,2x﹣4y+2mx=﹣10③,
①+③得,5x+2mx=﹣5,
整理得(5+2m)x=﹣5,
∵方程组有整数解,且m是整数,
∴5+2m=±1,5+2m=±5,
当5+2m=1时,m=﹣2,此时方程组的解为;
当5+2m=﹣1时,m=﹣3,此时方程组的解为;
当5+2m=5时,m=0,此时方程组的解为;
当5+2m=﹣5时,m=﹣5,此时方程组的解为;
综上所述:m=﹣2或m=0.
24.(1)解:
解不等式①得:,
解不等式②得:,
∴不等式组的解集为,
∴,整点为,
故答案为:;,;
(2)解:
解不等式得:,
当时,即时,,
∵,,,
∴,
解得:,
∴,
当时,即时,,
∵,,,
∴,
解得,,
∴
当时,方程组解为:,
满足题意,
综上所述:的取值范围.
(3)解:存在,理由如下:
当时,不等式的解集为,
∴,不符合,
当时,不等式的解集为,
∵,
∴,
解得:,
当时,不等式的解集为,
∴,
解得:,
当,不等式的解集为,
∴,
解得:,当时,,不符合,
当或,方程组无解,
综上所述:,
∴为,
解不等式组得:,
∵关于y的不等式组恰有4个“整点”,
∴,
解得:.
25.解:(1),
.
,
,
(2)①如图所示,当在上方时,延长交于,
,
,
,
,
;
②当在下方时,只需要在旋转40秒的基础上再旋转180度即有,;
综上所述,当旋转到时,的值是40或100;
(3)①如图,当时,
设直线与分别交于,
此时,
,
,
,
,
,即,解得:;
②如图,当时,延长,分别与交于,
此时,,
,
,
,即,
,
,
解得:;
③如图所示,当时,
设直线分别交、于、,
此时,,
,
,
,,
,
.
解得.
综上:所有满足条件的的值为15或60或105.
21世纪教育网(www.21cnjy.com)
同课章节目录
