人教版2024—2025学年七年级下册数学期末考试模拟试卷A卷(含答案)
文档属性
| 名称 | 人教版2024—2025学年七年级下册数学期末考试模拟试卷A卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 660.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版2024—2025学年七年级下册数学期末考试模拟试卷A卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.在平面直角坐标系中,点(2,﹣1)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.下列说法错误的是( )
A.若,则 B.若,则
C.若,则 D.若,则
3.若(m+1)x|m|+2>0是关于x的一元一次不等式,则该不等式的解集为( )
A.x=0 B.x<﹣3 C.x>﹣1 D.x<﹣1
4.下列图形中,由∠1=∠2能判定AB∥CD的是( )
A. B. C. D.
5.在平面直角坐标系中,若点A(2a﹣5,4﹣a)在x轴上.则点A的坐标为( )
A. B.(5,﹣1) C.(3,0) D.(0,3)
6.某校在一次演讲比赛中,将所有参赛学生的成绩绘制成如图所示的折线统计图,则下列说法错误的是( )
A.95分的人数最多
B.最高分与最低分的差是15分
C.参赛学生人数为8人
D.最高分为100分
7.若方程组的解互为相反数,则m的值是( )
A.﹣7 B.10 C.﹣10 D.﹣12
8.如图直线l∥m,直角三角板ABC的直角顶点C在直线m上,若已知∠B=45°,∠1=65°,则∠2的度数为( )
A.10° B.15° C.20° D.25°
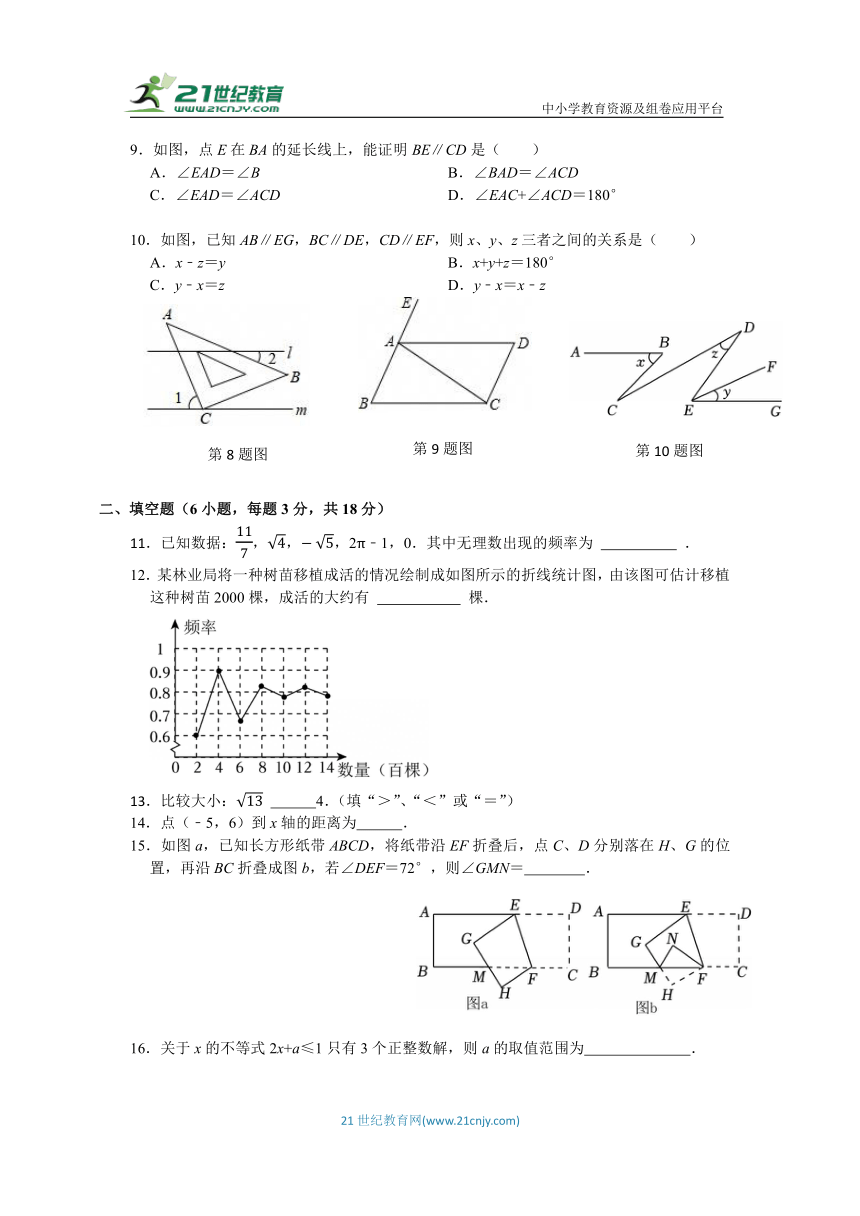
9.如图,点E在BA的延长线上,能证明BE∥CD是( )
A.∠EAD=∠B B.∠BAD=∠ACD
C.∠EAD=∠ACD D.∠EAC+∠ACD=180°
10.如图,已知AB∥EG,BC∥DE,CD∥EF,则x、y、z三者之间的关系是( )
A.x﹣z=y B.x+y+z=180°
C.y﹣x=z D.y﹣x=x﹣z
二、填空题(6小题,每题3分,共18分)
11.已知数据:,,,2π﹣1,0.其中无理数出现的频率为 .
12.某林业局将一种树苗移植成活的情况绘制成如图所示的折线统计图,由该图可估计移植这种树苗2000棵,成活的大约有 棵.
13.比较大小: 4.(填“>”、“<”或“=”)
14.点(﹣5,6)到x轴的距离为 .
15.如图a,已知长方形纸带ABCD,将纸带沿EF折叠后,点C、D分别落在H、G的位置,再沿BC折叠成图b,若∠DEF=72°,则∠GMN= .
16.关于x的不等式2x+a≤1只有3个正整数解,则a的取值范围为 .
第II卷
人教版2024—2025学年七年级下册数学期末考试模拟试卷A卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
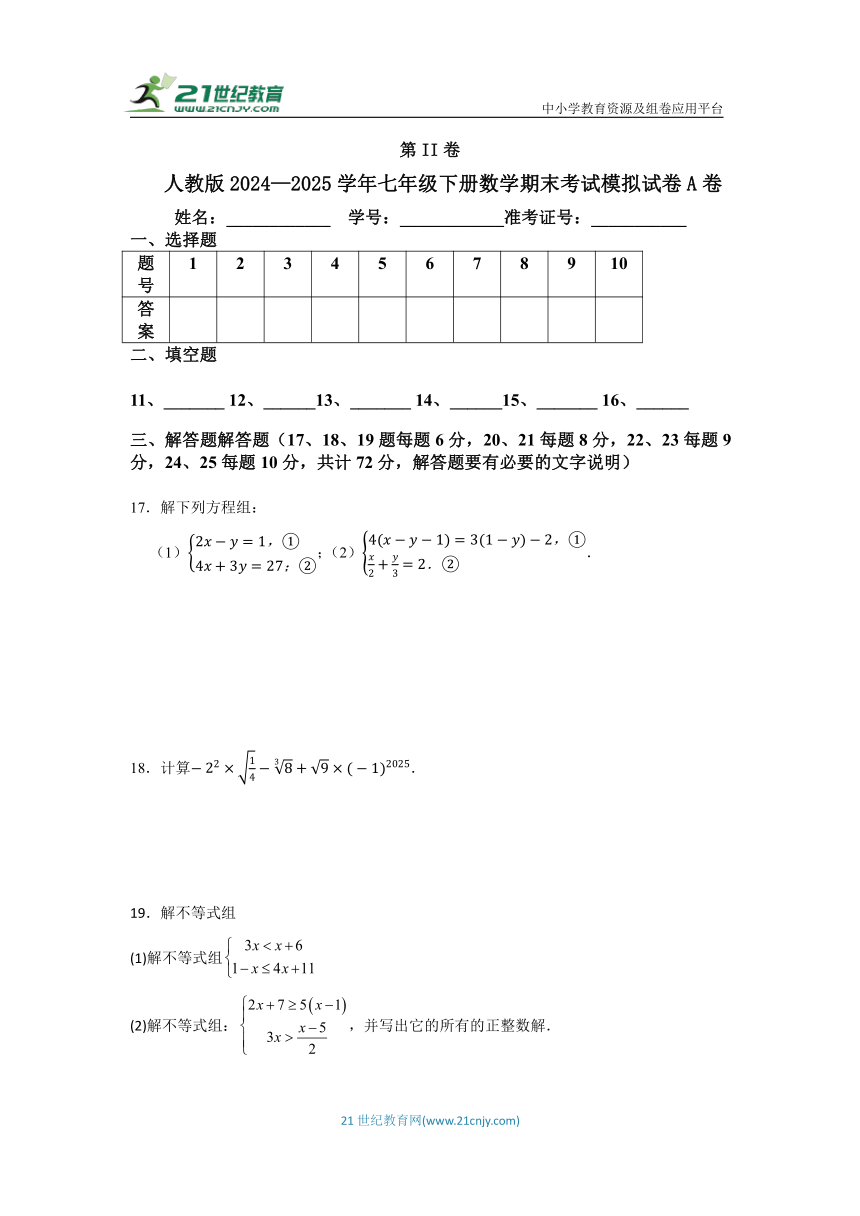
17.解下列方程组:
(1);(2).
18.计算.
19.解不等式组
(1)解不等式组
(2)解不等式组:,并写出它的所有的正整数解.
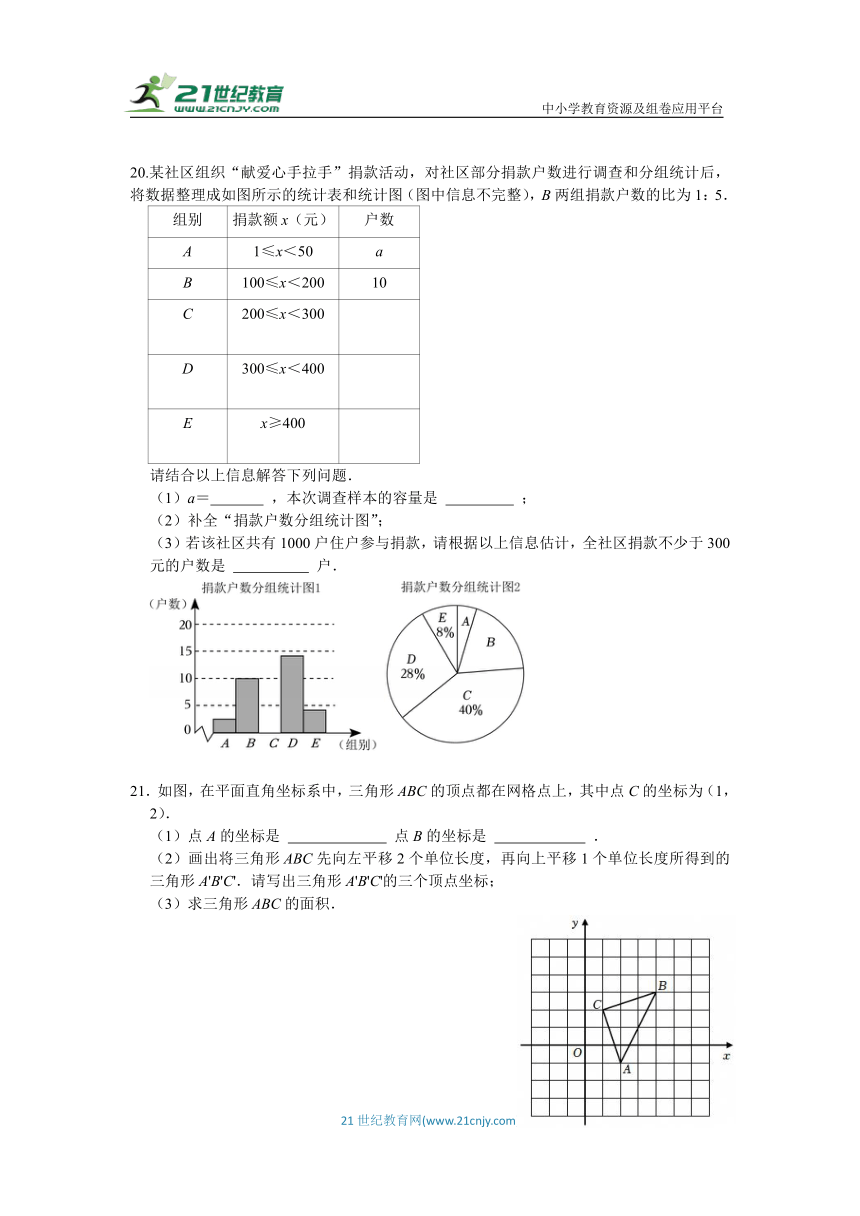
20.某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整),B两组捐款户数的比为1:5.
组别 捐款额x(元) 户数
A 1≤x<50 a
B 100≤x<200 10
C 200≤x<300
D 300≤x<400
E x≥400
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)补全“捐款户数分组统计图”;
(3)若该社区共有1000户住户参与捐款,请根据以上信息估计,全社区捐款不少于300元的户数是 户.
21.如图,在平面直角坐标系中,三角形ABC的顶点都在网格点上,其中点C的坐标为(1,2).
(1)点A的坐标是 点B的坐标是 .
(2)画出将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度所得到的三角形A'B'C'.请写出三角形A'B'C'的三个顶点坐标;
(3)求三角形ABC的面积.
22.已知关于x、y的方程满足方程组.
(1)若,求m的值;
(2)若x、y均为非负数,求m的取值范围.
23.为迎接六一儿童节,某儿童品牌玩具专卖店购进了A、B两种玩具,其中A类玩具5套B类玩具4套,需800元;A类玩具3套B类玩具2套,则需450元.
(1)求A、B两类玩具每套进价分别是多少元.
(2)该玩具店购进B类玩具比A类玩具的2倍多4套,若玩具店销售1套A类玩具获利30元,销售1套B类玩具获利20元,且全部售出后所获得利润不少于1200元.问该玩具店至少购进A类玩具多少件?
24.我们把关于x、y的两个二元一次方程与叫作互为共轭二元一次方程:二元一次方程组,叫做关于x、y共轭二元一次方程组.例如:与互为共轭二元一次方程,二元一次方程组,叫做关于x、y共轭二元一次方程组;与互为共轭二元一次方程,二元一次方程组,叫做关于、的共轭二元一次方程组.
(1)若关于x、y的方程组,为共轭方程组,则 , ;
(2)若二元一次方程中x、y的值满足下列表格:
则这个方程的共轭二元一次方程是 .
(3)解下列方程组(直接写出方程组的解即可):的解为 .
(4)发现:若方程组是共轭方程组,且方程组的解是,请化简.
25.已知关于的不等式组.
(1)当时,求该不等式组的解集.
(2)若该不等式组有且只有个整数解,求的所有整数解的和.
(3)在()的条件下,已知关于的方程组的解满足不等式,求的取值范围.
参考答案
选择题
1—10:DBCBC CCCDA
二、填空题
11.【解答】解:,
∴无理数有:,2π﹣1共2个,
故无理数出现的频率为:.
故答案为:0.4.
12.【解答】根据图形可以发现,频率在0.8附近波动,从而可以估计这种树苗移植成活的概率,再根据成活概率估算总体数量即可.
解:由图可得这种树苗成活的频率约为0.8,
∴这种树苗成活的概率为0.8,
∵移植这种树苗2000棵,
∴成活的大约有:2000×0.8=1600(棵),
故答案为:1600.
13.【解答】解:∵4,
∴4,
∴4.
故答案为:<.
14.【解答】解:点(﹣5,6)到x轴的距离为|6|=6.
故答案为:6.
15.【解答】解:∵AD∥CB,
∴∠EFC+∠DEF=180°,∠EFB=∠DEF,
即∠EFC=180°﹣72°=108°,∠EFB=72°,
∴∠BFH=108°﹣72°=36°.
∵∠H=∠D=90°,
∴∠HMF=180°﹣90°﹣36°=54°.
由折叠可得:∠NMF=∠HMF=54°,
∴∠GMN=72°.
故答案为:72.
16.【解答】解:由2x+a≤1,得:x,因为不等式只有3个正整数解,
所以不等式的正整数解为1、2、3,
∴34,
解得﹣7<a≤﹣5,
故答案为:﹣7<a≤﹣5.
三、解答题
17.【解答】解:(1)由①得,y=2x﹣1,③
把③代入②得,4x+3(2x﹣1)=27,
解得x=3,
把x=3代入③得,y=5,
所以原方程组的解为;
(2)原方程组可变为,
由①得,y=4x﹣5,③
把③代入②得,3x+2(4x﹣5)=12,
解得x=2,
把x=2代入③得,y=8﹣5=3,
所以原方程组的解为.
18.【解答】解:原式=﹣42+3×(﹣1)
=﹣2﹣2﹣3
=﹣7.
19.(1)解:,
解不等式①可得:,
解不等式②可得:,
∴不等式组的解为;
(2)解:,
解不等式①可得:,
解不等式②可得:,
∴不等式组的解集为:,
∴不等式组的正整数解为:,,,.
20.【解答】解:(1)B组捐款户数是10,则A组捐款户数为10×,样本容量为(2+10)÷(1﹣8%﹣40%﹣28%)=50,
故答案为:8、50;
(2)统计表C、D、E 组的户数分别为50×40%=20,50×8%=4.
组别 捐款额x(元) 户数
A 3≤x<100 a
B 100≤x<200 10
C 200≤x<300 20
D 300≤x<400 14
E x≥400 4
;
故答案为:20,14,4;
(3)估计全社区捐款不少于300元的户数是1000×(28%+2%)=360(户),
故答案为:360.
21.【解答】解:(1)A(2,﹣1),B(4,3);
故答案为(2,﹣1);(4,3);
(2)如图,三角形A'B'C'为所作;A′(0,0),B′(2,4),C′(﹣1,3);
(3)三角形ABC的面积=3×43×13×12×4=5.
22.(1)解:,
得:,
,
解得:;
(2)解:
得:,解得,
把代入②得:,解得,
∴原方程组的解为,
、均为非负数,
,,
∴,
解得:.
23.(1)解:设A、B两类玩具每套进价分别是x元,y元,
由题意得,,
解得:
答:A、B两类玩具每套进价分别是100元,75元.
(2)解:设购进A类玩具m件,则购进B类玩具套,
由题意得,,
解得:,
∴m的最小值为16,
答:至少购进A类玩具16件.
24.(1)解:由定义可得: , ,
∴, ,
故答案为:,;
(2)解:将, 代入, 得,解得,
∴二元一次方程为,
∴共轭二元一次方程为:,
故答案为:;
(3)解:
①②得: , 即③,
①③得: ,
解得,
将代入③得,
∴方程组的解为: ,
故答案为: ;
(4)解:∵由定义可得
∴
∵方程组是共轭方程组,
∴,
①②得,
,
又∵方程组的解是,
,即,
.
25.(1)解:当时,不等式组为,
由得,,
由得,,
∴不等式组的解集为;
(2)解:,
由得,,
由得,,
∴不等式组的解集为,
∵不等式组有且只有个整数解,
∴,
即,
解得,
∴的整数解为,,,
∴;
(3)解:,
方程组化简得,,
得,,
解得,
把代入得,,
∴,
∴方程组的解为,
把,代入不等式得,,
解得.
21世纪教育网(www.21cnjy.com)
人教版2024—2025学年七年级下册数学期末考试模拟试卷A卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.在平面直角坐标系中,点(2,﹣1)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.下列说法错误的是( )
A.若,则 B.若,则
C.若,则 D.若,则
3.若(m+1)x|m|+2>0是关于x的一元一次不等式,则该不等式的解集为( )
A.x=0 B.x<﹣3 C.x>﹣1 D.x<﹣1
4.下列图形中,由∠1=∠2能判定AB∥CD的是( )
A. B. C. D.
5.在平面直角坐标系中,若点A(2a﹣5,4﹣a)在x轴上.则点A的坐标为( )
A. B.(5,﹣1) C.(3,0) D.(0,3)
6.某校在一次演讲比赛中,将所有参赛学生的成绩绘制成如图所示的折线统计图,则下列说法错误的是( )
A.95分的人数最多
B.最高分与最低分的差是15分
C.参赛学生人数为8人
D.最高分为100分
7.若方程组的解互为相反数,则m的值是( )
A.﹣7 B.10 C.﹣10 D.﹣12
8.如图直线l∥m,直角三角板ABC的直角顶点C在直线m上,若已知∠B=45°,∠1=65°,则∠2的度数为( )
A.10° B.15° C.20° D.25°
9.如图,点E在BA的延长线上,能证明BE∥CD是( )
A.∠EAD=∠B B.∠BAD=∠ACD
C.∠EAD=∠ACD D.∠EAC+∠ACD=180°
10.如图,已知AB∥EG,BC∥DE,CD∥EF,则x、y、z三者之间的关系是( )
A.x﹣z=y B.x+y+z=180°
C.y﹣x=z D.y﹣x=x﹣z
二、填空题(6小题,每题3分,共18分)
11.已知数据:,,,2π﹣1,0.其中无理数出现的频率为 .
12.某林业局将一种树苗移植成活的情况绘制成如图所示的折线统计图,由该图可估计移植这种树苗2000棵,成活的大约有 棵.
13.比较大小: 4.(填“>”、“<”或“=”)
14.点(﹣5,6)到x轴的距离为 .
15.如图a,已知长方形纸带ABCD,将纸带沿EF折叠后,点C、D分别落在H、G的位置,再沿BC折叠成图b,若∠DEF=72°,则∠GMN= .
16.关于x的不等式2x+a≤1只有3个正整数解,则a的取值范围为 .
第II卷
人教版2024—2025学年七年级下册数学期末考试模拟试卷A卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解下列方程组:
(1);(2).
18.计算.
19.解不等式组
(1)解不等式组
(2)解不等式组:,并写出它的所有的正整数解.
20.某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整),B两组捐款户数的比为1:5.
组别 捐款额x(元) 户数
A 1≤x<50 a
B 100≤x<200 10
C 200≤x<300
D 300≤x<400
E x≥400
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)补全“捐款户数分组统计图”;
(3)若该社区共有1000户住户参与捐款,请根据以上信息估计,全社区捐款不少于300元的户数是 户.
21.如图,在平面直角坐标系中,三角形ABC的顶点都在网格点上,其中点C的坐标为(1,2).
(1)点A的坐标是 点B的坐标是 .
(2)画出将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度所得到的三角形A'B'C'.请写出三角形A'B'C'的三个顶点坐标;
(3)求三角形ABC的面积.
22.已知关于x、y的方程满足方程组.
(1)若,求m的值;
(2)若x、y均为非负数,求m的取值范围.
23.为迎接六一儿童节,某儿童品牌玩具专卖店购进了A、B两种玩具,其中A类玩具5套B类玩具4套,需800元;A类玩具3套B类玩具2套,则需450元.
(1)求A、B两类玩具每套进价分别是多少元.
(2)该玩具店购进B类玩具比A类玩具的2倍多4套,若玩具店销售1套A类玩具获利30元,销售1套B类玩具获利20元,且全部售出后所获得利润不少于1200元.问该玩具店至少购进A类玩具多少件?
24.我们把关于x、y的两个二元一次方程与叫作互为共轭二元一次方程:二元一次方程组,叫做关于x、y共轭二元一次方程组.例如:与互为共轭二元一次方程,二元一次方程组,叫做关于x、y共轭二元一次方程组;与互为共轭二元一次方程,二元一次方程组,叫做关于、的共轭二元一次方程组.
(1)若关于x、y的方程组,为共轭方程组,则 , ;
(2)若二元一次方程中x、y的值满足下列表格:
则这个方程的共轭二元一次方程是 .
(3)解下列方程组(直接写出方程组的解即可):的解为 .
(4)发现:若方程组是共轭方程组,且方程组的解是,请化简.
25.已知关于的不等式组.
(1)当时,求该不等式组的解集.
(2)若该不等式组有且只有个整数解,求的所有整数解的和.
(3)在()的条件下,已知关于的方程组的解满足不等式,求的取值范围.
参考答案
选择题
1—10:DBCBC CCCDA
二、填空题
11.【解答】解:,
∴无理数有:,2π﹣1共2个,
故无理数出现的频率为:.
故答案为:0.4.
12.【解答】根据图形可以发现,频率在0.8附近波动,从而可以估计这种树苗移植成活的概率,再根据成活概率估算总体数量即可.
解:由图可得这种树苗成活的频率约为0.8,
∴这种树苗成活的概率为0.8,
∵移植这种树苗2000棵,
∴成活的大约有:2000×0.8=1600(棵),
故答案为:1600.
13.【解答】解:∵4,
∴4,
∴4.
故答案为:<.
14.【解答】解:点(﹣5,6)到x轴的距离为|6|=6.
故答案为:6.
15.【解答】解:∵AD∥CB,
∴∠EFC+∠DEF=180°,∠EFB=∠DEF,
即∠EFC=180°﹣72°=108°,∠EFB=72°,
∴∠BFH=108°﹣72°=36°.
∵∠H=∠D=90°,
∴∠HMF=180°﹣90°﹣36°=54°.
由折叠可得:∠NMF=∠HMF=54°,
∴∠GMN=72°.
故答案为:72.
16.【解答】解:由2x+a≤1,得:x,因为不等式只有3个正整数解,
所以不等式的正整数解为1、2、3,
∴34,
解得﹣7<a≤﹣5,
故答案为:﹣7<a≤﹣5.
三、解答题
17.【解答】解:(1)由①得,y=2x﹣1,③
把③代入②得,4x+3(2x﹣1)=27,
解得x=3,
把x=3代入③得,y=5,
所以原方程组的解为;
(2)原方程组可变为,
由①得,y=4x﹣5,③
把③代入②得,3x+2(4x﹣5)=12,
解得x=2,
把x=2代入③得,y=8﹣5=3,
所以原方程组的解为.
18.【解答】解:原式=﹣42+3×(﹣1)
=﹣2﹣2﹣3
=﹣7.
19.(1)解:,
解不等式①可得:,
解不等式②可得:,
∴不等式组的解为;
(2)解:,
解不等式①可得:,
解不等式②可得:,
∴不等式组的解集为:,
∴不等式组的正整数解为:,,,.
20.【解答】解:(1)B组捐款户数是10,则A组捐款户数为10×,样本容量为(2+10)÷(1﹣8%﹣40%﹣28%)=50,
故答案为:8、50;
(2)统计表C、D、E 组的户数分别为50×40%=20,50×8%=4.
组别 捐款额x(元) 户数
A 3≤x<100 a
B 100≤x<200 10
C 200≤x<300 20
D 300≤x<400 14
E x≥400 4
;
故答案为:20,14,4;
(3)估计全社区捐款不少于300元的户数是1000×(28%+2%)=360(户),
故答案为:360.
21.【解答】解:(1)A(2,﹣1),B(4,3);
故答案为(2,﹣1);(4,3);
(2)如图,三角形A'B'C'为所作;A′(0,0),B′(2,4),C′(﹣1,3);
(3)三角形ABC的面积=3×43×13×12×4=5.
22.(1)解:,
得:,
,
解得:;
(2)解:
得:,解得,
把代入②得:,解得,
∴原方程组的解为,
、均为非负数,
,,
∴,
解得:.
23.(1)解:设A、B两类玩具每套进价分别是x元,y元,
由题意得,,
解得:
答:A、B两类玩具每套进价分别是100元,75元.
(2)解:设购进A类玩具m件,则购进B类玩具套,
由题意得,,
解得:,
∴m的最小值为16,
答:至少购进A类玩具16件.
24.(1)解:由定义可得: , ,
∴, ,
故答案为:,;
(2)解:将, 代入, 得,解得,
∴二元一次方程为,
∴共轭二元一次方程为:,
故答案为:;
(3)解:
①②得: , 即③,
①③得: ,
解得,
将代入③得,
∴方程组的解为: ,
故答案为: ;
(4)解:∵由定义可得
∴
∵方程组是共轭方程组,
∴,
①②得,
,
又∵方程组的解是,
,即,
.
25.(1)解:当时,不等式组为,
由得,,
由得,,
∴不等式组的解集为;
(2)解:,
由得,,
由得,,
∴不等式组的解集为,
∵不等式组有且只有个整数解,
∴,
即,
解得,
∴的整数解为,,,
∴;
(3)解:,
方程组化简得,,
得,,
解得,
把代入得,,
∴,
∴方程组的解为,
把,代入不等式得,,
解得.
21世纪教育网(www.21cnjy.com)
同课章节目录
