人教版2024—2025学年七年级下册数学期末复习检测卷(含答案)
文档属性
| 名称 | 人教版2024—2025学年七年级下册数学期末复习检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 715.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 07:36:05 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版2024—2025学年七年级下册数学期末复习检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列调查中,最适宜采用普查的是( )
A.某品牌灯泡的使用寿命
B.某班学生的身高
C.某市的空气质量
D.某电视节目的收视率
2.下列图形中,由∠1=∠2能判定AB∥CD的是( )
A. B. C. D.
3.要说明命题“若a>b,则a2>ab“是假命题,能举的一个反例是( )
A.a=1,b=﹣2 B.a=2,b=1 C.a=4,b=﹣1 D.a=﹣2,b=﹣3
4.在平面直角坐标系中,若点A(2a﹣5,4﹣a)在x轴上.则点A的坐标为( )
A. B.(5,﹣1) C.(3,0) D.(0,3)
5.为了调查我市某校学生的视力情况,在全校的2000名学生中随机抽取了300名学生,下列说法正确的是( )
A.此次调查属于全面调查
B.样本容量是300
C.2000名学生是总体
D.被抽取的每一名学生称为个体
6.已知:0.71,2.24,7.1,22.4,请根据以上规律得到的结果( )
A.0.071 B.0.224 C.0.025 D.0.0224
7.的算术平方根等于( )
A.4 B.±4 C.2 D.±2
8.若不等式组无解,则m的值可能为( )
A.3 B.5 C.7 D.9
9.在平面直角坐标系中,点A(﹣4,3)到y轴的距离是( )
A.4 B.3 C.﹣4 D.﹣3
10.若关于x的一元一次不等式组的解集为x≥,且关于y的方程3y﹣2=的解为非负整数,则符合条件的所有整数m的积为( )
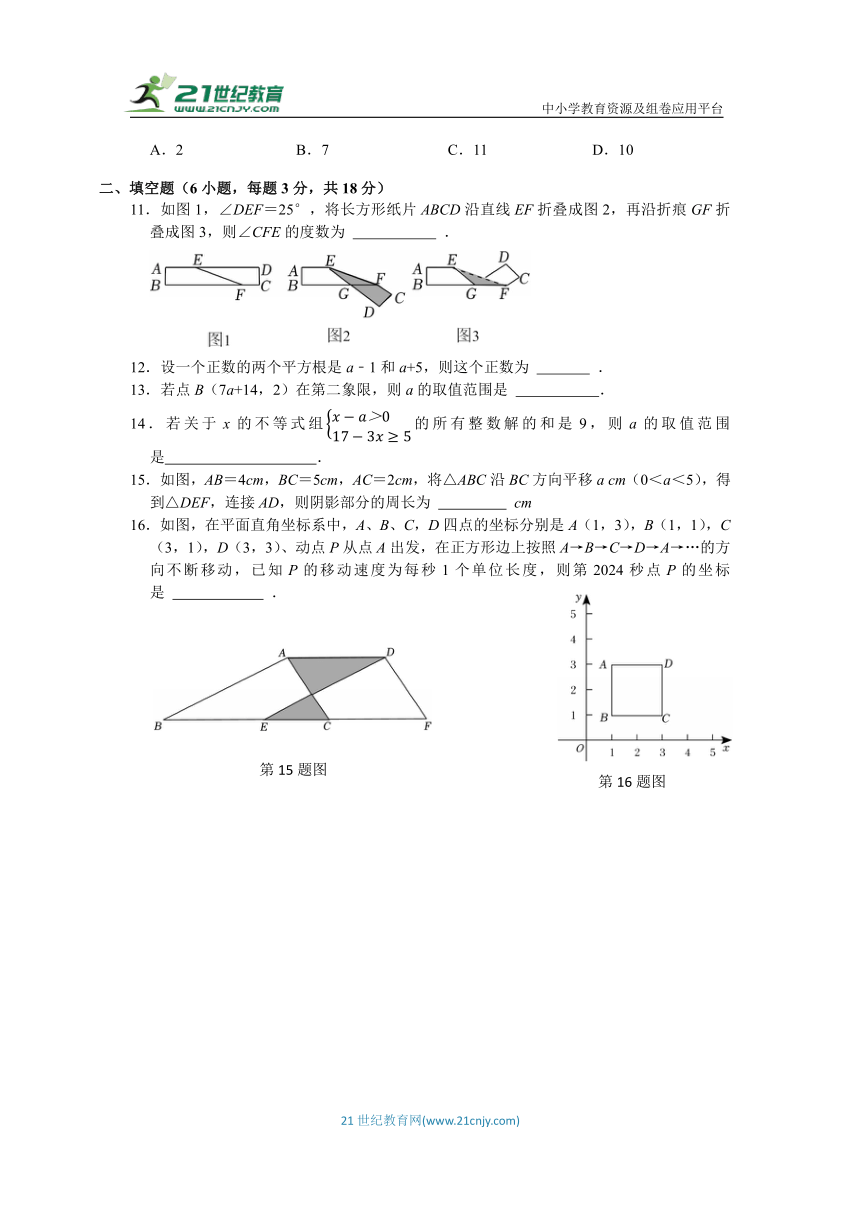
A.2 B.7 C.11 D.10
二、填空题(6小题,每题3分,共18分)
11.如图1,∠DEF=25°,将长方形纸片ABCD沿直线EF折叠成图2,再沿折痕GF折叠成图3,则∠CFE的度数为 .
12.设一个正数的两个平方根是a﹣1和a+5,则这个正数为 .
13.若点B(7a+14,2)在第二象限,则a的取值范围是 .
14.若关于x的不等式组的所有整数解的和是9,则a的取值范围是 .
15.如图,AB=4cm,BC=5cm,AC=2cm,将△ABC沿BC方向平移a cm(0<a<5),得到△DEF,连接AD,则阴影部分的周长为 cm
16.如图,在平面直角坐标系中,A、B、C,D四点的坐标分别是A(1,3),B(1,1),C(3,1),D(3,3)、动点P从点A出发,在正方形边上按照A→B→C→D→A→…的方向不断移动,已知P的移动速度为每秒1个单位长度,则第2024秒点P的坐标是 .
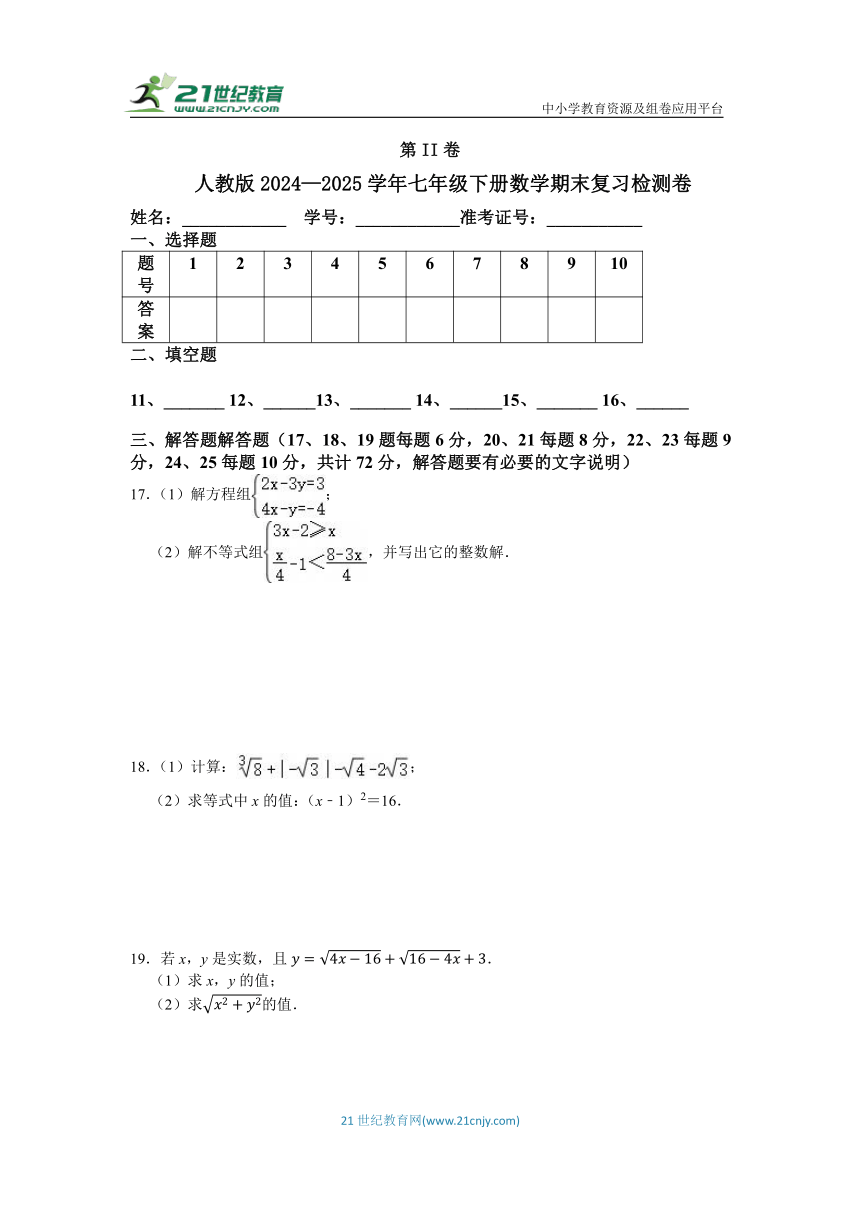
第II卷
人教版2024—2025学年七年级下册数学期末复习检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.(1)解方程组;
(2)解不等式组,并写出它的整数解.
18.(1)计算:;
(2)求等式中x的值:(x﹣1)2=16.
19.若x,y是实数,且.
(1)求x,y的值;
(2)求的值.
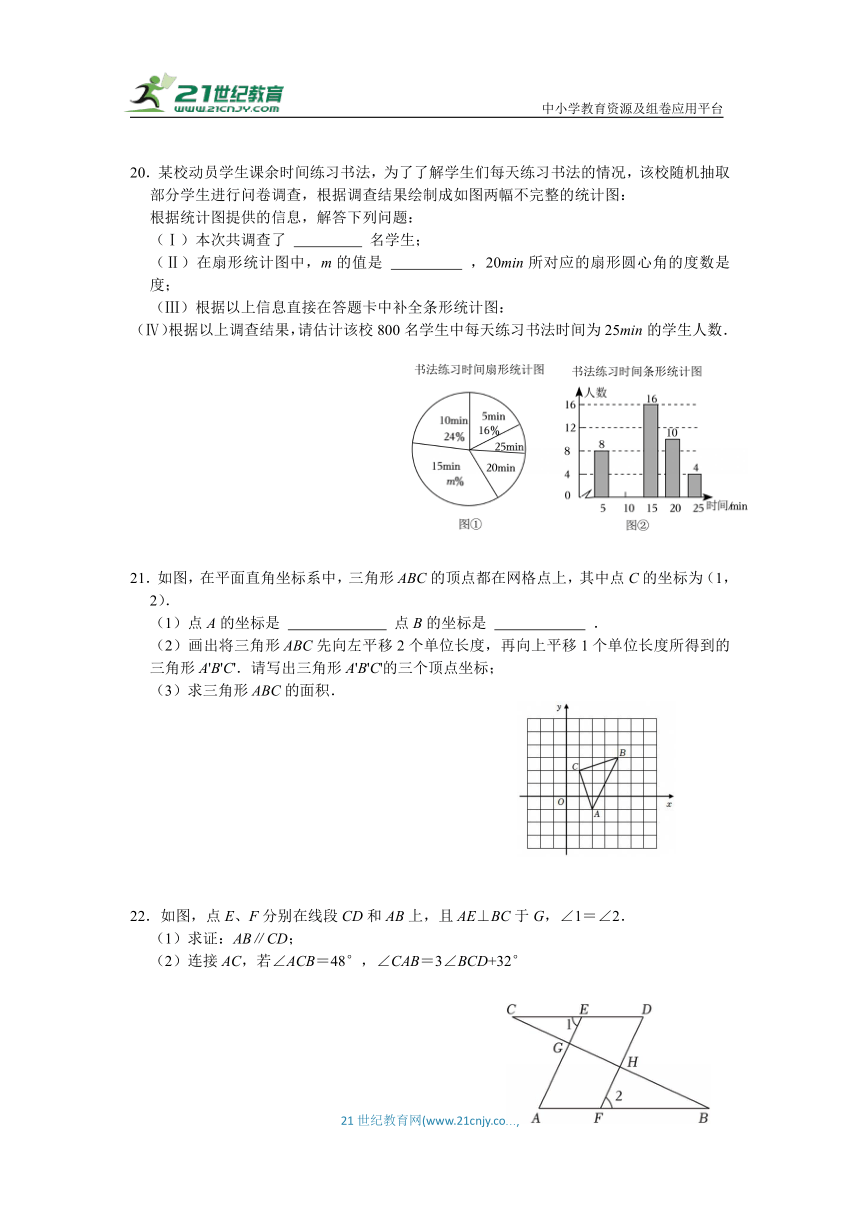
20.某校动员学生课余时间练习书法,为了了解学生们每天练习书法的情况,该校随机抽取部分学生进行问卷调查,根据调查结果绘制成如图两幅不完整的统计图:
根据统计图提供的信息,解答下列问题:
(Ⅰ)本次共调查了 名学生;
(Ⅱ)在扇形统计图中,m的值是 ,20min所对应的扇形圆心角的度数是 度;
(Ⅲ)根据以上信息直接在答题卡中补全条形统计图:
(Ⅳ)根据以上调查结果,请估计该校800名学生中每天练习书法时间为25min的学生人数.
21.如图,在平面直角坐标系中,三角形ABC的顶点都在网格点上,其中点C的坐标为(1,2).
(1)点A的坐标是 点B的坐标是 .
(2)画出将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度所得到的三角形A'B'C'.请写出三角形A'B'C'的三个顶点坐标;
(3)求三角形ABC的面积.
22.如图,点E、F分别在线段CD和AB上,且AE⊥BC于G,∠1=∠2.
(1)求证:AB∥CD;
(2)连接AC,若∠ACB=48°,∠CAB=3∠BCD+32°
23.某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:
销售时段 销售数量 销售收入
A种型号 B种型号
第一周 3台 4台 1200元
第二周 5台 6台 1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标?若能;若不能,请说明理由.
24.如果一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.例如:方程的解为,不等式组的解集为,因为,所以称方程为不等式组的关联方程.
(1)在方程①;②;③中,不等式组的关联方程是______;(填序号)
(2)若不等式组的一个关联方程的解是整数,且这个关联方程是,求常数的值;
(3)①解两个方程:和;②是否存在整数,使得方程和都是关于的不等式组的关联方程?若存在,直接写出所有符合条件的整数的值;若不存在,请说明理由.
25.对于关于x,y的二元一次方程组(其中是常数),若该方程组的解x,y满足,则称这个方程组为“和美方程组”.
(1)下列方程组是“和美方程组”的是_____________;(只填写序号)
①;②;③;④.
(2)若关于x,y的方程组是“和美方程组”,求的值;
(3)若对于任意实数,关于x,y的方程组都是“和美方程组”,求的值.
参考答案
一、选择题
1—10:BBDCB ACAAD
二、填空题
11.【解答】解:∵四边形ABCD为长方形,
∴AD∥BC,
∴∠BFE=∠DEF=25°.
由翻折的性质可知:
图2中,∠EFC=180°﹣∠BFE=155°,∠BFC=∠EFC﹣∠BFE=130°,
图3中,∠CFE=∠BFC﹣∠BFE=105°.
故答案为:105°.
12.【解答】解:∵一个正数的两个平方根是a﹣1和a+5,
∴a﹣1+a+5=0,
解得:a=﹣2,
∴这个数为(a﹣1)2=(﹣3)2=9,
故答案为:9.
13.【解答】解:∵点B(7a+14,2)在第二象限,
∴7a+14<0,
7a<﹣14,
a<﹣2,
故答案为:a<﹣2.
14.【解答】解:,
解不等式①得x>a,
解不等式②得x≤4,
∵所有整数解的和是9,
∴不等式组的整数解为2,3,4或﹣1,0,1,2,3,4,
∴1≤a<2或﹣2≤a<﹣1
故答案为:1≤a<2或﹣2≤a<﹣1.
15.【解答】解:由平移的性质可知:DE=AB=4cm,AD=BE=a cm,
∴EC=(5﹣a)cm,
∴阴影部分的周长=AD+EC+AC+DE=a+(5﹣a)+2+4=11(cm),
故答案为:11.
16.【解答】解:由题知,
因为A、B、C,D四点的坐标分别是A(1,3),B(1,1),C(3,1),D(3,3),
所以四边形ABCD是正方形,且边长为2.
又因为点P的速度为每秒1个单位长度,
所以2×4÷1=8,
即每运动8秒,点P的位置循环出现.
因为2024÷8=253,
所以第2024秒时点P的位置和第8秒时点P的位置相同.
又因为第8秒时点P的坐标为(1,3),
所以第2024秒点P的坐标是(1,3).
故答案为:(1,3).
三、解答题
17.【解答】解:(1),
①﹣②×6,得﹣10x=﹣15,
解得x=﹣,
把x=﹣代入②.
故原方程组的解为;
(2),
解不等式①,得:x≥6,
解不等式②,得:x<3,
则不等式组的解集为:1≤x<8,它的整数解为1,2.
18.【解答】解:(1)
=2+﹣2﹣2
=﹣;
(2)开平方,得x﹣1=±4,
解得x=4或x=﹣3.
19.【解答】解:(1)∵.
∴4x﹣16≥0,16﹣4x≥0,
∴4x﹣16=0,
∴x=4,
则y=3,
(2)∵x=4,y=3,
∴.
20.【解答】解:(Ⅰ)8÷16%=50(名),
故答案为:50;
(Ⅱ)16÷50×100%=32%,即m=32,
360°×=72°,
故答案为:32,72;
(Ⅲ)每天练习书法时间为10min的学生人数为:50﹣8﹣16﹣10﹣6=12(名),
补全条形统计图如下:
(Ⅳ)800×=64(人),
答:该校800名学生中每天练习书法时间为25min的学生人数大约有64人.
21.【解答】解:(1)A(2,﹣1),B(4,3);
故答案为(2,﹣1);(4,3);
(2)如图,三角形A'B'C'为所作;A′(0,0),B′(2,4),C′(﹣1,3);
(3)三角形ABC的面积=3×43×13×12×4=5.
22.【解答】(1)证明:∵AE⊥BC,DF⊥BC,
∴∠AGB=∠FHB=90°,
∴AE∥DF,
∴∠1=∠D,
∵∠1=∠6,
∴∠D=∠2,
∴AB∥CD;
(2)解:如图,
∵AB∥CD,
∴∠B=∠BCD,
∵∠CAB=3∠BCD+32°,
∴∠CAB=2∠B+32°,
∵∠ACB+∠CAB+∠B=180°,∠ACB=48°,
∴48°+3∠B+32°+∠B=180°,
∴∠B=25°.
23.【解答】解:(1)设A、B两种型号电风扇的销售单价分别为x元,
依题意得:,
解得:,
答:A、B两种型号电风扇的销售单价分别为200元.
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(50﹣a)台.
依题意得:160a+120(50﹣a)≤7500,
解得:a≤37,
∵a是整数,
∴a最大是37,
答:超市最多采购A种型号电风扇37台时,采购金额不多于7500元.
24.(1)解:方程①的解为;
方程②的解为;
方程③的解为;
不等式组的解集为,
∵,
∴不等式组的关联方程是方程③,
故答案为:③;
(2)解:解不等式组,得,
因此不等式组的整数解为.
将代入关联方程0,
得;
(3)解:①,
解得;
,
解得;
②不存在.理由如下:
解不等式组,
得,
假如方程和都是关于的不等式组的关联方程,
则且.
解得:且
∴不等式组无解,
不存在整数,使得方程和都是关于的不等式组的关联方程.
25.(1)解:由定义可知①④的解x,y满足,①④是“和美方程组”;
由②解得满足
∴②是“和美方程组”;
由③解得不满足
∴③不是“和美方程组”.
故答案为:①②④;
(2)解方程组
关于x,y的方程组是“和美方程组”,
,
解得;
(3)是“和美方程组”,
.
由得或.
①当时,代入,
得,
.
为任意实数,
;
②当时,代入,得,
.
为任意实数,
.
综上所述,的值为或.
21世纪教育网(www.21cnjy.com)
人教版2024—2025学年七年级下册数学期末复习检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列调查中,最适宜采用普查的是( )
A.某品牌灯泡的使用寿命
B.某班学生的身高
C.某市的空气质量
D.某电视节目的收视率
2.下列图形中,由∠1=∠2能判定AB∥CD的是( )
A. B. C. D.
3.要说明命题“若a>b,则a2>ab“是假命题,能举的一个反例是( )
A.a=1,b=﹣2 B.a=2,b=1 C.a=4,b=﹣1 D.a=﹣2,b=﹣3
4.在平面直角坐标系中,若点A(2a﹣5,4﹣a)在x轴上.则点A的坐标为( )
A. B.(5,﹣1) C.(3,0) D.(0,3)
5.为了调查我市某校学生的视力情况,在全校的2000名学生中随机抽取了300名学生,下列说法正确的是( )
A.此次调查属于全面调查
B.样本容量是300
C.2000名学生是总体
D.被抽取的每一名学生称为个体
6.已知:0.71,2.24,7.1,22.4,请根据以上规律得到的结果( )
A.0.071 B.0.224 C.0.025 D.0.0224
7.的算术平方根等于( )
A.4 B.±4 C.2 D.±2
8.若不等式组无解,则m的值可能为( )
A.3 B.5 C.7 D.9
9.在平面直角坐标系中,点A(﹣4,3)到y轴的距离是( )
A.4 B.3 C.﹣4 D.﹣3
10.若关于x的一元一次不等式组的解集为x≥,且关于y的方程3y﹣2=的解为非负整数,则符合条件的所有整数m的积为( )
A.2 B.7 C.11 D.10
二、填空题(6小题,每题3分,共18分)
11.如图1,∠DEF=25°,将长方形纸片ABCD沿直线EF折叠成图2,再沿折痕GF折叠成图3,则∠CFE的度数为 .
12.设一个正数的两个平方根是a﹣1和a+5,则这个正数为 .
13.若点B(7a+14,2)在第二象限,则a的取值范围是 .
14.若关于x的不等式组的所有整数解的和是9,则a的取值范围是 .
15.如图,AB=4cm,BC=5cm,AC=2cm,将△ABC沿BC方向平移a cm(0<a<5),得到△DEF,连接AD,则阴影部分的周长为 cm
16.如图,在平面直角坐标系中,A、B、C,D四点的坐标分别是A(1,3),B(1,1),C(3,1),D(3,3)、动点P从点A出发,在正方形边上按照A→B→C→D→A→…的方向不断移动,已知P的移动速度为每秒1个单位长度,则第2024秒点P的坐标是 .
第II卷
人教版2024—2025学年七年级下册数学期末复习检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.(1)解方程组;
(2)解不等式组,并写出它的整数解.
18.(1)计算:;
(2)求等式中x的值:(x﹣1)2=16.
19.若x,y是实数,且.
(1)求x,y的值;
(2)求的值.
20.某校动员学生课余时间练习书法,为了了解学生们每天练习书法的情况,该校随机抽取部分学生进行问卷调查,根据调查结果绘制成如图两幅不完整的统计图:
根据统计图提供的信息,解答下列问题:
(Ⅰ)本次共调查了 名学生;
(Ⅱ)在扇形统计图中,m的值是 ,20min所对应的扇形圆心角的度数是 度;
(Ⅲ)根据以上信息直接在答题卡中补全条形统计图:
(Ⅳ)根据以上调查结果,请估计该校800名学生中每天练习书法时间为25min的学生人数.
21.如图,在平面直角坐标系中,三角形ABC的顶点都在网格点上,其中点C的坐标为(1,2).
(1)点A的坐标是 点B的坐标是 .
(2)画出将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度所得到的三角形A'B'C'.请写出三角形A'B'C'的三个顶点坐标;
(3)求三角形ABC的面积.
22.如图,点E、F分别在线段CD和AB上,且AE⊥BC于G,∠1=∠2.
(1)求证:AB∥CD;
(2)连接AC,若∠ACB=48°,∠CAB=3∠BCD+32°
23.某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:
销售时段 销售数量 销售收入
A种型号 B种型号
第一周 3台 4台 1200元
第二周 5台 6台 1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标?若能;若不能,请说明理由.
24.如果一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.例如:方程的解为,不等式组的解集为,因为,所以称方程为不等式组的关联方程.
(1)在方程①;②;③中,不等式组的关联方程是______;(填序号)
(2)若不等式组的一个关联方程的解是整数,且这个关联方程是,求常数的值;
(3)①解两个方程:和;②是否存在整数,使得方程和都是关于的不等式组的关联方程?若存在,直接写出所有符合条件的整数的值;若不存在,请说明理由.
25.对于关于x,y的二元一次方程组(其中是常数),若该方程组的解x,y满足,则称这个方程组为“和美方程组”.
(1)下列方程组是“和美方程组”的是_____________;(只填写序号)
①;②;③;④.
(2)若关于x,y的方程组是“和美方程组”,求的值;
(3)若对于任意实数,关于x,y的方程组都是“和美方程组”,求的值.
参考答案
一、选择题
1—10:BBDCB ACAAD
二、填空题
11.【解答】解:∵四边形ABCD为长方形,
∴AD∥BC,
∴∠BFE=∠DEF=25°.
由翻折的性质可知:
图2中,∠EFC=180°﹣∠BFE=155°,∠BFC=∠EFC﹣∠BFE=130°,
图3中,∠CFE=∠BFC﹣∠BFE=105°.
故答案为:105°.
12.【解答】解:∵一个正数的两个平方根是a﹣1和a+5,
∴a﹣1+a+5=0,
解得:a=﹣2,
∴这个数为(a﹣1)2=(﹣3)2=9,
故答案为:9.
13.【解答】解:∵点B(7a+14,2)在第二象限,
∴7a+14<0,
7a<﹣14,
a<﹣2,
故答案为:a<﹣2.
14.【解答】解:,
解不等式①得x>a,
解不等式②得x≤4,
∵所有整数解的和是9,
∴不等式组的整数解为2,3,4或﹣1,0,1,2,3,4,
∴1≤a<2或﹣2≤a<﹣1
故答案为:1≤a<2或﹣2≤a<﹣1.
15.【解答】解:由平移的性质可知:DE=AB=4cm,AD=BE=a cm,
∴EC=(5﹣a)cm,
∴阴影部分的周长=AD+EC+AC+DE=a+(5﹣a)+2+4=11(cm),
故答案为:11.
16.【解答】解:由题知,
因为A、B、C,D四点的坐标分别是A(1,3),B(1,1),C(3,1),D(3,3),
所以四边形ABCD是正方形,且边长为2.
又因为点P的速度为每秒1个单位长度,
所以2×4÷1=8,
即每运动8秒,点P的位置循环出现.
因为2024÷8=253,
所以第2024秒时点P的位置和第8秒时点P的位置相同.
又因为第8秒时点P的坐标为(1,3),
所以第2024秒点P的坐标是(1,3).
故答案为:(1,3).
三、解答题
17.【解答】解:(1),
①﹣②×6,得﹣10x=﹣15,
解得x=﹣,
把x=﹣代入②.
故原方程组的解为;
(2),
解不等式①,得:x≥6,
解不等式②,得:x<3,
则不等式组的解集为:1≤x<8,它的整数解为1,2.
18.【解答】解:(1)
=2+﹣2﹣2
=﹣;
(2)开平方,得x﹣1=±4,
解得x=4或x=﹣3.
19.【解答】解:(1)∵.
∴4x﹣16≥0,16﹣4x≥0,
∴4x﹣16=0,
∴x=4,
则y=3,
(2)∵x=4,y=3,
∴.
20.【解答】解:(Ⅰ)8÷16%=50(名),
故答案为:50;
(Ⅱ)16÷50×100%=32%,即m=32,
360°×=72°,
故答案为:32,72;
(Ⅲ)每天练习书法时间为10min的学生人数为:50﹣8﹣16﹣10﹣6=12(名),
补全条形统计图如下:
(Ⅳ)800×=64(人),
答:该校800名学生中每天练习书法时间为25min的学生人数大约有64人.
21.【解答】解:(1)A(2,﹣1),B(4,3);
故答案为(2,﹣1);(4,3);
(2)如图,三角形A'B'C'为所作;A′(0,0),B′(2,4),C′(﹣1,3);
(3)三角形ABC的面积=3×43×13×12×4=5.
22.【解答】(1)证明:∵AE⊥BC,DF⊥BC,
∴∠AGB=∠FHB=90°,
∴AE∥DF,
∴∠1=∠D,
∵∠1=∠6,
∴∠D=∠2,
∴AB∥CD;
(2)解:如图,
∵AB∥CD,
∴∠B=∠BCD,
∵∠CAB=3∠BCD+32°,
∴∠CAB=2∠B+32°,
∵∠ACB+∠CAB+∠B=180°,∠ACB=48°,
∴48°+3∠B+32°+∠B=180°,
∴∠B=25°.
23.【解答】解:(1)设A、B两种型号电风扇的销售单价分别为x元,
依题意得:,
解得:,
答:A、B两种型号电风扇的销售单价分别为200元.
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(50﹣a)台.
依题意得:160a+120(50﹣a)≤7500,
解得:a≤37,
∵a是整数,
∴a最大是37,
答:超市最多采购A种型号电风扇37台时,采购金额不多于7500元.
24.(1)解:方程①的解为;
方程②的解为;
方程③的解为;
不等式组的解集为,
∵,
∴不等式组的关联方程是方程③,
故答案为:③;
(2)解:解不等式组,得,
因此不等式组的整数解为.
将代入关联方程0,
得;
(3)解:①,
解得;
,
解得;
②不存在.理由如下:
解不等式组,
得,
假如方程和都是关于的不等式组的关联方程,
则且.
解得:且
∴不等式组无解,
不存在整数,使得方程和都是关于的不等式组的关联方程.
25.(1)解:由定义可知①④的解x,y满足,①④是“和美方程组”;
由②解得满足
∴②是“和美方程组”;
由③解得不满足
∴③不是“和美方程组”.
故答案为:①②④;
(2)解方程组
关于x,y的方程组是“和美方程组”,
,
解得;
(3)是“和美方程组”,
.
由得或.
①当时,代入,
得,
.
为任意实数,
;
②当时,代入,得,
.
为任意实数,
.
综上所述,的值为或.
21世纪教育网(www.21cnjy.com)
同课章节目录
