湘教版2024—2025学年七年级下学期数学期末考试调研检测卷(含答案)
文档属性
| 名称 | 湘教版2024—2025学年七年级下学期数学期末考试调研检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 740.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 07:33:02 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
湘教版2024—2025学年七年级下学期数学期末考试调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
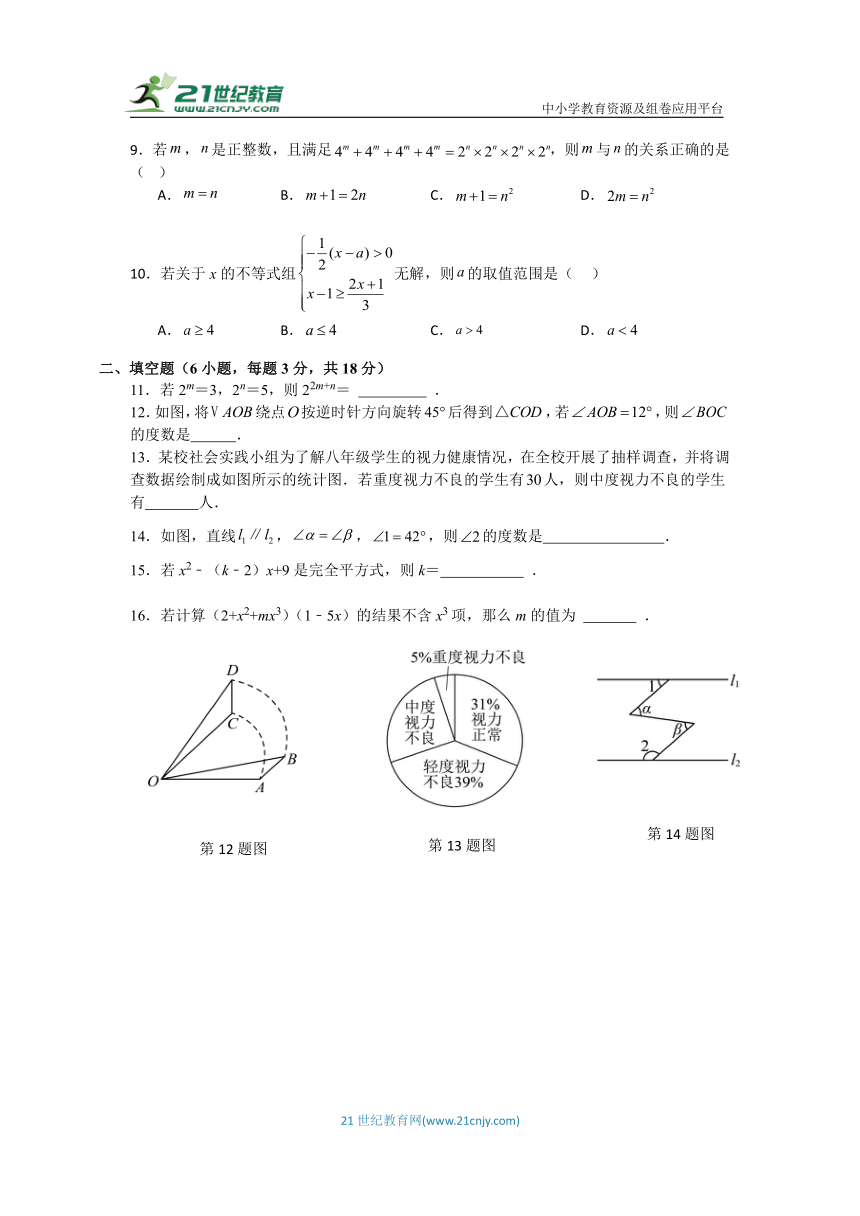
1.下列图形是轴对称图形的是( )
A. B. C. D.
2.农业科研人员在试验田里种植了新品种大麦,为了考察麦穗长度的分布情况,抽取了100个麦穗进行测量.这项调查中的样本是( )
A.新品种大麦长度的分布情况 B.100
C.从中抽取的100个麦穗的长度 D.100个麦穗中的某一个麦穗的长度
3.如图,四边形中,对角线与相交于点O.下列条件,能判定的是( )
A. B.
C. D.
4.如果关于x的不等式的解集为,那么a的取值范围是( )
A. B. C. D.
5.下列各式是求个位数为5的整数的算术平方根的运算:,,,,,,观察这些运算都有规律,试利用该规律直接写出运算的结果为( )
A.9595 B.9995 C.9955 D.5995
6.如图,绕点A逆时针旋转得到,若,则( )
A. B. C. D.
7.如图,已知,,,则的度数为( )
A. B. C. D.
8.如图,将一张长方形纸片进行折叠,若,则的度数为( )
A. B. C. D.
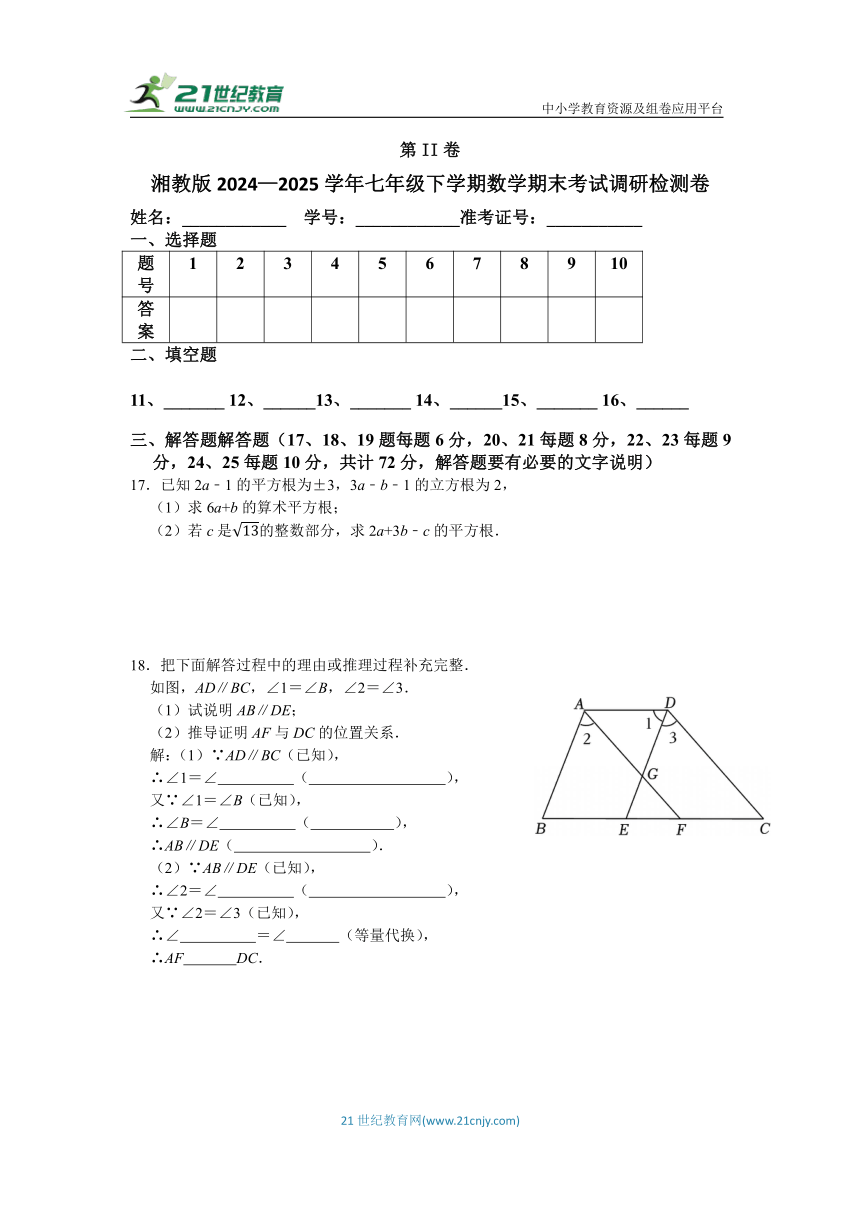
9.若,是正整数,且满足,则与的关系正确的是( )
A. B. C. D.
10.若关于x的不等式组无解,则的取值范围是( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.若2m=3,2n=5,则22m+n= .
12.如图,将绕点按逆时针方向旋转后得到,若,则的度数是 .
13.某校社会实践小组为了解八年级学生的视力健康情况,在全校开展了抽样调查,并将调查数据绘制成如图所示的统计图.若重度视力不良的学生有人,则中度视力不良的学生有 人.
14.如图,直线,,,则的度数是 .
15.若x2﹣(k﹣2)x+9是完全平方式,则k= .
16.若计算(2+x2+mx3)(1﹣5x)的结果不含x3项,那么m的值为 .
第II卷
湘教版2024—2025学年七年级下学期数学期末考试调研检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
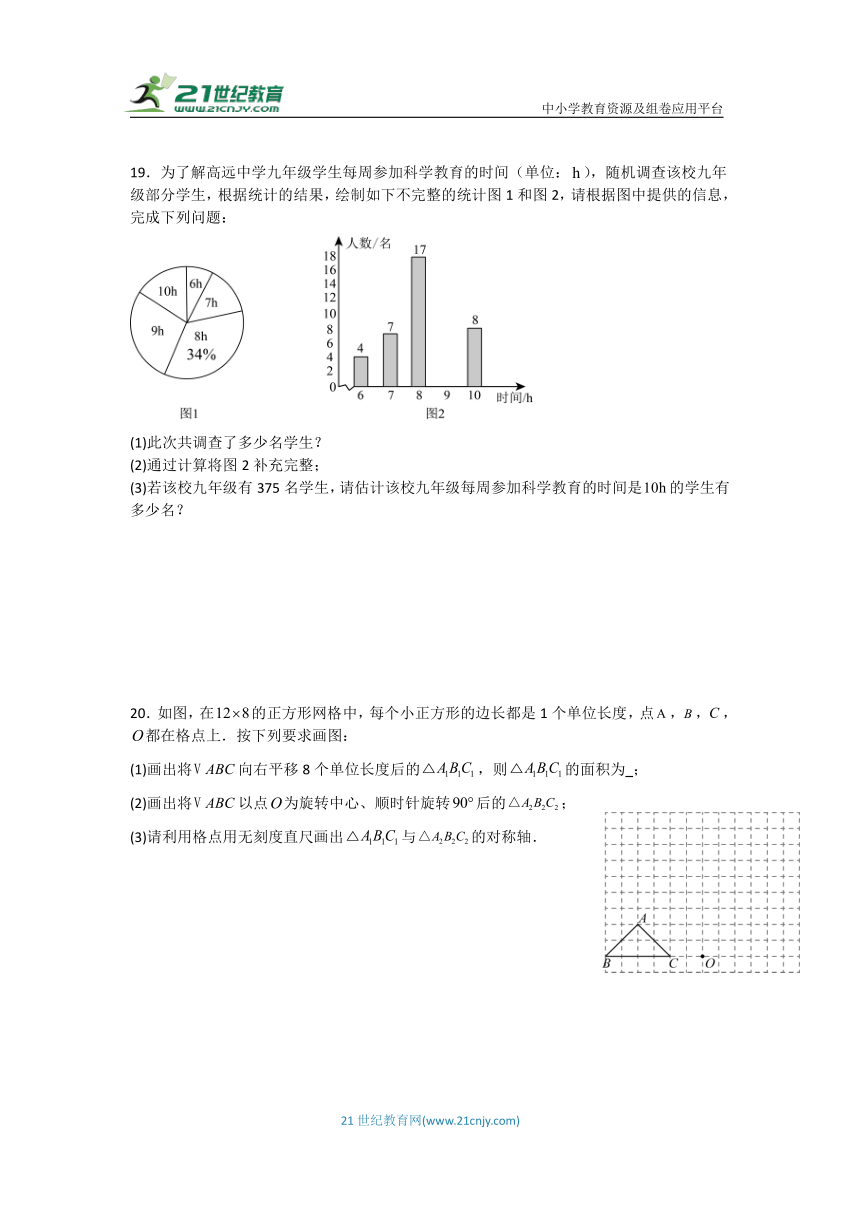
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.已知2a﹣1的平方根为±3,3a﹣b﹣1的立方根为2,
(1)求6a+b的算术平方根;
(2)若c是的整数部分,求2a+3b﹣c的平方根.
18.把下面解答过程中的理由或推理过程补充完整.
如图,AD∥BC,∠1=∠B,∠2=∠3.
(1)试说明AB∥DE;
(2)推导证明AF与DC的位置关系.
解:(1)∵AD∥BC(已知),
∴∠1=∠ ( ),
又∵∠1=∠B(已知),
∴∠B=∠ ( ),
∴AB∥DE( ).
(2)∵AB∥DE(已知),
∴∠2=∠ ( ),
又∵∠2=∠3(已知),
∴∠ =∠ (等量代换),
∴AF DC.
19.为了解高远中学九年级学生每周参加科学教育的时间(单位:),随机调查该校九年级部分学生,根据统计的结果,绘制如下不完整的统计图1和图2,请根据图中提供的信息,完成下列问题:
(1)此次共调查了多少名学生?
(2)通过计算将图2补充完整;
(3)若该校九年级有375名学生,请估计该校九年级每周参加科学教育的时间是的学生有多少名?
20.如图,在的正方形网格中,每个小正方形的边长都是1个单位长度,点,,,都在格点上.按下列要求画图:
(1)画出将向右平移8个单位长度后的,则的面积为 ;
(2)画出将以点为旋转中心、顺时针旋转后的;
(3)请利用格点用无刻度直尺画出与的对称轴.
21.已知关于x、y的方程组的解是非负数.
(1)求k的取值范围;
(2)化简:|2k﹣1|+|k﹣2|.
22.已知(m+2)x|m+3|﹣1>2是关于x的一元一次不等式.
(1)求m的值.
(2)求出原一元一次不等式的解集.
23.如图,已知AC∥FE,∠1+∠2=180°.
(1)求证:∠FAB=∠BDC;
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
24.若一个不等式(组)A有解且解集为a<x<b(a<b),则称为A的解集中点值,若A的解集中点值是不等式(组)B的解(即中点值满足不等式组),则称不等式(组)B对于不等式(组)A中点包含.
(1)已知关于x的不等式组A:,以及不等式B:﹣1<x≤5,请判断不等式B对于不等式组A是否中点包含,并写出判断过程;
(2)已知关于x的不等式组C:和不等式组D:,若D对于不等式组C中点包含,求m的取值范围.
(3)关于x的不等式组E:(n<m)和不等式组F:,若不等式组F对于不等式组E中点包含,且所有符合要求的整数m之和为14,求n的取值范围.
25.已知直线,点A,C在直线上,D在直线上.
(1)如图1,若,,且,则的度数为 ;
(2)如图2,若平分,,,,过点D作交于点F,求证:;
(3)如图3,若,直线和直线相交于点K,点H在直线上,试探究,和之间的数量关系,请直接写出结论
参考答案
一、选择题
1—10:CCBCB BACBB
二、填空题
11.【解答】解:22m+n=(2m)2 2n=32×5=45.
故答案为:45.
12.【解答】解:【详解】解:由题意及旋转变换的性质得,
又 ∵,
,
故答案为:.
13.【解答】解:【详解】解:由扇形统计图可知,中度视力不良的学生占比为,
重度视力不良的学生有人,
八年级的学生总数为:(人),
中度视力不良的学生有:(人),
中度视力不良的学生有人.
故答案为:.
14.【解答】解:延长交直线于点,
直线,,
,
,
,
,
.
故答案为:.
15.【解答】解:由题意得:x2﹣(k﹣2)x+9=(x±3)2,
∴x2﹣(k﹣2)x+9=x2±6x+9,
∴﹣(k﹣2)=±6,
k﹣2=±6,
解得:k=8或﹣4,
故答案为:8或﹣4.
16.【解答】解:∵多项式(2+x2+mx3)(1﹣5x)=﹣5mx4+(m﹣5)x3+x2﹣10x+2不含x3项,
∴m﹣5=0,
解得m=5.
故答案为:5.
三、解答题
17.【解答】解:(1)∵2a﹣1的平方根为±3,3a﹣b﹣1的立方根为2,
∴2a﹣1=9,3a﹣b﹣1=8,
解得a=5,b=6,
∴6a+b=36,
∵36的算术平方根为6,
∴6a+b的算术平方根是6;
(2)∵34,
∴的整数部分为3,
即c=3,
由(1)得a=5,b=6,
∴2a+3b﹣c=10+18﹣3=25,
而25的平方根为±5,
∴2a+3b﹣c的平方根±5.
18.【解答】解:(1)∵AD∥BC(已知),
∴∠1=∠DEC(两直线平行,内错角相等),
又∵∠1=∠B(已知),
∴∠B=∠DEC(等量代换),
∴AB∥DE(同位角相等,两直线平行),
故答案为:DEC;两直线平行,内错角相等;DEC;等量代换;同位角相等,两直线平行;
(2)∵AB∥DE(已知),
∴∠2=∠AGD(两直线平行,内错角相等),
又∵∠2=∠3(已知),
∴∠AGD=∠3(等量代换),
∴AF∥DC,
故答案为:AGD;两直线平行,内错角相等;AGD;3;∥.
19.(1)解:,
即此次共调查了50名学生;
(2)每周参加科学教育的时间为的学生有(名),
故可补画条形统计图如下图所示:
(3)(名),
即估计该校九年级每周参加科学教育的时间是的学生有60名.
20.(1)解:如图,即为所求:
面积为;
(2)解:如上图,即为所求;
(3)解:如上图,直线即为所求.
21.【解答】解:(1),
①+②得:4x=8k﹣4,即x=2k﹣1③,
将③代入②得:y=﹣4k+4,
则原方程组的解为:;
∵原方程组的解均为非负数,
∴,
解得:.
(2)∵,
∴2k﹣1>0,k﹣2<0,
∴|2k﹣1|+|k﹣2|.
=2k﹣1+2﹣k
=k+1.
22.【解答】解:(1)根据题意|m+3|=1且m+2≠0,解得m+3=±1且m≠﹣2,
所以m=﹣4.
(2)原一元一次不等式为﹣2x﹣1>2,
移项得﹣2x>2+1,
合并同类项得﹣2x>3,
解得.
23.【解答】(1)证明:∵AC∥EF,
∴∠1+∠FAC=180°,
又∵∠1+∠2=180°,
∴∠FAC=∠2,
∴FA∥CD,
∴∠FAB=∠BDC;
(2)解:∵AC平分∠FAD,
∴∠FAC=∠CAD,∠FAD=2∠FAC,
由(1)知∠FAC=∠2,
∴∠FAD=2∠2,
∴∠2∠FAD,
∵∠FAD=80°,
∴∠280°=40°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠2=50°.
24.【解答】解:(1)不等式B对于不等式组A中点包含,判断过程如下:
解不等式组A:,得4<x<6,
∴A的中点值为x=5,
∵x=5在﹣1<x≤5范围内,
∴不等式B对于不等式组A中点包含;
(2)∵D对于不等式组C中点包含,
∴不等式组C和不等式组D有解,
解不等式组C:,得,
不等式组D:,得,
∴,
解得:m>﹣4,
∴当m>﹣4时,不等式组C的解集为m﹣3<x<3m+5,不等式组D的解集为m﹣4<x,
∴C的中点值为2m+1,
∵D对于不等式组C中点包含,
∴m﹣4<2m+1,
解得:﹣5<m<10,
又∵m>﹣4,
∴﹣4<m<10.
(3)解不等式组E得,2n<x<2m,解不等式组F得,,
∴E的中点值为n+m,
∵不等式组F对于不等式组E中点包含,
∴,
解得:n<m<6,
∵所有符合要求的整数m之和为14,
∴整数m可取2,3、4,5,或整数m可取﹣1、0、1、2、3、4,5.
∴1≤n<2或﹣2≤n<﹣1.
25.(1)解:∵,,
∴,
∵,
∴,
∵,
∴,
故答案为:;
(2)证明:设,
∵,
∴,
∵平分,
∴,
∴.
∵,,
∴,,
∴,
∵,
∴,
∴.
(3)解:如图,当点H在点K上方时,则,
∴,,
,
∴,
∴,
∴;
如图,当点H在点C,过点H作,
∴,,
,
∴,
∴,
∴,即;
如图,当点H在点C,过点H作,
∴,,
,
∴,
∴,
∴,
综上所述,满足条件的关系是或.
21世纪教育网(www.21cnjy.com)
湘教版2024—2025学年七年级下学期数学期末考试调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形是轴对称图形的是( )
A. B. C. D.
2.农业科研人员在试验田里种植了新品种大麦,为了考察麦穗长度的分布情况,抽取了100个麦穗进行测量.这项调查中的样本是( )
A.新品种大麦长度的分布情况 B.100
C.从中抽取的100个麦穗的长度 D.100个麦穗中的某一个麦穗的长度
3.如图,四边形中,对角线与相交于点O.下列条件,能判定的是( )
A. B.
C. D.
4.如果关于x的不等式的解集为,那么a的取值范围是( )
A. B. C. D.
5.下列各式是求个位数为5的整数的算术平方根的运算:,,,,,,观察这些运算都有规律,试利用该规律直接写出运算的结果为( )
A.9595 B.9995 C.9955 D.5995
6.如图,绕点A逆时针旋转得到,若,则( )
A. B. C. D.
7.如图,已知,,,则的度数为( )
A. B. C. D.
8.如图,将一张长方形纸片进行折叠,若,则的度数为( )
A. B. C. D.
9.若,是正整数,且满足,则与的关系正确的是( )
A. B. C. D.
10.若关于x的不等式组无解,则的取值范围是( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.若2m=3,2n=5,则22m+n= .
12.如图,将绕点按逆时针方向旋转后得到,若,则的度数是 .
13.某校社会实践小组为了解八年级学生的视力健康情况,在全校开展了抽样调查,并将调查数据绘制成如图所示的统计图.若重度视力不良的学生有人,则中度视力不良的学生有 人.
14.如图,直线,,,则的度数是 .
15.若x2﹣(k﹣2)x+9是完全平方式,则k= .
16.若计算(2+x2+mx3)(1﹣5x)的结果不含x3项,那么m的值为 .
第II卷
湘教版2024—2025学年七年级下学期数学期末考试调研检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.已知2a﹣1的平方根为±3,3a﹣b﹣1的立方根为2,
(1)求6a+b的算术平方根;
(2)若c是的整数部分,求2a+3b﹣c的平方根.
18.把下面解答过程中的理由或推理过程补充完整.
如图,AD∥BC,∠1=∠B,∠2=∠3.
(1)试说明AB∥DE;
(2)推导证明AF与DC的位置关系.
解:(1)∵AD∥BC(已知),
∴∠1=∠ ( ),
又∵∠1=∠B(已知),
∴∠B=∠ ( ),
∴AB∥DE( ).
(2)∵AB∥DE(已知),
∴∠2=∠ ( ),
又∵∠2=∠3(已知),
∴∠ =∠ (等量代换),
∴AF DC.
19.为了解高远中学九年级学生每周参加科学教育的时间(单位:),随机调查该校九年级部分学生,根据统计的结果,绘制如下不完整的统计图1和图2,请根据图中提供的信息,完成下列问题:
(1)此次共调查了多少名学生?
(2)通过计算将图2补充完整;
(3)若该校九年级有375名学生,请估计该校九年级每周参加科学教育的时间是的学生有多少名?
20.如图,在的正方形网格中,每个小正方形的边长都是1个单位长度,点,,,都在格点上.按下列要求画图:
(1)画出将向右平移8个单位长度后的,则的面积为 ;
(2)画出将以点为旋转中心、顺时针旋转后的;
(3)请利用格点用无刻度直尺画出与的对称轴.
21.已知关于x、y的方程组的解是非负数.
(1)求k的取值范围;
(2)化简:|2k﹣1|+|k﹣2|.
22.已知(m+2)x|m+3|﹣1>2是关于x的一元一次不等式.
(1)求m的值.
(2)求出原一元一次不等式的解集.
23.如图,已知AC∥FE,∠1+∠2=180°.
(1)求证:∠FAB=∠BDC;
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
24.若一个不等式(组)A有解且解集为a<x<b(a<b),则称为A的解集中点值,若A的解集中点值是不等式(组)B的解(即中点值满足不等式组),则称不等式(组)B对于不等式(组)A中点包含.
(1)已知关于x的不等式组A:,以及不等式B:﹣1<x≤5,请判断不等式B对于不等式组A是否中点包含,并写出判断过程;
(2)已知关于x的不等式组C:和不等式组D:,若D对于不等式组C中点包含,求m的取值范围.
(3)关于x的不等式组E:(n<m)和不等式组F:,若不等式组F对于不等式组E中点包含,且所有符合要求的整数m之和为14,求n的取值范围.
25.已知直线,点A,C在直线上,D在直线上.
(1)如图1,若,,且,则的度数为 ;
(2)如图2,若平分,,,,过点D作交于点F,求证:;
(3)如图3,若,直线和直线相交于点K,点H在直线上,试探究,和之间的数量关系,请直接写出结论
参考答案
一、选择题
1—10:CCBCB BACBB
二、填空题
11.【解答】解:22m+n=(2m)2 2n=32×5=45.
故答案为:45.
12.【解答】解:【详解】解:由题意及旋转变换的性质得,
又 ∵,
,
故答案为:.
13.【解答】解:【详解】解:由扇形统计图可知,中度视力不良的学生占比为,
重度视力不良的学生有人,
八年级的学生总数为:(人),
中度视力不良的学生有:(人),
中度视力不良的学生有人.
故答案为:.
14.【解答】解:延长交直线于点,
直线,,
,
,
,
,
.
故答案为:.
15.【解答】解:由题意得:x2﹣(k﹣2)x+9=(x±3)2,
∴x2﹣(k﹣2)x+9=x2±6x+9,
∴﹣(k﹣2)=±6,
k﹣2=±6,
解得:k=8或﹣4,
故答案为:8或﹣4.
16.【解答】解:∵多项式(2+x2+mx3)(1﹣5x)=﹣5mx4+(m﹣5)x3+x2﹣10x+2不含x3项,
∴m﹣5=0,
解得m=5.
故答案为:5.
三、解答题
17.【解答】解:(1)∵2a﹣1的平方根为±3,3a﹣b﹣1的立方根为2,
∴2a﹣1=9,3a﹣b﹣1=8,
解得a=5,b=6,
∴6a+b=36,
∵36的算术平方根为6,
∴6a+b的算术平方根是6;
(2)∵34,
∴的整数部分为3,
即c=3,
由(1)得a=5,b=6,
∴2a+3b﹣c=10+18﹣3=25,
而25的平方根为±5,
∴2a+3b﹣c的平方根±5.
18.【解答】解:(1)∵AD∥BC(已知),
∴∠1=∠DEC(两直线平行,内错角相等),
又∵∠1=∠B(已知),
∴∠B=∠DEC(等量代换),
∴AB∥DE(同位角相等,两直线平行),
故答案为:DEC;两直线平行,内错角相等;DEC;等量代换;同位角相等,两直线平行;
(2)∵AB∥DE(已知),
∴∠2=∠AGD(两直线平行,内错角相等),
又∵∠2=∠3(已知),
∴∠AGD=∠3(等量代换),
∴AF∥DC,
故答案为:AGD;两直线平行,内错角相等;AGD;3;∥.
19.(1)解:,
即此次共调查了50名学生;
(2)每周参加科学教育的时间为的学生有(名),
故可补画条形统计图如下图所示:
(3)(名),
即估计该校九年级每周参加科学教育的时间是的学生有60名.
20.(1)解:如图,即为所求:
面积为;
(2)解:如上图,即为所求;
(3)解:如上图,直线即为所求.
21.【解答】解:(1),
①+②得:4x=8k﹣4,即x=2k﹣1③,
将③代入②得:y=﹣4k+4,
则原方程组的解为:;
∵原方程组的解均为非负数,
∴,
解得:.
(2)∵,
∴2k﹣1>0,k﹣2<0,
∴|2k﹣1|+|k﹣2|.
=2k﹣1+2﹣k
=k+1.
22.【解答】解:(1)根据题意|m+3|=1且m+2≠0,解得m+3=±1且m≠﹣2,
所以m=﹣4.
(2)原一元一次不等式为﹣2x﹣1>2,
移项得﹣2x>2+1,
合并同类项得﹣2x>3,
解得.
23.【解答】(1)证明:∵AC∥EF,
∴∠1+∠FAC=180°,
又∵∠1+∠2=180°,
∴∠FAC=∠2,
∴FA∥CD,
∴∠FAB=∠BDC;
(2)解:∵AC平分∠FAD,
∴∠FAC=∠CAD,∠FAD=2∠FAC,
由(1)知∠FAC=∠2,
∴∠FAD=2∠2,
∴∠2∠FAD,
∵∠FAD=80°,
∴∠280°=40°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠2=50°.
24.【解答】解:(1)不等式B对于不等式组A中点包含,判断过程如下:
解不等式组A:,得4<x<6,
∴A的中点值为x=5,
∵x=5在﹣1<x≤5范围内,
∴不等式B对于不等式组A中点包含;
(2)∵D对于不等式组C中点包含,
∴不等式组C和不等式组D有解,
解不等式组C:,得,
不等式组D:,得,
∴,
解得:m>﹣4,
∴当m>﹣4时,不等式组C的解集为m﹣3<x<3m+5,不等式组D的解集为m﹣4<x,
∴C的中点值为2m+1,
∵D对于不等式组C中点包含,
∴m﹣4<2m+1,
解得:﹣5<m<10,
又∵m>﹣4,
∴﹣4<m<10.
(3)解不等式组E得,2n<x<2m,解不等式组F得,,
∴E的中点值为n+m,
∵不等式组F对于不等式组E中点包含,
∴,
解得:n<m<6,
∵所有符合要求的整数m之和为14,
∴整数m可取2,3、4,5,或整数m可取﹣1、0、1、2、3、4,5.
∴1≤n<2或﹣2≤n<﹣1.
25.(1)解:∵,,
∴,
∵,
∴,
∵,
∴,
故答案为:;
(2)证明:设,
∵,
∴,
∵平分,
∴,
∴.
∵,,
∴,,
∴,
∵,
∴,
∴.
(3)解:如图,当点H在点K上方时,则,
∴,,
,
∴,
∴,
∴;
如图,当点H在点C,过点H作,
∴,,
,
∴,
∴,
∴,即;
如图,当点H在点C,过点H作,
∴,,
,
∴,
∴,
∴,
综上所述,满足条件的关系是或.
21世纪教育网(www.21cnjy.com)
同课章节目录
