浙教版2024—2025学年七年级下学期数学期末考试调研检测卷(含答案)
文档属性
| 名称 | 浙教版2024—2025学年七年级下学期数学期末考试调研检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 553.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 07:27:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年七年级下学期数学期末考试调研检测卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列四幅图案能通过基本图形平移得到的是( )
A. B. C. D.
2.石墨烯目前是世界上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000 000 000 34米,将这个数用科学记数法表示为( )
A.0.34×10﹣9 B.3.4×10﹣9 C.3.4×10﹣10 D.3.4×10﹣11
3.为了解某校八年级1000名学生在五一期间每天阅读名著所用的时间,随机抽取其中100名学生进行抽样调查.下列说法正确的是()
A.该校八年级全体学生是总体 B.从中抽取的100名学生是个体
C.每个八年级学生是总体的一个样本 D.样本容量是100
4.方程组的解为,则被遮住的两个数分别为( )
A.2,1 B.5,1 C.2,3 D.2,4
5.如果把分式中的x和y都扩大2倍,那么分式的值( )
A.缩小到原来的 B.扩大2倍
C.不变 D.缩小到原来的
6.关于x,y的二元一次方程组的解也是二元一次方程3x﹣2y=7的解,则k的值为( )
A. B. C. D.
7.解方程组时,一学生把c看错而得到,而正确的解是,那么a+b+c的值为( )
A.4 B.5 C.6 D.7
8.如果(2ambm+n)3=8a9b15成立,则( )
A.m=3,n=2 B.m=2,n=3 C.m=2,n=5 D.m=6,n=2
9.若a,b是正整数,且满足3a+3a+3a=3b×3b×3b,则下列a与b的关系正确的是( )
A.a=b B.a+1=3b C.a+1=b3 D.3a=b3
10.若关于y的分式方程的解为正数,且x2+2(a﹣1)x+16是一个完全平方式,则满足条件的整数a的值为( )
A.±3 B.5 C.﹣3 D.5或﹣3
二、填空题(每小题3分,满分18分)
11.因式分解4x2﹣4= .
12.若x2+2(m﹣3)x+9是一个完全平方式,则m的值为 .
13.如图,已知四边形ABCD、四边形ECGF都是正方形,△BCF的面积为5,BG的长为7,那么阴影部分的面积是 .
14.若关于a,b的方程组的解为,则关于x,y的方程组的解为 .
15.已知:m+2n﹣2=0,则3m 9n的值为 .
16.如图,AB∥CD,CE平分∠BCD,F是射线BA上一定点,G是射线CE上的动点,GH∥BC交CD于点H.∠ABC=120°,∠GFB=α°.在点G的运动过程中,当时,∠BGH= 度.(用含α的代数式表示)
浙教版2024—2025学年七年级下学期数学期末考试调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程(组):
(1); (2).
18.已知m+n=1,求代数式的值.
19.先化简,再求值:
(1),其中x;
(2),其中a,b=1.
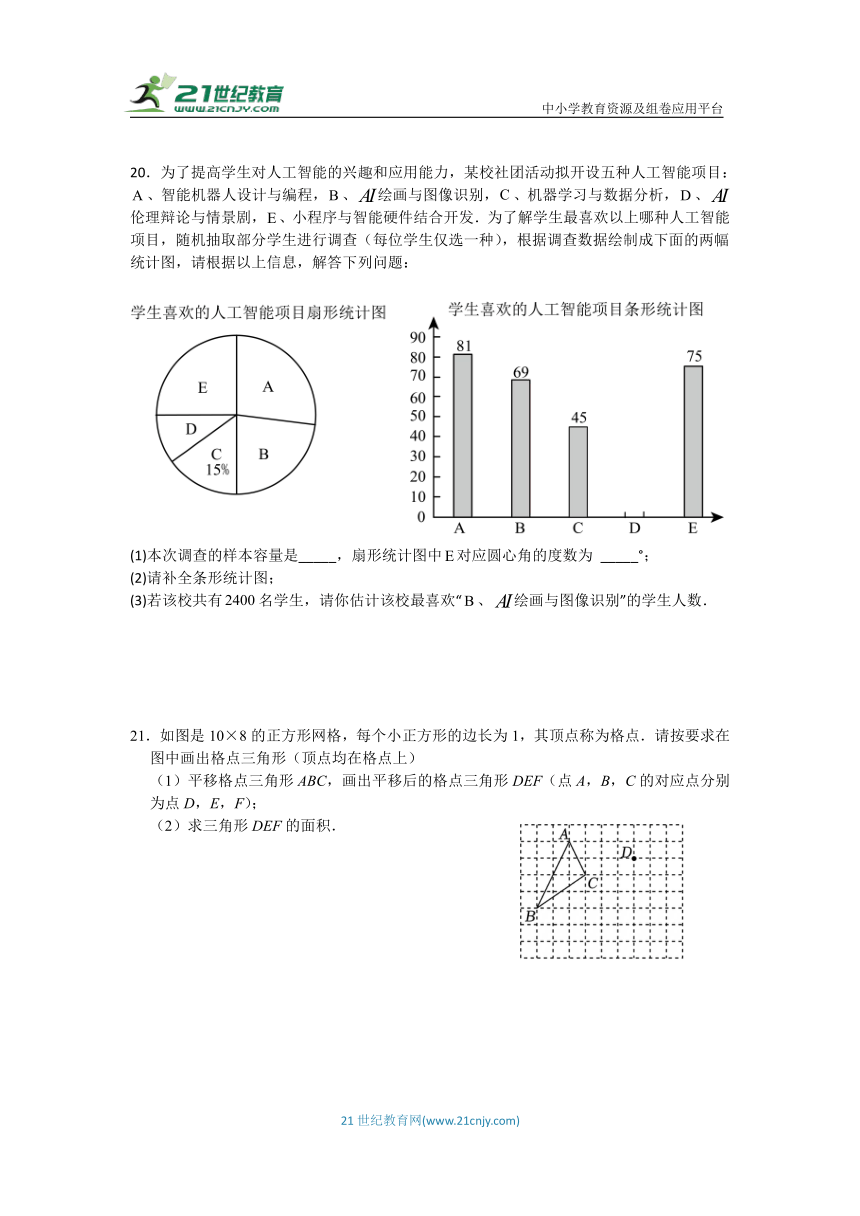
20.为了提高学生对人工智能的兴趣和应用能力,某校社团活动拟开设五种人工智能项目:、智能机器人设计与编程,、绘画与图像识别,、机器学习与数据分析,、伦理辩论与情景剧,、小程序与智能硬件结合开发.为了解学生最喜欢以上哪种人工智能项目,随机抽取部分学生进行调查(每位学生仅选一种),根据调查数据绘制成下面的两幅统计图,请根据以上信息,解答下列问题:
(1)本次调查的样本容量是_____,扇形统计图中对应圆心角的度数为 _____°;
(2)请补全条形统计图;
(3)若该校共有名学生,请你估计该校最喜欢“、绘画与图像识别”的学生人数.
21.如图是10×8的正方形网格,每个小正方形的边长为1,其顶点称为格点.请按要求在图中画出格点三角形(顶点均在格点上)
(1)平移格点三角形ABC,画出平移后的格点三角形DEF(点A,B,C的对应点分别为点D,E,F);
(2)求三角形DEF的面积.
22.某校组织七年级350名学生去研学,已知1辆A型车和2辆B型车可以载学生110人;3辆A型车和1辆B型车可以载学生130人.
(1)A、B型车每辆可分别载学生多少人?
(2)若租一辆A型车需要1000元,一辆B型车需1200元,请你设计租车方案,使得恰好送完学生,并且租车费用最少?
23.某工程队承接了老旧小区改造工程中1000平方米的外墙粉刷任务,选派甲、乙两人分别用A、B两种外墙漆各完成总粉刷任务的一半.据测算需要A、B两种外墙漆各300千克,购买外墙漆总费用为15000元,已知A种外墙漆每千克的价格比B种外墙漆每千克的价格多2元.
(1)求A、B两种外墙漆每千克的价格各是多少元?
(2)已知乙每小时粉刷外墙面积是甲每小时粉刷外墙面积的,乙完成粉刷任务所需时间比甲完成粉刷任务所需时间多5小时.问甲每小时粉刷外墙的面积是多少平方米?
24.某段铁路两旁安置了A,D两座可旋转探照灯.已知PQ∥CN,A,B为PQ上两点,连接AC,∠C=20°,AD平分∠CAB交CN于点D,E为AD上一点,连接BE.
(1)求∠EAP= .
(2)如图,G为CN上一点,连接AG.当,∠2=3∠1时,试说明:AC∥BE;
(3)探照灯A、D照出的光线在铁路所在平面旋转,探照灯射出的光线AC以每秒5度的速度逆时针转动,探照灯D射出的光线DN以每秒15度的速度逆时针转动,DN转至射线DC后立即以相同速度回转,若它们同时开始转动,设转动时间为t秒,当DN回到出发时的位置时同时停止转动,则在转动过程中,当AC与DN互相平行或垂直时,请直接写出此时t的值.
25.把几个图形拼成一个新的图形,通过图形面积的计算,常常可以得到一些等式,这是研究数学问题的一种常用方法.我们在学习“从面积到乘法公式”时,曾用两种不同的方法计算同一个图形的面积,探索了完全平方公式:(a+b)2=a2+2ab+b2(如图1).
(1)观察图2,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
拓展应用:根据(1)中的等量关系及课本所学的完全平方公式知识,解决如下问题:
(2)若,且x>y,求x﹣y的值;
(3)若(2025﹣m)2+(m﹣2024)2=7,求(2025﹣m)(m﹣2024)的值;
(4)如图3,在△BCE中,∠BCE=90°,CE=8,点M在边BC上,CM=3,在边CE上取一点Q,使BM=EQ,分别以BC,CQ为边在△BCE外部作正方形ABCD和正方形COPQ,连接BQ,若△BCQ的面积等于,设BM=x(x>0),求正方形ABCD和正方形COPQ的面积和.
参考答案
一、选择题
1—10:DCDBA DDABD
二、填空题
11.【解答】解:原式=4(x2﹣1)=4(x+1)(x﹣1),
故答案为:4(x+1)(x﹣1)
12.【解答】解:∵(x±3)2
=x2±6x+9
=x2+2(m﹣3)x+9,
∴2(m﹣3)=±6,
解得:m=0或m=6.
故答案为:0或6.
13.【解答】解:∵四边形ABCD和四边形CEFG均是正方形,
∴∠A=∠G=90°,AD=AB=BC=CD,CG=FG,
∴S△BCFBC FG=5,
∴BC FG=10,
∵BG=BC+CG=7,
∴BC2+CG2=(BC+CG)2﹣2BC CG=49﹣2×10=29,
∴S正方形ABCD+S正方形CEFG=29,
∵S△DEFEF DECG (AB﹣CG)CG ABCG2=5CG2,
∴S阴影=S正方形ABCD+S正方形CEFG+S△DEF﹣S△ABD﹣S△BCF=29+5CG2AB2﹣5=29(CG2+AB2)=2929=14.5.
故答案为:14.5.
14.【解答】解:设x﹣1=m,y+1=n,
则关于x,y的方程组为,
∵关于a,b的方程组的解为,
∴方程组的解是,
∴,
∴,
即关于x,y的方程组的解为,
故答案为:.
15.【解答】解:∵m+2n﹣2=0,
∴m+2n=2,
∴3m 9n=3m 32n=3m+2n=32=9.
故答案为:9.
16.【解答】解:如图1所示,设FG交CG于点I,
∵∠ABC=120°,AB∥CD,CE平分∠BCD,
∴∠BCD=120°,∠BCE=∠DCE=60°.
∵GH∥BC,
∴∠CGH=∠BCE=60°.
∵∠FIC=∠GFB+∠ABC=120°+α,
又∵∠FIC=∠BCE+∠CGF,
∴∠CGF=∠FIC﹣∠BCE=120°+α﹣60°=60°+α,
∴∠BGH=∠FGB+∠CGF+∠CGH60°+α+60°=120°.
故答案为:(120°).
三、解答题
17.【解答】解:(1),
①×2+②得:6x=3,
解得:x,
将x代入①得:1+3y=2,
解得:y,
故原方程组的解为;
(2)原方程去分母得:2﹣x=﹣1﹣2x+6,
解得:x=3,
检验:当x=3时,x﹣3=0,
则x=3是分式方程的增根,
故原方程无解.
18.【解答】解:3(m+n),
当m+n=1时,原式=3×1=3.
19.【解答】解:(1)
=3x3﹣x﹣6x2+2﹣3x3+6x2+36x
=35x+2,
当x时,原式=35×()+2=﹣7+2=﹣5;
(2)
,
当a,b=1时,原式2.
20.(1)解:由图可得组的人数为人,所占总人数的百分比为,
∴本次调查的样本容量是:(人),
∵图中组对应的人数为人,
∴图中组对应的圆心角的度数为,
故答案为:;.
(2)解:由(1)可得样本容量是人,
∴图中组对应的人数是:(人),
补全条形统计图如下:
(3)解:最喜欢“、绘画与图像识别”的学生所占百分比为,
∴当该校共名学生时,估计该校最喜欢“、绘画与图像识别”的学生人数为(人).
21.【解答】解:(1)如图,三角形DEF即为所求,
(2)三角形DEF的面积为.
22.【解答】解:(1)设每辆A型车可载学生x人,每辆B型车可载学生y人.
根据题意,得,
解得,
∴每辆A型车可载学生30人,每辆B型车可载学生40人.
(2)设租用A型车a辆,则租用B型车辆.
∴租用A型车1辆,租用B型车8辆使得恰好送完学生,并且租车费用最少.
23.【解答】解:(1)设A种外墙漆每千克的价格是x元,B种外墙漆每千克的价格是y元,
根据题意得:,
解得:.
答:A种外墙漆每千克的价格是26元,B种外墙漆每千克的价格是24元;
(2)设甲每小时粉刷外墙的面积是m平方米,则乙每小时粉刷外墙的面积是m方米,
根据题意得:5,
解得:m=25,
经检验,m=25是所列方程的解,且符合题意.
答:甲每小时粉刷外墙的面积是25平方米.
24.【解答】解:(1)∵PQ∥CN,
∴∠PAC=∠C=20°,
∴∠CAB=180°﹣20°=160°,
∵AD平分∠CAB,
∴,
∴∠EAP=∠PAC+∠CAD=20°+80°=100°,
故答案为:100°;
(2)证明:∵,
∴∠ADC=3∠1,
∵∠2=3∠1,
∴∠2=∠ADC,
∵PQ∥CN,
∴∠EAP+∠ADC=180°,
∴∠ADC=180°﹣100°=80°,
∴∠2=80°,
∵∠PAC=20°,∠EAP=100°,
∴∠CAE=100°﹣20°=80°,
∴∠CAE=∠2,
∴AC∥BE;
(3)360°÷15°=24s,当AC∥DN时,则∠ACD=∠HDN,如图,
∵PB∥CH,
∴∠PAC=∠ACD,
∴∠PAC=∠HDN,
由题意得,∠PAC=20°+5t,∠HDN=15°t,
∴20°+5t=15°t,
∴t=2;
当AC⊥DN时,则∠CND=90°,如图,
∵PA∥CD,
∴∠ACD=∠PAC=20+5t,
∵∠NDH=15t,
∴∠NDC=180°﹣15°t,
∴20+5t+180°﹣15t=90°,
∴t=11;
当ND∥AC时,则∠NDC=∠ACH,如图,
由题意得,∠MDN=15t﹣180°,∠PAC=20°+5°t,
∴∠NDC=180°﹣∠MDN=360°﹣15°t,
∴20°+5°t=360°﹣15°t,
∴t=17;
当DN⊥AC时,∠DNC=90°,如图,
∵∠NDC=360°﹣15°t,
∴∠NDC+∠DCN=90°,
∵∠NCD=180°﹣(20°+5t),
∴360°﹣15t+180°﹣(20°+5t)=90°,
∴t=21.5;
综上,t的值为2或11或17或21.5.
25.【解答】解:(1)由图可知:大正方形的面积等于4个长方形的面积加上阴影正方形的面积,
∴(a+b)2=(a﹣b)2+4ab;
故答案为:(a+b)2=(a﹣b)2+4ab;
(2)由(1)可得(x﹣y)2=(x+y)2﹣4xy,
∴(x﹣y)2=(x+y)2﹣4xy,
∵x>y,
∴x﹣y=3;
(3)由条件可知2ab=(a+b)2﹣(a2+b2),
∵(2025﹣m)2+(m﹣2024)2=7,
∴2(2025﹣m)(m﹣2024)
=(2025﹣m+m﹣2024)2﹣[(2025﹣m)2+(m﹣2024)2]
=1﹣7
=﹣6,
∴原式=﹣3;
(4)设BM=x,则BM=EQ=x,
∴CM=3,CE=8,
CQ=CE﹣EQ=8﹣x,BC=BM+CM=3+x,
∵,
∴(8﹣x)(3+x)=21,
令8﹣x=a,x+3=b,
∴a+b=11,ab=21,
∴正方形ABCD和正方形COPQ的面积和:
=a2+b2=(a+b)2﹣2ab=112﹣2×21=121﹣42=79.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年七年级下学期数学期末考试调研检测卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列四幅图案能通过基本图形平移得到的是( )
A. B. C. D.
2.石墨烯目前是世界上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000 000 000 34米,将这个数用科学记数法表示为( )
A.0.34×10﹣9 B.3.4×10﹣9 C.3.4×10﹣10 D.3.4×10﹣11
3.为了解某校八年级1000名学生在五一期间每天阅读名著所用的时间,随机抽取其中100名学生进行抽样调查.下列说法正确的是()
A.该校八年级全体学生是总体 B.从中抽取的100名学生是个体
C.每个八年级学生是总体的一个样本 D.样本容量是100
4.方程组的解为,则被遮住的两个数分别为( )
A.2,1 B.5,1 C.2,3 D.2,4
5.如果把分式中的x和y都扩大2倍,那么分式的值( )
A.缩小到原来的 B.扩大2倍
C.不变 D.缩小到原来的
6.关于x,y的二元一次方程组的解也是二元一次方程3x﹣2y=7的解,则k的值为( )
A. B. C. D.
7.解方程组时,一学生把c看错而得到,而正确的解是,那么a+b+c的值为( )
A.4 B.5 C.6 D.7
8.如果(2ambm+n)3=8a9b15成立,则( )
A.m=3,n=2 B.m=2,n=3 C.m=2,n=5 D.m=6,n=2
9.若a,b是正整数,且满足3a+3a+3a=3b×3b×3b,则下列a与b的关系正确的是( )
A.a=b B.a+1=3b C.a+1=b3 D.3a=b3
10.若关于y的分式方程的解为正数,且x2+2(a﹣1)x+16是一个完全平方式,则满足条件的整数a的值为( )
A.±3 B.5 C.﹣3 D.5或﹣3
二、填空题(每小题3分,满分18分)
11.因式分解4x2﹣4= .
12.若x2+2(m﹣3)x+9是一个完全平方式,则m的值为 .
13.如图,已知四边形ABCD、四边形ECGF都是正方形,△BCF的面积为5,BG的长为7,那么阴影部分的面积是 .
14.若关于a,b的方程组的解为,则关于x,y的方程组的解为 .
15.已知:m+2n﹣2=0,则3m 9n的值为 .
16.如图,AB∥CD,CE平分∠BCD,F是射线BA上一定点,G是射线CE上的动点,GH∥BC交CD于点H.∠ABC=120°,∠GFB=α°.在点G的运动过程中,当时,∠BGH= 度.(用含α的代数式表示)
浙教版2024—2025学年七年级下学期数学期末考试调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程(组):
(1); (2).
18.已知m+n=1,求代数式的值.
19.先化简,再求值:
(1),其中x;
(2),其中a,b=1.
20.为了提高学生对人工智能的兴趣和应用能力,某校社团活动拟开设五种人工智能项目:、智能机器人设计与编程,、绘画与图像识别,、机器学习与数据分析,、伦理辩论与情景剧,、小程序与智能硬件结合开发.为了解学生最喜欢以上哪种人工智能项目,随机抽取部分学生进行调查(每位学生仅选一种),根据调查数据绘制成下面的两幅统计图,请根据以上信息,解答下列问题:
(1)本次调查的样本容量是_____,扇形统计图中对应圆心角的度数为 _____°;
(2)请补全条形统计图;
(3)若该校共有名学生,请你估计该校最喜欢“、绘画与图像识别”的学生人数.
21.如图是10×8的正方形网格,每个小正方形的边长为1,其顶点称为格点.请按要求在图中画出格点三角形(顶点均在格点上)
(1)平移格点三角形ABC,画出平移后的格点三角形DEF(点A,B,C的对应点分别为点D,E,F);
(2)求三角形DEF的面积.
22.某校组织七年级350名学生去研学,已知1辆A型车和2辆B型车可以载学生110人;3辆A型车和1辆B型车可以载学生130人.
(1)A、B型车每辆可分别载学生多少人?
(2)若租一辆A型车需要1000元,一辆B型车需1200元,请你设计租车方案,使得恰好送完学生,并且租车费用最少?
23.某工程队承接了老旧小区改造工程中1000平方米的外墙粉刷任务,选派甲、乙两人分别用A、B两种外墙漆各完成总粉刷任务的一半.据测算需要A、B两种外墙漆各300千克,购买外墙漆总费用为15000元,已知A种外墙漆每千克的价格比B种外墙漆每千克的价格多2元.
(1)求A、B两种外墙漆每千克的价格各是多少元?
(2)已知乙每小时粉刷外墙面积是甲每小时粉刷外墙面积的,乙完成粉刷任务所需时间比甲完成粉刷任务所需时间多5小时.问甲每小时粉刷外墙的面积是多少平方米?
24.某段铁路两旁安置了A,D两座可旋转探照灯.已知PQ∥CN,A,B为PQ上两点,连接AC,∠C=20°,AD平分∠CAB交CN于点D,E为AD上一点,连接BE.
(1)求∠EAP= .
(2)如图,G为CN上一点,连接AG.当,∠2=3∠1时,试说明:AC∥BE;
(3)探照灯A、D照出的光线在铁路所在平面旋转,探照灯射出的光线AC以每秒5度的速度逆时针转动,探照灯D射出的光线DN以每秒15度的速度逆时针转动,DN转至射线DC后立即以相同速度回转,若它们同时开始转动,设转动时间为t秒,当DN回到出发时的位置时同时停止转动,则在转动过程中,当AC与DN互相平行或垂直时,请直接写出此时t的值.
25.把几个图形拼成一个新的图形,通过图形面积的计算,常常可以得到一些等式,这是研究数学问题的一种常用方法.我们在学习“从面积到乘法公式”时,曾用两种不同的方法计算同一个图形的面积,探索了完全平方公式:(a+b)2=a2+2ab+b2(如图1).
(1)观察图2,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
拓展应用:根据(1)中的等量关系及课本所学的完全平方公式知识,解决如下问题:
(2)若,且x>y,求x﹣y的值;
(3)若(2025﹣m)2+(m﹣2024)2=7,求(2025﹣m)(m﹣2024)的值;
(4)如图3,在△BCE中,∠BCE=90°,CE=8,点M在边BC上,CM=3,在边CE上取一点Q,使BM=EQ,分别以BC,CQ为边在△BCE外部作正方形ABCD和正方形COPQ,连接BQ,若△BCQ的面积等于,设BM=x(x>0),求正方形ABCD和正方形COPQ的面积和.
参考答案
一、选择题
1—10:DCDBA DDABD
二、填空题
11.【解答】解:原式=4(x2﹣1)=4(x+1)(x﹣1),
故答案为:4(x+1)(x﹣1)
12.【解答】解:∵(x±3)2
=x2±6x+9
=x2+2(m﹣3)x+9,
∴2(m﹣3)=±6,
解得:m=0或m=6.
故答案为:0或6.
13.【解答】解:∵四边形ABCD和四边形CEFG均是正方形,
∴∠A=∠G=90°,AD=AB=BC=CD,CG=FG,
∴S△BCFBC FG=5,
∴BC FG=10,
∵BG=BC+CG=7,
∴BC2+CG2=(BC+CG)2﹣2BC CG=49﹣2×10=29,
∴S正方形ABCD+S正方形CEFG=29,
∵S△DEFEF DECG (AB﹣CG)CG ABCG2=5CG2,
∴S阴影=S正方形ABCD+S正方形CEFG+S△DEF﹣S△ABD﹣S△BCF=29+5CG2AB2﹣5=29(CG2+AB2)=2929=14.5.
故答案为:14.5.
14.【解答】解:设x﹣1=m,y+1=n,
则关于x,y的方程组为,
∵关于a,b的方程组的解为,
∴方程组的解是,
∴,
∴,
即关于x,y的方程组的解为,
故答案为:.
15.【解答】解:∵m+2n﹣2=0,
∴m+2n=2,
∴3m 9n=3m 32n=3m+2n=32=9.
故答案为:9.
16.【解答】解:如图1所示,设FG交CG于点I,
∵∠ABC=120°,AB∥CD,CE平分∠BCD,
∴∠BCD=120°,∠BCE=∠DCE=60°.
∵GH∥BC,
∴∠CGH=∠BCE=60°.
∵∠FIC=∠GFB+∠ABC=120°+α,
又∵∠FIC=∠BCE+∠CGF,
∴∠CGF=∠FIC﹣∠BCE=120°+α﹣60°=60°+α,
∴∠BGH=∠FGB+∠CGF+∠CGH60°+α+60°=120°.
故答案为:(120°).
三、解答题
17.【解答】解:(1),
①×2+②得:6x=3,
解得:x,
将x代入①得:1+3y=2,
解得:y,
故原方程组的解为;
(2)原方程去分母得:2﹣x=﹣1﹣2x+6,
解得:x=3,
检验:当x=3时,x﹣3=0,
则x=3是分式方程的增根,
故原方程无解.
18.【解答】解:3(m+n),
当m+n=1时,原式=3×1=3.
19.【解答】解:(1)
=3x3﹣x﹣6x2+2﹣3x3+6x2+36x
=35x+2,
当x时,原式=35×()+2=﹣7+2=﹣5;
(2)
,
当a,b=1时,原式2.
20.(1)解:由图可得组的人数为人,所占总人数的百分比为,
∴本次调查的样本容量是:(人),
∵图中组对应的人数为人,
∴图中组对应的圆心角的度数为,
故答案为:;.
(2)解:由(1)可得样本容量是人,
∴图中组对应的人数是:(人),
补全条形统计图如下:
(3)解:最喜欢“、绘画与图像识别”的学生所占百分比为,
∴当该校共名学生时,估计该校最喜欢“、绘画与图像识别”的学生人数为(人).
21.【解答】解:(1)如图,三角形DEF即为所求,
(2)三角形DEF的面积为.
22.【解答】解:(1)设每辆A型车可载学生x人,每辆B型车可载学生y人.
根据题意,得,
解得,
∴每辆A型车可载学生30人,每辆B型车可载学生40人.
(2)设租用A型车a辆,则租用B型车辆.
∴租用A型车1辆,租用B型车8辆使得恰好送完学生,并且租车费用最少.
23.【解答】解:(1)设A种外墙漆每千克的价格是x元,B种外墙漆每千克的价格是y元,
根据题意得:,
解得:.
答:A种外墙漆每千克的价格是26元,B种外墙漆每千克的价格是24元;
(2)设甲每小时粉刷外墙的面积是m平方米,则乙每小时粉刷外墙的面积是m方米,
根据题意得:5,
解得:m=25,
经检验,m=25是所列方程的解,且符合题意.
答:甲每小时粉刷外墙的面积是25平方米.
24.【解答】解:(1)∵PQ∥CN,
∴∠PAC=∠C=20°,
∴∠CAB=180°﹣20°=160°,
∵AD平分∠CAB,
∴,
∴∠EAP=∠PAC+∠CAD=20°+80°=100°,
故答案为:100°;
(2)证明:∵,
∴∠ADC=3∠1,
∵∠2=3∠1,
∴∠2=∠ADC,
∵PQ∥CN,
∴∠EAP+∠ADC=180°,
∴∠ADC=180°﹣100°=80°,
∴∠2=80°,
∵∠PAC=20°,∠EAP=100°,
∴∠CAE=100°﹣20°=80°,
∴∠CAE=∠2,
∴AC∥BE;
(3)360°÷15°=24s,当AC∥DN时,则∠ACD=∠HDN,如图,
∵PB∥CH,
∴∠PAC=∠ACD,
∴∠PAC=∠HDN,
由题意得,∠PAC=20°+5t,∠HDN=15°t,
∴20°+5t=15°t,
∴t=2;
当AC⊥DN时,则∠CND=90°,如图,
∵PA∥CD,
∴∠ACD=∠PAC=20+5t,
∵∠NDH=15t,
∴∠NDC=180°﹣15°t,
∴20+5t+180°﹣15t=90°,
∴t=11;
当ND∥AC时,则∠NDC=∠ACH,如图,
由题意得,∠MDN=15t﹣180°,∠PAC=20°+5°t,
∴∠NDC=180°﹣∠MDN=360°﹣15°t,
∴20°+5°t=360°﹣15°t,
∴t=17;
当DN⊥AC时,∠DNC=90°,如图,
∵∠NDC=360°﹣15°t,
∴∠NDC+∠DCN=90°,
∵∠NCD=180°﹣(20°+5t),
∴360°﹣15t+180°﹣(20°+5t)=90°,
∴t=21.5;
综上,t的值为2或11或17或21.5.
25.【解答】解:(1)由图可知:大正方形的面积等于4个长方形的面积加上阴影正方形的面积,
∴(a+b)2=(a﹣b)2+4ab;
故答案为:(a+b)2=(a﹣b)2+4ab;
(2)由(1)可得(x﹣y)2=(x+y)2﹣4xy,
∴(x﹣y)2=(x+y)2﹣4xy,
∵x>y,
∴x﹣y=3;
(3)由条件可知2ab=(a+b)2﹣(a2+b2),
∵(2025﹣m)2+(m﹣2024)2=7,
∴2(2025﹣m)(m﹣2024)
=(2025﹣m+m﹣2024)2﹣[(2025﹣m)2+(m﹣2024)2]
=1﹣7
=﹣6,
∴原式=﹣3;
(4)设BM=x,则BM=EQ=x,
∴CM=3,CE=8,
CQ=CE﹣EQ=8﹣x,BC=BM+CM=3+x,
∵,
∴(8﹣x)(3+x)=21,
令8﹣x=a,x+3=b,
∴a+b=11,ab=21,
∴正方形ABCD和正方形COPQ的面积和:
=a2+b2=(a+b)2﹣2ab=112﹣2×21=121﹣42=79.
21世纪教育网(www.21cnjy.com)
同课章节目录
