浙教版2024—2025学年七年级下学期数学期末考试押题卷(含答案)
文档属性
| 名称 | 浙教版2024—2025学年七年级下学期数学期末考试押题卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 476.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 07:26:04 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年七年级下学期数学期末考试押题卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形,不能通过其中一个四边形平移得到的是( )
A. B. C. D.
2.下列方程中,是二元一次方程的是( )
A.3x﹣2y=4z B.6xy+9=0 C.x+4y=6 D.x1
3.下列调查中,适合用普查方法的是( )
A.学校在做校服前对八年级学生的衣服尺寸大小的调查
B.环保部门对长江水域的水污染情况的调查
C.质检部门对各厂家生产的电池使用寿命的调查
D.军工厂对该厂生产的某种型号的炮弹爆炸范围的调查
4.太空中微波理论上可以在0.000006秒内接收到相距约2km的信息,数据0.000006用科学记数法表示应为( )
A.0.6×10﹣7 B.0.6×10﹣6 C.6×10﹣6 D.6×10﹣7
5.下列计算正确的是( )
A.(3a3)2=9a6 B.a3+a2=2a5
C.(a+b)2=a2+b2 D.(a4)3=a7
6.如图,点E在AC的延长线上,下列条件能判断AB∥CD的是( )
A.∠3=∠4 B.∠1=∠2
C.∠BDC=∠DCE D.∠BDC+∠ACD=180°
7.农业科研人员在试验田里种植了新品种大麦,为了考察麦穗长度的分布情况,抽取了100个麦穗进行测量.这项调查中的样本是( )
A.新品种大麦长度的分布情况 B.100
C.从中抽取的100个麦穗的长度 D.100个麦穗中的某一个麦穗的长度
8.已知分式方程的解为x=3,则a的值为( )
A.2 B.3 C.7 D.13
9.若关于x的分式方程的解为正实数,则实数m的取值范围是( )
A.m<1 B.m>1 C.m<1且m≠﹣2 D.m>1且m≠3
10.若实数a,b满足a+b=2025,b≠a+1,则的值等于( )
A.2025 B. C. D.
二、填空题(每小题3分,满分18分)
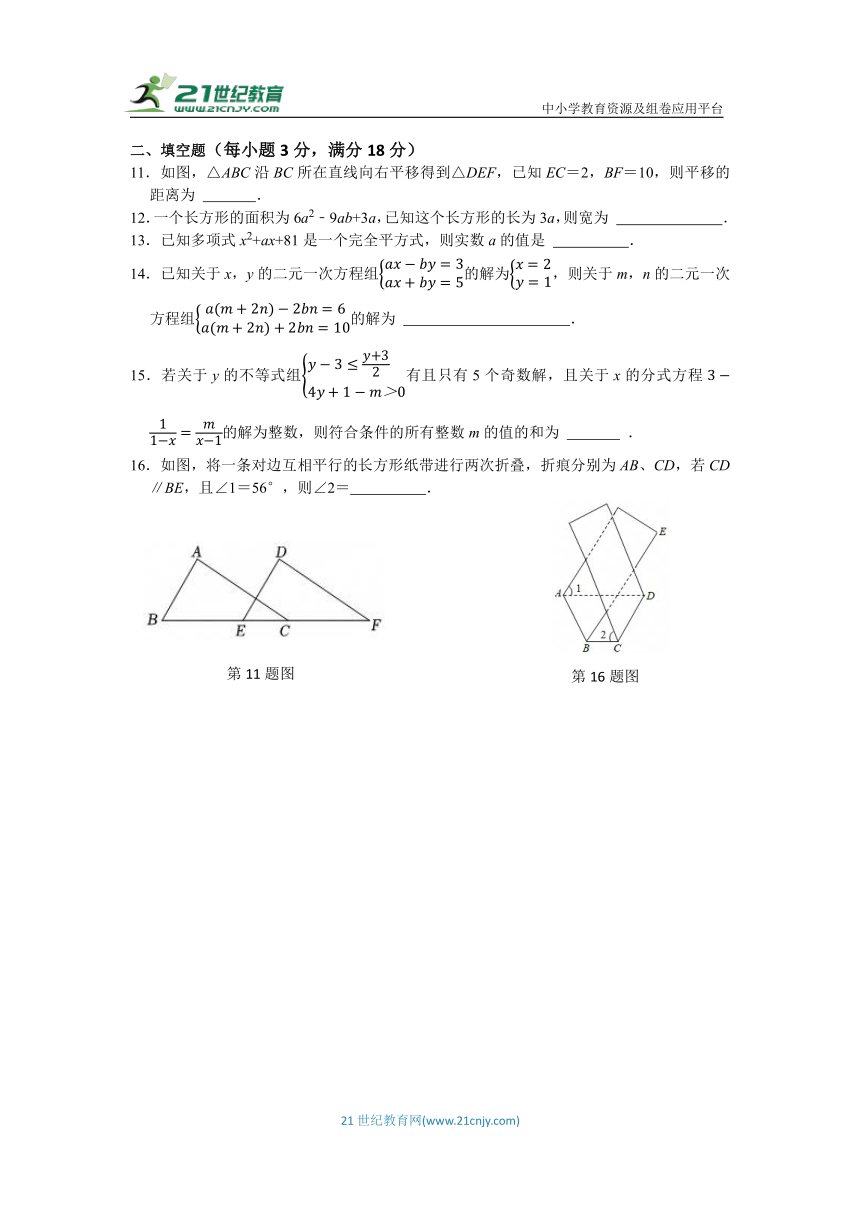
11.如图,△ABC沿BC所在直线向右平移得到△DEF,已知EC=2,BF=10,则平移的距离为 .
12.一个长方形的面积为6a2﹣9ab+3a,已知这个长方形的长为3a,则宽为 .
13.已知多项式x2+ax+81是一个完全平方式,则实数a的值是 .
14.已知关于x,y的二元一次方程组的解为,则关于m,n的二元一次方程组的解为 .
15.若关于y的不等式组有且只有5个奇数解,且关于x的分式方程的解为整数,则符合条件的所有整数m的值的和为 .
16.如图,将一条对边互相平行的长方形纸带进行两次折叠,折痕分别为AB、CD,若CD∥BE,且∠1=56°,则∠2= .
浙教版2024—2025学年七年级下学期数学期末考试押题卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程组:
(1); (2).
18.先化简,再求值:[(x﹣3y)(x+3y)﹣(x﹣y)2+2y(x﹣y)]÷4y,其中x=﹣2,y.
19.先化简:,然后从﹣1,0,1,2这四个数中选取一个合适的数作为x的值代入求值.
20.李、丁、楼、吕四位退休阿姨,一起合伙开了一家轻食餐饮店.她们的出资情况如下图.预计这家轻食餐饮店全年的营业额将达到80万元,房租、人工、材料等成本费预计支出53.6万元,还要按营业额的3%缴纳增值税,剩下的就是这家轻食餐厅店的净利润.
(1)这家轻食餐饮店这一年将交多少万元的增值税?
(2)如果按出资比例将这一年的净利润进行分配,李阿姨预计可以分到多少万元?
(3)如果成本费不变,要使丁阿姨按出资比例能分到5.7万元的净利润,那么这家餐饮店这一年的营业额至少要做到多少万元?(得数保留整数)
21.今年元旦期间某物流公司计划用两种车型运输新年物资,用2辆A型车和1辆B型车装满物资一次可运10吨:用1辆A型车和2辆B型车一次可运11吨.
(1)求每辆A型车和每辆B型车都装满物资一次可分别运多少吨.
(2)某物流公司现有31吨货物资,计划同时租用A型车a辆,B型车b辆,一次运完且恰好每辆车都装满.若A型车每辆需租金每次200元,B型车租金每次300元,求最少租车费用.
22.在正方形的网格中,每个小正方形的边长为1个单位长度,△ABC的三个顶点A,B,C都在格点(正方形网格的交点称为格点).现将△ABC平移.使点A平移到点D,点E、F分别是B、C的对应点.
(1)请在图中画出平移后的△DEF;
(2)分别连接AD,BE,则AD与BE的关系为 .
(3)求四边形ABED的面积.
23.已知关于的二元一次方程组.
(1)当时,求这个方程组的解.
(2)若该方程组的解满足等式,求的值.
(3)在(2)的条件下,某同学在解关于的方程组时,将中的看成了6,“”写成了“”,结果得到方程组的解为,而方程组正确的解为,求的值.
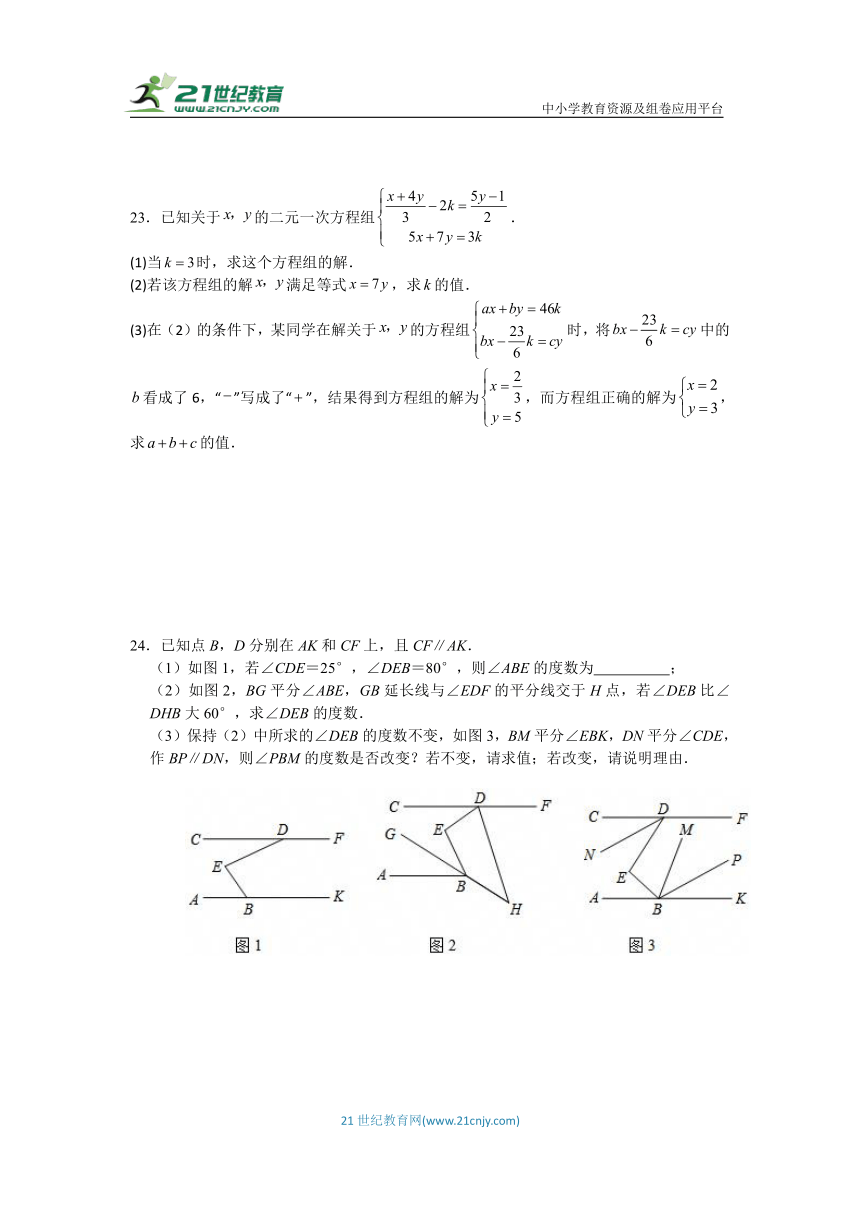
24.已知点B,D分别在AK和CF上,且CF∥AK.
(1)如图1,若∠CDE=25°,∠DEB=80°,则∠ABE的度数为 ;
(2)如图2,BG平分∠ABE,GB延长线与∠EDF的平分线交于H点,若∠DEB比∠DHB大60°,求∠DEB的度数.
(3)保持(2)中所求的∠DEB的度数不变,如图3,BM平分∠EBK,DN平分∠CDE,作BP∥DN,则∠PBM的度数是否改变?若不变,请求值;若改变,请说明理由.
25.用几个小的长方形、正方形拼成一个大的正方形,然后利用两种不同的方法计算这个大的正方形的面积,可以得到一个等式.例如:计算图1的面积,把图1看作一个大正方形,它的面积是(a+b)2;如果把图1看作是由2个长方形和2个小正方形组成的,它的面积为a2+2ab+b2,由此得到(a+b)2=a2+2ab+b2.
(1)如图2,由几个面积不等的小正方形和几个小长方形拼成一个边长为(a+b+c)的正方形,从中你能发现什么结论?该结论用等式表示为 ;
(2)利用(1)中的结论解决以下问题:已知a+b+c=10,ab+ac+bc=38,求a2+b2+c2的值;
(3)如图3,由正方形ABCD边长为a,正方形CEFG边长为b,点D,G,C在同一直线上,连接BD,DF,若a﹣b=2,ab=3,求图3中阴影部分的面积.
参考答案
一、选择题
1—10:DCACA BCCDC
二、填空题
11.【解答】解:由平移的性质可知:BE=CF,
∵EC=2,BF=10,
∴BE+CF=10﹣2=8,
∴BE=CF=4,
则平移的距离为4,
故答案为:4.
12.【解答】解:(6a2﹣9ab+3a)÷3a
=6a2÷3a﹣9ab÷3a+3a÷3a
=2a﹣3b+1.
故答案为:2a﹣3b+1.
13.【解答】解:∵多项式x2+ax+81是一个完全平方式,
∴a=±2×1×9=±18,
故答案为:±18.
14.【解答】解:∵关于x、y的二元一次方程组的解为,
∴关于m、n的二元一次方程组得到,,
∴,
∴解这个关于m、n的方程组得:.
故答案为:.
15.【解答】解:∵,
解①得:y≤9;
解②得,
∴不等式组的解集为,
∵不等式组有且只有5个奇数解,
解得:﹣3≤m<5;
∵,
解得:,
∵方程有整数解,且x≠1,﹣3≤m<5,
∴m的值为﹣2,4,
∴﹣2+4=2,
故答案为:2.
16.【解答】解:如图,延长BC到点F,
∵纸带对边互相平行,∠1=56°,
∴∠4=∠3=∠1=56°,
由折叠可得,∠DCF=∠5,
∵CD∥BE,
∴∠DCF=∠4=56°,
∴∠5=56°,
∴∠2=180°﹣∠DCF﹣∠5=180°﹣56°﹣56°=68°,
故答案为:68°.
三、解答题
17.【解答】解:(1),
①+②得5x=10,
解得:x=2,
将x=2代入①得8+2y=7,
解得:,
∴原方程组的解是;
(2),
由①得:3x﹣4x+4y=2,
整理得:x=4y﹣2 ③,
把③代入②得:2(4y﹣2)﹣3y=1,
解得:y=1
将y=1代入②得2x﹣3=1,
解得:x=2,
∴原方程组的解是.
18.【解答】解:原式=[x2﹣9y2﹣(x2﹣2xy+y2)+2xy﹣2y2]÷4y
=(x2﹣9y2﹣x2+2xy﹣y2+2xy﹣2y2)÷4y
=(4xy﹣12y2)÷4y
=x﹣3y;
当时,原式.
19.【解答】解:原式
,
∵x不能为±1和2,
∴x只能为0,
当x=0时,原式.
20.(1)解:(万元),
答:这家轻食餐饮店这一年将交2.4万元的增值税;
(2)解:,
(万元),
或(万元),
答:李阿姨预计可以分到10.8万元;
(3)解:设这家餐饮店这一年的营业额至少要做到万元,
,
,
答:这一年的营业额至少要做到85万元.
21.【解答】解:(1)设每辆A型车装满物资一次可运x吨,每辆B型车装满物资一次可运y吨,
依题意得:,
解得:,
答:每辆A型车装满物资一次可运3吨,每辆B型车装满物资一次可运4吨;
(2)依题意得:3a+4b=31,
∵a,b均为正整数,
∴或或,
∴该物流公司共有3种租车方案,
方案1:租用9辆A型车,1辆B型车,所需租金300×9+200×1=2900(元);
方案2:租用5辆A型车,4辆B型车,所需租金为300×5+200×4=2300(元);
方案3:租用1辆A型车,7辆B型车,所需租金为300×1+200×7=1700(元);
∵2900>2300>1700,
∴最省钱的租车方案为租用1辆A型车,7辆B型车,最少租车费为1700元.
22.【解答】解:(1)由题意得,△ABC向右平移6个单位长度,向下平移2个单位长度得到△DEF,
如图,△DEF即为所求.
(2)由平移得,AD与BE的关系为平行且相等.
故答案为:平行且相等.
(3)四边形ABED的面积为8×648﹣6﹣4﹣6﹣4=28.
23.(1)解:当时,,
整理得,
由①②得,
;
将代入①得,
;
当时,这个方程组的解为;
(2)解:,
整理得,
由①②得,
;
将代入①得,
;
,解得;
(3)解:在(2)的条件下,,
是关于的方程组的解,
;
是关于的方程组的解,
,
解得,
综上所述,,
.
24.【解答】解:(1)如图1,延长DE交AK于点G,
∵CF∥AK,
∴∠DGB=∠CDE=25°,
∵∠DGB+∠ABE=∠DEB,∠DEB=80°,
∴∠ABE=80°﹣25°=55°,
故答案为:55°;
(2)如图2,作EM∥CD,HN∥CD,
∵AB∥CD,
∴AB∥EM∥HN∥CD,
∴∠1+∠EDF=180°,∠MEB=∠ABE,
∵BG平分∠ABE,
∴∠ABG∠ABE,
∵AB∥HN,
∴∠2=∠ABG,
∵CF∥HN,
∴∠2+∠β=∠3,
∴∠ABE+∠β=∠3,
∵DH平分∠EDF,
∴∠3∠EDF,
∴∠ABE+∠β∠EDF,
∴∠β(∠EDF﹣∠ABE),
∴∠EDF﹣∠ABE=2∠β,
设∠DEB=∠α,
∵∠α=∠1+∠MEB=180°﹣∠EDF+∠ABE=180°﹣(∠EDF﹣∠ABE)=180°﹣2∠β,
∵∠DEB比∠DHB大60°,
∴∠α﹣60°=∠β,
∴∠α=180°﹣2(∠α﹣60°),
解得∠α=100°.
∴∠DEB的度数为100°;
(3)∠PBM的度数不变,理由如下:
如图3,过点E作ES∥CD,设直线DF和直线BP相交于点G,
∵BM平分∠EBK,DN平分∠CDE,
∴∠EBM=∠MBK∠EBK,
∠CDN=∠EDN∠CDE,
∵ES∥CD,AB∥CD,
∴ES∥AB∥CD,
∴∠DES=∠CDE,
∠BES=∠ABE=180°﹣∠EBK,
∠G=∠PBK,
由(2)可知:∠DEB=100°,
∴∠CDE+180°﹣∠EBK=100°,
∴∠EBK﹣∠CDE=80°,
∵BP∥DN,
∴∠CDN=∠G,
∴∠PBK=∠G=∠CDN∠CDE,
∴∠PBM=∠MBK﹣∠PBK
∠EBK∠CDE
(∠EBK﹣∠CDE)
80°
=40°.
∴∠PBM的度数不变,∠PBM=40°.
25.【解答】解:(1)图2中正方形的面积可以表示为:(a+6+c)2.
还可以表示为:a2+b2+c2+2ab+2ac+2bc.
.∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
(2)由(2)知:a2+b2+c2=(a+b+c)2﹣2ab﹣2ac﹣2bc=100﹣2(ab+ac+bc)=100﹣76=24.
(3)S阴影=SABCD﹣S△DGF﹣S△ABD﹣SFECG=AB ADEC CG=a2b(a﹣b)b2(a2﹣b2)(a+b)(a﹣b).
∵a﹣b=2,ab=3且(a+b)2=(a﹣b)2+4ab..
∵a+b>0,
∴a+b=4.
∴S阴影4×23.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年七年级下学期数学期末考试押题卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形,不能通过其中一个四边形平移得到的是( )
A. B. C. D.
2.下列方程中,是二元一次方程的是( )
A.3x﹣2y=4z B.6xy+9=0 C.x+4y=6 D.x1
3.下列调查中,适合用普查方法的是( )
A.学校在做校服前对八年级学生的衣服尺寸大小的调查
B.环保部门对长江水域的水污染情况的调查
C.质检部门对各厂家生产的电池使用寿命的调查
D.军工厂对该厂生产的某种型号的炮弹爆炸范围的调查
4.太空中微波理论上可以在0.000006秒内接收到相距约2km的信息,数据0.000006用科学记数法表示应为( )
A.0.6×10﹣7 B.0.6×10﹣6 C.6×10﹣6 D.6×10﹣7
5.下列计算正确的是( )
A.(3a3)2=9a6 B.a3+a2=2a5
C.(a+b)2=a2+b2 D.(a4)3=a7
6.如图,点E在AC的延长线上,下列条件能判断AB∥CD的是( )
A.∠3=∠4 B.∠1=∠2
C.∠BDC=∠DCE D.∠BDC+∠ACD=180°
7.农业科研人员在试验田里种植了新品种大麦,为了考察麦穗长度的分布情况,抽取了100个麦穗进行测量.这项调查中的样本是( )
A.新品种大麦长度的分布情况 B.100
C.从中抽取的100个麦穗的长度 D.100个麦穗中的某一个麦穗的长度
8.已知分式方程的解为x=3,则a的值为( )
A.2 B.3 C.7 D.13
9.若关于x的分式方程的解为正实数,则实数m的取值范围是( )
A.m<1 B.m>1 C.m<1且m≠﹣2 D.m>1且m≠3
10.若实数a,b满足a+b=2025,b≠a+1,则的值等于( )
A.2025 B. C. D.
二、填空题(每小题3分,满分18分)
11.如图,△ABC沿BC所在直线向右平移得到△DEF,已知EC=2,BF=10,则平移的距离为 .
12.一个长方形的面积为6a2﹣9ab+3a,已知这个长方形的长为3a,则宽为 .
13.已知多项式x2+ax+81是一个完全平方式,则实数a的值是 .
14.已知关于x,y的二元一次方程组的解为,则关于m,n的二元一次方程组的解为 .
15.若关于y的不等式组有且只有5个奇数解,且关于x的分式方程的解为整数,则符合条件的所有整数m的值的和为 .
16.如图,将一条对边互相平行的长方形纸带进行两次折叠,折痕分别为AB、CD,若CD∥BE,且∠1=56°,则∠2= .
浙教版2024—2025学年七年级下学期数学期末考试押题卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程组:
(1); (2).
18.先化简,再求值:[(x﹣3y)(x+3y)﹣(x﹣y)2+2y(x﹣y)]÷4y,其中x=﹣2,y.
19.先化简:,然后从﹣1,0,1,2这四个数中选取一个合适的数作为x的值代入求值.
20.李、丁、楼、吕四位退休阿姨,一起合伙开了一家轻食餐饮店.她们的出资情况如下图.预计这家轻食餐饮店全年的营业额将达到80万元,房租、人工、材料等成本费预计支出53.6万元,还要按营业额的3%缴纳增值税,剩下的就是这家轻食餐厅店的净利润.
(1)这家轻食餐饮店这一年将交多少万元的增值税?
(2)如果按出资比例将这一年的净利润进行分配,李阿姨预计可以分到多少万元?
(3)如果成本费不变,要使丁阿姨按出资比例能分到5.7万元的净利润,那么这家餐饮店这一年的营业额至少要做到多少万元?(得数保留整数)
21.今年元旦期间某物流公司计划用两种车型运输新年物资,用2辆A型车和1辆B型车装满物资一次可运10吨:用1辆A型车和2辆B型车一次可运11吨.
(1)求每辆A型车和每辆B型车都装满物资一次可分别运多少吨.
(2)某物流公司现有31吨货物资,计划同时租用A型车a辆,B型车b辆,一次运完且恰好每辆车都装满.若A型车每辆需租金每次200元,B型车租金每次300元,求最少租车费用.
22.在正方形的网格中,每个小正方形的边长为1个单位长度,△ABC的三个顶点A,B,C都在格点(正方形网格的交点称为格点).现将△ABC平移.使点A平移到点D,点E、F分别是B、C的对应点.
(1)请在图中画出平移后的△DEF;
(2)分别连接AD,BE,则AD与BE的关系为 .
(3)求四边形ABED的面积.
23.已知关于的二元一次方程组.
(1)当时,求这个方程组的解.
(2)若该方程组的解满足等式,求的值.
(3)在(2)的条件下,某同学在解关于的方程组时,将中的看成了6,“”写成了“”,结果得到方程组的解为,而方程组正确的解为,求的值.
24.已知点B,D分别在AK和CF上,且CF∥AK.
(1)如图1,若∠CDE=25°,∠DEB=80°,则∠ABE的度数为 ;
(2)如图2,BG平分∠ABE,GB延长线与∠EDF的平分线交于H点,若∠DEB比∠DHB大60°,求∠DEB的度数.
(3)保持(2)中所求的∠DEB的度数不变,如图3,BM平分∠EBK,DN平分∠CDE,作BP∥DN,则∠PBM的度数是否改变?若不变,请求值;若改变,请说明理由.
25.用几个小的长方形、正方形拼成一个大的正方形,然后利用两种不同的方法计算这个大的正方形的面积,可以得到一个等式.例如:计算图1的面积,把图1看作一个大正方形,它的面积是(a+b)2;如果把图1看作是由2个长方形和2个小正方形组成的,它的面积为a2+2ab+b2,由此得到(a+b)2=a2+2ab+b2.
(1)如图2,由几个面积不等的小正方形和几个小长方形拼成一个边长为(a+b+c)的正方形,从中你能发现什么结论?该结论用等式表示为 ;
(2)利用(1)中的结论解决以下问题:已知a+b+c=10,ab+ac+bc=38,求a2+b2+c2的值;
(3)如图3,由正方形ABCD边长为a,正方形CEFG边长为b,点D,G,C在同一直线上,连接BD,DF,若a﹣b=2,ab=3,求图3中阴影部分的面积.
参考答案
一、选择题
1—10:DCACA BCCDC
二、填空题
11.【解答】解:由平移的性质可知:BE=CF,
∵EC=2,BF=10,
∴BE+CF=10﹣2=8,
∴BE=CF=4,
则平移的距离为4,
故答案为:4.
12.【解答】解:(6a2﹣9ab+3a)÷3a
=6a2÷3a﹣9ab÷3a+3a÷3a
=2a﹣3b+1.
故答案为:2a﹣3b+1.
13.【解答】解:∵多项式x2+ax+81是一个完全平方式,
∴a=±2×1×9=±18,
故答案为:±18.
14.【解答】解:∵关于x、y的二元一次方程组的解为,
∴关于m、n的二元一次方程组得到,,
∴,
∴解这个关于m、n的方程组得:.
故答案为:.
15.【解答】解:∵,
解①得:y≤9;
解②得,
∴不等式组的解集为,
∵不等式组有且只有5个奇数解,
解得:﹣3≤m<5;
∵,
解得:,
∵方程有整数解,且x≠1,﹣3≤m<5,
∴m的值为﹣2,4,
∴﹣2+4=2,
故答案为:2.
16.【解答】解:如图,延长BC到点F,
∵纸带对边互相平行,∠1=56°,
∴∠4=∠3=∠1=56°,
由折叠可得,∠DCF=∠5,
∵CD∥BE,
∴∠DCF=∠4=56°,
∴∠5=56°,
∴∠2=180°﹣∠DCF﹣∠5=180°﹣56°﹣56°=68°,
故答案为:68°.
三、解答题
17.【解答】解:(1),
①+②得5x=10,
解得:x=2,
将x=2代入①得8+2y=7,
解得:,
∴原方程组的解是;
(2),
由①得:3x﹣4x+4y=2,
整理得:x=4y﹣2 ③,
把③代入②得:2(4y﹣2)﹣3y=1,
解得:y=1
将y=1代入②得2x﹣3=1,
解得:x=2,
∴原方程组的解是.
18.【解答】解:原式=[x2﹣9y2﹣(x2﹣2xy+y2)+2xy﹣2y2]÷4y
=(x2﹣9y2﹣x2+2xy﹣y2+2xy﹣2y2)÷4y
=(4xy﹣12y2)÷4y
=x﹣3y;
当时,原式.
19.【解答】解:原式
,
∵x不能为±1和2,
∴x只能为0,
当x=0时,原式.
20.(1)解:(万元),
答:这家轻食餐饮店这一年将交2.4万元的增值税;
(2)解:,
(万元),
或(万元),
答:李阿姨预计可以分到10.8万元;
(3)解:设这家餐饮店这一年的营业额至少要做到万元,
,
,
答:这一年的营业额至少要做到85万元.
21.【解答】解:(1)设每辆A型车装满物资一次可运x吨,每辆B型车装满物资一次可运y吨,
依题意得:,
解得:,
答:每辆A型车装满物资一次可运3吨,每辆B型车装满物资一次可运4吨;
(2)依题意得:3a+4b=31,
∵a,b均为正整数,
∴或或,
∴该物流公司共有3种租车方案,
方案1:租用9辆A型车,1辆B型车,所需租金300×9+200×1=2900(元);
方案2:租用5辆A型车,4辆B型车,所需租金为300×5+200×4=2300(元);
方案3:租用1辆A型车,7辆B型车,所需租金为300×1+200×7=1700(元);
∵2900>2300>1700,
∴最省钱的租车方案为租用1辆A型车,7辆B型车,最少租车费为1700元.
22.【解答】解:(1)由题意得,△ABC向右平移6个单位长度,向下平移2个单位长度得到△DEF,
如图,△DEF即为所求.
(2)由平移得,AD与BE的关系为平行且相等.
故答案为:平行且相等.
(3)四边形ABED的面积为8×648﹣6﹣4﹣6﹣4=28.
23.(1)解:当时,,
整理得,
由①②得,
;
将代入①得,
;
当时,这个方程组的解为;
(2)解:,
整理得,
由①②得,
;
将代入①得,
;
,解得;
(3)解:在(2)的条件下,,
是关于的方程组的解,
;
是关于的方程组的解,
,
解得,
综上所述,,
.
24.【解答】解:(1)如图1,延长DE交AK于点G,
∵CF∥AK,
∴∠DGB=∠CDE=25°,
∵∠DGB+∠ABE=∠DEB,∠DEB=80°,
∴∠ABE=80°﹣25°=55°,
故答案为:55°;
(2)如图2,作EM∥CD,HN∥CD,
∵AB∥CD,
∴AB∥EM∥HN∥CD,
∴∠1+∠EDF=180°,∠MEB=∠ABE,
∵BG平分∠ABE,
∴∠ABG∠ABE,
∵AB∥HN,
∴∠2=∠ABG,
∵CF∥HN,
∴∠2+∠β=∠3,
∴∠ABE+∠β=∠3,
∵DH平分∠EDF,
∴∠3∠EDF,
∴∠ABE+∠β∠EDF,
∴∠β(∠EDF﹣∠ABE),
∴∠EDF﹣∠ABE=2∠β,
设∠DEB=∠α,
∵∠α=∠1+∠MEB=180°﹣∠EDF+∠ABE=180°﹣(∠EDF﹣∠ABE)=180°﹣2∠β,
∵∠DEB比∠DHB大60°,
∴∠α﹣60°=∠β,
∴∠α=180°﹣2(∠α﹣60°),
解得∠α=100°.
∴∠DEB的度数为100°;
(3)∠PBM的度数不变,理由如下:
如图3,过点E作ES∥CD,设直线DF和直线BP相交于点G,
∵BM平分∠EBK,DN平分∠CDE,
∴∠EBM=∠MBK∠EBK,
∠CDN=∠EDN∠CDE,
∵ES∥CD,AB∥CD,
∴ES∥AB∥CD,
∴∠DES=∠CDE,
∠BES=∠ABE=180°﹣∠EBK,
∠G=∠PBK,
由(2)可知:∠DEB=100°,
∴∠CDE+180°﹣∠EBK=100°,
∴∠EBK﹣∠CDE=80°,
∵BP∥DN,
∴∠CDN=∠G,
∴∠PBK=∠G=∠CDN∠CDE,
∴∠PBM=∠MBK﹣∠PBK
∠EBK∠CDE
(∠EBK﹣∠CDE)
80°
=40°.
∴∠PBM的度数不变,∠PBM=40°.
25.【解答】解:(1)图2中正方形的面积可以表示为:(a+6+c)2.
还可以表示为:a2+b2+c2+2ab+2ac+2bc.
.∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
(2)由(2)知:a2+b2+c2=(a+b+c)2﹣2ab﹣2ac﹣2bc=100﹣2(ab+ac+bc)=100﹣76=24.
(3)S阴影=SABCD﹣S△DGF﹣S△ABD﹣SFECG=AB ADEC CG=a2b(a﹣b)b2(a2﹣b2)(a+b)(a﹣b).
∵a﹣b=2,ab=3且(a+b)2=(a﹣b)2+4ab..
∵a+b>0,
∴a+b=4.
∴S阴影4×23.
21世纪教育网(www.21cnjy.com)
同课章节目录
