浙教版2024—2025学年七年级下学期数学期末考试全真模拟试卷(含答案)
文档属性
| 名称 | 浙教版2024—2025学年七年级下学期数学期末考试全真模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 403.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 07:24:34 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年七年级下学期数学期末考试全真模拟试卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列各式不能使用平方差公式的是( )
A.(2a+3b)(2a﹣3b) B.(﹣2a+3b)(3b﹣2a)
C.(﹣2a+3b)(﹣2a﹣3b) D.(2a﹣3b)(﹣2a﹣3b)
2.某课题小组想用某种统计图表表达“2025年6月10日上海某气象站测得的每小时气温”并研究气温的变化规律,最好的统计图表为( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.以上都很合适
3.两条直线被第三条直线所截,下列条件不能判定这两条直线平行的( )
A.同位角相等 B.内错角相等
C.同旁内角相等 D.同旁内角互补
4.若是方程3x+ay=1的一个解,则a的值是( )
A.1 B.﹣1 C.2 D.﹣2
5.我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )
A. B.
C. D.
6.文明城市人人创建,文明成果人人共享.在某市高质量建设全国文明城市的过程中,为了解某学校七年级1200名学生对文明知识的了解情况,学校组织了相关知识测试,并从中随机抽取了100名学生的成绩进行统计分析,下列说法正确的是( )
A.此次调查方式属于抽样调查 B.1200名学生是总体
C.样本容量是1200 D.被抽取的100名学生是样本
7.如图,点E在CD的延长线上,BE与AD交于点F,下列条件能判断BC∥AD的是( )
A.∠1=∠3 B.∠A+∠CDA=180°
C.∠4=∠A D.∠2+∠5=180°
8.如图,已知AB∥CD,EF⊥AB于点E,∠AEH=∠FGH=20°,∠H=55°,则∠EFG的度数是( )
A.130° B.140° C.145° D.155°
9.已知,则的值为( )
A. B. C. D.
10.设x为实数,已知实数x满足x2=3x+1.则的值为( )
A.0 B.1 C.2 D.3
二、填空题(每小题3分,满分18分)
11.计算: .
12.因式分解:4x2﹣100= .
13.已知关于x,y的多项式x2﹣2kxy+16y2是完全平方式,则k= .
14.若3x=4,9y=7,则3x﹣2y的值为 .
15.已知方程组与有相同的解,则(m﹣n)2= .
16.已知关于x,y的二元一次方程(m+1)x+(2m﹣1)y+2﹣m=0,无论实数m取何值,此二元一次方程都有一个相同的解,则这个相同的解是 .
浙教版2024—2025学年七年级下学期数学期末考试全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:+(﹣1)2025
18.解方程组:
(1); (2).
19.先化简,再求值:
(1)(x+1)2+(x+2)(x﹣3),其中.
(2)已知2a2+3a﹣4=0,求代数式3a(2a+1)﹣(2a+1)(2a﹣1)的值.
20.我市某中学为了充分提高学生参与“大课间”活动的积极性,校体育组针对“你愿意参加哪一种‘大课间’活动(从跳绳、呼啦圈、篮球、排球四项中选一项)”进行了抽样调查,并将调查的结果绘制成如下的两幅不完整的统计图(图1,图2),请你根据图中提供的信息解答下列问题:
(1)在这次抽样调查中,一共调查了 名学生;
(2)补全频数分布折线统计图.
(3)喜欢排球的人数在扇形统计图中所占的圆心角是 度.
21.如图:已知,∠HCO=∠EBC,∠BHC+∠BEF=180°.
(1)求证:EF∥BH;
(2)若BH平分∠EBO,EF⊥AO于F,∠HCO=64°,求∠CHO的度数.
22.某玩具公司生产了“哪吒”和“敖丙”两款手办.已知每个“哪吒”手办的售价比每个“敖丙”手办的售价便宜20元,按售价购买3个“哪吒”手办和2个“敖丙”手办共需540元.
(1)每个“哪吒”和“敖丙”手办的售价分别是多少元?
(2)由于电影角色深受大家喜爱,所以玩具公司决定对两款手办进行降价促销,若降价后每个“敖丙”手办的售价是每个“哪吒”手办售价的1.3倍,且用800元购买“哪吒”手办的数量比用520元购买“敖丙”手办的数量多5个,求降价后每个“哪吒”手办的售价为多少元?
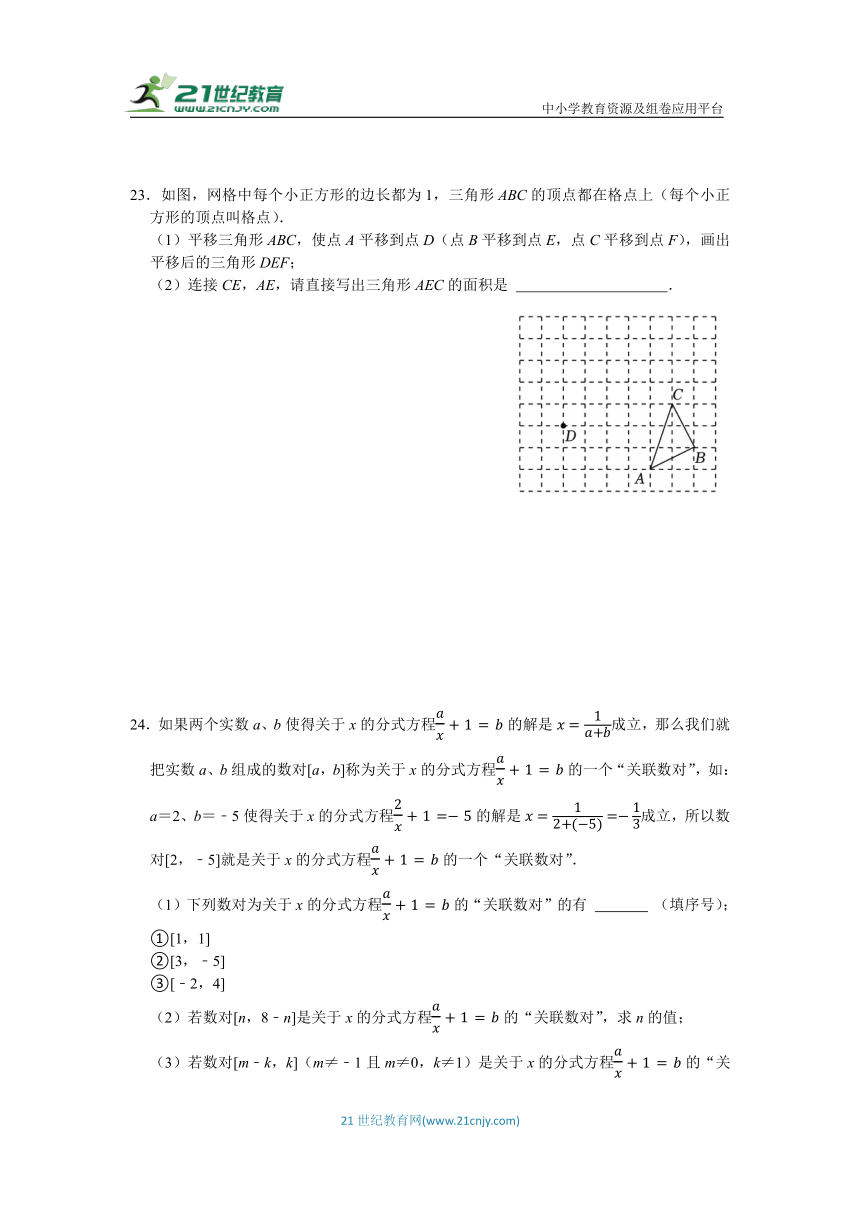
23.如图,网格中每个小正方形的边长都为1,三角形ABC的顶点都在格点上(每个小正方形的顶点叫格点).
(1)平移三角形ABC,使点A平移到点D(点B平移到点E,点C平移到点F),画出平移后的三角形DEF;
(2)连接CE,AE,请直接写出三角形AEC的面积是 .
24.如果两个实数a、b使得关于x的分式方程的解是成立,那么我们就把实数a、b组成的数对[a,b]称为关于x的分式方程的一个“关联数对”,如:a=2、b=﹣5使得关于x的分式方程的解是成立,所以数对[2,﹣5]就是关于x的分式方程的一个“关联数对”.
(1)下列数对为关于x的分式方程的“关联数对”的有 (填序号);
①[1,1]
②[3,﹣5]
③[﹣2,4]
(2)若数对[n,8﹣n]是关于x的分式方程的“关联数对”,求n的值;
(3)若数对[m﹣k,k](m≠﹣1且m≠0,k≠1)是关于x的分式方程的“关联数对”,且关于x的方程有整数解,求整数m的值.
25.【知识生成】通常情况下,通过用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.如图1,在边长为a的正方形中剪掉一个边长为b的小正方形.把余下的部分沿虚线剪开拼成一个长方形(如图2).图1中阴影部分面积可表示为:,图2中阴影部分面积可表示为,因为两个图中的阴影部分面积是相同的,所以可得到等式:.
【拓展探究】图3是一个长为,宽为的长方形,沿图中虚线用剪刀平均分成四个小长方形,然后按图4的形状拼成一个正方形.
(1)根据图形可得到一个关于、、的等量关系式是 ;
(2)结合以上信息,灵活运用公式,解决如下问题:
①已知,,则 .
②已知,求的值.
【知识迁移】
(3)如图5,红岭中学前不久举办了第一届“智启未来,科技筑梦”校园科技节活动,其中创意竞赛要求设计一款由两个正方形构成的光学元件模型.其中大正方形与小正方形的边长分别为a和b.已知两正方形边长之和,边长之积,且E为中点.模型中阴影部分为特殊光线吸收区域,其面积大小直接影响光学元件对光线的吸收效果,进而决定模型的光学性能.为优化设计,需精确计算图中阴影部分的面积总和,求该阴影部分面积总和.
参考答案
一、选择题
1—10:BCCCA ADCDB
二、填空题
11.【解答】解:原式=﹣()2023×52023×5
=﹣(5)2023×5
=﹣1×5
=﹣5.
故答案为:﹣5.
12.【解答】解:4x2﹣100=4(x2﹣25)=4(x+5)(x﹣5),
故答案为:4(x+5)(x﹣5).
13.【解答】解:∵x2﹣2kxy+16y2=x2﹣kxy+(4y)2,
∴﹣2kxy=±2x×4y,
解得k=±4.
故答案为:4和﹣4.
14.【解答】解:3x﹣2y=3x÷32y=3x÷9y.
故答案为:.
15.【解答】解:∵方程组与有相同的解,
∴与有相同的解,
①×2+②得:x=1,
把x=1代入①得:y=﹣2,
把x=1,y=﹣2代入③得:m=14,
把x=1,y=﹣2代入④得:n=2,
∴(m﹣n)2=(14﹣2)2=122=144,
故答案为:144.
16.【解答】解:方程整理得:mx+x+2my﹣y+2﹣m=0,
整理得:(x+2y﹣1)m+x﹣y+2=0,
由无论实数m取何值,此二元一次方程都有一个相同的解,
得到x+2y﹣1=0,x﹣y+2=0,
解得:,
故答案为:.
三、解答题
17.【解答】解:
=1﹣3+1
=-1.
18.【解答】解:(1),
把①代入②得:y=2(3y﹣2)﹣y,
解得:y=1,
∴x=3y﹣2=1,
故方程组的解为;
(2),
①×3﹣②×2得:﹣5y=﹣1,
解得:,
把代入①得:,
解得:,
故方程组的解为.
19.【解答】解:(1)(x+1)2+(x+2)(x﹣3)
=x2+2x+1+x2﹣x﹣6
=2x2+x﹣5;
(2)∵2a2+3a﹣4=0,
∴2a2+3a=4,
∴3a(2a+1)﹣(2a+1)(2a﹣1)
=6a2+3a﹣(4a2﹣1)
=6a2+3a﹣4a2+1
=2a2+3a+1
=4+1
=5.
20.(1)解:(名),
故答案为:100;
(2)解:喜欢篮球人数为:(人),
喜欢排球人数为:(人),
补全频数分布折线统计图如下:
;
(3)解:,
故答案为:;
21.【解答】证明:(1)∵∠HCO=∠EBC,
∴EB∥HC.
∴∠EBH=∠CHB.
∵∠BHC+∠BEF=180°,
∴∠EBH+∠BEF=180°.
∴EF∥BH.
(2)解:∵∠HCO=∠EBC,
∴∠HCO=∠EBC=64°,
∵BH平分∠EBO,
∴∠EBH=∠CHB∠EBC=32°.
∵EF⊥AO于F,EF∥BH,
∴∠BHA=90°.
∴∠FHC=∠BHA+∠CHB=122°.
∵∠CHO=180°﹣∠FHC
=180°﹣122°
=58°.
22.【解答】解:(1)设每个“哪吒”的售价是x元,“敖丙”手办的售价是y元,
由题意得:,
解得:,
答:每个“哪吒”的售价是100元,“敖丙”手办的售价是120元;
(2)降价后每个“哪吒”手办的售价为a元,则降价后每个“敖丙”手办的售价是1.3a元,
由题意得:,
解得:a=80,
经检验:a=80是所列方程的根,且符合题意;
答:降价后每个“哪吒”手办的售价为80元.
23.【解答】解:(1)由题意得,三角形ABC向左平移4个单位长度,向上平移2个单位长度得到三角形DEF.
如图,三角形DEF即为所求.
(2)三角形AEC的面积是.
故答案为:.
24.【解答】解:(1)①若a=1,b=1,分式方程1=1的解为无解,
不符合“关联数对”的定义,
故不正确,不符合题意;
②若a=3,b=﹣5,分式方程1=﹣5的解为x,
,符合“关联数对”的定义,
故正确,符合题意;
③若a=﹣2,b=4,分式方程的解为,
不符合“关联数对”的定义,
故不正确,不符合题意;
故答案为:②;
(2)∵数对[n,8﹣n]是关于x的分式方程的“关联数对”,
∴x是方程的解,
∴1=8﹣n,
整理得:8n+1=8﹣n,
解得:;
(3)∵数对[m﹣k,k](m≠﹣1且m≠0,k≠1)是关于x的分式方程的“关联数对”,
∴x是分式方程的解,
∴1=k,
整理可得m(m﹣k)+1=k,
解得k,
将方程整理为k(m+1)x﹣m(m+1)+m+1=﹣2mx,
解得x1,
∵方程有整数解,
∴m+1=±1,±2,
∴m=0或﹣2或1或﹣3,
又∵m≠0,k≠1,
∴m+1≠m2+1,
∴m≠1,
∴m=﹣2或﹣3.
25.解:(1)方法1:用大正方形面积减去四个小长方形面积列式可得:,
方法2:用小正方形的边长列式可得:;
故答案为:;;
∵方法1和方法2表示的图形面积相等,
∴;
故答案为:;
(2)①∵,,
∴,
∴
,
故答案为:24;
②∵,,
∴
,
∴;
(3)阴影部分面积和为:
,
∵,,
∴,
∴阴影部分面积和等于.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年七年级下学期数学期末考试全真模拟试卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列各式不能使用平方差公式的是( )
A.(2a+3b)(2a﹣3b) B.(﹣2a+3b)(3b﹣2a)
C.(﹣2a+3b)(﹣2a﹣3b) D.(2a﹣3b)(﹣2a﹣3b)
2.某课题小组想用某种统计图表表达“2025年6月10日上海某气象站测得的每小时气温”并研究气温的变化规律,最好的统计图表为( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.以上都很合适
3.两条直线被第三条直线所截,下列条件不能判定这两条直线平行的( )
A.同位角相等 B.内错角相等
C.同旁内角相等 D.同旁内角互补
4.若是方程3x+ay=1的一个解,则a的值是( )
A.1 B.﹣1 C.2 D.﹣2
5.我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )
A. B.
C. D.
6.文明城市人人创建,文明成果人人共享.在某市高质量建设全国文明城市的过程中,为了解某学校七年级1200名学生对文明知识的了解情况,学校组织了相关知识测试,并从中随机抽取了100名学生的成绩进行统计分析,下列说法正确的是( )
A.此次调查方式属于抽样调查 B.1200名学生是总体
C.样本容量是1200 D.被抽取的100名学生是样本
7.如图,点E在CD的延长线上,BE与AD交于点F,下列条件能判断BC∥AD的是( )
A.∠1=∠3 B.∠A+∠CDA=180°
C.∠4=∠A D.∠2+∠5=180°
8.如图,已知AB∥CD,EF⊥AB于点E,∠AEH=∠FGH=20°,∠H=55°,则∠EFG的度数是( )
A.130° B.140° C.145° D.155°
9.已知,则的值为( )
A. B. C. D.
10.设x为实数,已知实数x满足x2=3x+1.则的值为( )
A.0 B.1 C.2 D.3
二、填空题(每小题3分,满分18分)
11.计算: .
12.因式分解:4x2﹣100= .
13.已知关于x,y的多项式x2﹣2kxy+16y2是完全平方式,则k= .
14.若3x=4,9y=7,则3x﹣2y的值为 .
15.已知方程组与有相同的解,则(m﹣n)2= .
16.已知关于x,y的二元一次方程(m+1)x+(2m﹣1)y+2﹣m=0,无论实数m取何值,此二元一次方程都有一个相同的解,则这个相同的解是 .
浙教版2024—2025学年七年级下学期数学期末考试全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:+(﹣1)2025
18.解方程组:
(1); (2).
19.先化简,再求值:
(1)(x+1)2+(x+2)(x﹣3),其中.
(2)已知2a2+3a﹣4=0,求代数式3a(2a+1)﹣(2a+1)(2a﹣1)的值.
20.我市某中学为了充分提高学生参与“大课间”活动的积极性,校体育组针对“你愿意参加哪一种‘大课间’活动(从跳绳、呼啦圈、篮球、排球四项中选一项)”进行了抽样调查,并将调查的结果绘制成如下的两幅不完整的统计图(图1,图2),请你根据图中提供的信息解答下列问题:
(1)在这次抽样调查中,一共调查了 名学生;
(2)补全频数分布折线统计图.
(3)喜欢排球的人数在扇形统计图中所占的圆心角是 度.
21.如图:已知,∠HCO=∠EBC,∠BHC+∠BEF=180°.
(1)求证:EF∥BH;
(2)若BH平分∠EBO,EF⊥AO于F,∠HCO=64°,求∠CHO的度数.
22.某玩具公司生产了“哪吒”和“敖丙”两款手办.已知每个“哪吒”手办的售价比每个“敖丙”手办的售价便宜20元,按售价购买3个“哪吒”手办和2个“敖丙”手办共需540元.
(1)每个“哪吒”和“敖丙”手办的售价分别是多少元?
(2)由于电影角色深受大家喜爱,所以玩具公司决定对两款手办进行降价促销,若降价后每个“敖丙”手办的售价是每个“哪吒”手办售价的1.3倍,且用800元购买“哪吒”手办的数量比用520元购买“敖丙”手办的数量多5个,求降价后每个“哪吒”手办的售价为多少元?
23.如图,网格中每个小正方形的边长都为1,三角形ABC的顶点都在格点上(每个小正方形的顶点叫格点).
(1)平移三角形ABC,使点A平移到点D(点B平移到点E,点C平移到点F),画出平移后的三角形DEF;
(2)连接CE,AE,请直接写出三角形AEC的面积是 .
24.如果两个实数a、b使得关于x的分式方程的解是成立,那么我们就把实数a、b组成的数对[a,b]称为关于x的分式方程的一个“关联数对”,如:a=2、b=﹣5使得关于x的分式方程的解是成立,所以数对[2,﹣5]就是关于x的分式方程的一个“关联数对”.
(1)下列数对为关于x的分式方程的“关联数对”的有 (填序号);
①[1,1]
②[3,﹣5]
③[﹣2,4]
(2)若数对[n,8﹣n]是关于x的分式方程的“关联数对”,求n的值;
(3)若数对[m﹣k,k](m≠﹣1且m≠0,k≠1)是关于x的分式方程的“关联数对”,且关于x的方程有整数解,求整数m的值.
25.【知识生成】通常情况下,通过用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.如图1,在边长为a的正方形中剪掉一个边长为b的小正方形.把余下的部分沿虚线剪开拼成一个长方形(如图2).图1中阴影部分面积可表示为:,图2中阴影部分面积可表示为,因为两个图中的阴影部分面积是相同的,所以可得到等式:.
【拓展探究】图3是一个长为,宽为的长方形,沿图中虚线用剪刀平均分成四个小长方形,然后按图4的形状拼成一个正方形.
(1)根据图形可得到一个关于、、的等量关系式是 ;
(2)结合以上信息,灵活运用公式,解决如下问题:
①已知,,则 .
②已知,求的值.
【知识迁移】
(3)如图5,红岭中学前不久举办了第一届“智启未来,科技筑梦”校园科技节活动,其中创意竞赛要求设计一款由两个正方形构成的光学元件模型.其中大正方形与小正方形的边长分别为a和b.已知两正方形边长之和,边长之积,且E为中点.模型中阴影部分为特殊光线吸收区域,其面积大小直接影响光学元件对光线的吸收效果,进而决定模型的光学性能.为优化设计,需精确计算图中阴影部分的面积总和,求该阴影部分面积总和.
参考答案
一、选择题
1—10:BCCCA ADCDB
二、填空题
11.【解答】解:原式=﹣()2023×52023×5
=﹣(5)2023×5
=﹣1×5
=﹣5.
故答案为:﹣5.
12.【解答】解:4x2﹣100=4(x2﹣25)=4(x+5)(x﹣5),
故答案为:4(x+5)(x﹣5).
13.【解答】解:∵x2﹣2kxy+16y2=x2﹣kxy+(4y)2,
∴﹣2kxy=±2x×4y,
解得k=±4.
故答案为:4和﹣4.
14.【解答】解:3x﹣2y=3x÷32y=3x÷9y.
故答案为:.
15.【解答】解:∵方程组与有相同的解,
∴与有相同的解,
①×2+②得:x=1,
把x=1代入①得:y=﹣2,
把x=1,y=﹣2代入③得:m=14,
把x=1,y=﹣2代入④得:n=2,
∴(m﹣n)2=(14﹣2)2=122=144,
故答案为:144.
16.【解答】解:方程整理得:mx+x+2my﹣y+2﹣m=0,
整理得:(x+2y﹣1)m+x﹣y+2=0,
由无论实数m取何值,此二元一次方程都有一个相同的解,
得到x+2y﹣1=0,x﹣y+2=0,
解得:,
故答案为:.
三、解答题
17.【解答】解:
=1﹣3+1
=-1.
18.【解答】解:(1),
把①代入②得:y=2(3y﹣2)﹣y,
解得:y=1,
∴x=3y﹣2=1,
故方程组的解为;
(2),
①×3﹣②×2得:﹣5y=﹣1,
解得:,
把代入①得:,
解得:,
故方程组的解为.
19.【解答】解:(1)(x+1)2+(x+2)(x﹣3)
=x2+2x+1+x2﹣x﹣6
=2x2+x﹣5;
(2)∵2a2+3a﹣4=0,
∴2a2+3a=4,
∴3a(2a+1)﹣(2a+1)(2a﹣1)
=6a2+3a﹣(4a2﹣1)
=6a2+3a﹣4a2+1
=2a2+3a+1
=4+1
=5.
20.(1)解:(名),
故答案为:100;
(2)解:喜欢篮球人数为:(人),
喜欢排球人数为:(人),
补全频数分布折线统计图如下:
;
(3)解:,
故答案为:;
21.【解答】证明:(1)∵∠HCO=∠EBC,
∴EB∥HC.
∴∠EBH=∠CHB.
∵∠BHC+∠BEF=180°,
∴∠EBH+∠BEF=180°.
∴EF∥BH.
(2)解:∵∠HCO=∠EBC,
∴∠HCO=∠EBC=64°,
∵BH平分∠EBO,
∴∠EBH=∠CHB∠EBC=32°.
∵EF⊥AO于F,EF∥BH,
∴∠BHA=90°.
∴∠FHC=∠BHA+∠CHB=122°.
∵∠CHO=180°﹣∠FHC
=180°﹣122°
=58°.
22.【解答】解:(1)设每个“哪吒”的售价是x元,“敖丙”手办的售价是y元,
由题意得:,
解得:,
答:每个“哪吒”的售价是100元,“敖丙”手办的售价是120元;
(2)降价后每个“哪吒”手办的售价为a元,则降价后每个“敖丙”手办的售价是1.3a元,
由题意得:,
解得:a=80,
经检验:a=80是所列方程的根,且符合题意;
答:降价后每个“哪吒”手办的售价为80元.
23.【解答】解:(1)由题意得,三角形ABC向左平移4个单位长度,向上平移2个单位长度得到三角形DEF.
如图,三角形DEF即为所求.
(2)三角形AEC的面积是.
故答案为:.
24.【解答】解:(1)①若a=1,b=1,分式方程1=1的解为无解,
不符合“关联数对”的定义,
故不正确,不符合题意;
②若a=3,b=﹣5,分式方程1=﹣5的解为x,
,符合“关联数对”的定义,
故正确,符合题意;
③若a=﹣2,b=4,分式方程的解为,
不符合“关联数对”的定义,
故不正确,不符合题意;
故答案为:②;
(2)∵数对[n,8﹣n]是关于x的分式方程的“关联数对”,
∴x是方程的解,
∴1=8﹣n,
整理得:8n+1=8﹣n,
解得:;
(3)∵数对[m﹣k,k](m≠﹣1且m≠0,k≠1)是关于x的分式方程的“关联数对”,
∴x是分式方程的解,
∴1=k,
整理可得m(m﹣k)+1=k,
解得k,
将方程整理为k(m+1)x﹣m(m+1)+m+1=﹣2mx,
解得x1,
∵方程有整数解,
∴m+1=±1,±2,
∴m=0或﹣2或1或﹣3,
又∵m≠0,k≠1,
∴m+1≠m2+1,
∴m≠1,
∴m=﹣2或﹣3.
25.解:(1)方法1:用大正方形面积减去四个小长方形面积列式可得:,
方法2:用小正方形的边长列式可得:;
故答案为:;;
∵方法1和方法2表示的图形面积相等,
∴;
故答案为:;
(2)①∵,,
∴,
∴
,
故答案为:24;
②∵,,
∴
,
∴;
(3)阴影部分面积和为:
,
∵,,
∴,
∴阴影部分面积和等于.
21世纪教育网(www.21cnjy.com)
同课章节目录
