浙教版2024—2025学年七年级下学期数学期末复习综合卷(含答案)
文档属性
| 名称 | 浙教版2024—2025学年七年级下学期数学期末复习综合卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 459.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 07:24:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年七年级下学期数学期末复习综合卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
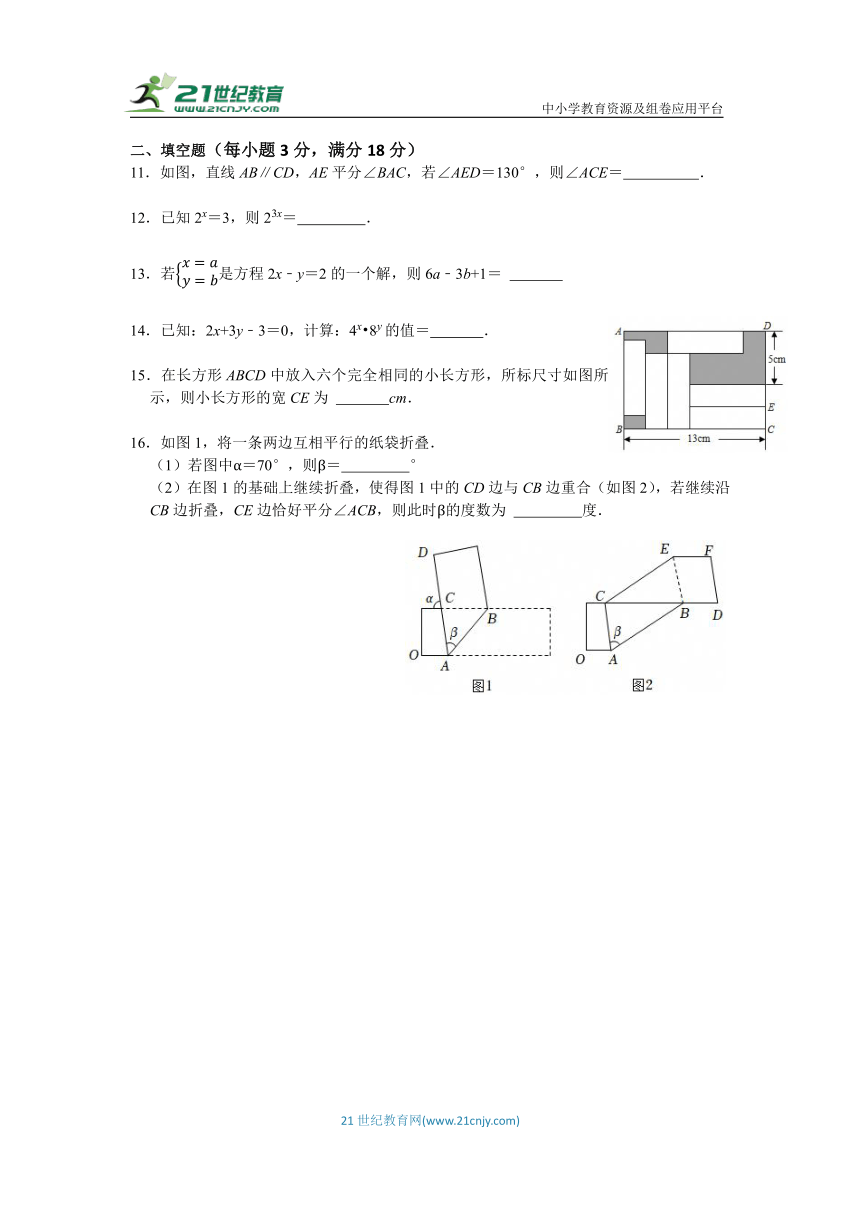
1.“白日不到处,青春恰自来,苔花如米小,也学牡丹开.”这是清朝袁枚所写五言绝句《苔》,这首咏物诗启示我们身处逆境也要努力绽放自己,要和苔花一样尽自己所能实现人生价值,袁枚所写的“苔花”很可能是苔类孢子体的苞荫,某孢子体的苞荫直径约为0.0000084m,将数据0.0000084用科学记数法表示为( )
A.0.84×10﹣5 B.84×10﹣7 C.8.4×10﹣5 D.8.4×10﹣6
2.农业科研人员在试验田里种植了新品种大麦,为了考察麦穗长度的分布情况,抽取了100个麦穗进行测量.这项调查中的样本是( )
A.新品种大麦长度的分布情况 B.100
C.从中抽取的100个麦穗的长度 D.100个麦穗中的某一个麦穗的长度
3.下列分式中,不论x取何值,一定有意义的是( )
A. B. C. D.
4.将分式中的a、b都扩大为原来的3倍,则分式的值( )
A.不变 B.是原来的3倍
C.是原来的9倍 D.是原来的6倍
5.某市为尽快了解义务教育阶段劳动课程开设及实施的情况,现面向全市义务教育阶段的学校进行抽样调查,下列抽样方式较合适的是( )
A.随机抽取城区三分之一的学校 B.随机抽取乡村三分之一的学校
C.调查全体学校 D.随机抽取三分之一的学校
6.运用平方差公式计算,下列变形正确的是( )
A. B.
C. D.
7.如图,点E在AC的延长线上,下列条件能判断AB∥CD的是( )
A.∠3=∠4 B.∠1=∠2
C.∠BDC=∠DCE D.∠BDC+∠ACD=180°
8.下列运动属于平移的是( )
A.冷水加热过程中小气泡变成大气泡
B.乘电梯从一楼到十楼
C.随风飘动的树叶在空中的运动
D.钟表上走动的分针
9.已知,,则的值为( )
A.10 B.4 C.2 D.1
10.已知,,,,则a、b、c、d的大小关系是( )
A. B. C. D.
二、填空题(每小题3分,满分18分)
11.如图,直线AB∥CD,AE平分∠BAC,若∠AED=130°,则∠ACE= .
12.已知2x=3,则23x= .
13.若是方程2x﹣y=2的一个解,则6a﹣3b+1=
14.已知:2x+3y﹣3=0,计算:4x 8y的值= .
15.在长方形ABCD中放入六个完全相同的小长方形,所标尺寸如图所示,则小长方形的宽CE为 cm.
16.如图1,将一条两边互相平行的纸袋折叠.
(1)若图中α=70°,则β= °
(2)在图1的基础上继续折叠,使得图1中的CD边与CB边重合(如图2),若继续沿CB边折叠,CE边恰好平分∠ACB,则此时β的度数为 度.
浙教版2024—2025学年七年级下学期数学期末复习综合卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______ ______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程(组):
(1) (2)1
18.(1)化简:(4ab3﹣8a2b2)÷(4ab);
(2)先化简,再求值:(2x﹣y)2﹣(x+y)(x﹣y),其中x=﹣2,y=1.
19.先化简,再求值:
(1)[(x﹣2y)2+(x﹣2y)(x+2y)﹣2x(2x﹣y)]÷2x,其中x=5,y=﹣6.
(2),并从0,﹣1,2中选一个合适的数作为a的值代入求值.
20.为增强师生的国家安全意识,闵行区某中学组织了“国家安全知识竞赛”,根据学生的成绩划分为、、、四个等级,并绘制了如下不完整的条形统计图和扇形统计图:
根据图中提供的信息,回答下列问题:
(1)参加知识竞赛的学生共有___________人,并补全条形统计图;
(2)扇形统计图中,___________,C等级对应的圆心角为___________度;
(3)成绩为A等级人数比成绩为B等级人数少百分之几?
21.“三头一掌”是衢州地方特色美食,其中最具代表性的是鸭头和兔头.在某品牌销售店中,已知一个鸭头的价格与一个兔头的价格和为23元,用40元购进鸭头的个数与用75元购进兔头的个数相同.
(1)求出鸭头和兔头的单价.
(2)某位游客在该销售店中购买鸭头和兔头恰好用了320元(鸭头和兔头都购买),请写出所有购买方案.
22.已知:如图,点E在直线DF上,点B在直线AC上,∠1=∠2,∠3=∠4.
①求证:BD∥CE.
②若∠A=40°,求∠F的值.
23.我们将(a+b)2=a2+2ab+b2进行变形,如:a2+b2=(a+b)2﹣2ab,ab等.根据以上变形解决下列问题:
(1)已知a2+b2=10,(a+b)2=18,则ab= .
(2)已知,若x满足(25﹣x)(x﹣10)=﹣15,求(25﹣x)2+(x﹣10)2的值.
(3)如图,长方形ABFD,DA⊥AB,FB⊥AB,AD=AC,BE=BC,连接CD,CE,若AC BC=10,则图中阴影部分的面积为 .
24.如图1,已知点A,B分别是直线MN,PQ上的点,∠BAN=45°,且PQ∥MN.
(1)∠PBA的度数为 .
(2)如图2,射线AC以每秒3°的速度绕点A从AM开始顺时针旋转,射线BD以每秒1°的速度绕点B从BP开始顺时针旋转,当射线AC旋转到与AN重合时,两条射线同时停止旋转.
①当0<t<45,是否存在t,使得AC∥BD?请说明理由.
②如图3,当t>45时,射线AC和射线BD交于点G,用含t的代数式表示∠AGB的度数.
③在②的条件上,过点G作GH⊥AG交PQ于点H,在转动过程中,∠BAG与∠BGH的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
25.阅读探索:
材料一:解方程组时,采用了一种“换元法”的解法,解法如下:
解:设,原方程组可化为解得,即,解得;
材料二:解方程组时,采用了一种“整体代换”的解法,解法如下:
解:将方程②,变形为③,把方程①代入③得,,则;把代入①得,,所以方程组的解为:;
根据上述材料,解决下列问题:
(1)运用换元法解求关于,的方程组:的解;
(2)若关于,的方程组的解为,求关于,的方程组的解.
(3)已知、、,满足,试求y的值.
参考答案
一、选择题
1—10:DCDBD CBBDB
二、填空题
11.【解答】解:∵AB∥CD,
∴∠BAE=∠AEC,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∴∠AEC=∠CAE,
∵∠AED=130°,
∴∠AEC=∠CAE=180°﹣∠AED=50°,
∴∠ACE=180°﹣50°﹣50°=80°
故答案为:80°.
12.【解答】解:∵2x=3,
∴23x=(2x)3=33=27,
故答案为:27.
13.【解答】解:把代入方程2x﹣y=2得:2a﹣b=2,
∴6a﹣3b+1
=3(2a﹣b)+1
=3×2+1
=6+1
=7,
故答案为:7.
14.【解答】解:∵2x+3y﹣3=0,
∴2x+3y=3,
∴4x 8y=22x 23y=22x+3y=23=8,
故答案为:8.
15.【解答】解:设小长方形的长为x cm,宽为y cm,
则AD=x+3y,AB=x+y=5+2y,
即x﹣y=5,
根据题意,得:,
解得:,
即CE=2cm,
故答案为:2.
16.【解答】解:(1)根据上下边互相平行可知,α=∠OAD,
∵α=70°,
∴∠OAD=70°.
又∠OAD+2β=180°,
∴β=55°.
故答案为:55.
(2)根据折叠的性质可知,折叠两次后形成的三个角都相等,
根据题意可知,折叠两次后形成的三个角与折叠后的∠ACE都相等,而这四个角的和为180°,故每个角为45°,
∴∠ACB=90°,即α=90°,
由(1)中可得,β(180°﹣90°)=45°.
故答案为:45.
三、解答题
17.【解答】解:(1),
①×2+②得:6x=3,
解得:x,
将x代入①得:1+3y=2,
解得:y,
故原方程组的解为;
(2)原方程去分母得:2﹣x=﹣1﹣2x+6,
解得:x=3,
检验:当x=3时,x﹣3=0,
则x=3是分式方程的增根,
故原方程无解.
18.【解答】解:3(m+n),
当m+n=1时,原式=3×1=3.
19.【解答】解:(1)
=3x3﹣x﹣6x2+2﹣3x3+6x2+36x
=35x+2,
当x时,原式=35×()+2=﹣7+2=﹣5;
(2)
,
当a,b=1时,原式2.
20.(1)解:参加知识竞赛的学生共有人,
故等级的人数为人,
补全条形统计图如图所示:
;
(2)解:,即;
C等级对应的圆心角为;
(3)解:成绩为A等级人数比成绩为B等级人数少.
21.【解答】解:(1)设鸭头的单价为x元,则兔头的单价为(23﹣x)元,
由题意得:,
解得:x=8,
经检验,x=8是原方程的解,且符合题意,
∴23﹣x=15,
答:鸭头的单价为8元,兔头的单价为15元;
(2)设购买鸭头m个,兔头n个,
由题意得:8m+15n=320,
整理得:m=40n,
∵m、n均为正整数,
∴或,
∴有2种购买方案:
①购买鸭头25个,兔头8个;
②购买鸭头10个,兔头16个.
22.【解答】解:如图,
①证明:
∵∠1=∠2,∠1=∠5,
∴∠2=∠5,
∴BD∥CE;
②∵BD∥CE,
∴∠3+∠C=180°,
∵∠3=∠4,
∴∠4+∠C=180°,
∴DF∥AC,
∴∠F=∠A=40°,
答:∠F的值为40°.
23.【解答】解:(1)由题意得,ab4,
故答案为:4;
(2)由a2+b2=(a+b)2﹣2ab得,
(25﹣x)2+(x﹣10)2
=[(25﹣x)+(x﹣10)]2﹣2(25﹣x)(x﹣10)
=152﹣2×(﹣15)
=225+30
=255;
(3)设AC=a,BC=b,根据ab可得,
图中阴影部分的面积为:
=ab
=AC BC
=10,
故答案为:10.
24.【解答】(1)解:∵∠BAN=45°,且PQ∥MN,
∴∠PBA=180°﹣∠BAN=135°,
故答案为:135°;
(2)解:①不存在t,使得AC∥BD,理由如下:
由题意可得∠MAC=3t,∠PBD=t,
∵∠PBA=135°,
∴∠DBA=135°﹣t,
∵BAN=45°,
∴∠BAC=180°﹣∠MAC﹣∠BAN=135°﹣3t,
∵要使AC∥BD,
∴∠BAC=∠ABD,即 35°﹣3t=135°﹣t,
解得t=0,
∵0<t<45,
∴不存在t,使得AC∥BD;
②过点G作GH∥PQ,
∵∠MAC=3t,∠MAC+∠GAN=180°,
∴∠GAN=180°﹣3t,
∵PQ∥MN,GH∥PQ,
∴PQ∥MN∥GH,
∴∠HGB=∠PBD=t,∠HGA=∠NAC=180°﹣3t,
∴∠AGB=∠AGH+∠BGH=180°﹣3t+t=180°﹣2t;
③,保持不变,理由如下:
∵GH⊥AG,
∴∠AGH=90°,
∴∠BGH=90°﹣∠AGB=90°﹣(180°﹣2t)=2t﹣90°,
∵∠BAG=3t﹣135°,
∴.
25.(1)解:设,则原方程组变形得,
解得,,
∴,
解得,;
(2)解:关于,的方程组的解为,
∴,
∴,
解得,;
(3)解:∵,,
∴,
∴,
解得,.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年七年级下学期数学期末复习综合卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.“白日不到处,青春恰自来,苔花如米小,也学牡丹开.”这是清朝袁枚所写五言绝句《苔》,这首咏物诗启示我们身处逆境也要努力绽放自己,要和苔花一样尽自己所能实现人生价值,袁枚所写的“苔花”很可能是苔类孢子体的苞荫,某孢子体的苞荫直径约为0.0000084m,将数据0.0000084用科学记数法表示为( )
A.0.84×10﹣5 B.84×10﹣7 C.8.4×10﹣5 D.8.4×10﹣6
2.农业科研人员在试验田里种植了新品种大麦,为了考察麦穗长度的分布情况,抽取了100个麦穗进行测量.这项调查中的样本是( )
A.新品种大麦长度的分布情况 B.100
C.从中抽取的100个麦穗的长度 D.100个麦穗中的某一个麦穗的长度
3.下列分式中,不论x取何值,一定有意义的是( )
A. B. C. D.
4.将分式中的a、b都扩大为原来的3倍,则分式的值( )
A.不变 B.是原来的3倍
C.是原来的9倍 D.是原来的6倍
5.某市为尽快了解义务教育阶段劳动课程开设及实施的情况,现面向全市义务教育阶段的学校进行抽样调查,下列抽样方式较合适的是( )
A.随机抽取城区三分之一的学校 B.随机抽取乡村三分之一的学校
C.调查全体学校 D.随机抽取三分之一的学校
6.运用平方差公式计算,下列变形正确的是( )
A. B.
C. D.
7.如图,点E在AC的延长线上,下列条件能判断AB∥CD的是( )
A.∠3=∠4 B.∠1=∠2
C.∠BDC=∠DCE D.∠BDC+∠ACD=180°
8.下列运动属于平移的是( )
A.冷水加热过程中小气泡变成大气泡
B.乘电梯从一楼到十楼
C.随风飘动的树叶在空中的运动
D.钟表上走动的分针
9.已知,,则的值为( )
A.10 B.4 C.2 D.1
10.已知,,,,则a、b、c、d的大小关系是( )
A. B. C. D.
二、填空题(每小题3分,满分18分)
11.如图,直线AB∥CD,AE平分∠BAC,若∠AED=130°,则∠ACE= .
12.已知2x=3,则23x= .
13.若是方程2x﹣y=2的一个解,则6a﹣3b+1=
14.已知:2x+3y﹣3=0,计算:4x 8y的值= .
15.在长方形ABCD中放入六个完全相同的小长方形,所标尺寸如图所示,则小长方形的宽CE为 cm.
16.如图1,将一条两边互相平行的纸袋折叠.
(1)若图中α=70°,则β= °
(2)在图1的基础上继续折叠,使得图1中的CD边与CB边重合(如图2),若继续沿CB边折叠,CE边恰好平分∠ACB,则此时β的度数为 度.
浙教版2024—2025学年七年级下学期数学期末复习综合卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______ ______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程(组):
(1) (2)1
18.(1)化简:(4ab3﹣8a2b2)÷(4ab);
(2)先化简,再求值:(2x﹣y)2﹣(x+y)(x﹣y),其中x=﹣2,y=1.
19.先化简,再求值:
(1)[(x﹣2y)2+(x﹣2y)(x+2y)﹣2x(2x﹣y)]÷2x,其中x=5,y=﹣6.
(2),并从0,﹣1,2中选一个合适的数作为a的值代入求值.
20.为增强师生的国家安全意识,闵行区某中学组织了“国家安全知识竞赛”,根据学生的成绩划分为、、、四个等级,并绘制了如下不完整的条形统计图和扇形统计图:
根据图中提供的信息,回答下列问题:
(1)参加知识竞赛的学生共有___________人,并补全条形统计图;
(2)扇形统计图中,___________,C等级对应的圆心角为___________度;
(3)成绩为A等级人数比成绩为B等级人数少百分之几?
21.“三头一掌”是衢州地方特色美食,其中最具代表性的是鸭头和兔头.在某品牌销售店中,已知一个鸭头的价格与一个兔头的价格和为23元,用40元购进鸭头的个数与用75元购进兔头的个数相同.
(1)求出鸭头和兔头的单价.
(2)某位游客在该销售店中购买鸭头和兔头恰好用了320元(鸭头和兔头都购买),请写出所有购买方案.
22.已知:如图,点E在直线DF上,点B在直线AC上,∠1=∠2,∠3=∠4.
①求证:BD∥CE.
②若∠A=40°,求∠F的值.
23.我们将(a+b)2=a2+2ab+b2进行变形,如:a2+b2=(a+b)2﹣2ab,ab等.根据以上变形解决下列问题:
(1)已知a2+b2=10,(a+b)2=18,则ab= .
(2)已知,若x满足(25﹣x)(x﹣10)=﹣15,求(25﹣x)2+(x﹣10)2的值.
(3)如图,长方形ABFD,DA⊥AB,FB⊥AB,AD=AC,BE=BC,连接CD,CE,若AC BC=10,则图中阴影部分的面积为 .
24.如图1,已知点A,B分别是直线MN,PQ上的点,∠BAN=45°,且PQ∥MN.
(1)∠PBA的度数为 .
(2)如图2,射线AC以每秒3°的速度绕点A从AM开始顺时针旋转,射线BD以每秒1°的速度绕点B从BP开始顺时针旋转,当射线AC旋转到与AN重合时,两条射线同时停止旋转.
①当0<t<45,是否存在t,使得AC∥BD?请说明理由.
②如图3,当t>45时,射线AC和射线BD交于点G,用含t的代数式表示∠AGB的度数.
③在②的条件上,过点G作GH⊥AG交PQ于点H,在转动过程中,∠BAG与∠BGH的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
25.阅读探索:
材料一:解方程组时,采用了一种“换元法”的解法,解法如下:
解:设,原方程组可化为解得,即,解得;
材料二:解方程组时,采用了一种“整体代换”的解法,解法如下:
解:将方程②,变形为③,把方程①代入③得,,则;把代入①得,,所以方程组的解为:;
根据上述材料,解决下列问题:
(1)运用换元法解求关于,的方程组:的解;
(2)若关于,的方程组的解为,求关于,的方程组的解.
(3)已知、、,满足,试求y的值.
参考答案
一、选择题
1—10:DCDBD CBBDB
二、填空题
11.【解答】解:∵AB∥CD,
∴∠BAE=∠AEC,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∴∠AEC=∠CAE,
∵∠AED=130°,
∴∠AEC=∠CAE=180°﹣∠AED=50°,
∴∠ACE=180°﹣50°﹣50°=80°
故答案为:80°.
12.【解答】解:∵2x=3,
∴23x=(2x)3=33=27,
故答案为:27.
13.【解答】解:把代入方程2x﹣y=2得:2a﹣b=2,
∴6a﹣3b+1
=3(2a﹣b)+1
=3×2+1
=6+1
=7,
故答案为:7.
14.【解答】解:∵2x+3y﹣3=0,
∴2x+3y=3,
∴4x 8y=22x 23y=22x+3y=23=8,
故答案为:8.
15.【解答】解:设小长方形的长为x cm,宽为y cm,
则AD=x+3y,AB=x+y=5+2y,
即x﹣y=5,
根据题意,得:,
解得:,
即CE=2cm,
故答案为:2.
16.【解答】解:(1)根据上下边互相平行可知,α=∠OAD,
∵α=70°,
∴∠OAD=70°.
又∠OAD+2β=180°,
∴β=55°.
故答案为:55.
(2)根据折叠的性质可知,折叠两次后形成的三个角都相等,
根据题意可知,折叠两次后形成的三个角与折叠后的∠ACE都相等,而这四个角的和为180°,故每个角为45°,
∴∠ACB=90°,即α=90°,
由(1)中可得,β(180°﹣90°)=45°.
故答案为:45.
三、解答题
17.【解答】解:(1),
①×2+②得:6x=3,
解得:x,
将x代入①得:1+3y=2,
解得:y,
故原方程组的解为;
(2)原方程去分母得:2﹣x=﹣1﹣2x+6,
解得:x=3,
检验:当x=3时,x﹣3=0,
则x=3是分式方程的增根,
故原方程无解.
18.【解答】解:3(m+n),
当m+n=1时,原式=3×1=3.
19.【解答】解:(1)
=3x3﹣x﹣6x2+2﹣3x3+6x2+36x
=35x+2,
当x时,原式=35×()+2=﹣7+2=﹣5;
(2)
,
当a,b=1时,原式2.
20.(1)解:参加知识竞赛的学生共有人,
故等级的人数为人,
补全条形统计图如图所示:
;
(2)解:,即;
C等级对应的圆心角为;
(3)解:成绩为A等级人数比成绩为B等级人数少.
21.【解答】解:(1)设鸭头的单价为x元,则兔头的单价为(23﹣x)元,
由题意得:,
解得:x=8,
经检验,x=8是原方程的解,且符合题意,
∴23﹣x=15,
答:鸭头的单价为8元,兔头的单价为15元;
(2)设购买鸭头m个,兔头n个,
由题意得:8m+15n=320,
整理得:m=40n,
∵m、n均为正整数,
∴或,
∴有2种购买方案:
①购买鸭头25个,兔头8个;
②购买鸭头10个,兔头16个.
22.【解答】解:如图,
①证明:
∵∠1=∠2,∠1=∠5,
∴∠2=∠5,
∴BD∥CE;
②∵BD∥CE,
∴∠3+∠C=180°,
∵∠3=∠4,
∴∠4+∠C=180°,
∴DF∥AC,
∴∠F=∠A=40°,
答:∠F的值为40°.
23.【解答】解:(1)由题意得,ab4,
故答案为:4;
(2)由a2+b2=(a+b)2﹣2ab得,
(25﹣x)2+(x﹣10)2
=[(25﹣x)+(x﹣10)]2﹣2(25﹣x)(x﹣10)
=152﹣2×(﹣15)
=225+30
=255;
(3)设AC=a,BC=b,根据ab可得,
图中阴影部分的面积为:
=ab
=AC BC
=10,
故答案为:10.
24.【解答】(1)解:∵∠BAN=45°,且PQ∥MN,
∴∠PBA=180°﹣∠BAN=135°,
故答案为:135°;
(2)解:①不存在t,使得AC∥BD,理由如下:
由题意可得∠MAC=3t,∠PBD=t,
∵∠PBA=135°,
∴∠DBA=135°﹣t,
∵BAN=45°,
∴∠BAC=180°﹣∠MAC﹣∠BAN=135°﹣3t,
∵要使AC∥BD,
∴∠BAC=∠ABD,即 35°﹣3t=135°﹣t,
解得t=0,
∵0<t<45,
∴不存在t,使得AC∥BD;
②过点G作GH∥PQ,
∵∠MAC=3t,∠MAC+∠GAN=180°,
∴∠GAN=180°﹣3t,
∵PQ∥MN,GH∥PQ,
∴PQ∥MN∥GH,
∴∠HGB=∠PBD=t,∠HGA=∠NAC=180°﹣3t,
∴∠AGB=∠AGH+∠BGH=180°﹣3t+t=180°﹣2t;
③,保持不变,理由如下:
∵GH⊥AG,
∴∠AGH=90°,
∴∠BGH=90°﹣∠AGB=90°﹣(180°﹣2t)=2t﹣90°,
∵∠BAG=3t﹣135°,
∴.
25.(1)解:设,则原方程组变形得,
解得,,
∴,
解得,;
(2)解:关于,的方程组的解为,
∴,
∴,
解得,;
(3)解:∵,,
∴,
∴,
解得,.
21世纪教育网(www.21cnjy.com)
同课章节目录
