浙教版2024—2025学年七年级下学期数学期末总复习强化训练(含答案)
文档属性
| 名称 | 浙教版2024—2025学年七年级下学期数学期末总复习强化训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 284.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年七年级下学期数学期末总复习强化训练
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.若分式的值为0,则x的值是( )
A.2 B.﹣2 C.0 D.±2
2.大国工匠年度人物胡胜实现了0.000004米精度的数控雕刻,完美诠释了新时代工匠精神.将数0.000004用科学记数法表示为( )
A.4×10﹣5 B.﹣4×106 C.4×10﹣6 D.0.4×10﹣5
3.下列各式不能使用平方差公式的是( )
A.(2a+3b)(2a﹣3b) B.(﹣2a+3b)(3b﹣2a)
C.(﹣2a+3b)(﹣2a﹣3b) D.(2a﹣3b)(﹣2a﹣3b)
4.已知方程组,则x+y+z的值是( )
A.3 B.4 C.5 D.6
5.《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸:屈绳量之,不足一尺,木长几何?”意思是:“用一根绳子去量一根木条的长,绳子还剩余4.5尺:将绳子对折再量木条,则木条还剩余1尺,问木条长多少尺?”现设木条长尺,绳子长y尺,则可列方程组为( )
A. B.
C. D.
6.计算的结果是( )
A. B. C. D.
7.若,则的值为( )
A. B. C. D.
8.若,是正整数,且满足,则下列与的关系正确的是( )
A. B. C. D.
9.已知:m2﹣m﹣2025=0,则的值为( )
A. B. C.2025 D.﹣2025
10.已知一列均不为1的数a1,a2,a3,…,an满足如下关系:a2,a3,a4,…,an+1,若a1=2,则a2025的值是( )
A. B. C.﹣3 D.2
二、填空题(每小题3分,满分18分)
11.已知多项式x2+ax+81是一个完全平方式,则实数a的值是 .
12.已知关于x,y的二元一次方程组的解为,则关于m,n的二元一次方程组的解为 .
13.如果单项式3xa+3y2b+10与﹣6x1﹣by4﹣a能合并成一个单项式,那么a= ,b= .
14.若关于x,y的二元一次方程组的解互为相反数,则常数k= .
15.购买铅笔7支,作业本6个,中性笔4支共需33元;购买铅笔5支,作业本5个,中性笔3支共需26元;则购买铅笔2支,作业本1个,中性笔1支共需 元.
16.如图1,∠DEF=24°,将长方形纸片ABCD沿直线EF折叠成图2,再沿直线GF折叠成图3,则图3中∠CFE= .
浙教版2024—2025学年七年级下学期数学期末总复习强化训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简:,再从﹣2,﹣1,0,1,2中选择一个合适的数代入求值.
18.解下列方程组:
(1); (2).
19.先化简,再求值:[(x﹣3y)(x+3y)﹣(x﹣y)2+2y(x﹣y)]÷4y,其中x=﹣2,y.
20.某水果销售商前往水果批发市场进货,已知苹果的批发价格为每箱40元,橙子的批发价格为每箱50元.他花了3500元购进苹果和橙子共80箱.
(1)问苹果、橙子各购买了多少箱?
(2)该水果销售商有甲、乙两家店铺,因地段不同,每售出一箱苹果和橙子的获利也不同,甲店分别可获利12元和18元,乙店分别可获利10元和15元.现将购进的80箱水果中的a箱苹果和b箱橙子分配到甲店,其余的分配到乙店.由于口碑良好,两家店都很快卖完这批水果.若此次销售过程中销售商在甲店获利600元,那么在乙店获利多少元?
21.如图,AB∥CD∥EF,点O在CD上,AO平分∠BAC,EO平分∠CEF.
(1)若CD平分∠ACE,求证:∠BAO=∠FEO;
(2)若AC⊥CE,求∠AOE的度数.
22.已知,关于x的分式方程1.
(1)当a=2,b=1时,求分式方程的解;
(2)当a=1时,求b为何值时分式方程1无解;
(3)若a=3b,且a、b为正整数,当分式方程1的解为整数时,求b的值.
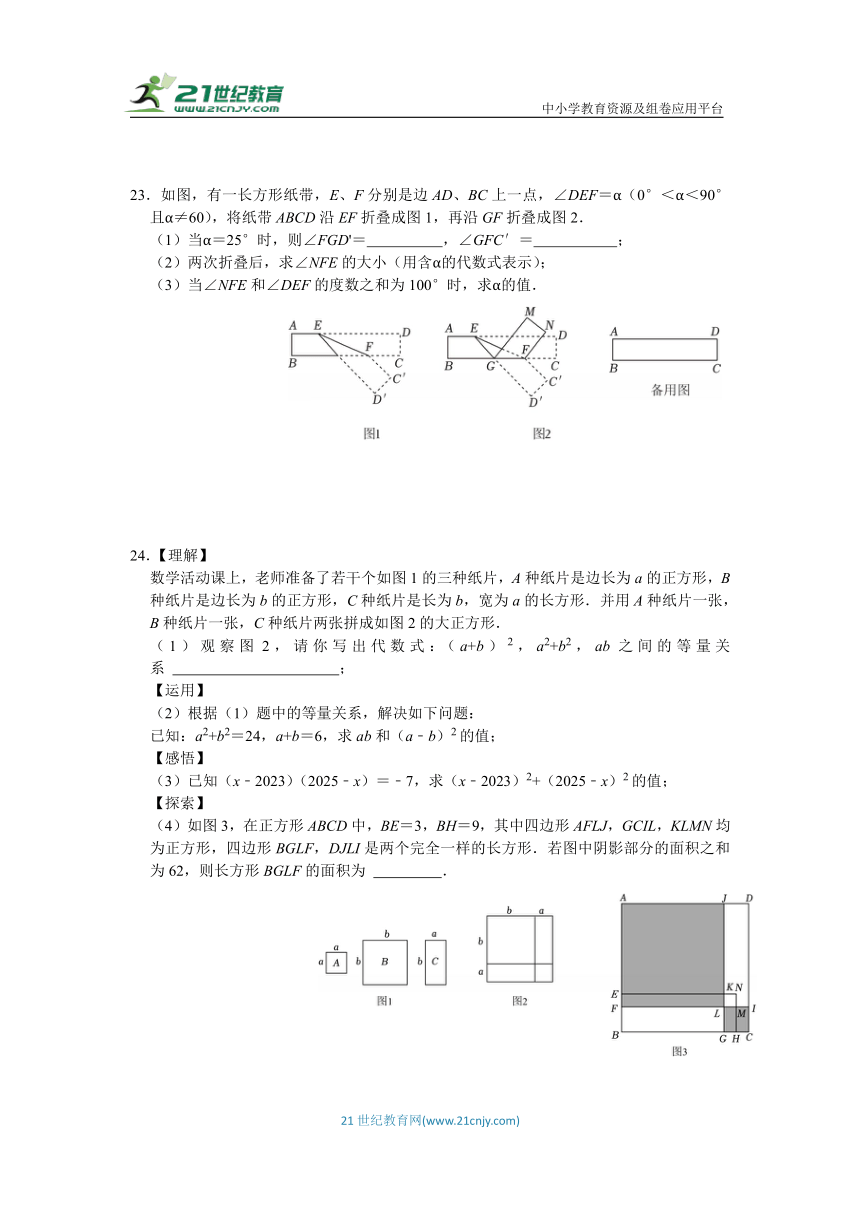
23.如图,有一长方形纸带,E、F分别是边AD、BC上一点,∠DEF=α(0°<α<90°且α≠60),将纸带ABCD沿EF折叠成图1,再沿GF折叠成图2.
(1)当α=25°时,则∠FGD'= ,∠GFC′= ;
(2)两次折叠后,求∠NFE的大小(用含α的代数式表示);
(3)当∠NFE和∠DEF的度数之和为100°时,求α的值.
24.【理解】
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)观察图2,请你写出代数式:(a+b)2,a2+b2,ab之间的等量关系 ;
【运用】
(2)根据(1)题中的等量关系,解决如下问题:
已知:a2+b2=24,a+b=6,求ab和(a﹣b)2的值;
【感悟】
(3)已知(x﹣2023)(2025﹣x)=﹣7,求(x﹣2023)2+(2025﹣x)2的值;
【探索】
(4)如图3,在正方形ABCD中,BE=3,BH=9,其中四边形AFLJ,GCIL,KLMN均为正方形,四边形BGLF,DJLI是两个完全一样的长方形.若图中阴影部分的面积之和为62,则长方形BGLF的面积为 .
25.如图1,已知AB∥CD,连结AD和BC交于点E.
(1)求证:∠BAD+∠BCD=∠AEC;
(2)如图2,∠AEC=60°,点F,G分别在线段BE,ED上,∠EAF=2∠BAF=2x,∠DCG=2∠ECG=2y.
①请直接写出∠AFE和∠EGC(用含x,y的代数式表示);
②请判断∠AFE+2∠EGC是否为定值,若是,请求出该定值;若不是,请说明理由.
参考答案
一、选择题
1—10:BCBAA BCBDD
二、填空题
11.【解答】解:∵多项式x2+ax+81是一个完全平方式,
∴a=±2×1×9=±18,
故答案为:±18.
12.【解答】解:∵关于x、y的二元一次方程组的解为,
∴关于m、n的二元一次方程组得到,,
∴,
∴解这个关于m、n的方程组得:.
故答案为:.
13.【解答】解:∵单项式3xa+3y2b+10与﹣6x1﹣by4﹣a是同类项,
∴,
解得.
故答案是:2,﹣4.
14.【解答】解:∵关于x,y的二元一次方程组的解互为相反数,
∴x=﹣y,
代入x﹣y=3,得:﹣y﹣y=3,
解得:,
∴,
将:,代入2x+y=3k,得:,
解得:;
故答案为:.
15.【解答】解:设铅笔的单价是x元,作业本的单价是y元,中性笔的单价是z元.购买铅笔2支,作业本1本,中性笔1支共需a元.
则由题意得:
,
由①﹣②得2x+y+z=7,
于是:a=7,
故答案为:7.
16.【解答】解:∵四边形ABCD为长方形,
∴AD∥BC,
∴∠BFE=∠DEF=24°.
由翻折的性质可知:
图2中,∠EFC=180°﹣∠BFE=156°,∠BFC=∠EFC﹣∠BFE=132°,
图3中,∠CFE=∠BFC﹣∠BFE=108°.
故答案为:108°.
三、解答题
17.【解答】解:原式
,
当x=2时,
原式.
18.【解答】解:(1),
将②式代入①式得:
x+x﹣3=5,
2x=8,
x=4,
∴y=x﹣3=4﹣3=1,
∴该方程组的解为:;
(2),
①+2×②得:
,
x+2y+x+1﹣2y=5,
2x=4,
x=2,
将x=2代入①得:2+2y=9,
解得:,
∴该方程组的解为:.
19.【解答】解:原式=[x2﹣9y2﹣(x2﹣2xy+y2)+2xy﹣2y2]÷4y
=(x2﹣9y2﹣x2+2xy﹣y2+2xy﹣2y2)÷4y
=(4xy﹣12y2)÷4y
=x﹣3y;
当时,原式.
20.【解答】解:(1)设苹果购买了x箱,橙子购买了y箱,
根据题意得,,
解得,,
答:苹果、橙子各购买了50箱、30箱.
(2)由题意可得销售商在甲店获利为:12a+18b=600(元),
整理得,2a+3b=100,
销售商在乙店获利为:10(50﹣a)+15(30﹣b)
=950﹣10a﹣15b
=950﹣5(2a+3b)
=950﹣5×100
=450(元),
即在乙店获利450元.
答:在乙店获利450元.
21.【解答】(1)证明:∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵CD∥EF,
∴∠DCE+∠CEF=180°,
∵CD平分∠ACE,
∴∠ACD=∠DCE,
∴∠BAC=∠CEF,
∵AO平分∠BAC,EO平分∠CEF,
∴∠BAO=∠BAC,∠FEO=∠CEF,
∴∠BAO=∠FEO;
(2)解:∵AC⊥CE,
∴∠ACE=90°,
∴∠ACD+∠DCE=90°,
由(1)可得:∠BAC+∠ACD=180°,∠DCE+∠CEF=180°,
∴∠BAC+∠CEF=360°﹣(∠ACD+∠DCE)=270°,
∵∠BAO=∠BAC,∠FEO=∠CEF,
∴∠BAO+∠FEO=∠BAC+∠CEF=135°,
∵AB∥CD,
∴∠BAO=∠AOC,
∵CD∥EF,
∴∠COE=∠FEO,
∴∠AOE=∠AOC+∠COE
=∠BAO+∠FEO
=135°,
∴∠AOE的度数为135°.
22.【解答】解:(1)把a=2,b=1代入分式方程 中,得,
方程两边同时乘以(2x+3)(x﹣5),
2(x﹣5)﹣(1﹣x)(2x+3)=(2x+3)(x﹣5),
2x2+3x﹣13=2x2﹣7x﹣15,
10x=﹣2,
x,
检验:把x 代入(2x+3)(x﹣5)≠0,所以原分式方程的解是x.
答:分式方程的解是x.
(2)把a=1代入分式方程 得,
方程两边同时乘以(2x+3)(x﹣5),
(x﹣5)﹣(b﹣x)(2x+3)=(2x+3)(x﹣5),
x﹣5+2x2+3x﹣2bx﹣3b=2x2﹣7x﹣15,
(11﹣2b)x=3b﹣10,
①当11﹣2b=0时,即,方程无解;
②当11﹣2b≠0时,,
时,分式方程无解,即,b不存在;
x=5时,分式方程无解,即,b=5.
综上所述,或b=5时,分式方程 无解.
(3)把a=3b代入分式方程 中,得:
方程两边同时乘以(2x+3)(x﹣5),
3b(x﹣5)+(x﹣b)(2x+3)=(2x+3)(x﹣5),
整理得:(10+b)x=18b﹣15,
∴,
∵,且b为正整数,x为整数,
∴10+b必为195的因数,10+b≥11,
∵195=3×5×13,
∴195的因数有1、3、5、13、15、39、65、195,
但1、3、5 小于11,不合题意,故10+b可以取13、15、39、65、195这五个数.
对应地,方程的解x为3、5、13、15、17,
由于x=5为分式方程的增根,故应舍去.
对应地,b只可以取3、29、55、185,
所以满足条件的b可取3、29、55、185这四个数.
23.【解答】解:(1)如图2,由折叠可得,∠DEF=∠GEF=α,
∴∠DEG=2α,
∵AD∥BC,
∴∠FGD'=∠DEG=2α,
当α=25°时,则∠FGD'=50°;
又∵FC'∥GD,
∴∠GFC'=180°﹣50°=130°;
故答案为:50°;130°;
(2)分两种情况:
当α<60°时,如图2,由折叠可得,∠DEF=∠GEF=α,
∴∠DEG=2α,
∵AD∥BC,
∴∠FGD'=∠DEG=2α,∠EFG=∠DEF=α,
又∵FC'∥GD,
∴∠GFC'=180°﹣∠FGD'=180°﹣2α,
∴∠GFN=180°﹣2α,
∴∠NFE=∠GFN﹣∠EFG=180°﹣2α﹣α=180°﹣3α;
当60°<α<90°时,如图所示,同理可得,∠GFN=180°﹣2α,∠EFG=α,
∴∠NFE=∠EFG﹣∠GFN=α﹣(180°﹣2α)=3α﹣180°;
综上所述,∠NFE的度数为180°﹣3α或3α﹣180°;
(3)当∠NFE和∠DEF的度数之和为100°时,180°﹣3α+α=100°或3α﹣180°+α=100°,
解得α=40°或α=70°,
即α的值为40°或70°.
24.【解答】解:(1)由题意得:(a+b)2=a2+b2+2ab,
故答案为:(a+b)2=a2+b2+2ab;
(2)∵a2+b2=24,a+b=6,
∴2ab=(a+b)2﹣(a2+b2)
=62﹣24
=36﹣24
=12,
∴ab=6,
∴(a﹣b)2=a2﹣2ab+b2=24﹣12=12;
(3)设x﹣2023=a,2025﹣x=b,
∴a+b=x﹣2023+2025﹣x=2,
∵(x﹣2023)(2025﹣x)=﹣7,
∴ab=﹣7,
∴(x﹣2023)2+(2025﹣x)2=a2+b2
=(a+b)2﹣2ab
=22﹣2×(﹣7)
=4+14
=18;
(4)设正方形KLMN的边长为x,
∵BE=3,BH=9,
∴BG=FL=9﹣x,BF=LG=3﹣x,
设9﹣x=a,3﹣x=b,
∴a﹣b=9﹣x﹣(3﹣x)=6,
∵阴影部分的面积之和为62,
∴FL2+LG2=62,
∴(9﹣x)2+(3﹣x)2=62,
∴a2+b2=62,
∴2ab=a2+b2﹣(a﹣b)2
=62﹣62
=62﹣36
=26,
∴ab=13,
∴长方形BGLF的面积=BG LG=ab=13,
故答案为:13.
25.【解答】(1)证明:∵AB∥CD,
∴∠ABC=∠BCD,
∵∠BAD+∠ABC=∠AEC,
∴∠BAD+∠BCD=∠AEC.
(2)解:①∵∠EAF+∠AFE=∠AEC,∠EAF=2∠BAF=2x,∠AEC=60°,
∴2x+∠AFE=60°,
即∠AFE=60°﹣2x,
∵∠DCG=2∠ECG=2y,
∴∠ECG=y,
又∵∠EGC+∠ECG=∠AEC,∠AEC=60°,
∴y+∠EGC=60°,
即∠AFE=60°﹣y,
故∠AFE=60°﹣2x,∠EGC=60°﹣y;
②∠AFE+2∠EGC是定值.
∵AB∥CD,
∴∠ABC=∠DCB,
∵∠DCG=2∠ECG=2y,
∴∠DCB=∠DCG+∠ECG=3y,
∴∠ABC=3y,
∵∠EAF=2∠BAF=2x,
∴∠BAF=x,
∵∠BAF+∠ABC=∠AFC,∠AFE=60°﹣2x,
∴3y+x=60°﹣2x,
化简得x+y=20°,
∵∠AFE=60°﹣2x,∠EGC=60°﹣y,
∴∠AFE+2∠EGC=60°﹣2x+2(60°﹣y)=180°﹣2(x+y),
∵x+y=20°,
∴∠AFE+2∠EGC=180°﹣2×20°=140°,
∴∠AFE+2∠EGC是定值140°.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年七年级下学期数学期末总复习强化训练
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.若分式的值为0,则x的值是( )
A.2 B.﹣2 C.0 D.±2
2.大国工匠年度人物胡胜实现了0.000004米精度的数控雕刻,完美诠释了新时代工匠精神.将数0.000004用科学记数法表示为( )
A.4×10﹣5 B.﹣4×106 C.4×10﹣6 D.0.4×10﹣5
3.下列各式不能使用平方差公式的是( )
A.(2a+3b)(2a﹣3b) B.(﹣2a+3b)(3b﹣2a)
C.(﹣2a+3b)(﹣2a﹣3b) D.(2a﹣3b)(﹣2a﹣3b)
4.已知方程组,则x+y+z的值是( )
A.3 B.4 C.5 D.6
5.《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸:屈绳量之,不足一尺,木长几何?”意思是:“用一根绳子去量一根木条的长,绳子还剩余4.5尺:将绳子对折再量木条,则木条还剩余1尺,问木条长多少尺?”现设木条长尺,绳子长y尺,则可列方程组为( )
A. B.
C. D.
6.计算的结果是( )
A. B. C. D.
7.若,则的值为( )
A. B. C. D.
8.若,是正整数,且满足,则下列与的关系正确的是( )
A. B. C. D.
9.已知:m2﹣m﹣2025=0,则的值为( )
A. B. C.2025 D.﹣2025
10.已知一列均不为1的数a1,a2,a3,…,an满足如下关系:a2,a3,a4,…,an+1,若a1=2,则a2025的值是( )
A. B. C.﹣3 D.2
二、填空题(每小题3分,满分18分)
11.已知多项式x2+ax+81是一个完全平方式,则实数a的值是 .
12.已知关于x,y的二元一次方程组的解为,则关于m,n的二元一次方程组的解为 .
13.如果单项式3xa+3y2b+10与﹣6x1﹣by4﹣a能合并成一个单项式,那么a= ,b= .
14.若关于x,y的二元一次方程组的解互为相反数,则常数k= .
15.购买铅笔7支,作业本6个,中性笔4支共需33元;购买铅笔5支,作业本5个,中性笔3支共需26元;则购买铅笔2支,作业本1个,中性笔1支共需 元.
16.如图1,∠DEF=24°,将长方形纸片ABCD沿直线EF折叠成图2,再沿直线GF折叠成图3,则图3中∠CFE= .
浙教版2024—2025学年七年级下学期数学期末总复习强化训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简:,再从﹣2,﹣1,0,1,2中选择一个合适的数代入求值.
18.解下列方程组:
(1); (2).
19.先化简,再求值:[(x﹣3y)(x+3y)﹣(x﹣y)2+2y(x﹣y)]÷4y,其中x=﹣2,y.
20.某水果销售商前往水果批发市场进货,已知苹果的批发价格为每箱40元,橙子的批发价格为每箱50元.他花了3500元购进苹果和橙子共80箱.
(1)问苹果、橙子各购买了多少箱?
(2)该水果销售商有甲、乙两家店铺,因地段不同,每售出一箱苹果和橙子的获利也不同,甲店分别可获利12元和18元,乙店分别可获利10元和15元.现将购进的80箱水果中的a箱苹果和b箱橙子分配到甲店,其余的分配到乙店.由于口碑良好,两家店都很快卖完这批水果.若此次销售过程中销售商在甲店获利600元,那么在乙店获利多少元?
21.如图,AB∥CD∥EF,点O在CD上,AO平分∠BAC,EO平分∠CEF.
(1)若CD平分∠ACE,求证:∠BAO=∠FEO;
(2)若AC⊥CE,求∠AOE的度数.
22.已知,关于x的分式方程1.
(1)当a=2,b=1时,求分式方程的解;
(2)当a=1时,求b为何值时分式方程1无解;
(3)若a=3b,且a、b为正整数,当分式方程1的解为整数时,求b的值.
23.如图,有一长方形纸带,E、F分别是边AD、BC上一点,∠DEF=α(0°<α<90°且α≠60),将纸带ABCD沿EF折叠成图1,再沿GF折叠成图2.
(1)当α=25°时,则∠FGD'= ,∠GFC′= ;
(2)两次折叠后,求∠NFE的大小(用含α的代数式表示);
(3)当∠NFE和∠DEF的度数之和为100°时,求α的值.
24.【理解】
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)观察图2,请你写出代数式:(a+b)2,a2+b2,ab之间的等量关系 ;
【运用】
(2)根据(1)题中的等量关系,解决如下问题:
已知:a2+b2=24,a+b=6,求ab和(a﹣b)2的值;
【感悟】
(3)已知(x﹣2023)(2025﹣x)=﹣7,求(x﹣2023)2+(2025﹣x)2的值;
【探索】
(4)如图3,在正方形ABCD中,BE=3,BH=9,其中四边形AFLJ,GCIL,KLMN均为正方形,四边形BGLF,DJLI是两个完全一样的长方形.若图中阴影部分的面积之和为62,则长方形BGLF的面积为 .
25.如图1,已知AB∥CD,连结AD和BC交于点E.
(1)求证:∠BAD+∠BCD=∠AEC;
(2)如图2,∠AEC=60°,点F,G分别在线段BE,ED上,∠EAF=2∠BAF=2x,∠DCG=2∠ECG=2y.
①请直接写出∠AFE和∠EGC(用含x,y的代数式表示);
②请判断∠AFE+2∠EGC是否为定值,若是,请求出该定值;若不是,请说明理由.
参考答案
一、选择题
1—10:BCBAA BCBDD
二、填空题
11.【解答】解:∵多项式x2+ax+81是一个完全平方式,
∴a=±2×1×9=±18,
故答案为:±18.
12.【解答】解:∵关于x、y的二元一次方程组的解为,
∴关于m、n的二元一次方程组得到,,
∴,
∴解这个关于m、n的方程组得:.
故答案为:.
13.【解答】解:∵单项式3xa+3y2b+10与﹣6x1﹣by4﹣a是同类项,
∴,
解得.
故答案是:2,﹣4.
14.【解答】解:∵关于x,y的二元一次方程组的解互为相反数,
∴x=﹣y,
代入x﹣y=3,得:﹣y﹣y=3,
解得:,
∴,
将:,代入2x+y=3k,得:,
解得:;
故答案为:.
15.【解答】解:设铅笔的单价是x元,作业本的单价是y元,中性笔的单价是z元.购买铅笔2支,作业本1本,中性笔1支共需a元.
则由题意得:
,
由①﹣②得2x+y+z=7,
于是:a=7,
故答案为:7.
16.【解答】解:∵四边形ABCD为长方形,
∴AD∥BC,
∴∠BFE=∠DEF=24°.
由翻折的性质可知:
图2中,∠EFC=180°﹣∠BFE=156°,∠BFC=∠EFC﹣∠BFE=132°,
图3中,∠CFE=∠BFC﹣∠BFE=108°.
故答案为:108°.
三、解答题
17.【解答】解:原式
,
当x=2时,
原式.
18.【解答】解:(1),
将②式代入①式得:
x+x﹣3=5,
2x=8,
x=4,
∴y=x﹣3=4﹣3=1,
∴该方程组的解为:;
(2),
①+2×②得:
,
x+2y+x+1﹣2y=5,
2x=4,
x=2,
将x=2代入①得:2+2y=9,
解得:,
∴该方程组的解为:.
19.【解答】解:原式=[x2﹣9y2﹣(x2﹣2xy+y2)+2xy﹣2y2]÷4y
=(x2﹣9y2﹣x2+2xy﹣y2+2xy﹣2y2)÷4y
=(4xy﹣12y2)÷4y
=x﹣3y;
当时,原式.
20.【解答】解:(1)设苹果购买了x箱,橙子购买了y箱,
根据题意得,,
解得,,
答:苹果、橙子各购买了50箱、30箱.
(2)由题意可得销售商在甲店获利为:12a+18b=600(元),
整理得,2a+3b=100,
销售商在乙店获利为:10(50﹣a)+15(30﹣b)
=950﹣10a﹣15b
=950﹣5(2a+3b)
=950﹣5×100
=450(元),
即在乙店获利450元.
答:在乙店获利450元.
21.【解答】(1)证明:∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵CD∥EF,
∴∠DCE+∠CEF=180°,
∵CD平分∠ACE,
∴∠ACD=∠DCE,
∴∠BAC=∠CEF,
∵AO平分∠BAC,EO平分∠CEF,
∴∠BAO=∠BAC,∠FEO=∠CEF,
∴∠BAO=∠FEO;
(2)解:∵AC⊥CE,
∴∠ACE=90°,
∴∠ACD+∠DCE=90°,
由(1)可得:∠BAC+∠ACD=180°,∠DCE+∠CEF=180°,
∴∠BAC+∠CEF=360°﹣(∠ACD+∠DCE)=270°,
∵∠BAO=∠BAC,∠FEO=∠CEF,
∴∠BAO+∠FEO=∠BAC+∠CEF=135°,
∵AB∥CD,
∴∠BAO=∠AOC,
∵CD∥EF,
∴∠COE=∠FEO,
∴∠AOE=∠AOC+∠COE
=∠BAO+∠FEO
=135°,
∴∠AOE的度数为135°.
22.【解答】解:(1)把a=2,b=1代入分式方程 中,得,
方程两边同时乘以(2x+3)(x﹣5),
2(x﹣5)﹣(1﹣x)(2x+3)=(2x+3)(x﹣5),
2x2+3x﹣13=2x2﹣7x﹣15,
10x=﹣2,
x,
检验:把x 代入(2x+3)(x﹣5)≠0,所以原分式方程的解是x.
答:分式方程的解是x.
(2)把a=1代入分式方程 得,
方程两边同时乘以(2x+3)(x﹣5),
(x﹣5)﹣(b﹣x)(2x+3)=(2x+3)(x﹣5),
x﹣5+2x2+3x﹣2bx﹣3b=2x2﹣7x﹣15,
(11﹣2b)x=3b﹣10,
①当11﹣2b=0时,即,方程无解;
②当11﹣2b≠0时,,
时,分式方程无解,即,b不存在;
x=5时,分式方程无解,即,b=5.
综上所述,或b=5时,分式方程 无解.
(3)把a=3b代入分式方程 中,得:
方程两边同时乘以(2x+3)(x﹣5),
3b(x﹣5)+(x﹣b)(2x+3)=(2x+3)(x﹣5),
整理得:(10+b)x=18b﹣15,
∴,
∵,且b为正整数,x为整数,
∴10+b必为195的因数,10+b≥11,
∵195=3×5×13,
∴195的因数有1、3、5、13、15、39、65、195,
但1、3、5 小于11,不合题意,故10+b可以取13、15、39、65、195这五个数.
对应地,方程的解x为3、5、13、15、17,
由于x=5为分式方程的增根,故应舍去.
对应地,b只可以取3、29、55、185,
所以满足条件的b可取3、29、55、185这四个数.
23.【解答】解:(1)如图2,由折叠可得,∠DEF=∠GEF=α,
∴∠DEG=2α,
∵AD∥BC,
∴∠FGD'=∠DEG=2α,
当α=25°时,则∠FGD'=50°;
又∵FC'∥GD,
∴∠GFC'=180°﹣50°=130°;
故答案为:50°;130°;
(2)分两种情况:
当α<60°时,如图2,由折叠可得,∠DEF=∠GEF=α,
∴∠DEG=2α,
∵AD∥BC,
∴∠FGD'=∠DEG=2α,∠EFG=∠DEF=α,
又∵FC'∥GD,
∴∠GFC'=180°﹣∠FGD'=180°﹣2α,
∴∠GFN=180°﹣2α,
∴∠NFE=∠GFN﹣∠EFG=180°﹣2α﹣α=180°﹣3α;
当60°<α<90°时,如图所示,同理可得,∠GFN=180°﹣2α,∠EFG=α,
∴∠NFE=∠EFG﹣∠GFN=α﹣(180°﹣2α)=3α﹣180°;
综上所述,∠NFE的度数为180°﹣3α或3α﹣180°;
(3)当∠NFE和∠DEF的度数之和为100°时,180°﹣3α+α=100°或3α﹣180°+α=100°,
解得α=40°或α=70°,
即α的值为40°或70°.
24.【解答】解:(1)由题意得:(a+b)2=a2+b2+2ab,
故答案为:(a+b)2=a2+b2+2ab;
(2)∵a2+b2=24,a+b=6,
∴2ab=(a+b)2﹣(a2+b2)
=62﹣24
=36﹣24
=12,
∴ab=6,
∴(a﹣b)2=a2﹣2ab+b2=24﹣12=12;
(3)设x﹣2023=a,2025﹣x=b,
∴a+b=x﹣2023+2025﹣x=2,
∵(x﹣2023)(2025﹣x)=﹣7,
∴ab=﹣7,
∴(x﹣2023)2+(2025﹣x)2=a2+b2
=(a+b)2﹣2ab
=22﹣2×(﹣7)
=4+14
=18;
(4)设正方形KLMN的边长为x,
∵BE=3,BH=9,
∴BG=FL=9﹣x,BF=LG=3﹣x,
设9﹣x=a,3﹣x=b,
∴a﹣b=9﹣x﹣(3﹣x)=6,
∵阴影部分的面积之和为62,
∴FL2+LG2=62,
∴(9﹣x)2+(3﹣x)2=62,
∴a2+b2=62,
∴2ab=a2+b2﹣(a﹣b)2
=62﹣62
=62﹣36
=26,
∴ab=13,
∴长方形BGLF的面积=BG LG=ab=13,
故答案为:13.
25.【解答】(1)证明:∵AB∥CD,
∴∠ABC=∠BCD,
∵∠BAD+∠ABC=∠AEC,
∴∠BAD+∠BCD=∠AEC.
(2)解:①∵∠EAF+∠AFE=∠AEC,∠EAF=2∠BAF=2x,∠AEC=60°,
∴2x+∠AFE=60°,
即∠AFE=60°﹣2x,
∵∠DCG=2∠ECG=2y,
∴∠ECG=y,
又∵∠EGC+∠ECG=∠AEC,∠AEC=60°,
∴y+∠EGC=60°,
即∠AFE=60°﹣y,
故∠AFE=60°﹣2x,∠EGC=60°﹣y;
②∠AFE+2∠EGC是定值.
∵AB∥CD,
∴∠ABC=∠DCB,
∵∠DCG=2∠ECG=2y,
∴∠DCB=∠DCG+∠ECG=3y,
∴∠ABC=3y,
∵∠EAF=2∠BAF=2x,
∴∠BAF=x,
∵∠BAF+∠ABC=∠AFC,∠AFE=60°﹣2x,
∴3y+x=60°﹣2x,
化简得x+y=20°,
∵∠AFE=60°﹣2x,∠EGC=60°﹣y,
∴∠AFE+2∠EGC=60°﹣2x+2(60°﹣y)=180°﹣2(x+y),
∵x+y=20°,
∴∠AFE+2∠EGC=180°﹣2×20°=140°,
∴∠AFE+2∠EGC是定值140°.
21世纪教育网(www.21cnjy.com)
同课章节目录
