浙教版2024—2025学年八年级下册数学期末考试重难点练习卷(含答案)
文档属性
| 名称 | 浙教版2024—2025学年八年级下册数学期末考试重难点练习卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 774.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 13:01:45 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年八年级下册数学期末考试重难点练习卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列四幅图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.下列说法正确的是( )
A.菱形的四个内角都是直角 B.矩形的对角线互相垂直
C.正方形的每一条对角线平分一组对角 D.平行四边形是轴对称图形
3.一元二次方程3x2﹣2x+1=0的根的情况为( )
A.有两个相等的实数根 B.有两个不相等的实根数
C.只有一个实数根 D.没有实数根
4.若关于x的方程(m+1)x2+x+m2﹣2m﹣3=0有一个根为0,则m的值是( )
A.﹣1 B.3 C.﹣1或3 D.1或﹣3
5.已知x1,x2,x3,x4,x5的方差为m,则2x1+1,2x2+1,2x3+1,2x4+1,2x5+1的方差是( )
A.2m+1 B.2m C.4m D.4m+1
6.用反证法证明命题结论“a<0”时,应先假设( )
A.a>0 B.a≥0 C.a=0 D.a≠0
7.一个多边形的内角和是外角和的2倍,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
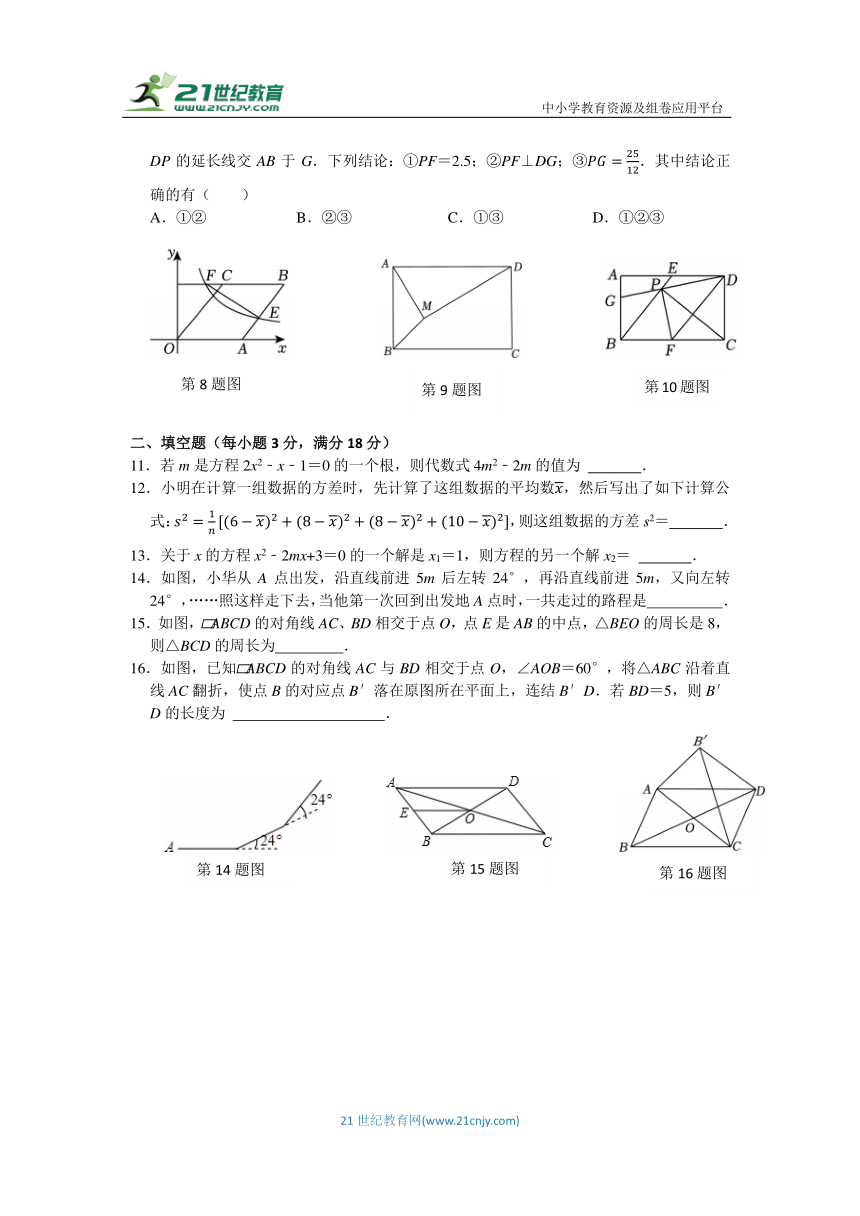
8.如图,在直角坐标系中,菱形OABC的顶点C(3,4),反比例函数图象交线段AB,射线BC于点E,F,连接EF,则S△BEF的值是( )
A.6 B.7 C.8 D.9
9.如图,在矩形ABCD中,M是矩形内一点,设△ABM,△ADM,△CDM,△BCM的面积分别表示S1,S2,S3,S4,要求出S3﹣S4的值,只需知道( )
A.S4﹣S1 B.S2﹣S1 C.S3+S2 D.S3﹣S2
10.如图,矩形ABCD中,AB=3,AD=5,E,F分别是边AD,BC的中点,CP⊥BE于P,DP的延长线交AB于G.下列结论:①PF=2.5;②PF⊥DG;③.其中结论正确的有( )
A.①② B.②③ C.①③ D.①②③
二、填空题(每小题3分,满分18分)
11.若m是方程2x2﹣x﹣1=0的一个根,则代数式4m2﹣2m的值为 .
12.小明在计算一组数据的方差时,先计算了这组数据的平均数,然后写出了如下计算公式:,则这组数据的方差s2= .
13.关于x的方程x2﹣2mx+3=0的一个解是x1=1,则方程的另一个解x2= .
14.如图,小华从A点出发,沿直线前进5m后左转24°,再沿直线前进5m,又向左转24°,……照这样走下去,当他第一次回到出发地A点时,一共走过的路程是 .
15.如图, ABCD的对角线AC、BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为 .
16.如图,已知 ABCD的对角线AC与BD相交于点O,∠AOB=60°,将△ABC沿着直线AC翻折,使点B的对应点B′落在原图所在平面上,连结B′D.若BD=5,则B′D的长度为 .
第II卷
浙教版2024—2025学年八年级下册数学期末考试重难点练习卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
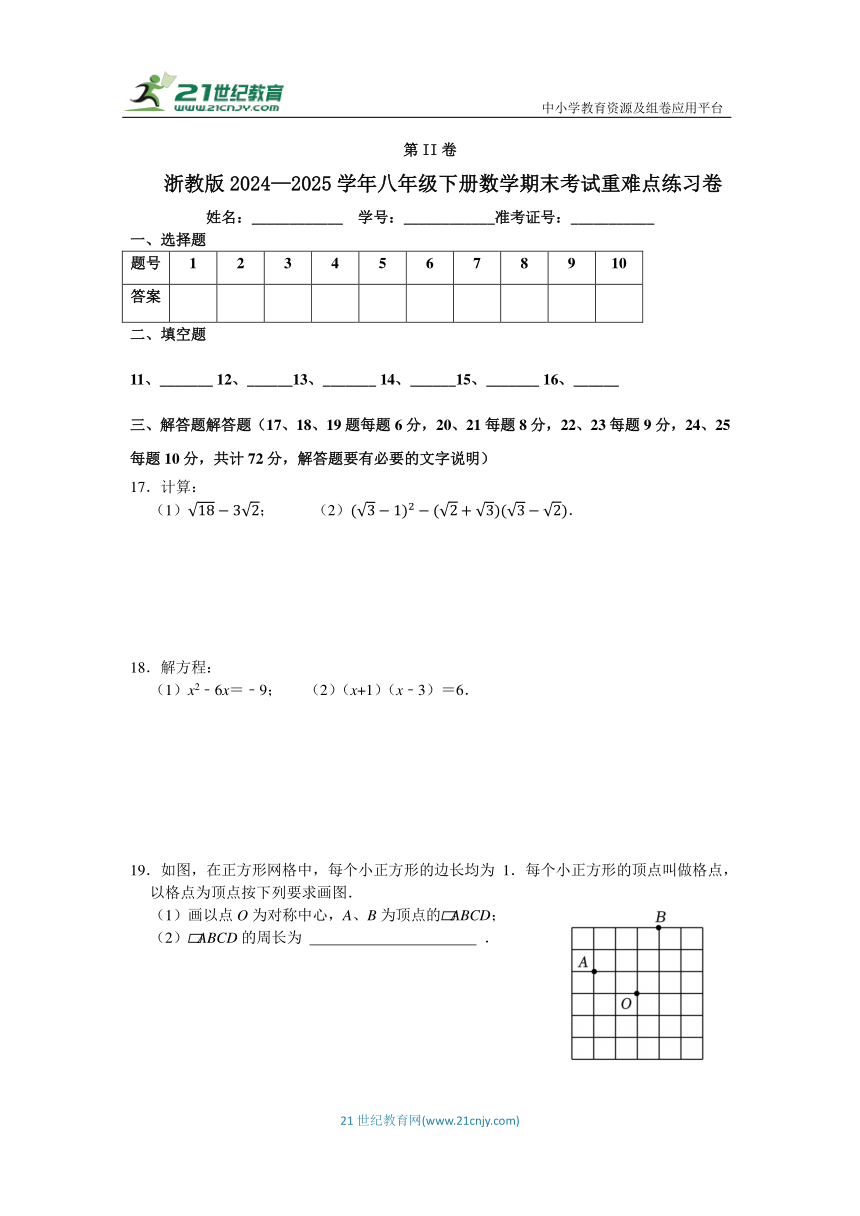
17.计算:
(1); (2).
18.解方程:
(1)x2﹣6x=﹣9; (2)(x+1)(x﹣3)=6.
19.如图,在正方形网格中,每个小正方形的边长均为1.每个小正方形的顶点叫做格点,以格点为顶点按下列要求画图.
(1)画以点O为对称中心,A、B为顶点的 ABCD;
(2) ABCD的周长为 .
20.今年6月26日是第37个国际禁毒日,某校八年级1,2班开展了一次禁毒知识竞赛,每班选25名同学参赛,成绩评为A,B,C,D四个等级,相应等级的得分依次为100分,90分,80分,70分,将两个班的成绩整理后,绘制成如所示统计图表:
平均数 中位数 众数
1班 a b 90
2班 87.6 80 c
(1)请把1班竞赛成绩统计图补充完整.
(2)计算出表格中a,b,c的值:a= ,b= ,c= .
(3)请你根据平均数和众数,分析比较1班和2班的竞赛成绩.
21.已知关于x的方程x2﹣(m+2)x+(2m﹣1)=0.
(1)求证:方程一定有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求出以此两根为边长的直角三角形的周长.
22.诸暨某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“五一”国际劳动节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售 件,每件盈利 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天盈利1200元.
(3)要想平均每天盈利2000元,可能吗?请说明理由.
23.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,BD=2AD,点E在线段OC上,且OE=CE.
(1)求证:∠ADO=2∠OBE;
(2)若F,G分别是OD,AB的中点,
①求证:△EFG是等腰三角形;
②当EF⊥EG时,BC=10时,求平行四边形ABCD的面积.
24.如图,已知A(﹣3,2),B(n,﹣3)是一次函数y=kx+b的图象与反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)在x轴上是否存在一点P,使△AOP是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
25.如图1,正方形ABCD中,C(﹣2,0),D(0,3).过A点作AF⊥y轴于F点,过B点作x轴的垂线交过A点的反比例函数的图象于E点,交x轴于G点.
(1)求证:△CDO≌△DAF;
(2)求反比例函数的表达式及点E的坐标;
(3)如图2,过点C作直线l∥AE,点P是直线l上的一点,在平面内是否存在点Q,使得点A、C、P、Q四个点依次连接构成的四边形是菱形,若存在,请直接写出点Q的横坐标,若不存在,请说明理由.
参考答案
一、选择题
1—10:BCDCC BDCBD
二、填空题
11.【解答】解:把x=m代入方程2x2﹣x﹣1=0,可得:2m2﹣m=1,
4m2﹣2m=2(2m2﹣m)=2×1=2.
故答案为:2.
12.【解答】解:∵计算公式:,
∴这组数据为6、8、8、10,
∴这组数据的平均数为:(6+8+8+10)=8.
∴S2[(6﹣8)2+(8﹣8)2+(8﹣8)2+(10﹣8)2]=2.
故答案为:2.
13.【解答】解:根据根与系数的关系得x1x2=3,
而x1=1,
所以x2=3.
故答案为:3.
14.【解答】解:由题意可知,当小华回到出发地A点时,行走的路线是正多边形,
∵多边形的外角和为360°,而每一个外角为24°,
∴多边形的边数为360°÷24°=15,
∴小华一共走的路程:15×5=75,
故答案为:75m.
15.【解答】解:∵ ABCD的对角线AC、BD相交于点O,
∴BO=DOBD,BD=2OB,
∴O为BD中点,
∵点E是AB的中点,
∴AB=2BE,BC=2OE,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴CD=2BE.
∵△BEO的周长为8,
∴OB+OE+BE=8,
∴BD+BC+CD=2OB+2OE+2BE=2(OB+OE+BE)=16,
∴△BCD的周长是16,
故答案为16.
16.【解答】解:∵四边形ABCD是平行四边形,BD=5,
∴.
如图,连接OB′.
根据折叠的性质知:∠AOB=∠AOB′=60°,BO=B′O,
∴∠BOB′=∠AOB+∠AOB′=120°,
∴∠B′OD=180°﹣∠BOB′=60°,
∵BO=B′O,DO=BO,
∴B′O=OD,
∴△B′OD是等边三角形,
∴,
故答案为:.
三、解答题
17.【解答】解:(1)原式
=0;
(2)
.
18.【解答】解:(1)x2﹣6x=﹣9,
x2﹣6x+9=0,
(x﹣3)2=0,
∴x1=x2=3;
(2)(x+1)(x﹣3)=6,
x2+x﹣3x﹣3=6,
x2﹣2x﹣3=6,
∴x2﹣2x=9,
∴(x﹣1)2=9+1,
∴x﹣1,
∴x1=1,x2=1.
19.【解答】(1)如图, ABCD即为所求.
(2)由勾股定理得,AB=CD,BC=AD,
∴ ABCD的周长为AB+CD+BC+AD.
故答案为:.
20.【解答】解:(1)∵每班选25名同学参加比赛,
∴(1)班C等级的人数是:25﹣6﹣12﹣5=2(人),
补充统计图如图:
(2)a=(6×100+12×90+2×80+5×70)=87.6,
∵(1)班有6人100分,12人90分,2人80分,5人70分,
∴按照从小到大的顺序将成绩排列,正中间的成绩为90分,
∴b=90,
∵由扇形统计图可知:(2)班等级为A的占44%,为最多,
∴(2)班成绩为100分的人数最多,
∴c=100,
(3)②∵(1)班和(2)班的平均成绩均为87.6分,而(1)班的众数是90分,(2)班的众数是100分,
∴从平均数和众数方面进行比较,(2)班成绩更好.
21.【解答】(1)证明:
∵方程x2﹣(m+2)x+(2m﹣1)=0,
∴Δ=(m+2)2﹣4(2m﹣1)=m2+4m+4﹣8m+4=m2﹣4m+4+4=(m﹣2)2+4>0,
∴方程一定有两个不相等的实数根;
(2)解:把x=1代入方程可得1﹣(m+2)+2m﹣1=0,解得m=2,
∴方程为x2﹣4x+3=0,解得x=1或x=3,
∴方程的另一根为x=3,
当边长为1和3的线段为直角三角形的直角边时,则斜边,此时直角三角形的周长=4,
当边长为3的直角三角形斜边时,则另一直角边2,此时直角三角形的周长=4+2,
综上可知直角三角形的周长为4或4+2.
22.【解答】解:(1)设每件童装降价x元时,每天可销售(20+2x)件,每件盈利(40﹣x)元,
故答案为:(20+2x),(40﹣x);
(2)根据题意,得:(20+2x)(40﹣x)=1200,
解得:x1=20,x2=10,
∵要扩大销售量,
∴x=20,
答:每件童装降价20元,平均每天盈利1200元;
(3)不能,理由如下:
(20+2x)(40﹣x)=2000,
整理,得:x2﹣30x+600=0,
∵Δ=(﹣30)2﹣4×600=﹣1500<0,
∴此方程无实数根,
故不可能做到平均每天盈利2000元.
23.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,BD=2DO=2BO,
∴∠ADO=∠CBO,
∵BD=2AD,
∴AD=BO=BC,
∴△BOC是等腰三角形,
∵OE=CE,
∴∠OBE=∠CBE∠ADO,
∴∠ADO=2∠OBE.
(2)①证明:∵△BOC是等腰三角形,E是CO中点,
∴EB⊥CO,
∴∠BEA=90°,
∵G为AB中点,
∴EGAB,
∵E、F分别是OC、OD的中点,
∴EFCD,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴EG=EF,
∴△EFG是等腰三角形.
②解:由题意知,EF∥CD∥BG,
∴EFAB=BG,
∴四边形BEFG是平行四边形,
∴∠EFG=∠GBE,
∵∠FEG=∠AEB=90°,
∴△ABE是等腰三角形,
∴∠BAE=∠ABE=45°,
∴EG⊥AB,
设AG=GE=x,则BE=AEx,CE,
在Rt△BCE中,由勾股定理得,BC2=BE2+CE2,即,
解得x=3或x=﹣3(不合题意,舍去),
∴BE=3,AC=4CE=4,
∴S平行四边形ABCD=2120,
∴平行四边形ABCD的面积为120.
24.【解答】解:(1)将A(﹣3,2)代入得:m=﹣6,
∴反比例函数的解析式是,
将B(n,﹣3)代入得:n=2,
∴B的坐标为B(2,﹣3),
将A(﹣3,2),B(2,﹣3)代入y=kx+b得:
,
∴,
∴一次函数的解析式为y=﹣x﹣1;
(2)根据图像,结合题意,得:﹣3<x<0或x>2;
(3)存在一点P,使△AOP是等腰三角形;P点坐标为(﹣6,0),(,0),(,0),(,0);理由如下:
如图2,
在x轴上存在点P,使△AOP 是等腰三角形由A(﹣3,2)可得:OA,
当△AOP是等腰三角形时,分三种情况讨论:
①当AO=AP时(图2中P1),作AS⊥x轴于点S,由A(﹣3,2),等腰三角形三线合一的性质得:OS=P1S=3,由AS=2,OS=3,
∴P1O=6,
故P1(﹣6,0);
②当AO=PO时(图2中P2),P点在O点左侧时,P2(,0);
P点在O点右侧时,P3(,0);
③当PA=PO时(AP'=P'O)时,即AP'2=P'O2,
∴22+(3﹣OP')2=OP'2,
∴OP',
∴P'(,0),
综上所述,存在一点P,使△AOP是等腰三角形;P点坐标为(﹣6,0),(,0),(,0),(,0).
25.【解答】(1)证明:如图1,∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ADF+∠CDO=90°,
∵AF⊥y轴,
∴∠AFD=∠DOC=90°,
∴∠CDO+∠DCO=90°,
∴∠ADF=∠DCO,
在△CDO和△DAF中,
,
∴△CDO≌△DAF(AAS);
(2)解:∵C(﹣2,0),D(0,3),
∴OC=2,OD=3,
∵△CDO≌△DAF,
∴DF=OC,AF=OD,
∴OG=OF=OD+DF=3+2=5,
∴A(﹣3,5),
设反比例函数的表达式为y(k≠0),把A(﹣3,5)代入,得k=﹣15,
∴y,
当x=﹣5时,y3,
∴点E的坐标为(﹣5,3);
(3)在平面内存在点Q,使得点A、C、P、Q四个点依次连接构成的四边形是菱形.理由如下:
设直线AE的解析式为y=k′x+b,把A(﹣3,5),E(﹣5,3)代入,
得,
解得:,
∴直线AE的解析式为y=x+8,
∵直线l∥AE,
∴设直线l的解析式为y=x+b′,把C(﹣2,0)代入得﹣2+b′=0,
解得:b′=2,
∴直线l的解析式为y=x+2,
∵点P是直线l上的一点,点Q是平面内一点,
∴设P(m,m+2),Q(t,s),
又A(﹣3,5),C(﹣2,0),
当AC、PQ为对角线时,
,
解得:,
∴Q(,);
当CP、AQ为对角线时,
,
解得:或(舍去),
∴Q(3,﹣1);
当AP、CQ为对角线时,
,
解得:或,
∴Q(﹣3,5)或(﹣3,5);
综上所述,在平面内存在点Q,使得点A、C、P、Q四个点依次连接构成的四边形是菱形,点Q的横坐标为或3或﹣3或﹣3.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年八年级下册数学期末考试重难点练习卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列四幅图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.下列说法正确的是( )
A.菱形的四个内角都是直角 B.矩形的对角线互相垂直
C.正方形的每一条对角线平分一组对角 D.平行四边形是轴对称图形
3.一元二次方程3x2﹣2x+1=0的根的情况为( )
A.有两个相等的实数根 B.有两个不相等的实根数
C.只有一个实数根 D.没有实数根
4.若关于x的方程(m+1)x2+x+m2﹣2m﹣3=0有一个根为0,则m的值是( )
A.﹣1 B.3 C.﹣1或3 D.1或﹣3
5.已知x1,x2,x3,x4,x5的方差为m,则2x1+1,2x2+1,2x3+1,2x4+1,2x5+1的方差是( )
A.2m+1 B.2m C.4m D.4m+1
6.用反证法证明命题结论“a<0”时,应先假设( )
A.a>0 B.a≥0 C.a=0 D.a≠0
7.一个多边形的内角和是外角和的2倍,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
8.如图,在直角坐标系中,菱形OABC的顶点C(3,4),反比例函数图象交线段AB,射线BC于点E,F,连接EF,则S△BEF的值是( )
A.6 B.7 C.8 D.9
9.如图,在矩形ABCD中,M是矩形内一点,设△ABM,△ADM,△CDM,△BCM的面积分别表示S1,S2,S3,S4,要求出S3﹣S4的值,只需知道( )
A.S4﹣S1 B.S2﹣S1 C.S3+S2 D.S3﹣S2
10.如图,矩形ABCD中,AB=3,AD=5,E,F分别是边AD,BC的中点,CP⊥BE于P,DP的延长线交AB于G.下列结论:①PF=2.5;②PF⊥DG;③.其中结论正确的有( )
A.①② B.②③ C.①③ D.①②③
二、填空题(每小题3分,满分18分)
11.若m是方程2x2﹣x﹣1=0的一个根,则代数式4m2﹣2m的值为 .
12.小明在计算一组数据的方差时,先计算了这组数据的平均数,然后写出了如下计算公式:,则这组数据的方差s2= .
13.关于x的方程x2﹣2mx+3=0的一个解是x1=1,则方程的另一个解x2= .
14.如图,小华从A点出发,沿直线前进5m后左转24°,再沿直线前进5m,又向左转24°,……照这样走下去,当他第一次回到出发地A点时,一共走过的路程是 .
15.如图, ABCD的对角线AC、BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为 .
16.如图,已知 ABCD的对角线AC与BD相交于点O,∠AOB=60°,将△ABC沿着直线AC翻折,使点B的对应点B′落在原图所在平面上,连结B′D.若BD=5,则B′D的长度为 .
第II卷
浙教版2024—2025学年八年级下册数学期末考试重难点练习卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2).
18.解方程:
(1)x2﹣6x=﹣9; (2)(x+1)(x﹣3)=6.
19.如图,在正方形网格中,每个小正方形的边长均为1.每个小正方形的顶点叫做格点,以格点为顶点按下列要求画图.
(1)画以点O为对称中心,A、B为顶点的 ABCD;
(2) ABCD的周长为 .
20.今年6月26日是第37个国际禁毒日,某校八年级1,2班开展了一次禁毒知识竞赛,每班选25名同学参赛,成绩评为A,B,C,D四个等级,相应等级的得分依次为100分,90分,80分,70分,将两个班的成绩整理后,绘制成如所示统计图表:
平均数 中位数 众数
1班 a b 90
2班 87.6 80 c
(1)请把1班竞赛成绩统计图补充完整.
(2)计算出表格中a,b,c的值:a= ,b= ,c= .
(3)请你根据平均数和众数,分析比较1班和2班的竞赛成绩.
21.已知关于x的方程x2﹣(m+2)x+(2m﹣1)=0.
(1)求证:方程一定有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求出以此两根为边长的直角三角形的周长.
22.诸暨某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“五一”国际劳动节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售 件,每件盈利 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天盈利1200元.
(3)要想平均每天盈利2000元,可能吗?请说明理由.
23.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,BD=2AD,点E在线段OC上,且OE=CE.
(1)求证:∠ADO=2∠OBE;
(2)若F,G分别是OD,AB的中点,
①求证:△EFG是等腰三角形;
②当EF⊥EG时,BC=10时,求平行四边形ABCD的面积.
24.如图,已知A(﹣3,2),B(n,﹣3)是一次函数y=kx+b的图象与反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)在x轴上是否存在一点P,使△AOP是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
25.如图1,正方形ABCD中,C(﹣2,0),D(0,3).过A点作AF⊥y轴于F点,过B点作x轴的垂线交过A点的反比例函数的图象于E点,交x轴于G点.
(1)求证:△CDO≌△DAF;
(2)求反比例函数的表达式及点E的坐标;
(3)如图2,过点C作直线l∥AE,点P是直线l上的一点,在平面内是否存在点Q,使得点A、C、P、Q四个点依次连接构成的四边形是菱形,若存在,请直接写出点Q的横坐标,若不存在,请说明理由.
参考答案
一、选择题
1—10:BCDCC BDCBD
二、填空题
11.【解答】解:把x=m代入方程2x2﹣x﹣1=0,可得:2m2﹣m=1,
4m2﹣2m=2(2m2﹣m)=2×1=2.
故答案为:2.
12.【解答】解:∵计算公式:,
∴这组数据为6、8、8、10,
∴这组数据的平均数为:(6+8+8+10)=8.
∴S2[(6﹣8)2+(8﹣8)2+(8﹣8)2+(10﹣8)2]=2.
故答案为:2.
13.【解答】解:根据根与系数的关系得x1x2=3,
而x1=1,
所以x2=3.
故答案为:3.
14.【解答】解:由题意可知,当小华回到出发地A点时,行走的路线是正多边形,
∵多边形的外角和为360°,而每一个外角为24°,
∴多边形的边数为360°÷24°=15,
∴小华一共走的路程:15×5=75,
故答案为:75m.
15.【解答】解:∵ ABCD的对角线AC、BD相交于点O,
∴BO=DOBD,BD=2OB,
∴O为BD中点,
∵点E是AB的中点,
∴AB=2BE,BC=2OE,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴CD=2BE.
∵△BEO的周长为8,
∴OB+OE+BE=8,
∴BD+BC+CD=2OB+2OE+2BE=2(OB+OE+BE)=16,
∴△BCD的周长是16,
故答案为16.
16.【解答】解:∵四边形ABCD是平行四边形,BD=5,
∴.
如图,连接OB′.
根据折叠的性质知:∠AOB=∠AOB′=60°,BO=B′O,
∴∠BOB′=∠AOB+∠AOB′=120°,
∴∠B′OD=180°﹣∠BOB′=60°,
∵BO=B′O,DO=BO,
∴B′O=OD,
∴△B′OD是等边三角形,
∴,
故答案为:.
三、解答题
17.【解答】解:(1)原式
=0;
(2)
.
18.【解答】解:(1)x2﹣6x=﹣9,
x2﹣6x+9=0,
(x﹣3)2=0,
∴x1=x2=3;
(2)(x+1)(x﹣3)=6,
x2+x﹣3x﹣3=6,
x2﹣2x﹣3=6,
∴x2﹣2x=9,
∴(x﹣1)2=9+1,
∴x﹣1,
∴x1=1,x2=1.
19.【解答】(1)如图, ABCD即为所求.
(2)由勾股定理得,AB=CD,BC=AD,
∴ ABCD的周长为AB+CD+BC+AD.
故答案为:.
20.【解答】解:(1)∵每班选25名同学参加比赛,
∴(1)班C等级的人数是:25﹣6﹣12﹣5=2(人),
补充统计图如图:
(2)a=(6×100+12×90+2×80+5×70)=87.6,
∵(1)班有6人100分,12人90分,2人80分,5人70分,
∴按照从小到大的顺序将成绩排列,正中间的成绩为90分,
∴b=90,
∵由扇形统计图可知:(2)班等级为A的占44%,为最多,
∴(2)班成绩为100分的人数最多,
∴c=100,
(3)②∵(1)班和(2)班的平均成绩均为87.6分,而(1)班的众数是90分,(2)班的众数是100分,
∴从平均数和众数方面进行比较,(2)班成绩更好.
21.【解答】(1)证明:
∵方程x2﹣(m+2)x+(2m﹣1)=0,
∴Δ=(m+2)2﹣4(2m﹣1)=m2+4m+4﹣8m+4=m2﹣4m+4+4=(m﹣2)2+4>0,
∴方程一定有两个不相等的实数根;
(2)解:把x=1代入方程可得1﹣(m+2)+2m﹣1=0,解得m=2,
∴方程为x2﹣4x+3=0,解得x=1或x=3,
∴方程的另一根为x=3,
当边长为1和3的线段为直角三角形的直角边时,则斜边,此时直角三角形的周长=4,
当边长为3的直角三角形斜边时,则另一直角边2,此时直角三角形的周长=4+2,
综上可知直角三角形的周长为4或4+2.
22.【解答】解:(1)设每件童装降价x元时,每天可销售(20+2x)件,每件盈利(40﹣x)元,
故答案为:(20+2x),(40﹣x);
(2)根据题意,得:(20+2x)(40﹣x)=1200,
解得:x1=20,x2=10,
∵要扩大销售量,
∴x=20,
答:每件童装降价20元,平均每天盈利1200元;
(3)不能,理由如下:
(20+2x)(40﹣x)=2000,
整理,得:x2﹣30x+600=0,
∵Δ=(﹣30)2﹣4×600=﹣1500<0,
∴此方程无实数根,
故不可能做到平均每天盈利2000元.
23.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,BD=2DO=2BO,
∴∠ADO=∠CBO,
∵BD=2AD,
∴AD=BO=BC,
∴△BOC是等腰三角形,
∵OE=CE,
∴∠OBE=∠CBE∠ADO,
∴∠ADO=2∠OBE.
(2)①证明:∵△BOC是等腰三角形,E是CO中点,
∴EB⊥CO,
∴∠BEA=90°,
∵G为AB中点,
∴EGAB,
∵E、F分别是OC、OD的中点,
∴EFCD,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴EG=EF,
∴△EFG是等腰三角形.
②解:由题意知,EF∥CD∥BG,
∴EFAB=BG,
∴四边形BEFG是平行四边形,
∴∠EFG=∠GBE,
∵∠FEG=∠AEB=90°,
∴△ABE是等腰三角形,
∴∠BAE=∠ABE=45°,
∴EG⊥AB,
设AG=GE=x,则BE=AEx,CE,
在Rt△BCE中,由勾股定理得,BC2=BE2+CE2,即,
解得x=3或x=﹣3(不合题意,舍去),
∴BE=3,AC=4CE=4,
∴S平行四边形ABCD=2120,
∴平行四边形ABCD的面积为120.
24.【解答】解:(1)将A(﹣3,2)代入得:m=﹣6,
∴反比例函数的解析式是,
将B(n,﹣3)代入得:n=2,
∴B的坐标为B(2,﹣3),
将A(﹣3,2),B(2,﹣3)代入y=kx+b得:
,
∴,
∴一次函数的解析式为y=﹣x﹣1;
(2)根据图像,结合题意,得:﹣3<x<0或x>2;
(3)存在一点P,使△AOP是等腰三角形;P点坐标为(﹣6,0),(,0),(,0),(,0);理由如下:
如图2,
在x轴上存在点P,使△AOP 是等腰三角形由A(﹣3,2)可得:OA,
当△AOP是等腰三角形时,分三种情况讨论:
①当AO=AP时(图2中P1),作AS⊥x轴于点S,由A(﹣3,2),等腰三角形三线合一的性质得:OS=P1S=3,由AS=2,OS=3,
∴P1O=6,
故P1(﹣6,0);
②当AO=PO时(图2中P2),P点在O点左侧时,P2(,0);
P点在O点右侧时,P3(,0);
③当PA=PO时(AP'=P'O)时,即AP'2=P'O2,
∴22+(3﹣OP')2=OP'2,
∴OP',
∴P'(,0),
综上所述,存在一点P,使△AOP是等腰三角形;P点坐标为(﹣6,0),(,0),(,0),(,0).
25.【解答】(1)证明:如图1,∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ADF+∠CDO=90°,
∵AF⊥y轴,
∴∠AFD=∠DOC=90°,
∴∠CDO+∠DCO=90°,
∴∠ADF=∠DCO,
在△CDO和△DAF中,
,
∴△CDO≌△DAF(AAS);
(2)解:∵C(﹣2,0),D(0,3),
∴OC=2,OD=3,
∵△CDO≌△DAF,
∴DF=OC,AF=OD,
∴OG=OF=OD+DF=3+2=5,
∴A(﹣3,5),
设反比例函数的表达式为y(k≠0),把A(﹣3,5)代入,得k=﹣15,
∴y,
当x=﹣5时,y3,
∴点E的坐标为(﹣5,3);
(3)在平面内存在点Q,使得点A、C、P、Q四个点依次连接构成的四边形是菱形.理由如下:
设直线AE的解析式为y=k′x+b,把A(﹣3,5),E(﹣5,3)代入,
得,
解得:,
∴直线AE的解析式为y=x+8,
∵直线l∥AE,
∴设直线l的解析式为y=x+b′,把C(﹣2,0)代入得﹣2+b′=0,
解得:b′=2,
∴直线l的解析式为y=x+2,
∵点P是直线l上的一点,点Q是平面内一点,
∴设P(m,m+2),Q(t,s),
又A(﹣3,5),C(﹣2,0),
当AC、PQ为对角线时,
,
解得:,
∴Q(,);
当CP、AQ为对角线时,
,
解得:或(舍去),
∴Q(3,﹣1);
当AP、CQ为对角线时,
,
解得:或,
∴Q(﹣3,5)或(﹣3,5);
综上所述,在平面内存在点Q,使得点A、C、P、Q四个点依次连接构成的四边形是菱形,点Q的横坐标为或3或﹣3或﹣3.
21世纪教育网(www.21cnjy.com)
同课章节目录
