浙教版2024—2025学年八年级下学期数学期末素养检测卷(含答案)
文档属性
| 名称 | 浙教版2024—2025学年八年级下学期数学期末素养检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 628.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 13:02:51 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年八年级下学期数学期末素养检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形中既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.下列二次根式中,属于最简二次根式的是( )
A. B. C. D.
3.一个多边形的内角和是外角和的2倍,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
4.体育课上,体育老师记录了40位同学的实心球成绩,数据分别为x1,x2,……x40.但由于场地布置失误,导致每位同学的成绩都少记录了10cm,其实际数据分别为y1,y2,……y40,比较记录成绩和实际成绩这两组数据,统计量不会发生变化的是( )
A.方差 B.中位数 C.众数 D.平均数
5.已知反比例函数,下列结论中不正确的是( )
A.图象必经过点(﹣3,2)
B.图象位于第二、四象限
C.x<0,则y>0
D.y随x的增大而增大
6.公安部交管局部署“一盔一带”安全守护行动,某头盔经销商经统计发现某品牌头盔5月份销售量144个,7月份销售量225个,从5月份到7月份销售量的月增长率相同,则此月增长率为( )
A.83% B.69% C.25% D.20%
7.用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,首先应假设这个直角三角形中( )
A.两个锐角都大于45°
B.两个锐角都小于45°
C.两个锐角都不大于45°
D.两个锐角都等于45°
8.已知(x1,y1),B(x2,y2),C(x3,y3)是反比例函数的图象上的三个点,并且x1<x2<0,x3>0,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y3<y1<y2
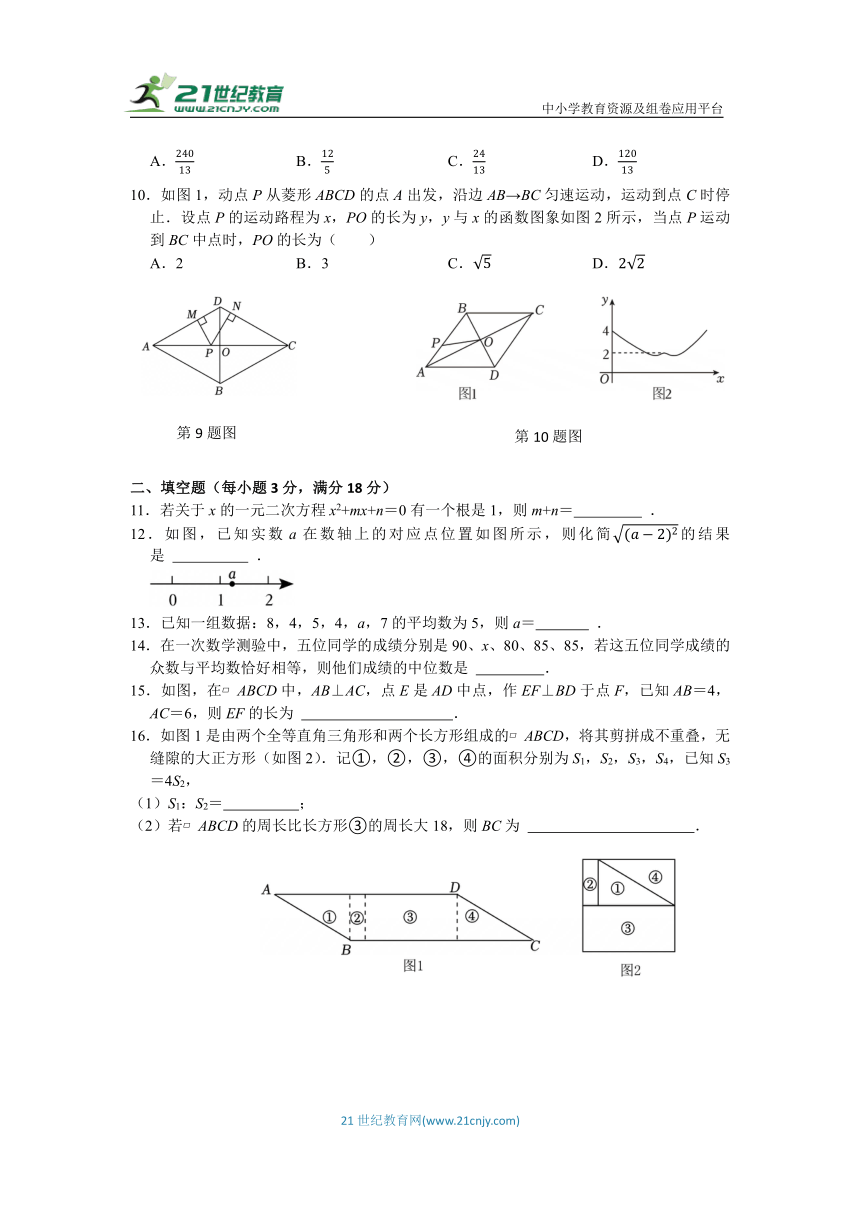
9.如图,在菱形ABCD中,AC、BD交于O点,AC=24,BD=10,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,作PN⊥DC于点N,则PM+PN的值为( )
A. B. C. D.
10.如图1,动点P从菱形ABCD的点A出发,沿边AB→BC匀速运动,运动到点C时停止.设点P的运动路程为x,PO的长为y,y与x的函数图象如图2所示,当点P运动到BC中点时,PO的长为( )
A.2 B.3 C. D.
二、填空题(每小题3分,满分18分)
11.若关于x的一元二次方程x2+mx+n=0有一个根是1,则m+n= .
12.如图,已知实数a在数轴上的对应点位置如图所示,则化简的结果是 .
13.已知一组数据:8,4,5,4,a,7的平均数为5,则a= .
14.在一次数学测验中,五位同学的成绩分别是90、x、80、85、85,若这五位同学成绩的众数与平均数恰好相等,则他们成绩的中位数是 .
15.如图,在 ABCD中,AB⊥AC,点E是AD中点,作EF⊥BD于点F,已知AB=4,AC=6,则EF的长为 .
16.如图1是由两个全等直角三角形和两个长方形组成的 ABCD,将其剪拼成不重叠,无缝隙的大正方形(如图2).记①,②,③,④的面积分别为S1,S2,S3,S4,已知S3=4S2,
(1)S1:S2= ;
(2)若 ABCD的周长比长方形③的周长大18,则BC为 .
第II卷
浙教版2024—2025学年八年级下学期数学期末素养检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.选择合适的方法解下列方程:
(1)x2﹣2x﹣8=0.(2)3x(x﹣1)=2(x﹣1).
18.计算:
(1); (2).
19.已知:,,求下列代数式的值:
(1)x2﹣y2;
(2)x2﹣3xy+y2.
20.每年的4月15日是我国全民国家安全教育日,某中学七、八年级共1200名学生全部参加“国家安全法”知识竞赛,并从七、八年级学生中各随机抽取20名学生,统计这部分学生的竞赛成绩(竞赛成绩均为整数,满分10分,6分及以上为合格,8分及以上为优秀),八年级抽取的学生的竞赛成绩:4,4,6,6,6,6,7,7,8,8,8,8,8,8,8,9,9,9,9,10.相关数据整理如下:
年级 七年级 八年级
平均数 7.4 7.4
中位数 a b
众数 7 c
合格率 d 90%
根据以上信息,解答下列问题:
(1)填空:a= ;b= ;c= ;d= .
(2)若该校七、八年级各有600名学生,请估计该校七、八年级学生中竞赛成绩达到8分及以上的人数.
21.已知关于x的方程mx2﹣(m+2)x+2=0(m≠0).
(1)求证:方程总有两个实数根;
(2)如果方程有一个根为2,求方程两根的乘积.
22.如图,在 ABCD中,M,N是对角线BD的三等分点.
(1)求证:四边形AMCN是平行四边形;
(2)若AM⊥BD,AD=13,BD=18,求CD的长.
23.第19届亚洲运动会于2023年9月23日晚在浙江省杭州市隆重开幕,亚运会吉祥物是一组承载深厚底蕴和充满时代活力的机器人,由“琮琮”、“莲莲”、“宸宸”共间组成“江南忆”组合,三个吉祥物造型形象生动,深受大家的喜爱,某网店购进一批亚运会吉祥物“宸宸”和“琮琮”,进货价和销售价如下表:
吉祥物 宸宸 琮琮
进货价(元/个) 59 66
销售价(元/个) 79 88
(1)该网店第一次用3160元购进“宸宸”和“琮琮”共50个,则购进“宸宸” 个,购进“琮琮” 个;
(2)亚运会临近结束时,该网店打算把“宸宸”调价销售,如果按照原价销售,平均每天可售8个,经调查发现,每降价1元,平均每天可多售2个,将销售价定为每个多少元时,才能使“宸宸”平均每天销售利润为288元.
24.如图,一次函数y=ax+b的图象与反比例函数的图象交于A,B两点与x轴交于点C,与y轴交于点D,已知点A坐标为(3,1),点B的坐标为(﹣2,m).
(1)求反比例函数的表达式和一次函数的表达式;
(2)观察图象直接写出时x的取值范围是 ;
(3)若P为x轴上一动点,请直接写出当△OAP是以OA为腰的等腰三角形时,点P的坐标.
25.如图,动点M在函数的图象,过点M分别作x轴和y轴的平行线交反比例函数y的图象于点B、C,作直线BC,设直线BC的函数表达式为y=kx+b(k≠0).
(1)若点M的坐标为(1,4),
①求直线BC的函数解析式;
②点D在x轴上,点E在y轴上,且以点B、C、D、E为顶点的四边形是平行四边形,请直接写出点D、E的坐标;
(2)连接BO、CO,试探究点M在运动过程中,△BOC的面积是否是定值?若是,求出该定值;若不是,请说明理由.
参考答案
一、选择题
1—10:DDDAD CADDC
二、填空题
11.【解答】解:把x=1代入原方程可得:
1+m+n=0,
∴m+n=﹣1,
故答案为:﹣1.
12.【解答】解:由实数a在数轴上的对应点位置可知1<a<2,
∴2﹣a.
故答案为:2﹣a.
13.【解答】解:∵一组数据:8,4,5,4,a,7的平均数为5,
∴,
解得a=2.
故答案为:2.
14.【解答】解:因为众数与平均数恰好相等,说明众数是一个数,
所以x=85,
将这5个数从小到大排列如下:
80,85,85,85,90,
中间的数是85,
所以成绩的中位数是85,
故答案为:85.
15.【解答】解:如图,连接OE,
∵四边形ABCD是平行四边形,AC=6,
∴OAAC=3,OB=OD,
∴S△OAD=S△OABAB OA4×3=6,
∵AB⊥AC,
∴∠OAB=90°,
∴OB5,
∴OD=5,
∵点E是AD中点,
∴S△OAE=S△ODE6=3,
∵EF⊥BD,
∴S△ODEOD EF=3,
∴OD EF=6,
即5EF=6,
∴EF,
故答案为:.
16.【解答】解:(1)如图,
由题意设PE=x,则FG=EH=4x,PH=3x,HQ=QG=2x,
∵,,
∴S1:S2=3:2,
故答案为:3:2;
(2)如图,由勾股定理可得,
∵AD=BC=8x,EF=FG=GH=EH=4x,
又∵平行四边形的周长比长方形③的周长大18,
∴,
∴,
∴,
故答案为:.
三、解答题
17.【解答】解:(1)x2﹣2x﹣8=0,
(x﹣4)(x+2)=0,
x﹣4=0或x+2=0,
∴x1=4,x2=﹣2;
(2)3x(x﹣1)=2(x﹣1),
3x(x﹣1)﹣2(x﹣1)=0,
(x﹣1)(3x﹣2)=0,
x﹣1=0或3x﹣2=0,
∴x1=1,.
18.【解答】解:(1)
=24
;
(2)
2
=3+2
=5.
19.【解答】解:(1)∵,,
∴,
∴x2﹣y2;
(2)∵,,
∴xy=2﹣9=﹣7,x﹣y=6,
∴x2﹣3xy+y2
=(x﹣y)2﹣xy
=36+7
=43.
20.【解答】解:(1)把七年级学生的竞赛成绩从小到大排列,中位数是第10、11个数的平均数,
则a7.5,b8,
因为8出现了7次,出现的次数最多,
所以众数是8,即c=8;
d100%=85%;
故答案为:7.5,8,8,85%;
(2)根据题意得:
600600
=360+300
=660(人),
答:估计该校七、八年级学生中竞赛成绩达到8分及以上的人数有660人.
21.【解答】解:(1)证明:∵关于x的方程mx2﹣(m+2)x+2=0(m≠0),
∴Δ=[﹣(m+2)]2﹣4m×2
=(m+2)2﹣8m
=m2+4+4m﹣8m
=(m﹣2)2≥0,
∴方程总有两个实数根;
(2)∵方程有一个根为2,
∴4m﹣2(m+2)+2=0,
解得m=1,
∴原方程可化为x2﹣3x+2=0,
∴方程两根的乘积=2.
22.【解答】(1)证明:连接AC交BD于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵M,N是对角线BD的三等分点,
∴BM=DN,
∴OM=ON,
∴四边形AMCN是平行四边形;
(2)解:∵AD=13,BD=18,M,N是对角线BD的三等分点,
∴DM=12,BM=6,
∵AM⊥BD,
∴AM,
∴AB,
∵四边形ABCD是平行四边形,
∴CD=AB.
23.【解答】解:(1)设购进x个“宸宸”,y个“琮琮”,
根据题意得:,
解得:.
答:购进20个“宸宸”,30个“琮琮”;
(2)设销售价下降m元,则每个的销售利润为(79﹣m﹣59)元,平均每天可售出(8+2m)个,
根据题意得:(79﹣m﹣59)(8+2m)=288,
整理得:m2﹣16m+64=0,
解得:m1=m2=8,
∴79﹣m=79﹣8=71(元).
答:销售价定为每个71元.
24.【解答】解:(1)根据题意将点A坐标(3,1)代入中得:k=3,
∴反比例函数的表达式:,
∵点B的坐标为(﹣2,m),
∴,
∴点B的坐标为,
∴将点A(3,1),点B代入y=ax+b中得:
,
解得:,
∴一次函数的表达式:;
(2)∵一次函数y=ax+b的图象与反比例函数的图象交于A,B两点,
∵点A(3,1),点B,
由图象可知,当﹣2<x<0或x>3时,,
故答案为:﹣2<x<0或x>3;
(3)
当△OAP是以OA为腰的等腰三角形时,点P的坐标为P(6,0)或或;理由如下:
∵点A(3,1),
∴,
∵P为x轴上一动点,
∴过点A作AM⊥x轴,△OAP是以OA为腰的等腰三角形,
∴当P在x轴正半轴时,PM=OM=3,
∴OP=6,即P(6,0),
∴当P在x轴负半轴时,,
∴,
∴当P在x轴正半轴时,,
∴,
综上所述:点P的坐标为P(6,0)或或.
25.【解答】解:(1)①当M(1,4)时,则B(,4),C(1,2),
∴,
解得,
∴直线BC的解析式为y=﹣4x+6;
②设D(m,0),E(0,n),
当BD、CE为对角线时,
,
∴,
∴D(,0)E(0,2),
当BC、DE为对角线时,,
∴,
此时点B、C、D、E共线,故舍去,
当BE、CD为对角线时,
,
∴,
∴D(,0),E(0,﹣2),
综上:D(,0),E(0,2)或D(,0),E(0,﹣2);
(2)证明:延长MC、MB分别交x轴于G,交y轴于H,设M(a,),
∴B(,),C(a,),
∴S△OBC=S矩形OGMH﹣S△OCG﹣S△BCM﹣S△BHO
=a 1() (a)﹣1
=4﹣11
,
∴△BOC的面积是个定值.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年八年级下学期数学期末素养检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形中既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.下列二次根式中,属于最简二次根式的是( )
A. B. C. D.
3.一个多边形的内角和是外角和的2倍,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
4.体育课上,体育老师记录了40位同学的实心球成绩,数据分别为x1,x2,……x40.但由于场地布置失误,导致每位同学的成绩都少记录了10cm,其实际数据分别为y1,y2,……y40,比较记录成绩和实际成绩这两组数据,统计量不会发生变化的是( )
A.方差 B.中位数 C.众数 D.平均数
5.已知反比例函数,下列结论中不正确的是( )
A.图象必经过点(﹣3,2)
B.图象位于第二、四象限
C.x<0,则y>0
D.y随x的增大而增大
6.公安部交管局部署“一盔一带”安全守护行动,某头盔经销商经统计发现某品牌头盔5月份销售量144个,7月份销售量225个,从5月份到7月份销售量的月增长率相同,则此月增长率为( )
A.83% B.69% C.25% D.20%
7.用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,首先应假设这个直角三角形中( )
A.两个锐角都大于45°
B.两个锐角都小于45°
C.两个锐角都不大于45°
D.两个锐角都等于45°
8.已知(x1,y1),B(x2,y2),C(x3,y3)是反比例函数的图象上的三个点,并且x1<x2<0,x3>0,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y3<y1<y2
9.如图,在菱形ABCD中,AC、BD交于O点,AC=24,BD=10,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,作PN⊥DC于点N,则PM+PN的值为( )
A. B. C. D.
10.如图1,动点P从菱形ABCD的点A出发,沿边AB→BC匀速运动,运动到点C时停止.设点P的运动路程为x,PO的长为y,y与x的函数图象如图2所示,当点P运动到BC中点时,PO的长为( )
A.2 B.3 C. D.
二、填空题(每小题3分,满分18分)
11.若关于x的一元二次方程x2+mx+n=0有一个根是1,则m+n= .
12.如图,已知实数a在数轴上的对应点位置如图所示,则化简的结果是 .
13.已知一组数据:8,4,5,4,a,7的平均数为5,则a= .
14.在一次数学测验中,五位同学的成绩分别是90、x、80、85、85,若这五位同学成绩的众数与平均数恰好相等,则他们成绩的中位数是 .
15.如图,在 ABCD中,AB⊥AC,点E是AD中点,作EF⊥BD于点F,已知AB=4,AC=6,则EF的长为 .
16.如图1是由两个全等直角三角形和两个长方形组成的 ABCD,将其剪拼成不重叠,无缝隙的大正方形(如图2).记①,②,③,④的面积分别为S1,S2,S3,S4,已知S3=4S2,
(1)S1:S2= ;
(2)若 ABCD的周长比长方形③的周长大18,则BC为 .
第II卷
浙教版2024—2025学年八年级下学期数学期末素养检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.选择合适的方法解下列方程:
(1)x2﹣2x﹣8=0.(2)3x(x﹣1)=2(x﹣1).
18.计算:
(1); (2).
19.已知:,,求下列代数式的值:
(1)x2﹣y2;
(2)x2﹣3xy+y2.
20.每年的4月15日是我国全民国家安全教育日,某中学七、八年级共1200名学生全部参加“国家安全法”知识竞赛,并从七、八年级学生中各随机抽取20名学生,统计这部分学生的竞赛成绩(竞赛成绩均为整数,满分10分,6分及以上为合格,8分及以上为优秀),八年级抽取的学生的竞赛成绩:4,4,6,6,6,6,7,7,8,8,8,8,8,8,8,9,9,9,9,10.相关数据整理如下:
年级 七年级 八年级
平均数 7.4 7.4
中位数 a b
众数 7 c
合格率 d 90%
根据以上信息,解答下列问题:
(1)填空:a= ;b= ;c= ;d= .
(2)若该校七、八年级各有600名学生,请估计该校七、八年级学生中竞赛成绩达到8分及以上的人数.
21.已知关于x的方程mx2﹣(m+2)x+2=0(m≠0).
(1)求证:方程总有两个实数根;
(2)如果方程有一个根为2,求方程两根的乘积.
22.如图,在 ABCD中,M,N是对角线BD的三等分点.
(1)求证:四边形AMCN是平行四边形;
(2)若AM⊥BD,AD=13,BD=18,求CD的长.
23.第19届亚洲运动会于2023年9月23日晚在浙江省杭州市隆重开幕,亚运会吉祥物是一组承载深厚底蕴和充满时代活力的机器人,由“琮琮”、“莲莲”、“宸宸”共间组成“江南忆”组合,三个吉祥物造型形象生动,深受大家的喜爱,某网店购进一批亚运会吉祥物“宸宸”和“琮琮”,进货价和销售价如下表:
吉祥物 宸宸 琮琮
进货价(元/个) 59 66
销售价(元/个) 79 88
(1)该网店第一次用3160元购进“宸宸”和“琮琮”共50个,则购进“宸宸” 个,购进“琮琮” 个;
(2)亚运会临近结束时,该网店打算把“宸宸”调价销售,如果按照原价销售,平均每天可售8个,经调查发现,每降价1元,平均每天可多售2个,将销售价定为每个多少元时,才能使“宸宸”平均每天销售利润为288元.
24.如图,一次函数y=ax+b的图象与反比例函数的图象交于A,B两点与x轴交于点C,与y轴交于点D,已知点A坐标为(3,1),点B的坐标为(﹣2,m).
(1)求反比例函数的表达式和一次函数的表达式;
(2)观察图象直接写出时x的取值范围是 ;
(3)若P为x轴上一动点,请直接写出当△OAP是以OA为腰的等腰三角形时,点P的坐标.
25.如图,动点M在函数的图象,过点M分别作x轴和y轴的平行线交反比例函数y的图象于点B、C,作直线BC,设直线BC的函数表达式为y=kx+b(k≠0).
(1)若点M的坐标为(1,4),
①求直线BC的函数解析式;
②点D在x轴上,点E在y轴上,且以点B、C、D、E为顶点的四边形是平行四边形,请直接写出点D、E的坐标;
(2)连接BO、CO,试探究点M在运动过程中,△BOC的面积是否是定值?若是,求出该定值;若不是,请说明理由.
参考答案
一、选择题
1—10:DDDAD CADDC
二、填空题
11.【解答】解:把x=1代入原方程可得:
1+m+n=0,
∴m+n=﹣1,
故答案为:﹣1.
12.【解答】解:由实数a在数轴上的对应点位置可知1<a<2,
∴2﹣a.
故答案为:2﹣a.
13.【解答】解:∵一组数据:8,4,5,4,a,7的平均数为5,
∴,
解得a=2.
故答案为:2.
14.【解答】解:因为众数与平均数恰好相等,说明众数是一个数,
所以x=85,
将这5个数从小到大排列如下:
80,85,85,85,90,
中间的数是85,
所以成绩的中位数是85,
故答案为:85.
15.【解答】解:如图,连接OE,
∵四边形ABCD是平行四边形,AC=6,
∴OAAC=3,OB=OD,
∴S△OAD=S△OABAB OA4×3=6,
∵AB⊥AC,
∴∠OAB=90°,
∴OB5,
∴OD=5,
∵点E是AD中点,
∴S△OAE=S△ODE6=3,
∵EF⊥BD,
∴S△ODEOD EF=3,
∴OD EF=6,
即5EF=6,
∴EF,
故答案为:.
16.【解答】解:(1)如图,
由题意设PE=x,则FG=EH=4x,PH=3x,HQ=QG=2x,
∵,,
∴S1:S2=3:2,
故答案为:3:2;
(2)如图,由勾股定理可得,
∵AD=BC=8x,EF=FG=GH=EH=4x,
又∵平行四边形的周长比长方形③的周长大18,
∴,
∴,
∴,
故答案为:.
三、解答题
17.【解答】解:(1)x2﹣2x﹣8=0,
(x﹣4)(x+2)=0,
x﹣4=0或x+2=0,
∴x1=4,x2=﹣2;
(2)3x(x﹣1)=2(x﹣1),
3x(x﹣1)﹣2(x﹣1)=0,
(x﹣1)(3x﹣2)=0,
x﹣1=0或3x﹣2=0,
∴x1=1,.
18.【解答】解:(1)
=24
;
(2)
2
=3+2
=5.
19.【解答】解:(1)∵,,
∴,
∴x2﹣y2;
(2)∵,,
∴xy=2﹣9=﹣7,x﹣y=6,
∴x2﹣3xy+y2
=(x﹣y)2﹣xy
=36+7
=43.
20.【解答】解:(1)把七年级学生的竞赛成绩从小到大排列,中位数是第10、11个数的平均数,
则a7.5,b8,
因为8出现了7次,出现的次数最多,
所以众数是8,即c=8;
d100%=85%;
故答案为:7.5,8,8,85%;
(2)根据题意得:
600600
=360+300
=660(人),
答:估计该校七、八年级学生中竞赛成绩达到8分及以上的人数有660人.
21.【解答】解:(1)证明:∵关于x的方程mx2﹣(m+2)x+2=0(m≠0),
∴Δ=[﹣(m+2)]2﹣4m×2
=(m+2)2﹣8m
=m2+4+4m﹣8m
=(m﹣2)2≥0,
∴方程总有两个实数根;
(2)∵方程有一个根为2,
∴4m﹣2(m+2)+2=0,
解得m=1,
∴原方程可化为x2﹣3x+2=0,
∴方程两根的乘积=2.
22.【解答】(1)证明:连接AC交BD于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵M,N是对角线BD的三等分点,
∴BM=DN,
∴OM=ON,
∴四边形AMCN是平行四边形;
(2)解:∵AD=13,BD=18,M,N是对角线BD的三等分点,
∴DM=12,BM=6,
∵AM⊥BD,
∴AM,
∴AB,
∵四边形ABCD是平行四边形,
∴CD=AB.
23.【解答】解:(1)设购进x个“宸宸”,y个“琮琮”,
根据题意得:,
解得:.
答:购进20个“宸宸”,30个“琮琮”;
(2)设销售价下降m元,则每个的销售利润为(79﹣m﹣59)元,平均每天可售出(8+2m)个,
根据题意得:(79﹣m﹣59)(8+2m)=288,
整理得:m2﹣16m+64=0,
解得:m1=m2=8,
∴79﹣m=79﹣8=71(元).
答:销售价定为每个71元.
24.【解答】解:(1)根据题意将点A坐标(3,1)代入中得:k=3,
∴反比例函数的表达式:,
∵点B的坐标为(﹣2,m),
∴,
∴点B的坐标为,
∴将点A(3,1),点B代入y=ax+b中得:
,
解得:,
∴一次函数的表达式:;
(2)∵一次函数y=ax+b的图象与反比例函数的图象交于A,B两点,
∵点A(3,1),点B,
由图象可知,当﹣2<x<0或x>3时,,
故答案为:﹣2<x<0或x>3;
(3)
当△OAP是以OA为腰的等腰三角形时,点P的坐标为P(6,0)或或;理由如下:
∵点A(3,1),
∴,
∵P为x轴上一动点,
∴过点A作AM⊥x轴,△OAP是以OA为腰的等腰三角形,
∴当P在x轴正半轴时,PM=OM=3,
∴OP=6,即P(6,0),
∴当P在x轴负半轴时,,
∴,
∴当P在x轴正半轴时,,
∴,
综上所述:点P的坐标为P(6,0)或或.
25.【解答】解:(1)①当M(1,4)时,则B(,4),C(1,2),
∴,
解得,
∴直线BC的解析式为y=﹣4x+6;
②设D(m,0),E(0,n),
当BD、CE为对角线时,
,
∴,
∴D(,0)E(0,2),
当BC、DE为对角线时,,
∴,
此时点B、C、D、E共线,故舍去,
当BE、CD为对角线时,
,
∴,
∴D(,0),E(0,﹣2),
综上:D(,0),E(0,2)或D(,0),E(0,﹣2);
(2)证明:延长MC、MB分别交x轴于G,交y轴于H,设M(a,),
∴B(,),C(a,),
∴S△OBC=S矩形OGMH﹣S△OCG﹣S△BCM﹣S△BHO
=a 1() (a)﹣1
=4﹣11
,
∴△BOC的面积是个定值.
21世纪教育网(www.21cnjy.com)
同课章节目录
