浙教版2024—2025学年八年级下学期数学期末考试调研检测卷(含答案)
文档属性
| 名称 | 浙教版2024—2025学年八年级下学期数学期末考试调研检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 580.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 13:03:36 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年八年级下学期数学期末考试调研检测卷
满分:120分 时间:120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列电视台标志是中心对称图形的是( )
A. B. C. D.
2.方程x2﹣x﹣1=0的根的情况是( )
A.没有实数根 B.两个不相等的实数根
C.两个相等的实数根 D.无法确定
3.如图,根据平行四边形中所标注的角的度数、边的长度,能判定其为菱形的是( )
A. B. C. D.
4.用反证法证明命题“一个多边形最多有四个内角是直角”时,我们可以先假设( )
A.有三个直角
B.有四个直角
C.至少有四个内角是直角
D.至少有五个内角是直角
5.已知实数a,b在数轴上的位置如图所示,化简的正确结果是( )
A.a+b﹣1 B.1﹣a﹣b C.a﹣b+3 D.b﹣a﹣3
6.保障国家粮食安全是一个永恒的课题,任何时候这根弦都不能松.某农科实验基地,大力开展种子实验,让农民能得到高产、易发芽的种子.该农科实验基地两年前有81种农作物种子,经过两年不断的努力培育新品种,现在有100种农作物种子.若这两年培育新品种数量的平均年增长率为x,则根据题意列出的符合题意的方程是( )
A.100(1﹣2x)=81 B.100(1+2x)=81
C.81(1﹣x)2=100 D.81(1+x)2=100
7.下列说法正确的是( )
A.菱形的四个内角都是直角
B.矩形的对角线互相垂直
C.正方形的每一条对角线平分一组对角
D.平行四边形是轴对称图形
8.已知x1,x2,x3,x4,x5的方差为m,则2x1+1,2x2+1,2x3+1,2x4+1,2x5+1的方差是( )
A.2m+1 B.2m C.4m D.4m+1
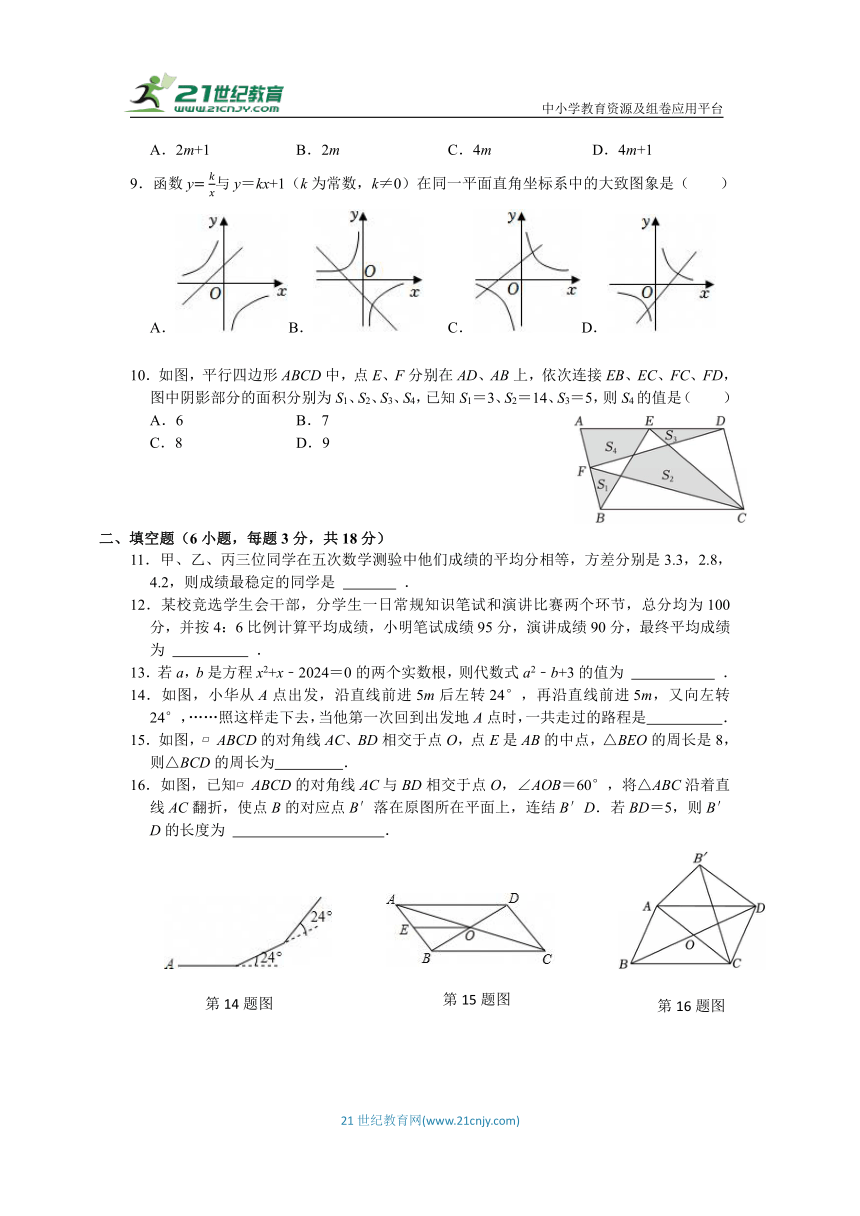
9.函数y与y=kx+1(k为常数,k≠0)在同一平面直角坐标系中的大致图象是( )
A.B. C.D.
10.如图,平行四边形ABCD中,点E、F分别在AD、AB上,依次连接EB、EC、FC、FD,图中阴影部分的面积分别为S1、S2、S3、S4,已知S1=3、S2=14、S3=5,则S4的值是( )
A.6 B.7
C.8 D.9
二、填空题(6小题,每题3分,共18分)
11.甲、乙、丙三位同学在五次数学测验中他们成绩的平均分相等,方差分别是3.3,2.8,4.2,则成绩最稳定的同学是 .
12.某校竞选学生会干部,分学生一日常规知识笔试和演讲比赛两个环节,总分均为100分,并按4:6比例计算平均成绩,小明笔试成绩95分,演讲成绩90分,最终平均成绩为 .
13.若a,b是方程x2+x﹣2024=0的两个实数根,则代数式a2﹣b+3的值为 .
14.如图,小华从A点出发,沿直线前进5m后左转24°,再沿直线前进5m,又向左转24°,……照这样走下去,当他第一次回到出发地A点时,一共走过的路程是 .
15.如图, ABCD的对角线AC、BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为 .
16.如图,已知 ABCD的对角线AC与BD相交于点O,∠AOB=60°,将△ABC沿着直线AC翻折,使点B的对应点B′落在原图所在平面上,连结B′D.若BD=5,则B′D的长度为 .
浙教版2024—2025学年八年级下学期数学期末考试调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1);(2).
18.解方程:
(1)x2﹣4x+3=0;(2)2x2﹣3x﹣1=0.
19.某校为了了解初三学生寒假期间参加体育锻炼的天数,随机抽取了部分初三学生进行调查,并绘制了如下的扇形统计图和条形统计图(部分信息未给出),请根据图中提供的信息,回答下列问题:
(1)本次调查中,体育锻炼天数的众数为 天,中位数为 天.
(2)请补全条形统计图.
(3)如果该校初三有1600名学生,请你估计初三约有多少名学生参加体育锻炼的天数不少于7天.
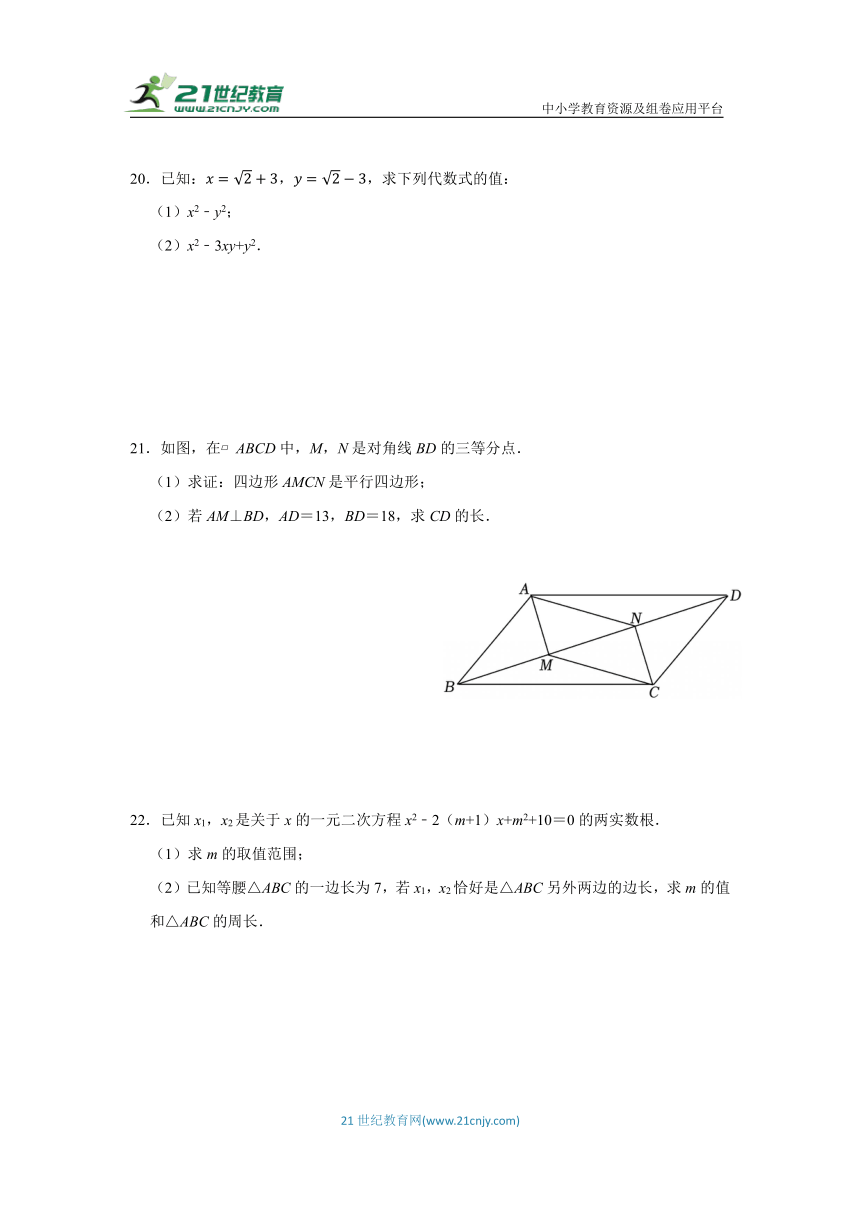
20.已知:,,求下列代数式的值:
(1)x2﹣y2;
(2)x2﹣3xy+y2.
21.如图,在 ABCD中,M,N是对角线BD的三等分点.
(1)求证:四边形AMCN是平行四边形;
(2)若AM⊥BD,AD=13,BD=18,求CD的长.
22.已知x1,x2是关于x的一元二次方程x2﹣2(m+1)x+m2+10=0的两实数根.
(1)求m的取值范围;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求m的值和△ABC的周长.
23.我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a,b,c,记,则其面积.这个公式也被称为海伦﹣秦九韶公式.
(1)当三角形的三边a=3,b=5,c=6时,请你利用公式计算出三角形的面积;
(2)一个三角形的三边长依次为、,,请求出三角形的面积;
(3)若p=8,a=4,求此时三角形面积的最大值.
24.如图,在正方形ABCD中,点E在边AB上,点F在边BC的延长线上,且CF=AE,连接EF交边CD于点N,过点D作DH⊥EF,垂足为H,交BC于点M.
(1)求∠DEF的度数;
(2)当BE=4,CN=1时,求CM的长;
(3)若点M是BC的中点,求证:DN﹣NC=BE.
25.如图,一次函数的图象与反比例函数的图象交于点A(a,3),与y轴交于点B.
(1)求a,k的值;
(2)直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,连接CB.
①求△ABC的面积;
②利用图象信息,直接写出不等式的解集.
③点P在反比例函数的图象上,点Q在x轴上,若以点A,B,P,Q为顶点的四边形是平行四边形,请求出所有符合条件的点P坐标.
参考答案
一、选择题
1—10:ABBBC DCCCA
二、填空题
11.【解答】解:∵S甲2=3.3,S乙2=2.8,S丙2=4.2,
∴S丙2>S甲2>S乙2,
∴成绩比较稳定的是乙;
故答案为:乙.
12.【解答】解:(95×4+90×6)÷(4+6)=92(分),
即最终平均成绩为92分.
故答案为:92分.
13.【解答】解:∵a,b是方程x2+x﹣2024=0的两个实数根,
∴a2+a﹣2024=0,a+b=﹣1,
∴a2=2024﹣a,
∴a2﹣b+3
=2024﹣a﹣b+3
=2024﹣(a+b)+3
=2024+1+3
=2028.
故答案为:2028.
14.【解答】解:由题意可知,当小华回到出发地A点时,行走的路线是正多边形,
∵多边形的外角和为360°,而每一个外角为24°,
∴多边形的边数为360°÷24°=15,
∴小华一共走的路程:15×5=75,
故答案为:75m.
15.【解答】解:∵ ABCD的对角线AC、BD相交于点O,
∴BO=DOBD,BD=2OB,
∴O为BD中点,
∵点E是AB的中点,
∴AB=2BE,BC=2OE,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴CD=2BE.
∵△BEO的周长为8,
∴OB+OE+BE=8,
∴BD+BC+CD=2OB+2OE+2BE=2(OB+OE+BE)=16,
∴△BCD的周长是16,
故答案为16.
16.【解答】解:∵四边形ABCD是平行四边形,BD=5,
∴.
如图,连接OB′.
根据折叠的性质知:∠AOB=∠AOB′=60°,BO=B′O,
∴∠BOB′=∠AOB+∠AOB′=120°,
∴∠B′OD=180°﹣∠BOB′=60°,
∵BO=B′O,DO=BO,
∴B′O=OD,
∴△B′OD是等边三角形,
∴,
故答案为:.
三、解答题
17.【解答】解:(1)
=2﹣3
=﹣1;
(2)
=2﹣21﹣5+3
=1﹣2.
18.【解答】解:(1)x2﹣4x+3=0,
(x﹣3)(x﹣1)=0,
∴x﹣3=0或x﹣1=0,
∴x1=3,x2=1;
(2)2x2﹣3x﹣1=0,
∵a=2,b=﹣3,c=﹣1,
∴Δ=9﹣4×2×(﹣1)=17>0,
∴x,
∴x1,x2.
19.【解答】解:(1)调查的总人数为240÷40%=600(人),
体育锻炼为8天的有:600﹣240﹣120﹣150﹣30=60(人),
参加体育锻炼为5天的人数最多,所以众数是5,
600人中,按照参加体育锻炼的天数从少到多排列,第300人和301人都是6天,所以中位数是6;
故答案为:5,6;
(2)补全的条形统计图如图所示:
20.【解答】解:(1)∵,,
∴,
∴x2﹣y2;
(2)∵,,
∴xy=2﹣9=﹣7,x﹣y=6,
∴x2﹣3xy+y2
=(x﹣y)2﹣xy
=36+7
=43.
21.【解答】(1)证明:连接AC交BD于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵M,N是对角线BD的三等分点,
∴BM=DN,
∴OM=ON,
∴四边形AMCN是平行四边形;
(2)解:∵AD=13,BD=18,M,N是对角线BD的三等分点,
∴DM=12,BM=6,
∵AM⊥BD,
∴AM,
∴AB,
∵四边形ABCD是平行四边形,
∴CD=AB.
22.【解答】解:(1)根据题意得Δ=4(m+1)2﹣4(m2+10)≥0,
解得;
(2)当腰长为7时,则x=7是一元二次方程x2﹣2(m+1)x+m2+10=0的一个解,
把x=7代入方程得49﹣14(m+1)+m2+10=0,
整理得m2﹣14m+45=0,
解得m1=9,m2=5,
当m=9时,x1+x2=2(m+1)=20,解得x2=13,
则三角形周长为13+7+7=27;
当m=5时,x1+x2=2(m+1)=12,解得x2=5,
则三角形周长为5+7+7=19;
当7为等腰三角形的底边时,则x1=x2,所以,方程化为4x2﹣44x+121=0,
解得,三边长为,
其周长为,
综上所述,m的值是9或5或,这个三角形的周长为27或19或18.
23.【解答】解:(1)∵a=3,b=5,c=6,
则:,
∴;
,
则三边长依次为、,,代入可得:;
(3)∵,p=8,a=4,
∴b+c=12,则c=12﹣b,
∴
,
∴当b=6时,S有最大值,为.
24.【解答】(1)解:连接DF,
在正方形ABCD中,AD=CD,∠A=∠BCD=∠ADC=90°,
∴∠DCF=90°,
∴∠A=∠DCF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS),
∴DE=DF,∠ADE=∠CDF,
∵∠ADE+∠EDC=90°,
∴∠CDF+∠EDC=∠EDF=90°,
∴∠DEF=45°;
(2)解:∵△DEF为等腰直角三角形,DH⊥EF,
∴DH=FH,∠DHN=∠FHM=90°,
∴∠FMH+∠MFH=90°,
∵∠DCF=90°,∠DNH=∠CNF,
∴∠MFH+∠CNF=∠MFH+∠DNH=90°,
∴∠FMH=∠DNH.
在△FMH和△DNH中.
,
∴△FMH≌△DNH(AAS),
∴FM=DN,
∵BE=4,CN=1,
∴CM=FM﹣CF=DN﹣AE=CD﹣CN﹣AE=BE﹣CN=4﹣1=3;
(3)证明:∵M是BC的中点,
∴BC=2CM=2BM,
设BM=CM=a,AE=CF=b,则AB=CD=BC=2a,BE=2a﹣b,FM=a+b,
∵CM=BE﹣NC,
∴NC=BE﹣CM=2a﹣b﹣a=a﹣b,
∴DN=CD﹣NC=2a﹣(a﹣b)=a+b,
∴DN﹣NC=(a+b)﹣(a﹣b)=2b,
连接EM,
∵DH垂直平分EF,
∴EM=FM=a+b,
∵BM2+BE2=EM2,
∴a2+(2a﹣b)2=(a+b)2,
∴2a=3b,
∴BE=2a﹣b=2b,
∴DN﹣NC=BE.
25.【解答】解:(1)一次函数的图象与反比例函数的图象交于点A(a,3),与y轴交于点B.把x=a,y=3代入得:
,
解得:a=4,
把x=4,y=3代入得:
,
解得:k=12;
(2)直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,点A(4,3),D点的纵坐标是0,
∴点C的纵坐标是3×2﹣0=6,把y=6代入,得x=2,
∴C(2,6),
①如图,作CF⊥x轴于F,交AB于E,作AM⊥y轴于M,
当x=2时,,
∴E(2,2),
∵C(2,6),A(4,3),
∴CE=6﹣2=4,AM=4,
∴;
②由图象可得,当x≥4时,一次函数的图象在反比例函数的图象上或上方,
∴当x≥4时,;
③设,Q(n,0),
∵A(4,3),B(0,1).
当AB为对角线时,,
∴,
∴P(3,4);
当AP为对角线时,
解得,
∴P(﹣6,﹣2),
∵﹣6<0,
∴不合题意,舍去;
当AQ为对角线时,
解得:,
∴P(6,2),
综上P点坐标为(3,4)或(6,2).
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年八年级下学期数学期末考试调研检测卷
满分:120分 时间:120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列电视台标志是中心对称图形的是( )
A. B. C. D.
2.方程x2﹣x﹣1=0的根的情况是( )
A.没有实数根 B.两个不相等的实数根
C.两个相等的实数根 D.无法确定
3.如图,根据平行四边形中所标注的角的度数、边的长度,能判定其为菱形的是( )
A. B. C. D.
4.用反证法证明命题“一个多边形最多有四个内角是直角”时,我们可以先假设( )
A.有三个直角
B.有四个直角
C.至少有四个内角是直角
D.至少有五个内角是直角
5.已知实数a,b在数轴上的位置如图所示,化简的正确结果是( )
A.a+b﹣1 B.1﹣a﹣b C.a﹣b+3 D.b﹣a﹣3
6.保障国家粮食安全是一个永恒的课题,任何时候这根弦都不能松.某农科实验基地,大力开展种子实验,让农民能得到高产、易发芽的种子.该农科实验基地两年前有81种农作物种子,经过两年不断的努力培育新品种,现在有100种农作物种子.若这两年培育新品种数量的平均年增长率为x,则根据题意列出的符合题意的方程是( )
A.100(1﹣2x)=81 B.100(1+2x)=81
C.81(1﹣x)2=100 D.81(1+x)2=100
7.下列说法正确的是( )
A.菱形的四个内角都是直角
B.矩形的对角线互相垂直
C.正方形的每一条对角线平分一组对角
D.平行四边形是轴对称图形
8.已知x1,x2,x3,x4,x5的方差为m,则2x1+1,2x2+1,2x3+1,2x4+1,2x5+1的方差是( )
A.2m+1 B.2m C.4m D.4m+1
9.函数y与y=kx+1(k为常数,k≠0)在同一平面直角坐标系中的大致图象是( )
A.B. C.D.
10.如图,平行四边形ABCD中,点E、F分别在AD、AB上,依次连接EB、EC、FC、FD,图中阴影部分的面积分别为S1、S2、S3、S4,已知S1=3、S2=14、S3=5,则S4的值是( )
A.6 B.7
C.8 D.9
二、填空题(6小题,每题3分,共18分)
11.甲、乙、丙三位同学在五次数学测验中他们成绩的平均分相等,方差分别是3.3,2.8,4.2,则成绩最稳定的同学是 .
12.某校竞选学生会干部,分学生一日常规知识笔试和演讲比赛两个环节,总分均为100分,并按4:6比例计算平均成绩,小明笔试成绩95分,演讲成绩90分,最终平均成绩为 .
13.若a,b是方程x2+x﹣2024=0的两个实数根,则代数式a2﹣b+3的值为 .
14.如图,小华从A点出发,沿直线前进5m后左转24°,再沿直线前进5m,又向左转24°,……照这样走下去,当他第一次回到出发地A点时,一共走过的路程是 .
15.如图, ABCD的对角线AC、BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为 .
16.如图,已知 ABCD的对角线AC与BD相交于点O,∠AOB=60°,将△ABC沿着直线AC翻折,使点B的对应点B′落在原图所在平面上,连结B′D.若BD=5,则B′D的长度为 .
浙教版2024—2025学年八年级下学期数学期末考试调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1);(2).
18.解方程:
(1)x2﹣4x+3=0;(2)2x2﹣3x﹣1=0.
19.某校为了了解初三学生寒假期间参加体育锻炼的天数,随机抽取了部分初三学生进行调查,并绘制了如下的扇形统计图和条形统计图(部分信息未给出),请根据图中提供的信息,回答下列问题:
(1)本次调查中,体育锻炼天数的众数为 天,中位数为 天.
(2)请补全条形统计图.
(3)如果该校初三有1600名学生,请你估计初三约有多少名学生参加体育锻炼的天数不少于7天.
20.已知:,,求下列代数式的值:
(1)x2﹣y2;
(2)x2﹣3xy+y2.
21.如图,在 ABCD中,M,N是对角线BD的三等分点.
(1)求证:四边形AMCN是平行四边形;
(2)若AM⊥BD,AD=13,BD=18,求CD的长.
22.已知x1,x2是关于x的一元二次方程x2﹣2(m+1)x+m2+10=0的两实数根.
(1)求m的取值范围;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求m的值和△ABC的周长.
23.我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a,b,c,记,则其面积.这个公式也被称为海伦﹣秦九韶公式.
(1)当三角形的三边a=3,b=5,c=6时,请你利用公式计算出三角形的面积;
(2)一个三角形的三边长依次为、,,请求出三角形的面积;
(3)若p=8,a=4,求此时三角形面积的最大值.
24.如图,在正方形ABCD中,点E在边AB上,点F在边BC的延长线上,且CF=AE,连接EF交边CD于点N,过点D作DH⊥EF,垂足为H,交BC于点M.
(1)求∠DEF的度数;
(2)当BE=4,CN=1时,求CM的长;
(3)若点M是BC的中点,求证:DN﹣NC=BE.
25.如图,一次函数的图象与反比例函数的图象交于点A(a,3),与y轴交于点B.
(1)求a,k的值;
(2)直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,连接CB.
①求△ABC的面积;
②利用图象信息,直接写出不等式的解集.
③点P在反比例函数的图象上,点Q在x轴上,若以点A,B,P,Q为顶点的四边形是平行四边形,请求出所有符合条件的点P坐标.
参考答案
一、选择题
1—10:ABBBC DCCCA
二、填空题
11.【解答】解:∵S甲2=3.3,S乙2=2.8,S丙2=4.2,
∴S丙2>S甲2>S乙2,
∴成绩比较稳定的是乙;
故答案为:乙.
12.【解答】解:(95×4+90×6)÷(4+6)=92(分),
即最终平均成绩为92分.
故答案为:92分.
13.【解答】解:∵a,b是方程x2+x﹣2024=0的两个实数根,
∴a2+a﹣2024=0,a+b=﹣1,
∴a2=2024﹣a,
∴a2﹣b+3
=2024﹣a﹣b+3
=2024﹣(a+b)+3
=2024+1+3
=2028.
故答案为:2028.
14.【解答】解:由题意可知,当小华回到出发地A点时,行走的路线是正多边形,
∵多边形的外角和为360°,而每一个外角为24°,
∴多边形的边数为360°÷24°=15,
∴小华一共走的路程:15×5=75,
故答案为:75m.
15.【解答】解:∵ ABCD的对角线AC、BD相交于点O,
∴BO=DOBD,BD=2OB,
∴O为BD中点,
∵点E是AB的中点,
∴AB=2BE,BC=2OE,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴CD=2BE.
∵△BEO的周长为8,
∴OB+OE+BE=8,
∴BD+BC+CD=2OB+2OE+2BE=2(OB+OE+BE)=16,
∴△BCD的周长是16,
故答案为16.
16.【解答】解:∵四边形ABCD是平行四边形,BD=5,
∴.
如图,连接OB′.
根据折叠的性质知:∠AOB=∠AOB′=60°,BO=B′O,
∴∠BOB′=∠AOB+∠AOB′=120°,
∴∠B′OD=180°﹣∠BOB′=60°,
∵BO=B′O,DO=BO,
∴B′O=OD,
∴△B′OD是等边三角形,
∴,
故答案为:.
三、解答题
17.【解答】解:(1)
=2﹣3
=﹣1;
(2)
=2﹣21﹣5+3
=1﹣2.
18.【解答】解:(1)x2﹣4x+3=0,
(x﹣3)(x﹣1)=0,
∴x﹣3=0或x﹣1=0,
∴x1=3,x2=1;
(2)2x2﹣3x﹣1=0,
∵a=2,b=﹣3,c=﹣1,
∴Δ=9﹣4×2×(﹣1)=17>0,
∴x,
∴x1,x2.
19.【解答】解:(1)调查的总人数为240÷40%=600(人),
体育锻炼为8天的有:600﹣240﹣120﹣150﹣30=60(人),
参加体育锻炼为5天的人数最多,所以众数是5,
600人中,按照参加体育锻炼的天数从少到多排列,第300人和301人都是6天,所以中位数是6;
故答案为:5,6;
(2)补全的条形统计图如图所示:
20.【解答】解:(1)∵,,
∴,
∴x2﹣y2;
(2)∵,,
∴xy=2﹣9=﹣7,x﹣y=6,
∴x2﹣3xy+y2
=(x﹣y)2﹣xy
=36+7
=43.
21.【解答】(1)证明:连接AC交BD于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵M,N是对角线BD的三等分点,
∴BM=DN,
∴OM=ON,
∴四边形AMCN是平行四边形;
(2)解:∵AD=13,BD=18,M,N是对角线BD的三等分点,
∴DM=12,BM=6,
∵AM⊥BD,
∴AM,
∴AB,
∵四边形ABCD是平行四边形,
∴CD=AB.
22.【解答】解:(1)根据题意得Δ=4(m+1)2﹣4(m2+10)≥0,
解得;
(2)当腰长为7时,则x=7是一元二次方程x2﹣2(m+1)x+m2+10=0的一个解,
把x=7代入方程得49﹣14(m+1)+m2+10=0,
整理得m2﹣14m+45=0,
解得m1=9,m2=5,
当m=9时,x1+x2=2(m+1)=20,解得x2=13,
则三角形周长为13+7+7=27;
当m=5时,x1+x2=2(m+1)=12,解得x2=5,
则三角形周长为5+7+7=19;
当7为等腰三角形的底边时,则x1=x2,所以,方程化为4x2﹣44x+121=0,
解得,三边长为,
其周长为,
综上所述,m的值是9或5或,这个三角形的周长为27或19或18.
23.【解答】解:(1)∵a=3,b=5,c=6,
则:,
∴;
,
则三边长依次为、,,代入可得:;
(3)∵,p=8,a=4,
∴b+c=12,则c=12﹣b,
∴
,
∴当b=6时,S有最大值,为.
24.【解答】(1)解:连接DF,
在正方形ABCD中,AD=CD,∠A=∠BCD=∠ADC=90°,
∴∠DCF=90°,
∴∠A=∠DCF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS),
∴DE=DF,∠ADE=∠CDF,
∵∠ADE+∠EDC=90°,
∴∠CDF+∠EDC=∠EDF=90°,
∴∠DEF=45°;
(2)解:∵△DEF为等腰直角三角形,DH⊥EF,
∴DH=FH,∠DHN=∠FHM=90°,
∴∠FMH+∠MFH=90°,
∵∠DCF=90°,∠DNH=∠CNF,
∴∠MFH+∠CNF=∠MFH+∠DNH=90°,
∴∠FMH=∠DNH.
在△FMH和△DNH中.
,
∴△FMH≌△DNH(AAS),
∴FM=DN,
∵BE=4,CN=1,
∴CM=FM﹣CF=DN﹣AE=CD﹣CN﹣AE=BE﹣CN=4﹣1=3;
(3)证明:∵M是BC的中点,
∴BC=2CM=2BM,
设BM=CM=a,AE=CF=b,则AB=CD=BC=2a,BE=2a﹣b,FM=a+b,
∵CM=BE﹣NC,
∴NC=BE﹣CM=2a﹣b﹣a=a﹣b,
∴DN=CD﹣NC=2a﹣(a﹣b)=a+b,
∴DN﹣NC=(a+b)﹣(a﹣b)=2b,
连接EM,
∵DH垂直平分EF,
∴EM=FM=a+b,
∵BM2+BE2=EM2,
∴a2+(2a﹣b)2=(a+b)2,
∴2a=3b,
∴BE=2a﹣b=2b,
∴DN﹣NC=BE.
25.【解答】解:(1)一次函数的图象与反比例函数的图象交于点A(a,3),与y轴交于点B.把x=a,y=3代入得:
,
解得:a=4,
把x=4,y=3代入得:
,
解得:k=12;
(2)直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,点A(4,3),D点的纵坐标是0,
∴点C的纵坐标是3×2﹣0=6,把y=6代入,得x=2,
∴C(2,6),
①如图,作CF⊥x轴于F,交AB于E,作AM⊥y轴于M,
当x=2时,,
∴E(2,2),
∵C(2,6),A(4,3),
∴CE=6﹣2=4,AM=4,
∴;
②由图象可得,当x≥4时,一次函数的图象在反比例函数的图象上或上方,
∴当x≥4时,;
③设,Q(n,0),
∵A(4,3),B(0,1).
当AB为对角线时,,
∴,
∴P(3,4);
当AP为对角线时,
解得,
∴P(﹣6,﹣2),
∵﹣6<0,
∴不合题意,舍去;
当AQ为对角线时,
解得:,
∴P(6,2),
综上P点坐标为(3,4)或(6,2).
21世纪教育网(www.21cnjy.com)
同课章节目录
