2024-2025学年期末模拟试卷(含解析)六年级下册数学(苏教版)
文档属性
| 名称 | 2024-2025学年期末模拟试卷(含解析)六年级下册数学(苏教版) |  | |
| 格式 | docx | ||
| 文件大小 | 201.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 09:52:32 | ||
图片预览




文档简介
2024-2025学年期末模拟试卷(试题)六年级下册数学(苏教版)
一、单选题
1. 亮亮家住在八楼,为了锻炼身体,他每天都步行上楼,上一层楼大约需要15秒,那么他从一楼到家大约需要( )秒。
A.120 B.105 C.135
2.有一张正方形的彩纸,要在它的里面剪出一个最大的圆,这个圆的面积占整张纸的( )。
A. B.2π C.4/π D.π/2
3.在设计运动场平面图时,先确定( )。
A.比例尺 B.起跑线 C.足球场 D.占地面积
4.连续六个自然数,前三个数的和是90,那么后三个数的和是( )
A.93 B.96 C.99 D.90
5.下面的图形中,( )是圆柱。
A. B. C. D.
6.装饰教室时在一条彩带上挂灯笼,每隔3分米系上一个,刚好系了18个,那么这条彩带最长可以是( )
A.51分米 B.54分米 C.57分米 D.60分米
7.小明从家到学校要走15分钟,他每天要在7∶40到校,他应该在什么时候从家出发,才能准时到校?正确的解答是( )
A.7∶45 B.7∶25 C.7∶15 D.7∶55
8.将一个正方体的6个面都涂上红色,然后把它切成大小相等的27个小正方体,只有一个面涂上红色的小正方体有( )个。
A.4 B.6 C.8 D.10
二、判断题
9.如果,那么5B=6A。( )
10. 一个圆柱与一个圆锥的体积之比是3:1,那么这个圆柱与圆锥一定是等底等高。( )
11.一个圆锥的底面半径扩大2倍,体积也就扩大2倍。( )
12.比值一定,比的前项和后项成正比例。( )
13.折线统计图不但可表示数量的多少,而且能够表示数量增减变化的情况。( )
14.用小正方体拼大正方体,所取的小正方体的个数一定是立方数。( )
15.鸡和狗共8个头,22只脚,则鸡和狗的只数一样多。( )
16.圆的半径增加2厘米,周长就增加12.56厘米,面积也增加12.56平方厘米。( )
三、填空题
17.如果×a=b×(a、b均不为0),则 a:b= ,a比b多 %。
18.天都峰比海平面高1830米,可以记作 米;吐鲁番盆地的海拔为-154米,意思是它的高度比海平面 米。
19.5个棱长是1dm的正方体的表面积之和是 dm ,把它们排成一行拼成一个长方体,这个长方体的表面积是 dm 。
A.5 B.30 C.26 D.22
20.在一幅地图上量得甲、乙两地间的距离为3cm,丙、丁两地间的距离为8cm。已知甲、乙两地间的实际距离为120 km,那么丙、丁两地间的实际距离为 km,这幅地图的比例尺是 。
21.暑假里小丽每3天去一次图书馆,小芳每4天去同一家图书馆,如果7月10日她们在图书馆相遇,那么下次相遇是 月 日。
22.把3米长的圆柱形木料锯成2段,表面积增加了6.28平方分米,原来木料的体积是 立方分米。
23.自然数A除以3余1,除以7余1,除以5余1。A最小是 。
24.小明与小强进行扑克牌点数大小比赛,小强的牌为8、6、4,小明如果按9、7、5的顺序出牌,小强分别按 、 、 出牌可以获胜.
四、口算与估算
25.直接写出得数。
1.98×0.1= 5.6÷0.56= 8.76-7.6= 6.3+5.7÷0.3=
21.21÷7= 0.8×2.5= 0.56÷0.07= 0.7×0.9÷0.7×0.9=
五、竖式计算
26.用竖式计算(得数保留两位小数)
(1)2.04×5.22≈
(2)0.926÷2.3≈
六、脱式计算
27.用简便方法计算。
⑴0.125×0.25×8×4 ⑵
七、解方程
28.求未知数x。
(1)12+6x=36
(2) x﹣x=10
(3) x:=14
八、操作题
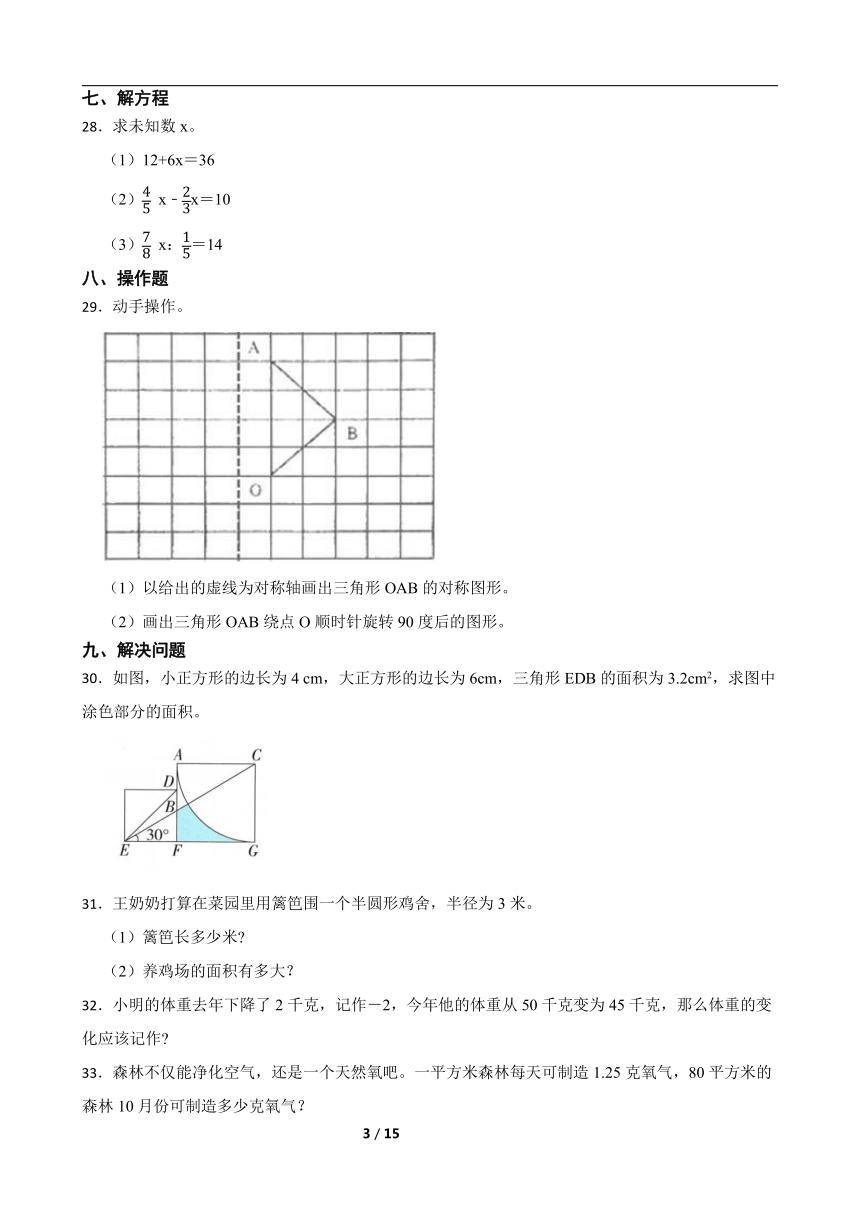
29.动手操作。
(1)以给出的虚线为对称轴画出三角形OAB的对称图形。
(2)画出三角形OAB绕点O顺时针旋转90度后的图形。
九、解决问题
30.如图,小正方形的边长为4 cm,大正方形的边长为6cm,三角形EDB的面积为3.2cm2,求图中涂色部分的面积。
31.王奶奶打算在菜园里用篱笆围一个半圆形鸡舍,半径为3米。
(1)篱笆长多少米
(2)养鸡场的面积有多大?
32.小明的体重去年下降了2千克,记作-2,今年他的体重从50千克变为45千克,那么体重的变化应该记作
33.森林不仅能净化空气,还是一个天然氧吧。一平方米森林每天可制造1.25克氧气,80平方米的森林10月份可制造多少克氧气?
34.如图是一个直角三角形,以一条直角边所在直线为轴旋转一周得到一个圆锥,圆锥的底面直径和高分别为多少?怎样旋转得到的圆锥底面周长最大?
35.一根长6米的圆柱体钢材,如果沿着与底面平行的方向截成相等的三段,表面积就增加25.12平方厘米。已知1立方厘米的钢约重8克,求每段钢材重多少千克? (结果保留整数)
36.一个工程队铺一段铁路,实际工作效率与原计划工作效率的比是6:5,实际工作90天,原计划需要工作多少天?
37.一个卫生间长5m,宽2m,高2.7m,门窗的面积为2.5m2。要在卫生间的四周墙壁贴上墙砖,贴墙砖的高度为2.5m,贴墙砖的面积至少有多少平方米?
答案解析部分
1.【答案】B
【解析】【解答】解:家住在八楼,有7层,
15×7=105(秒)
他从一楼到家大约需要105秒。
故答案为:B。
【分析】上一层楼需要的时间×7=他从一楼到八楼需要的时间。
2.【答案】A
【解析】【解答】解:假设这个正方形彩纸的边长是1,那么剪出一个最大圆的直径是1,半径是1÷2=0.5;
(π×0.5×0.5)÷(1×1)
=π÷1
=。
故答案为:A。
【分析】假设这个正方形彩纸的边长是1,那么剪出一个最大圆的直径是1,半径=直径÷2,这个圆的面积占整张纸的分率=圆的面积÷整张纸的面积;其中,圆的面积=π×半径×半径,整张纸的面积=边长×边长。
3.【答案】A
【解析】【解答】解:在设计运动场平面图时,先确定比例尺。
故答案为:A
【分析】在设计运动场的平面图时,要根据一定的比例把各部分缩小,因此先确定比例尺。
4.【答案】C
【解析】【解答】解:前三个数中间的数为:90÷3=30,所以前三个数为29,30,31;
后三个数应为32,33,34;
后三个数的和为:32+33+34=99;
故答案为:C。
【分析】前三个数的和是90,根据“三个数的和÷数的个数=平均数”求出前三个数中间的数,为90÷3=30,进而得出前三个数和后三个数,然后求出和即可选择。
5.【答案】A
【解析】【解答】解: 是圆柱。
故答案为:A。
【分析】圆柱是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。它有2个大小相同、相互平行的圆形底面和1个曲面侧面。其侧面展开是矩形。本题据此解答。
6.【答案】C
【解析】【解答】解:(18+1)×3
=19×3
=57(分米)。
故答案为:C。
【分析】这条彩带最长时是两端不挂灯笼时的长度,彩带最长=(灯笼的个数+1)×间距。
7.【答案】B
【解析】40-15=25(分)
答:他应该在7∶25从家出发,才能准时到校.
8.【答案】B
【解析】【解答】解:把它切成大小相等的27个小正方体,说明一条棱上有3个小正方体,
6×=6×1=6(个)。
故答案为:B。
【分析】用n表示大正方体每条棱上小正方体的块数,小正方体的涂色规律为:
三面涂色的小正方体的块数=8块(顶点的个数);
两面涂色的小正方体的块数=12(n-2);
一面涂色的小正方体的块数=6乘(n-2)的平方;
没有涂色的小正方体的块数=(n-2)的立方。
9.【答案】正确
【解析】【解答】解:=,所以6A=5B。
故答案为:正确。
【分析】香江除法改写成分数的形式,再根据比例的基本性质得出结果。比例的基本性质:两外项的积等于两内项的积。
10.【答案】错误
【解析】【解答】解:设圆柱的底面积为12,高为3,则圆柱的体积为:12×3=36
圆锥的底面积为6,高为6,则圆锥的体积为:6×6×=12
此时圆柱的体积:圆锥的体积=36:12=3:1,但是它们的底面积与高都不相等,原题干说法错误。
故答案为:错误。
【分析】解决此类问题,采用举反例的方法是一种有效的简洁的方法,这要求学生要熟练掌握圆柱与圆锥的体积公式。
11.【答案】错误
【解析】【解答】 一个圆锥的底面半径扩大2倍,高不变,体积会扩大2×2=4倍,原题说法错误。
故答案为:错误。
【分析】圆锥的体积公式:V=πr2h,一个圆锥的体积大小受底面半径和高的大小影响,据此判断。
12.【答案】正确
【解析】【解答】解:前项:后项=比值(一定),前项和后项成正比例,原题说法正确。
故答案为:正确。
【分析】前项和后项的商就是比值,前项和后项的商一定,前项和后项就成正比例关系。
13.【答案】正确
【解析】【解答】解:折线统计图不但可表示数量的多少,而且能够表示数量增减变化的情况。
故答案为:正确。
【分析】折线统计图用折线的起伏表示数据的增减变化情况。它不仅可以表示数量的多少,而且可以反映数据的增减变化情况。
14.【答案】正确
【解析】【解答】解:用小正方体拼大正方体,所取的小正方体的个数一定是立方数。
故答案为:正确。
【分析】大正方体需要小正方体的个数有23、33、43、……,所以用小正方体拼大正方体,所取的小正方体的个数一定是立方数。
15.【答案】错误
【解析】【解答】解:假设全是鸡,那么狗的只数是:(22-8×2)÷(4-2)=3(只),8-3=5(只),所以鸡和狗的只数不一样多。
故答案为:错误。
【分析】假设全是鸡,那么狗的只数=(一共有脚的只数-一只鸡有脚的只数×一共有头的个数)÷一只狗比一只鸡多的脚的只数,鸡的只数=一共有头的个数-狗的只数,然后比较鸡和狗的只数。
16.【答案】错误
【解析】【解答】3.14×2×2=12.56(厘米),故周长增加12.56厘米。
但,面积的增加,并不确定。
故答案为:错误
【分析】圆的周长,C=2πr,当r增加2厘米时,C=2π(r+2)=2πr+4π。半径增加2厘米时,增加的部分是一个圆环,圆环的面积,S=π(R -r ),圆的半径不能确定的情况下,无法确定圆环的面积。
17.【答案】2:1;100
【解析】【解答】解:a:b=:=2:1;
(2-1)÷1
=1÷1
=100%。
故答案为:2:1;100。
【分析】比例的基本性质:在比例里,两个内项积等于两个外项积,因为×a=b×,所以 a:b=:=2:1; a比b多的百分率=(a-b)÷b。
18.【答案】+1830;低154
【解析】【解答】解:天都峰比海平面高1830米,可以记作+1830米;吐鲁番盆地的海拔为-154米,意思是它的高度比海平面底154米
故答案为:+1830,低154。
【分析】以海平面作为基准,高于海平面的高度用正数表示,低于海平面的高度用负数表示,据此解答即可。
19.【答案】B;D
【解析】【解答】解:1×1×6×5=30(平方分米)
排成一排,长是5分米,宽是1分米,高是1分米
(5×1+5×1+1×1)×2=11×2=22(平方分米)
故答案为:B;D。
【分析】正方体的棱长×棱长×6=正方体的表面积,;正方体的表面积×5=5个正方体的表面积;
(长×宽+长×高+宽×高)×2=长方体的表面积。
20.【答案】320;1:4000000
【解析】【解答】解:比例尺=3cm:120km
=3cm:12000000cm
=1:4000000
8÷=32000000(cm)=320km
故答案为:320,1:4000000。
【分析】分析题干,已知甲、乙两地的图上距离是3cm,实际距离是120km,根据比例尺=图上距离:实际距离,得到这幅地图的比例尺是3cm:120km,根据1km=100000cm和比的性质,化简得到比例尺=1:4000000;又已知丙、丁两地的图上距离,然后根据实际距离=图上距离÷比例尺,代入数据计算即可得到丙、丁两地的实际距离。
21.【答案】7;22
【解析】【解答】解:3和4的最小公倍数是12,7月10日过12天是7月22日,下次相遇是7月22日。
故答案为:7;22。
【分析】两人下次相遇经过的天数一定是3和4的最小公倍数,由此确定3和4的最小公倍数,再从7月10日起推算下次相遇的日期即可。
22.【答案】94.2
【解析】【解答】解:3米=30分米
6.28÷2×30
=3.14×30
=94.2(立方分米)。
故答案为:94.2。
【分析】先单位换算3米=30分米,原来木料的体积=底面积×高;其中,底面积=增加的表面积÷增加底面的个数。
23.【答案】106
【解析】【解答】3×7×5
=21×5
=105
105+1=106
故答案为:106。
【分析】此题主要考查了最小公倍数的应用,先求出这三个数的最小公倍数,然后用它们的最小公倍数加余数,即可得到A最小是多少。
24.【答案】4;8;6
【解析】【解答】解:小明出9,小强出4,小强输;小明出7,小强出8,小强胜;小明出5,小强出6,小强胜。小强按4、8、6出牌可以获胜。
故答案为:4;8;6.
【分析】小强的牌整体比小明的小,因为小明的出牌顺序一定,那么小强合理出牌即可确保三局两胜。
25.【答案】
1.98×0.1=0.198 5.6÷0.56=10 8.76-7.6=1.16 6.3+5.7÷0.3=25.3
21.21÷7=3.03 0.8×2.5=2 0.56÷0.07=8 0.7×0.9÷0.7×0.9=0.81
【解析】【分析】计算小数的加法和减法,先把各数的小数点对齐, 再按照整数加减法的法则进行计算,最后在得数里对齐横线上的小数点点上小数点;
除数是整数的小数除法:从被除数的高位除起,除数有几位,就看被除数的前几位;除到被除数的哪一位,就把商写在哪一位的上面;商的小数点和被除数的小数点对齐;
一个数除以小数,先移动除数的小数点,使它变成整数;除数的小数点向右移动几位,被除数的小数点也向右移动几位;位数不够时,在被除数的末尾用0补足;最后按照除数是整数的除法进行计算。
26.【答案】(1)2.04×5.22≈10.65;
(2)0.926÷2.3≈0.40;
【解析】【分析】小数乘法计算法则:先按照整数乘法的计算法则进行计算,再看因数中有几位小数,积的末尾就有几位小数。
除数是小数的计算方法:①移动除数的小数点,使它变成整数;②看除数原来有几位小数,就把被除数小数点向右移动相同的几位(位数不够时补0);③按照除数是整数的除法进行计算;④商的小数点与被除数的小数点对齐。
保留两位小数,即是对千分位上的数字四舍五入。
27.【答案】解:⑴
⑵
【解析】【分析】第一题:利用乘法交换律和结合律计算;
第二题:把除法化成乘法,再利用乘法分配律进行简算。
乘法分配律:a×b+a×c=a×(b+c)
28.【答案】(1)解:12+6x=36
12+6x-12=36-12
6x=24
6x÷6=24÷6
x=4
(2)解: x- x=10
x=10
x÷ =10÷
x=75
(3)解: x: =14
x= ×14
x÷ = ÷
x=3.2
【解析】【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
(1)综合应用等式的性质解方程;
(2)应用等式的性质2解方程;
比例的基本性质:在比例里,两个内项积等于两个外项积,(3)依据比例的基本性质解比例。
29.【答案】(1)
(2)
【解析】【分析】(1)画轴对称图形的步骤:①点出关键点,找出所有的关键点,即图形中所有线段的端点;②确定关键点到对称轴的距离,关键点离对称轴多远,对称点就离对称轴多远;③点出对称点;④连线,按照给出的一半图形将所有对称点连接成线段,据此作图;
(2)画旋转图形的方法:把图形的关键点与旋转中心连接,再量出题目要求旋转的角度,最后依次连接各对应点即可,据此作图。
30.【答案】解:4-3.2×2÷4
=4-6.4÷4
=4-1.6
=2.4( cm)
(2.4+6)×6÷2
=8.4×6÷2
=50.4÷2
=25.2(cm2)
180°-90°-30°=60°
25.2-18.84
=6.36(cm2)
答: 涂色部分的面积为6.36cm2。
【解析】【分析】根据三角形 EDB 的面积及其底边DB上的高,可求出底边 DB的长度,于是可求出梯形BFGC 的上底BF的长,可得梯形 BFGC的面积。而梯形BFGC中空白部分扇形的面积占其所在圆的面积的 ,因此可得空白部分扇形的面积,用梯形 BFGC 的面积减去空白部分扇形的面积,就是涂色部分的面积。
31.【答案】(1)解:2×π×3÷2+3×2
=9.42+6
=15.42(米)
答:篱笆长15.42米。
(2)解:×π×32
=28.26÷2
=14.13(平方米)
答:养鸡场的面积有14.13平方米。
【解析】【分析】(1)根据半圆的周长=2πr÷2+2r可计算出篱笆的长度;
(2)根据半圆的面积=πr2计算出养鸡场的面积即可。
32.【答案】解:从50千克变成45千克,减轻了5千克,所以应该记作-5
【解析】【解答】从50千克变成45千克,减轻了5千克,所以应该记作-5
【分析】考查了对负数的理解和应用
33.【答案】解:10月份=31天
1.25×80×31
=100×31
=3100(克)
答:80平方米的森林10月份可制造3100克氧气。
【解析】【分析】80平方米的森林10月份可制造氧气的质量=平均一平方米森林每天可制造氧气的质量×森林的面积×10月份的天数。
34.【答案】解:5×2=10(cm) 2×3.14×5=31.4(cm)
4×2=8(cm) 2×3.14×4=25.12(cm)
31.4>25.12
答:圆锥的底面直径为10cm,高为4cm或底面直径为8cm,高为5cm。
将三角形以4cm的直角边所在直线为轴旋转得到的圆锥底面周长最大。
【解析】【分析】如果以3cm的边为轴旋转,那么底面直径为4×2=8(cm),高为3cm。如果以4cm的边为轴旋转,那么底面直径为3×2=6(cm),高为4cm。
如果以3cm的边为轴旋转,那么底面周长为3.14×8=25.12(cm)。如果以4cm的边为轴旋转,那么底面周长为3.14×6=18.84(cm)。
将三角形以4cm的直角边所在直线为轴旋转得到的圆锥底面周长最大
35.【答案】解:6米÷3=2米=200厘米
25.12÷4=6.28(平方厘米)
6.28×200=1256(立方厘米)
1256×8=10048(克)≈10(千克)
答:每段钢材重10千克。
【解析】【分析】沿着与底面平行的方向截成相等的三段,增加了4个底面积,增加的面积÷4=圆柱的底面积,圆柱的底面积×一段的高度=一段的体积,一段的体积×每立方厘米的质量=一段的质量。
36.【答案】解:根据实际工作效率与原计划工作效率的比是6:5可得出实际工作时间:原计划时间=5:6;
90:原计划需要的时间=5:6
5×原计划需要的时间=90×6
原计划的时间=90×6÷5
原计划的时间=108
答:原计划需要工作108天。
【解析】【分析】工作总量=工作效率×工作时间,工作总量一定,则工作效率和工作时间成反比例,根据实际工作效率与原计划工作效率的比,即可得出实际工作时间与原计划工作时间的比,再根据实际工作时间即可得出原计划需要工作的时间。
37.【答案】解:(5×2.5+2×2.5)×2-2.5
=(12.5+5)×2-2.5
=17.5×2-2.5
=35-2.5
=32.5(平方米)
答:贴墙砖的面积至少有32.5平方米。
【解析】【分析】贴墙砖的面积至少=(长×高+宽×高)×2-门窗面积。
1 / 1
一、单选题
1. 亮亮家住在八楼,为了锻炼身体,他每天都步行上楼,上一层楼大约需要15秒,那么他从一楼到家大约需要( )秒。
A.120 B.105 C.135
2.有一张正方形的彩纸,要在它的里面剪出一个最大的圆,这个圆的面积占整张纸的( )。
A. B.2π C.4/π D.π/2
3.在设计运动场平面图时,先确定( )。
A.比例尺 B.起跑线 C.足球场 D.占地面积
4.连续六个自然数,前三个数的和是90,那么后三个数的和是( )
A.93 B.96 C.99 D.90
5.下面的图形中,( )是圆柱。
A. B. C. D.
6.装饰教室时在一条彩带上挂灯笼,每隔3分米系上一个,刚好系了18个,那么这条彩带最长可以是( )
A.51分米 B.54分米 C.57分米 D.60分米
7.小明从家到学校要走15分钟,他每天要在7∶40到校,他应该在什么时候从家出发,才能准时到校?正确的解答是( )
A.7∶45 B.7∶25 C.7∶15 D.7∶55
8.将一个正方体的6个面都涂上红色,然后把它切成大小相等的27个小正方体,只有一个面涂上红色的小正方体有( )个。
A.4 B.6 C.8 D.10
二、判断题
9.如果,那么5B=6A。( )
10. 一个圆柱与一个圆锥的体积之比是3:1,那么这个圆柱与圆锥一定是等底等高。( )
11.一个圆锥的底面半径扩大2倍,体积也就扩大2倍。( )
12.比值一定,比的前项和后项成正比例。( )
13.折线统计图不但可表示数量的多少,而且能够表示数量增减变化的情况。( )
14.用小正方体拼大正方体,所取的小正方体的个数一定是立方数。( )
15.鸡和狗共8个头,22只脚,则鸡和狗的只数一样多。( )
16.圆的半径增加2厘米,周长就增加12.56厘米,面积也增加12.56平方厘米。( )
三、填空题
17.如果×a=b×(a、b均不为0),则 a:b= ,a比b多 %。
18.天都峰比海平面高1830米,可以记作 米;吐鲁番盆地的海拔为-154米,意思是它的高度比海平面 米。
19.5个棱长是1dm的正方体的表面积之和是 dm ,把它们排成一行拼成一个长方体,这个长方体的表面积是 dm 。
A.5 B.30 C.26 D.22
20.在一幅地图上量得甲、乙两地间的距离为3cm,丙、丁两地间的距离为8cm。已知甲、乙两地间的实际距离为120 km,那么丙、丁两地间的实际距离为 km,这幅地图的比例尺是 。
21.暑假里小丽每3天去一次图书馆,小芳每4天去同一家图书馆,如果7月10日她们在图书馆相遇,那么下次相遇是 月 日。
22.把3米长的圆柱形木料锯成2段,表面积增加了6.28平方分米,原来木料的体积是 立方分米。
23.自然数A除以3余1,除以7余1,除以5余1。A最小是 。
24.小明与小强进行扑克牌点数大小比赛,小强的牌为8、6、4,小明如果按9、7、5的顺序出牌,小强分别按 、 、 出牌可以获胜.
四、口算与估算
25.直接写出得数。
1.98×0.1= 5.6÷0.56= 8.76-7.6= 6.3+5.7÷0.3=
21.21÷7= 0.8×2.5= 0.56÷0.07= 0.7×0.9÷0.7×0.9=
五、竖式计算
26.用竖式计算(得数保留两位小数)
(1)2.04×5.22≈
(2)0.926÷2.3≈
六、脱式计算
27.用简便方法计算。
⑴0.125×0.25×8×4 ⑵
七、解方程
28.求未知数x。
(1)12+6x=36
(2) x﹣x=10
(3) x:=14
八、操作题
29.动手操作。
(1)以给出的虚线为对称轴画出三角形OAB的对称图形。
(2)画出三角形OAB绕点O顺时针旋转90度后的图形。
九、解决问题
30.如图,小正方形的边长为4 cm,大正方形的边长为6cm,三角形EDB的面积为3.2cm2,求图中涂色部分的面积。
31.王奶奶打算在菜园里用篱笆围一个半圆形鸡舍,半径为3米。
(1)篱笆长多少米
(2)养鸡场的面积有多大?
32.小明的体重去年下降了2千克,记作-2,今年他的体重从50千克变为45千克,那么体重的变化应该记作
33.森林不仅能净化空气,还是一个天然氧吧。一平方米森林每天可制造1.25克氧气,80平方米的森林10月份可制造多少克氧气?
34.如图是一个直角三角形,以一条直角边所在直线为轴旋转一周得到一个圆锥,圆锥的底面直径和高分别为多少?怎样旋转得到的圆锥底面周长最大?
35.一根长6米的圆柱体钢材,如果沿着与底面平行的方向截成相等的三段,表面积就增加25.12平方厘米。已知1立方厘米的钢约重8克,求每段钢材重多少千克? (结果保留整数)
36.一个工程队铺一段铁路,实际工作效率与原计划工作效率的比是6:5,实际工作90天,原计划需要工作多少天?
37.一个卫生间长5m,宽2m,高2.7m,门窗的面积为2.5m2。要在卫生间的四周墙壁贴上墙砖,贴墙砖的高度为2.5m,贴墙砖的面积至少有多少平方米?
答案解析部分
1.【答案】B
【解析】【解答】解:家住在八楼,有7层,
15×7=105(秒)
他从一楼到家大约需要105秒。
故答案为:B。
【分析】上一层楼需要的时间×7=他从一楼到八楼需要的时间。
2.【答案】A
【解析】【解答】解:假设这个正方形彩纸的边长是1,那么剪出一个最大圆的直径是1,半径是1÷2=0.5;
(π×0.5×0.5)÷(1×1)
=π÷1
=。
故答案为:A。
【分析】假设这个正方形彩纸的边长是1,那么剪出一个最大圆的直径是1,半径=直径÷2,这个圆的面积占整张纸的分率=圆的面积÷整张纸的面积;其中,圆的面积=π×半径×半径,整张纸的面积=边长×边长。
3.【答案】A
【解析】【解答】解:在设计运动场平面图时,先确定比例尺。
故答案为:A
【分析】在设计运动场的平面图时,要根据一定的比例把各部分缩小,因此先确定比例尺。
4.【答案】C
【解析】【解答】解:前三个数中间的数为:90÷3=30,所以前三个数为29,30,31;
后三个数应为32,33,34;
后三个数的和为:32+33+34=99;
故答案为:C。
【分析】前三个数的和是90,根据“三个数的和÷数的个数=平均数”求出前三个数中间的数,为90÷3=30,进而得出前三个数和后三个数,然后求出和即可选择。
5.【答案】A
【解析】【解答】解: 是圆柱。
故答案为:A。
【分析】圆柱是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。它有2个大小相同、相互平行的圆形底面和1个曲面侧面。其侧面展开是矩形。本题据此解答。
6.【答案】C
【解析】【解答】解:(18+1)×3
=19×3
=57(分米)。
故答案为:C。
【分析】这条彩带最长时是两端不挂灯笼时的长度,彩带最长=(灯笼的个数+1)×间距。
7.【答案】B
【解析】40-15=25(分)
答:他应该在7∶25从家出发,才能准时到校.
8.【答案】B
【解析】【解答】解:把它切成大小相等的27个小正方体,说明一条棱上有3个小正方体,
6×=6×1=6(个)。
故答案为:B。
【分析】用n表示大正方体每条棱上小正方体的块数,小正方体的涂色规律为:
三面涂色的小正方体的块数=8块(顶点的个数);
两面涂色的小正方体的块数=12(n-2);
一面涂色的小正方体的块数=6乘(n-2)的平方;
没有涂色的小正方体的块数=(n-2)的立方。
9.【答案】正确
【解析】【解答】解:=,所以6A=5B。
故答案为:正确。
【分析】香江除法改写成分数的形式,再根据比例的基本性质得出结果。比例的基本性质:两外项的积等于两内项的积。
10.【答案】错误
【解析】【解答】解:设圆柱的底面积为12,高为3,则圆柱的体积为:12×3=36
圆锥的底面积为6,高为6,则圆锥的体积为:6×6×=12
此时圆柱的体积:圆锥的体积=36:12=3:1,但是它们的底面积与高都不相等,原题干说法错误。
故答案为:错误。
【分析】解决此类问题,采用举反例的方法是一种有效的简洁的方法,这要求学生要熟练掌握圆柱与圆锥的体积公式。
11.【答案】错误
【解析】【解答】 一个圆锥的底面半径扩大2倍,高不变,体积会扩大2×2=4倍,原题说法错误。
故答案为:错误。
【分析】圆锥的体积公式:V=πr2h,一个圆锥的体积大小受底面半径和高的大小影响,据此判断。
12.【答案】正确
【解析】【解答】解:前项:后项=比值(一定),前项和后项成正比例,原题说法正确。
故答案为:正确。
【分析】前项和后项的商就是比值,前项和后项的商一定,前项和后项就成正比例关系。
13.【答案】正确
【解析】【解答】解:折线统计图不但可表示数量的多少,而且能够表示数量增减变化的情况。
故答案为:正确。
【分析】折线统计图用折线的起伏表示数据的增减变化情况。它不仅可以表示数量的多少,而且可以反映数据的增减变化情况。
14.【答案】正确
【解析】【解答】解:用小正方体拼大正方体,所取的小正方体的个数一定是立方数。
故答案为:正确。
【分析】大正方体需要小正方体的个数有23、33、43、……,所以用小正方体拼大正方体,所取的小正方体的个数一定是立方数。
15.【答案】错误
【解析】【解答】解:假设全是鸡,那么狗的只数是:(22-8×2)÷(4-2)=3(只),8-3=5(只),所以鸡和狗的只数不一样多。
故答案为:错误。
【分析】假设全是鸡,那么狗的只数=(一共有脚的只数-一只鸡有脚的只数×一共有头的个数)÷一只狗比一只鸡多的脚的只数,鸡的只数=一共有头的个数-狗的只数,然后比较鸡和狗的只数。
16.【答案】错误
【解析】【解答】3.14×2×2=12.56(厘米),故周长增加12.56厘米。
但,面积的增加,并不确定。
故答案为:错误
【分析】圆的周长,C=2πr,当r增加2厘米时,C=2π(r+2)=2πr+4π。半径增加2厘米时,增加的部分是一个圆环,圆环的面积,S=π(R -r ),圆的半径不能确定的情况下,无法确定圆环的面积。
17.【答案】2:1;100
【解析】【解答】解:a:b=:=2:1;
(2-1)÷1
=1÷1
=100%。
故答案为:2:1;100。
【分析】比例的基本性质:在比例里,两个内项积等于两个外项积,因为×a=b×,所以 a:b=:=2:1; a比b多的百分率=(a-b)÷b。
18.【答案】+1830;低154
【解析】【解答】解:天都峰比海平面高1830米,可以记作+1830米;吐鲁番盆地的海拔为-154米,意思是它的高度比海平面底154米
故答案为:+1830,低154。
【分析】以海平面作为基准,高于海平面的高度用正数表示,低于海平面的高度用负数表示,据此解答即可。
19.【答案】B;D
【解析】【解答】解:1×1×6×5=30(平方分米)
排成一排,长是5分米,宽是1分米,高是1分米
(5×1+5×1+1×1)×2=11×2=22(平方分米)
故答案为:B;D。
【分析】正方体的棱长×棱长×6=正方体的表面积,;正方体的表面积×5=5个正方体的表面积;
(长×宽+长×高+宽×高)×2=长方体的表面积。
20.【答案】320;1:4000000
【解析】【解答】解:比例尺=3cm:120km
=3cm:12000000cm
=1:4000000
8÷=32000000(cm)=320km
故答案为:320,1:4000000。
【分析】分析题干,已知甲、乙两地的图上距离是3cm,实际距离是120km,根据比例尺=图上距离:实际距离,得到这幅地图的比例尺是3cm:120km,根据1km=100000cm和比的性质,化简得到比例尺=1:4000000;又已知丙、丁两地的图上距离,然后根据实际距离=图上距离÷比例尺,代入数据计算即可得到丙、丁两地的实际距离。
21.【答案】7;22
【解析】【解答】解:3和4的最小公倍数是12,7月10日过12天是7月22日,下次相遇是7月22日。
故答案为:7;22。
【分析】两人下次相遇经过的天数一定是3和4的最小公倍数,由此确定3和4的最小公倍数,再从7月10日起推算下次相遇的日期即可。
22.【答案】94.2
【解析】【解答】解:3米=30分米
6.28÷2×30
=3.14×30
=94.2(立方分米)。
故答案为:94.2。
【分析】先单位换算3米=30分米,原来木料的体积=底面积×高;其中,底面积=增加的表面积÷增加底面的个数。
23.【答案】106
【解析】【解答】3×7×5
=21×5
=105
105+1=106
故答案为:106。
【分析】此题主要考查了最小公倍数的应用,先求出这三个数的最小公倍数,然后用它们的最小公倍数加余数,即可得到A最小是多少。
24.【答案】4;8;6
【解析】【解答】解:小明出9,小强出4,小强输;小明出7,小强出8,小强胜;小明出5,小强出6,小强胜。小强按4、8、6出牌可以获胜。
故答案为:4;8;6.
【分析】小强的牌整体比小明的小,因为小明的出牌顺序一定,那么小强合理出牌即可确保三局两胜。
25.【答案】
1.98×0.1=0.198 5.6÷0.56=10 8.76-7.6=1.16 6.3+5.7÷0.3=25.3
21.21÷7=3.03 0.8×2.5=2 0.56÷0.07=8 0.7×0.9÷0.7×0.9=0.81
【解析】【分析】计算小数的加法和减法,先把各数的小数点对齐, 再按照整数加减法的法则进行计算,最后在得数里对齐横线上的小数点点上小数点;
除数是整数的小数除法:从被除数的高位除起,除数有几位,就看被除数的前几位;除到被除数的哪一位,就把商写在哪一位的上面;商的小数点和被除数的小数点对齐;
一个数除以小数,先移动除数的小数点,使它变成整数;除数的小数点向右移动几位,被除数的小数点也向右移动几位;位数不够时,在被除数的末尾用0补足;最后按照除数是整数的除法进行计算。
26.【答案】(1)2.04×5.22≈10.65;
(2)0.926÷2.3≈0.40;
【解析】【分析】小数乘法计算法则:先按照整数乘法的计算法则进行计算,再看因数中有几位小数,积的末尾就有几位小数。
除数是小数的计算方法:①移动除数的小数点,使它变成整数;②看除数原来有几位小数,就把被除数小数点向右移动相同的几位(位数不够时补0);③按照除数是整数的除法进行计算;④商的小数点与被除数的小数点对齐。
保留两位小数,即是对千分位上的数字四舍五入。
27.【答案】解:⑴
⑵
【解析】【分析】第一题:利用乘法交换律和结合律计算;
第二题:把除法化成乘法,再利用乘法分配律进行简算。
乘法分配律:a×b+a×c=a×(b+c)
28.【答案】(1)解:12+6x=36
12+6x-12=36-12
6x=24
6x÷6=24÷6
x=4
(2)解: x- x=10
x=10
x÷ =10÷
x=75
(3)解: x: =14
x= ×14
x÷ = ÷
x=3.2
【解析】【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
(1)综合应用等式的性质解方程;
(2)应用等式的性质2解方程;
比例的基本性质:在比例里,两个内项积等于两个外项积,(3)依据比例的基本性质解比例。
29.【答案】(1)
(2)
【解析】【分析】(1)画轴对称图形的步骤:①点出关键点,找出所有的关键点,即图形中所有线段的端点;②确定关键点到对称轴的距离,关键点离对称轴多远,对称点就离对称轴多远;③点出对称点;④连线,按照给出的一半图形将所有对称点连接成线段,据此作图;
(2)画旋转图形的方法:把图形的关键点与旋转中心连接,再量出题目要求旋转的角度,最后依次连接各对应点即可,据此作图。
30.【答案】解:4-3.2×2÷4
=4-6.4÷4
=4-1.6
=2.4( cm)
(2.4+6)×6÷2
=8.4×6÷2
=50.4÷2
=25.2(cm2)
180°-90°-30°=60°
25.2-18.84
=6.36(cm2)
答: 涂色部分的面积为6.36cm2。
【解析】【分析】根据三角形 EDB 的面积及其底边DB上的高,可求出底边 DB的长度,于是可求出梯形BFGC 的上底BF的长,可得梯形 BFGC的面积。而梯形BFGC中空白部分扇形的面积占其所在圆的面积的 ,因此可得空白部分扇形的面积,用梯形 BFGC 的面积减去空白部分扇形的面积,就是涂色部分的面积。
31.【答案】(1)解:2×π×3÷2+3×2
=9.42+6
=15.42(米)
答:篱笆长15.42米。
(2)解:×π×32
=28.26÷2
=14.13(平方米)
答:养鸡场的面积有14.13平方米。
【解析】【分析】(1)根据半圆的周长=2πr÷2+2r可计算出篱笆的长度;
(2)根据半圆的面积=πr2计算出养鸡场的面积即可。
32.【答案】解:从50千克变成45千克,减轻了5千克,所以应该记作-5
【解析】【解答】从50千克变成45千克,减轻了5千克,所以应该记作-5
【分析】考查了对负数的理解和应用
33.【答案】解:10月份=31天
1.25×80×31
=100×31
=3100(克)
答:80平方米的森林10月份可制造3100克氧气。
【解析】【分析】80平方米的森林10月份可制造氧气的质量=平均一平方米森林每天可制造氧气的质量×森林的面积×10月份的天数。
34.【答案】解:5×2=10(cm) 2×3.14×5=31.4(cm)
4×2=8(cm) 2×3.14×4=25.12(cm)
31.4>25.12
答:圆锥的底面直径为10cm,高为4cm或底面直径为8cm,高为5cm。
将三角形以4cm的直角边所在直线为轴旋转得到的圆锥底面周长最大。
【解析】【分析】如果以3cm的边为轴旋转,那么底面直径为4×2=8(cm),高为3cm。如果以4cm的边为轴旋转,那么底面直径为3×2=6(cm),高为4cm。
如果以3cm的边为轴旋转,那么底面周长为3.14×8=25.12(cm)。如果以4cm的边为轴旋转,那么底面周长为3.14×6=18.84(cm)。
将三角形以4cm的直角边所在直线为轴旋转得到的圆锥底面周长最大
35.【答案】解:6米÷3=2米=200厘米
25.12÷4=6.28(平方厘米)
6.28×200=1256(立方厘米)
1256×8=10048(克)≈10(千克)
答:每段钢材重10千克。
【解析】【分析】沿着与底面平行的方向截成相等的三段,增加了4个底面积,增加的面积÷4=圆柱的底面积,圆柱的底面积×一段的高度=一段的体积,一段的体积×每立方厘米的质量=一段的质量。
36.【答案】解:根据实际工作效率与原计划工作效率的比是6:5可得出实际工作时间:原计划时间=5:6;
90:原计划需要的时间=5:6
5×原计划需要的时间=90×6
原计划的时间=90×6÷5
原计划的时间=108
答:原计划需要工作108天。
【解析】【分析】工作总量=工作效率×工作时间,工作总量一定,则工作效率和工作时间成反比例,根据实际工作效率与原计划工作效率的比,即可得出实际工作时间与原计划工作时间的比,再根据实际工作时间即可得出原计划需要工作的时间。
37.【答案】解:(5×2.5+2×2.5)×2-2.5
=(12.5+5)×2-2.5
=17.5×2-2.5
=35-2.5
=32.5(平方米)
答:贴墙砖的面积至少有32.5平方米。
【解析】【分析】贴墙砖的面积至少=(长×高+宽×高)×2-门窗面积。
1 / 1
同课章节目录
