人教版(2024)七年级下册数学期末考试试题(含答案)
文档属性
| 名称 | 人教版(2024)七年级下册数学期末考试试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 15:07:19 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版七年级下册数学期末考试试题
一、单选题:(每小题只有一个答案正确,每小题3分,共36分)
1.下列各数中,无理数是( )
A. B. C. D.
2.如图,直线,被直线所截,若,,则( )
A. B. C. D.
3.在下列各式中正确的是( )
A. B. C. D.
4.在平面直角坐标系中,如果点在第三象限,那么的取值范围为( )
A. B. C. D.
5.如图,将沿水平方向向右平移到的位置,已知点A和D之间的距离为1,,则的长为( )
A.2 B.3 C.4 D.5
6.中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹两,牛每头两,根据题意可列方程组为( )
A. B. C. D.
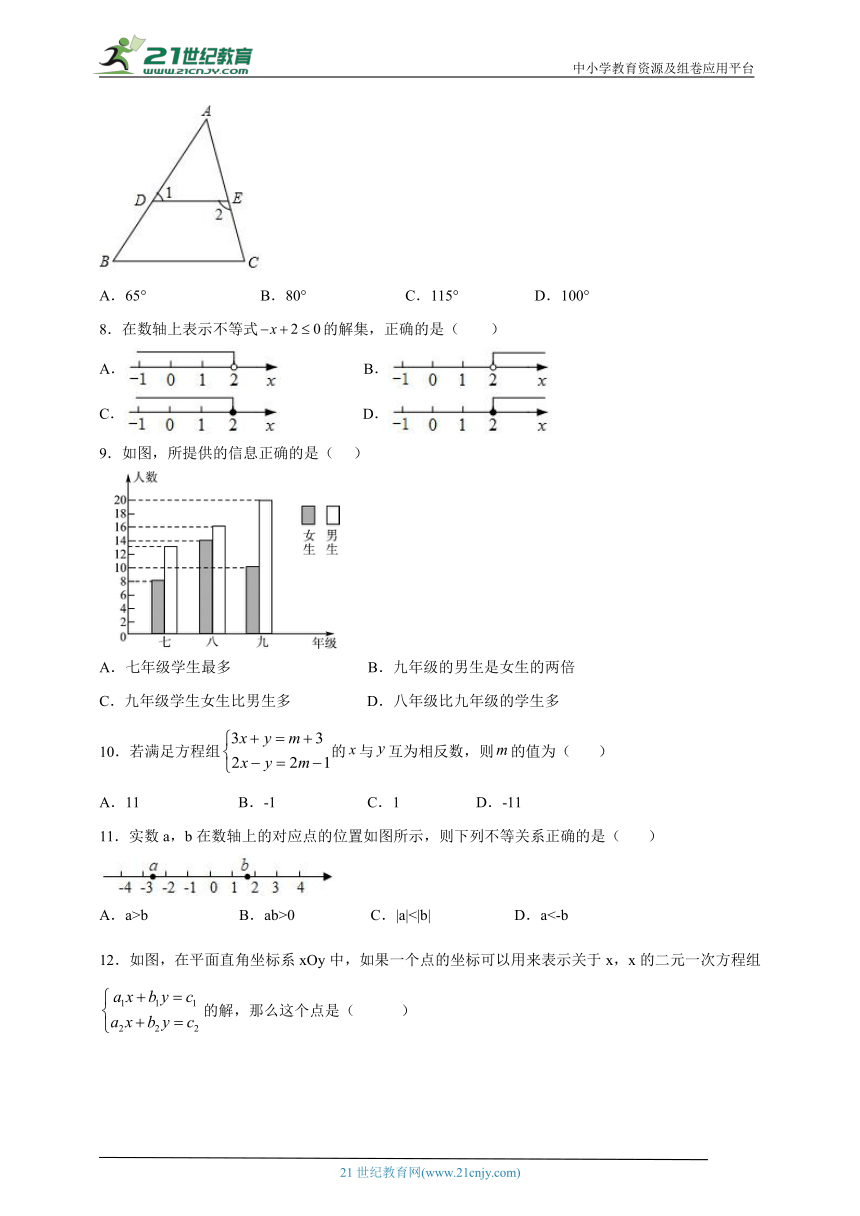
7.如图,,,,则的度数为( )
A.65° B.80° C.115° D.100°
8.在数轴上表示不等式的解集,正确的是( )
A. B.
C. D.
9.如图,所提供的信息正确的是( )
A.七年级学生最多 B.九年级的男生是女生的两倍
C.九年级学生女生比男生多 D.八年级比九年级的学生多
10.若满足方程组的与互为相反数,则的值为( )
A.11 B.-1 C.1 D.-11
11.实数a,b在数轴上的对应点的位置如图所示,则下列不等关系正确的是( )
A.a>b B.ab>0 C.|a|<|b| D.a<-b
12.如图,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x,x的二元一次方程组 的解,那么这个点是( )
A.M B.N C.E D.F
二、填空题:(每小题3分,共12分)
13.比较实数大小:_________(填“>”或“<”).
14.如图,将长为,宽为的长方形先向右平移,再向下平移,得到长方形,则阴影部分的面积为________.
15.在平面直角坐标系中,点A(2,﹣3)位于第_____象限.
16.如图,己知,与的平分线相交于点,若,则的度数是__________.
三、解答题:(本大题共9小题,共72分)
17.(8分)计算.
(1) (2)
18.(8分)解下列方程组:
(1) (2)
19.(6分)解不等式组,并写出它的整数解.
20.(8分)某电器超市销售每台进价分别200元,170元的,两种型号的电风扇,下表是近两周的销售情况:
销售时段 销售数量 销售收入
种型号 种型号
第一周 3台 5台 1800元
第二周 4台 10台 3100元
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求,两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求种型号的电风扇最多能采购多少台;
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
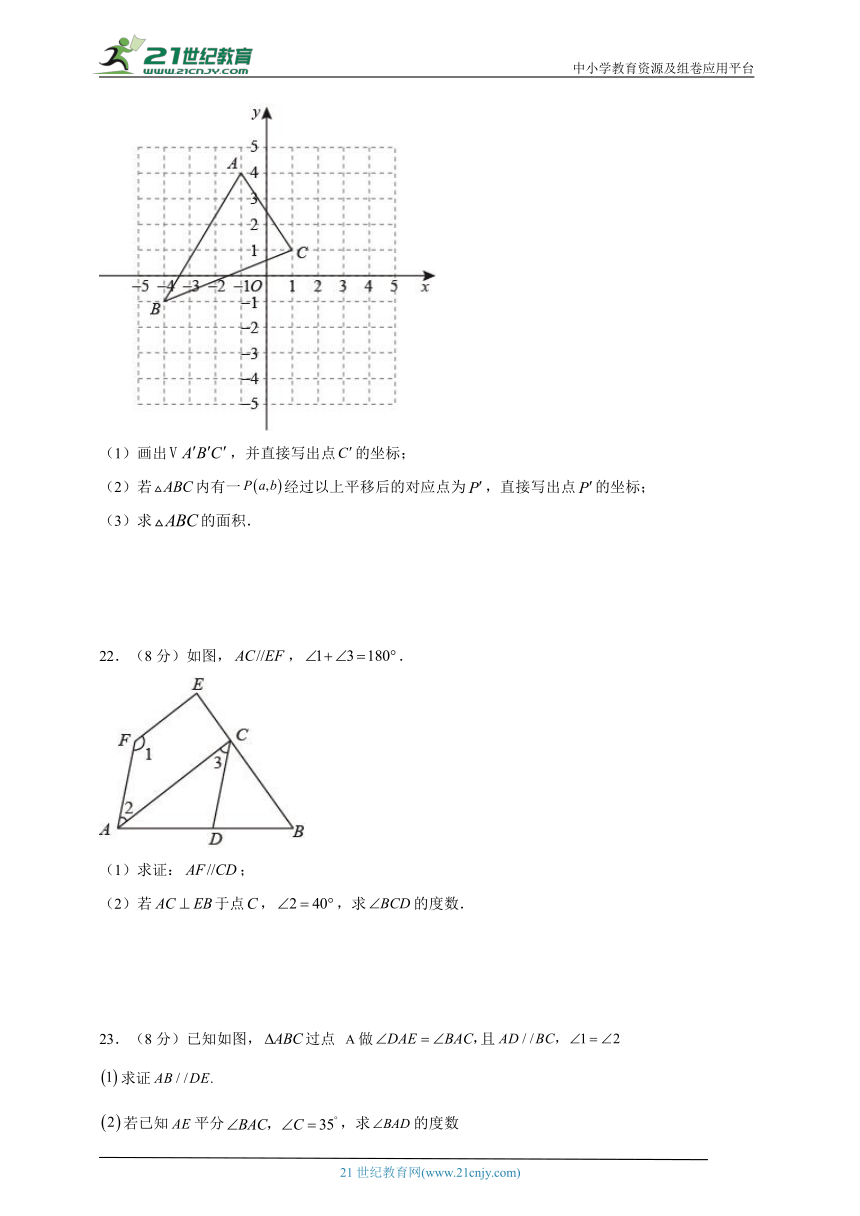
21.(8分)如图,的顶点,,.若向右平移4个单位长度,再向下平移3个单位长度得到,且点的对应点坐标是.
(1)画出,并直接写出点的坐标;
(2)若内有一经过以上平移后的对应点为,直接写出点的坐标;
(3)求的面积.
22.(8分)如图,,.
(1)求证:;
(2)若于点,,求的度数.
23.(8分)已知如图,过点 做且
求证
若已知平分,求的度数
24.(9分)某中学对七年级(1)班学生上学主要交通方式做了全面调查,调查结果分4个类别,A:乘坐地铁;B:乘坐公交车;C:乘坐私家车;D:步行.根据调查的结果绘制了不完整的条形统计图和扇形统计图(如图①、图②)如下,请根据图中所给的信息,解答下列问题:
(1)求七年级(1)班学生人数;
(2)将条形统计图补充完整;
(3)求扇形统计图中表示“B类别”的圆心角的度数;
(4)若该中学七年级有学生480人,请估计七年级学生上学主要交通方式是“步行”的有多少人?
25.(9分)已知,点为平面内一点,于.
(1)如图1,求证:;
(2)如图2,过点作的延长线于点,求证:;
(3)如图3,在(2)问的条件下,点、在上,连接、、,且平分,平分,若,,求的度数.
参考答案
一、单选题:(每小题只有一个答案正确,每小题3分,共36分)
1.下列各数中,无理数是( )
A. B. C. D.
【答案】1.D
2.如图,直线,被直线所截,若,,则( )
A. B. C. D.
【答案】2.A
3.在下列各式中正确的是( )
A. B. C. D.
【答案】3.D
4.在平面直角坐标系中,如果点在第三象限,那么的取值范围为( )
A. B. C. D.
【答案】4.A
5.如图,将沿水平方向向右平移到的位置,已知点A和D之间的距离为1,,则的长为( )
A.2 B.3 C.4 D.5
【答案】5.C
6.中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹两,牛每头两,根据题意可列方程组为( )
A. B.
C. D.
【答案】6.C
7.如图,,,,则的度数为( )
A.65° B.80° C.115° D.100°
【答案】7.D
8.在数轴上表示不等式的解集,正确的是( )
A. B.
C. D.
【答案】8.D
9.如图,所提供的信息正确的是( )
A.七年级学生最多 B.九年级的男生是女生的两倍
C.九年级学生女生比男生多 D.八年级比九年级的学生多
【答案】9.B
10.若满足方程组的与互为相反数,则的值为( )
A.11 B.-1 C.1 D.-11
【答案】10.A
11.实数a,b在数轴上的对应点的位置如图所示,则下列不等关系正确的是( )
A.a>b B.ab>0 C.|a|<|b| D.a<-b
【答案】11.D
12.如图,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x,x的二元一次方程组 的解,那么这个点是( )
A.M B.N C.E D.F
【答案】12.C
二、填空题:(每小题3分,共12分)
13.比较实数大小:_________(填“>”或“<”).
【答案】13.<
14.如图,将长为,宽为的长方形先向右平移,再向下平移,得到长方形,则阴影部分的面积为________.
【答案】14.6
15.在平面直角坐标系中,点A(2,﹣3)位于第_____象限.
【答案】15.四
16.如图,己知,与的平分线相交于点,若,则的度数是__________.
【答案】16.59°
三、解答题:(本大题共9小题,共72分)
17.(8分)计算.
(1) (2)
【答案】17.
解:(1)原式=7-3+3
=7
(2)原式=
=24
18.(8分)解下列方程组:
(1) (2)
【答案】18.
解:(1)
①×2-②,得-9y=9
解得y=-1
把y=-1代入①,得x+3=4
解得x=1
故方程组的解为:
(2)
将①代入②,得13x-12x+42=8
解得:x=-34
把x=-34代入①,得y=2×(-34) 7
解得y=-75
故方程组的解为:
19.(6分)解不等式组,并写出它的整数解.
【答案】19.不等式组的解集是-1≤x<,整数解是-1,0,1
【详解】
解:
解不等式①,得x≥-1
解不等式②,得x<
所以不等式组的解集是-1≤x<
所以不等式组的整数解是-1,0,1.
20.(8分)某电器超市销售每台进价分别200元,170元的,两种型号的电风扇,下表是近两周的销售情况:
销售时段 销售数量 销售收入
种型号 种型号
第一周 3台 5台 1800元
第二周 4台 10台 3100元
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求,两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求种型号的电风扇最多能采购多少台;
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
【答案】20.(1)A、B两种型号电风扇的销售单价分别为250元,210元;
(2)A型号电风扇最多能采购10台;
(3)在(2)的条件下,超市不能实现利润为1400元的目标,理由见详解:
【详解】
(1)设A、B两种型号的电风扇销售单价分别为元、元.
解得:
答:A、B两种型号电风扇的销售单价分别为250元,210元.
(2)设采购A种型号电风扇台.
200+170(30-)≤5400 解得:≤10
答:A型号电风扇最多能采购10台.
(3)依题意解(250-200)+(210-170)(30-)=1400
解得:=20 ∵≤10
∴在(2)的条件下,超市不能实现利润为1400元的目标.
21.(8分)如图,的顶点,,.若向右平移4个单位长度,再向下平移3个单位长度得到,且点的对应点坐标是.
(1)画出,并直接写出点的坐标;
(2)若内有一经过以上平移后的对应点为,直接写出点的坐标;
(3)求的面积.
【答案】21.
(1)(5,-2) 如图
(2)∵是P(a,b)经过向右平移4个单位,向下平移3个单位得到的
∴的坐标为(a+4,b-3)
(3)
.
22.(8分)如图,,.
(1)求证:;
(2)若于点,,求的度数.
【答案】22.
(1)证明:∵,
∴,
又∵,
∴,
∴;
(2),
,
由(1)可知,
,
.
23.(8分)已知如图,过点 做且
求证
若已知平分,求的度数
【答案】23.
(1)∵
∴
∵
∴
∵
∴
∴
(2)∵平分
∴
∵
∴
∴
故答案为:105°
24.(9分)某中学对七年级(1)班学生上学主要交通方式做了全面调查,调查结果分4个类别,A:乘坐地铁;B:乘坐公交车;C:乘坐私家车;D:步行.根据调查的结果绘制了不完整的条形统计图和扇形统计图(如图①、图②)如下,请根据图中所给的信息,解答下列问题:
(1)求七年级(1)班学生人数;
(2)将条形统计图补充完整;
(3)求扇形统计图中表示“B类别”的圆心角的度数;
(4)若该中学七年级有学生480人,请估计七年级学生上学主要交通方式是“步行”的有多少人?
【答案】24.
解:(1)8÷20%=40(人),
即七年级(1)班有学生40人;
(2)选择B的学生有:40-8-5-15=12(人),
补全的条形统计图如图所示:
(3)扇形统计图中表示“B类别”的圆心角的度数是:360°×=108°;
(4)480×=180(人),
答:估计七年级学生上学主要交通方式是“步行”的有180人.
25.(9分)已知,点为平面内一点,于.
(1)如图1,求证:;
(2)如图2,过点作的延长线于点,求证:;
(3)如图3,在(2)问的条件下,点、在上,连接、、,且平分,平分,若,,求的度数.
【答案】25.
(1)证明:∵,
∴,
∵于,
∴,
∴,
∴;
(2)证明:过作,
∵,
∴,
又∵,
∴,
∴,
∵,
∴,
∴,
∴;
(3)设∠DBE=a,则∠BFC=3a,
∵BE平分∠ABD,
∴∠ABD=∠C=2a,
又∵AB⊥BC,BF平分∠DBC,
∴∠DBC=∠ABD+∠ABC=2a+90,即:∠FBC=∠DBC=a+45°
又∵∠BFC+∠FBC+∠BCF=180°,即:3a+a+45°+∠BCF=180°
∴∠BCF=135°-4a,
∴∠AFC=∠BCF=135°-4a,
又∵AM//CN,
∴∠AFC+∠ NCF=180°,即:∠AFC+∠BCN+∠BCF=180°,
∴135°-4a+135°-4a+2a=180,解得a=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版七年级下册数学期末考试试题
一、单选题:(每小题只有一个答案正确,每小题3分,共36分)
1.下列各数中,无理数是( )
A. B. C. D.
2.如图,直线,被直线所截,若,,则( )
A. B. C. D.
3.在下列各式中正确的是( )
A. B. C. D.
4.在平面直角坐标系中,如果点在第三象限,那么的取值范围为( )
A. B. C. D.
5.如图,将沿水平方向向右平移到的位置,已知点A和D之间的距离为1,,则的长为( )
A.2 B.3 C.4 D.5
6.中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹两,牛每头两,根据题意可列方程组为( )
A. B. C. D.
7.如图,,,,则的度数为( )
A.65° B.80° C.115° D.100°
8.在数轴上表示不等式的解集,正确的是( )
A. B.
C. D.
9.如图,所提供的信息正确的是( )
A.七年级学生最多 B.九年级的男生是女生的两倍
C.九年级学生女生比男生多 D.八年级比九年级的学生多
10.若满足方程组的与互为相反数,则的值为( )
A.11 B.-1 C.1 D.-11
11.实数a,b在数轴上的对应点的位置如图所示,则下列不等关系正确的是( )
A.a>b B.ab>0 C.|a|<|b| D.a<-b
12.如图,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x,x的二元一次方程组 的解,那么这个点是( )
A.M B.N C.E D.F
二、填空题:(每小题3分,共12分)
13.比较实数大小:_________(填“>”或“<”).
14.如图,将长为,宽为的长方形先向右平移,再向下平移,得到长方形,则阴影部分的面积为________.
15.在平面直角坐标系中,点A(2,﹣3)位于第_____象限.
16.如图,己知,与的平分线相交于点,若,则的度数是__________.
三、解答题:(本大题共9小题,共72分)
17.(8分)计算.
(1) (2)
18.(8分)解下列方程组:
(1) (2)
19.(6分)解不等式组,并写出它的整数解.
20.(8分)某电器超市销售每台进价分别200元,170元的,两种型号的电风扇,下表是近两周的销售情况:
销售时段 销售数量 销售收入
种型号 种型号
第一周 3台 5台 1800元
第二周 4台 10台 3100元
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求,两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求种型号的电风扇最多能采购多少台;
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
21.(8分)如图,的顶点,,.若向右平移4个单位长度,再向下平移3个单位长度得到,且点的对应点坐标是.
(1)画出,并直接写出点的坐标;
(2)若内有一经过以上平移后的对应点为,直接写出点的坐标;
(3)求的面积.
22.(8分)如图,,.
(1)求证:;
(2)若于点,,求的度数.
23.(8分)已知如图,过点 做且
求证
若已知平分,求的度数
24.(9分)某中学对七年级(1)班学生上学主要交通方式做了全面调查,调查结果分4个类别,A:乘坐地铁;B:乘坐公交车;C:乘坐私家车;D:步行.根据调查的结果绘制了不完整的条形统计图和扇形统计图(如图①、图②)如下,请根据图中所给的信息,解答下列问题:
(1)求七年级(1)班学生人数;
(2)将条形统计图补充完整;
(3)求扇形统计图中表示“B类别”的圆心角的度数;
(4)若该中学七年级有学生480人,请估计七年级学生上学主要交通方式是“步行”的有多少人?
25.(9分)已知,点为平面内一点,于.
(1)如图1,求证:;
(2)如图2,过点作的延长线于点,求证:;
(3)如图3,在(2)问的条件下,点、在上,连接、、,且平分,平分,若,,求的度数.
参考答案
一、单选题:(每小题只有一个答案正确,每小题3分,共36分)
1.下列各数中,无理数是( )
A. B. C. D.
【答案】1.D
2.如图,直线,被直线所截,若,,则( )
A. B. C. D.
【答案】2.A
3.在下列各式中正确的是( )
A. B. C. D.
【答案】3.D
4.在平面直角坐标系中,如果点在第三象限,那么的取值范围为( )
A. B. C. D.
【答案】4.A
5.如图,将沿水平方向向右平移到的位置,已知点A和D之间的距离为1,,则的长为( )
A.2 B.3 C.4 D.5
【答案】5.C
6.中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹两,牛每头两,根据题意可列方程组为( )
A. B.
C. D.
【答案】6.C
7.如图,,,,则的度数为( )
A.65° B.80° C.115° D.100°
【答案】7.D
8.在数轴上表示不等式的解集,正确的是( )
A. B.
C. D.
【答案】8.D
9.如图,所提供的信息正确的是( )
A.七年级学生最多 B.九年级的男生是女生的两倍
C.九年级学生女生比男生多 D.八年级比九年级的学生多
【答案】9.B
10.若满足方程组的与互为相反数,则的值为( )
A.11 B.-1 C.1 D.-11
【答案】10.A
11.实数a,b在数轴上的对应点的位置如图所示,则下列不等关系正确的是( )
A.a>b B.ab>0 C.|a|<|b| D.a<-b
【答案】11.D
12.如图,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x,x的二元一次方程组 的解,那么这个点是( )
A.M B.N C.E D.F
【答案】12.C
二、填空题:(每小题3分,共12分)
13.比较实数大小:_________(填“>”或“<”).
【答案】13.<
14.如图,将长为,宽为的长方形先向右平移,再向下平移,得到长方形,则阴影部分的面积为________.
【答案】14.6
15.在平面直角坐标系中,点A(2,﹣3)位于第_____象限.
【答案】15.四
16.如图,己知,与的平分线相交于点,若,则的度数是__________.
【答案】16.59°
三、解答题:(本大题共9小题,共72分)
17.(8分)计算.
(1) (2)
【答案】17.
解:(1)原式=7-3+3
=7
(2)原式=
=24
18.(8分)解下列方程组:
(1) (2)
【答案】18.
解:(1)
①×2-②,得-9y=9
解得y=-1
把y=-1代入①,得x+3=4
解得x=1
故方程组的解为:
(2)
将①代入②,得13x-12x+42=8
解得:x=-34
把x=-34代入①,得y=2×(-34) 7
解得y=-75
故方程组的解为:
19.(6分)解不等式组,并写出它的整数解.
【答案】19.不等式组的解集是-1≤x<,整数解是-1,0,1
【详解】
解:
解不等式①,得x≥-1
解不等式②,得x<
所以不等式组的解集是-1≤x<
所以不等式组的整数解是-1,0,1.
20.(8分)某电器超市销售每台进价分别200元,170元的,两种型号的电风扇,下表是近两周的销售情况:
销售时段 销售数量 销售收入
种型号 种型号
第一周 3台 5台 1800元
第二周 4台 10台 3100元
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求,两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求种型号的电风扇最多能采购多少台;
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
【答案】20.(1)A、B两种型号电风扇的销售单价分别为250元,210元;
(2)A型号电风扇最多能采购10台;
(3)在(2)的条件下,超市不能实现利润为1400元的目标,理由见详解:
【详解】
(1)设A、B两种型号的电风扇销售单价分别为元、元.
解得:
答:A、B两种型号电风扇的销售单价分别为250元,210元.
(2)设采购A种型号电风扇台.
200+170(30-)≤5400 解得:≤10
答:A型号电风扇最多能采购10台.
(3)依题意解(250-200)+(210-170)(30-)=1400
解得:=20 ∵≤10
∴在(2)的条件下,超市不能实现利润为1400元的目标.
21.(8分)如图,的顶点,,.若向右平移4个单位长度,再向下平移3个单位长度得到,且点的对应点坐标是.
(1)画出,并直接写出点的坐标;
(2)若内有一经过以上平移后的对应点为,直接写出点的坐标;
(3)求的面积.
【答案】21.
(1)(5,-2) 如图
(2)∵是P(a,b)经过向右平移4个单位,向下平移3个单位得到的
∴的坐标为(a+4,b-3)
(3)
.
22.(8分)如图,,.
(1)求证:;
(2)若于点,,求的度数.
【答案】22.
(1)证明:∵,
∴,
又∵,
∴,
∴;
(2),
,
由(1)可知,
,
.
23.(8分)已知如图,过点 做且
求证
若已知平分,求的度数
【答案】23.
(1)∵
∴
∵
∴
∵
∴
∴
(2)∵平分
∴
∵
∴
∴
故答案为:105°
24.(9分)某中学对七年级(1)班学生上学主要交通方式做了全面调查,调查结果分4个类别,A:乘坐地铁;B:乘坐公交车;C:乘坐私家车;D:步行.根据调查的结果绘制了不完整的条形统计图和扇形统计图(如图①、图②)如下,请根据图中所给的信息,解答下列问题:
(1)求七年级(1)班学生人数;
(2)将条形统计图补充完整;
(3)求扇形统计图中表示“B类别”的圆心角的度数;
(4)若该中学七年级有学生480人,请估计七年级学生上学主要交通方式是“步行”的有多少人?
【答案】24.
解:(1)8÷20%=40(人),
即七年级(1)班有学生40人;
(2)选择B的学生有:40-8-5-15=12(人),
补全的条形统计图如图所示:
(3)扇形统计图中表示“B类别”的圆心角的度数是:360°×=108°;
(4)480×=180(人),
答:估计七年级学生上学主要交通方式是“步行”的有180人.
25.(9分)已知,点为平面内一点,于.
(1)如图1,求证:;
(2)如图2,过点作的延长线于点,求证:;
(3)如图3,在(2)问的条件下,点、在上,连接、、,且平分,平分,若,,求的度数.
【答案】25.
(1)证明:∵,
∴,
∵于,
∴,
∴,
∴;
(2)证明:过作,
∵,
∴,
又∵,
∴,
∴,
∵,
∴,
∴,
∴;
(3)设∠DBE=a,则∠BFC=3a,
∵BE平分∠ABD,
∴∠ABD=∠C=2a,
又∵AB⊥BC,BF平分∠DBC,
∴∠DBC=∠ABD+∠ABC=2a+90,即:∠FBC=∠DBC=a+45°
又∵∠BFC+∠FBC+∠BCF=180°,即:3a+a+45°+∠BCF=180°
∴∠BCF=135°-4a,
∴∠AFC=∠BCF=135°-4a,
又∵AM//CN,
∴∠AFC+∠ NCF=180°,即:∠AFC+∠BCN+∠BCF=180°,
∴135°-4a+135°-4a+2a=180,解得a=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
