【期末押题卷】期末素养评价预测卷(含解析)2024-2025学年五年级下册数学苏教版
文档属性
| 名称 | 【期末押题卷】期末素养评价预测卷(含解析)2024-2025学年五年级下册数学苏教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 749.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末素养评价预测卷(含解析)2024-2025学年五年级下册数学苏教版
一、单选题
1.一位小数“”比大,比小。这个小数中被挡住的数字是( )。
A.4 B.5 C.6 D.7
2.红星小学一年级在学校吃午饭的学生有 210 人, 比六年级在学校吃午饭的人数的 2 倍还多 8 人, 求六年级学生在学校吃午饭的有多少人 设六年级学生在学校吃午饭的人数是 人,下面 ( ) 是正确的。
A. B. C. D.
3.用一些相同的小正方形卡片拼长方形,每次都用上所有的小正方形卡片。如果刚好可以摆出4种不同的长方形(含正方形),则小正方形卡片的个数一定( )。
A.是质数 B.含有因数5
C.只有5个因数 D.有7个或8个因数
4.下面不是质数的是( ).
A.23 B.73 C.91
5.下面( )的积可以根据“16×20=320”的积直接写出来。
A.160×20 B.20×19 C.12×60
6.仓库里有15本、16本、18本、19本、20车和30本等6堆书。小钱和小塘取走其中5堆。如果小钱取走的本数是小塘的2倍,那么仓库里还剩下( )本那堆书。
A.30 B.20 C.19 D.18
7.水果店运来两筐橘子,将甲筐的 倒入乙筐,则甲、乙两筐橘子同样重,甲筐橘子的质量比乙筐多( )。
A. B. C.
二、判断题
8.半径是2m的圆,它的周长和面积相等。( )
9.最简分数的分子和分母都是质数。( )
10.两个数的最小公倍数一定能被这两个数整除。( )
11.大于0的所有的偶数都是合数。( )
12.火车比汽车快 ,汽车就比火车慢 。(
)
13.用三根同样长的铁丝分别围成一个长方形、一个正方形和一个圆形,所围成的这三个图形的面积中,圆的面积最大。( )
三、填空题
14.如果数m=2×5×7,n=2×3×7,那么m和n的最小公倍数是 。
15.一个两位数,既是3的倍数,又有因数5,这个两位数最小是 ,最大是 。
16.要使五位数19□□0是30的倍数,方框里最大填 ,最小填 。
17.一袋糖重千克,吃去它的,还剩下它的 ;若吃去千克,还剩下 千克。
18.一个两位数同时是2、3和5的倍数,这个最大是 。
19.有两个不同的质数,它们的和刚好是20,这两个质数的积最大是 ,最小是 。
20.在下列方框内填上适当的数,使不等式成立。
(1)
(2)
21.一个时钟的分针长4厘米,时针长2厘米。每经过一小时,时针扫过的面积是 平方厘米,分针的尖端走了 厘米。
四、作图题
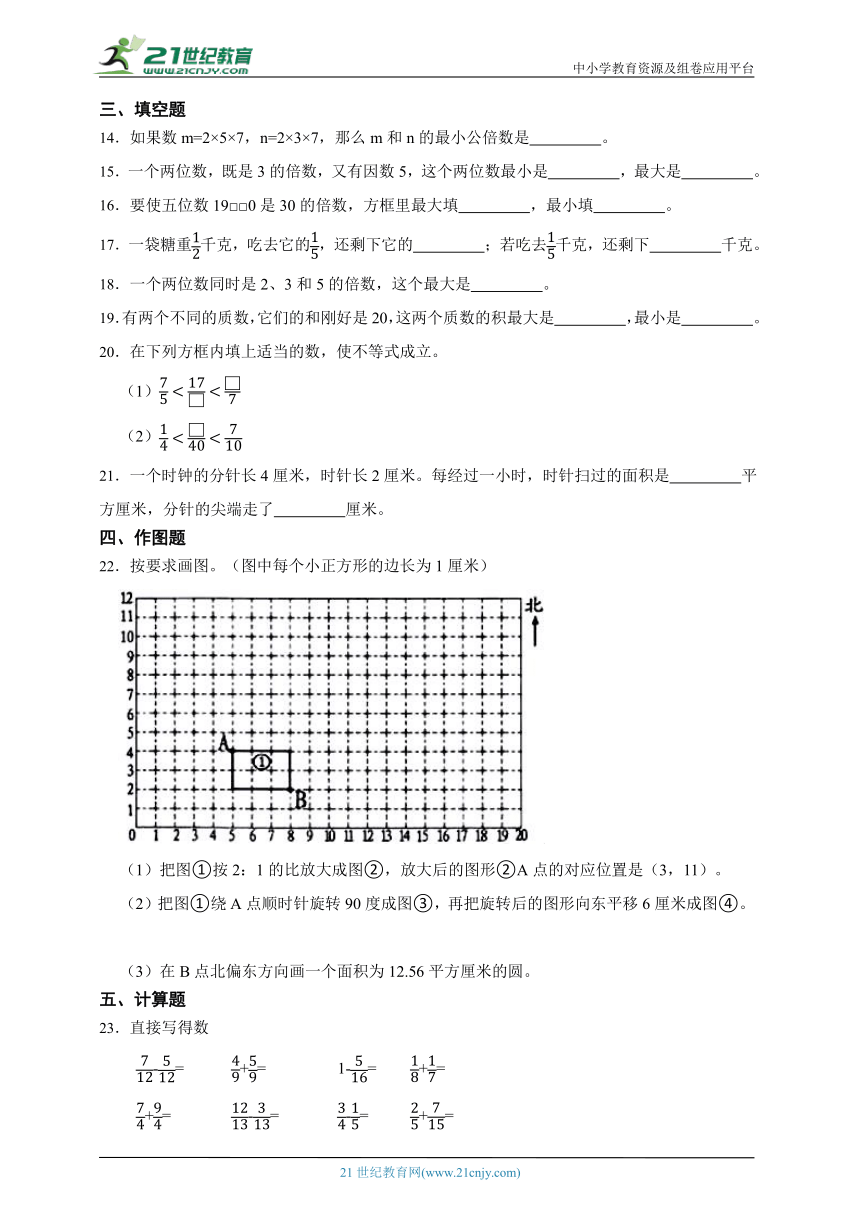
22.按要求画图。(图中每个小正方形的边长为1厘米)
(1)把图①按2:1的比放大成图②,放大后的图形②A点的对应位置是(3,11)。
(2)把图①绕A点顺时针旋转90度成图③,再把旋转后的图形向东平移6厘米成图④。
(3)在B点北偏东方向画一个面积为12.56平方厘米的圆。
五、计算题
23.直接写得数
-= += 1-= +=
+= -= -= +=
24.选择合适的方法计算下面各题。
25.解方程.
(1) x= (2)x+ x=
26.把下列分数化成最简分数。
27.看图列方程解答。
28.求下面图形阴影部分的周长和面积。
六、解决问题
29.修一条水渠,甲队修了总长的 ,乙队修了总长的 ,其余的由丙队修,甲、乙两队共修了总长的几分之几 丙队修了总长的几分之几
30.《三国志》由西晋史学家陈寿所著,是记载中国三国时期的断代史,全书一共有六十五卷,《魏书》有三十卷,《蜀书》有十五卷,《吴书》有二十卷。《魏书》《蜀书》《吴书》的卷数各占总卷数的几分之几
31.热爱劳动的小红和小东周六帮农民伯伯的菜地松土,上午松了 ,下午松了 ,还剩下几分之几没有松?
32. 五年级同学分组参加植树.每6人一组或每8人一组都没有剩余。已知该班的人数在30~50人之间,该班学生有多少人
33.下面是五(1)班同学最喜欢的水果统计表。
苹果 西瓜 葡萄 香蕉
占全班人数 几分之几
(1)喜欢吃苹果和喜欢吃香蕉的同学共占全班人数的几分之几?
(2)喜欢吃西瓜的比喜欢吃葡萄的多占全班人数的几分之几?
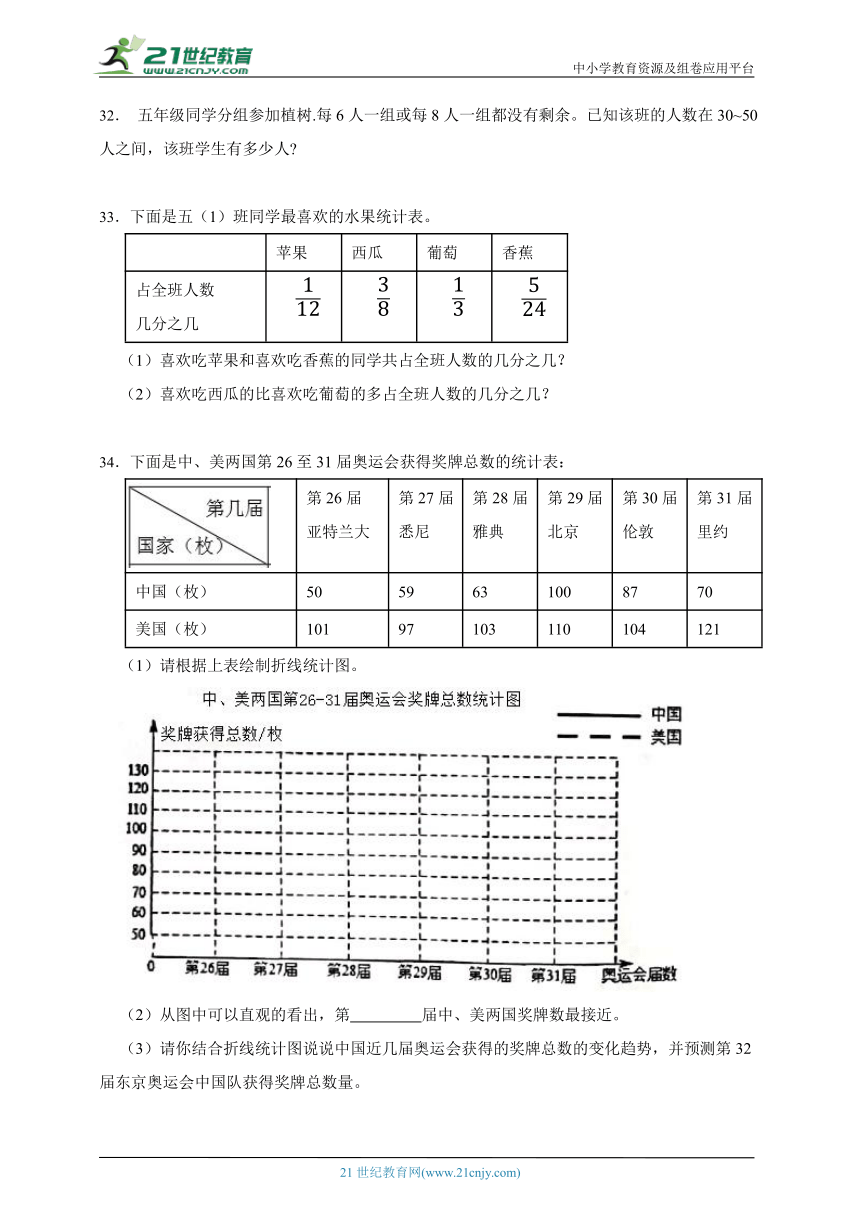
34.下面是中、美两国第26至31届奥运会获得奖牌总数的统计表:
第26届 亚特兰大 第27届 悉尼 第28届 雅典 第29届 北京 第30届 伦敦 第31届 里约
中国(枚) 50 59 63 100 87 70
美国(枚) 101 97 103 110 104 121
(1)请根据上表绘制折线统计图。
(2)从图中可以直观的看出,第 届中、美两国奖牌数最接近。
(3)请你结合折线统计图说说中国近几届奥运会获得的奖牌总数的变化趋势,并预测第32届东京奥运会中国队获得奖牌总数量。
答案解析
1.【答案】C
【知识点】多位小数的大小比较;分数与小数的互化
【解析】【解答】解:=1÷2=0.5,=2÷3=0.666.......,
比大,比小的一位数是0.6,
这个小数中被挡住的数字是6。
故答案为:C。
【分析】分数化小数:用分子除以分母,商写成小数的形式;
小数比较大小,先比较小数的整数部分,整数部分大的这个小数就大,如果整数部分相同,就比较十分位,十分位大的这个小数就大。
2.【答案】A
【知识点】列方程解含有一个未知数的应用题
【解析】【解答】解:A:等量关系:六年级吃午饭的人数×2+多的8人=一年级在校吃午饭的人数,方程正确。
B、C、D中的方程都不符合等量关系,都不正确。
故答案为:A。
【分析】等量关系:六年级吃午饭的人数×2+多的8人=一年级在校吃午饭的人数、六年级在校吃午饭的人数×2=一年级在校吃午饭的人数-多的8人、一年级在校吃无法的人数-六年级在校吃午饭的人数×2=8人,根据这些等量关系列方程即可。
3.【答案】D
【知识点】因数与倍数的关系;因数的特点及求法;倍数的特点及求法
【解析】【解答】解:A.是质数。质数只有两个因数,1和它自己,所以不能形成4种不同的长方形。
B.含有因数5。这并不直接说明它可以形成4种不同的长方形,因为这取决于n的总因数个数。
C.只有5个因数。这意味着n是一个形式为的数,其中p是一个质数。这样的数确实可以形成4种不同的长方形(包括1x, p,x,x,x1),但这也意味着n是一个完全平方数,但这种情况下n的因数个数为5,这与我们的条件不符,因为我们要求的是4种不同的长方形,而这里实际上是5种,不过其中x只算作一种。
D.有7个或8个因数。这是正确的。如果n有7个因数,这意味着n的形式是(p是一个质数),这种情况下n是一个完全平方数,它可以形成4种不同的长方形(1x, p,x,x)。如果n有8个因数,这可能是因为n是两个不同质数的乘积的平方(),这种情况下n也可以形成4种不同的长方形。
故答案为:D
【分析】设小正方形卡片的个数为n。因为可以摆出4种不同的长方形(含正方形),所以n的因数个数至少为4。 对于一个数n,如果它可以分解成,那么a和b都是n的因数。一个数的因数是成对出现的,除非这个数是完全平方数,此时会有一个因数重复。
4.【答案】C
【知识点】合数与质数的特征
【解析】【解答】因为91÷13=7,所以91不是质数。
故答案为:C。
【分析】一个数,如果只有1和它本身两个因数,这样的数叫做质数;一个数,如果除了1和它本身还有别的因数,这样的数叫做合数,据此解答。
5.【答案】A
【知识点】因数与倍数的关系
【解析】【解答】原题中一个因数由16变成160,另一个因数不变。
故答案为:A
【分析】一个因数变成原来的10倍,另一个因数不变,积变为原来积的10倍。
6.【答案】B
【知识点】3的倍数的特征
【解析】【解答】解:小钱取走的本数是小塘的2倍,说明小钱和小塘取走的5堆是3的倍数,则一定有15本和18本这两堆,
剩下的4堆分别是16本,19本,20本,31本,其中只有16+19+31=66(本),66是3的倍数,
66÷(15+18)
=66÷33
=2
仓库里还剩下20本那堆书。
故答案为:B。
【分析】3的倍数的特征是这个数的所有数位上的数字之和是3的倍数。
7.【答案】B
【知识点】分数除法的应用
【解析】【解答】7-2-2=3份;
(7-3)÷3=4÷3=.
故答案为:B。
【分析】甲筐橘子看做单位1,平均分成7份,根据题意可知,甲筐比乙筐多4份,乙筐是3份,(甲筐-乙筐)÷乙筐= 甲筐橘子的质量比乙筐的分率。
8.【答案】错误
【知识点】圆的周长;圆的面积
【解析】【解答】解:圆的周长和面积:①意义不同,圆的面积是指圆所占平面的大小,而圆的周长是指围成圆一周的长度;②计算方法不同,圆的面积=π×半径2,而圆的周长=π×直径;③计量单位不同,面积用面积单位,而周长用长度单位;所以原题干说法错误。
故答案为:错误。
【分析】圆的周长和面积无法比较大小。
9.【答案】错误
【知识点】合数与质数的特征;最简分数的特征
【解析】【解答】解:最简分数的分子和分母不一定都是质数。
故答案为:错误。
【分析】最简分数是指分数的分子和分母没有公约数,例如是最简分数,但是4是合数。
10.【答案】正确
【知识点】公倍数与最小公倍数
【解析】 【解答】 两个数的最小公倍数一定能被这两个数整除。
故答案为:正确。
【分析】几个数公有的倍数叫做这几个数的公倍数。其中最大的一个叫这几个数的最大公倍数。
11.【答案】错误
【知识点】奇数和偶数;合数与质数的特征
【解析】【解答】解:2是偶数,但2是质数。
故答案为:错误。
【分析】偶数是指是2的倍数的整数,合数是指这个数除了1和它本身之外还有其他因数的数,2是偶数,但不是合数。
12.【答案】错误
【知识点】单位“1”的认识及确定
【解析】【解答】把汽车速度看作单位“1”,则火车速度是1+=;
(-1)÷
=÷
=
原题说法错误。
故答案为:错误。
【分析】根据条件“火车比汽车快”可知,把汽车速度看作单位“1”,则火车速度是1+=,要求汽车比火车慢几分之几,用(火车的速度-汽车的速度)÷火车的速度=汽车比火车慢几分之几,据此列式解答。
13.【答案】正确
【知识点】圆的面积
【解析】【解答】解:假设铁丝的长是6.28米,设长方形的长是2米,宽是1.14米,则面积:2×1.14=2.28平方米;正方形的面积为:(6.28÷4)×(6.28÷4)=2.4649平方米;圆的面积为:3.14×(6.28÷3.14÷2)2=3.14平方米;因为:3.14>2.4649>2.28,所以圆的面积最大。
故答案为:正确。
【分析】设铁丝的长是6.28米,长方形的周长=(长+宽)×2,正方形的周长=正方形的边长×4,长方形的面积=长×宽,正方形的面积=正方形的边长×正方形的边长,可得出长方形的长和宽约接近,面积越大,可设长方形的长是2米,宽是1.14米,计算出长方形的面积,再计算出正方形的面积;圆的周长=π×圆的半径×2计算出圆的半径,再根据圆的面积=π×圆的半径的平方,计算出圆的面积,最后将三者的面积进行比较即可得出答案。
14.【答案】210
【知识点】公倍数与最小公倍数
【解析】【解答】解:m和n的最小公倍数是:2×7×5×3=210。
故答案为:210。
【分析】两个数的最小公倍数是把这两个数公有的质因数和它们各自独有的质因数相乘。
15.【答案】15;90
【知识点】2、5的倍数的特征;3的倍数的特征
【解析】【解答】解:3×5=15;
15×6=90。
故答案为:15;90。
【分析】既是3的倍数,又有因数5的最小两位数是3和5的最小公倍数=3×5=15;最大的两位数是15×6=90。
16.【答案】98;02
【知识点】3的倍数的特征
【解析】【解答】解:要使五位数19□□0是30的倍数,即19□□0÷30商是一个整数,根据商不变的规律将被除数和除数同时除以10,即19□□要是3的倍数:因为1+9=10,要最大则每一位都要最大,10+9+9=28,28不是3的倍数,舍去;10+9+8=27,27是3的倍数,所以最大的五位数是19980;要最小则每一位都要最小,10+0+0=10,10+0+1=11,11,10都不是3的倍数,舍去;10+0+2=12,12是3的倍数,所以最小的五位数是19020。
故答案为:98;02。
【分析】3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数;
商的变化规律:被除数和除数同时乘或除以相同的数(0除外),商不变;
先根据商的变化规律将五位数与30同时除以10,则转化成四位数是3的倍数,再根据3的倍数特征去找即可。
17.【答案】;
【知识点】异分母分数加减法
【解析】【解答】解:1-=
(千克)
故答案为,。
【分析】把一袋糖看作单位“1”,用单位“1”减去吃的,即可求出还剩下的是几分之几;用一袋糖的总重量减去吃去的重量,即可求出还剩下的重量。
18.【答案】90
【知识点】公倍数与最小公倍数
【解析】【解答】解:2×3×5=30,
30的倍数有30, 60, 90…,90是两位数范围内30的最大倍数;
故答案为:90。
【分析】先求出2、3和5的最小公倍数,再找出两位数范围内最小公倍数的最大倍数即可。
19.【答案】91;51
【知识点】合数与质数的特征
20.【答案】(1)12|10(答案不唯一)
(2)11~27
【知识点】异分子分母分数大小比较
【解析】【解答】解:(1),,要使,那么7×<85,<85÷7,<12.1…,所以可以是12;
,,所以第三个分数的分子可以是10;
(2),,所以第二个分数的分子可以是11~27。
故答案为:(1)12;10;(2)11~27(答案不唯一)。
【分析】异分母分数比较大小,先通分,然后按照同分母分数大小的比较方法比较大小。同分母分数比较大小,分子大的分数比较大。
21.【答案】;25.12
【知识点】圆的面积
【解析】【解答】解:3.14×(2×2)×
=3.14×4×
=12.56×
=(平方厘米);
3.14×4×2
=12.56×2
=25.12(厘米)。
故答案为:;25.12。
【分析】时针扫过的面积=π×(半径×半径)×;分针尖端走过的距离=2×π×半径。
22.【答案】(1)
(2)
(3) (答案不唯一)
【知识点】图形的缩放;画圆
【解析】【分析】(1)先找到(3,11)位置,把图形①的长、宽扩大2倍,画图形②;(2)旋转、平移图形的一条线段,再画出图形;(3) 在B点北偏东方向画出半径是2厘米的圆即可。
23.【答案】
- = + =1 1- = + =
+ =4 - = - = + =
【知识点】异分母分数加减法
【解析】【分析】同分母分数相加减,分母不变,把分子相加减,能约分的要约分;
异分母分数相加减,先通分,化成同分母分数,然后按照同分母分数的加减法作答即可。
24.【答案】解:++
=++
=1+
=1
+-
=
=
-(+)
=-
=
【知识点】分数加减混合运算及应用;分数加法运算律
【解析】【分析】加法交换律:两个加数相加交换两个加数的位置,和不变,用字母表示为:a+b=b+a;
分数加减混合运算:没有括号,从左往右依次计算;有括号,先算括号里面的,再算括号外面的;
第一题:运用加法交换律交换加数的位置会使计算简便;
第二题:没有括号,从左往右依次计算;
第三题:先算括号里面的加法,再算括号外面的减法。
25.【答案】(1) x= 解: x÷ =
x=
(2)x+ x= 解: x= 1 x÷1 = ÷
x=
【知识点】除数是分数的分数除法;应用等式的性质2解方程
【解析】【分析】解方程要掌握等式的性质,即等式两边同时加上或减去同一个数,左右两边仍然相等;等式两边同时乘或除以同一个不是0的数,等式两边仍然相等。由此结合分数的四则运算方法解方程即可。
26.【答案】解:
【知识点】最简分数的特征
【解析】【分析】先确定分子和分母的最大公因数,根据分数的基本性质把分子和分母同时除以他们的最大公因数即可化成最简分数。
27.【答案】解:3x-30=120
3x=150
x=150÷3
x=50
【知识点】列方程解含有一个未知数的应用题
【解析】【分析】依据等量关系式:女生人数×3-少的人数=男生人数,列方程,解方程。
28.【答案】解:周长:3.14×3×2=18.84(cm)
面积:3.14×32×=14.13(cm2)
【知识点】组合图形面积的巧算;组合图形的周长的巧算;圆的周长;圆的面积
【解析】【分析】阴影部分的周长=半径为3厘米的圆的周长=π×半径×2;
阴影部分的面积=圆的面积的一半=π×半径的平方÷2。
29.【答案】解:+=
1-=
答:甲、乙两队共修了总长的;丙队修了总长的。
【知识点】分数加减混合运算及应用;单位“1”的认识及确定
【解析】【分析】将水渠的总长度看作单位“1”,求甲、乙两队共修了几分之几,用甲队修了总长的几分之几+乙队修了总长的几分之几=甲乙共修了总长的几分之几;求丙队修了总长的几分之几,用减法,就是:1-甲乙共修了总长的几分之几=丙队修了总长的几分之几。
30.【答案】解:《魏书》:
《蜀书》:
《吴书》:
答:《魏书》的卷数占总卷数的,《蜀书》的卷数占总卷数的,《吴书》的卷数占总卷数的。
【知识点】分数的简单应用--占总数的几分之几;约分的认识与应用
【解析】【分析】此题主要考查了分数的简单应用,求一个数是另一个数的几分之几,用除法计算。
31.【答案】解:1-()
=1-()
=1-
=
答:还剩没有松。
【知识点】分数加减混合运算及应用
【解析】【分析】还剩几分之几=单位“1”-(上午松的几分之几+下午松的几分之几)。
32.【答案】解:6和8的最小公倍数是24,公倍数有24、48、72、……,48在30~50之间。
答:该班学生有48人。
【知识点】最小公倍数的应用
【解析】【分析】因为每6人一组或每8人一组都没有剩余,说明总人数一定是6和8的公倍数。先找出6和8的最小公倍数,然后找出6和8在30~50之间的公倍数,就是这个班的学生数。
33.【答案】(1)解;+=
答:喜欢吃苹果和喜欢吃香蕉的同学共占全班人数的。
(2)解:-=
答:喜欢吃西瓜的比喜欢吃葡萄的多占全班人数的。
【知识点】异分母分数加减法
【解析】【分析】(1)用加法计算喜欢吃苹果和喜欢吃香蕉的同学共占全班人数的几分之几;
(2)用减法计算喜欢吃西瓜的比喜欢吃葡萄的多占全班人数的几分之几。
34.【答案】(1)
(2)29
(3)解:从统计图中可以看出中国奖牌数基本是逐年增加的,预测第32届东京奥运会中国队获得奖牌总数量为88枚。
【知识点】复式折线统计图的特点及绘制;从复式折线统计图获取信息
【解析】【解答】解:(2)第29届中、美两国奖牌数最接近。
故答案为:(2)29。
【分析】(1)依据统计图中的数据描出各点,然后连接成线,并且标上数据;
(2)第29届中、美两国奖牌数折线上的点距离最近,所以这一届奖牌数最接近。
(3)中国奖牌数基本是逐年增加的,预测第32届东京奥运会中国队获得奖牌总数量为88枚。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末素养评价预测卷(含解析)2024-2025学年五年级下册数学苏教版
一、单选题
1.一位小数“”比大,比小。这个小数中被挡住的数字是( )。
A.4 B.5 C.6 D.7
2.红星小学一年级在学校吃午饭的学生有 210 人, 比六年级在学校吃午饭的人数的 2 倍还多 8 人, 求六年级学生在学校吃午饭的有多少人 设六年级学生在学校吃午饭的人数是 人,下面 ( ) 是正确的。
A. B. C. D.
3.用一些相同的小正方形卡片拼长方形,每次都用上所有的小正方形卡片。如果刚好可以摆出4种不同的长方形(含正方形),则小正方形卡片的个数一定( )。
A.是质数 B.含有因数5
C.只有5个因数 D.有7个或8个因数
4.下面不是质数的是( ).
A.23 B.73 C.91
5.下面( )的积可以根据“16×20=320”的积直接写出来。
A.160×20 B.20×19 C.12×60
6.仓库里有15本、16本、18本、19本、20车和30本等6堆书。小钱和小塘取走其中5堆。如果小钱取走的本数是小塘的2倍,那么仓库里还剩下( )本那堆书。
A.30 B.20 C.19 D.18
7.水果店运来两筐橘子,将甲筐的 倒入乙筐,则甲、乙两筐橘子同样重,甲筐橘子的质量比乙筐多( )。
A. B. C.
二、判断题
8.半径是2m的圆,它的周长和面积相等。( )
9.最简分数的分子和分母都是质数。( )
10.两个数的最小公倍数一定能被这两个数整除。( )
11.大于0的所有的偶数都是合数。( )
12.火车比汽车快 ,汽车就比火车慢 。(
)
13.用三根同样长的铁丝分别围成一个长方形、一个正方形和一个圆形,所围成的这三个图形的面积中,圆的面积最大。( )
三、填空题
14.如果数m=2×5×7,n=2×3×7,那么m和n的最小公倍数是 。
15.一个两位数,既是3的倍数,又有因数5,这个两位数最小是 ,最大是 。
16.要使五位数19□□0是30的倍数,方框里最大填 ,最小填 。
17.一袋糖重千克,吃去它的,还剩下它的 ;若吃去千克,还剩下 千克。
18.一个两位数同时是2、3和5的倍数,这个最大是 。
19.有两个不同的质数,它们的和刚好是20,这两个质数的积最大是 ,最小是 。
20.在下列方框内填上适当的数,使不等式成立。
(1)
(2)
21.一个时钟的分针长4厘米,时针长2厘米。每经过一小时,时针扫过的面积是 平方厘米,分针的尖端走了 厘米。
四、作图题
22.按要求画图。(图中每个小正方形的边长为1厘米)
(1)把图①按2:1的比放大成图②,放大后的图形②A点的对应位置是(3,11)。
(2)把图①绕A点顺时针旋转90度成图③,再把旋转后的图形向东平移6厘米成图④。
(3)在B点北偏东方向画一个面积为12.56平方厘米的圆。
五、计算题
23.直接写得数
-= += 1-= +=
+= -= -= +=
24.选择合适的方法计算下面各题。
25.解方程.
(1) x= (2)x+ x=
26.把下列分数化成最简分数。
27.看图列方程解答。
28.求下面图形阴影部分的周长和面积。
六、解决问题
29.修一条水渠,甲队修了总长的 ,乙队修了总长的 ,其余的由丙队修,甲、乙两队共修了总长的几分之几 丙队修了总长的几分之几
30.《三国志》由西晋史学家陈寿所著,是记载中国三国时期的断代史,全书一共有六十五卷,《魏书》有三十卷,《蜀书》有十五卷,《吴书》有二十卷。《魏书》《蜀书》《吴书》的卷数各占总卷数的几分之几
31.热爱劳动的小红和小东周六帮农民伯伯的菜地松土,上午松了 ,下午松了 ,还剩下几分之几没有松?
32. 五年级同学分组参加植树.每6人一组或每8人一组都没有剩余。已知该班的人数在30~50人之间,该班学生有多少人
33.下面是五(1)班同学最喜欢的水果统计表。
苹果 西瓜 葡萄 香蕉
占全班人数 几分之几
(1)喜欢吃苹果和喜欢吃香蕉的同学共占全班人数的几分之几?
(2)喜欢吃西瓜的比喜欢吃葡萄的多占全班人数的几分之几?
34.下面是中、美两国第26至31届奥运会获得奖牌总数的统计表:
第26届 亚特兰大 第27届 悉尼 第28届 雅典 第29届 北京 第30届 伦敦 第31届 里约
中国(枚) 50 59 63 100 87 70
美国(枚) 101 97 103 110 104 121
(1)请根据上表绘制折线统计图。
(2)从图中可以直观的看出,第 届中、美两国奖牌数最接近。
(3)请你结合折线统计图说说中国近几届奥运会获得的奖牌总数的变化趋势,并预测第32届东京奥运会中国队获得奖牌总数量。
答案解析
1.【答案】C
【知识点】多位小数的大小比较;分数与小数的互化
【解析】【解答】解:=1÷2=0.5,=2÷3=0.666.......,
比大,比小的一位数是0.6,
这个小数中被挡住的数字是6。
故答案为:C。
【分析】分数化小数:用分子除以分母,商写成小数的形式;
小数比较大小,先比较小数的整数部分,整数部分大的这个小数就大,如果整数部分相同,就比较十分位,十分位大的这个小数就大。
2.【答案】A
【知识点】列方程解含有一个未知数的应用题
【解析】【解答】解:A:等量关系:六年级吃午饭的人数×2+多的8人=一年级在校吃午饭的人数,方程正确。
B、C、D中的方程都不符合等量关系,都不正确。
故答案为:A。
【分析】等量关系:六年级吃午饭的人数×2+多的8人=一年级在校吃午饭的人数、六年级在校吃午饭的人数×2=一年级在校吃午饭的人数-多的8人、一年级在校吃无法的人数-六年级在校吃午饭的人数×2=8人,根据这些等量关系列方程即可。
3.【答案】D
【知识点】因数与倍数的关系;因数的特点及求法;倍数的特点及求法
【解析】【解答】解:A.是质数。质数只有两个因数,1和它自己,所以不能形成4种不同的长方形。
B.含有因数5。这并不直接说明它可以形成4种不同的长方形,因为这取决于n的总因数个数。
C.只有5个因数。这意味着n是一个形式为的数,其中p是一个质数。这样的数确实可以形成4种不同的长方形(包括1x, p,x,x,x1),但这也意味着n是一个完全平方数,但这种情况下n的因数个数为5,这与我们的条件不符,因为我们要求的是4种不同的长方形,而这里实际上是5种,不过其中x只算作一种。
D.有7个或8个因数。这是正确的。如果n有7个因数,这意味着n的形式是(p是一个质数),这种情况下n是一个完全平方数,它可以形成4种不同的长方形(1x, p,x,x)。如果n有8个因数,这可能是因为n是两个不同质数的乘积的平方(),这种情况下n也可以形成4种不同的长方形。
故答案为:D
【分析】设小正方形卡片的个数为n。因为可以摆出4种不同的长方形(含正方形),所以n的因数个数至少为4。 对于一个数n,如果它可以分解成,那么a和b都是n的因数。一个数的因数是成对出现的,除非这个数是完全平方数,此时会有一个因数重复。
4.【答案】C
【知识点】合数与质数的特征
【解析】【解答】因为91÷13=7,所以91不是质数。
故答案为:C。
【分析】一个数,如果只有1和它本身两个因数,这样的数叫做质数;一个数,如果除了1和它本身还有别的因数,这样的数叫做合数,据此解答。
5.【答案】A
【知识点】因数与倍数的关系
【解析】【解答】原题中一个因数由16变成160,另一个因数不变。
故答案为:A
【分析】一个因数变成原来的10倍,另一个因数不变,积变为原来积的10倍。
6.【答案】B
【知识点】3的倍数的特征
【解析】【解答】解:小钱取走的本数是小塘的2倍,说明小钱和小塘取走的5堆是3的倍数,则一定有15本和18本这两堆,
剩下的4堆分别是16本,19本,20本,31本,其中只有16+19+31=66(本),66是3的倍数,
66÷(15+18)
=66÷33
=2
仓库里还剩下20本那堆书。
故答案为:B。
【分析】3的倍数的特征是这个数的所有数位上的数字之和是3的倍数。
7.【答案】B
【知识点】分数除法的应用
【解析】【解答】7-2-2=3份;
(7-3)÷3=4÷3=.
故答案为:B。
【分析】甲筐橘子看做单位1,平均分成7份,根据题意可知,甲筐比乙筐多4份,乙筐是3份,(甲筐-乙筐)÷乙筐= 甲筐橘子的质量比乙筐的分率。
8.【答案】错误
【知识点】圆的周长;圆的面积
【解析】【解答】解:圆的周长和面积:①意义不同,圆的面积是指圆所占平面的大小,而圆的周长是指围成圆一周的长度;②计算方法不同,圆的面积=π×半径2,而圆的周长=π×直径;③计量单位不同,面积用面积单位,而周长用长度单位;所以原题干说法错误。
故答案为:错误。
【分析】圆的周长和面积无法比较大小。
9.【答案】错误
【知识点】合数与质数的特征;最简分数的特征
【解析】【解答】解:最简分数的分子和分母不一定都是质数。
故答案为:错误。
【分析】最简分数是指分数的分子和分母没有公约数,例如是最简分数,但是4是合数。
10.【答案】正确
【知识点】公倍数与最小公倍数
【解析】 【解答】 两个数的最小公倍数一定能被这两个数整除。
故答案为:正确。
【分析】几个数公有的倍数叫做这几个数的公倍数。其中最大的一个叫这几个数的最大公倍数。
11.【答案】错误
【知识点】奇数和偶数;合数与质数的特征
【解析】【解答】解:2是偶数,但2是质数。
故答案为:错误。
【分析】偶数是指是2的倍数的整数,合数是指这个数除了1和它本身之外还有其他因数的数,2是偶数,但不是合数。
12.【答案】错误
【知识点】单位“1”的认识及确定
【解析】【解答】把汽车速度看作单位“1”,则火车速度是1+=;
(-1)÷
=÷
=
原题说法错误。
故答案为:错误。
【分析】根据条件“火车比汽车快”可知,把汽车速度看作单位“1”,则火车速度是1+=,要求汽车比火车慢几分之几,用(火车的速度-汽车的速度)÷火车的速度=汽车比火车慢几分之几,据此列式解答。
13.【答案】正确
【知识点】圆的面积
【解析】【解答】解:假设铁丝的长是6.28米,设长方形的长是2米,宽是1.14米,则面积:2×1.14=2.28平方米;正方形的面积为:(6.28÷4)×(6.28÷4)=2.4649平方米;圆的面积为:3.14×(6.28÷3.14÷2)2=3.14平方米;因为:3.14>2.4649>2.28,所以圆的面积最大。
故答案为:正确。
【分析】设铁丝的长是6.28米,长方形的周长=(长+宽)×2,正方形的周长=正方形的边长×4,长方形的面积=长×宽,正方形的面积=正方形的边长×正方形的边长,可得出长方形的长和宽约接近,面积越大,可设长方形的长是2米,宽是1.14米,计算出长方形的面积,再计算出正方形的面积;圆的周长=π×圆的半径×2计算出圆的半径,再根据圆的面积=π×圆的半径的平方,计算出圆的面积,最后将三者的面积进行比较即可得出答案。
14.【答案】210
【知识点】公倍数与最小公倍数
【解析】【解答】解:m和n的最小公倍数是:2×7×5×3=210。
故答案为:210。
【分析】两个数的最小公倍数是把这两个数公有的质因数和它们各自独有的质因数相乘。
15.【答案】15;90
【知识点】2、5的倍数的特征;3的倍数的特征
【解析】【解答】解:3×5=15;
15×6=90。
故答案为:15;90。
【分析】既是3的倍数,又有因数5的最小两位数是3和5的最小公倍数=3×5=15;最大的两位数是15×6=90。
16.【答案】98;02
【知识点】3的倍数的特征
【解析】【解答】解:要使五位数19□□0是30的倍数,即19□□0÷30商是一个整数,根据商不变的规律将被除数和除数同时除以10,即19□□要是3的倍数:因为1+9=10,要最大则每一位都要最大,10+9+9=28,28不是3的倍数,舍去;10+9+8=27,27是3的倍数,所以最大的五位数是19980;要最小则每一位都要最小,10+0+0=10,10+0+1=11,11,10都不是3的倍数,舍去;10+0+2=12,12是3的倍数,所以最小的五位数是19020。
故答案为:98;02。
【分析】3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数;
商的变化规律:被除数和除数同时乘或除以相同的数(0除外),商不变;
先根据商的变化规律将五位数与30同时除以10,则转化成四位数是3的倍数,再根据3的倍数特征去找即可。
17.【答案】;
【知识点】异分母分数加减法
【解析】【解答】解:1-=
(千克)
故答案为,。
【分析】把一袋糖看作单位“1”,用单位“1”减去吃的,即可求出还剩下的是几分之几;用一袋糖的总重量减去吃去的重量,即可求出还剩下的重量。
18.【答案】90
【知识点】公倍数与最小公倍数
【解析】【解答】解:2×3×5=30,
30的倍数有30, 60, 90…,90是两位数范围内30的最大倍数;
故答案为:90。
【分析】先求出2、3和5的最小公倍数,再找出两位数范围内最小公倍数的最大倍数即可。
19.【答案】91;51
【知识点】合数与质数的特征
20.【答案】(1)12|10(答案不唯一)
(2)11~27
【知识点】异分子分母分数大小比较
【解析】【解答】解:(1),,要使,那么7×<85,<85÷7,<12.1…,所以可以是12;
,,所以第三个分数的分子可以是10;
(2),,所以第二个分数的分子可以是11~27。
故答案为:(1)12;10;(2)11~27(答案不唯一)。
【分析】异分母分数比较大小,先通分,然后按照同分母分数大小的比较方法比较大小。同分母分数比较大小,分子大的分数比较大。
21.【答案】;25.12
【知识点】圆的面积
【解析】【解答】解:3.14×(2×2)×
=3.14×4×
=12.56×
=(平方厘米);
3.14×4×2
=12.56×2
=25.12(厘米)。
故答案为:;25.12。
【分析】时针扫过的面积=π×(半径×半径)×;分针尖端走过的距离=2×π×半径。
22.【答案】(1)
(2)
(3) (答案不唯一)
【知识点】图形的缩放;画圆
【解析】【分析】(1)先找到(3,11)位置,把图形①的长、宽扩大2倍,画图形②;(2)旋转、平移图形的一条线段,再画出图形;(3) 在B点北偏东方向画出半径是2厘米的圆即可。
23.【答案】
- = + =1 1- = + =
+ =4 - = - = + =
【知识点】异分母分数加减法
【解析】【分析】同分母分数相加减,分母不变,把分子相加减,能约分的要约分;
异分母分数相加减,先通分,化成同分母分数,然后按照同分母分数的加减法作答即可。
24.【答案】解:++
=++
=1+
=1
+-
=
=
-(+)
=-
=
【知识点】分数加减混合运算及应用;分数加法运算律
【解析】【分析】加法交换律:两个加数相加交换两个加数的位置,和不变,用字母表示为:a+b=b+a;
分数加减混合运算:没有括号,从左往右依次计算;有括号,先算括号里面的,再算括号外面的;
第一题:运用加法交换律交换加数的位置会使计算简便;
第二题:没有括号,从左往右依次计算;
第三题:先算括号里面的加法,再算括号外面的减法。
25.【答案】(1) x= 解: x÷ =
x=
(2)x+ x= 解: x= 1 x÷1 = ÷
x=
【知识点】除数是分数的分数除法;应用等式的性质2解方程
【解析】【分析】解方程要掌握等式的性质,即等式两边同时加上或减去同一个数,左右两边仍然相等;等式两边同时乘或除以同一个不是0的数,等式两边仍然相等。由此结合分数的四则运算方法解方程即可。
26.【答案】解:
【知识点】最简分数的特征
【解析】【分析】先确定分子和分母的最大公因数,根据分数的基本性质把分子和分母同时除以他们的最大公因数即可化成最简分数。
27.【答案】解:3x-30=120
3x=150
x=150÷3
x=50
【知识点】列方程解含有一个未知数的应用题
【解析】【分析】依据等量关系式:女生人数×3-少的人数=男生人数,列方程,解方程。
28.【答案】解:周长:3.14×3×2=18.84(cm)
面积:3.14×32×=14.13(cm2)
【知识点】组合图形面积的巧算;组合图形的周长的巧算;圆的周长;圆的面积
【解析】【分析】阴影部分的周长=半径为3厘米的圆的周长=π×半径×2;
阴影部分的面积=圆的面积的一半=π×半径的平方÷2。
29.【答案】解:+=
1-=
答:甲、乙两队共修了总长的;丙队修了总长的。
【知识点】分数加减混合运算及应用;单位“1”的认识及确定
【解析】【分析】将水渠的总长度看作单位“1”,求甲、乙两队共修了几分之几,用甲队修了总长的几分之几+乙队修了总长的几分之几=甲乙共修了总长的几分之几;求丙队修了总长的几分之几,用减法,就是:1-甲乙共修了总长的几分之几=丙队修了总长的几分之几。
30.【答案】解:《魏书》:
《蜀书》:
《吴书》:
答:《魏书》的卷数占总卷数的,《蜀书》的卷数占总卷数的,《吴书》的卷数占总卷数的。
【知识点】分数的简单应用--占总数的几分之几;约分的认识与应用
【解析】【分析】此题主要考查了分数的简单应用,求一个数是另一个数的几分之几,用除法计算。
31.【答案】解:1-()
=1-()
=1-
=
答:还剩没有松。
【知识点】分数加减混合运算及应用
【解析】【分析】还剩几分之几=单位“1”-(上午松的几分之几+下午松的几分之几)。
32.【答案】解:6和8的最小公倍数是24,公倍数有24、48、72、……,48在30~50之间。
答:该班学生有48人。
【知识点】最小公倍数的应用
【解析】【分析】因为每6人一组或每8人一组都没有剩余,说明总人数一定是6和8的公倍数。先找出6和8的最小公倍数,然后找出6和8在30~50之间的公倍数,就是这个班的学生数。
33.【答案】(1)解;+=
答:喜欢吃苹果和喜欢吃香蕉的同学共占全班人数的。
(2)解:-=
答:喜欢吃西瓜的比喜欢吃葡萄的多占全班人数的。
【知识点】异分母分数加减法
【解析】【分析】(1)用加法计算喜欢吃苹果和喜欢吃香蕉的同学共占全班人数的几分之几;
(2)用减法计算喜欢吃西瓜的比喜欢吃葡萄的多占全班人数的几分之几。
34.【答案】(1)
(2)29
(3)解:从统计图中可以看出中国奖牌数基本是逐年增加的,预测第32届东京奥运会中国队获得奖牌总数量为88枚。
【知识点】复式折线统计图的特点及绘制;从复式折线统计图获取信息
【解析】【解答】解:(2)第29届中、美两国奖牌数最接近。
故答案为:(2)29。
【分析】(1)依据统计图中的数据描出各点,然后连接成线,并且标上数据;
(2)第29届中、美两国奖牌数折线上的点距离最近,所以这一届奖牌数最接近。
(3)中国奖牌数基本是逐年增加的,预测第32届东京奥运会中国队获得奖牌总数量为88枚。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
