2024-2025学年小升初重点校分班考全真模拟提分卷(含解析)六年级下册数学(北师大版)
文档属性
| 名称 | 2024-2025学年小升初重点校分班考全真模拟提分卷(含解析)六年级下册数学(北师大版) |  | |
| 格式 | docx | ||
| 文件大小 | 421.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 15:11:37 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年六年级下册数学小升初重点校分班考全真模拟提分卷
一、填空题
1.如图,三角形ABC是一个等腰直角三角形,它与一个正方形叠放在一起,已知AE,EF,FB三条线段一样长,三角形EFD(阴影部分)面积是4平方米,三角形ABC面积是 平方米。
2.如图,涂色部分是一个长方形,周长是30cm。若分别以它的长和宽为边长画出两个正方形,两个正方形的面积之和是137 cm2,则涂色部分的面积是 cm2。
3. ÷ == = (填小数)
4.把“1”平均分成100份,其中的37份是 (填分数),也可以表示为 (填小数)。
5.体育课每星期上两节,两节课的安排要满足如下要求:①每天只能上一节;②不能连续两天都有体育课;③每天可以在1 ~6节的任意一节上这门课;④星期六和星期日不能安排。则这门课一共有 种安排方式。
6.一幅城市地图中两地的图上距离为10cm,表示实际距离30km,该幅地图的比例尺是 。
7.有一根电线, 第一次用去 32 m , 第二次用去 28 m , 还剩下 , 这根电线原来有 m
8.某工厂去年生产电视机20000台,今年比去年增产二成五,今年生产 台。
9.小芳将米的丝带剪成同样长的8段,每段丝带长 米,每段是全长的 。
10. 每套《中国首次载人航天飞行成功》纪念邮票是2.8元,购买15套一共花 元。
11.加工一批零件,甲先加工了这批零件的,接着乙加工了余下的,已知乙加工的个数比甲少200个,这批零件共有 个。
12.
摆一个△用3根小棒,摆2个△用5根小棒,摆3个△用7根小棒。照这样摆下去,摆6个△用 根小棒,用21根小棒可以摆 个△。
★一个正方体木块,表面积是50平方厘米,如果把它截成体积相等的27个小正方体木块,27个小正方体木块的表面积之和是 平方厘米。
13.一个长方形的周长为36厘米,如果长减少4厘米,宽增加2厘米,长方形就变成了正方形,则原来长方形的面积是 平方厘米。
二、判断题
14.六(1)班学生在植树活动中共栽树苗99棵,树苗全部成活,成活率是99%。( )
15.一个平行四边形和一个三角形的面积相等,高也相等。若平行四边形的底是6厘米,则三角形的底是3厘米。( )
16.在一个三角形中,已知两个内角分别是55°和33°,这个三角形一定是锐角三角形。( )
17.把一个长方体切成两个小长方体,它的表面积不变。( )
18.把一个长方形木框架拉成平行四边形,周长不变,面积变小了.( )
19.被除数相当于分数的分子,除数相当于分数的分母。(
)
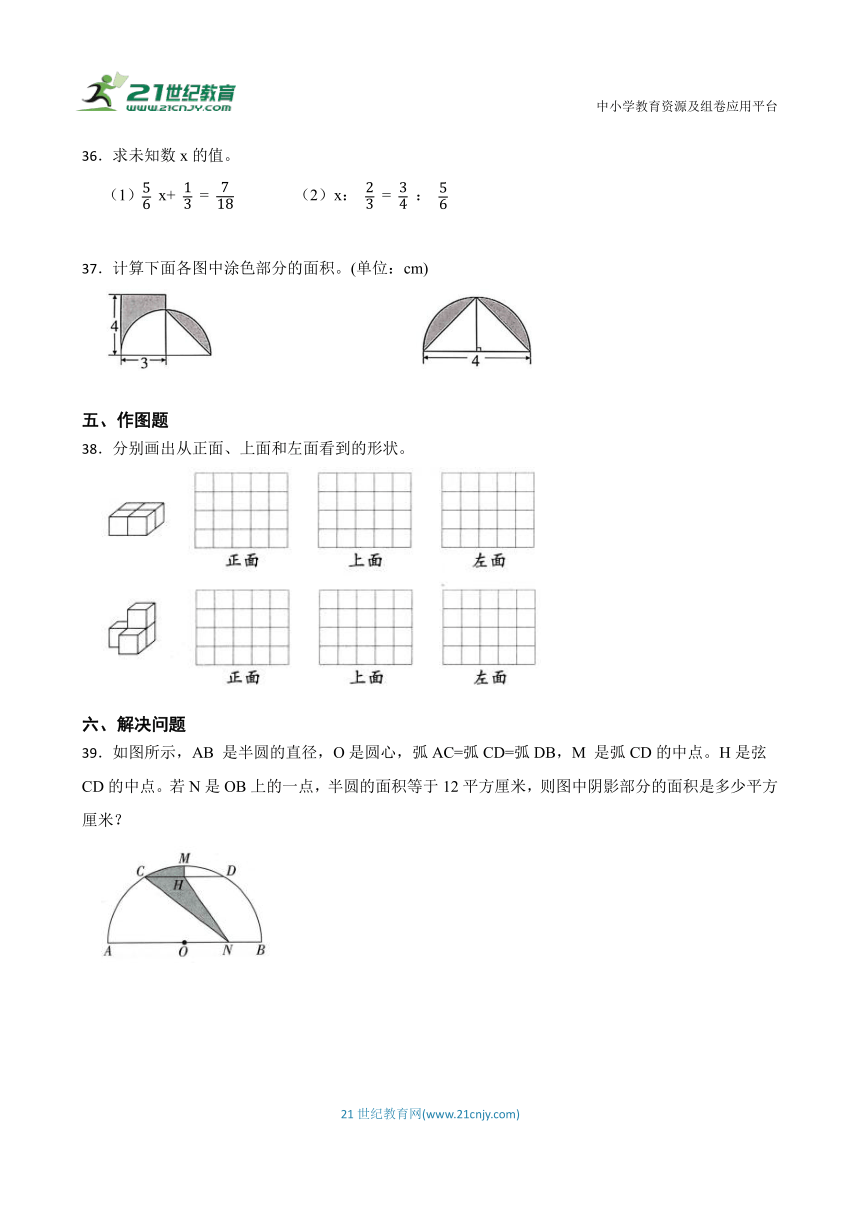
20.用同样长的铁丝围成两个长方形,甲长方形的长与宽之比为6:1,乙长方形的长与宽之比为2:1。那么,甲长方形的面积大于乙长方形的面积。( )
21.平年的上半年有181天。( )
三、单选题
22.如图,甲和乙都是由若干个相同的小正方体组成的,甲的体积 乙的体积,甲的表面积 乙的表面积。
A.> B.= C.< D.无法比较
23.甲地到乙地的距离是5千米28米,与这个距离相等的是( )。
A.5028米 B.5280米 C.528米 D.5208米
24.学校图书室长9.7m,宽5.8m,用边长为0.9m的正方形瓷砖铺地,需要准备多少块瓷砖 在解决这个问题的时候,同学们认为不用精确计算,估算就可以。下面估算合理的是( )。
A.9.7 m≈9 m,9÷0.9=10(块),5.8m≈5. 4m,5.4÷0.9=6(块), (块)
B.9.7m≈9.9m,9.9÷0.9=11(块),5.8m≈5. 4m ,5.4÷0.9=6(块), (块)
C.9.7 m≈9.9 m,9.9÷0.9=11(块),5.8m≈6. 3m ,6.3÷0.9=7(块), (块)
D.9.7 m≈9 m,9÷0.9=10(块),5.8m≈7. 2m,7.2÷0.9=8(块), (块)
25.一个底面内直径为6cm的瓶子里,水的高度是5cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是16cm。这个瓶子的容积是( )mL。
A.593.46 B.310.86 C.2373.84 D.1808.64
26.两种不同的新冠疫苗A和B,已经在两个医院都做过了临床试验。试验结果表明,在两个医院中,A疫苗均比B疫苗效果好。但令人奇怪的是,当人们把结果合并(即把两个医院看作一个医院)后发现,B疫苗却比A疫苗效果好,这是否可能( )。
A.不可能 B.可能 C.一定是 D.一定不是
E.无法确定
27.一辆汽车的油箱储油102升,行驶了56千米正好耗油8升,照这样计算,剩下的油还可以行驶多少千米?设剩下的油还可以行驶x千米,可以列式为( )。
A.56:8=102:x B.56:8=x:102
C.56:8=x:(102-8) D.56:8=(102+8):x
28.把一个棱长是 adm的正方体,任意截成两个长方体,这两个长方体的表面积之和是( ) dm2。
A.2a2 B.7a2 C.8a2 D.10a2
29.春晚分会场在西安设立,将西安文创销量再次推向顶峰,甲文创厂的产值由第一季度的35万增长到第二季度的63万,乙文创厂第一季度的产值是20万,增长速度比甲文创厂快,乙文创厂第二季度的产值可能是( )万。
A.35 B.36 C.37
30.下面图形不是正方体展开图的是( )。
A. B. C.
31.下面说法正确的是( )。
A.每两个计数单位之间的进率是10。
B.直线比射线长。
C.只有一组对边平行的四边形叫做梯形。
32.有( )个正方形中含有“”。
A.5 B.6 C.7
33.一根圆柱形木料的底面半径是2厘米,长是40厘米。如图所示,将它截成5段( )平方厘米。
A.200.96 B.100.48 C.80 D.50.24
四、计算题
34.直接写出得数。
- = 3.14×0.12= 2-0.08= 2.5×40%= 50×20%
3.75+ = 72× = 24÷ = ÷ = 10÷10%=
35.计算下面各题,能简算的要简算。
36.求未知数x的值。
(1) x+ = (2)x: = :
37.计算下面各图中涂色部分的面积。(单位:cm)
五、作图题
38.分别画出从正面、上面和左面看到的形状。
六、解决问题
39.如图所示,AB 是半圆的直径,O是圆心,弧AC=弧CD=弧DB,M 是弧CD的中点。H是弦CD的中点。若N是OB上的一点,半圆的面积等于12平方厘米,则图中阴影部分的面积是多少平方厘米?
40.盒子灯,又称宫廷盒子灯,是起源于河北省沧州市海兴县的花灯技艺。硕大的纸质古式食盒之内,暗藏着一层层花灯:或状如玲珑雅致的宝塔,或似寓意吉祥的花盆……孙师傅制作盒子灯中的一个长方体框架时,用了52dm长的竹条,已知它的长是8dm,宽是3dm,则高是多少分米?
41.四位姐姐在一片荷塘里采莲,一共需要8日可以完成;若再加上乐乐,则只需8日就可以完成。乐乐采一日的数量是一位姐姐采一日的几分之几 (每位姐姐每日采的数量相同)
42. 一根88cm长的绳子每隔6cm做一个红色的记号,每隔5cm做一个蓝色的记号,每隔7cm做一个绿色的记号。那么这根绳子共有多少个记号 (开端不做记号,重合的记号记为1个记号)
43.张老师做红花和黄花,红花的朵数是黄花的4倍。____________,红花和黄花各有多少朵?(从下面选择一个你喜欢的条件,将序号填在横线上,再列方程解答)
①红花和黄花一共300朵 ②红花比黄花多180朵
44.智能音箱可以在人们语音指引下,提供点歌、听书、定闹钟等功能。超市某款智能音箱的价格为300元,中秋节降价 出售,中秋节买这款智能音箱需要多少元
45.某班有若干人参加一次智力竞赛,共a、b、c三题,每题或者得满分或者得0分,其中题a、题b、题c满分分别为 20 分、25分,25分。竞赛结果,每个学生至少答对了一题,三题全答对的有1人只答对其中两道题的有 15 人,答对题a的人数与答对题b的人数之和为 29,答对题a的人数与答对题。的人数之和为 25,答对题b的人数与答对题c的人数之和为 20,求这个班参赛同学的平均成绩是多少分?
46.甲、乙两个城市相距120 km。一只蚂蚁在这幅地图上仅用了5秒便从乙城市爬行到甲城市,已知蚂蚁每秒爬行1.2cm,则这幅地图的比例尺是多少?
47.如图,自行车上的两个齿轮通过链条转动,在同一时间内,大、小齿轮转过的齿数是相同的。
(1)当转过的总齿数一定时,每个齿轮的齿数与转过的圈数成什么比例,为什么?
(2)大齿轮有50个齿,小齿轮有20个齿,如果大齿轮每分转12圈,那么小齿轮每分转多少圈呢?
(3)骑自行车时,自行车后轮随大齿轮的转动而转动,已知后轮与大齿轮圈数之比为2∶3,如果后轮直径为80厘米,请问骑行该自行车走1256米时,小齿轮转了几圈?
参考答案及试题解析
1.【答案】36
【解析】解:如图,
与等高,则
则
则
故答案为:36
【分析】因为AE,EF,FB三条线段一样长,所以用它们作斜边的三个等腰直角三角形面积相等,E是线段AF的中点。等腰直角△ADE的面积与△DEF的面积相等,即面积为4。不难看出,叠放的正方形是由8个这样的等腰直角三角形组成如图。而△ABC是由9个这样的等腰直角三角形组成,面积是4×9=36。
2.【答案】44
【解析】解:根据题意,可得
[(30÷2)2-137]÷2
=[152-137]÷2
=[225-137]÷2
=88÷2
=44(cm2)答:涂色部分的面积是44平方厘米
故答案为:44
【分析】如图,把这个图形通过作辅助线补成一个边长为阴影部分长、宽之和的正方形,用阴影部分的周长除以2就是阴影部分的长、宽之和,即补成的正方形的边长,用补成的正方形的面积减137 cm2,再除以2就是阴影部分的面积
3.【答案】2;5;6;0.4
【解析】解:根据题意,可得
故答案为:2;5;6;0.4
【分析】(1)根据分数的性质:分子分母同时扩大相同的倍数,分数的结果不变;
(2)分数化小数的方法:用分子除以分母,然后再进行求解即可
4.【答案】;0.37
5.【答案】216
【解析】解:由题意可知,这节体育课可以安排在:周一和周三;周一和周四;周一和周五;周二和周四;周二和周五;周三和周五共6种情况。因为每一节体育课都有6种情况,从第一节到第六节,这门课共有:6×6×6=216(种)安排方式。
故答案为:216
【分析】 从安排在哪天来说有6种情况,而每一节体育课又有6种情况,然后可得答案.
6.【答案】1:300000
【解析】解:根据题意,可得
30km=3000000cm
10:3000000=1:300000
故答案为:1:300000
【分析】先将30km化成3000000cm,然后再根据比例尺=图上距离÷实际距离,代入数据即可求解
7.【答案】100
【解析】解:(32+28)÷(1-40%)
=60÷0.6
=100(米)
这根电线原来有100米
故答案为:100。
【分析】一共用去的长度÷一共用去的长度占这根电线原来长度的百分率=这根电线原来的长度。
8.【答案】25000
9.【答案】;
【解析】解:根据题意,可得
故答案为:;
【分析】用总长度除以平均分的段数,就是每段的长度。把总长度看作单位“1”,用1除以平均分的段数,就是每段是全长的几分之几。
10.【答案】42
【解析】解:2.8×15=42(元)
答:购买15套一共花42元。
故答案为:42。
【分析】根据“单价×数量=总价”列式2.8×15=42(元)。
11.【答案】1500
【解析】解:(1-)×
=×
=
200÷(-)
=200÷
=1500(个)
故答案为:1500。
【分析】首先,将这批零件看作单位“1”计算乙加工的零件所占的比例。由于甲先加工了这批零件的,那么剩余的零件比例就是1-=。乙加工了这剩余零件的,所以乙加工的零件所占的比例为×=;用甲加工的减去乙加工的,得到甲比乙多加工的数量占总数的多少,进而根据分数除法,用200除以该分数比例即可得出这批零件的总数。
12.【答案】13;10;2n+1
【解析】解:6×2+1=13根,所以 摆6个△用13根小棒;(21-1)÷2=10个,所以用21根小棒可以摆10个△;
3×3×3=27块,2×2×3=12,50÷6×12+50=150平方米,所以27个小正方体木块的表面积之和是150平方厘米。
故答案为:13;10;2n+1。
【分析】(1)摆1个△用小棒的根数:3=2+1;
摆2个△用小棒的根数:5=2×2+1;
摆3个△用小棒的根数:7=2×3+1;
……
摆n个△用小棒的根数:2n+1。
(2)3×3×3=27块,所以这个大正方体沿着高、宽、长都截了2次,每截一次,增加2个大正方体一个面的面积,所以增加大正方体一个面的个数=2×2×3=12个,所以27个小正方体木块的表面积之和=正方体的表面积÷6×增加大正方体一个面的个数+大正方体的表面积。
13.【答案】72
【解析】解:36÷2=18(厘米)
18-4+2
=14+2
=16(厘米)
长:16÷2+4
=8+4
=12(厘米)
宽:16÷2-2
=8-2
=6(厘米)
12×6=72(平方厘米)
故答案为:72。
【分析】长方形的周长=(长+宽)×2,所以,长方形的周长÷2=长+宽,因此,当长减少时长与宽的和也减少,当宽增加时长与宽的和也增加,所以,长与宽的和-长减少的长度+宽增加的长度=变成正方形后长与宽的和,变成正方形后长与宽的和÷2=此时的长与宽,变成正方形后长与宽的和÷2+长减少的长度=原长方形的长,变成正方形后长与宽的和÷2-宽增加的长度=原长方形的宽,所以,原长方形的面积=原长方形的长×原长方形的宽。
14.【答案】错误
【解析】解:99÷99=100%,全部成活,成活率是100%。原题说法错误。
故答案为:错误。
【分析】树苗的成活棵数÷种的棵数=成活率。
15.【答案】错误
【解析】解:一个平行四边形和一个三角形的面积相等,高也相等。若平行四边形的底是6厘米,则三角形的底是12厘米。原题说法错误。
故答案为:错误。
【分析】平行四边形面积=底×高,三角形面积=底×高÷2,等底等高的平行四边形面积是三角形面积的2倍。如果面积相等,高也相等,那么三角形的底就是平行四边形底的2倍。
16.【答案】错误
【解析】180°-(55°+33°)
=180°-88°
=92°
这个三角形是一个钝角三角形,原题说法错误。
故答案为:错误。
【分析】三角形的内角和是180°,已知三角形的两个内角,要求第三个内角,三角形的内角和-两个内角的度数之和=第三个内角度数;三角形按角分类,可以分为锐角三角形、直角三角形、钝角三角形;有一个角是直角的三角形是直角三角形;有一个角是钝角的三角形是钝角三角形;三个角都是锐角的三角形是锐角三角形,据此解答。
17.【答案】错误
【解析】解:把一个长方体切成两个小长方体,它的表面积比原来大。
故答案为:错误。
【分析】把一个长方体切成两个小长方体,它的表面积增加了2个横截面的面积,所以它的表面积比原来大。
18.【答案】正确
【解析】解:把一个长方形木框架拉成平行四边形,周长不变,面积变小了,说法正确。
故答案为:正确。
【分析】一个长方形框架拉成平行四边形,四条边的边长不变则周长不变;再拉的过程中,底不变,高减小,根据平行四边形的面积=底×高即可得出答案。
19.【答案】正确
【解析】被除数相当于分数的分子,除数相当于分数的分母。本题说法正确。
故答案为:正确。
【分析】根据分数与除法的关系判断,a÷b=。
20.【答案】错误
【解析】解:6÷1=6,2÷1=2,2<6,甲长方形的面积<乙长方形的面积,原题干说法错误。
故答案为:错误。
【分析】周长相等的长方形中,长与宽最接近,面积最大,即长与宽的比值最小时,面积最大。
21.【答案】正确
【解析】解:31+28+31+30+31+30=181(天),原题说法正确。
故答案为:正确。
【分析】一年中1、3、5、7、8、10、12是大月,每个大月是31天;4、6、9、11是小月,每个小月是30天;还有一个特殊月2月,平年的2月是28天,闰年的2月是29天。据此解答。
22.【答案】C;A
【解析】解:甲和乙都是由若干个相同的小正方体组成的,甲的体积<乙的体积,甲的表面积>乙的表面积。
故答案为:C;A。
【分析】甲是由26个小正方体组成,乙是由27个小正方体组成,所以甲的体积小于乙的体积;甲的表面积比乙的表面积多出两个小正方体的面,所以甲的表面积大于乙的表面积。
23.【答案】A
24.【答案】C
【解析】解:9.7 m≈9.9 m,9.9÷0.9=11(块),5.8m≈6. 3m ,6.3÷0.9=7(块),11×7=77 (块)。
长和宽都合理估了,计算更加准确。
故答案为:C。
【分析】根据题意,贴瓷砖的块数=长贴的块数×宽贴的块数,长贴的块数=长÷边长,宽贴的块数=宽÷边长,估算时既要方便计算,又要减少误差,这样才与精确结果接近,才会更加合理。
25.【答案】A
【解析】解:3.14×(6÷2)2×(5+16)
=3.14×9×21
=593.46(cm3)
=593.46mL
故答案为:A。
【分析】瓶子的体积=水的体积+倒置是无水部分圆柱的体积,圆柱的体积=底面积×高,代入数据计算即可。
26.【答案】B
【解析】解:这是有可能的,分两种情况讨论:
⑴若A疫苗在甲医院有n个人接受试验,a个人有效; B疫苗在甲医院有n个人接受试验,b个人有效,则 所以a>b.
A疫苗和B疫苗在乙医院都有m个人接受试验,分别有c和d个人有效,依题意 所以c >d. 于是
在这种情况下,把结果合并后A疫苗仍比B疫苗效果好.
⑵若A疫苗在甲医院有20个人接受试验,6个人有效; B疫苗在甲医院有10个人接受试验,2个人有效,显然
A疫苗在乙医院有80个人接受试验,40 个人有效; B疫苗在医院有990个人接受试验,478个人有效,显然
然而把结果合并后却可得 即 B 疫苗比 A 疫苗效果好。
故答案为:B。
【分析】因为两个医院的测试人数可能会有所不同,并且每个人接受的疫苗有效人数也可能不同,这可能导致两个医院之间存在差异,从而影响结论的准确性。所以可以分两种情况讨论:①假设两个医院接受测试的人数相等;②假设两个医院接受测试的人数不相等。通过这两种情况分别讨论合并后的结果情况。
27.【答案】C
【解析】解:56:8=x:(102-8)
故答案为:C。
【分析】根据已知“照这样计算”可知每升油能行驶的距离一定,即行驶的距离:油耗=每升油能行驶的距离(一定),比值一定,所以行驶的距离和油耗成正比例关系,因此,油箱储油量-已经用的油=剩下的油,已经行驶的距离:已经用了的油=剩下的距离:(油箱储油量-已经用的油),据此可以判断。
28.【答案】C
【解析】解:6×a×a+2×a×a
=6a2+2a2
=8a2(dm2);
故答案为:C。
【分析】两个长方体的表面积之和就是原正方体的表面积+增加的两个面的面积,正方体表面积=棱长×棱长×棱长,据此求解。
29.【答案】C
【解析】解:(63-35)÷35=80%,
20×(1+80%)=36万,
35<36<37。
故答案为:C
【分析】本题考查的是对百分比增长率的理解与计算。根据题目信息,首先需要计算出甲文创厂的产值增长百分比,然后分析乙文创厂的产值增长百分比是否大于甲文创厂,从而判断乙文创厂第二季度产值的可能值。
30.【答案】B
31.【答案】C
32.【答案】B
【解析】解:1+4+1=6(个)。
故答案为:B。
【分析】包含○的正方形个数=1个最小的正方形+四个小的正方形组成4个稍大的正方形+整个正方形。
33.【答案】B
【解析】解:3.14×22×8
=3.14×4×8
=100.48(平方厘米);
故答案为:B。
【分析】每截一次木料,都会新增两个圆形截面,截成5段就是截了4次,新增8个圆形截面,圆的面积=,据此求解即可。
34.【答案】 - = 3.14×0.12=0.0314 2-0.08=1.92 2.5×40%=1 50×20%=10
3.75+ =4 72× =40 24÷ =30 ÷ = 10÷10%=100
【解析】计算含有分数、小数的运算时,可以先统一化成分数或小数,再计算。
含百分数的计算,通常把百分数化成小数或分数后,再计算;
分数乘法的计算法则:分数乘分数,用分子相乘的积作分子,分母相乘的积作分母。
分数除法的计算法则:甲数除以乙数(0除外),等于甲数乘乙数的倒数。
异分母分数加减法计算方法:先通分,然后按照同分母分数加减法的的法则进行计算。
35.【答案】解:(1)
=
=
=
=
(2)
=
=
=15+14-16
=13
(3)
=2-1
=1
(4)
=
=
=28+72
=100
(5)
=
=
=
【解析】(1)首先将题目中的除法运算转换为乘法运算,便于观察和提取公因式,通过转换可以将题目简化为乘法的组合,从而应用提取公因式的技巧来简化计算过程。
(2)首先需要将除法转化为乘法,然后利用分数乘法分配律,对每一项进行计算,最后求出最终结果。
(3)根据加法交换律将同分母分数凑在一起,可以进行简便计算。
(4)利用分配律将式子展开,发现可以通过约分进行简便运算。
(5)按照数学运算的优先级,首先处理括号内的加法运算,然后将分数除法转化为分数乘法,进行计算。
36.【答案】(1) x+=
解:x+-=-
x=
x÷=÷
x=
(2) x:=:
解:x=×
x=
x÷=÷
x=
【解析】(1)根据等式性质1消掉方程左边的已知数,然后根据等式性质2使未知项的系数变成1,可得方程的解;
(2)根据比例的基本性质将比例式化成乘积式,再按照解方程的方法计算。
37.【答案】解:(4-3+4)×3÷2
=5×3÷2
=7.5(cm2);
4÷2=2(cm)
3.14×22×
=6.28(cm2)
4×2×=4(cm2)
6.28-4=2.28(cm2)。
【解析】如图将右边涂色部分剪下后拼到左边,则涂色部分就是一个梯形,梯形的上底是4-3=1cm,下底是4cm,高是3cm,因此,(上底+下底)×高÷2=梯形的面积;
第二幅图外面是一个直径为4cm的半圆,空白部分是一个底是4cm,高是半圆半径的三角形,因此,直径÷2=半径,圆周率×半径的平方×=外面半圆的面积,底×高×=空白部分三角形的面积,外面半圆的面积-空白部分三角形的面积=涂色部分的面积。
38.【答案】
【解析】分别从不同的方向观察图形,判断出观察到的图形有几个正方形以及每个正方形的位置,然后画出看到的图形即可。
39.【答案】12÷3÷2
=4÷2
=2(平方厘米)
【解析】如图,连接OC,OD,OH,则扇形AOC,COD,BOD 的面积相等,且都等于半圆面积的 又因为△COH与△CNH等底等高,则,因此阴影部分的面积等于扇形COD面积的一半,依此求解。
40.【答案】解:52÷4-8-3
=13-8-3
=2(dm)
答:高是2分米。
【解析】根据题意可知竹条的长度就是长方体框架的棱长之和,因为长方体的棱长之和=(长+宽+高)×4,所以,竹条的长度÷4-长-宽=高,据此可以解答。
41.【答案】解:设姐姐的工作效率为x,乐乐的工作效率为y
32x+8y=34x
8y=2x
答:乐乐采一日的数量是一位姐姐采一日的
【解析】设姐姐的工作效率为x,乐乐的工作效率为y,根据工作总量=工作时间×工作效率,结合题目中的等量关系,列出方程,解出y,即可求出答案。
42.【答案】解:根据题意,在这88 cm长的绳子上,
每隔6的倍数做一个红色记号,
则88÷6=14(个)……4(cm), 有 14个红色记号;
每隔5的倍数做一个蓝色记号,
则88÷5=17(个)……3(cm), 有17个蓝色记号;
每隔7的倍数做一个绿色记号,
则88÷7=12(个)……4(cm), 有12个绿色记号;
重合的记号长度即分别是6和5的最小公倍数、5和7的最小公倍数、6和7的最小公倍数、6和5和7的最小公倍数,
[6,5]=30, 88÷30=2(个)……28(cm), 红色和蓝色重合的记号有2个,
[5,7]=35, 88÷35=2(个)……18(cm), 蓝色和绿色重合的记号有2个,
[6,7]=42, 88÷42=2(个)……4(cm), 红色和绿色重合的记号有2个,
[5,6,7]=210, 210>88, 所以没有三种颜色重合的记号,
一共有记号:14+17+12-2-2-2=37(个)。
答:这根绳子共有37个记号。
【解析】先根据绳子长度和每种间隔距离求出各自做记号的数量。因为重合的地方在各自计算时被重复计算,所以通过求最小公倍数来确定两两重合的记号数量。最后考虑三种颜色重合的情况,由于6、5、7的最小公倍数大于绳子长度,所以没有三种颜色重合的记号。将各自做记号的数量相加,再减去两两重合多算的数量,就得到绳子上记号的总数。
43.【答案】①(或②);红花240朵,黄花60朵
44.【答案】解:根据题意,得
300×(1-)
=300×(1-)
=300×
=270(元)
答:中秋节买这款智能音箱需要270元。
【解析】本题考查分数乘法的计算及应用。把智能音箱的原价看作单位“1”,降价出售,现价是原价的(1-),用智能音箱的原价乘(1-),即可求出中秋节这款智能音箱的价格是多少。
45.【答案】 解:设答对 a 题的有 x 人,答对 b 题的有 y 人,答对 c 题的有 z 人,
根据题意得:
x + y =29
x + z =25,
y + z =20
解得:
x =17
y =12.
z =8
全班总得分为17×20+(12+8)×25=840(分),
全班总人数为17+12+8-1×15-2×1=20(人),
全班的平均成绩为840÷20=42(分).
答: 这个班参赛同学的平均成绩是42分 。
【解析】 设答对 a 题的有 x 人,答对 b 题的有 y 人,答对 c 题的有 z 人,根据"答对题 a 的人数与答对题 b 的人数之和为29,答对题 a 的人数与答对题 c 的人数之和为25,答对题 b 的人数与答对题 c 的人数之和为20",即可得出关于 x 、 y 、 z 的三元一次方程组,解之即可得出 x 、 y 、 z 的值,由 x 、 y 、 z 的值结合 a 、 b 、 c 三题的分值可求出全班总得分,由 x 、 y 、 z 的值结合答对两题及答对三题的人数可求出全班总人数,再利用平均分=总分÷人数,即可求出结论.
46.【答案】解:5×1.2=6(cm)
120km=12000000cm
6:1000000=1:2000000
答:这幅地图的比例尺是1:2000000。
【解析】用蚂蚁爬行的时间乘爬行的速度,求出图上距离,然后根据“比例尺=图上距离:实际距离”即可算出比例尺。
47.【答案】(1)反比例;每个齿轮的齿数×转过的圈数=转过的总齿数(一定)
(2)30圈
(3)1875圈
21世纪教育网(www.21cnjy.com)
2024-2025学年六年级下册数学小升初重点校分班考全真模拟提分卷
一、填空题
1.如图,三角形ABC是一个等腰直角三角形,它与一个正方形叠放在一起,已知AE,EF,FB三条线段一样长,三角形EFD(阴影部分)面积是4平方米,三角形ABC面积是 平方米。
2.如图,涂色部分是一个长方形,周长是30cm。若分别以它的长和宽为边长画出两个正方形,两个正方形的面积之和是137 cm2,则涂色部分的面积是 cm2。
3. ÷ == = (填小数)
4.把“1”平均分成100份,其中的37份是 (填分数),也可以表示为 (填小数)。
5.体育课每星期上两节,两节课的安排要满足如下要求:①每天只能上一节;②不能连续两天都有体育课;③每天可以在1 ~6节的任意一节上这门课;④星期六和星期日不能安排。则这门课一共有 种安排方式。
6.一幅城市地图中两地的图上距离为10cm,表示实际距离30km,该幅地图的比例尺是 。
7.有一根电线, 第一次用去 32 m , 第二次用去 28 m , 还剩下 , 这根电线原来有 m
8.某工厂去年生产电视机20000台,今年比去年增产二成五,今年生产 台。
9.小芳将米的丝带剪成同样长的8段,每段丝带长 米,每段是全长的 。
10. 每套《中国首次载人航天飞行成功》纪念邮票是2.8元,购买15套一共花 元。
11.加工一批零件,甲先加工了这批零件的,接着乙加工了余下的,已知乙加工的个数比甲少200个,这批零件共有 个。
12.
摆一个△用3根小棒,摆2个△用5根小棒,摆3个△用7根小棒。照这样摆下去,摆6个△用 根小棒,用21根小棒可以摆 个△。
★一个正方体木块,表面积是50平方厘米,如果把它截成体积相等的27个小正方体木块,27个小正方体木块的表面积之和是 平方厘米。
13.一个长方形的周长为36厘米,如果长减少4厘米,宽增加2厘米,长方形就变成了正方形,则原来长方形的面积是 平方厘米。
二、判断题
14.六(1)班学生在植树活动中共栽树苗99棵,树苗全部成活,成活率是99%。( )
15.一个平行四边形和一个三角形的面积相等,高也相等。若平行四边形的底是6厘米,则三角形的底是3厘米。( )
16.在一个三角形中,已知两个内角分别是55°和33°,这个三角形一定是锐角三角形。( )
17.把一个长方体切成两个小长方体,它的表面积不变。( )
18.把一个长方形木框架拉成平行四边形,周长不变,面积变小了.( )
19.被除数相当于分数的分子,除数相当于分数的分母。(
)
20.用同样长的铁丝围成两个长方形,甲长方形的长与宽之比为6:1,乙长方形的长与宽之比为2:1。那么,甲长方形的面积大于乙长方形的面积。( )
21.平年的上半年有181天。( )
三、单选题
22.如图,甲和乙都是由若干个相同的小正方体组成的,甲的体积 乙的体积,甲的表面积 乙的表面积。
A.> B.= C.< D.无法比较
23.甲地到乙地的距离是5千米28米,与这个距离相等的是( )。
A.5028米 B.5280米 C.528米 D.5208米
24.学校图书室长9.7m,宽5.8m,用边长为0.9m的正方形瓷砖铺地,需要准备多少块瓷砖 在解决这个问题的时候,同学们认为不用精确计算,估算就可以。下面估算合理的是( )。
A.9.7 m≈9 m,9÷0.9=10(块),5.8m≈5. 4m,5.4÷0.9=6(块), (块)
B.9.7m≈9.9m,9.9÷0.9=11(块),5.8m≈5. 4m ,5.4÷0.9=6(块), (块)
C.9.7 m≈9.9 m,9.9÷0.9=11(块),5.8m≈6. 3m ,6.3÷0.9=7(块), (块)
D.9.7 m≈9 m,9÷0.9=10(块),5.8m≈7. 2m,7.2÷0.9=8(块), (块)
25.一个底面内直径为6cm的瓶子里,水的高度是5cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是16cm。这个瓶子的容积是( )mL。
A.593.46 B.310.86 C.2373.84 D.1808.64
26.两种不同的新冠疫苗A和B,已经在两个医院都做过了临床试验。试验结果表明,在两个医院中,A疫苗均比B疫苗效果好。但令人奇怪的是,当人们把结果合并(即把两个医院看作一个医院)后发现,B疫苗却比A疫苗效果好,这是否可能( )。
A.不可能 B.可能 C.一定是 D.一定不是
E.无法确定
27.一辆汽车的油箱储油102升,行驶了56千米正好耗油8升,照这样计算,剩下的油还可以行驶多少千米?设剩下的油还可以行驶x千米,可以列式为( )。
A.56:8=102:x B.56:8=x:102
C.56:8=x:(102-8) D.56:8=(102+8):x
28.把一个棱长是 adm的正方体,任意截成两个长方体,这两个长方体的表面积之和是( ) dm2。
A.2a2 B.7a2 C.8a2 D.10a2
29.春晚分会场在西安设立,将西安文创销量再次推向顶峰,甲文创厂的产值由第一季度的35万增长到第二季度的63万,乙文创厂第一季度的产值是20万,增长速度比甲文创厂快,乙文创厂第二季度的产值可能是( )万。
A.35 B.36 C.37
30.下面图形不是正方体展开图的是( )。
A. B. C.
31.下面说法正确的是( )。
A.每两个计数单位之间的进率是10。
B.直线比射线长。
C.只有一组对边平行的四边形叫做梯形。
32.有( )个正方形中含有“”。
A.5 B.6 C.7
33.一根圆柱形木料的底面半径是2厘米,长是40厘米。如图所示,将它截成5段( )平方厘米。
A.200.96 B.100.48 C.80 D.50.24
四、计算题
34.直接写出得数。
- = 3.14×0.12= 2-0.08= 2.5×40%= 50×20%
3.75+ = 72× = 24÷ = ÷ = 10÷10%=
35.计算下面各题,能简算的要简算。
36.求未知数x的值。
(1) x+ = (2)x: = :
37.计算下面各图中涂色部分的面积。(单位:cm)
五、作图题
38.分别画出从正面、上面和左面看到的形状。
六、解决问题
39.如图所示,AB 是半圆的直径,O是圆心,弧AC=弧CD=弧DB,M 是弧CD的中点。H是弦CD的中点。若N是OB上的一点,半圆的面积等于12平方厘米,则图中阴影部分的面积是多少平方厘米?
40.盒子灯,又称宫廷盒子灯,是起源于河北省沧州市海兴县的花灯技艺。硕大的纸质古式食盒之内,暗藏着一层层花灯:或状如玲珑雅致的宝塔,或似寓意吉祥的花盆……孙师傅制作盒子灯中的一个长方体框架时,用了52dm长的竹条,已知它的长是8dm,宽是3dm,则高是多少分米?
41.四位姐姐在一片荷塘里采莲,一共需要8日可以完成;若再加上乐乐,则只需8日就可以完成。乐乐采一日的数量是一位姐姐采一日的几分之几 (每位姐姐每日采的数量相同)
42. 一根88cm长的绳子每隔6cm做一个红色的记号,每隔5cm做一个蓝色的记号,每隔7cm做一个绿色的记号。那么这根绳子共有多少个记号 (开端不做记号,重合的记号记为1个记号)
43.张老师做红花和黄花,红花的朵数是黄花的4倍。____________,红花和黄花各有多少朵?(从下面选择一个你喜欢的条件,将序号填在横线上,再列方程解答)
①红花和黄花一共300朵 ②红花比黄花多180朵
44.智能音箱可以在人们语音指引下,提供点歌、听书、定闹钟等功能。超市某款智能音箱的价格为300元,中秋节降价 出售,中秋节买这款智能音箱需要多少元
45.某班有若干人参加一次智力竞赛,共a、b、c三题,每题或者得满分或者得0分,其中题a、题b、题c满分分别为 20 分、25分,25分。竞赛结果,每个学生至少答对了一题,三题全答对的有1人只答对其中两道题的有 15 人,答对题a的人数与答对题b的人数之和为 29,答对题a的人数与答对题。的人数之和为 25,答对题b的人数与答对题c的人数之和为 20,求这个班参赛同学的平均成绩是多少分?
46.甲、乙两个城市相距120 km。一只蚂蚁在这幅地图上仅用了5秒便从乙城市爬行到甲城市,已知蚂蚁每秒爬行1.2cm,则这幅地图的比例尺是多少?
47.如图,自行车上的两个齿轮通过链条转动,在同一时间内,大、小齿轮转过的齿数是相同的。
(1)当转过的总齿数一定时,每个齿轮的齿数与转过的圈数成什么比例,为什么?
(2)大齿轮有50个齿,小齿轮有20个齿,如果大齿轮每分转12圈,那么小齿轮每分转多少圈呢?
(3)骑自行车时,自行车后轮随大齿轮的转动而转动,已知后轮与大齿轮圈数之比为2∶3,如果后轮直径为80厘米,请问骑行该自行车走1256米时,小齿轮转了几圈?
参考答案及试题解析
1.【答案】36
【解析】解:如图,
与等高,则
则
则
故答案为:36
【分析】因为AE,EF,FB三条线段一样长,所以用它们作斜边的三个等腰直角三角形面积相等,E是线段AF的中点。等腰直角△ADE的面积与△DEF的面积相等,即面积为4。不难看出,叠放的正方形是由8个这样的等腰直角三角形组成如图。而△ABC是由9个这样的等腰直角三角形组成,面积是4×9=36。
2.【答案】44
【解析】解:根据题意,可得
[(30÷2)2-137]÷2
=[152-137]÷2
=[225-137]÷2
=88÷2
=44(cm2)答:涂色部分的面积是44平方厘米
故答案为:44
【分析】如图,把这个图形通过作辅助线补成一个边长为阴影部分长、宽之和的正方形,用阴影部分的周长除以2就是阴影部分的长、宽之和,即补成的正方形的边长,用补成的正方形的面积减137 cm2,再除以2就是阴影部分的面积
3.【答案】2;5;6;0.4
【解析】解:根据题意,可得
故答案为:2;5;6;0.4
【分析】(1)根据分数的性质:分子分母同时扩大相同的倍数,分数的结果不变;
(2)分数化小数的方法:用分子除以分母,然后再进行求解即可
4.【答案】;0.37
5.【答案】216
【解析】解:由题意可知,这节体育课可以安排在:周一和周三;周一和周四;周一和周五;周二和周四;周二和周五;周三和周五共6种情况。因为每一节体育课都有6种情况,从第一节到第六节,这门课共有:6×6×6=216(种)安排方式。
故答案为:216
【分析】 从安排在哪天来说有6种情况,而每一节体育课又有6种情况,然后可得答案.
6.【答案】1:300000
【解析】解:根据题意,可得
30km=3000000cm
10:3000000=1:300000
故答案为:1:300000
【分析】先将30km化成3000000cm,然后再根据比例尺=图上距离÷实际距离,代入数据即可求解
7.【答案】100
【解析】解:(32+28)÷(1-40%)
=60÷0.6
=100(米)
这根电线原来有100米
故答案为:100。
【分析】一共用去的长度÷一共用去的长度占这根电线原来长度的百分率=这根电线原来的长度。
8.【答案】25000
9.【答案】;
【解析】解:根据题意,可得
故答案为:;
【分析】用总长度除以平均分的段数,就是每段的长度。把总长度看作单位“1”,用1除以平均分的段数,就是每段是全长的几分之几。
10.【答案】42
【解析】解:2.8×15=42(元)
答:购买15套一共花42元。
故答案为:42。
【分析】根据“单价×数量=总价”列式2.8×15=42(元)。
11.【答案】1500
【解析】解:(1-)×
=×
=
200÷(-)
=200÷
=1500(个)
故答案为:1500。
【分析】首先,将这批零件看作单位“1”计算乙加工的零件所占的比例。由于甲先加工了这批零件的,那么剩余的零件比例就是1-=。乙加工了这剩余零件的,所以乙加工的零件所占的比例为×=;用甲加工的减去乙加工的,得到甲比乙多加工的数量占总数的多少,进而根据分数除法,用200除以该分数比例即可得出这批零件的总数。
12.【答案】13;10;2n+1
【解析】解:6×2+1=13根,所以 摆6个△用13根小棒;(21-1)÷2=10个,所以用21根小棒可以摆10个△;
3×3×3=27块,2×2×3=12,50÷6×12+50=150平方米,所以27个小正方体木块的表面积之和是150平方厘米。
故答案为:13;10;2n+1。
【分析】(1)摆1个△用小棒的根数:3=2+1;
摆2个△用小棒的根数:5=2×2+1;
摆3个△用小棒的根数:7=2×3+1;
……
摆n个△用小棒的根数:2n+1。
(2)3×3×3=27块,所以这个大正方体沿着高、宽、长都截了2次,每截一次,增加2个大正方体一个面的面积,所以增加大正方体一个面的个数=2×2×3=12个,所以27个小正方体木块的表面积之和=正方体的表面积÷6×增加大正方体一个面的个数+大正方体的表面积。
13.【答案】72
【解析】解:36÷2=18(厘米)
18-4+2
=14+2
=16(厘米)
长:16÷2+4
=8+4
=12(厘米)
宽:16÷2-2
=8-2
=6(厘米)
12×6=72(平方厘米)
故答案为:72。
【分析】长方形的周长=(长+宽)×2,所以,长方形的周长÷2=长+宽,因此,当长减少时长与宽的和也减少,当宽增加时长与宽的和也增加,所以,长与宽的和-长减少的长度+宽增加的长度=变成正方形后长与宽的和,变成正方形后长与宽的和÷2=此时的长与宽,变成正方形后长与宽的和÷2+长减少的长度=原长方形的长,变成正方形后长与宽的和÷2-宽增加的长度=原长方形的宽,所以,原长方形的面积=原长方形的长×原长方形的宽。
14.【答案】错误
【解析】解:99÷99=100%,全部成活,成活率是100%。原题说法错误。
故答案为:错误。
【分析】树苗的成活棵数÷种的棵数=成活率。
15.【答案】错误
【解析】解:一个平行四边形和一个三角形的面积相等,高也相等。若平行四边形的底是6厘米,则三角形的底是12厘米。原题说法错误。
故答案为:错误。
【分析】平行四边形面积=底×高,三角形面积=底×高÷2,等底等高的平行四边形面积是三角形面积的2倍。如果面积相等,高也相等,那么三角形的底就是平行四边形底的2倍。
16.【答案】错误
【解析】180°-(55°+33°)
=180°-88°
=92°
这个三角形是一个钝角三角形,原题说法错误。
故答案为:错误。
【分析】三角形的内角和是180°,已知三角形的两个内角,要求第三个内角,三角形的内角和-两个内角的度数之和=第三个内角度数;三角形按角分类,可以分为锐角三角形、直角三角形、钝角三角形;有一个角是直角的三角形是直角三角形;有一个角是钝角的三角形是钝角三角形;三个角都是锐角的三角形是锐角三角形,据此解答。
17.【答案】错误
【解析】解:把一个长方体切成两个小长方体,它的表面积比原来大。
故答案为:错误。
【分析】把一个长方体切成两个小长方体,它的表面积增加了2个横截面的面积,所以它的表面积比原来大。
18.【答案】正确
【解析】解:把一个长方形木框架拉成平行四边形,周长不变,面积变小了,说法正确。
故答案为:正确。
【分析】一个长方形框架拉成平行四边形,四条边的边长不变则周长不变;再拉的过程中,底不变,高减小,根据平行四边形的面积=底×高即可得出答案。
19.【答案】正确
【解析】被除数相当于分数的分子,除数相当于分数的分母。本题说法正确。
故答案为:正确。
【分析】根据分数与除法的关系判断,a÷b=。
20.【答案】错误
【解析】解:6÷1=6,2÷1=2,2<6,甲长方形的面积<乙长方形的面积,原题干说法错误。
故答案为:错误。
【分析】周长相等的长方形中,长与宽最接近,面积最大,即长与宽的比值最小时,面积最大。
21.【答案】正确
【解析】解:31+28+31+30+31+30=181(天),原题说法正确。
故答案为:正确。
【分析】一年中1、3、5、7、8、10、12是大月,每个大月是31天;4、6、9、11是小月,每个小月是30天;还有一个特殊月2月,平年的2月是28天,闰年的2月是29天。据此解答。
22.【答案】C;A
【解析】解:甲和乙都是由若干个相同的小正方体组成的,甲的体积<乙的体积,甲的表面积>乙的表面积。
故答案为:C;A。
【分析】甲是由26个小正方体组成,乙是由27个小正方体组成,所以甲的体积小于乙的体积;甲的表面积比乙的表面积多出两个小正方体的面,所以甲的表面积大于乙的表面积。
23.【答案】A
24.【答案】C
【解析】解:9.7 m≈9.9 m,9.9÷0.9=11(块),5.8m≈6. 3m ,6.3÷0.9=7(块),11×7=77 (块)。
长和宽都合理估了,计算更加准确。
故答案为:C。
【分析】根据题意,贴瓷砖的块数=长贴的块数×宽贴的块数,长贴的块数=长÷边长,宽贴的块数=宽÷边长,估算时既要方便计算,又要减少误差,这样才与精确结果接近,才会更加合理。
25.【答案】A
【解析】解:3.14×(6÷2)2×(5+16)
=3.14×9×21
=593.46(cm3)
=593.46mL
故答案为:A。
【分析】瓶子的体积=水的体积+倒置是无水部分圆柱的体积,圆柱的体积=底面积×高,代入数据计算即可。
26.【答案】B
【解析】解:这是有可能的,分两种情况讨论:
⑴若A疫苗在甲医院有n个人接受试验,a个人有效; B疫苗在甲医院有n个人接受试验,b个人有效,则 所以a>b.
A疫苗和B疫苗在乙医院都有m个人接受试验,分别有c和d个人有效,依题意 所以c >d. 于是
在这种情况下,把结果合并后A疫苗仍比B疫苗效果好.
⑵若A疫苗在甲医院有20个人接受试验,6个人有效; B疫苗在甲医院有10个人接受试验,2个人有效,显然
A疫苗在乙医院有80个人接受试验,40 个人有效; B疫苗在医院有990个人接受试验,478个人有效,显然
然而把结果合并后却可得 即 B 疫苗比 A 疫苗效果好。
故答案为:B。
【分析】因为两个医院的测试人数可能会有所不同,并且每个人接受的疫苗有效人数也可能不同,这可能导致两个医院之间存在差异,从而影响结论的准确性。所以可以分两种情况讨论:①假设两个医院接受测试的人数相等;②假设两个医院接受测试的人数不相等。通过这两种情况分别讨论合并后的结果情况。
27.【答案】C
【解析】解:56:8=x:(102-8)
故答案为:C。
【分析】根据已知“照这样计算”可知每升油能行驶的距离一定,即行驶的距离:油耗=每升油能行驶的距离(一定),比值一定,所以行驶的距离和油耗成正比例关系,因此,油箱储油量-已经用的油=剩下的油,已经行驶的距离:已经用了的油=剩下的距离:(油箱储油量-已经用的油),据此可以判断。
28.【答案】C
【解析】解:6×a×a+2×a×a
=6a2+2a2
=8a2(dm2);
故答案为:C。
【分析】两个长方体的表面积之和就是原正方体的表面积+增加的两个面的面积,正方体表面积=棱长×棱长×棱长,据此求解。
29.【答案】C
【解析】解:(63-35)÷35=80%,
20×(1+80%)=36万,
35<36<37。
故答案为:C
【分析】本题考查的是对百分比增长率的理解与计算。根据题目信息,首先需要计算出甲文创厂的产值增长百分比,然后分析乙文创厂的产值增长百分比是否大于甲文创厂,从而判断乙文创厂第二季度产值的可能值。
30.【答案】B
31.【答案】C
32.【答案】B
【解析】解:1+4+1=6(个)。
故答案为:B。
【分析】包含○的正方形个数=1个最小的正方形+四个小的正方形组成4个稍大的正方形+整个正方形。
33.【答案】B
【解析】解:3.14×22×8
=3.14×4×8
=100.48(平方厘米);
故答案为:B。
【分析】每截一次木料,都会新增两个圆形截面,截成5段就是截了4次,新增8个圆形截面,圆的面积=,据此求解即可。
34.【答案】 - = 3.14×0.12=0.0314 2-0.08=1.92 2.5×40%=1 50×20%=10
3.75+ =4 72× =40 24÷ =30 ÷ = 10÷10%=100
【解析】计算含有分数、小数的运算时,可以先统一化成分数或小数,再计算。
含百分数的计算,通常把百分数化成小数或分数后,再计算;
分数乘法的计算法则:分数乘分数,用分子相乘的积作分子,分母相乘的积作分母。
分数除法的计算法则:甲数除以乙数(0除外),等于甲数乘乙数的倒数。
异分母分数加减法计算方法:先通分,然后按照同分母分数加减法的的法则进行计算。
35.【答案】解:(1)
=
=
=
=
(2)
=
=
=15+14-16
=13
(3)
=2-1
=1
(4)
=
=
=28+72
=100
(5)
=
=
=
【解析】(1)首先将题目中的除法运算转换为乘法运算,便于观察和提取公因式,通过转换可以将题目简化为乘法的组合,从而应用提取公因式的技巧来简化计算过程。
(2)首先需要将除法转化为乘法,然后利用分数乘法分配律,对每一项进行计算,最后求出最终结果。
(3)根据加法交换律将同分母分数凑在一起,可以进行简便计算。
(4)利用分配律将式子展开,发现可以通过约分进行简便运算。
(5)按照数学运算的优先级,首先处理括号内的加法运算,然后将分数除法转化为分数乘法,进行计算。
36.【答案】(1) x+=
解:x+-=-
x=
x÷=÷
x=
(2) x:=:
解:x=×
x=
x÷=÷
x=
【解析】(1)根据等式性质1消掉方程左边的已知数,然后根据等式性质2使未知项的系数变成1,可得方程的解;
(2)根据比例的基本性质将比例式化成乘积式,再按照解方程的方法计算。
37.【答案】解:(4-3+4)×3÷2
=5×3÷2
=7.5(cm2);
4÷2=2(cm)
3.14×22×
=6.28(cm2)
4×2×=4(cm2)
6.28-4=2.28(cm2)。
【解析】如图将右边涂色部分剪下后拼到左边,则涂色部分就是一个梯形,梯形的上底是4-3=1cm,下底是4cm,高是3cm,因此,(上底+下底)×高÷2=梯形的面积;
第二幅图外面是一个直径为4cm的半圆,空白部分是一个底是4cm,高是半圆半径的三角形,因此,直径÷2=半径,圆周率×半径的平方×=外面半圆的面积,底×高×=空白部分三角形的面积,外面半圆的面积-空白部分三角形的面积=涂色部分的面积。
38.【答案】
【解析】分别从不同的方向观察图形,判断出观察到的图形有几个正方形以及每个正方形的位置,然后画出看到的图形即可。
39.【答案】12÷3÷2
=4÷2
=2(平方厘米)
【解析】如图,连接OC,OD,OH,则扇形AOC,COD,BOD 的面积相等,且都等于半圆面积的 又因为△COH与△CNH等底等高,则,因此阴影部分的面积等于扇形COD面积的一半,依此求解。
40.【答案】解:52÷4-8-3
=13-8-3
=2(dm)
答:高是2分米。
【解析】根据题意可知竹条的长度就是长方体框架的棱长之和,因为长方体的棱长之和=(长+宽+高)×4,所以,竹条的长度÷4-长-宽=高,据此可以解答。
41.【答案】解:设姐姐的工作效率为x,乐乐的工作效率为y
32x+8y=34x
8y=2x
答:乐乐采一日的数量是一位姐姐采一日的
【解析】设姐姐的工作效率为x,乐乐的工作效率为y,根据工作总量=工作时间×工作效率,结合题目中的等量关系,列出方程,解出y,即可求出答案。
42.【答案】解:根据题意,在这88 cm长的绳子上,
每隔6的倍数做一个红色记号,
则88÷6=14(个)……4(cm), 有 14个红色记号;
每隔5的倍数做一个蓝色记号,
则88÷5=17(个)……3(cm), 有17个蓝色记号;
每隔7的倍数做一个绿色记号,
则88÷7=12(个)……4(cm), 有12个绿色记号;
重合的记号长度即分别是6和5的最小公倍数、5和7的最小公倍数、6和7的最小公倍数、6和5和7的最小公倍数,
[6,5]=30, 88÷30=2(个)……28(cm), 红色和蓝色重合的记号有2个,
[5,7]=35, 88÷35=2(个)……18(cm), 蓝色和绿色重合的记号有2个,
[6,7]=42, 88÷42=2(个)……4(cm), 红色和绿色重合的记号有2个,
[5,6,7]=210, 210>88, 所以没有三种颜色重合的记号,
一共有记号:14+17+12-2-2-2=37(个)。
答:这根绳子共有37个记号。
【解析】先根据绳子长度和每种间隔距离求出各自做记号的数量。因为重合的地方在各自计算时被重复计算,所以通过求最小公倍数来确定两两重合的记号数量。最后考虑三种颜色重合的情况,由于6、5、7的最小公倍数大于绳子长度,所以没有三种颜色重合的记号。将各自做记号的数量相加,再减去两两重合多算的数量,就得到绳子上记号的总数。
43.【答案】①(或②);红花240朵,黄花60朵
44.【答案】解:根据题意,得
300×(1-)
=300×(1-)
=300×
=270(元)
答:中秋节买这款智能音箱需要270元。
【解析】本题考查分数乘法的计算及应用。把智能音箱的原价看作单位“1”,降价出售,现价是原价的(1-),用智能音箱的原价乘(1-),即可求出中秋节这款智能音箱的价格是多少。
45.【答案】 解:设答对 a 题的有 x 人,答对 b 题的有 y 人,答对 c 题的有 z 人,
根据题意得:
x + y =29
x + z =25,
y + z =20
解得:
x =17
y =12.
z =8
全班总得分为17×20+(12+8)×25=840(分),
全班总人数为17+12+8-1×15-2×1=20(人),
全班的平均成绩为840÷20=42(分).
答: 这个班参赛同学的平均成绩是42分 。
【解析】 设答对 a 题的有 x 人,答对 b 题的有 y 人,答对 c 题的有 z 人,根据"答对题 a 的人数与答对题 b 的人数之和为29,答对题 a 的人数与答对题 c 的人数之和为25,答对题 b 的人数与答对题 c 的人数之和为20",即可得出关于 x 、 y 、 z 的三元一次方程组,解之即可得出 x 、 y 、 z 的值,由 x 、 y 、 z 的值结合 a 、 b 、 c 三题的分值可求出全班总得分,由 x 、 y 、 z 的值结合答对两题及答对三题的人数可求出全班总人数,再利用平均分=总分÷人数,即可求出结论.
46.【答案】解:5×1.2=6(cm)
120km=12000000cm
6:1000000=1:2000000
答:这幅地图的比例尺是1:2000000。
【解析】用蚂蚁爬行的时间乘爬行的速度,求出图上距离,然后根据“比例尺=图上距离:实际距离”即可算出比例尺。
47.【答案】(1)反比例;每个齿轮的齿数×转过的圈数=转过的总齿数(一定)
(2)30圈
(3)1875圈
21世纪教育网(www.21cnjy.com)
同课章节目录
