初中数学苏科版(2024)七年级下册12.4 三角形内角和定理(14张PPT)
文档属性
| 名称 | 初中数学苏科版(2024)七年级下册12.4 三角形内角和定理(14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 14:41:46 | ||
图片预览


文档简介
(共14张PPT)
7.5.1 三角形内角和定理
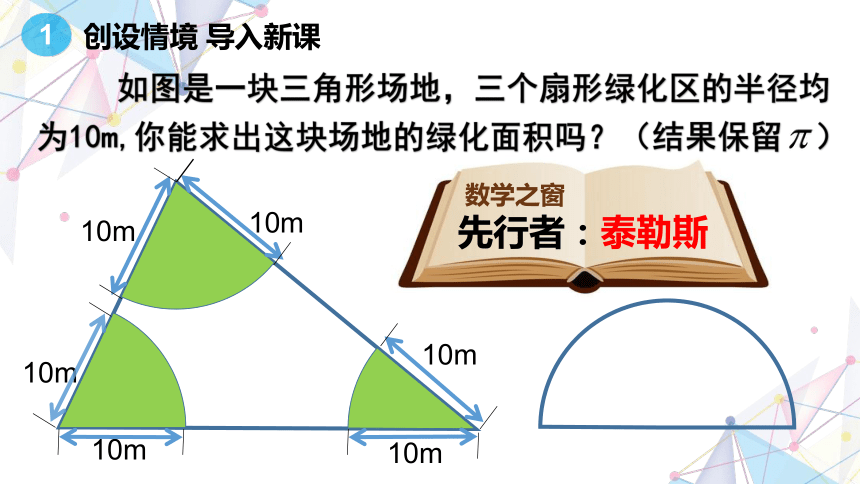
如图是一块三角形场地,三个扇形绿化区的半径均
为10m,你能求出这块场地的绿化面积吗?
10m
10m
10m
10m
10m
10m
1
创设情境 导入新课
(结果保留 )
数学之窗
先行者:泰勒斯
2
回顾旧知 实践探索
命题:三角形的内角和等于180°
问题:如何得出这一结论?
测量
探索:动手操作并思考
撕拼
2.你有哪些拼法?请你继续拼一拼.
3.从上述操作的过程中,你能发现证明的思路吗?请你想一想.
3
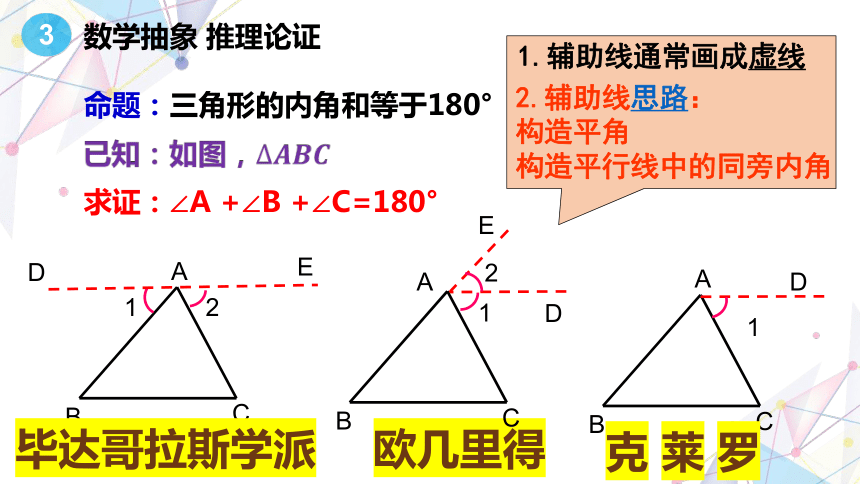
数学抽象 推理论证
命题:三角形的内角和等于180°
求证:∠A +∠B +∠C=180°
A
B
C
D
E
2
1
A
B
C
E
1
2
毕达哥拉斯学派
欧几里得
A
B
C
克 莱 罗
D
D
1
1.辅助线通常画成虚线
2.辅助线思路:
构造平角
构造平行线中的同旁内角
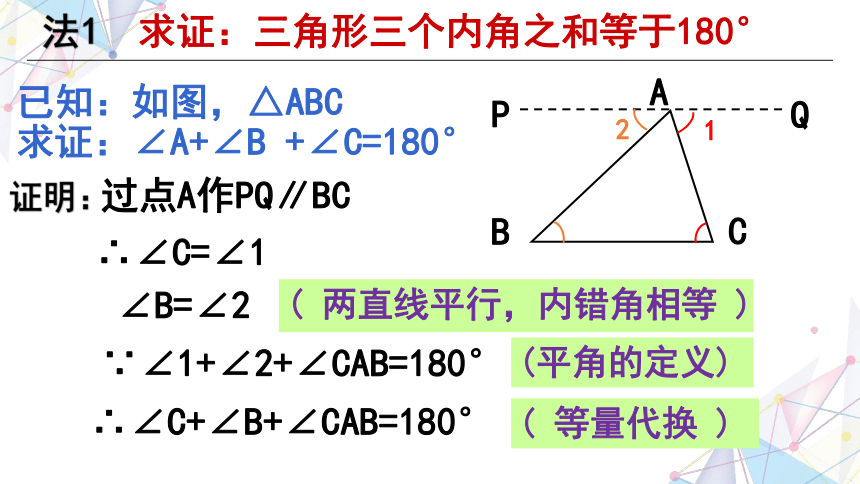
已知:如图,△ABC
求证:∠A+∠B +∠C=180°
证明:
∴∠C=∠1
过点A作PQ∥BC
∵∠1+∠2+∠CAB=180°
(平角的定义)
∴∠C+∠B+∠CAB=180°
( 等量代换 )
A
B
C
∠B=∠2
( 两直线平行,内错角相等 )
P
Q
2
1
法1 求证:三角形三个内角之和等于180°
A
B
C
1
2
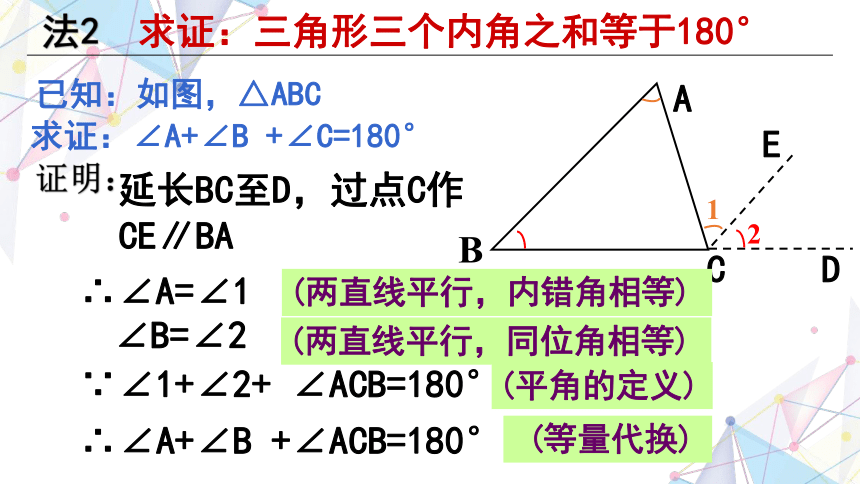
∴∠A=∠1
延长BC至D,过点C作
CE∥BA
∵∠1+∠2+ ∠ACB=180°
(平角的定义)
∴∠A+∠B +∠ACB=180°
(等量代换)
∠B=∠2
(两直线平行,内错角相等)
D
E
已知:如图,△ABC
求证:∠A+∠B +∠C=180°
证明:
法2 求证:三角形三个内角之和等于180°
(两直线平行,同位角相等)
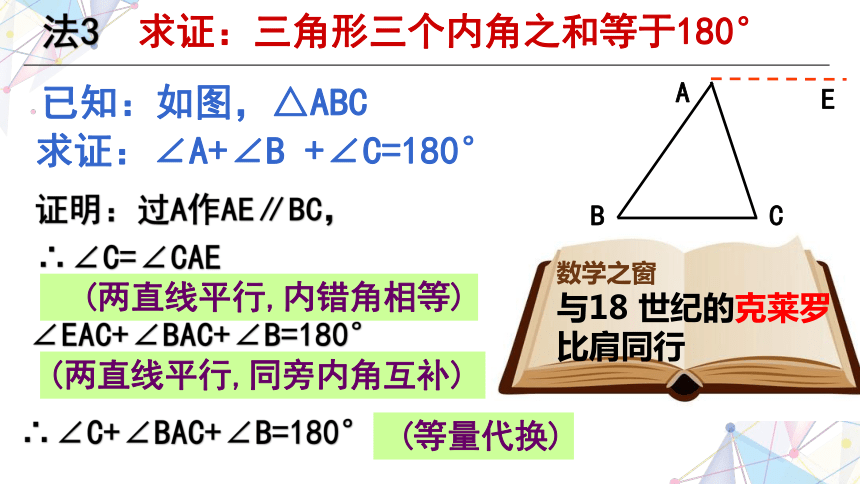
证明:过A作AE∥BC,
E
∴∠C=∠CAE
(两直线平行,内错角相等)
∠EAC+∠BAC+∠B=180°
(两直线平行,同旁内角互补)
∴∠C+∠BAC+∠B=180°
(等量代换)
已知:如图,△ABC
求证:∠A+∠B +∠C=180°
A
B
C
法3 求证:三角形三个内角之和等于180°
数学之窗
与18 世纪的克莱罗
比肩同行
直角三角形的两锐角之和是多少度?证明你的结论.
小试牛刀
直角三角形两锐角和为90°
已知:如图,在Rt△ABC中,∠C=90
求证: ∠A+∠B=90°
4
开放训练 体现应用
(等式的性质)
正三角形的一个内角是多少度?请说明理由.
已知:如图,△ABC为正三角形
求证: ∠A=∠B=∠C=60°
等边三角形三个内角都等于60°
小试牛刀
4
开放训练 体现应用
A
B
C
例1 如图,在 ABC中,∠B=38 ,∠C=62 ,
(1)求∠BAC的度数;
(2)AD是 ABC的角平分线,求∠ADB度数;
D
4
开放训练 体现应用
(3)DE⊥AC,求∠ADE的度数.
E
A
B
C
例1 如图,在 ABC中,∠B=38 ,∠C=62 ,
D
4
开放训练 体现应用
变式:DF∥AC交AC于点F,AD是 ABC的
角平分线,求∠BFD和∠FDA的度数.
F
5
课堂总结 联系拓广
第一层
知识:
第二层
方法:
第三层
思想:
三角形的内角和定理的证明及简单应用
1.辅助线的作法与思路
2.一题多解,一题多变
数学抽象 转化
6
布置作业
1.练习册:课时作业(12、13题选做)
2.(思考)在证明三角形内角和定理时,是否可以把三角形的三个角的顶点“凑”到BC 边上的一点P(如图(1))?如果把三个角的顶点“凑”到三角形内一点呢(如图(2))?“凑”到三角形外一点呢(如图(3))?你还能想出其他证法吗?
谢谢观看
7.5.1 三角形内角和定理
如图是一块三角形场地,三个扇形绿化区的半径均
为10m,你能求出这块场地的绿化面积吗?
10m
10m
10m
10m
10m
10m
1
创设情境 导入新课
(结果保留 )
数学之窗
先行者:泰勒斯
2
回顾旧知 实践探索
命题:三角形的内角和等于180°
问题:如何得出这一结论?
测量
探索:动手操作并思考
撕拼
2.你有哪些拼法?请你继续拼一拼.
3.从上述操作的过程中,你能发现证明的思路吗?请你想一想.
3
数学抽象 推理论证
命题:三角形的内角和等于180°
求证:∠A +∠B +∠C=180°
A
B
C
D
E
2
1
A
B
C
E
1
2
毕达哥拉斯学派
欧几里得
A
B
C
克 莱 罗
D
D
1
1.辅助线通常画成虚线
2.辅助线思路:
构造平角
构造平行线中的同旁内角
已知:如图,△ABC
求证:∠A+∠B +∠C=180°
证明:
∴∠C=∠1
过点A作PQ∥BC
∵∠1+∠2+∠CAB=180°
(平角的定义)
∴∠C+∠B+∠CAB=180°
( 等量代换 )
A
B
C
∠B=∠2
( 两直线平行,内错角相等 )
P
Q
2
1
法1 求证:三角形三个内角之和等于180°
A
B
C
1
2
∴∠A=∠1
延长BC至D,过点C作
CE∥BA
∵∠1+∠2+ ∠ACB=180°
(平角的定义)
∴∠A+∠B +∠ACB=180°
(等量代换)
∠B=∠2
(两直线平行,内错角相等)
D
E
已知:如图,△ABC
求证:∠A+∠B +∠C=180°
证明:
法2 求证:三角形三个内角之和等于180°
(两直线平行,同位角相等)
证明:过A作AE∥BC,
E
∴∠C=∠CAE
(两直线平行,内错角相等)
∠EAC+∠BAC+∠B=180°
(两直线平行,同旁内角互补)
∴∠C+∠BAC+∠B=180°
(等量代换)
已知:如图,△ABC
求证:∠A+∠B +∠C=180°
A
B
C
法3 求证:三角形三个内角之和等于180°
数学之窗
与18 世纪的克莱罗
比肩同行
直角三角形的两锐角之和是多少度?证明你的结论.
小试牛刀
直角三角形两锐角和为90°
已知:如图,在Rt△ABC中,∠C=90
求证: ∠A+∠B=90°
4
开放训练 体现应用
(等式的性质)
正三角形的一个内角是多少度?请说明理由.
已知:如图,△ABC为正三角形
求证: ∠A=∠B=∠C=60°
等边三角形三个内角都等于60°
小试牛刀
4
开放训练 体现应用
A
B
C
例1 如图,在 ABC中,∠B=38 ,∠C=62 ,
(1)求∠BAC的度数;
(2)AD是 ABC的角平分线,求∠ADB度数;
D
4
开放训练 体现应用
(3)DE⊥AC,求∠ADE的度数.
E
A
B
C
例1 如图,在 ABC中,∠B=38 ,∠C=62 ,
D
4
开放训练 体现应用
变式:DF∥AC交AC于点F,AD是 ABC的
角平分线,求∠BFD和∠FDA的度数.
F
5
课堂总结 联系拓广
第一层
知识:
第二层
方法:
第三层
思想:
三角形的内角和定理的证明及简单应用
1.辅助线的作法与思路
2.一题多解,一题多变
数学抽象 转化
6
布置作业
1.练习册:课时作业(12、13题选做)
2.(思考)在证明三角形内角和定理时,是否可以把三角形的三个角的顶点“凑”到BC 边上的一点P(如图(1))?如果把三个角的顶点“凑”到三角形内一点呢(如图(2))?“凑”到三角形外一点呢(如图(3))?你还能想出其他证法吗?
谢谢观看
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
