初中数学苏科版(2024)七年级下册12.4 三角形内角和定理 教学设计
文档属性
| 名称 | 初中数学苏科版(2024)七年级下册12.4 三角形内角和定理 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 249.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-21 14:43:31 | ||
图片预览

文档简介
《三角形内角和定理》教学设计
课 型:新授课
一、教学目标
经历探索与证明三角形内角和定理的过程,掌握三角形内角和定理的证明及简单应用,培养学生直观想象和逻辑推理的核心素养.
通过一题多证、一题多变,形成独立思考、合作交流的学习模式,培养说理能力.
培养学生的创造性,体验解决问题的成就感,感悟推理的数学价值.
二、教材分析
重点:三角形内角和定理的证明及其应用.
难点:添加辅助线证明三角形内角和定理.
学情分析
小学阶段学生已经学习过“三角形内角和等于”,七年级学生又通过活动再次验证了这一结论,有一定的活动经验积累;
大多数学生乐于尝试、探索、思考,但推理不严密,需加以引导;少部分学生不擅于交流与合作,归纳与总结,应多加鼓励,让学生有成就感.
教师教法
讲授法,实验法,讨论法,练习法
学生学法
实验探究,讨论交流,总结归纳,类比迁移
六、教学过程
1.创设情境,导入新课
[数学抽象] 如图是一块三角形场地,三个扇形绿化区的半径均为10m,你能求出这块场地的绿化面积吗?(结果保留)
设计意图:设疑激趣,导入新课.
[数学史材料] 同学们知道历史上是哪位科学家最先发现三角形内角和定理吗?
泰勒斯也和我们一样在“拼角”的过程中发现了三角形内角和定理,但是他只是发现没有证明,而我们已经学习过,命题经过证明为真才是定理,今天我们就来一起尝试证明三角形内角和定理,来完成科学家泰勒斯都没有完成的事情.
设计意图:融入数学史,强调科学家都没有完成的事情我们今天要来尝试,培养学习兴趣,提升学习成就感.
2.实践探究,交流新知
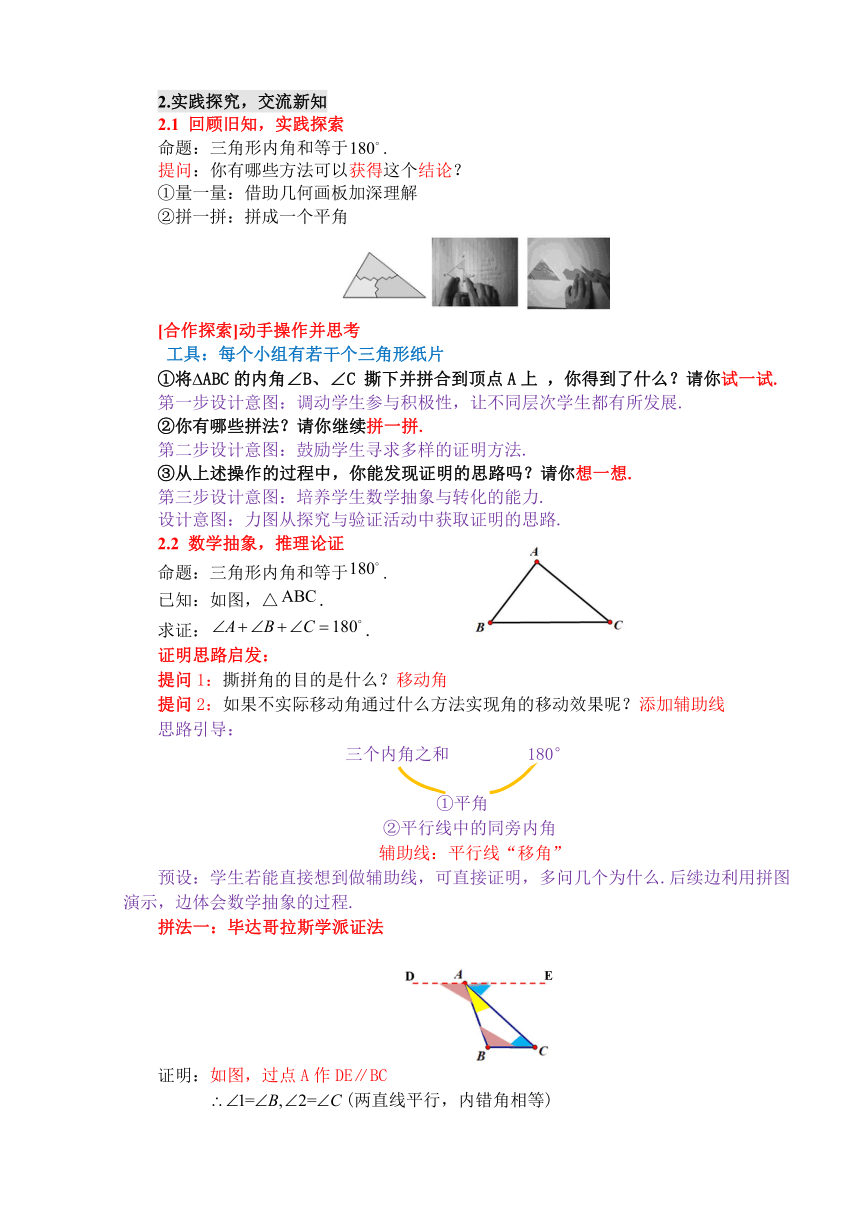
2.1 回顾旧知,实践探索
命题:三角形内角和等于.
提问:你有哪些方法可以获得这个结论?
①量一量:借助几何画板加深理解
②拼一拼:拼成一个平角
[合作探索]动手操作并思考
工具:每个小组有若干个三角形纸片
①将 ABC的内角∠B、∠C 撕下并拼合到顶点A上 ,你得到了什么?请你试一试.
第一步设计意图:调动学生参与积极性,让不同层次学生都有所发展.
②你有哪些拼法?请你继续拼一拼.
第二步设计意图:鼓励学生寻求多样的证明方法.
③从上述操作的过程中,你能发现证明的思路吗?请你想一想.
第三步设计意图:培养学生数学抽象与转化的能力.
设计意图:力图从探究与验证活动中获取证明的思路.
2.2 数学抽象,推理论证
命题:三角形内角和等于.
已知:如图,△.
求证:.
证明思路启发:
提问1:撕拼角的目的是什么?移动角
提问2:如果不实际移动角通过什么方法实现角的移动效果呢?添加辅助线
思路引导:
三个内角之和 180°
①平角
②平行线中的同旁内角
辅助线:平行线“移角”
预设:学生若能直接想到做辅助线,可直接证明,多问几个为什么.后续边利用拼图演示,边体会数学抽象的过程.
拼法一:毕达哥拉斯学派证法
证明:如图,过点A作DE∥BC
(两直线平行,内错角相等)
又(平角的定义)
(等量代换)
预设:学生对射线AD和AE是否在同一直线上提出质疑.
总结:(提问)他们是如何从拼图中找到证明思路的呢?(拿下角,留下痕迹,进而抽象出几何图形.)
设计意图:强化学生数学抽象的核心素养.
拼法二:欧几里得证法
(要求:独立思考并证明.)
提问1:这两种方法有什么共同特点?
(添加辅助线,构造平角.)
提问2:辅助线起什么作业?(移角)
拼法三: 拼法四:
以上两种拼法能否为证明带来启发?为什么?
没有平行线,达不到移角的目的.
预设:除这两种证明方法外,你还有没有其他证明方法?
拼法五:十八世纪克莱罗的证法
提问:能为你提供证明思路吗?
(将三角形的三个内角转化为平行线中的同旁内角)
设计意图:合情拓展,一题多证.
找共性:将分散的要素集中在一起.
2.3 开放训练,体现应用
小试牛刀
1.直角三角形的两锐角之和是多少度?证明你的结论?
2.正三角形的一个内角是多少度?请说明理由.
设计意图:学生自主解决. 既是对一般结论的巩固,又是一个重要的思考问题的方式.
一题多变
例1 如图,在 ABC中,∠B=38 ,∠C=62 ,
(1)求∠BAC的度数;
(2)AD是 ABC的角平分线,求∠ADB度数;
(3)DE⊥AC,求∠ADE的度数.
(4)DF∥AC交AC于点F,AD是 ABC的角平分线,求∠BFD和∠FDA的度数.
设计意图:在一题多变中提升应用能力和说理能力.
3.课堂总结,布置作业
3.1 课堂总结
提问:同学们在今天的学习中都有哪些收获 证明三角形内角和定理的主要思路是?主要体现哪些数学思想?
第一层
知识:三角形的内角和定理的证明及简单应用.
第二层
方法:1.辅助线的作法与思路;
2.一题多解,一题多变.
第三层
思想:数学抽象,转化.
3.2 布置作业
①练习册:课时作业(12、13题选做)
②[思考]在证明三角形内角和定理时,是否可以把三角形的三个角的顶点“凑”到BC 边上的一点P(如图(1))?如果把三个角的顶点“凑”到三角形内一点呢(如图(2))?“凑”到三角形外一点呢(如图(3))?你还能想出其他证法吗?
七、板书设计(使用课件:是)
八、教学反思
①[授课流程反思]
创设情境,设疑激趣,在撕拼实验中娓娓道来三角形内角和定理的证明,一题多证,一题多变,培养了学生数学抽象的核心素养和转化、化归的数学思想。.
②[讲授效果反思]
通过撕拼操作,在实验中观察、探索三角形内角和定理的证明,让学生切身感受到自己是学习的主人,为学生今后获取知识、探索发现和创造打下了良好的基础.在合作讨论中,培养学生的一题多思、一题多解的创新精神,让学生体会数学辅助线的桥梁作用,添加辅助线是教学中的一个难点,如何添加辅助线充分引导并留足时间让学生思考迁移.
③[师生互动反思]
回顾探索环节,让同桌之间互相讨论交流,并展示对三角形内角和定理的验证方法;抽象推理环节,问题串层层深入,思维碰撞,共同探讨三角形内角和定理的证明,课堂时间充足的情况下,应让学生充分思考,总结方法,类比迁移,一题多证.
④[习题设计反思]
一题多变,让学生的思维在条件的变换中不断发展;题目应少而精,将课堂训练落到实处.
课 型:新授课
一、教学目标
经历探索与证明三角形内角和定理的过程,掌握三角形内角和定理的证明及简单应用,培养学生直观想象和逻辑推理的核心素养.
通过一题多证、一题多变,形成独立思考、合作交流的学习模式,培养说理能力.
培养学生的创造性,体验解决问题的成就感,感悟推理的数学价值.
二、教材分析
重点:三角形内角和定理的证明及其应用.
难点:添加辅助线证明三角形内角和定理.
学情分析
小学阶段学生已经学习过“三角形内角和等于”,七年级学生又通过活动再次验证了这一结论,有一定的活动经验积累;
大多数学生乐于尝试、探索、思考,但推理不严密,需加以引导;少部分学生不擅于交流与合作,归纳与总结,应多加鼓励,让学生有成就感.
教师教法
讲授法,实验法,讨论法,练习法
学生学法
实验探究,讨论交流,总结归纳,类比迁移
六、教学过程
1.创设情境,导入新课
[数学抽象] 如图是一块三角形场地,三个扇形绿化区的半径均为10m,你能求出这块场地的绿化面积吗?(结果保留)
设计意图:设疑激趣,导入新课.
[数学史材料] 同学们知道历史上是哪位科学家最先发现三角形内角和定理吗?
泰勒斯也和我们一样在“拼角”的过程中发现了三角形内角和定理,但是他只是发现没有证明,而我们已经学习过,命题经过证明为真才是定理,今天我们就来一起尝试证明三角形内角和定理,来完成科学家泰勒斯都没有完成的事情.
设计意图:融入数学史,强调科学家都没有完成的事情我们今天要来尝试,培养学习兴趣,提升学习成就感.
2.实践探究,交流新知
2.1 回顾旧知,实践探索
命题:三角形内角和等于.
提问:你有哪些方法可以获得这个结论?
①量一量:借助几何画板加深理解
②拼一拼:拼成一个平角
[合作探索]动手操作并思考
工具:每个小组有若干个三角形纸片
①将 ABC的内角∠B、∠C 撕下并拼合到顶点A上 ,你得到了什么?请你试一试.
第一步设计意图:调动学生参与积极性,让不同层次学生都有所发展.
②你有哪些拼法?请你继续拼一拼.
第二步设计意图:鼓励学生寻求多样的证明方法.
③从上述操作的过程中,你能发现证明的思路吗?请你想一想.
第三步设计意图:培养学生数学抽象与转化的能力.
设计意图:力图从探究与验证活动中获取证明的思路.
2.2 数学抽象,推理论证
命题:三角形内角和等于.
已知:如图,△.
求证:.
证明思路启发:
提问1:撕拼角的目的是什么?移动角
提问2:如果不实际移动角通过什么方法实现角的移动效果呢?添加辅助线
思路引导:
三个内角之和 180°
①平角
②平行线中的同旁内角
辅助线:平行线“移角”
预设:学生若能直接想到做辅助线,可直接证明,多问几个为什么.后续边利用拼图演示,边体会数学抽象的过程.
拼法一:毕达哥拉斯学派证法
证明:如图,过点A作DE∥BC
(两直线平行,内错角相等)
又(平角的定义)
(等量代换)
预设:学生对射线AD和AE是否在同一直线上提出质疑.
总结:(提问)他们是如何从拼图中找到证明思路的呢?(拿下角,留下痕迹,进而抽象出几何图形.)
设计意图:强化学生数学抽象的核心素养.
拼法二:欧几里得证法
(要求:独立思考并证明.)
提问1:这两种方法有什么共同特点?
(添加辅助线,构造平角.)
提问2:辅助线起什么作业?(移角)
拼法三: 拼法四:
以上两种拼法能否为证明带来启发?为什么?
没有平行线,达不到移角的目的.
预设:除这两种证明方法外,你还有没有其他证明方法?
拼法五:十八世纪克莱罗的证法
提问:能为你提供证明思路吗?
(将三角形的三个内角转化为平行线中的同旁内角)
设计意图:合情拓展,一题多证.
找共性:将分散的要素集中在一起.
2.3 开放训练,体现应用
小试牛刀
1.直角三角形的两锐角之和是多少度?证明你的结论?
2.正三角形的一个内角是多少度?请说明理由.
设计意图:学生自主解决. 既是对一般结论的巩固,又是一个重要的思考问题的方式.
一题多变
例1 如图,在 ABC中,∠B=38 ,∠C=62 ,
(1)求∠BAC的度数;
(2)AD是 ABC的角平分线,求∠ADB度数;
(3)DE⊥AC,求∠ADE的度数.
(4)DF∥AC交AC于点F,AD是 ABC的角平分线,求∠BFD和∠FDA的度数.
设计意图:在一题多变中提升应用能力和说理能力.
3.课堂总结,布置作业
3.1 课堂总结
提问:同学们在今天的学习中都有哪些收获 证明三角形内角和定理的主要思路是?主要体现哪些数学思想?
第一层
知识:三角形的内角和定理的证明及简单应用.
第二层
方法:1.辅助线的作法与思路;
2.一题多解,一题多变.
第三层
思想:数学抽象,转化.
3.2 布置作业
①练习册:课时作业(12、13题选做)
②[思考]在证明三角形内角和定理时,是否可以把三角形的三个角的顶点“凑”到BC 边上的一点P(如图(1))?如果把三个角的顶点“凑”到三角形内一点呢(如图(2))?“凑”到三角形外一点呢(如图(3))?你还能想出其他证法吗?
七、板书设计(使用课件:是)
八、教学反思
①[授课流程反思]
创设情境,设疑激趣,在撕拼实验中娓娓道来三角形内角和定理的证明,一题多证,一题多变,培养了学生数学抽象的核心素养和转化、化归的数学思想。.
②[讲授效果反思]
通过撕拼操作,在实验中观察、探索三角形内角和定理的证明,让学生切身感受到自己是学习的主人,为学生今后获取知识、探索发现和创造打下了良好的基础.在合作讨论中,培养学生的一题多思、一题多解的创新精神,让学生体会数学辅助线的桥梁作用,添加辅助线是教学中的一个难点,如何添加辅助线充分引导并留足时间让学生思考迁移.
③[师生互动反思]
回顾探索环节,让同桌之间互相讨论交流,并展示对三角形内角和定理的验证方法;抽象推理环节,问题串层层深入,思维碰撞,共同探讨三角形内角和定理的证明,课堂时间充足的情况下,应让学生充分思考,总结方法,类比迁移,一题多证.
④[习题设计反思]
一题多变,让学生的思维在条件的变换中不断发展;题目应少而精,将课堂训练落到实处.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
