1.1.1 空间向量及其线性运算 练习 (含答案)2025-2026学年高二数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 1.1.1 空间向量及其线性运算 练习 (含答案)2025-2026学年高二数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | docx | ||
| 文件大小 | 282.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 21:29:02 | ||
图片预览




文档简介
1.1.1 空间向量及其线性运算(1)
一、 单项选择题
1 给出下列命题:①零向量的方向是任意的;②若两个空间向量相等,则它们的起点相同,终点也相同;③若空间向量a,b满足|a|=|b|,则a=b;④空间中任意两个单位向量必相等.其中正确命题的个数为( )
A. 4 B. 3 C. 2 D. 1
2 关于空间向量,下列说法中正确的是( )
A. 单位向量都相等
B. 若|a|=|b|,则a,b的长度相等,方向相同或相反
C. 若向量,满足||>||,则>
D. 相等向量其方向必相同
3 在平行六面体ABCD-A1B1C1D1中,(+)-等于( )
A. B. C. D.
4 如图,在直三棱柱ABC-A1B1C1中,若=a,=b,=c,则等于( )
A. -a+b-c
B. a-b+c
C. -a+b+c
D. a+b-c
5 如图,在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点,若=a,=b,=c,则下列向量中与相等的是( )
A. -a+b+c
B. a+b+c
C. -a-b+c
D. a-b+c
6 如图,在平行六面体ABCD-A1B1C1D1中,下列关系式中错误的是( )
A. =
B. =-
C. =-
D. ++=
7如图,在四面体OABC中,=a,=b,=c,且OM=2MA,BN=NC,则等于( )
A. a+b+c
B. a+b-c
C. -a+b+c
D. a-b+c
8 在平行六面体ABCD-A1B1C1D1中,M,N分别为线段A1B,A1C上的点,则“=且=”是“M,N,D1三点共线”的( )
A. 充要条件
B. 充分不必要条件
C. 必要不充分条件
D. 既不充分也不必要条件
二、 多项选择题
9 如图,已知在四面体ABCD中,E,F分别是棱BC,CD的中点,则下列等式中正确的有( )
A. ++=
B. +-=
C. +(+)=
D. -+=
(第9题) (第10题)
10 如图,在三棱柱ABC-A1B1C1中,P为空间内一点,且满足=λ+μ,λ∈[0,1],μ∈[0,1],则下列说法中正确的有( )
A. 当λ=1时,点P在棱BB1上
B. 当μ=1时,点P在棱B1C1上
C. 当λ+μ=1时,点P在线段B1C上
D. 当λ=μ时,点P在线段BC1上
三、填空题
11 在三棱柱ABC-A1B1C1中,点M在线段CB1上,且CM=2MB1,若用,,表示,则=________.
12 在四棱柱ABCD-A1B1C1D1中,=x+y+z,则x-y-z=________.
13 已知空间中互不平行的三个向量i,j,k,a=4i+λj+μk,b=μi+2j+3k,若a∥b,则μ=________.
四、 解答题
14 如图,在平行六面体ABCD-A1B1C1D1中,=a,=b,=c. M是棱C1D1的中点,N是线段CA1上的点,且CN∶NA1=4∶1.用a,b,c表示以下向量:
(1) ;
(2) .
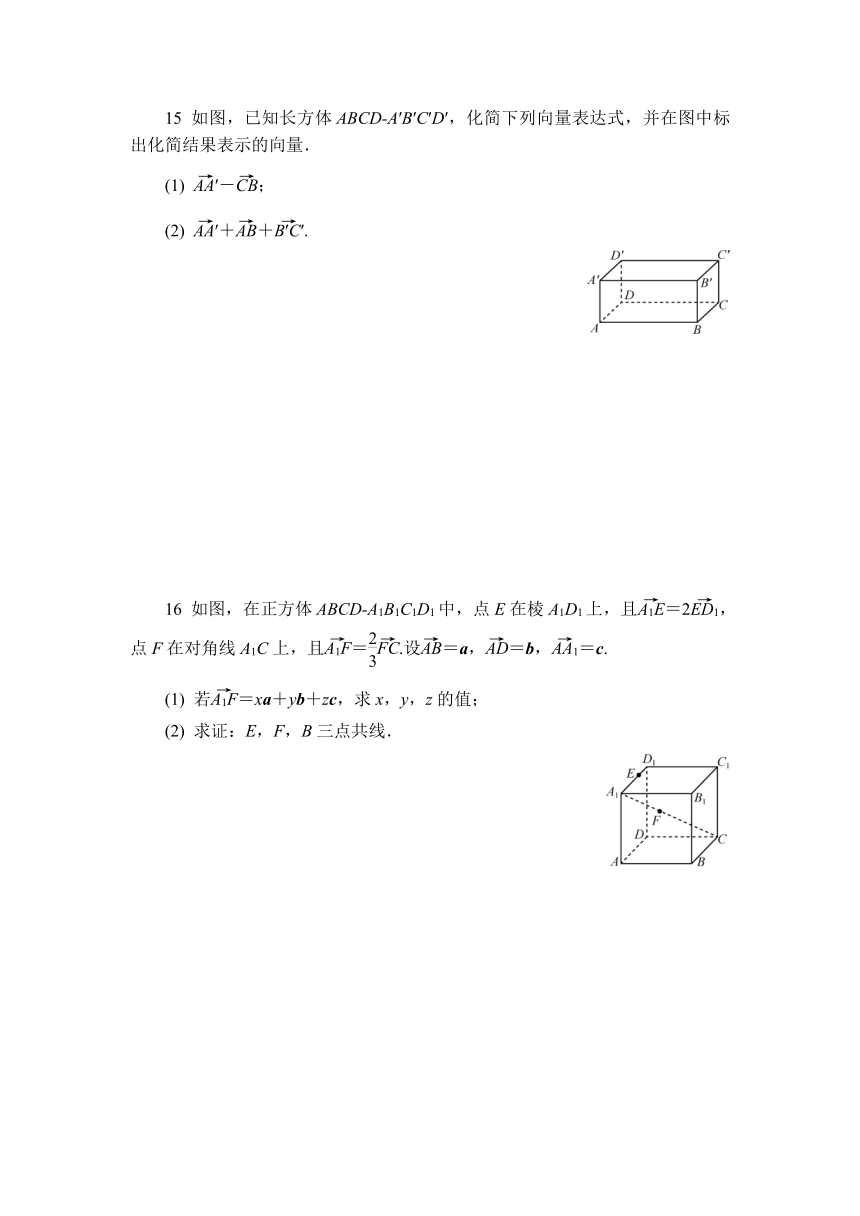
15 如图,已知长方体ABCD-A′B′C′D′,化简下列向量表达式,并在图中标出化简结果表示的向量.
(1) -;
(2) ++.
16 如图,在正方体ABCD-A1B1C1D1中,点E在棱A1D1上,且=2,点F在对角线A1C上,且=.设=a,=b,=c.
(1) 若=xa+yb+zc,求x,y,z的值;
(2) 求证:E,F,B三点共线.
1.1.1 空间向量及其线性运算(2)
一、 单项选择题
1 (吉林四校月考)下列关于空间向量的说法中,错误的是( )
A. 平行于同一个平面的向量叫做共面向量
B. 直线可以由其上一点和它的方向向量确定
C. 任意两个空间向量不一定共面
D. 任意两个空间向量都可以通过平移转化为同一平面内的向量
2 (江阴六校期中)设a,b,c为空间内三个不共面的向量,=2a+3b+5c,=a+2b-2c,=ka+b+3c,若,,共面,则k的值为( )
A. B. C. D.
3 如图,在三棱柱ABC-A1B1C1中,P为平面A1BC内一动点,且=x+y+z,则x+y+z的值为( )
A. 0
B. 1
C. 3
D. -1
4 (浙江四校月考)三个非零向量a,b,c,则“a,b,c共面”是“c=λa+μb(λ,μ∈R)”的( )
A. 充分不必要条件
B. 必要不充分条件
C. 充要条件
D. 既不充分也不必要条件
5 (雅礼中学月考)已知a,b,c为空间内不共面的三个向量,则下列选项中与向量m=a-2c,n=a+2c不共面的向量是( )
A. a B. b C. c D. a-c
6 (南京玄武高级中学月考)已知a,b,c不共面,则下列向量中不共面的是( )
A. a+b,a-b,b
B. a-b,a-b+c,-c
C. a+2b,a-2b,a+c
D. a-2b,4b-2a,a+c
7 (文山期末)对三维空间中不共线的三点A,B,C和任一点O,点P在平面ABC内的充要条件是存在唯一有序实数组(x,y,z),使=x+y+z且x+y+z=1.已知A,B,C,D四点共面,O为空间中任意一点,且满足=3-x-y,其中x>0,y>0,则+的最小值为( )
A. B. 1 C. D. 4
8 (厦门一中月考)如图,在三棱锥O-ABC中,点G为底面三角形ABC的重心,M是线段OG上靠近点G的三等分点,过点M的平面分别交棱OA,OB,OC于点D,E,F,若=k,=m,=n,则++的值为( )
A.
B.
C.
D.
二、 多项选择题
9 已知正方体ABCD-A1B1C1D1,则下列选项中,不共面的一组向量有( )
A. ,,
B. ,,
C. ,,
D. ,,
10 (温州十校联考)已知A,B,C三点不共线,对平面ABC外的任一点O,下列条件中能确定点M,A,B,C共面的是( )
A. =+-
B. =++
C. =++
D. =3--
三、填空题
11 (泰安二中期初)已知A,B,C三点不共线,O为平面ABC外一点,若由向量=++λ确定的点P与A,B,C共面,则λ=________.
12 已知a,b,c是空间中三个不共面的向量,下列各组向量:①la,mb,nc(lmn≠0);②a+2b,2b+3c,-9c+3a;③a+2b,b+2c,c+2a.其中不共面的是__________(填序号).
13 (南师大附中期末)已知正四面体PABC的棱长为1,空间中一点M满足=x+y+z,其中x,y,z∈R,且x+y+z=1,则||的最小值为__________.
四、 解答题
14 如图,在平行六面体ABCD-A1B1C1D1中,点E,F分别在棱B1B和D1D上,且=,=.
(1) 求证:A,E,C1,F四点共面;
(2) 若=x+y+z,求x+y+z的值.
15 如图,在平行六面体ABCD-A1B1C1D1中,M是棱C1D1的中点,判断AC1上是否存在一点N,使得B,C,M,N四点共面,若存在,求的值;若不存在,请说明理由.
16 (连云港惠泽高级中学月考)已知a,b,c是空间中不共面的向量,若=2a-b+c,=a+2b-c,=-a+mb+nc.
(1) 若B,C,D三点共线,求m,n的值;
(2) 若A,B,C,D四点共面,求mn的最大值.
1.1.1 空间向量及其线性运算(1)
1. D 对于①,零向量的方向是任意的,故①正确;对于②,若两个空间向量相等,则它们方向相同,模长相等,故②错误;对于③,若空间向量a,b满足|a|=|b|,则不一定满足向量a与b方向相同,故③错误;对于④,空间中任意两个单位向量的模相等,方向不一定相同,则向量不一定相等,故④错误.故正确命题的个数为1.
2. D 对于A,单位向量不一定同向,故A不正确;对于B,因为|a|=|b|,所以a与b的长度相等,方向不一定相同或相反,故B错误;对于C,向量作为矢量不能比较大小,故C错误;对于D,由相等向量的定义知,相等向量的方向必相同,故D正确.
3. C 如图,结合向量加法的几何意义可得(+)-=+=.
4. A 由题意,得=+=+-=-+-=-a+b-c.
5. A 在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点,=a,=b,=c,则=++=-++=-++(+)=-+++=-++=-a+b+c,所以=-a+b+c.
6. C 对于A,由向量相等可知=,故A正确;对于B,==-,故B正确;对于C,因为=-,==+,则-=--,所以≠-,故C错误;对于D,++=+=,故D正确.
7. C 由题意,得=++=+(-)+=-++(-)=-++=-a+b+c.
8. B 设=a,=b,=c,则=-=a-c.又=,所以==(a-c),=+=-b+(a-c)=(a-3b-c).因为=+=a-c+b,=,所以==(a-c+b),所以=+=-b+(a-c+b)=(a-3b-c),所以=,即∥.又D1是直线D1M和D1N的公共点,所以D1M和D1N共线,即M,N,D1三点在一条直线上.易知由M,N,D1共线无法得到=且=.故“=且=”是“M,N,D1三点共线”的充分不必要条件.
9. AC 对于A,++=+=,故A正确;对于B,+-=-≠,故B错误;对于C,+(+)=+=,故C正确;对于D,-+=+≠,故D错误.故选AC.
10. BCD 当λ=1时,=+μ,所以=μ,则∥,即点P在棱CC1上,故A错误;同理当μ=1时,∥,故点P在棱B1C1上,故B正确;当λ+μ=1时,μ=1-λ,所以=λ+(1-λ),即=λ,故点P在线段B1C上,故C正确;当λ=μ时,=λ(+)=λ,故点P在线段BC1上,故D正确.故选BCD.
11. ++ 因为点M在线段CB1上,且CM=2MB1,所以==(+)=(-+),所以=+=+-+=++.
12. -3 如图,在四棱柱ABCD-A1B1C1D1中,=+=-+=-++,所以x=-1,y=1,z=1,所以x-y-z=-3.
13. ±2 由题意,得a=4i+λj+μk,b=μi+2j+3k,显然b不是零向量.若a∥b,则存在实数t使得a=tb,即解得μ=±2.
14. (1) =(+)
=[(++)+(+)]
=(+2+2)
=a+b+c.
(2) =+
=+(-)
=++
=a+b+c.
15. (1) -=-
=+=+=.
(2) ++=++
=+=.
向量,如图所示.
16. (1) 因为=,
所以=,
故=(-)=(+-)=a+b-c.
又=xa+yb+zc,
所以x=,y=,z=-.
(2) 因为=2,
所以=,所以==b.
由(1)知,=a+b-c,
所以=-=a-b-c=(a-b-c).
又=++=-b-c+a=a-b-c,
所以=.
因为与有公共点E,
所以E,F,B三点共线.
1.1.1 空间向量及其线性运算(2)
1. C 任意两个空间向量一定共面,故C错误. 根据空间向量的概念可知,其余选项均正确.
2. D 若,,共面,则存在实数λ,μ,使得=λ+μ,即2a+3b+5c=λ(a+2b-2c)+μ(ka+b+3c)=(λ+kμ)a+(2λ+μ)b+(-2λ+3μ)c,则解得
3. B 因为P为平面A1BC内一动点,则P,A1,B,C四点共面,且=x+y+z,所以x+y+z=1.
4. B 若a,b,c共面,当a与b共线时,c=λa+μb(λ,μ∈R)不一定成立,所以充分性不成立;若c=λa+μb(λ,μ∈R),根据向量线性运算的性质,可知c可以由a和b线性表示,则a,b,c必然共面,所以必要性成立,故“a,b,c共面”是“c=λa+μb(λ,μ∈R)”的必要不充分条件.
5. B 对于A,由题意,得a=(a-2c)+(a+2c),故A错误;对于B,设b=s(a-2c)+t(a+2c),易得s,t不存在,故B正确;对于C,由题意,得c=-(a-2c)+(a+2c),故C错误;对于D,设a-c=x(a-2c)+y(a+2c)=(x+y)a+(2y-2x)c,则所以x=,y=,所以a-c=(a-2c)+(a+2c),故D错误.
6. C 因为b=[(a+b)-(a-b)],所以a+b,a-b,b共面,故A错误;因为a-b+c=a-b-(-c),所以a-b,a-b+c,-c共面,故B错误;因为4b-2a=-2(a-2b)+0(a+c),所以a-2b,4b-2a,a+c共面,故D错误;对于C,不存在实数λ,μ,使得a+2b=λ(a-2b)+μ(a+c)成立,所以a+2b,a-2b,a+c不共面.
7. A 由题意,得-=3-x-y,即=4-x-y.因为A,B,C,D四点共面,所以4-x-y=1,即x+y=3,所以+=(x+y)=≥,当且仅当x=y=时,等号成立,所以+的最小值为.
8. D 由题意,得==(+)=[+×(+)]=[+(-)+(-)]=++.因为D,E,F,M四点共面,所以存在实数λ,μ,使=λ+μ,所以-=λ(-)+μ(-),所以=(1-λ-μ)·+λ+μ=(1-λ-μ)k+λm+μn,所以所以++=(1-λ-μ)+λ+μ=.
9. AC 对于A,,,两两正交,所以,,不共面,故A正确;对于B,因为=,所以=+=+,所以,,共面,故B错误;对于C,因为,在平面A1BCD1上,DC与平面A1BCD1不平行,所以,,不共面,故C正确;对于D,因为=,所以=+=+,故,,共面,故D错误.故选AC.
10. ABD 因为A,B,C三点不共线,所以由共面向量定理可得对平面ABC外的任一点O,存在唯一一对实数λ,μ,使得=λ+μ,即=(1-λ-μ)+λ+μ,所以(1-λ-μ)+λ+μ=1,所以ABD符合题意.故选ABD.
11. 若由向量=++λ确定的点P与A,B,C共面,则根据空间向量共面定理,得++λ=1,解得λ=.
12. ①③ 对于①,因为 a,b,c 是空间中三个不共面的向量,且 lmn≠0,所以 la,mb,nc 不共面,所以①符合题意;对于②,因为 -9c+3a=3[(a+2b)-(2b+3c)],所以 a+2b,2b+3c,-9c+3a 是共面向量,所以②不符合题意;对于③,若 a+2b,b+2c,c+2a 是共面向量,则存在实数 λ,μ,使c+2a=λ(a+2b)+μ(b+2c),即 (1-2μ)c=(λ-2)a+(2λ+μ)b.因为 a,b,c 是空间中三个不共面的向量,所以 1-2μ=λ-2=2λ+μ=0,不成立,所以 a+2b,b+2c,c+2a 不共面,所以③符合题意.
13. 因为正四面体P-ABC的棱长为1,空间中一点M满足=x+y+z,其中x,y,z∈R,且x+y+z=1,所以M,A,B,C四点共面,则||的最小值为三棱锥的高.如图,设点O为点P在平面ABC上的射影,连接OC并延长交AB于点H,则CH⊥AB,所以CH=,所以CO=,故三棱锥的高为=,所以||的最小值为.
14. (1) 由题意,得=+,=+.
因为=,=,
所以=+,=+.
由平行六面体ABCD-A1B1C1D1,
可知=,=,即=,
所以=+=+,
故A,E,C1,F四点共面.
(2) 因为=+=++
=++-
=-+-
=-++
=x+y+z,
所以x=-1,y=1,z=,
故x+y+z=.
15. 存在,理由如下:
令=a,=b,=c,
设=λ=λ(a+b+c),则=-b,=+=c+(-a)=c-a,
且=++=-b+(-a)+λ(a+b+c)=(λ-1)a+(λ-1)b+λc.
若B,C,M,N四点共面,则存在实数x,y,使得=x+y成立,
则(λ-1)a+(λ-1)b+λc=x(-b)+y(c-a),
则解得λ=,即=2.
故AC1上存在点N,使得B,C,M,N四点共面.
16. (1) 因为B,C,D三点共线,所以=λ.
又=-=-a+3b-2c,=-=-3a+(m+1)b+(n-1)c,
则解得
(2) 因为A,B,C,D四点共面,
所以=x+y,
所以-a+mb+nc=x(2a-b+c)+y(a+2b-c),
所以解得3m+5n=-1,
所以mn=m·=(-3m2-m),
当m=-时,取到最大值.
一、 单项选择题
1 给出下列命题:①零向量的方向是任意的;②若两个空间向量相等,则它们的起点相同,终点也相同;③若空间向量a,b满足|a|=|b|,则a=b;④空间中任意两个单位向量必相等.其中正确命题的个数为( )
A. 4 B. 3 C. 2 D. 1
2 关于空间向量,下列说法中正确的是( )
A. 单位向量都相等
B. 若|a|=|b|,则a,b的长度相等,方向相同或相反
C. 若向量,满足||>||,则>
D. 相等向量其方向必相同
3 在平行六面体ABCD-A1B1C1D1中,(+)-等于( )
A. B. C. D.
4 如图,在直三棱柱ABC-A1B1C1中,若=a,=b,=c,则等于( )
A. -a+b-c
B. a-b+c
C. -a+b+c
D. a+b-c
5 如图,在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点,若=a,=b,=c,则下列向量中与相等的是( )
A. -a+b+c
B. a+b+c
C. -a-b+c
D. a-b+c
6 如图,在平行六面体ABCD-A1B1C1D1中,下列关系式中错误的是( )
A. =
B. =-
C. =-
D. ++=
7如图,在四面体OABC中,=a,=b,=c,且OM=2MA,BN=NC,则等于( )
A. a+b+c
B. a+b-c
C. -a+b+c
D. a-b+c
8 在平行六面体ABCD-A1B1C1D1中,M,N分别为线段A1B,A1C上的点,则“=且=”是“M,N,D1三点共线”的( )
A. 充要条件
B. 充分不必要条件
C. 必要不充分条件
D. 既不充分也不必要条件
二、 多项选择题
9 如图,已知在四面体ABCD中,E,F分别是棱BC,CD的中点,则下列等式中正确的有( )
A. ++=
B. +-=
C. +(+)=
D. -+=
(第9题) (第10题)
10 如图,在三棱柱ABC-A1B1C1中,P为空间内一点,且满足=λ+μ,λ∈[0,1],μ∈[0,1],则下列说法中正确的有( )
A. 当λ=1时,点P在棱BB1上
B. 当μ=1时,点P在棱B1C1上
C. 当λ+μ=1时,点P在线段B1C上
D. 当λ=μ时,点P在线段BC1上
三、填空题
11 在三棱柱ABC-A1B1C1中,点M在线段CB1上,且CM=2MB1,若用,,表示,则=________.
12 在四棱柱ABCD-A1B1C1D1中,=x+y+z,则x-y-z=________.
13 已知空间中互不平行的三个向量i,j,k,a=4i+λj+μk,b=μi+2j+3k,若a∥b,则μ=________.
四、 解答题
14 如图,在平行六面体ABCD-A1B1C1D1中,=a,=b,=c. M是棱C1D1的中点,N是线段CA1上的点,且CN∶NA1=4∶1.用a,b,c表示以下向量:
(1) ;
(2) .
15 如图,已知长方体ABCD-A′B′C′D′,化简下列向量表达式,并在图中标出化简结果表示的向量.
(1) -;
(2) ++.
16 如图,在正方体ABCD-A1B1C1D1中,点E在棱A1D1上,且=2,点F在对角线A1C上,且=.设=a,=b,=c.
(1) 若=xa+yb+zc,求x,y,z的值;
(2) 求证:E,F,B三点共线.
1.1.1 空间向量及其线性运算(2)
一、 单项选择题
1 (吉林四校月考)下列关于空间向量的说法中,错误的是( )
A. 平行于同一个平面的向量叫做共面向量
B. 直线可以由其上一点和它的方向向量确定
C. 任意两个空间向量不一定共面
D. 任意两个空间向量都可以通过平移转化为同一平面内的向量
2 (江阴六校期中)设a,b,c为空间内三个不共面的向量,=2a+3b+5c,=a+2b-2c,=ka+b+3c,若,,共面,则k的值为( )
A. B. C. D.
3 如图,在三棱柱ABC-A1B1C1中,P为平面A1BC内一动点,且=x+y+z,则x+y+z的值为( )
A. 0
B. 1
C. 3
D. -1
4 (浙江四校月考)三个非零向量a,b,c,则“a,b,c共面”是“c=λa+μb(λ,μ∈R)”的( )
A. 充分不必要条件
B. 必要不充分条件
C. 充要条件
D. 既不充分也不必要条件
5 (雅礼中学月考)已知a,b,c为空间内不共面的三个向量,则下列选项中与向量m=a-2c,n=a+2c不共面的向量是( )
A. a B. b C. c D. a-c
6 (南京玄武高级中学月考)已知a,b,c不共面,则下列向量中不共面的是( )
A. a+b,a-b,b
B. a-b,a-b+c,-c
C. a+2b,a-2b,a+c
D. a-2b,4b-2a,a+c
7 (文山期末)对三维空间中不共线的三点A,B,C和任一点O,点P在平面ABC内的充要条件是存在唯一有序实数组(x,y,z),使=x+y+z且x+y+z=1.已知A,B,C,D四点共面,O为空间中任意一点,且满足=3-x-y,其中x>0,y>0,则+的最小值为( )
A. B. 1 C. D. 4
8 (厦门一中月考)如图,在三棱锥O-ABC中,点G为底面三角形ABC的重心,M是线段OG上靠近点G的三等分点,过点M的平面分别交棱OA,OB,OC于点D,E,F,若=k,=m,=n,则++的值为( )
A.
B.
C.
D.
二、 多项选择题
9 已知正方体ABCD-A1B1C1D1,则下列选项中,不共面的一组向量有( )
A. ,,
B. ,,
C. ,,
D. ,,
10 (温州十校联考)已知A,B,C三点不共线,对平面ABC外的任一点O,下列条件中能确定点M,A,B,C共面的是( )
A. =+-
B. =++
C. =++
D. =3--
三、填空题
11 (泰安二中期初)已知A,B,C三点不共线,O为平面ABC外一点,若由向量=++λ确定的点P与A,B,C共面,则λ=________.
12 已知a,b,c是空间中三个不共面的向量,下列各组向量:①la,mb,nc(lmn≠0);②a+2b,2b+3c,-9c+3a;③a+2b,b+2c,c+2a.其中不共面的是__________(填序号).
13 (南师大附中期末)已知正四面体PABC的棱长为1,空间中一点M满足=x+y+z,其中x,y,z∈R,且x+y+z=1,则||的最小值为__________.
四、 解答题
14 如图,在平行六面体ABCD-A1B1C1D1中,点E,F分别在棱B1B和D1D上,且=,=.
(1) 求证:A,E,C1,F四点共面;
(2) 若=x+y+z,求x+y+z的值.
15 如图,在平行六面体ABCD-A1B1C1D1中,M是棱C1D1的中点,判断AC1上是否存在一点N,使得B,C,M,N四点共面,若存在,求的值;若不存在,请说明理由.
16 (连云港惠泽高级中学月考)已知a,b,c是空间中不共面的向量,若=2a-b+c,=a+2b-c,=-a+mb+nc.
(1) 若B,C,D三点共线,求m,n的值;
(2) 若A,B,C,D四点共面,求mn的最大值.
1.1.1 空间向量及其线性运算(1)
1. D 对于①,零向量的方向是任意的,故①正确;对于②,若两个空间向量相等,则它们方向相同,模长相等,故②错误;对于③,若空间向量a,b满足|a|=|b|,则不一定满足向量a与b方向相同,故③错误;对于④,空间中任意两个单位向量的模相等,方向不一定相同,则向量不一定相等,故④错误.故正确命题的个数为1.
2. D 对于A,单位向量不一定同向,故A不正确;对于B,因为|a|=|b|,所以a与b的长度相等,方向不一定相同或相反,故B错误;对于C,向量作为矢量不能比较大小,故C错误;对于D,由相等向量的定义知,相等向量的方向必相同,故D正确.
3. C 如图,结合向量加法的几何意义可得(+)-=+=.
4. A 由题意,得=+=+-=-+-=-a+b-c.
5. A 在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点,=a,=b,=c,则=++=-++=-++(+)=-+++=-++=-a+b+c,所以=-a+b+c.
6. C 对于A,由向量相等可知=,故A正确;对于B,==-,故B正确;对于C,因为=-,==+,则-=--,所以≠-,故C错误;对于D,++=+=,故D正确.
7. C 由题意,得=++=+(-)+=-++(-)=-++=-a+b+c.
8. B 设=a,=b,=c,则=-=a-c.又=,所以==(a-c),=+=-b+(a-c)=(a-3b-c).因为=+=a-c+b,=,所以==(a-c+b),所以=+=-b+(a-c+b)=(a-3b-c),所以=,即∥.又D1是直线D1M和D1N的公共点,所以D1M和D1N共线,即M,N,D1三点在一条直线上.易知由M,N,D1共线无法得到=且=.故“=且=”是“M,N,D1三点共线”的充分不必要条件.
9. AC 对于A,++=+=,故A正确;对于B,+-=-≠,故B错误;对于C,+(+)=+=,故C正确;对于D,-+=+≠,故D错误.故选AC.
10. BCD 当λ=1时,=+μ,所以=μ,则∥,即点P在棱CC1上,故A错误;同理当μ=1时,∥,故点P在棱B1C1上,故B正确;当λ+μ=1时,μ=1-λ,所以=λ+(1-λ),即=λ,故点P在线段B1C上,故C正确;当λ=μ时,=λ(+)=λ,故点P在线段BC1上,故D正确.故选BCD.
11. ++ 因为点M在线段CB1上,且CM=2MB1,所以==(+)=(-+),所以=+=+-+=++.
12. -3 如图,在四棱柱ABCD-A1B1C1D1中,=+=-+=-++,所以x=-1,y=1,z=1,所以x-y-z=-3.
13. ±2 由题意,得a=4i+λj+μk,b=μi+2j+3k,显然b不是零向量.若a∥b,则存在实数t使得a=tb,即解得μ=±2.
14. (1) =(+)
=[(++)+(+)]
=(+2+2)
=a+b+c.
(2) =+
=+(-)
=++
=a+b+c.
15. (1) -=-
=+=+=.
(2) ++=++
=+=.
向量,如图所示.
16. (1) 因为=,
所以=,
故=(-)=(+-)=a+b-c.
又=xa+yb+zc,
所以x=,y=,z=-.
(2) 因为=2,
所以=,所以==b.
由(1)知,=a+b-c,
所以=-=a-b-c=(a-b-c).
又=++=-b-c+a=a-b-c,
所以=.
因为与有公共点E,
所以E,F,B三点共线.
1.1.1 空间向量及其线性运算(2)
1. C 任意两个空间向量一定共面,故C错误. 根据空间向量的概念可知,其余选项均正确.
2. D 若,,共面,则存在实数λ,μ,使得=λ+μ,即2a+3b+5c=λ(a+2b-2c)+μ(ka+b+3c)=(λ+kμ)a+(2λ+μ)b+(-2λ+3μ)c,则解得
3. B 因为P为平面A1BC内一动点,则P,A1,B,C四点共面,且=x+y+z,所以x+y+z=1.
4. B 若a,b,c共面,当a与b共线时,c=λa+μb(λ,μ∈R)不一定成立,所以充分性不成立;若c=λa+μb(λ,μ∈R),根据向量线性运算的性质,可知c可以由a和b线性表示,则a,b,c必然共面,所以必要性成立,故“a,b,c共面”是“c=λa+μb(λ,μ∈R)”的必要不充分条件.
5. B 对于A,由题意,得a=(a-2c)+(a+2c),故A错误;对于B,设b=s(a-2c)+t(a+2c),易得s,t不存在,故B正确;对于C,由题意,得c=-(a-2c)+(a+2c),故C错误;对于D,设a-c=x(a-2c)+y(a+2c)=(x+y)a+(2y-2x)c,则所以x=,y=,所以a-c=(a-2c)+(a+2c),故D错误.
6. C 因为b=[(a+b)-(a-b)],所以a+b,a-b,b共面,故A错误;因为a-b+c=a-b-(-c),所以a-b,a-b+c,-c共面,故B错误;因为4b-2a=-2(a-2b)+0(a+c),所以a-2b,4b-2a,a+c共面,故D错误;对于C,不存在实数λ,μ,使得a+2b=λ(a-2b)+μ(a+c)成立,所以a+2b,a-2b,a+c不共面.
7. A 由题意,得-=3-x-y,即=4-x-y.因为A,B,C,D四点共面,所以4-x-y=1,即x+y=3,所以+=(x+y)=≥,当且仅当x=y=时,等号成立,所以+的最小值为.
8. D 由题意,得==(+)=[+×(+)]=[+(-)+(-)]=++.因为D,E,F,M四点共面,所以存在实数λ,μ,使=λ+μ,所以-=λ(-)+μ(-),所以=(1-λ-μ)·+λ+μ=(1-λ-μ)k+λm+μn,所以所以++=(1-λ-μ)+λ+μ=.
9. AC 对于A,,,两两正交,所以,,不共面,故A正确;对于B,因为=,所以=+=+,所以,,共面,故B错误;对于C,因为,在平面A1BCD1上,DC与平面A1BCD1不平行,所以,,不共面,故C正确;对于D,因为=,所以=+=+,故,,共面,故D错误.故选AC.
10. ABD 因为A,B,C三点不共线,所以由共面向量定理可得对平面ABC外的任一点O,存在唯一一对实数λ,μ,使得=λ+μ,即=(1-λ-μ)+λ+μ,所以(1-λ-μ)+λ+μ=1,所以ABD符合题意.故选ABD.
11. 若由向量=++λ确定的点P与A,B,C共面,则根据空间向量共面定理,得++λ=1,解得λ=.
12. ①③ 对于①,因为 a,b,c 是空间中三个不共面的向量,且 lmn≠0,所以 la,mb,nc 不共面,所以①符合题意;对于②,因为 -9c+3a=3[(a+2b)-(2b+3c)],所以 a+2b,2b+3c,-9c+3a 是共面向量,所以②不符合题意;对于③,若 a+2b,b+2c,c+2a 是共面向量,则存在实数 λ,μ,使c+2a=λ(a+2b)+μ(b+2c),即 (1-2μ)c=(λ-2)a+(2λ+μ)b.因为 a,b,c 是空间中三个不共面的向量,所以 1-2μ=λ-2=2λ+μ=0,不成立,所以 a+2b,b+2c,c+2a 不共面,所以③符合题意.
13. 因为正四面体P-ABC的棱长为1,空间中一点M满足=x+y+z,其中x,y,z∈R,且x+y+z=1,所以M,A,B,C四点共面,则||的最小值为三棱锥的高.如图,设点O为点P在平面ABC上的射影,连接OC并延长交AB于点H,则CH⊥AB,所以CH=,所以CO=,故三棱锥的高为=,所以||的最小值为.
14. (1) 由题意,得=+,=+.
因为=,=,
所以=+,=+.
由平行六面体ABCD-A1B1C1D1,
可知=,=,即=,
所以=+=+,
故A,E,C1,F四点共面.
(2) 因为=+=++
=++-
=-+-
=-++
=x+y+z,
所以x=-1,y=1,z=,
故x+y+z=.
15. 存在,理由如下:
令=a,=b,=c,
设=λ=λ(a+b+c),则=-b,=+=c+(-a)=c-a,
且=++=-b+(-a)+λ(a+b+c)=(λ-1)a+(λ-1)b+λc.
若B,C,M,N四点共面,则存在实数x,y,使得=x+y成立,
则(λ-1)a+(λ-1)b+λc=x(-b)+y(c-a),
则解得λ=,即=2.
故AC1上存在点N,使得B,C,M,N四点共面.
16. (1) 因为B,C,D三点共线,所以=λ.
又=-=-a+3b-2c,=-=-3a+(m+1)b+(n-1)c,
则解得
(2) 因为A,B,C,D四点共面,
所以=x+y,
所以-a+mb+nc=x(2a-b+c)+y(a+2b-c),
所以解得3m+5n=-1,
所以mn=m·=(-3m2-m),
当m=-时,取到最大值.
