2.1.1 倾斜角与斜率 同步练习 (含答案) 2025-2026学年高二数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.1.1 倾斜角与斜率 同步练习 (含答案) 2025-2026学年高二数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | docx | ||
| 文件大小 | 302.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 00:00:00 | ||
图片预览


文档简介
2.1.1 倾斜角与斜率
一、 单项选择题
1 已知点A(1,y1),B(2,y2)在斜率为的直线l上,则y2-y1的值为( )
A. - B. - C. D.
2 已知两点A(2,t),B(1,0),t∈R,直线AB的倾斜角为120°,则实数t的值为( )
A. - B. - C. D.
3 若A(-2,3),B(3,-2),C三点共线,则实数m的值为( )
A. B. - C. -2 D. 2
4 若将直线l沿x轴正方向平移2个单位长度,再沿y轴负方向平移3个单位长度,又回到了原来的位置,则直线l的斜率是( )
A. - B. C. - D.
5 经过A(0,2),B(a,0)两点的直线的方向向量为n=(1,2),则实数a的值为( )
A. -1 B. 0 C. 1 D. 2
6 已知两点M(3,-1),N(2,5),直线l过点P(1,1)且与线段MN相交,则直线l的斜率k的取值范围是( )
A. (-∞,-1]
B. [4,+∞)
C. [-1,4]
D. (-∞,-1]∪[4,+∞)
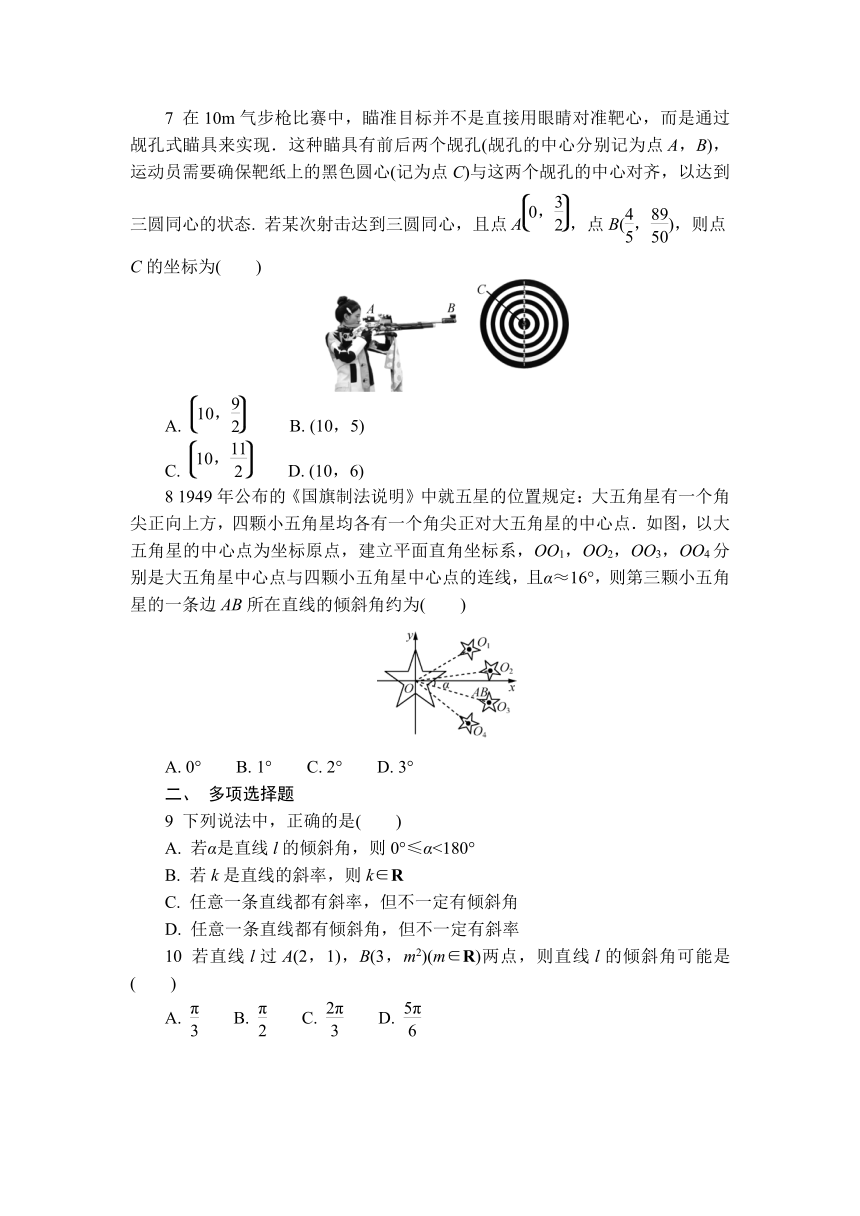
7 在10m气步枪比赛中,瞄准目标并不是直接用眼睛对准靶心,而是通过觇孔式瞄具来实现.这种瞄具有前后两个觇孔(觇孔的中心分别记为点A,B),运动员需要确保靶纸上的黑色圆心(记为点C)与这两个觇孔的中心对齐,以达到三圆同心的状态. 若某次射击达到三圆同心,且点A,点B(,),则点C的坐标为( )
A. B. (10,5)
C. D. (10,6)
8 1949年公布的《国旗制法说明》中就五星的位置规定:大五角星有一个角尖正向上方,四颗小五角星均各有一个角尖正对大五角星的中心点.如图,以大五角星的中心点为坐标原点,建立平面直角坐标系,OO1,OO2,OO3,OO4分别是大五角星中心点与四颗小五角星中心点的连线,且α≈16°,则第三颗小五角星的一条边AB所在直线的倾斜角约为( )
A. 0° B. 1° C. 2° D. 3°
二、 多项选择题
9 下列说法中,正确的是( )
A. 若α是直线l的倾斜角,则0°≤α<180°
B. 若k是直线的斜率,则k∈R
C. 任意一条直线都有斜率,但不一定有倾斜角
D. 任意一条直线都有倾斜角,但不一定有斜率
10 若直线l过A(2,1),B(3,m2)(m∈R)两点,则直线l的倾斜角可能是( )
A. B. C. D.
三、填空题
11 若倾斜角为的直线过点(1,3)和(2,m),则实数m=________.
12 已知θ是斜率为-1的直线的倾斜角,则sin =________.
13已知过点(0,-2)的直线l与以点A(3,1)和B(-2,4)为端点的线段相交,则直线l的斜率的取值范围是________.
四、解答题
14 (建平实验中学月考)根据下列条件,求直线l的倾斜角α的大小:
(1) 直线l的斜率为-;
(2) 直线l经过A(-2,0),B(-5,3)两点;
(3) 直线l的一个方向向量为=(2,).
15 已知A(1,2),B(2,1),C(0,m)三点.
(1) 若过A,C两点的直线的倾斜角为45°,求实数m的值;
(2) A,B,C三点可能共线吗?若能,求出实数m的值;若不能,请说明理由.
16 已知平面直角坐标系内三点A(-1,1),B(1,1),C(2,+1).
(1) 求直线AB,BC,AC的斜率和倾斜角;
(2) 若D为△ABC的边AB上一动点,求直线CD的倾斜角的取值范围.
2.1.1 倾斜角与斜率
1. D
2. B 由题意,得直线AB的斜率为k==t.又k=tan 120°=-,所以t=-.
3. A 因为A(-2,3),B(3,-2),C三点共线,所以kAB=kAC,即=,解得m=.
4. A 设A(a,b)是直线l上任意一点,则平移后得点A′(a+2,b-3),所以直线l的斜率为k=kAA′==-.
5. A 由点A(0,2),B(a,0),得=(a,-2).由直线AB的方向向量为n=(1,2),得∥n,所以2a=-2,解得a=-1.
6. C 如图,由题意可知kPM==-1,kPN==4,所以直线l的斜率k的取值范围是[-1,4].
7. B 由题意,得A,B,C三点共线.设点C(10,t),因为点A,B,所以kAB===kAC=,解得t=5,所以点C的坐标为(10,5).
8. C 因为O,O3分别为大五角星和第三颗小五角星的中心点,所以OO3平分第三颗小五角星的一个角.又五角星的角尖为36°,所以∠BAO3=18°. 过点O3作x轴的平行线O3E,如图,则∠OO3E=α≈16°,所以直线AB的倾斜角约为18°-16°=2°.
9. ABD 直线的倾斜角α必定存在,且满足0≤α<180°;直线的斜率k∈R,但不是所有直线都存在斜率,故A,B,D正确,C错误.故选ABD.
10. AD 设l的倾斜角为α,所以直线l的斜率为k==m2-1,所以tan α=m2-1≥-1.又α∈[0,π),所以直线l的倾斜角的取值范围是∪.故选AD.
11. 3+
12. 因为θ是斜率为-1的直线的倾斜角,所以tan θ=-1,θ∈[0,π),所以θ=,所以sin (θ-)=sin =sin =.
13. (-∞,-]∪[1,+∞) 如图,设点P(0,-2),由题意,得kPA==1,kPB==-.因为当直线l与y轴重合时,斜率不存在,所以当直线l与线段AB有交点时,kl≤-或kl≥1.故直线l的斜率的取值范围是(-∞,-]∪[1,+∞).
14. (1) α= (2) α= (3) α=
15. (1) 因为过A,C两点的直线斜率为k=tan 45°=1,
所以k==1,解得m=1.
(2) 由题意,得kAB==-1,kAC==2-m.
若A,B,C三点共线,则kAB=kAC,
即2-m=-1,解得m=3,
所以当m=3时,A,B,C三点共线.
16. (1) 由斜率公式,得kAB==0,kBC==,kAC==,
所以直线AB的倾斜角为0,直线BC的倾斜角为,直线AC的倾斜角为.
(2) 如图,当直线CD绕点C由CA逆时针转到CB时,直线CD与线段AB恒有交点,即点D在线段AB上,此时kCD由kAC增大到kBC,
所以kCD的取值范围为,
即直线CD的倾斜角的取值范围为.
一、 单项选择题
1 已知点A(1,y1),B(2,y2)在斜率为的直线l上,则y2-y1的值为( )
A. - B. - C. D.
2 已知两点A(2,t),B(1,0),t∈R,直线AB的倾斜角为120°,则实数t的值为( )
A. - B. - C. D.
3 若A(-2,3),B(3,-2),C三点共线,则实数m的值为( )
A. B. - C. -2 D. 2
4 若将直线l沿x轴正方向平移2个单位长度,再沿y轴负方向平移3个单位长度,又回到了原来的位置,则直线l的斜率是( )
A. - B. C. - D.
5 经过A(0,2),B(a,0)两点的直线的方向向量为n=(1,2),则实数a的值为( )
A. -1 B. 0 C. 1 D. 2
6 已知两点M(3,-1),N(2,5),直线l过点P(1,1)且与线段MN相交,则直线l的斜率k的取值范围是( )
A. (-∞,-1]
B. [4,+∞)
C. [-1,4]
D. (-∞,-1]∪[4,+∞)
7 在10m气步枪比赛中,瞄准目标并不是直接用眼睛对准靶心,而是通过觇孔式瞄具来实现.这种瞄具有前后两个觇孔(觇孔的中心分别记为点A,B),运动员需要确保靶纸上的黑色圆心(记为点C)与这两个觇孔的中心对齐,以达到三圆同心的状态. 若某次射击达到三圆同心,且点A,点B(,),则点C的坐标为( )
A. B. (10,5)
C. D. (10,6)
8 1949年公布的《国旗制法说明》中就五星的位置规定:大五角星有一个角尖正向上方,四颗小五角星均各有一个角尖正对大五角星的中心点.如图,以大五角星的中心点为坐标原点,建立平面直角坐标系,OO1,OO2,OO3,OO4分别是大五角星中心点与四颗小五角星中心点的连线,且α≈16°,则第三颗小五角星的一条边AB所在直线的倾斜角约为( )
A. 0° B. 1° C. 2° D. 3°
二、 多项选择题
9 下列说法中,正确的是( )
A. 若α是直线l的倾斜角,则0°≤α<180°
B. 若k是直线的斜率,则k∈R
C. 任意一条直线都有斜率,但不一定有倾斜角
D. 任意一条直线都有倾斜角,但不一定有斜率
10 若直线l过A(2,1),B(3,m2)(m∈R)两点,则直线l的倾斜角可能是( )
A. B. C. D.
三、填空题
11 若倾斜角为的直线过点(1,3)和(2,m),则实数m=________.
12 已知θ是斜率为-1的直线的倾斜角,则sin =________.
13已知过点(0,-2)的直线l与以点A(3,1)和B(-2,4)为端点的线段相交,则直线l的斜率的取值范围是________.
四、解答题
14 (建平实验中学月考)根据下列条件,求直线l的倾斜角α的大小:
(1) 直线l的斜率为-;
(2) 直线l经过A(-2,0),B(-5,3)两点;
(3) 直线l的一个方向向量为=(2,).
15 已知A(1,2),B(2,1),C(0,m)三点.
(1) 若过A,C两点的直线的倾斜角为45°,求实数m的值;
(2) A,B,C三点可能共线吗?若能,求出实数m的值;若不能,请说明理由.
16 已知平面直角坐标系内三点A(-1,1),B(1,1),C(2,+1).
(1) 求直线AB,BC,AC的斜率和倾斜角;
(2) 若D为△ABC的边AB上一动点,求直线CD的倾斜角的取值范围.
2.1.1 倾斜角与斜率
1. D
2. B 由题意,得直线AB的斜率为k==t.又k=tan 120°=-,所以t=-.
3. A 因为A(-2,3),B(3,-2),C三点共线,所以kAB=kAC,即=,解得m=.
4. A 设A(a,b)是直线l上任意一点,则平移后得点A′(a+2,b-3),所以直线l的斜率为k=kAA′==-.
5. A 由点A(0,2),B(a,0),得=(a,-2).由直线AB的方向向量为n=(1,2),得∥n,所以2a=-2,解得a=-1.
6. C 如图,由题意可知kPM==-1,kPN==4,所以直线l的斜率k的取值范围是[-1,4].
7. B 由题意,得A,B,C三点共线.设点C(10,t),因为点A,B,所以kAB===kAC=,解得t=5,所以点C的坐标为(10,5).
8. C 因为O,O3分别为大五角星和第三颗小五角星的中心点,所以OO3平分第三颗小五角星的一个角.又五角星的角尖为36°,所以∠BAO3=18°. 过点O3作x轴的平行线O3E,如图,则∠OO3E=α≈16°,所以直线AB的倾斜角约为18°-16°=2°.
9. ABD 直线的倾斜角α必定存在,且满足0≤α<180°;直线的斜率k∈R,但不是所有直线都存在斜率,故A,B,D正确,C错误.故选ABD.
10. AD 设l的倾斜角为α,所以直线l的斜率为k==m2-1,所以tan α=m2-1≥-1.又α∈[0,π),所以直线l的倾斜角的取值范围是∪.故选AD.
11. 3+
12. 因为θ是斜率为-1的直线的倾斜角,所以tan θ=-1,θ∈[0,π),所以θ=,所以sin (θ-)=sin =sin =.
13. (-∞,-]∪[1,+∞) 如图,设点P(0,-2),由题意,得kPA==1,kPB==-.因为当直线l与y轴重合时,斜率不存在,所以当直线l与线段AB有交点时,kl≤-或kl≥1.故直线l的斜率的取值范围是(-∞,-]∪[1,+∞).
14. (1) α= (2) α= (3) α=
15. (1) 因为过A,C两点的直线斜率为k=tan 45°=1,
所以k==1,解得m=1.
(2) 由题意,得kAB==-1,kAC==2-m.
若A,B,C三点共线,则kAB=kAC,
即2-m=-1,解得m=3,
所以当m=3时,A,B,C三点共线.
16. (1) 由斜率公式,得kAB==0,kBC==,kAC==,
所以直线AB的倾斜角为0,直线BC的倾斜角为,直线AC的倾斜角为.
(2) 如图,当直线CD绕点C由CA逆时针转到CB时,直线CD与线段AB恒有交点,即点D在线段AB上,此时kCD由kAC增大到kBC,
所以kCD的取值范围为,
即直线CD的倾斜角的取值范围为.
