2.2.2 直线的两点式方程 同步练习 (含答案) 2025-2026学年高二数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.2.2 直线的两点式方程 同步练习 (含答案) 2025-2026学年高二数学人教A版(2019)选择性必修第一册 |
|
|
| 格式 | docx | ||
| 文件大小 | 70.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 00:00:00 | ||
图片预览



文档简介
2.2.2 直线的两点式方程
一、 单项选择题
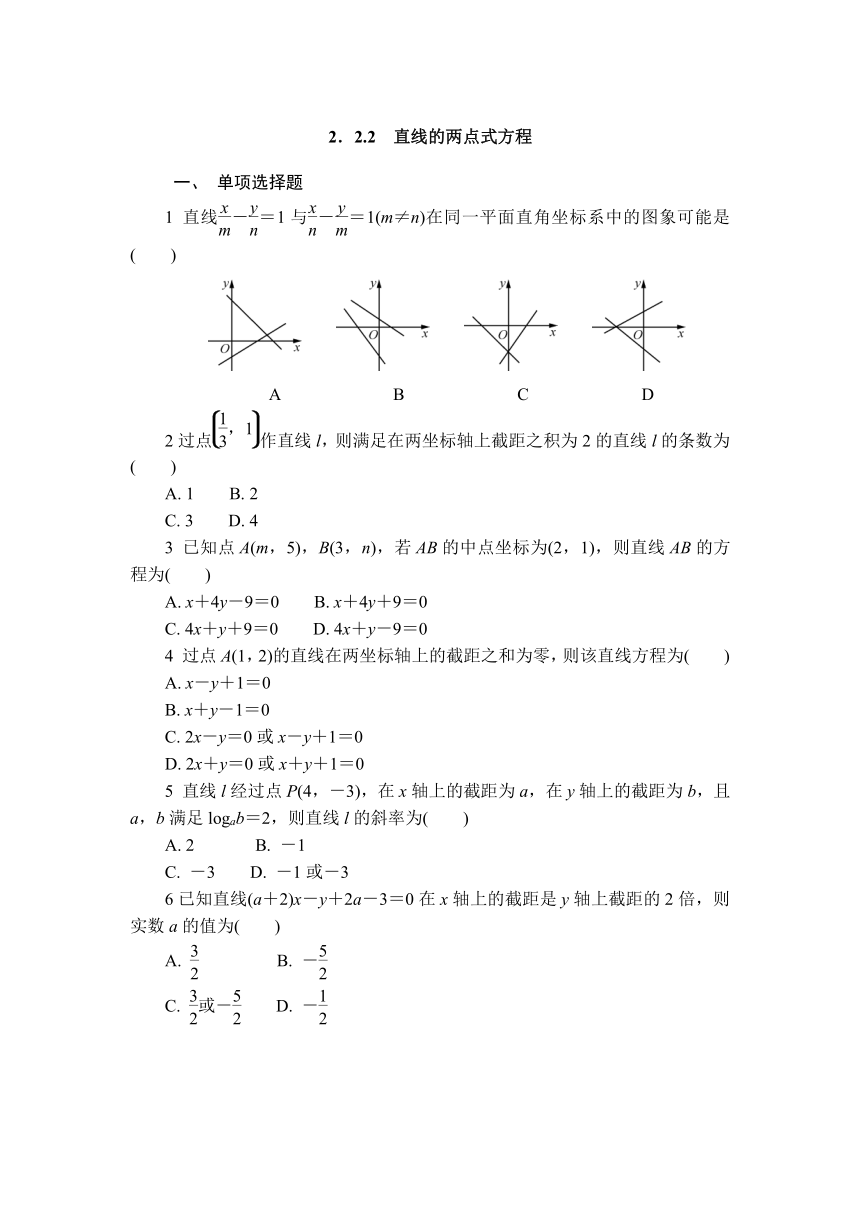
1 直线-=1与-=1(m≠n)在同一平面直角坐标系中的图象可能是( )
A B C D
2过点作直线l,则满足在两坐标轴上截距之积为2的直线l的条数为( )
A. 1 B. 2
C. 3 D. 4
3 已知点A(m,5),B(3,n),若AB的中点坐标为(2,1),则直线AB的方程为( )
A. x+4y-9=0 B. x+4y+9=0
C. 4x+y+9=0 D. 4x+y-9=0
4 过点A(1,2)的直线在两坐标轴上的截距之和为零,则该直线方程为( )
A. x-y+1=0
B. x+y-1=0
C. 2x-y=0或x-y+1=0
D. 2x+y=0或x+y+1=0
5 直线l经过点P(4,-3),在x轴上的截距为a,在y轴上的截距为b,且a,b满足logab=2,则直线l的斜率为( )
A. 2 B. -1
C. -3 D. -1或-3
6已知直线(a+2)x-y+2a-3=0在x轴上的截距是y轴上截距的2倍,则实数a的值为( )
A. B. -
C. 或- D. -
7 已知直线l经过点P(1,2),与两坐标轴的正半轴分别交于A,B两点,O为坐标原点,则△OAB面积的最小值为( )
A. 2 B. 3
C. 4 D. 8
8 瑞士数学家欧拉在《三角形的几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上.这条直线被称为欧拉线.已知△ABC的顶点A(-3,0),B(3,0),C(3,3),则△ABC的欧拉线的方程为( )
A. 2x-y-1=0 B. 2x+y-=0
C. x+2y-3=0 D. x-2y+1=0
二、 多项选择题
9 过定点(2,3)且在两坐标轴上截距的绝对值相等的直线为( )
A. 3x-2y=0
B. x+y-5=0
C. x-y+1=0
D. x-y-5=0
10 已知直线l过点(0,2),(,1),则下列结论中正确的是( )
A. 直线l的倾斜角为150°
B. 直线l的两点式方程为=
C. 直线l的一个方向向量为(1,-)
D. 直线l的截距式方程为+=1
三、填空题
11 已知直线l的两点式方程为=,则直线l的斜率为________.
12已知直线l在x轴与y轴上的截距分别为4,9,若点E(1,b)在直线l上,则实数b=________.
13 已知△ABC的顶点坐标分别为A(4,3),B(-2,-5),C(8,0),则角A的平分线所在的直线方程为________.
四、解答题
14 过点P(2,1)作直线l分别交x轴,y轴的正半轴于A,B两点.
(1) 求△ABO面积的最小值及相应的直线l的方程;
(2) 当OA+OB取最小值时,求直线l的方程.
15 已知点A(3,4).
(1) 求经过点A(3,4),且在x轴上的截距是y轴上截距的2倍的直线的方程;
(2) 光线自点A(3,4)射到y轴上的点B(0,1)后被y轴反射,求反射光线所在直线的方程.
16 已知三角形的三个顶点是A(4,0),B(6,7),C(0,3).
(1) 求边AC所在的直线方程;
(2) 求边AC上的高所在的直线方程;
(3) 求经过两边AB和BC中点的直线的方程.
2.2.2 直线的两点式方程
1. B 易知直线-=1的斜率为,直线-=1的斜率为,所以两直线的倾斜角同为锐角或者同为钝角,且斜率的绝对值一个大于1,一个小于1,故只有B满足题意.
2. B 设直线l的方程为+=1(a≠0),将点代入,可得+=1(a≠0),即3a2-6a+2=0.因为Δ=36-4×3×2=12>0,所以方程3a2-6a+2=0有两个不相等的实数根,故满足题意的直线l的条数为2.
3. D 由题意,得解得m=1,n=-3,即点A(1,5),B(3,-3). 将点A,B的坐标代入两点式方程可得=,即4x+y-9=0.
4. C 当直线过原点时在两坐标轴上的截距都为0,满足题意.因为直线过点A(1,2),所以直线的斜率为=2,所以直线方程为y=2x,即2x- y=0;当直线不过原点时,设直线方程为+= 1,因为点A(1,2)在直线上,所以+=1,解得a=-1,所以直线方程为x-y+1=0.故所求直线方程为2x-y=0或x-y+1=0.
5. C 由题意,设直线l的方程为+=1,则+=1①.又logab=2,所以b=a2②.由①②解得a=3,b=9或a=1,b=1.又由logab=2可知a>0,a≠1,b>0,所以a=3,b=9,则直线l的斜率为-=-3.
6. C 由题意,得a≠-2,当a=时,直线l为x-y=0,此时横、纵截距都等于0,满足题意;当a≠时,将直线l的方程化为截距式方程可得+=1,直线l在x轴上的截距为,在y轴上截距为2a-3,则=2×(2a-3),解得a=-或a=(舍去).综上,实数a的值为-或.
7. C 不妨设直线l分别交x轴,y轴于点A(a,0),B(0,b),则a>0,b>0,所以直线l的截距式方程为+=1.因为点P在直线l上,所以+=1,由基本不等式可得1=+≥2=,可得ab≥8,则S△OAB=ab≥4,当且仅当,即时,等号成立,故△OAB面积的最小值为4.
8. C 由△ABC的顶点A(-3,0),B(3,0),C(3,3)知,△ABC的重心为,即(1,1).因为BC⊥AB,所以△ABC为直角三角形,所以外心为斜边的中点, 即,所以△ABC的欧拉线的方程为=,即x+2y-3=0.
9. ABC 由题意,得直线不与坐标轴垂直,设所求的直线方程为y=k(x-2)+3,当y=0时,横截距为x=2-,当x=0时,纵截距为y=3-2k.因为过点(2,3)的直线在两坐标轴上截距的绝对值相等,所以=|3-2k|,解得k=-1或k=或k=1,所以直线的方程为x+y-5=0或3x-2y=0或x-y+1=0.故选ABC.
10. ABD 因为直线l过点(0,2),(,1),所以直线l的斜率为=-,倾斜角为150°,故A正确,C错误;直线l的两点式方程为=,整理,得截距式方程为+=1,故B,D正确.故选ABD.
11. - 原方程可化为=-x,即y=-x-3,所以直线l的斜率为-.
12. 由题意,得直线的截距式方程为+=1.又点E(1,b)在直线l上,所以+=1,解得b=.
13. 7x+y-31=0 如图,角A的平分线与BC交于点D.由题意,得AB==10,AC==5.由角平分线定理,得==2,所以=.设点D的坐标为(x,y),则(x-8,y-0)=(-2-8,-5),所以x-8=-,y=-,即点D,所以直线AD的方程为=,整理,得7x+y-31=0.
14. (1) 显然直线 l斜率存在且不过原点.
由题意可设直线 l的方程为+=1(a>0,b>0),
又点P(2,1)在直线 l上,所以+=1,
由基本不等式可得+=1≥2,
即ab≥8,当且仅当a=4,b=2时,等号成立.
又S△ABO=OA·OB=ab,
所以S△ABO=ab≥×8=4,当且仅当a=4,b=2时,等号成立,
此时相应的直线 l的方程为x+2y-4=0.
(2) 由(1)可知+=1(a>0,b>0).
又OA+OB=a+b,
所以OA+OB=a+b=(a+b)=3++ ≥3+2,
当且仅当a=2+,b=+1时,等号成立,
此时相应的直线 l的方程为x+y-2-=0.
15. (1) 当直线过原点时,满足在x轴上的截距是y轴上截距的2倍,
此时直线方程为y=kx,将点A(3,4)代入,
可得k=,化简可得4x-3y=0;
当直线不过原点时,设直线方程为+=1,且a=2b,
即+=1,将点A(3,4)代入,
可得+=1,解得b=,
则直线方程为+=1,化简可得x+2y-11=0.
综上,直线方程为4x-3y=0或x+2y-11=0.
(2) 点A关于y轴的对称点的坐标为A′(-3,4).
由题意可知,反射光线所在的直线经过点A′(-3,4),B(0,1),
所以反射光线所在的直线斜率为kA′B==-1,
故反射光线所在的直线方程为y-1=-1(x-0),即x+y-1=0.
16. (1) 由题意可知点A(4,0),C(0,3),
则由直线的截距式方程可得+=1,即3x+4y-12=0.
(2) 设高所在的直线方程的斜率为k,直线AC斜率为kAC,
由(1)可知直线AC的斜率为kAC=-.
因为高所在的直线的斜率与直线AC的斜率的乘积为-1,
即k·kAC=-1,则k=.
又由点斜式方程可得y-7=(x-6),
所以高所在的直线方程为3y-4x+3=0.
(3) 设AB和BC的中点分别为D(x1,y1),E(x2,y2).
因为A(4,0),B(6,7),C(0,3),
所以x1==5,y1==,x2==3,y2==5,
则由点斜式方程可得直线DE的方程为y-5=(x-3),
即4y+3x-29=0.
一、 单项选择题
1 直线-=1与-=1(m≠n)在同一平面直角坐标系中的图象可能是( )
A B C D
2过点作直线l,则满足在两坐标轴上截距之积为2的直线l的条数为( )
A. 1 B. 2
C. 3 D. 4
3 已知点A(m,5),B(3,n),若AB的中点坐标为(2,1),则直线AB的方程为( )
A. x+4y-9=0 B. x+4y+9=0
C. 4x+y+9=0 D. 4x+y-9=0
4 过点A(1,2)的直线在两坐标轴上的截距之和为零,则该直线方程为( )
A. x-y+1=0
B. x+y-1=0
C. 2x-y=0或x-y+1=0
D. 2x+y=0或x+y+1=0
5 直线l经过点P(4,-3),在x轴上的截距为a,在y轴上的截距为b,且a,b满足logab=2,则直线l的斜率为( )
A. 2 B. -1
C. -3 D. -1或-3
6已知直线(a+2)x-y+2a-3=0在x轴上的截距是y轴上截距的2倍,则实数a的值为( )
A. B. -
C. 或- D. -
7 已知直线l经过点P(1,2),与两坐标轴的正半轴分别交于A,B两点,O为坐标原点,则△OAB面积的最小值为( )
A. 2 B. 3
C. 4 D. 8
8 瑞士数学家欧拉在《三角形的几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上.这条直线被称为欧拉线.已知△ABC的顶点A(-3,0),B(3,0),C(3,3),则△ABC的欧拉线的方程为( )
A. 2x-y-1=0 B. 2x+y-=0
C. x+2y-3=0 D. x-2y+1=0
二、 多项选择题
9 过定点(2,3)且在两坐标轴上截距的绝对值相等的直线为( )
A. 3x-2y=0
B. x+y-5=0
C. x-y+1=0
D. x-y-5=0
10 已知直线l过点(0,2),(,1),则下列结论中正确的是( )
A. 直线l的倾斜角为150°
B. 直线l的两点式方程为=
C. 直线l的一个方向向量为(1,-)
D. 直线l的截距式方程为+=1
三、填空题
11 已知直线l的两点式方程为=,则直线l的斜率为________.
12已知直线l在x轴与y轴上的截距分别为4,9,若点E(1,b)在直线l上,则实数b=________.
13 已知△ABC的顶点坐标分别为A(4,3),B(-2,-5),C(8,0),则角A的平分线所在的直线方程为________.
四、解答题
14 过点P(2,1)作直线l分别交x轴,y轴的正半轴于A,B两点.
(1) 求△ABO面积的最小值及相应的直线l的方程;
(2) 当OA+OB取最小值时,求直线l的方程.
15 已知点A(3,4).
(1) 求经过点A(3,4),且在x轴上的截距是y轴上截距的2倍的直线的方程;
(2) 光线自点A(3,4)射到y轴上的点B(0,1)后被y轴反射,求反射光线所在直线的方程.
16 已知三角形的三个顶点是A(4,0),B(6,7),C(0,3).
(1) 求边AC所在的直线方程;
(2) 求边AC上的高所在的直线方程;
(3) 求经过两边AB和BC中点的直线的方程.
2.2.2 直线的两点式方程
1. B 易知直线-=1的斜率为,直线-=1的斜率为,所以两直线的倾斜角同为锐角或者同为钝角,且斜率的绝对值一个大于1,一个小于1,故只有B满足题意.
2. B 设直线l的方程为+=1(a≠0),将点代入,可得+=1(a≠0),即3a2-6a+2=0.因为Δ=36-4×3×2=12>0,所以方程3a2-6a+2=0有两个不相等的实数根,故满足题意的直线l的条数为2.
3. D 由题意,得解得m=1,n=-3,即点A(1,5),B(3,-3). 将点A,B的坐标代入两点式方程可得=,即4x+y-9=0.
4. C 当直线过原点时在两坐标轴上的截距都为0,满足题意.因为直线过点A(1,2),所以直线的斜率为=2,所以直线方程为y=2x,即2x- y=0;当直线不过原点时,设直线方程为+= 1,因为点A(1,2)在直线上,所以+=1,解得a=-1,所以直线方程为x-y+1=0.故所求直线方程为2x-y=0或x-y+1=0.
5. C 由题意,设直线l的方程为+=1,则+=1①.又logab=2,所以b=a2②.由①②解得a=3,b=9或a=1,b=1.又由logab=2可知a>0,a≠1,b>0,所以a=3,b=9,则直线l的斜率为-=-3.
6. C 由题意,得a≠-2,当a=时,直线l为x-y=0,此时横、纵截距都等于0,满足题意;当a≠时,将直线l的方程化为截距式方程可得+=1,直线l在x轴上的截距为,在y轴上截距为2a-3,则=2×(2a-3),解得a=-或a=(舍去).综上,实数a的值为-或.
7. C 不妨设直线l分别交x轴,y轴于点A(a,0),B(0,b),则a>0,b>0,所以直线l的截距式方程为+=1.因为点P在直线l上,所以+=1,由基本不等式可得1=+≥2=,可得ab≥8,则S△OAB=ab≥4,当且仅当,即时,等号成立,故△OAB面积的最小值为4.
8. C 由△ABC的顶点A(-3,0),B(3,0),C(3,3)知,△ABC的重心为,即(1,1).因为BC⊥AB,所以△ABC为直角三角形,所以外心为斜边的中点, 即,所以△ABC的欧拉线的方程为=,即x+2y-3=0.
9. ABC 由题意,得直线不与坐标轴垂直,设所求的直线方程为y=k(x-2)+3,当y=0时,横截距为x=2-,当x=0时,纵截距为y=3-2k.因为过点(2,3)的直线在两坐标轴上截距的绝对值相等,所以=|3-2k|,解得k=-1或k=或k=1,所以直线的方程为x+y-5=0或3x-2y=0或x-y+1=0.故选ABC.
10. ABD 因为直线l过点(0,2),(,1),所以直线l的斜率为=-,倾斜角为150°,故A正确,C错误;直线l的两点式方程为=,整理,得截距式方程为+=1,故B,D正确.故选ABD.
11. - 原方程可化为=-x,即y=-x-3,所以直线l的斜率为-.
12. 由题意,得直线的截距式方程为+=1.又点E(1,b)在直线l上,所以+=1,解得b=.
13. 7x+y-31=0 如图,角A的平分线与BC交于点D.由题意,得AB==10,AC==5.由角平分线定理,得==2,所以=.设点D的坐标为(x,y),则(x-8,y-0)=(-2-8,-5),所以x-8=-,y=-,即点D,所以直线AD的方程为=,整理,得7x+y-31=0.
14. (1) 显然直线 l斜率存在且不过原点.
由题意可设直线 l的方程为+=1(a>0,b>0),
又点P(2,1)在直线 l上,所以+=1,
由基本不等式可得+=1≥2,
即ab≥8,当且仅当a=4,b=2时,等号成立.
又S△ABO=OA·OB=ab,
所以S△ABO=ab≥×8=4,当且仅当a=4,b=2时,等号成立,
此时相应的直线 l的方程为x+2y-4=0.
(2) 由(1)可知+=1(a>0,b>0).
又OA+OB=a+b,
所以OA+OB=a+b=(a+b)=3++ ≥3+2,
当且仅当a=2+,b=+1时,等号成立,
此时相应的直线 l的方程为x+y-2-=0.
15. (1) 当直线过原点时,满足在x轴上的截距是y轴上截距的2倍,
此时直线方程为y=kx,将点A(3,4)代入,
可得k=,化简可得4x-3y=0;
当直线不过原点时,设直线方程为+=1,且a=2b,
即+=1,将点A(3,4)代入,
可得+=1,解得b=,
则直线方程为+=1,化简可得x+2y-11=0.
综上,直线方程为4x-3y=0或x+2y-11=0.
(2) 点A关于y轴的对称点的坐标为A′(-3,4).
由题意可知,反射光线所在的直线经过点A′(-3,4),B(0,1),
所以反射光线所在的直线斜率为kA′B==-1,
故反射光线所在的直线方程为y-1=-1(x-0),即x+y-1=0.
16. (1) 由题意可知点A(4,0),C(0,3),
则由直线的截距式方程可得+=1,即3x+4y-12=0.
(2) 设高所在的直线方程的斜率为k,直线AC斜率为kAC,
由(1)可知直线AC的斜率为kAC=-.
因为高所在的直线的斜率与直线AC的斜率的乘积为-1,
即k·kAC=-1,则k=.
又由点斜式方程可得y-7=(x-6),
所以高所在的直线方程为3y-4x+3=0.
(3) 设AB和BC的中点分别为D(x1,y1),E(x2,y2).
因为A(4,0),B(6,7),C(0,3),
所以x1==5,y1==,x2==3,y2==5,
则由点斜式方程可得直线DE的方程为y-5=(x-3),
即4y+3x-29=0.
