专题一 空间向量的综合应用(含答案) 高二数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 专题一 空间向量的综合应用(含答案) 高二数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | docx | ||
| 文件大小 | 308.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 21:33:56 | ||
图片预览




文档简介
空间向量的综合应用
一、 单项选择题
1 如图,在正三棱柱ABC-A1B1C1中,若AB=BB1=2,则点C到直线AB1的距离为( )
A. B. C. D.
2 设平面α的法向量为n,直线l的方向向量为m,则“〈m,n〉=60°”是“直线l与平面α的夹角为30°”的( )
A. 充分不必要条件
B. 必要不充分条件
C. 充要条件
D. 既不充分也不必要条件
3 阅读材料:在空间直角坐标系O-xyz中,过点P(x0,y0,z0)且一个法向量为n=(a,b,c)的平面α的方程为a(x-x0)+b(y-y0)+c(z-z0)=0,阅读上面材料,解决下面问题:已知平面α的方程为2x-y+z=2,点M(-1,2,1),则点M到平面α的距离为( )
A. B. C. D.
4 如图,在四棱锥A-BCDE中,AD⊥平面BCDE,底面BCDE为直角梯形,DE∥BC,∠CDE=90°,BC=3,CD=DE=2,AD=4.则点E到平面ABC的距离为( )
A. B. C. D. 2
(第4题) (第5题)
5 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F,G分别为BC,CC1,BB1的中点,则下列说法中正确的是( )
A. 直线D1D与直线AF垂直
B. 直线A1G与平面AEF平行
C. 三棱锥F-ABE的体积为
D. 直线BC与平面AEF所成的角为45°
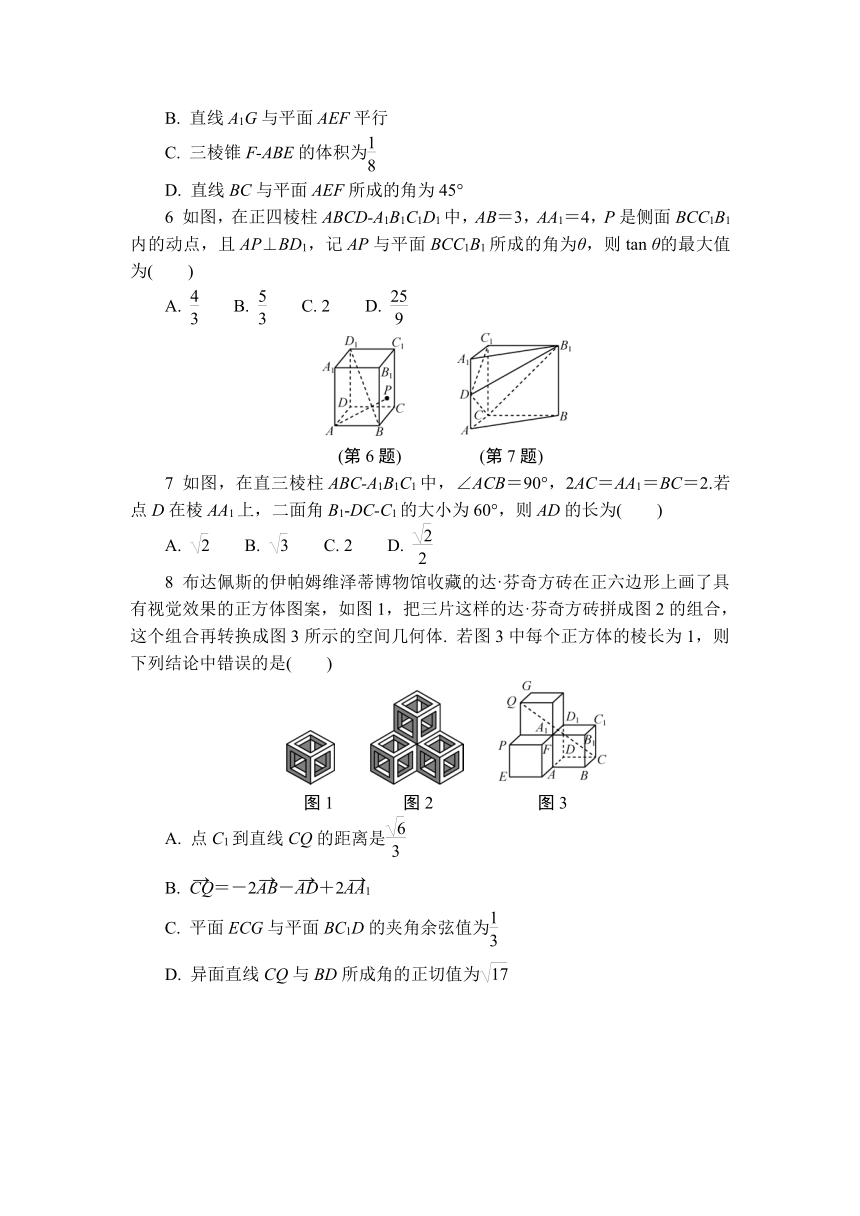
6 如图,在正四棱柱ABCD-A1B1C1D1中,AB=3,AA1=4,P是侧面BCC1B1内的动点,且AP⊥BD1,记AP与平面BCC1B1所成的角为θ,则tan θ的最大值为( )
A. B. C. 2 D.
(第6题) (第7题)
7 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2.若点D在棱AA1上,二面角B1-DC-C1的大小为60°,则AD的长为( )
A. B. C. 2 D.
8 布达佩斯的伊帕姆维泽蒂博物馆收藏的达·芬奇方砖在正六边形上画了具有视觉效果的正方体图案,如图1,把三片这样的达·芬奇方砖拼成图2的组合,这个组合再转换成图3所示的空间几何体. 若图3中每个正方体的棱长为1,则下列结论中错误的是( )
图1 图2 图3
A. 点C1到直线CQ的距离是
B. =-2-+2
C. 平面ECG与平面BC1D的夹角余弦值为
D. 异面直线CQ与BD所成角的正切值为
二、 多项选择题
9在空间直角坐标系O-xyz中,已知点A(2,0,0),B(1,1,-2),C(2,3,1),则下列说法中正确的有( )
A. ·=-3
B. 异面直线OB与AC所成角的余弦值为
C. ||=
D. 点C到直线AB的距离为
10如图,AE⊥平面ABCD,CF∥AE,AD∥BC,AD⊥AB,AE=BC=2,AB=AD=1,CF=,则下列说法中正确的是( )
A. BD⊥EC
B. BF∥平面ADE
C. 平面EBD与平面ABCD夹角的余弦值为
D. 直线CE与平面BDE所成角的正弦值为
三、填空题
11 如图,在正三棱柱ABC-A1B1C1中,AB=AA1,则A1B与B1C所成角的余弦值为________.
(第11题) (第12题)
12(涟水一中月考)如图,在四棱锥P-ABCD中,PB⊥平面ABCD,AB⊥BC,PB=AB=2BC=2,则点C到直线PA的距离为________.
13 在三棱锥P-ABC中,PA,AB,AC两两垂直,D为棱PC上一动点,PA=AC=2,AB=3.当BD与平面PAC所成角最大时,AD与平面PBC所成角的正弦值为________.
四、 解答题
14如图,在几何体B-ACDE中,CD∥AE,∠EAC=90°,平面EACD⊥平面ABC,CD=2EA=2,AB=AC=2,BC=2,F为BD的中点.
(1) 求证:EF∥平面ABC;
(2) 求直线AB与平面BDE所成角的正弦值.
15 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠DAB=60°,PD⊥底面ABCD,F为棱PD的中点,二面角D-FC-B的余弦值为.
(1) 求PD的长;
(2) 求异面直线BF与PA所成角的余弦值;
(3) 求直线AF与平面BCF所成角的正弦值.
16 如图,已知SA垂直于梯形ABCD所在的平面,矩形SADE的对角线交于点F,G为SB的中点,∠ABC=∠BAD=,SA=AB=BC=AD=1.
(1) 求证:BD∥平面AEG;
(2) 求二面角C-SD-E的余弦值;
(3) 在线段EG上是否存在一点H,使得BH与平面SCD所成角的大小为?若存在,求出GH的长;若不存在,请说明理由.
1.4.3 空间向量的综合应用
1. D 因为AB=BB1=2,所以BB1=,取AC的中点O,连接BO,则BO⊥AC,BO=,建立如图所示的空间直角坐标系O-xyz,则A(0,-1,0),B1(,0,),C(0,1,0),所以=(,1,)=(0,-2,0),所以在上的投影的长度为==,所以点C到直线AB1的距离为d==.
2. A 若直线l与平面α的夹角为30°,平面α的法向量为n,直线l的方向向量为m,则〈m,n〉=60°或120°,故“〈m,n〉=60°”是“直线l与平面α的夹角为30°”的充分不必要条件.
3. C 由题意可知平面α的法向量为n=(2,-1,1),在平面α上任取一点A(0,0,2),则=(1,-2,1),所以点M到平面α的距离为d====.
4. C 由题意,以D为坐标原点,DE,DC,DA所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,则E(2,0,0),A(0,0,4),B(3,2,0),C(0,2,0),所以=(2,0,-4),=(3,2,-4),=(0,2,-4).设平面ABC的法向量为n=(x,y,z),则令z=1,则x=0,y=2,所以n=(0,2,1),所以点E到平面ABC的距离为d===.
5. B 对于A,因为ABCD-A1B1C1D1为正方体,所以DD1∥CC1,直线AF与直线CC1不垂直,所以直线AF与直线DD1不垂直,故A错误;如图,建立空间直角坐标系,则A(1,0,0),E(,1,0),F(0,1,),G,A1(1,0,1),对于B,设平面AEF的法向量为n=(x,y,z).又=,=,所以令y=1,则x=2,z=2,所以n=(2,1,2).因为=,所以·n=0×2+1×1-×2=0,所以⊥n.因为A1G在平面AEF外,所以直线A1G与平面AEF平行,故B正确;对于C,因为S△ABE=BE·AB=×1×=,所以三棱锥F-ABE的体积为S△AEB·d=××=,故C错误;对于D,因为B(1,1,0),C(0,1,0),所以=(-1,0,0),设直线BC与平面AEF所成的角为θ,则sin θ===,故D错误.
6. B 以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系.设P(x,3,z),A(3,0,0),B(3,3,0),D1(0,0,4),则=(x-3,3,z),=(-3,-3,4),因为AP⊥BD1,所以·=-3(x-3)-3×3+4z=0,所以z=x,所以BP===≥.连接BP,易知AB⊥平面BCC1B1,所以AP与平面BCC1B1所成的角即为∠APB,所以tan θ=≤,所以tan θ的最大值为.
7. A 以C为坐标原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴建立如图直角坐标系,设AD=t,则C(0,0,0),D(1,0,t),B1(0,2,2),C1(0,0,2),易知平面CDC1的法向量为=(0,2,0).设平面CDB1的法向量为m=(x,y,z),则 即令z=-1,则x=t,y=1,所以平面 CDB1的法向量为m=(t,1,-1),则cos 60°= ==,解得t=.
8. A 由题意,得=+=-+2=-+2(-)=-2-+2,故B正确;如图,以A1为坐标原点,建立空间直角坐标系,则B1(0,1,0),C1(-1,1,0),D1(-1,0,0),Q(0,-1,1),C(-1,1,-1),E(1,-1,-1),G(-1,-1,1),B(0,1,-1),D(-1,0,-1),所以=(-2,0,2),=(-2,2,0),=(-1,-1,0),=(-1,0,1).设平面ECG的法向量为n1=(x,y,z),则令x=1,则y=1,z=1,故平面ECG的一个法向量 n1=(1,1,1),设平面BC1D的法向量为n2=(a,b,c),则令a=1,则b=-1,c=1,故平面BC1D的一个法向量为n2=(1,-1,1),则|cos 〈n1,n2〉|==,故C正确;因为=(-1,-1,0),=(1,-2,2),所以cos 〈,〉==,所以tan 〈,〉=,故D正确;因为=(-1,2,-1),设m==,所以点C1到直线CQ的距离为d===,故A错误.
9. BC 因为=(-1,1,-2),=(1,2,3),所以·=-1+2-6=-5,故A错误;因为=(1,1,-2),=(0,3,1),所以||==,故C正确;cos 〈,〉===,故B正确;点C到直线AB的距离为==,故D错误.故选BC.
10. BCD 由题意可知AE,AB,AD两两垂直,以A为坐标原点,AB,AD,AE所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,则B(1,0,0),C(1,2,0),D(0,1,0),E(0,0,2),F(1,2,),则=(-1,1,0),=(1,2,-2),=(-1,0,2),所以·=-1×1+1×2+0×(-2)=1≠0,所以BD,EC不垂直,故A错误;由题意,得=(1,0,0)是平面ADE的法向量.又=,所以·=0,则BF⊥AB.又因为直线BF 平面ADE,所以BF∥平面ADE,故B正确;设m=(a,b,c)为平面BDE的一个法向量,则令b=2,则a=2,c=1,所以m=(2,2,1).又易知底面ABCD的一个法向量为=(0,0,2),设平面EBD与平面ABCD夹角为α,则cos α=|cos 〈m,〉|===,故C正确;设直线CE与平面BDE所成角为θ,=(-1,-2,2),则sin θ=|cos 〈,m〉|==,故D正确.故选BCD.
11. 0 以A为坐标原点,在平面ABC内过点A作AC的垂线为x轴,AC所在直线为y轴,AA1所在直线为z轴,建立如图所示的空间直角坐标系,在正三棱柱ABC-A1B1C1中,设AA1=,AB=2,则A(0,0,0),A1(0,0,),B(,1,0),B1(,1,),C(0,2,0),所以=(,1,-),=(-,1,-).设异面直线A1B与B1C所成的角为θ,则θ∈,所以cos θ===0,所以异面直线A1B与B1C所成角的余弦值为0.
12. 由题意,以B为坐标原点,BC,BA,BP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,则C(1,0,0),A(0,2,0),P(0,0,2),所以=(1,0,-2),=(0,2,-2),即·=4,||=,所以在上的投影向量的长度为==,故点C到直线PA的距离为=.
13. 易证AB⊥平面PAC,则BD与平面PAC所成角为∠ADB,则tan ∠ADB==,当AD取得最小值时,∠ADB取得最大值.在等腰直角三角形△PAC中,当D为PC的中点时,AD取得最小值,以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(3,0,0),C(0,2,0),P(0,0,2),D(0,1,1),则=(0,1,1),=(0,2,-2),=(-3,2,0).设平面PBC的法向量为n=(x,y,z),则即令y=3,则x=2,z=3,所以n=(2,3,3).因为cos 〈n,〉==,所以AD与平面PBC所成角的正弦值为.
14. (1) 取BC的中点G,连接FG,AG.
因为F为BD的中点,CD=2EA,CD∥AE,
所以FG=CD=EA,且FG∥CD∥AE,
所以四边形AGFE是平行四边形,
所以EF∥AG.
又EF 平面ABC,AG 平面ABC,
所以EF∥平面ABC.
(2) 因为∠EAC=90°,平面EACD⊥平面ABC,平面EACD∩平面ABC=AC,EA 平面EACD,
所以EA⊥平面ABC,
由(1)可知FG∥AE,
所以FG⊥平面ABC.
又AB=AC,G为BC的中点,
所以AG⊥BC,所以GA,GB,GF两两垂直.
以G为坐标原点,GA,GB,GF所在直线分别为 x轴,y轴,z轴,建立如图所示的空间直角坐标系,
则A(1,0,0),B(0,,0),D(0,-,2),E(1,0,1),
所以=(-1,,0),=(0,-2,2),=(1,-,1).
设平面BDE的法向量为n=(x,y,z),
则即
令y=1,得n=(0,1,),
设直线AB与平面BDE所成的角为α,
则sin α=|cos 〈,n〉|==.
所以直线AB与平面BDE所成角的正弦值为.
15. (1) 取AB的中点M,连接DM,易知DM⊥DC,以D为坐标原点,DM,DC,DP所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.
设FD=a,则D(0,0,0),F(0,0,a),C(0,2,0),B(,1,0),A(,-1,0),
所以=(0,2,-a),=(,-1,0).
设平面BCF的法向量为m=(x,y,z).
由令x=1,则y=,z=,所以m=.
取平面DFC的一个法向量为n=(1,0,0).
由题意,得|cos 〈m,n〉|===,解得a=,
所以PD=2FD=2.
(2) 由题意,得P(0,0,2),=(,1,-),=(,-1,-2).
设异面直线BF与PA所成的角为θ1,
则cos θ1=|cos 〈,〉|===,
即异面直线BF与PA所成角的余弦值为.
(3) 由题意,得=(,-1,-).
设直线AF与平面BCF所成的角为θ2,
则sin θ2=|cos 〈m,〉|=== ,
即直线AF与平面BCF所成角的正弦值为.
16. (1) 连接FG.
在△SBD中,F,G分别为SD,SB的中点,
所以FG∥BD.
又因为FG 平面AEG,BD 平面AEG,
所以BD∥平面AEG.
(2) 因为SA⊥平面ABCD,AB 平面ABCD,AD 平面ABCD,
所以SA⊥AB,SA⊥AD.
又∠BAD=,所以AB⊥AD,
以{,,}为正交基底,建立空间直角坐标系A-xyz,
则A(0,0,0),B(1,0,0),C(1,1,0),D(0,2,0),S(0,0,1),E(0,2,1),G,
所以=(-1,1,0),=(1,1,-1).
设平面SCD的法向量为m=(x,y,z),
则 即
令x=1,得y=1,z=2,
所以平面SCD的一个法向量为m=(1,1,2).
易知平面ESD的一个法向量为=(1,0,0),
所以cos 〈m,〉===,
又由图可知,二面角C-SD-E为钝二面角,故二面角C-SD-E的余弦值为-.
(3) 存在,理由如下:
假设存在点H,设=λ=,
则=+λ=,
由(2)知,平面SCD的一个法向量为m=(1,1,2),
则sin =|cos 〈m,〉|===,
解得λ=1,
则==,
故存在满足题意的点H,此时GH=||=.
一、 单项选择题
1 如图,在正三棱柱ABC-A1B1C1中,若AB=BB1=2,则点C到直线AB1的距离为( )
A. B. C. D.
2 设平面α的法向量为n,直线l的方向向量为m,则“〈m,n〉=60°”是“直线l与平面α的夹角为30°”的( )
A. 充分不必要条件
B. 必要不充分条件
C. 充要条件
D. 既不充分也不必要条件
3 阅读材料:在空间直角坐标系O-xyz中,过点P(x0,y0,z0)且一个法向量为n=(a,b,c)的平面α的方程为a(x-x0)+b(y-y0)+c(z-z0)=0,阅读上面材料,解决下面问题:已知平面α的方程为2x-y+z=2,点M(-1,2,1),则点M到平面α的距离为( )
A. B. C. D.
4 如图,在四棱锥A-BCDE中,AD⊥平面BCDE,底面BCDE为直角梯形,DE∥BC,∠CDE=90°,BC=3,CD=DE=2,AD=4.则点E到平面ABC的距离为( )
A. B. C. D. 2
(第4题) (第5题)
5 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F,G分别为BC,CC1,BB1的中点,则下列说法中正确的是( )
A. 直线D1D与直线AF垂直
B. 直线A1G与平面AEF平行
C. 三棱锥F-ABE的体积为
D. 直线BC与平面AEF所成的角为45°
6 如图,在正四棱柱ABCD-A1B1C1D1中,AB=3,AA1=4,P是侧面BCC1B1内的动点,且AP⊥BD1,记AP与平面BCC1B1所成的角为θ,则tan θ的最大值为( )
A. B. C. 2 D.
(第6题) (第7题)
7 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2.若点D在棱AA1上,二面角B1-DC-C1的大小为60°,则AD的长为( )
A. B. C. 2 D.
8 布达佩斯的伊帕姆维泽蒂博物馆收藏的达·芬奇方砖在正六边形上画了具有视觉效果的正方体图案,如图1,把三片这样的达·芬奇方砖拼成图2的组合,这个组合再转换成图3所示的空间几何体. 若图3中每个正方体的棱长为1,则下列结论中错误的是( )
图1 图2 图3
A. 点C1到直线CQ的距离是
B. =-2-+2
C. 平面ECG与平面BC1D的夹角余弦值为
D. 异面直线CQ与BD所成角的正切值为
二、 多项选择题
9在空间直角坐标系O-xyz中,已知点A(2,0,0),B(1,1,-2),C(2,3,1),则下列说法中正确的有( )
A. ·=-3
B. 异面直线OB与AC所成角的余弦值为
C. ||=
D. 点C到直线AB的距离为
10如图,AE⊥平面ABCD,CF∥AE,AD∥BC,AD⊥AB,AE=BC=2,AB=AD=1,CF=,则下列说法中正确的是( )
A. BD⊥EC
B. BF∥平面ADE
C. 平面EBD与平面ABCD夹角的余弦值为
D. 直线CE与平面BDE所成角的正弦值为
三、填空题
11 如图,在正三棱柱ABC-A1B1C1中,AB=AA1,则A1B与B1C所成角的余弦值为________.
(第11题) (第12题)
12(涟水一中月考)如图,在四棱锥P-ABCD中,PB⊥平面ABCD,AB⊥BC,PB=AB=2BC=2,则点C到直线PA的距离为________.
13 在三棱锥P-ABC中,PA,AB,AC两两垂直,D为棱PC上一动点,PA=AC=2,AB=3.当BD与平面PAC所成角最大时,AD与平面PBC所成角的正弦值为________.
四、 解答题
14如图,在几何体B-ACDE中,CD∥AE,∠EAC=90°,平面EACD⊥平面ABC,CD=2EA=2,AB=AC=2,BC=2,F为BD的中点.
(1) 求证:EF∥平面ABC;
(2) 求直线AB与平面BDE所成角的正弦值.
15 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠DAB=60°,PD⊥底面ABCD,F为棱PD的中点,二面角D-FC-B的余弦值为.
(1) 求PD的长;
(2) 求异面直线BF与PA所成角的余弦值;
(3) 求直线AF与平面BCF所成角的正弦值.
16 如图,已知SA垂直于梯形ABCD所在的平面,矩形SADE的对角线交于点F,G为SB的中点,∠ABC=∠BAD=,SA=AB=BC=AD=1.
(1) 求证:BD∥平面AEG;
(2) 求二面角C-SD-E的余弦值;
(3) 在线段EG上是否存在一点H,使得BH与平面SCD所成角的大小为?若存在,求出GH的长;若不存在,请说明理由.
1.4.3 空间向量的综合应用
1. D 因为AB=BB1=2,所以BB1=,取AC的中点O,连接BO,则BO⊥AC,BO=,建立如图所示的空间直角坐标系O-xyz,则A(0,-1,0),B1(,0,),C(0,1,0),所以=(,1,)=(0,-2,0),所以在上的投影的长度为==,所以点C到直线AB1的距离为d==.
2. A 若直线l与平面α的夹角为30°,平面α的法向量为n,直线l的方向向量为m,则〈m,n〉=60°或120°,故“〈m,n〉=60°”是“直线l与平面α的夹角为30°”的充分不必要条件.
3. C 由题意可知平面α的法向量为n=(2,-1,1),在平面α上任取一点A(0,0,2),则=(1,-2,1),所以点M到平面α的距离为d====.
4. C 由题意,以D为坐标原点,DE,DC,DA所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,则E(2,0,0),A(0,0,4),B(3,2,0),C(0,2,0),所以=(2,0,-4),=(3,2,-4),=(0,2,-4).设平面ABC的法向量为n=(x,y,z),则令z=1,则x=0,y=2,所以n=(0,2,1),所以点E到平面ABC的距离为d===.
5. B 对于A,因为ABCD-A1B1C1D1为正方体,所以DD1∥CC1,直线AF与直线CC1不垂直,所以直线AF与直线DD1不垂直,故A错误;如图,建立空间直角坐标系,则A(1,0,0),E(,1,0),F(0,1,),G,A1(1,0,1),对于B,设平面AEF的法向量为n=(x,y,z).又=,=,所以令y=1,则x=2,z=2,所以n=(2,1,2).因为=,所以·n=0×2+1×1-×2=0,所以⊥n.因为A1G在平面AEF外,所以直线A1G与平面AEF平行,故B正确;对于C,因为S△ABE=BE·AB=×1×=,所以三棱锥F-ABE的体积为S△AEB·d=××=,故C错误;对于D,因为B(1,1,0),C(0,1,0),所以=(-1,0,0),设直线BC与平面AEF所成的角为θ,则sin θ===,故D错误.
6. B 以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系.设P(x,3,z),A(3,0,0),B(3,3,0),D1(0,0,4),则=(x-3,3,z),=(-3,-3,4),因为AP⊥BD1,所以·=-3(x-3)-3×3+4z=0,所以z=x,所以BP===≥.连接BP,易知AB⊥平面BCC1B1,所以AP与平面BCC1B1所成的角即为∠APB,所以tan θ=≤,所以tan θ的最大值为.
7. A 以C为坐标原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴建立如图直角坐标系,设AD=t,则C(0,0,0),D(1,0,t),B1(0,2,2),C1(0,0,2),易知平面CDC1的法向量为=(0,2,0).设平面CDB1的法向量为m=(x,y,z),则 即令z=-1,则x=t,y=1,所以平面 CDB1的法向量为m=(t,1,-1),则cos 60°= ==,解得t=.
8. A 由题意,得=+=-+2=-+2(-)=-2-+2,故B正确;如图,以A1为坐标原点,建立空间直角坐标系,则B1(0,1,0),C1(-1,1,0),D1(-1,0,0),Q(0,-1,1),C(-1,1,-1),E(1,-1,-1),G(-1,-1,1),B(0,1,-1),D(-1,0,-1),所以=(-2,0,2),=(-2,2,0),=(-1,-1,0),=(-1,0,1).设平面ECG的法向量为n1=(x,y,z),则令x=1,则y=1,z=1,故平面ECG的一个法向量 n1=(1,1,1),设平面BC1D的法向量为n2=(a,b,c),则令a=1,则b=-1,c=1,故平面BC1D的一个法向量为n2=(1,-1,1),则|cos 〈n1,n2〉|==,故C正确;因为=(-1,-1,0),=(1,-2,2),所以cos 〈,〉==,所以tan 〈,〉=,故D正确;因为=(-1,2,-1),设m==,所以点C1到直线CQ的距离为d===,故A错误.
9. BC 因为=(-1,1,-2),=(1,2,3),所以·=-1+2-6=-5,故A错误;因为=(1,1,-2),=(0,3,1),所以||==,故C正确;cos 〈,〉===,故B正确;点C到直线AB的距离为==,故D错误.故选BC.
10. BCD 由题意可知AE,AB,AD两两垂直,以A为坐标原点,AB,AD,AE所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,则B(1,0,0),C(1,2,0),D(0,1,0),E(0,0,2),F(1,2,),则=(-1,1,0),=(1,2,-2),=(-1,0,2),所以·=-1×1+1×2+0×(-2)=1≠0,所以BD,EC不垂直,故A错误;由题意,得=(1,0,0)是平面ADE的法向量.又=,所以·=0,则BF⊥AB.又因为直线BF 平面ADE,所以BF∥平面ADE,故B正确;设m=(a,b,c)为平面BDE的一个法向量,则令b=2,则a=2,c=1,所以m=(2,2,1).又易知底面ABCD的一个法向量为=(0,0,2),设平面EBD与平面ABCD夹角为α,则cos α=|cos 〈m,〉|===,故C正确;设直线CE与平面BDE所成角为θ,=(-1,-2,2),则sin θ=|cos 〈,m〉|==,故D正确.故选BCD.
11. 0 以A为坐标原点,在平面ABC内过点A作AC的垂线为x轴,AC所在直线为y轴,AA1所在直线为z轴,建立如图所示的空间直角坐标系,在正三棱柱ABC-A1B1C1中,设AA1=,AB=2,则A(0,0,0),A1(0,0,),B(,1,0),B1(,1,),C(0,2,0),所以=(,1,-),=(-,1,-).设异面直线A1B与B1C所成的角为θ,则θ∈,所以cos θ===0,所以异面直线A1B与B1C所成角的余弦值为0.
12. 由题意,以B为坐标原点,BC,BA,BP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,则C(1,0,0),A(0,2,0),P(0,0,2),所以=(1,0,-2),=(0,2,-2),即·=4,||=,所以在上的投影向量的长度为==,故点C到直线PA的距离为=.
13. 易证AB⊥平面PAC,则BD与平面PAC所成角为∠ADB,则tan ∠ADB==,当AD取得最小值时,∠ADB取得最大值.在等腰直角三角形△PAC中,当D为PC的中点时,AD取得最小值,以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(3,0,0),C(0,2,0),P(0,0,2),D(0,1,1),则=(0,1,1),=(0,2,-2),=(-3,2,0).设平面PBC的法向量为n=(x,y,z),则即令y=3,则x=2,z=3,所以n=(2,3,3).因为cos 〈n,〉==,所以AD与平面PBC所成角的正弦值为.
14. (1) 取BC的中点G,连接FG,AG.
因为F为BD的中点,CD=2EA,CD∥AE,
所以FG=CD=EA,且FG∥CD∥AE,
所以四边形AGFE是平行四边形,
所以EF∥AG.
又EF 平面ABC,AG 平面ABC,
所以EF∥平面ABC.
(2) 因为∠EAC=90°,平面EACD⊥平面ABC,平面EACD∩平面ABC=AC,EA 平面EACD,
所以EA⊥平面ABC,
由(1)可知FG∥AE,
所以FG⊥平面ABC.
又AB=AC,G为BC的中点,
所以AG⊥BC,所以GA,GB,GF两两垂直.
以G为坐标原点,GA,GB,GF所在直线分别为 x轴,y轴,z轴,建立如图所示的空间直角坐标系,
则A(1,0,0),B(0,,0),D(0,-,2),E(1,0,1),
所以=(-1,,0),=(0,-2,2),=(1,-,1).
设平面BDE的法向量为n=(x,y,z),
则即
令y=1,得n=(0,1,),
设直线AB与平面BDE所成的角为α,
则sin α=|cos 〈,n〉|==.
所以直线AB与平面BDE所成角的正弦值为.
15. (1) 取AB的中点M,连接DM,易知DM⊥DC,以D为坐标原点,DM,DC,DP所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.
设FD=a,则D(0,0,0),F(0,0,a),C(0,2,0),B(,1,0),A(,-1,0),
所以=(0,2,-a),=(,-1,0).
设平面BCF的法向量为m=(x,y,z).
由令x=1,则y=,z=,所以m=.
取平面DFC的一个法向量为n=(1,0,0).
由题意,得|cos 〈m,n〉|===,解得a=,
所以PD=2FD=2.
(2) 由题意,得P(0,0,2),=(,1,-),=(,-1,-2).
设异面直线BF与PA所成的角为θ1,
则cos θ1=|cos 〈,〉|===,
即异面直线BF与PA所成角的余弦值为.
(3) 由题意,得=(,-1,-).
设直线AF与平面BCF所成的角为θ2,
则sin θ2=|cos 〈m,〉|=== ,
即直线AF与平面BCF所成角的正弦值为.
16. (1) 连接FG.
在△SBD中,F,G分别为SD,SB的中点,
所以FG∥BD.
又因为FG 平面AEG,BD 平面AEG,
所以BD∥平面AEG.
(2) 因为SA⊥平面ABCD,AB 平面ABCD,AD 平面ABCD,
所以SA⊥AB,SA⊥AD.
又∠BAD=,所以AB⊥AD,
以{,,}为正交基底,建立空间直角坐标系A-xyz,
则A(0,0,0),B(1,0,0),C(1,1,0),D(0,2,0),S(0,0,1),E(0,2,1),G,
所以=(-1,1,0),=(1,1,-1).
设平面SCD的法向量为m=(x,y,z),
则 即
令x=1,得y=1,z=2,
所以平面SCD的一个法向量为m=(1,1,2).
易知平面ESD的一个法向量为=(1,0,0),
所以cos 〈m,〉===,
又由图可知,二面角C-SD-E为钝二面角,故二面角C-SD-E的余弦值为-.
(3) 存在,理由如下:
假设存在点H,设=λ=,
则=+λ=,
由(2)知,平面SCD的一个法向量为m=(1,1,2),
则sin =|cos 〈m,〉|===,
解得λ=1,
则==,
故存在满足题意的点H,此时GH=||=.
