广西大学附中2024-2025学年九年级(下)第九次段考中考模拟数学试卷(含答案)
文档属性
| 名称 | 广西大学附中2024-2025学年九年级(下)第九次段考中考模拟数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 178.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 19:00:34 | ||
图片预览



文档简介
2024-2025学年广西大学附中九年级(下)第九次段考中考模拟数学试卷
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的相反数为( )
A. B. C. D.
2.下列图形均表示医疗或救援的标识,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.据统计,年我国新能源汽车产量超过万辆,其中万用科学记数法表示为( )
A. B. C. D.
4.下列几何体中,其俯视图与主视图完全相同的是( )
A. B. C. D.
5.成语是中国语言文化的缩影,有着深厚丰富的文化底蕴,学习成语,运用成语,了解成语当中所包含的语言文化现象,是我们学习语言、学习中国传统文化必不可少的一个环节和目的下列成语所描述的事件中,属于必然事件的是( )
A. 百步穿杨 B. 缘木求鱼 C. 旭日东升 D. 拔苗助长
6.下列计算正确的是( )
A. B. C. D.
7.如图,点在的延长线上,下列条件能判断的是( )
A.
B.
C.
D.
8.如图,已知一次函数的图象分别与、轴交于、两点,若,,则关于的方程的解为( )
A. B. C. D.
9.若满足,则代数式的值为( )
A. B. C. D.
10.“我市为处理污水,需要铺设一条长为米的管道,为了尽量减少施工对交通所造成的影响,实际施工时每天比原计划多铺设米,结果提前天完成任务”根据题意可得方程,则方程中表示( )
A. 实际每天铺设管道的长度 B. 实际施工的天数
C. 原计划每天铺设管道的长度 D. 原计划施工的天数
11.将抛物线,先向右平移个单位长度,再向上平移个单位长度后所得抛物线的解析式为( )
A. B. C. D.
12.如图,点在反比例函数的图象上,点在轴负半轴上,直线交轴于点,若,的面积为,则的值为( )
A.
B.
C.
D.
二、填空题:本题共4小题,每小题3分,共12分。
13.若式子在实数范围内有意义,则的取值范围是______.
14.分解因式:______.
15.如图,在中,的垂直平分线交于点,交于点,连接若,,则的度数为______.
16.如图,是的切线,为切点,与交于点,以点为圆心、以的长为半径作,分别交,于点,若,,则图中阴影部分的面积为 .
三、解答题:本题共7小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:;
解不等式:.
18.本小题分
如图,是 中的角平分线,交于点.
作的角平分线,交于点尺规作图,不写作法,保留作图痕迹;
证明:.
19.本小题分
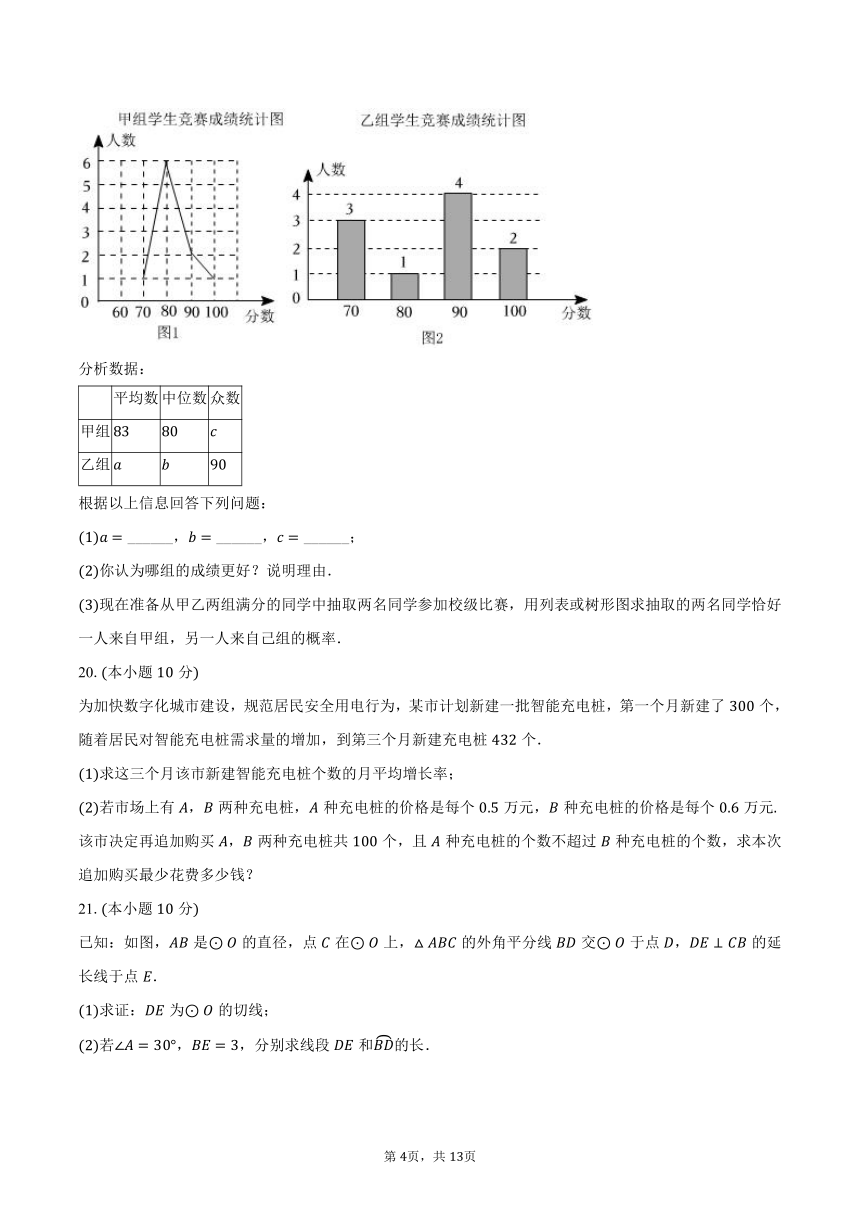
某校在开展“网络安全知识教育周”期间,在九年级随机抽取了名学生分成甲、乙两组,每组各人,进行“网络安全”现场知识竞赛,把甲、乙两组的成绩进行整理分析满分分,竞赛得分用表示:为网络安全意识非常强,为网络安全意识强,为网络安全意识一般,收集整理的数据制成如下两幅统计图:
分析数据:
平均数 中位数 众数
甲组
乙组
根据以上信息回答下列问题:
______, ______, ______;
你认为哪组的成绩更好?说明理由.
现在准备从甲乙两组满分的同学中抽取两名同学参加校级比赛,用列表或树形图求抽取的两名同学恰好一人来自甲组,另一人来自己组的概率.
20.本小题分
为加快数字化城市建设,规范居民安全用电行为,某市计划新建一批智能充电桩,第一个月新建了个,随着居民对智能充电桩需求量的增加,到第三个月新建充电桩个.
求这三个月该市新建智能充电桩个数的月平均增长率;
若市场上有,两种充电桩,种充电桩的价格是每个万元,种充电桩的价格是每个万元该市决定再追加购买,两种充电桩共个,且种充电桩的个数不超过种充电桩的个数,求本次追加购买最少花费多少钱?
21.本小题分
已知:如图,是的直径,点在上,的外角平分线交于点,的延长线于点.
求证:为的切线;
若,,分别求线段和的长.
22.本小题分
如图,在直角三角形纸片中,,,将三角形纸片进行以下操作:第一步:折叠三角形纸片使点与点重合,然后展开铺平,得到折痕;第二步:将绕点顺时针方向旋转得到,点,的对应点分别是点,,直线与边交于点点不与点重合,与边交于点.
【观察思考】折痕的长为______;
【实验探究】在绕点旋转的过程中,探究下列问题:
如图,当直线经过点时,求的长;
如图,当直线时,求的长;
【挑战自我】在绕点旋转的过程中,连接,则的最小值为______.
23.本小题分
【发现问题】
某景观公园内圆形人工湖中心有一喷泉,在人工湖中央垂直于水面安装一个柱子,安置在柱子顶端的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下爱思考的小敏发现,如果设距喷水柱子的水平距离为米,喷出的抛物线形水线距离湖面高度为米,与的数量变化有一定规律.
【提出问题】
喷出的抛物线形水线距离湖面高度为米与距喷水的柱子的水平距离米,与之间有怎样的函数关系?
【分析问题】
小敏对某个方向喷水的路径测量和计算得出如下数据:
米
米
【解决问题】
在建立如图所示的平面直角坐标系,根据已知数据描点,并用平滑曲线连接;
结合表中所给数据和所画出的图象,验证前面的抛物线形状的判断,并求出与之间的函数关系式;
现公园想通过喷泉设立一个新的游玩项目,使公园的平顶游船能从喷泉最高点的正下方通过如果游船宽度为米,顶棚到水面的高度为米,为了避免游船被淋到,顶棚到水柱的垂直距离不小于米,问游船在能否顺利通过?说明理由.
如图,若从安全的角度考虑,需要在这个喷泉外围设立一圈圆形护栏,这个喷泉的任何一条水柱在湖面上的落点到护栏的距离不能小于,请通过计算说明公园至少需要准备多少米的护栏?结果保留
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【解析】原式
;
,
,
,
,
,
则.
18.【答案】解:如图所示,射线即为所作.
证明四边形是平行四边形,
,,.
平分,平分,
,,
,
≌,
.
19.【解析】解:由图可知,甲组学生得分的人数最多,
故甲组的众数为,即;
由图的数据得,平均数;
图的数据从小到大排序为,,,,,,,,,,
位于中间的两个数为,,
中位数为,
故答案为:;;;
乙组的成绩更好;理由如下:
乙组的平均数和中位数都高于甲组,说明乙组的一般水平和中等水平都高于甲组,乙组的网络安全意识非常强的人数为人,高于甲组的人,所以乙组的成绩更好.
从甲乙两组满分的同学中抽取两名同学参加校级比赛,列表如下:
甲 乙 乙
甲 乙甲 乙甲
乙 甲乙 乙乙
乙 甲乙 乙乙
共有种等可能出现的结果,其中两名同学恰好一人来自甲组,另一人来自乙组的有种,
两名同学恰好一人来自甲组,另一人来自乙组的概率为.
20.【答案】解:设这三个月该市新建智能充电桩个数的月平均增长率为,
根据题意得:,
解得:,不符合题意,舍去.
答:这三个月该市新建智能充电桩个数的月平均增长率为;
设本次追加购买个种充电桩,则追加购买个种充电桩,
根据题意得:,
解得:.
设本次追加购买共花费万元,则,
即,
,
随的增大而减小,
当时,取得最小值,最小值为万元.
答:本次追加购买最少花费万元.
21.证明:连接,
,
,
是的外角平分线,
.
,
.
,
,
且点在上,
直线与相切;
解:,,
,
平分,
,
,
,,
,,
是等边三角形,,
.
22.【解析】由折叠的性质得:,,
,
,
,
是的中位线,
,
故答案为:;
由旋转的性质得:,,
,
,
,
,
,
设,
在中,,
即,
解得:,
,
故答案为:;
如图,过作于,交于.
则四边形是矩形,
,
,,,
,
,
,
,
,
,
∽,
,
即,
解得:;
如图,连接,
则,
当、、三点共线时,,
此时的值最小,最小,
,,
,
,
的最小值,
故答案为:.
23.【解析】描点、连线、图象如图;
;
该函数是二次函数,由和可知,抛物线的对称轴为直线,
当时,,
水柱最高点距离湖面的高度是米;
由图象可得,顶点,
设二次函数的关系式为,
把代入可得,
;
将和代入抛物线关系式,左边等于右边,所有的点都在二次函数图象上,
可以确认该函数是二次函数;
游船宽带米,在抛物线的正下方通过,令,
代入抛物线得,
由已知,顶棚到水面的高度为米,顶棚到水柱的垂直距离不小于米,
,
,
不能正常通过;
当时,即,
解得舍去或,
圆的半径为米,
至少需要准备栏杆米,
公园至少需要准备米的护栏.
第10页,共13页
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的相反数为( )
A. B. C. D.
2.下列图形均表示医疗或救援的标识,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.据统计,年我国新能源汽车产量超过万辆,其中万用科学记数法表示为( )
A. B. C. D.
4.下列几何体中,其俯视图与主视图完全相同的是( )
A. B. C. D.
5.成语是中国语言文化的缩影,有着深厚丰富的文化底蕴,学习成语,运用成语,了解成语当中所包含的语言文化现象,是我们学习语言、学习中国传统文化必不可少的一个环节和目的下列成语所描述的事件中,属于必然事件的是( )
A. 百步穿杨 B. 缘木求鱼 C. 旭日东升 D. 拔苗助长
6.下列计算正确的是( )
A. B. C. D.
7.如图,点在的延长线上,下列条件能判断的是( )
A.
B.
C.
D.
8.如图,已知一次函数的图象分别与、轴交于、两点,若,,则关于的方程的解为( )
A. B. C. D.
9.若满足,则代数式的值为( )
A. B. C. D.
10.“我市为处理污水,需要铺设一条长为米的管道,为了尽量减少施工对交通所造成的影响,实际施工时每天比原计划多铺设米,结果提前天完成任务”根据题意可得方程,则方程中表示( )
A. 实际每天铺设管道的长度 B. 实际施工的天数
C. 原计划每天铺设管道的长度 D. 原计划施工的天数
11.将抛物线,先向右平移个单位长度,再向上平移个单位长度后所得抛物线的解析式为( )
A. B. C. D.
12.如图,点在反比例函数的图象上,点在轴负半轴上,直线交轴于点,若,的面积为,则的值为( )
A.
B.
C.
D.
二、填空题:本题共4小题,每小题3分,共12分。
13.若式子在实数范围内有意义,则的取值范围是______.
14.分解因式:______.
15.如图,在中,的垂直平分线交于点,交于点,连接若,,则的度数为______.
16.如图,是的切线,为切点,与交于点,以点为圆心、以的长为半径作,分别交,于点,若,,则图中阴影部分的面积为 .
三、解答题:本题共7小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:;
解不等式:.
18.本小题分
如图,是 中的角平分线,交于点.
作的角平分线,交于点尺规作图,不写作法,保留作图痕迹;
证明:.
19.本小题分
某校在开展“网络安全知识教育周”期间,在九年级随机抽取了名学生分成甲、乙两组,每组各人,进行“网络安全”现场知识竞赛,把甲、乙两组的成绩进行整理分析满分分,竞赛得分用表示:为网络安全意识非常强,为网络安全意识强,为网络安全意识一般,收集整理的数据制成如下两幅统计图:
分析数据:
平均数 中位数 众数
甲组
乙组
根据以上信息回答下列问题:
______, ______, ______;
你认为哪组的成绩更好?说明理由.
现在准备从甲乙两组满分的同学中抽取两名同学参加校级比赛,用列表或树形图求抽取的两名同学恰好一人来自甲组,另一人来自己组的概率.
20.本小题分
为加快数字化城市建设,规范居民安全用电行为,某市计划新建一批智能充电桩,第一个月新建了个,随着居民对智能充电桩需求量的增加,到第三个月新建充电桩个.
求这三个月该市新建智能充电桩个数的月平均增长率;
若市场上有,两种充电桩,种充电桩的价格是每个万元,种充电桩的价格是每个万元该市决定再追加购买,两种充电桩共个,且种充电桩的个数不超过种充电桩的个数,求本次追加购买最少花费多少钱?
21.本小题分
已知:如图,是的直径,点在上,的外角平分线交于点,的延长线于点.
求证:为的切线;
若,,分别求线段和的长.
22.本小题分
如图,在直角三角形纸片中,,,将三角形纸片进行以下操作:第一步:折叠三角形纸片使点与点重合,然后展开铺平,得到折痕;第二步:将绕点顺时针方向旋转得到,点,的对应点分别是点,,直线与边交于点点不与点重合,与边交于点.
【观察思考】折痕的长为______;
【实验探究】在绕点旋转的过程中,探究下列问题:
如图,当直线经过点时,求的长;
如图,当直线时,求的长;
【挑战自我】在绕点旋转的过程中,连接,则的最小值为______.
23.本小题分
【发现问题】
某景观公园内圆形人工湖中心有一喷泉,在人工湖中央垂直于水面安装一个柱子,安置在柱子顶端的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下爱思考的小敏发现,如果设距喷水柱子的水平距离为米,喷出的抛物线形水线距离湖面高度为米,与的数量变化有一定规律.
【提出问题】
喷出的抛物线形水线距离湖面高度为米与距喷水的柱子的水平距离米,与之间有怎样的函数关系?
【分析问题】
小敏对某个方向喷水的路径测量和计算得出如下数据:
米
米
【解决问题】
在建立如图所示的平面直角坐标系,根据已知数据描点,并用平滑曲线连接;
结合表中所给数据和所画出的图象,验证前面的抛物线形状的判断,并求出与之间的函数关系式;
现公园想通过喷泉设立一个新的游玩项目,使公园的平顶游船能从喷泉最高点的正下方通过如果游船宽度为米,顶棚到水面的高度为米,为了避免游船被淋到,顶棚到水柱的垂直距离不小于米,问游船在能否顺利通过?说明理由.
如图,若从安全的角度考虑,需要在这个喷泉外围设立一圈圆形护栏,这个喷泉的任何一条水柱在湖面上的落点到护栏的距离不能小于,请通过计算说明公园至少需要准备多少米的护栏?结果保留
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【解析】原式
;
,
,
,
,
,
则.
18.【答案】解:如图所示,射线即为所作.
证明四边形是平行四边形,
,,.
平分,平分,
,,
,
≌,
.
19.【解析】解:由图可知,甲组学生得分的人数最多,
故甲组的众数为,即;
由图的数据得,平均数;
图的数据从小到大排序为,,,,,,,,,,
位于中间的两个数为,,
中位数为,
故答案为:;;;
乙组的成绩更好;理由如下:
乙组的平均数和中位数都高于甲组,说明乙组的一般水平和中等水平都高于甲组,乙组的网络安全意识非常强的人数为人,高于甲组的人,所以乙组的成绩更好.
从甲乙两组满分的同学中抽取两名同学参加校级比赛,列表如下:
甲 乙 乙
甲 乙甲 乙甲
乙 甲乙 乙乙
乙 甲乙 乙乙
共有种等可能出现的结果,其中两名同学恰好一人来自甲组,另一人来自乙组的有种,
两名同学恰好一人来自甲组,另一人来自乙组的概率为.
20.【答案】解:设这三个月该市新建智能充电桩个数的月平均增长率为,
根据题意得:,
解得:,不符合题意,舍去.
答:这三个月该市新建智能充电桩个数的月平均增长率为;
设本次追加购买个种充电桩,则追加购买个种充电桩,
根据题意得:,
解得:.
设本次追加购买共花费万元,则,
即,
,
随的增大而减小,
当时,取得最小值,最小值为万元.
答:本次追加购买最少花费万元.
21.证明:连接,
,
,
是的外角平分线,
.
,
.
,
,
且点在上,
直线与相切;
解:,,
,
平分,
,
,
,,
,,
是等边三角形,,
.
22.【解析】由折叠的性质得:,,
,
,
,
是的中位线,
,
故答案为:;
由旋转的性质得:,,
,
,
,
,
,
设,
在中,,
即,
解得:,
,
故答案为:;
如图,过作于,交于.
则四边形是矩形,
,
,,,
,
,
,
,
,
,
∽,
,
即,
解得:;
如图,连接,
则,
当、、三点共线时,,
此时的值最小,最小,
,,
,
,
的最小值,
故答案为:.
23.【解析】描点、连线、图象如图;
;
该函数是二次函数,由和可知,抛物线的对称轴为直线,
当时,,
水柱最高点距离湖面的高度是米;
由图象可得,顶点,
设二次函数的关系式为,
把代入可得,
;
将和代入抛物线关系式,左边等于右边,所有的点都在二次函数图象上,
可以确认该函数是二次函数;
游船宽带米,在抛物线的正下方通过,令,
代入抛物线得,
由已知,顶棚到水面的高度为米,顶棚到水柱的垂直距离不小于米,
,
,
不能正常通过;
当时,即,
解得舍去或,
圆的半径为米,
至少需要准备栏杆米,
公园至少需要准备米的护栏.
第10页,共13页
同课章节目录
