2025年河南省鼎城名校联盟中考数学适应性试卷(二)(含答案)
文档属性
| 名称 | 2025年河南省鼎城名校联盟中考数学适应性试卷(二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 120.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 20:17:25 | ||
图片预览




文档简介
2025年河南省鼎城名校联盟中考数学适应性试卷(二)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的绝对值是( )
A. B. C. D.
2.年“五一”假期河南接待游客万人次,旅游收入亿元数据“亿”用科学记数法可表示为( )
A. B. C. D.
3.欹器是古代一种倾斜易覆的盛水器,水少则倾,中则正,满则覆,寓意“满招损,谦受益”如图是一件欹器,它的主视图为( )
A. B.
C. D.
4.如图,直线,被直线,所截,下列条件能判定的是( )
A.
B.
C.
D.
5.“体重管理年”三年活动由国家卫健委联合个部门共同发起,宣传口号是“健康体重,一起行动”某校组织各班开展板报宣传活动,并对各班的宣传板报按如图所示的占比进行评分,每一项满分分已知九班“主题内容”“排版设计”“文字书写”三项的得分分别为分,分,分,则该班的最终得分为( )
A. 分 B. 分 C. 分 D. 分
6.一元二次方程有两个相等的实数根,则的值是( )
A. B. C. D.
7.我们规定关于任意正整数,的一种新运算:,若,则( )
A. B. C. D.
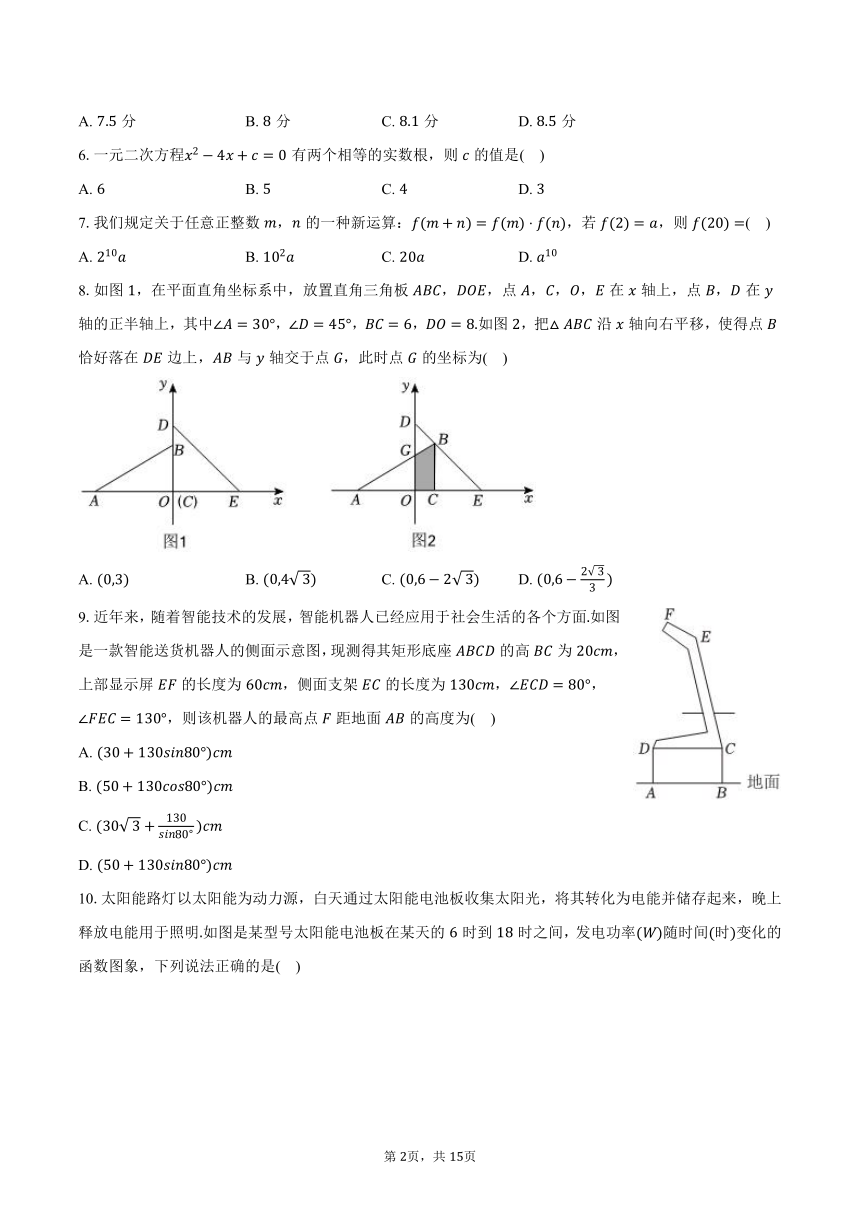
8.如图,在平面直角坐标系中,放置直角三角板,,点,,,在轴上,点,在轴的正半轴上,其中,,,如图,把沿轴向右平移,使得点恰好落在边上,与轴交于点,此时点的坐标为( )
A. B. C. D.
9.近年来,随着智能技术的发展,智能机器人已经应用于社会生活的各个方面如图是一款智能送货机器人的侧面示意图,现测得其矩形底座的高为,上部显示屏的长度为,侧面支架的长度为,,,则该机器人的最高点距地面的高度为( )
A.
B.
C.
D.
10.太阳能路灯以太阳能为动力源,白天通过太阳能电池板收集太阳光,将其转化为电能并储存起来,晚上释放电能用于照明如图是某型号太阳能电池板在某天的时到时之间,发电功率随时间时变化的函数图象,下列说法正确的是( )
A. 最大发电功率和最小发电功率相差
B. 时和时太阳能电池板的发电功率相同
C. 从时到时太阳能电池板的发电功率逐渐增大
D. 当天发电功率超过的时长为
二、填空题:本题共5小题,每小题3分,共15分。
11.请写出一个比小的无理数:______.
12.不等式组的解集为______.
13.如图,某教室的开关控制板上有四个外形完全相同的开关,其中两个分别控制两盏电灯,另两个分别控制两个电扇已知电灯、电扇均正常,且处于不工作状态,开关与电灯、电扇的对应关系未知若随机按下两个开关,则恰好打开一盏电灯和一个电扇的概率为______.
14.如图,在的正方形网格中,每个小正方形的边长均为,点,,,均在格点小正方形的顶点上,且点在上,为的中点,连接,,则图中阴影部分的面积为______.
15.如图,在中,,是射线上的一个动点,连接,将线段绕点逆时针旋转得到线段分别是,的对应点连接,,,当是以为腰的等腰三角形时,的长为______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:.
化简:.
17.本小题分
我国力争年前实现碳达峰,年前实现碳中和“碳达峰”“碳中和”倡导绿色、环保、低碳的生活方式为调查八、九年级学生对“碳达峰”和“碳中和”的了解程度,某校组织了一次测试,满分分,测试后随机抽取两个年级各名学生的成绩整理、分析如下:
【收集、整理数据】
八年级:,,,,,,,,,.
九年级:,,,,,,,,,.
【分析数据】
统计量
年级 平均数 中位数 众数
八年级
九年级
请根据以上信息,解决下列问题:
上表中______,______.
根据上表中的统计量,判断哪个年级的学生对“碳达峰”和“碳中和”的了解程度更深,并说明理由.
该校八年级有名学生、九年级有名学生参加测试,若分及以上为优秀,估计两个年级测试成绩为优秀的学生共多少名.
18.本小题分
如图,,平分交于点.
请用无刻度的直尺和圆规作的平分线,交于点,连接保留作图痕迹,不写作法
在的条件下,求证:四边形是菱形.
19.本小题分
如图,正方形的两个顶点,都在反比例函数的图象上.
求这个反比例函数的表达式.
反比例函数的图象经过点,直线分别与反比例函数,的图象交于点,若,求的长的取值范围.
20.本小题分
年月日,中央广播电视总台年春节联欢晚会发布官方吉祥物形象“巳升升”,祝福全球华人在新的一年如意康宁,好事连连某商店销售,两款“巳升升”吉祥物,已知款吉祥物的单价比款吉祥物的单价高元,花元购买款吉祥物的数量与花元购买款吉祥物的数量相同.
分别求出,两款吉祥物的单价.
某班级举办爱心义卖活动,准备从该商店购进,两款吉祥物共个进行售卖,且将每个款吉祥物的售价定为元,每个款吉祥物的售价定为元若本次购进款吉祥物的数量不少于款吉祥物数量的倍,则应如何设计购买方案才能获得最大利润?最大利润是多少?
21.本小题分
如图,已知内接于,是的直径,点在上不与点,重合,过点作的切线,交的延长线于点,连接,.
若要使,需要添加一个条件请从“条件:平分;条件:;条件:”中选择一个你认为正确的条件添加,并写出相应的证明过程.
在的条件下,若,,求的长.
22.本小题分
已知抛物线与轴交于点,与轴交于点.
求该抛物线的函数表达式及对称轴.
在如图所示的平面直角坐标系中,先描出该二次函数图象上的三个点,再画出该二次函数的图象;
在同一坐标系中画出直线,并根据图象直接写出关于的不等式的解集.
若关于的一元二次方程在的范围内有实数根,请结合图象直接写出的取值范围.
23.本小题分
综合与探究.
问题情境:
“综合与实践”课上,老师提出如下问题:将图中的直角三角形纸片折叠,使点的对应点落在边上,折痕分别交,于点,再将该纸片沿过点的直线折叠,使点的对应点落在的延长线上,折痕交于点,如图所示.
数学思考:
四边形的形状为______.
深入探究:
“善思小组”将图展开后,连接,得到图若为的中点,试猜想线段与的位置关系和数量关系,并说明理由.
“智慧小组”提出问题:若点的对应点落在射线上,其他条件不变,当,时,请直接写出面积的最大值和此时的长.
答案和解析
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】答案不唯一
12.【答案】
13.【答案】
14.【答案】
15.【答案】或
16.【解析】
;
原式
.
17.【解析】排序得:,,,,,,,,,,
位于中间的两个数为,,
,
九年级名学生的成绩中出现次数最多的是,
;
故答案为:,;
九年级学生对“碳达峰”和“碳中和”的了解程度更深.
理由:九年级学生测试成绩的平均数、中位数、众数均高于八年级,所以九年级学生对“碳达峰”和“碳中和”的了解程度更深.
由九年级与八年级的总人数分别乘以优秀学生的占比可得:
名.
答:两个年级测试成绩为优秀的学生共约名.
18.【解析】解:如图:即为所求;
证明:,
,
平分,
.
,
,
同理可证,
.
又,
四边形是平行四边形,
又,
四边形是菱形,
19.【解析】由条件可知,
点,是正方形的两个顶点,
,
,
联立,
解得:,
,,
,
这个反比例函数的表达式为;
由条件可知,
反比例函数的图象经过点,
,
即,
,,
,
,
,
,
的长的取值范围是.
20.【解析】设款吉祥物的单价为元,则款吉祥物的单价为元.
根据题意列分式方程得,,
整理得,,
解得.
经检验,是所列分式方程的解,且符合题意.
.
答:款吉祥物的单价为元,款吉祥物的单价为元.
设该班级本次购进款吉祥物个,则购进款吉祥物个,所获利润为元.
由题意,得.
,
随的增大而减小.
由题意列一元一次不等式得,,
整理得,,
解得.
为正整数,
当取时,的值最大,最大值为,此时.
答:购买个款吉祥物和个款吉祥物才能获得最大利润,最大利润是元.
21.【解析】解:选择条件,
证明:连接交于点,如解图所示.
.
.
是的直径,
.
,.
.
,
.
平分,
.
.
或选择条件,
证明:连接交于点,如解图所示.
为的切线,
.
.
是的直径,
.
,.
.
,
.
,
.
,
.
解:设的半径为,
则,.
在中,,
解得.
,,
.
若选择条件,此步可替换为“,”
.
.
.
又,
为的中位线.
.
,
,
即,
解得.
.
22.【解析】解:把点代入,得,
解得.
该抛物线的函数表达式为.
对称轴为直线;
解:描点,画出二次函数的图象如解图所示.
画出直线如解图所示.
由图象可得:出关于的不等式的解集为或;
由题意可得:
在的范围内,抛物线与直线有交点.
抛物线的对称轴为直线,开口向上,
抛物线在时取得最小值.
当时,,当时,.
当时,.
的取值范围为.
23【解析】将图中的直角三角形纸片折叠,使点的对应点落在边上,再将该纸片沿过点的直线折叠,使点的对应点落在的延长线上,
,,
,
四边形矩形,
故答案为:矩形;
,;理由如下:
如图,连接.
由知四边形是矩形,则,.
为的中点,
.
在和中,
,
≌,
,
由折叠的性质,得,,
,,
,,
,
又,
∽,
,
,
,;
面积的最大值为,此时;理由如下:
设,则,,
,,
∽,
则,
,,
,
,
,
,
当时,取最大值,最大值为此时.
第13页,共15页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的绝对值是( )
A. B. C. D.
2.年“五一”假期河南接待游客万人次,旅游收入亿元数据“亿”用科学记数法可表示为( )
A. B. C. D.
3.欹器是古代一种倾斜易覆的盛水器,水少则倾,中则正,满则覆,寓意“满招损,谦受益”如图是一件欹器,它的主视图为( )
A. B.
C. D.
4.如图,直线,被直线,所截,下列条件能判定的是( )
A.
B.
C.
D.
5.“体重管理年”三年活动由国家卫健委联合个部门共同发起,宣传口号是“健康体重,一起行动”某校组织各班开展板报宣传活动,并对各班的宣传板报按如图所示的占比进行评分,每一项满分分已知九班“主题内容”“排版设计”“文字书写”三项的得分分别为分,分,分,则该班的最终得分为( )
A. 分 B. 分 C. 分 D. 分
6.一元二次方程有两个相等的实数根,则的值是( )
A. B. C. D.
7.我们规定关于任意正整数,的一种新运算:,若,则( )
A. B. C. D.
8.如图,在平面直角坐标系中,放置直角三角板,,点,,,在轴上,点,在轴的正半轴上,其中,,,如图,把沿轴向右平移,使得点恰好落在边上,与轴交于点,此时点的坐标为( )
A. B. C. D.
9.近年来,随着智能技术的发展,智能机器人已经应用于社会生活的各个方面如图是一款智能送货机器人的侧面示意图,现测得其矩形底座的高为,上部显示屏的长度为,侧面支架的长度为,,,则该机器人的最高点距地面的高度为( )
A.
B.
C.
D.
10.太阳能路灯以太阳能为动力源,白天通过太阳能电池板收集太阳光,将其转化为电能并储存起来,晚上释放电能用于照明如图是某型号太阳能电池板在某天的时到时之间,发电功率随时间时变化的函数图象,下列说法正确的是( )
A. 最大发电功率和最小发电功率相差
B. 时和时太阳能电池板的发电功率相同
C. 从时到时太阳能电池板的发电功率逐渐增大
D. 当天发电功率超过的时长为
二、填空题:本题共5小题,每小题3分,共15分。
11.请写出一个比小的无理数:______.
12.不等式组的解集为______.
13.如图,某教室的开关控制板上有四个外形完全相同的开关,其中两个分别控制两盏电灯,另两个分别控制两个电扇已知电灯、电扇均正常,且处于不工作状态,开关与电灯、电扇的对应关系未知若随机按下两个开关,则恰好打开一盏电灯和一个电扇的概率为______.
14.如图,在的正方形网格中,每个小正方形的边长均为,点,,,均在格点小正方形的顶点上,且点在上,为的中点,连接,,则图中阴影部分的面积为______.
15.如图,在中,,是射线上的一个动点,连接,将线段绕点逆时针旋转得到线段分别是,的对应点连接,,,当是以为腰的等腰三角形时,的长为______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:.
化简:.
17.本小题分
我国力争年前实现碳达峰,年前实现碳中和“碳达峰”“碳中和”倡导绿色、环保、低碳的生活方式为调查八、九年级学生对“碳达峰”和“碳中和”的了解程度,某校组织了一次测试,满分分,测试后随机抽取两个年级各名学生的成绩整理、分析如下:
【收集、整理数据】
八年级:,,,,,,,,,.
九年级:,,,,,,,,,.
【分析数据】
统计量
年级 平均数 中位数 众数
八年级
九年级
请根据以上信息,解决下列问题:
上表中______,______.
根据上表中的统计量,判断哪个年级的学生对“碳达峰”和“碳中和”的了解程度更深,并说明理由.
该校八年级有名学生、九年级有名学生参加测试,若分及以上为优秀,估计两个年级测试成绩为优秀的学生共多少名.
18.本小题分
如图,,平分交于点.
请用无刻度的直尺和圆规作的平分线,交于点,连接保留作图痕迹,不写作法
在的条件下,求证:四边形是菱形.
19.本小题分
如图,正方形的两个顶点,都在反比例函数的图象上.
求这个反比例函数的表达式.
反比例函数的图象经过点,直线分别与反比例函数,的图象交于点,若,求的长的取值范围.
20.本小题分
年月日,中央广播电视总台年春节联欢晚会发布官方吉祥物形象“巳升升”,祝福全球华人在新的一年如意康宁,好事连连某商店销售,两款“巳升升”吉祥物,已知款吉祥物的单价比款吉祥物的单价高元,花元购买款吉祥物的数量与花元购买款吉祥物的数量相同.
分别求出,两款吉祥物的单价.
某班级举办爱心义卖活动,准备从该商店购进,两款吉祥物共个进行售卖,且将每个款吉祥物的售价定为元,每个款吉祥物的售价定为元若本次购进款吉祥物的数量不少于款吉祥物数量的倍,则应如何设计购买方案才能获得最大利润?最大利润是多少?
21.本小题分
如图,已知内接于,是的直径,点在上不与点,重合,过点作的切线,交的延长线于点,连接,.
若要使,需要添加一个条件请从“条件:平分;条件:;条件:”中选择一个你认为正确的条件添加,并写出相应的证明过程.
在的条件下,若,,求的长.
22.本小题分
已知抛物线与轴交于点,与轴交于点.
求该抛物线的函数表达式及对称轴.
在如图所示的平面直角坐标系中,先描出该二次函数图象上的三个点,再画出该二次函数的图象;
在同一坐标系中画出直线,并根据图象直接写出关于的不等式的解集.
若关于的一元二次方程在的范围内有实数根,请结合图象直接写出的取值范围.
23.本小题分
综合与探究.
问题情境:
“综合与实践”课上,老师提出如下问题:将图中的直角三角形纸片折叠,使点的对应点落在边上,折痕分别交,于点,再将该纸片沿过点的直线折叠,使点的对应点落在的延长线上,折痕交于点,如图所示.
数学思考:
四边形的形状为______.
深入探究:
“善思小组”将图展开后,连接,得到图若为的中点,试猜想线段与的位置关系和数量关系,并说明理由.
“智慧小组”提出问题:若点的对应点落在射线上,其他条件不变,当,时,请直接写出面积的最大值和此时的长.
答案和解析
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】答案不唯一
12.【答案】
13.【答案】
14.【答案】
15.【答案】或
16.【解析】
;
原式
.
17.【解析】排序得:,,,,,,,,,,
位于中间的两个数为,,
,
九年级名学生的成绩中出现次数最多的是,
;
故答案为:,;
九年级学生对“碳达峰”和“碳中和”的了解程度更深.
理由:九年级学生测试成绩的平均数、中位数、众数均高于八年级,所以九年级学生对“碳达峰”和“碳中和”的了解程度更深.
由九年级与八年级的总人数分别乘以优秀学生的占比可得:
名.
答:两个年级测试成绩为优秀的学生共约名.
18.【解析】解:如图:即为所求;
证明:,
,
平分,
.
,
,
同理可证,
.
又,
四边形是平行四边形,
又,
四边形是菱形,
19.【解析】由条件可知,
点,是正方形的两个顶点,
,
,
联立,
解得:,
,,
,
这个反比例函数的表达式为;
由条件可知,
反比例函数的图象经过点,
,
即,
,,
,
,
,
,
的长的取值范围是.
20.【解析】设款吉祥物的单价为元,则款吉祥物的单价为元.
根据题意列分式方程得,,
整理得,,
解得.
经检验,是所列分式方程的解,且符合题意.
.
答:款吉祥物的单价为元,款吉祥物的单价为元.
设该班级本次购进款吉祥物个,则购进款吉祥物个,所获利润为元.
由题意,得.
,
随的增大而减小.
由题意列一元一次不等式得,,
整理得,,
解得.
为正整数,
当取时,的值最大,最大值为,此时.
答:购买个款吉祥物和个款吉祥物才能获得最大利润,最大利润是元.
21.【解析】解:选择条件,
证明:连接交于点,如解图所示.
.
.
是的直径,
.
,.
.
,
.
平分,
.
.
或选择条件,
证明:连接交于点,如解图所示.
为的切线,
.
.
是的直径,
.
,.
.
,
.
,
.
,
.
解:设的半径为,
则,.
在中,,
解得.
,,
.
若选择条件,此步可替换为“,”
.
.
.
又,
为的中位线.
.
,
,
即,
解得.
.
22.【解析】解:把点代入,得,
解得.
该抛物线的函数表达式为.
对称轴为直线;
解:描点,画出二次函数的图象如解图所示.
画出直线如解图所示.
由图象可得:出关于的不等式的解集为或;
由题意可得:
在的范围内,抛物线与直线有交点.
抛物线的对称轴为直线,开口向上,
抛物线在时取得最小值.
当时,,当时,.
当时,.
的取值范围为.
23【解析】将图中的直角三角形纸片折叠,使点的对应点落在边上,再将该纸片沿过点的直线折叠,使点的对应点落在的延长线上,
,,
,
四边形矩形,
故答案为:矩形;
,;理由如下:
如图,连接.
由知四边形是矩形,则,.
为的中点,
.
在和中,
,
≌,
,
由折叠的性质,得,,
,,
,,
,
又,
∽,
,
,
,;
面积的最大值为,此时;理由如下:
设,则,,
,,
∽,
则,
,,
,
,
,
,
当时,取最大值,最大值为此时.
第13页,共15页
同课章节目录
