7.4平移 教学课件(共21张PPT) 人教版七年级数学下册
文档属性
| 名称 | 7.4平移 教学课件(共21张PPT) 人教版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 817.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 21:23:45 | ||
图片预览





文档简介
(共21张PPT)
7.4平移
1.掌握平移的性质特征.能按要求作出简单的平面图形平移后的图形.(重点)
2.运用平移性质解决生活中的实际问题.(难点)
学习目标
五星红旗冉冉升起
这些运动现象都给我们带来了怎样一种感觉?
窗户沿着滑槽移动
情境导入
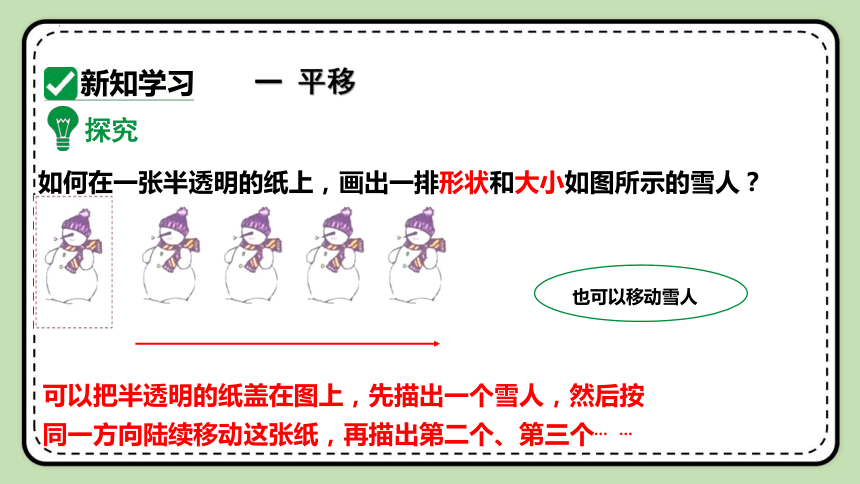
如何在一张半透明的纸上,画出一排形状和大小如图所示的雪人?
探究
也可以移动雪人
新知学习
可以把半透明的纸盖在图上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个
一 平移
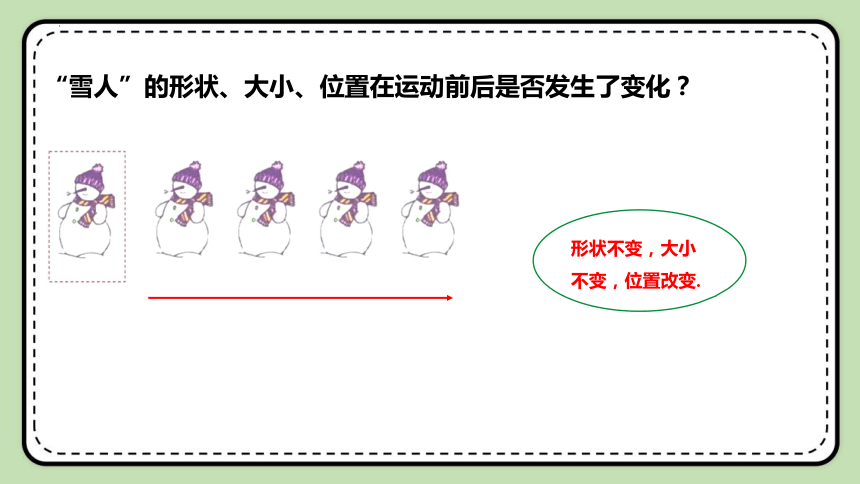
形状不变,大小不变,位置改变.
“雪人”的形状、大小、位置在运动前后是否发生了变化?
思考
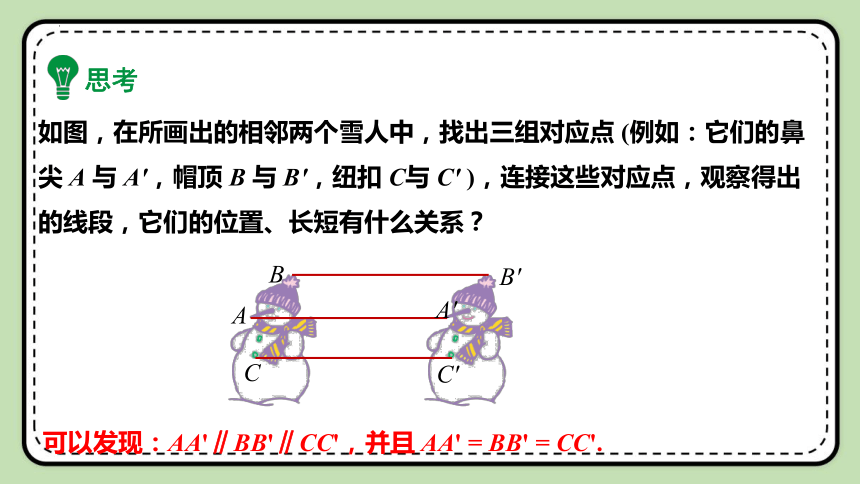
如图,在所画出的相邻两个雪人中,找出三组对应点 (例如:它们的鼻尖 A 与 A',帽顶 B 与 B',纽扣 C与 C' ),连接这些对应点,观察得出的线段,它们的位置、长短有什么关系?
A
B
C
A'
C'
B'
可以发现:AA'∥BB'∥CC',并且 AA' = BB' = CC'.
探究新知
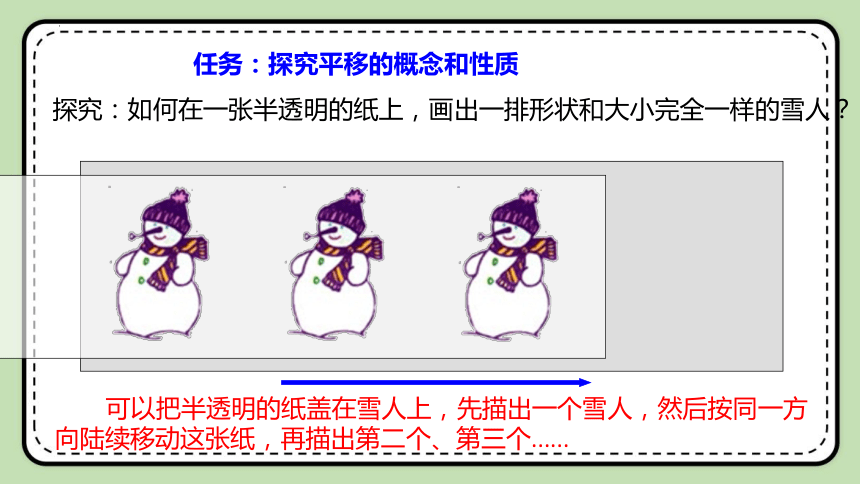
任务:探究平移的概念和性质
探究:如何在一张半透明的纸上,画出一排形状和大小完全一样的雪人?
可以把半透明的纸盖在雪人上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个......
探究新知
任务:探究平移的概念和性质
探究:如何在一张半透明的纸上,画出一排形状和大小完全一样的雪人?
可以把半透明的纸盖在雪人上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个......
探究新知
任务:探究平移的概念和性质
探究:如何在一张半透明的纸上,画出一排形状和大小完全一样的雪人?
可以把半透明的纸盖在雪人上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个......
如图,图中哪条线段可以由线段b经过平移得到?如何进行平移?
解:线段c,可由线段b向右平移3个单位,再向上平移2个单位得到.
或由线段b先向上平移2个单位,再向右平移3个单位得到.
典型例题
如图,平移△ABC,使点A移动到点A',画出平移后的△A'B'C'.
A
B
C
A'
B'
C'
连接A'A;过点B,做l∥AA',在l上截取BB' =AA'
同理作CC',连接A'B' ,B'C',C'A'则△A'B'C'即为所求.
l
平移作图的一般步骤:
(1)确定平移的方向和距离;
(2)确定构成图形的关键点(线段两个端点,三角形三个顶点,n边形n个顶点);
(3)按照平移的方向和距离平移各个关键点;
(4)顺次连接各个关键点的对应点,所得的图形就是平移后的图形.
归纳
1.下面生活中的物体的运动情况可以看成平移的是( )
A.摆动的钟摆
B.在笔直的公路上行驶的汽车
C.随风摆动的旗帜
D.汽车玻璃上雨刷的运动
B
2.下列四个图形中,不能通过其中一个四边形平移得到的是( )
D
A.
B.
C.
D.
3.如图,三角形ABC沿着BE的方向,平移得到三角形DEF,已知BC=5,EC=3,那么平移的距离为 .
2
课堂练习
【知识技能类作业】
——必做题:
1.下列运动属于平移的是( )
A.荡秋千
B.地球绕着太阳转
C.风筝在空中随风飘动
D.急刹车时,汽车在地面上的滑动
D
课堂练习
【知识技能类作业】
——必做题:
2.如图,可以看作是沿直线平移得到的.如果,,那么线段的长是( )
A.2.5 B.4
C.4.5 D.5
B
课堂练习
【知识技能类作业】
——必做题:
解:(1)如图,即为所求.
(2)由平移可知,.
的面积为.
3.如图,在的正方形网格中,每个小正方形的边长都为1,的顶点均在小正方形的顶点上.
(1)把先向右移动5个单位长度,再向下移动3个单位长度得到,画出(其中点A的对应点为
,点B的对应点为,点C的对应点为);
(2)连接,,判定与的位置关
系,并写出的面积.
A
B
C
A'
C'
B'
D
2.已知:如图,三角形ABC中,CA=3,CB=4 ,将三角形ABC沿CB方向平移得三角形A'B'C',若平移距离是2,且A'D=
填空:
(1)A'C'=______,B'C'=_____
3
4
(2)四边形A'DBB'的面积=____
3. 亚运会赛艇项目在富阳水上运动中心举行,如图,若将场馆外绿化区域的一条等宽的笔直通道改为同样宽度的等宽弯曲通道,则绿化区域的面积_______,改造后小路的长度_______(填“变大”,“不变”或“变小”).
变大
例题图
不变
4. 如图,三角形 ABC 沿 BC 所在直线向右平移得到三角形 DEF,已知 EC=2,BF=8,则平移的距离为 .
3
B
E
C
F
A
D
解析:三角形 ABC平移得到三角形 DEF,对应点点B 移动到了点E,平移的距离就是线段BE的长,
∵BC=EF,即BE+EC=EC+CF,
∴BE=CF
BF=BE+EC+CF=8,EC=2,
∴BE=CF=3
即平移的距离为3.
7.4平移
1.掌握平移的性质特征.能按要求作出简单的平面图形平移后的图形.(重点)
2.运用平移性质解决生活中的实际问题.(难点)
学习目标
五星红旗冉冉升起
这些运动现象都给我们带来了怎样一种感觉?
窗户沿着滑槽移动
情境导入
如何在一张半透明的纸上,画出一排形状和大小如图所示的雪人?
探究
也可以移动雪人
新知学习
可以把半透明的纸盖在图上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个
一 平移
形状不变,大小不变,位置改变.
“雪人”的形状、大小、位置在运动前后是否发生了变化?
思考
如图,在所画出的相邻两个雪人中,找出三组对应点 (例如:它们的鼻尖 A 与 A',帽顶 B 与 B',纽扣 C与 C' ),连接这些对应点,观察得出的线段,它们的位置、长短有什么关系?
A
B
C
A'
C'
B'
可以发现:AA'∥BB'∥CC',并且 AA' = BB' = CC'.
探究新知
任务:探究平移的概念和性质
探究:如何在一张半透明的纸上,画出一排形状和大小完全一样的雪人?
可以把半透明的纸盖在雪人上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个......
探究新知
任务:探究平移的概念和性质
探究:如何在一张半透明的纸上,画出一排形状和大小完全一样的雪人?
可以把半透明的纸盖在雪人上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个......
探究新知
任务:探究平移的概念和性质
探究:如何在一张半透明的纸上,画出一排形状和大小完全一样的雪人?
可以把半透明的纸盖在雪人上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个......
如图,图中哪条线段可以由线段b经过平移得到?如何进行平移?
解:线段c,可由线段b向右平移3个单位,再向上平移2个单位得到.
或由线段b先向上平移2个单位,再向右平移3个单位得到.
典型例题
如图,平移△ABC,使点A移动到点A',画出平移后的△A'B'C'.
A
B
C
A'
B'
C'
连接A'A;过点B,做l∥AA',在l上截取BB' =AA'
同理作CC',连接A'B' ,B'C',C'A'则△A'B'C'即为所求.
l
平移作图的一般步骤:
(1)确定平移的方向和距离;
(2)确定构成图形的关键点(线段两个端点,三角形三个顶点,n边形n个顶点);
(3)按照平移的方向和距离平移各个关键点;
(4)顺次连接各个关键点的对应点,所得的图形就是平移后的图形.
归纳
1.下面生活中的物体的运动情况可以看成平移的是( )
A.摆动的钟摆
B.在笔直的公路上行驶的汽车
C.随风摆动的旗帜
D.汽车玻璃上雨刷的运动
B
2.下列四个图形中,不能通过其中一个四边形平移得到的是( )
D
A.
B.
C.
D.
3.如图,三角形ABC沿着BE的方向,平移得到三角形DEF,已知BC=5,EC=3,那么平移的距离为 .
2
课堂练习
【知识技能类作业】
——必做题:
1.下列运动属于平移的是( )
A.荡秋千
B.地球绕着太阳转
C.风筝在空中随风飘动
D.急刹车时,汽车在地面上的滑动
D
课堂练习
【知识技能类作业】
——必做题:
2.如图,可以看作是沿直线平移得到的.如果,,那么线段的长是( )
A.2.5 B.4
C.4.5 D.5
B
课堂练习
【知识技能类作业】
——必做题:
解:(1)如图,即为所求.
(2)由平移可知,.
的面积为.
3.如图,在的正方形网格中,每个小正方形的边长都为1,的顶点均在小正方形的顶点上.
(1)把先向右移动5个单位长度,再向下移动3个单位长度得到,画出(其中点A的对应点为
,点B的对应点为,点C的对应点为);
(2)连接,,判定与的位置关
系,并写出的面积.
A
B
C
A'
C'
B'
D
2.已知:如图,三角形ABC中,CA=3,CB=4 ,将三角形ABC沿CB方向平移得三角形A'B'C',若平移距离是2,且A'D=
填空:
(1)A'C'=______,B'C'=_____
3
4
(2)四边形A'DBB'的面积=____
3. 亚运会赛艇项目在富阳水上运动中心举行,如图,若将场馆外绿化区域的一条等宽的笔直通道改为同样宽度的等宽弯曲通道,则绿化区域的面积_______,改造后小路的长度_______(填“变大”,“不变”或“变小”).
变大
例题图
不变
4. 如图,三角形 ABC 沿 BC 所在直线向右平移得到三角形 DEF,已知 EC=2,BF=8,则平移的距离为 .
3
B
E
C
F
A
D
解析:三角形 ABC平移得到三角形 DEF,对应点点B 移动到了点E,平移的距离就是线段BE的长,
∵BC=EF,即BE+EC=EC+CF,
∴BE=CF
BF=BE+EC+CF=8,EC=2,
∴BE=CF=3
即平移的距离为3.
同课章节目录
