17.1勾股定理 同步练习(含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 17.1勾股定理 同步练习(含答案) 2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 179.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 22:13:43 | ||
图片预览


文档简介
17.1勾股定理
第1课时勾股定理
自主预习
1.如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 .若直角三角形两直角边长为5 和 12,则它的斜边长为 .
2.在 Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
(1)若a=3,b=4,则c= ;(2)若b=6,c=10,则a= ;
(3)若a=5,c=13,则b= ;(4)若a=1,b=2,则c= .
3.在△ABC中,∠C=90°,AC=BC=m,AB=n,m与n的关系是 .
基础优练
知识点1 勾股定理的认识及验证
1.在△ABC中,若∠ABC=90°,则下列正确的是【点拨 1】 ( )
A. BC=AB+AC
2.下列选项中,不能用来证明勾股定理的是【点拨2】 ( )
3“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图17--1--1--1所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短 图1直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为 ( )
A.9 B.6 C.4 D.3
知识点2 利用勾股定理进行计算
4.一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则该三角形的面积为【点拨 3】 ( )
A.8 B.10 C.24 D.48
5.在△ABC中,∠B=90°,若BC=3,AC=5,则AB等于【点拨4】 ( )
A.2 B.3 C.4
6.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)若b=2,c=4,则a= ;
(2)若a:b=3: 4,c=20,则a= ,b= .
名师点拨
点拨1 ((1)勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
(2)勾股定理的表达式:如果直角三角形的两直角边分别用a,b表示,斜边用c表示,那么勾股定理可表示为:
点拨2 证明勾股定理时,用几个全等的直角三角形拼成一个规则的图形,然后利用大图形的面积等于几个小图形的面积之和得出等量关系,再进行化简整理证明勾股定理.
点拨3 已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
点拨4 勾股定理的变形:(已知两边,求第三边的方法)
点拨5 直角三角形中已知两边求第三边时因未分类讨论而出错:利用勾股定理解题一定要找准斜边、直角边,直角边和斜边分不清是常见的错误,应当重视.
整合集训
7.在△ABC中, 则两直角边a,b的关系是 ( )
A. ab
C. a=b D.以上三种情况都有可能
8.如图17-1-1-2,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB 交BC 于点 E,. 则AC= ( )
A.1 B.2 C.3 D.4
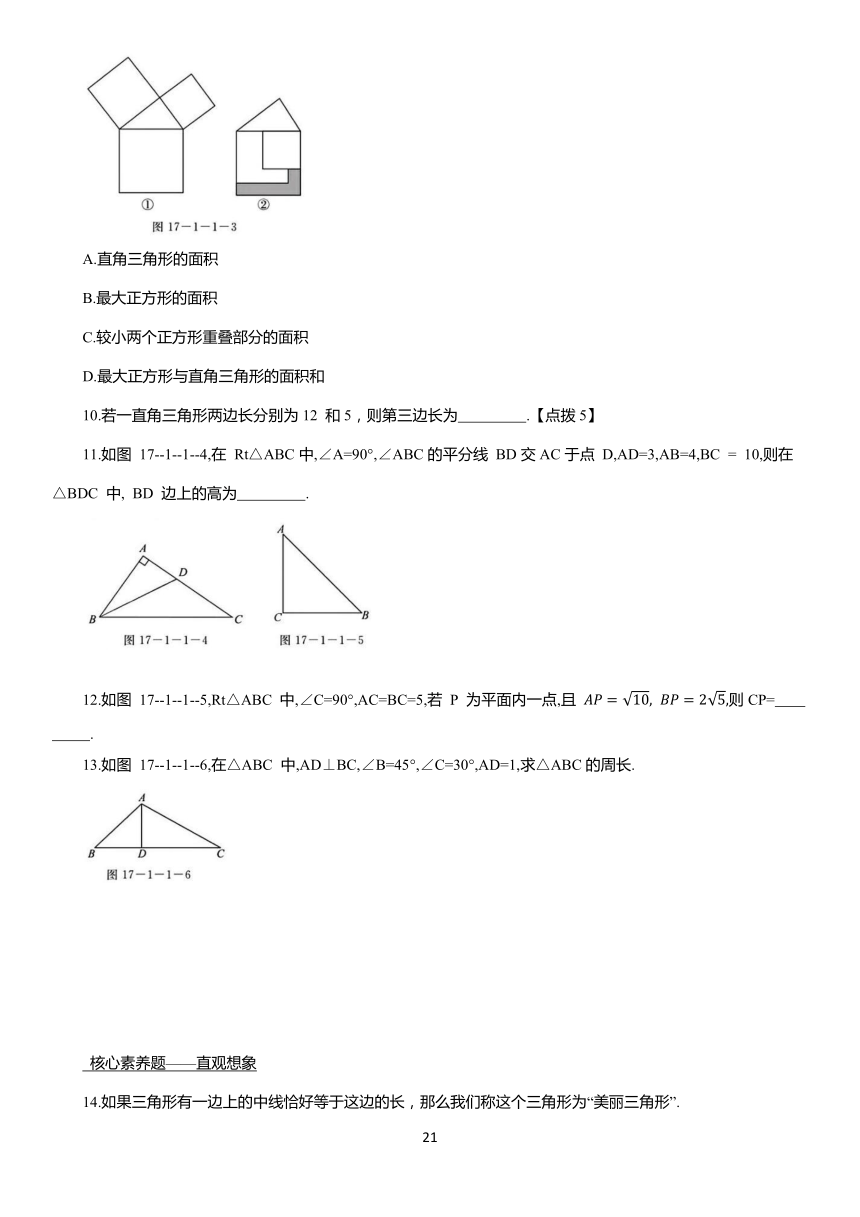
9.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图17-1-1-3①,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按17-1-1-3②的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出 ( )
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
10.若一直角三角形两边长分别为12 和5,则第三边长为 .【点拨5】
11.如图 17--1--1--4,在 Rt△ABC中,∠A=90°,∠ABC的平分线 BD交AC于点 D,AD=3,AB=4,BC = 10,则在 △BDC 中, BD 边上的高为 .
12.如图 17--1--1--5,Rt△ABC 中,∠C=90°,AC=BC=5,若 P 为平面内一点,且 则CP= .
13.如图 17--1--1--6,在△ABC 中,AD⊥BC,∠B=45°,∠C=30°,AD=1,求△ABC的周长.
核心素养题——直观想象
14.如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“美丽三角形”.
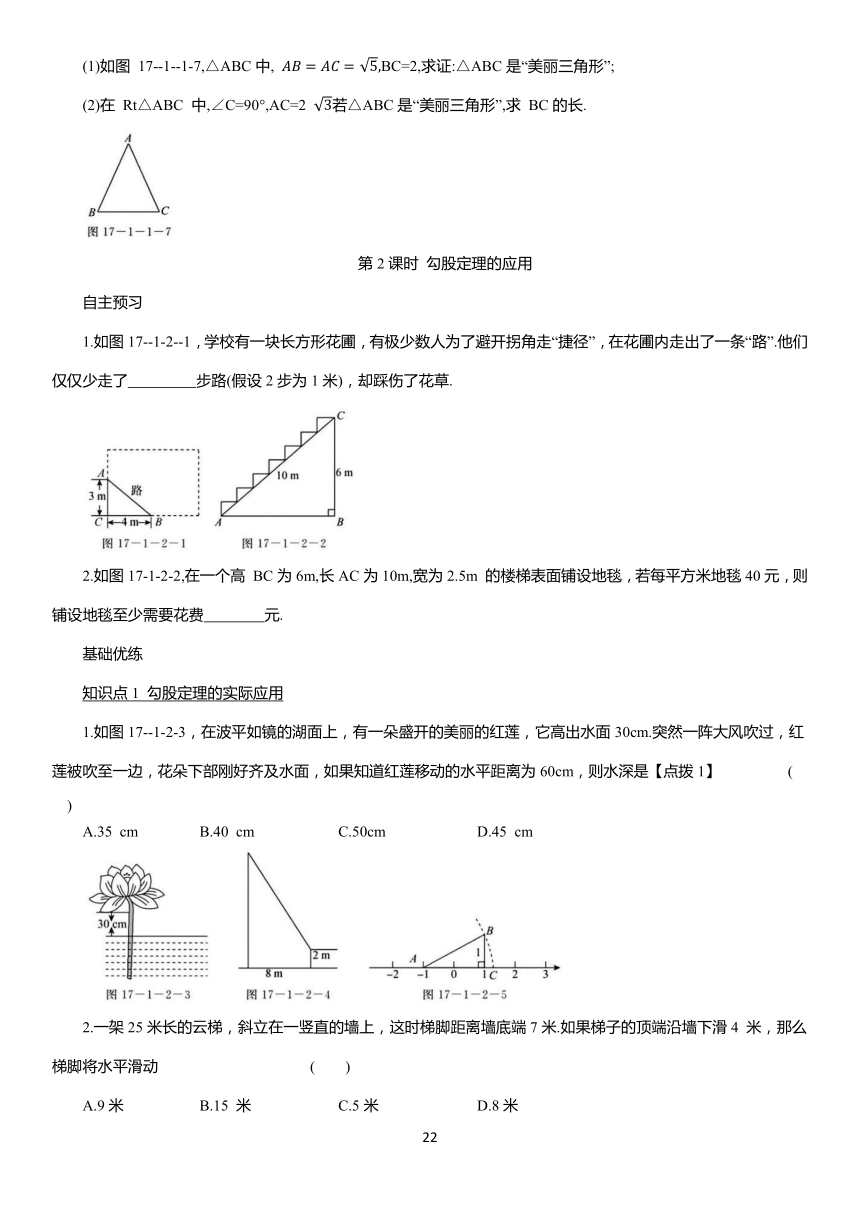
(1)如图 17--1--1-7,△ABC中, BC=2,求证:△ABC是“美丽三角形”;
(2)在 Rt△ABC 中,∠C=90°,AC=2 若△ABC是“美丽三角形”,求 BC的长.
第2课时 勾股定理的应用
自主预习
1.如图17--1-2--1,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.
2.如图17-1-2-2,在一个高 BC为6m,长AC为10m,宽为2.5m 的楼梯表面铺设地毯,若每平方米地毯40元,则铺设地毯至少需要花费 元.
基础优练
知识点1 勾股定理的实际应用
1.如图17--1-2-3,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面30cm.突然一阵大风吹过,红莲被吹至一边,花朵下部刚好齐及水面,如果知道红莲移动的水平距离为60cm,则水深是【点拨1】 ( )
A.35 cm B.40 cm C.50cm D.45 cm
2.一架25米长的云梯,斜立在一竖直的墙上,这时梯脚距离墙底端7米.如果梯子的顶端沿墙下滑4 米,那么梯脚将水平滑动 ( )
A.9米 B.15 米 C.5米 D.8米
3.如图17-1-2-4,小华将升旗的绳子拉到竖直旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,此时绳子末端距离地面2m,则绳子的总长度为 m.
知识点2 在数轴上表示无理数
4.如图17--1-2-5,AB=AC,则数轴上点C所表示的数为【点拨2】 ( )
5.如图17--1-2-6,在数轴上作出表示 的点(不写作法,要求保留作图痕迹).
名师点拨
点拨1 利用勾股定理解决实际问题时,要注意以下几点:
(1)在不规则的几何图形中,通常添加辅助线得到直角三角形;(2)勾股定理与方程的结合是解决实际问题常用的方法;(3)在应用勾股定理解决实际问题时,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图,体会数形结合思想的应用.
点拨2 在数轴上表示无理数时,将在数轴上表示无理数的问题转化为画长为无理数的线段问题.第一步:利用勾股定理拆分出哪两条线段长的平方和等于所画线段(斜边)长的平方,注意一般其中两条线段的长是整数;第二步:以数轴原点为直角三角形斜边的顶点,构造直角三角形;第三步:以数轴原点为圆心,以斜边长为半径画弧,即可在数轴上找到表示该无理数的点.
点拨3解决最短路径问题时,要将立体图形的侧面展开转化为平面图形问题,然后利用勾股定理求解,应考虑经过的面,然后选择最短路径.
整合集训 *
6.“折竹抵地”问题源自《九章算术》,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何 意思是:一根竹子,原高一丈(1丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4 尺远,则折断处离地面的高度为 ( )
A.5.8尺 B.4.2尺 C.3尺 D.7尺
7.如图17--1-2-7所示的正方体中,Q,R,S是棱PB 上的点,一只蚂蚁从 A 点出发,沿着正方体的侧面爬行,经过 PB上一点,爬行到 C点,若此蚂蚁所爬行的路线最短,那么 P,Q,R,S四个点中,它最有可能经过的点是 ( )
A. P B. Q C. R D. S
8.如图17-1-2-8,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 米(结果精确到0.1米,参考数据:
9如图17-1-2-9,在平面直角坐标系中,A(4,0),B(0,3),以点 A 为圆心,AB长为半径画弧,交x轴的负半轴于点 C,则点 C的坐标为 .
10.如图17-1-2-10,一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A 点沿纸箱外表面爬到 B点,求它所爬行的最短路线的长.【点拨3】
11.超速行驶是引发交通事故的主要原因,上周末,小鹏等三位同学在滨海大道红树林路段,尝试用自己所学的知识检测车速.如图17-1-2--11,观测点设在到公路l的距离为100m的 P 处.这时,一辆富康轿车由西向东匀速驶来,测得此车从A 处行驶到 B 处所用的时间为3s ,并测得∠APO=60°,∠BPO=45°,试判断此车是否超过了每小时80千米的限制速度
核心素养题——数学建模
12.如图17-1-2-12,在笔直的铁路上 A,B两点相距25 km,C,D为两村庄,DA=10 km,CB=15 km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站 E,使得 C,D两村到E 站的距离相等.求E应建在距A 多远处
第十七章勾股定理
17.1勾股定理
第1课时勾股定理
自主预习
1. a +b =r 13 2.(1)5 (2)8 (3)12 (1) 3.2m =n 基础优练
1.1) 2.1) 3.1) 4.( 5. C 6.(1)2 (2)12 16整合集训
7. C8. B 9. C
10.13或 11.6 12. 或5
13.解:∵AD⊥BC.
∴∠ADB=∠AIX'=90°.在 Rt△ADB 中.∵∠B+∠BAI)=90°,∠B=45°,∴∠B=∠BAD=15'.∴AD=BD=1,AB= 在Rt△ADC中.∵∠C=30°,∴AC=2AD=2.∴CD=
14.(1)证明:如答图17-1-1-1.过点A 作AD⊥BC于D.∵AB 由勾股定理,得AD= 即△ABC是“美丽三角形”.
(2)解:如答图17-1-1-2.当AC边上的中线BD 等于AC时 当BC边上的中线AE等于BC时。AC=AE°. CE,即 解得BC=4.综上所述,BC=3或BC=4.
第2课时勾股定理的应用
白主预习
1.4 2.1 400
基础优练
1.1) 2.1) 3.17 4. B
5.
解:如答图17-1-2-1. A点即为所求.
整合集训
6. B 7. C 8.2.9 9.(-1.0)
10.解:如答图 17-1-2-2①所示. 如答图 17 - 1-2-2②所示 。最短路线的长是10.
11.解:在 Rt△APO中.∠APO=60'.则∠PAO=30'.
在Rt△BOP中.∠BPO=45°,则BO=OP=100m.∴AB=AO-B()=100 -100≈73(m).∴从A到B小车行驶的速度为73÷3≈21.3m/s=87.48 km/h>80 km'h.∴此车超过每小时80千米的限制速度.
12.解:设AE=. r km.则 BE=(25-. r) km.由勾股定理.得在Rt△ADE中. 在 Rt△BCE 中. 由题意可知 DE=CE,所 解得. r=15.所以,E应建在距A点 15 km处.
第1课时勾股定理
自主预习
1.如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 .若直角三角形两直角边长为5 和 12,则它的斜边长为 .
2.在 Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
(1)若a=3,b=4,则c= ;(2)若b=6,c=10,则a= ;
(3)若a=5,c=13,则b= ;(4)若a=1,b=2,则c= .
3.在△ABC中,∠C=90°,AC=BC=m,AB=n,m与n的关系是 .
基础优练
知识点1 勾股定理的认识及验证
1.在△ABC中,若∠ABC=90°,则下列正确的是【点拨 1】 ( )
A. BC=AB+AC
2.下列选项中,不能用来证明勾股定理的是【点拨2】 ( )
3“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图17--1--1--1所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短 图1直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为 ( )
A.9 B.6 C.4 D.3
知识点2 利用勾股定理进行计算
4.一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则该三角形的面积为【点拨 3】 ( )
A.8 B.10 C.24 D.48
5.在△ABC中,∠B=90°,若BC=3,AC=5,则AB等于【点拨4】 ( )
A.2 B.3 C.4
6.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)若b=2,c=4,则a= ;
(2)若a:b=3: 4,c=20,则a= ,b= .
名师点拨
点拨1 ((1)勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
(2)勾股定理的表达式:如果直角三角形的两直角边分别用a,b表示,斜边用c表示,那么勾股定理可表示为:
点拨2 证明勾股定理时,用几个全等的直角三角形拼成一个规则的图形,然后利用大图形的面积等于几个小图形的面积之和得出等量关系,再进行化简整理证明勾股定理.
点拨3 已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
点拨4 勾股定理的变形:(已知两边,求第三边的方法)
点拨5 直角三角形中已知两边求第三边时因未分类讨论而出错:利用勾股定理解题一定要找准斜边、直角边,直角边和斜边分不清是常见的错误,应当重视.
整合集训
7.在△ABC中, 则两直角边a,b的关系是 ( )
A. ab
C. a=b D.以上三种情况都有可能
8.如图17-1-1-2,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB 交BC 于点 E,. 则AC= ( )
A.1 B.2 C.3 D.4
9.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图17-1-1-3①,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按17-1-1-3②的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出 ( )
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
10.若一直角三角形两边长分别为12 和5,则第三边长为 .【点拨5】
11.如图 17--1--1--4,在 Rt△ABC中,∠A=90°,∠ABC的平分线 BD交AC于点 D,AD=3,AB=4,BC = 10,则在 △BDC 中, BD 边上的高为 .
12.如图 17--1--1--5,Rt△ABC 中,∠C=90°,AC=BC=5,若 P 为平面内一点,且 则CP= .
13.如图 17--1--1--6,在△ABC 中,AD⊥BC,∠B=45°,∠C=30°,AD=1,求△ABC的周长.
核心素养题——直观想象
14.如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“美丽三角形”.
(1)如图 17--1--1-7,△ABC中, BC=2,求证:△ABC是“美丽三角形”;
(2)在 Rt△ABC 中,∠C=90°,AC=2 若△ABC是“美丽三角形”,求 BC的长.
第2课时 勾股定理的应用
自主预习
1.如图17--1-2--1,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.
2.如图17-1-2-2,在一个高 BC为6m,长AC为10m,宽为2.5m 的楼梯表面铺设地毯,若每平方米地毯40元,则铺设地毯至少需要花费 元.
基础优练
知识点1 勾股定理的实际应用
1.如图17--1-2-3,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面30cm.突然一阵大风吹过,红莲被吹至一边,花朵下部刚好齐及水面,如果知道红莲移动的水平距离为60cm,则水深是【点拨1】 ( )
A.35 cm B.40 cm C.50cm D.45 cm
2.一架25米长的云梯,斜立在一竖直的墙上,这时梯脚距离墙底端7米.如果梯子的顶端沿墙下滑4 米,那么梯脚将水平滑动 ( )
A.9米 B.15 米 C.5米 D.8米
3.如图17-1-2-4,小华将升旗的绳子拉到竖直旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,此时绳子末端距离地面2m,则绳子的总长度为 m.
知识点2 在数轴上表示无理数
4.如图17--1-2-5,AB=AC,则数轴上点C所表示的数为【点拨2】 ( )
5.如图17--1-2-6,在数轴上作出表示 的点(不写作法,要求保留作图痕迹).
名师点拨
点拨1 利用勾股定理解决实际问题时,要注意以下几点:
(1)在不规则的几何图形中,通常添加辅助线得到直角三角形;(2)勾股定理与方程的结合是解决实际问题常用的方法;(3)在应用勾股定理解决实际问题时,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图,体会数形结合思想的应用.
点拨2 在数轴上表示无理数时,将在数轴上表示无理数的问题转化为画长为无理数的线段问题.第一步:利用勾股定理拆分出哪两条线段长的平方和等于所画线段(斜边)长的平方,注意一般其中两条线段的长是整数;第二步:以数轴原点为直角三角形斜边的顶点,构造直角三角形;第三步:以数轴原点为圆心,以斜边长为半径画弧,即可在数轴上找到表示该无理数的点.
点拨3解决最短路径问题时,要将立体图形的侧面展开转化为平面图形问题,然后利用勾股定理求解,应考虑经过的面,然后选择最短路径.
整合集训 *
6.“折竹抵地”问题源自《九章算术》,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何 意思是:一根竹子,原高一丈(1丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4 尺远,则折断处离地面的高度为 ( )
A.5.8尺 B.4.2尺 C.3尺 D.7尺
7.如图17--1-2-7所示的正方体中,Q,R,S是棱PB 上的点,一只蚂蚁从 A 点出发,沿着正方体的侧面爬行,经过 PB上一点,爬行到 C点,若此蚂蚁所爬行的路线最短,那么 P,Q,R,S四个点中,它最有可能经过的点是 ( )
A. P B. Q C. R D. S
8.如图17-1-2-8,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 米(结果精确到0.1米,参考数据:
9如图17-1-2-9,在平面直角坐标系中,A(4,0),B(0,3),以点 A 为圆心,AB长为半径画弧,交x轴的负半轴于点 C,则点 C的坐标为 .
10.如图17-1-2-10,一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A 点沿纸箱外表面爬到 B点,求它所爬行的最短路线的长.【点拨3】
11.超速行驶是引发交通事故的主要原因,上周末,小鹏等三位同学在滨海大道红树林路段,尝试用自己所学的知识检测车速.如图17-1-2--11,观测点设在到公路l的距离为100m的 P 处.这时,一辆富康轿车由西向东匀速驶来,测得此车从A 处行驶到 B 处所用的时间为3s ,并测得∠APO=60°,∠BPO=45°,试判断此车是否超过了每小时80千米的限制速度
核心素养题——数学建模
12.如图17-1-2-12,在笔直的铁路上 A,B两点相距25 km,C,D为两村庄,DA=10 km,CB=15 km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站 E,使得 C,D两村到E 站的距离相等.求E应建在距A 多远处
第十七章勾股定理
17.1勾股定理
第1课时勾股定理
自主预习
1. a +b =r 13 2.(1)5 (2)8 (3)12 (1) 3.2m =n 基础优练
1.1) 2.1) 3.1) 4.( 5. C 6.(1)2 (2)12 16整合集训
7. C8. B 9. C
10.13或 11.6 12. 或5
13.解:∵AD⊥BC.
∴∠ADB=∠AIX'=90°.在 Rt△ADB 中.∵∠B+∠BAI)=90°,∠B=45°,∴∠B=∠BAD=15'.∴AD=BD=1,AB= 在Rt△ADC中.∵∠C=30°,∴AC=2AD=2.∴CD=
14.(1)证明:如答图17-1-1-1.过点A 作AD⊥BC于D.∵AB 由勾股定理,得AD= 即△ABC是“美丽三角形”.
(2)解:如答图17-1-1-2.当AC边上的中线BD 等于AC时 当BC边上的中线AE等于BC时。AC=AE°. CE,即 解得BC=4.综上所述,BC=3或BC=4.
第2课时勾股定理的应用
白主预习
1.4 2.1 400
基础优练
1.1) 2.1) 3.17 4. B
5.
解:如答图17-1-2-1. A点即为所求.
整合集训
6. B 7. C 8.2.9 9.(-1.0)
10.解:如答图 17-1-2-2①所示. 如答图 17 - 1-2-2②所示 。最短路线的长是10.
11.解:在 Rt△APO中.∠APO=60'.则∠PAO=30'.
在Rt△BOP中.∠BPO=45°,则BO=OP=100m.∴AB=AO-B()=100 -100≈73(m).∴从A到B小车行驶的速度为73÷3≈21.3m/s=87.48 km/h>80 km'h.∴此车超过每小时80千米的限制速度.
12.解:设AE=. r km.则 BE=(25-. r) km.由勾股定理.得在Rt△ADE中. 在 Rt△BCE 中. 由题意可知 DE=CE,所 解得. r=15.所以,E应建在距A点 15 km处.
