第十七章 勾股定理本章考点分类集训 (含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第十七章 勾股定理本章考点分类集训 (含答案) 2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 134.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 22:19:31 | ||
图片预览

文档简介
第十七章 勾股定理本章考点分类集训
考点1 勾股定理
1.在直角三角形中,若勾为3,股为4,则弦为 ( )
A.5 B.6 C.7 D.8
2.如图K--17--1,将两个大小、形状完全相同的△ABC和△A'B'C'拼在一起,其中点 A'与点A 重合,点C落在边 AB上,连接B'C.若∠ACB=∠AC'B'=90°,AC=BC=3,则B'C的长为 ( )
A.3 B.6
3.如图K-17-2,在△ABC中,AB=AC=5,BC=8,D是线段BC 上的动点(不含端点 B,C).若线段AD长为正整数,则点 D的位置共有 ( )
A.5个 B.4个 C.3个 D.2个
4.为了比较 与 的大小,可以构造如图K-17-3所示的图形进行推算,其中∠C=90°,BC=3,D在BC 上且BD=AC=1.通过计算可得 (填“>”或“<”或“=”)
5.已知等腰三角形的底角是30°,腰长为2,则它的周长是 .
6.把两个同样大小的含45°角的三角尺按如图K-17-4所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点 A,且另三个锐角顶点 B,C,D在同一直线上.若AB= ,则CD= .
7.已知:如图K-17-5,∠B=∠D=90°,∠A=60°,AB=4,CD=2.求四边形ABCD的面积.
考点2 勾股定理的应用
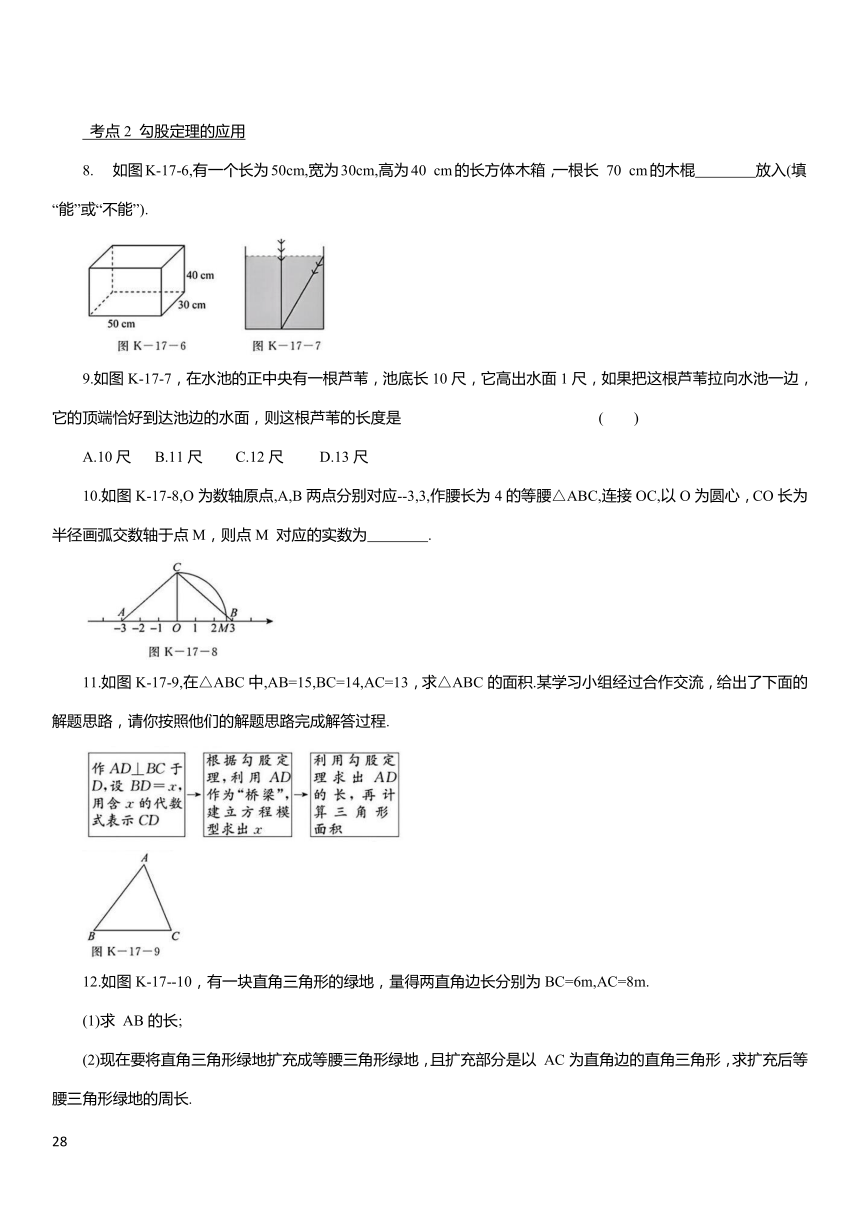
如图K-17-6,有一个长为50cm,宽为30cm,高为40 cm的长方体木箱,一根长 70 cm的木棍 放入(填“能”或“不能”).
9.如图K-17-7,在水池的正中央有一根芦苇,池底长10尺,它高出水面1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,则这根芦苇的长度是 ( )
A.10尺 B.11尺 C.12尺 D.13尺
10.如图K-17-8,O为数轴原点,A,B两点分别对应--3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,CO长为半径画弧交数轴于点M,则点M 对应的实数为 .
11.如图K-17-9,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
12.如图K-17--10,有一块直角三角形的绿地,量得两直角边长分别为BC=6m,AC=8m.
(1)求 AB的长;
(2)现在要将直角三角形绿地扩充成等腰三角形绿地,且扩充部分是以 AC为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
考点3 命题与互逆定理
13.下列各命题中,逆命题不成立的是 ( )
A.全等三角形的对应边相等
B.等腰三角形的两个底角相等
C.若a-b>0,则a>b
D.若a=b,则
14.“角平分线上的点到这个角的两边距离相等”的逆命题是 ,它是 命题(填“真”或“假”).
考点4 勾股定理的逆定理
15.满足下列条件的△ABC,不是直角三角形的是( )
A.∠C=∠A+∠B
B.∠C=∠A-∠B
C. a:b:c=3:4:5
D.∠A:∠B:∠C=3:4:5
16.在数学活动课上,老师要求学生在如图K-17-11 的4×4 的正方形 ABCD 网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB和 AD都不平行,则画出的形状不同的直角三角形有
A.3种 B.4 种 C.5种 D.6种
17.如图K--17-12,△ABC为 等 腰 直 角 三 角 形,∠ACB=90°,AC=BC.在∠ACB 的内部任意作∠ECF=45°,交 AB 于点E,F,则以AE,EF,BF为边的三角形的形状是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
18.已知△ABC的三边长为a,b,c,满足a+b=10,ab=18,c=8,则此三角形为 三角形.
19.如图K-17-13,小明的家位于一条南北走向的河流 MN的东侧A 处,某一天小明从家出发沿南偏西30°方向走60m到达河边 B处取水,然后沿另一方向走 80 m到达菜地 C处浇水,最后沿第三方向走 100m回到家A处,问小明在河边 B处取水后是沿哪个方向行走的 并说明理由.
20.台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图K--17--14,有一台风中心沿东西方向AB由点A 行驶向点B,已知点C为一海港,且点C与直线AB上两点A,B的距离分别为300 km和400 km,又AB=500 km,以台风中心为圆心周围250 km以内为受影响区域.
(1)海港C受台风影响吗 为什么
(2)若台风的速度为20km/h,则台风影响该海港持续的时间有多长
本章考点分类集训
1. A 2. A 3. C 4.> 5.6+4 6. -1
7.解:如答图 K-17--1.延长AD. BC.相交于点 E.在Rt△ABE中.∠A=60°. AB=1.∴∠E=30°,AE=2AB=8.∴BE=
在 Rt△DCE中,∠E-30°,(1)=2.
∴CE=2CD=1.
8.能 9. D 10.
11.解:在△ABC中,AB=15,BC=14. AC=13.
设BD=x,则CD=14-x.
由勾股定理。得/ 故 解得x=9.
12.解:
(2)①如答图K--17-2①.延长BC到D.使CD=BC=6m。连接AD.则AB=AD=10m,得△ABD的周长为32m ②如答图K--17-2②.当AB=BD时,可求(1)=4m,由勾股定理得: 得△ABD的周长为 如答图K--17-2③,当AD=BD时,设AD=BD= xm,则CD=(x-6)m。由勾股定理得((x· 6)' 18'-x'.解得: 得△ABD的周长为 m.
13. D 14.到角两边距离相等的点在这个角的平分线上 真15. D 16. C 17. B
18.直角
19.解:小明在河边B处取水后是沿南偏东60°方向行走的.
理由:∵AB=60 m,BC=80 m. AC= 100m.∴AB→BC”=AC∵,∴∠ABC-90°,∴∠NBA=30°,∴∠MBC=180°-90°..30°-60°,∴小明在河边B处取水后是沿南偏东60°方向行走的.
20.解:(1)海港C受台风影响.理由:如答图 K-17-3.过点C作CDJAB于D.∵AC≌300 km. BC=400km. AB=500 km.∴AC+BC'=AB',∴△ABC'是直角三角形.
∴AC·BC=CD·AB.
∴300×400-CD×500.
∵以台风中心为圆心周围250 km以内为受影响区域。
∴海港(`受到台风影响.
(2)如图K-17-14,当EC=250 km. FC=250 km时,正好影响(港|口.
∴EF=140 km.∵台风的速度为20 km/h.
∴台风影响该海港持续的时间为110÷20=7(h).
考点1 勾股定理
1.在直角三角形中,若勾为3,股为4,则弦为 ( )
A.5 B.6 C.7 D.8
2.如图K--17--1,将两个大小、形状完全相同的△ABC和△A'B'C'拼在一起,其中点 A'与点A 重合,点C落在边 AB上,连接B'C.若∠ACB=∠AC'B'=90°,AC=BC=3,则B'C的长为 ( )
A.3 B.6
3.如图K-17-2,在△ABC中,AB=AC=5,BC=8,D是线段BC 上的动点(不含端点 B,C).若线段AD长为正整数,则点 D的位置共有 ( )
A.5个 B.4个 C.3个 D.2个
4.为了比较 与 的大小,可以构造如图K-17-3所示的图形进行推算,其中∠C=90°,BC=3,D在BC 上且BD=AC=1.通过计算可得 (填“>”或“<”或“=”)
5.已知等腰三角形的底角是30°,腰长为2,则它的周长是 .
6.把两个同样大小的含45°角的三角尺按如图K-17-4所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点 A,且另三个锐角顶点 B,C,D在同一直线上.若AB= ,则CD= .
7.已知:如图K-17-5,∠B=∠D=90°,∠A=60°,AB=4,CD=2.求四边形ABCD的面积.
考点2 勾股定理的应用
如图K-17-6,有一个长为50cm,宽为30cm,高为40 cm的长方体木箱,一根长 70 cm的木棍 放入(填“能”或“不能”).
9.如图K-17-7,在水池的正中央有一根芦苇,池底长10尺,它高出水面1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,则这根芦苇的长度是 ( )
A.10尺 B.11尺 C.12尺 D.13尺
10.如图K-17-8,O为数轴原点,A,B两点分别对应--3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,CO长为半径画弧交数轴于点M,则点M 对应的实数为 .
11.如图K-17-9,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
12.如图K-17--10,有一块直角三角形的绿地,量得两直角边长分别为BC=6m,AC=8m.
(1)求 AB的长;
(2)现在要将直角三角形绿地扩充成等腰三角形绿地,且扩充部分是以 AC为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
考点3 命题与互逆定理
13.下列各命题中,逆命题不成立的是 ( )
A.全等三角形的对应边相等
B.等腰三角形的两个底角相等
C.若a-b>0,则a>b
D.若a=b,则
14.“角平分线上的点到这个角的两边距离相等”的逆命题是 ,它是 命题(填“真”或“假”).
考点4 勾股定理的逆定理
15.满足下列条件的△ABC,不是直角三角形的是( )
A.∠C=∠A+∠B
B.∠C=∠A-∠B
C. a:b:c=3:4:5
D.∠A:∠B:∠C=3:4:5
16.在数学活动课上,老师要求学生在如图K-17-11 的4×4 的正方形 ABCD 网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB和 AD都不平行,则画出的形状不同的直角三角形有
A.3种 B.4 种 C.5种 D.6种
17.如图K--17-12,△ABC为 等 腰 直 角 三 角 形,∠ACB=90°,AC=BC.在∠ACB 的内部任意作∠ECF=45°,交 AB 于点E,F,则以AE,EF,BF为边的三角形的形状是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
18.已知△ABC的三边长为a,b,c,满足a+b=10,ab=18,c=8,则此三角形为 三角形.
19.如图K-17-13,小明的家位于一条南北走向的河流 MN的东侧A 处,某一天小明从家出发沿南偏西30°方向走60m到达河边 B处取水,然后沿另一方向走 80 m到达菜地 C处浇水,最后沿第三方向走 100m回到家A处,问小明在河边 B处取水后是沿哪个方向行走的 并说明理由.
20.台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图K--17--14,有一台风中心沿东西方向AB由点A 行驶向点B,已知点C为一海港,且点C与直线AB上两点A,B的距离分别为300 km和400 km,又AB=500 km,以台风中心为圆心周围250 km以内为受影响区域.
(1)海港C受台风影响吗 为什么
(2)若台风的速度为20km/h,则台风影响该海港持续的时间有多长
本章考点分类集训
1. A 2. A 3. C 4.> 5.6+4 6. -1
7.解:如答图 K-17--1.延长AD. BC.相交于点 E.在Rt△ABE中.∠A=60°. AB=1.∴∠E=30°,AE=2AB=8.∴BE=
在 Rt△DCE中,∠E-30°,(1)=2.
∴CE=2CD=1.
8.能 9. D 10.
11.解:在△ABC中,AB=15,BC=14. AC=13.
设BD=x,则CD=14-x.
由勾股定理。得/ 故 解得x=9.
12.解:
(2)①如答图K--17-2①.延长BC到D.使CD=BC=6m。连接AD.则AB=AD=10m,得△ABD的周长为32m ②如答图K--17-2②.当AB=BD时,可求(1)=4m,由勾股定理得: 得△ABD的周长为 如答图K--17-2③,当AD=BD时,设AD=BD= xm,则CD=(x-6)m。由勾股定理得((x· 6)' 18'-x'.解得: 得△ABD的周长为 m.
13. D 14.到角两边距离相等的点在这个角的平分线上 真15. D 16. C 17. B
18.直角
19.解:小明在河边B处取水后是沿南偏东60°方向行走的.
理由:∵AB=60 m,BC=80 m. AC= 100m.∴AB→BC”=AC∵,∴∠ABC-90°,∴∠NBA=30°,∴∠MBC=180°-90°..30°-60°,∴小明在河边B处取水后是沿南偏东60°方向行走的.
20.解:(1)海港C受台风影响.理由:如答图 K-17-3.过点C作CDJAB于D.∵AC≌300 km. BC=400km. AB=500 km.∴AC+BC'=AB',∴△ABC'是直角三角形.
∴AC·BC=CD·AB.
∴300×400-CD×500.
∵以台风中心为圆心周围250 km以内为受影响区域。
∴海港(`受到台风影响.
(2)如图K-17-14,当EC=250 km. FC=250 km时,正好影响(港|口.
∴EF=140 km.∵台风的速度为20 km/h.
∴台风影响该海港持续的时间为110÷20=7(h).
