人教版(2024版)八上数学 13.3.1 三角形的内角(第2课时)同步练习(含解析)
文档属性
| 名称 | 人教版(2024版)八上数学 13.3.1 三角形的内角(第2课时)同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 685.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
13.3.1 三角形的内角(第2课时) 同步练习
班级:________ 姓名:________
一、单选题
1.在一个直角三角形中,若一个锐角是,则另一个锐角是( )
A. B. C. D.
2.如图,在中,,,则是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.钝角三角形
第2题图 第3题图 第4题图
3.在中,平分,则等于( )
A. B. C. D.
4.将三角尺按如图位置摆放,顶点落在直线上,顶点落在直线上.若,,则的度数是( )
A. B. C. D.
5.满足下列条件的不是直角三角形的是( )
A. B.
C. D.
二、填空题
6.如图,将直尺与30°角的三角尺叠放在一起,若,则的大小是 °.
第6题图 第7题图 第9题图
7.如图,在Rt△ABC 中,∠B=90°,直线 DE 与 AC,BC 分别交于 D,E 两点.若∠DEC=∠A,则△EDC 是 .
8.在一个直角三角形中,已知一个锐角比另一个锐角的倍多,则较小锐角的度数为 .
9.把一块直尺与一块三角板按如图所示的方式放置.若,则的度数是 .
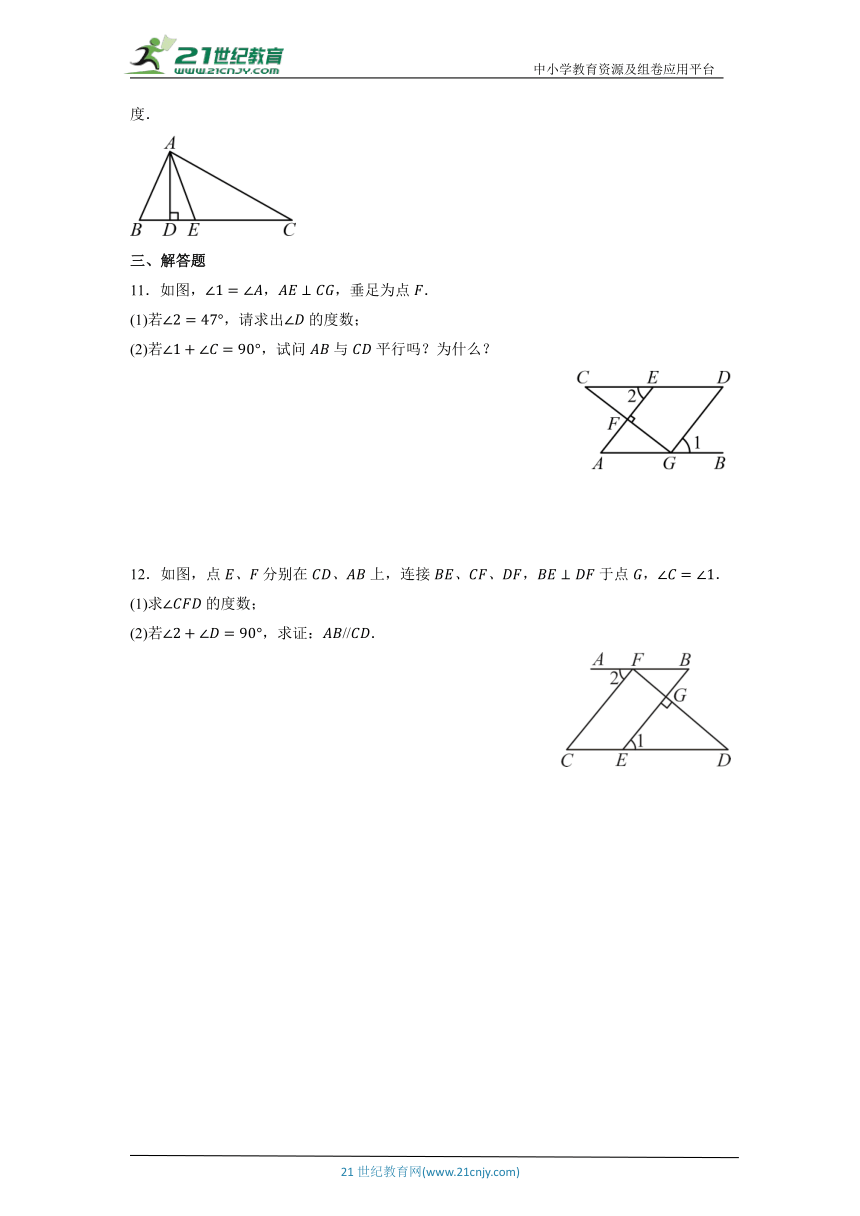
10.如图,中,是上的高,平分,,则 度.
三、解答题
11.如图,,,垂足为点.
(1)若,请求出的度数;
(2)若,试问与平行吗?为什么?
12.如图,点分别在上,连接,于点,.
(1)求的度数;
(2)若,求证:.
答案与解析
13.3.1 三角形的内角(第2课时) 同步练习
班级:________ 姓名:________
一、单选题
1.在一个直角三角形中,若一个锐角是,则另一个锐角是( )
A. B. C. D.
【答案】B
【解析】本题考查了直角三角形两锐角互余,理解互余的概念,根据直角三角形两锐角互余求解即可.
解:在一个直角三角形中,若一个锐角是,则另一个锐角,
故选:B .
2.如图,在中,,,则是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.钝角三角形
【答案】C
【解析】本题考查了三角形内角和定理,利用三角形内角和定理,找出是解题的关键.
在中,利用三角形内角和定理,可得出,结合,可得出,再利用三角形内角和定理,可得出,进而可得出是直角三角形.
解:在中,,
∴,
又∵,
,
∴,
是直角三角形.
故选:C.
3.在中,平分,则等于( )
A. B. C. D.
【答案】B
【解析】本题主要考查直角三角形的性质(两锐角互余)以及角平分线的定义,先根据直角三角形两锐角互余求出的度数,再利用角平分线的性质求出的度数.
解:在中,,,
,
平分,
.
故选:B.
4.将三角尺按如图位置摆放,顶点落在直线上,顶点落在直线上.若,,则的度数是( )
A. B. C. D.
【答案】C
【解析】本题考查了直角三角形两锐角互余,平行线的性质,掌握平行线的性质求角度的计算是关键.
根据题意,得到,根据平行线的性质得到,由此即可求解.
解:如图所示,
,
∴,
∵,
∴,
故选:C .
5.满足下列条件的不是直角三角形的是( )
A. B.
C. D.
【答案】B
【解析】本题考查直角三角形的识别,根据三角形内角和定理以及直角三角形的判定逐项判断,即可得到结论.
解:A,,是直角三角形,不合题意;
B,时,最大的角,不是直角三角形,符合题意;
C,,则,是直角三角形,不合题意;
D,,则,是直角三角形,不合题意;
故选B.
二、填空题
6.如图,将直尺与30°角的三角尺叠放在一起,若,则的大小是 °.
【答案】55
【解析】本题主要考查了平行线的性质,由三角尺可知,由平角可求,再根据平行线的性质可知.
解:如图:
由的三角尺可知,
∴.
由平行线的性质可知.
故答案为:55.
7.如图,在Rt△ABC 中,∠B=90°,直线 DE 与 AC,BC 分别交于 D,E 两点.若∠DEC=∠A,则△EDC 是 .
【答案】直角三角形
【解析】根据直角三角形的两个锐角互余可知∠A+∠C=90°,再由∠DEC=∠A进而可得出结论.
解:解: 在Rt△ABC 中,
∵∠B=90°,
∴∠A+∠C=90°,
∵∠DEC=∠A,
∴∠DEC+∠C=90°,
∴∠EDC=90°,
∴△EDC 是直角三角形,
故答案为 直角三角形.
8.在一个直角三角形中,已知一个锐角比另一个锐角的倍多,则较小锐角的度数为 .
【答案】/15度
【解析】本题考查了直角三角形两锐角互余的性质,关键步骤是正确设定变量并准确列方程,最终求出较小的锐角度数.本题设定未知数,根据直角三角形两锐角互余的性质,建立方程求解较小的锐角度数.
解:设较小的锐角为,则较大的锐角为,
根据直角三角形两锐角之和为,得:
,
解得:,
所以较小锐角的度数为.
故答案为:.
9.把一块直尺与一块三角板按如图所示的方式放置.若,则的度数是 .
【答案】/128度
【解析】本题考查平行线的性质、直角三角形的两个锐角互余,根据平行线的性质、直角三角形的两个锐角互余,结合邻补角求解即可.
解:如图,
由题意,,,,
∵,
∴,则,
∴,
∴,
故答案为:.
10.如图,中,是上的高,平分,,则 度.
【答案】10
【解析】本题考查的是三角形内角和定理,三角形的角平分线的定义,三角形高的含义.先由三角形的内角和定理求解的大小,再由角平分线的性质求解的大小,再利用直角三角形的两锐角互余求出,最后利用角的和差关系可得答案.
解:在中,,
∴,
∵平分,
∴.,
∵是上的高,
∴,
∴,
∴.
故答案为:10.
三、解答题
11.如图,,,垂足为点.
(1)若,请求出的度数;
(2)若,试问与平行吗?为什么?
【答案】(1)
(2),理由见解析
【解析】本题主要考查了平行线的性质与判定、同角或等角的余角相等、直角三角形的性质.
(1)因为,根据同位角相等,两直线平行可证,根据两直线平行,同位角相等可知;
(2)根据垂直的定义可知,根据直角三角形两锐角互余可得,因为,根据同角的余角相等可证,等量代换可得,根据内错角相等,两直线平行可证.
解:(1)∵,
∴,
∴,
∵,
∴.
(2),理由如下:
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
12.如图,点分别在上,连接,于点,.
(1)求的度数;
(2)若,求证:.
【答案】(1)
(2)见解析
【解析】本题考查了平行线的判定,垂直的定义,直角三角形特征,熟练掌握平行线的判定,同角的余角相等是解题的关键;
(1)根据垂直的定义和直角三角形特征可得,再通过等量代换即可求出;
(2)根据同角的余角相等可得,再通过等量代换可得,即可证明.
解:(1),
,
,
,
,
;
(2)证明:,
,
,
,
,
,
,
.
21世纪教育网(www.21cnjy.com)
13.3.1 三角形的内角(第2课时) 同步练习
班级:________ 姓名:________
一、单选题
1.在一个直角三角形中,若一个锐角是,则另一个锐角是( )
A. B. C. D.
2.如图,在中,,,则是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.钝角三角形
第2题图 第3题图 第4题图
3.在中,平分,则等于( )
A. B. C. D.
4.将三角尺按如图位置摆放,顶点落在直线上,顶点落在直线上.若,,则的度数是( )
A. B. C. D.
5.满足下列条件的不是直角三角形的是( )
A. B.
C. D.
二、填空题
6.如图,将直尺与30°角的三角尺叠放在一起,若,则的大小是 °.
第6题图 第7题图 第9题图
7.如图,在Rt△ABC 中,∠B=90°,直线 DE 与 AC,BC 分别交于 D,E 两点.若∠DEC=∠A,则△EDC 是 .
8.在一个直角三角形中,已知一个锐角比另一个锐角的倍多,则较小锐角的度数为 .
9.把一块直尺与一块三角板按如图所示的方式放置.若,则的度数是 .
10.如图,中,是上的高,平分,,则 度.
三、解答题
11.如图,,,垂足为点.
(1)若,请求出的度数;
(2)若,试问与平行吗?为什么?
12.如图,点分别在上,连接,于点,.
(1)求的度数;
(2)若,求证:.
答案与解析
13.3.1 三角形的内角(第2课时) 同步练习
班级:________ 姓名:________
一、单选题
1.在一个直角三角形中,若一个锐角是,则另一个锐角是( )
A. B. C. D.
【答案】B
【解析】本题考查了直角三角形两锐角互余,理解互余的概念,根据直角三角形两锐角互余求解即可.
解:在一个直角三角形中,若一个锐角是,则另一个锐角,
故选:B .
2.如图,在中,,,则是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.钝角三角形
【答案】C
【解析】本题考查了三角形内角和定理,利用三角形内角和定理,找出是解题的关键.
在中,利用三角形内角和定理,可得出,结合,可得出,再利用三角形内角和定理,可得出,进而可得出是直角三角形.
解:在中,,
∴,
又∵,
,
∴,
是直角三角形.
故选:C.
3.在中,平分,则等于( )
A. B. C. D.
【答案】B
【解析】本题主要考查直角三角形的性质(两锐角互余)以及角平分线的定义,先根据直角三角形两锐角互余求出的度数,再利用角平分线的性质求出的度数.
解:在中,,,
,
平分,
.
故选:B.
4.将三角尺按如图位置摆放,顶点落在直线上,顶点落在直线上.若,,则的度数是( )
A. B. C. D.
【答案】C
【解析】本题考查了直角三角形两锐角互余,平行线的性质,掌握平行线的性质求角度的计算是关键.
根据题意,得到,根据平行线的性质得到,由此即可求解.
解:如图所示,
,
∴,
∵,
∴,
故选:C .
5.满足下列条件的不是直角三角形的是( )
A. B.
C. D.
【答案】B
【解析】本题考查直角三角形的识别,根据三角形内角和定理以及直角三角形的判定逐项判断,即可得到结论.
解:A,,是直角三角形,不合题意;
B,时,最大的角,不是直角三角形,符合题意;
C,,则,是直角三角形,不合题意;
D,,则,是直角三角形,不合题意;
故选B.
二、填空题
6.如图,将直尺与30°角的三角尺叠放在一起,若,则的大小是 °.
【答案】55
【解析】本题主要考查了平行线的性质,由三角尺可知,由平角可求,再根据平行线的性质可知.
解:如图:
由的三角尺可知,
∴.
由平行线的性质可知.
故答案为:55.
7.如图,在Rt△ABC 中,∠B=90°,直线 DE 与 AC,BC 分别交于 D,E 两点.若∠DEC=∠A,则△EDC 是 .
【答案】直角三角形
【解析】根据直角三角形的两个锐角互余可知∠A+∠C=90°,再由∠DEC=∠A进而可得出结论.
解:解: 在Rt△ABC 中,
∵∠B=90°,
∴∠A+∠C=90°,
∵∠DEC=∠A,
∴∠DEC+∠C=90°,
∴∠EDC=90°,
∴△EDC 是直角三角形,
故答案为 直角三角形.
8.在一个直角三角形中,已知一个锐角比另一个锐角的倍多,则较小锐角的度数为 .
【答案】/15度
【解析】本题考查了直角三角形两锐角互余的性质,关键步骤是正确设定变量并准确列方程,最终求出较小的锐角度数.本题设定未知数,根据直角三角形两锐角互余的性质,建立方程求解较小的锐角度数.
解:设较小的锐角为,则较大的锐角为,
根据直角三角形两锐角之和为,得:
,
解得:,
所以较小锐角的度数为.
故答案为:.
9.把一块直尺与一块三角板按如图所示的方式放置.若,则的度数是 .
【答案】/128度
【解析】本题考查平行线的性质、直角三角形的两个锐角互余,根据平行线的性质、直角三角形的两个锐角互余,结合邻补角求解即可.
解:如图,
由题意,,,,
∵,
∴,则,
∴,
∴,
故答案为:.
10.如图,中,是上的高,平分,,则 度.
【答案】10
【解析】本题考查的是三角形内角和定理,三角形的角平分线的定义,三角形高的含义.先由三角形的内角和定理求解的大小,再由角平分线的性质求解的大小,再利用直角三角形的两锐角互余求出,最后利用角的和差关系可得答案.
解:在中,,
∴,
∵平分,
∴.,
∵是上的高,
∴,
∴,
∴.
故答案为:10.
三、解答题
11.如图,,,垂足为点.
(1)若,请求出的度数;
(2)若,试问与平行吗?为什么?
【答案】(1)
(2),理由见解析
【解析】本题主要考查了平行线的性质与判定、同角或等角的余角相等、直角三角形的性质.
(1)因为,根据同位角相等,两直线平行可证,根据两直线平行,同位角相等可知;
(2)根据垂直的定义可知,根据直角三角形两锐角互余可得,因为,根据同角的余角相等可证,等量代换可得,根据内错角相等,两直线平行可证.
解:(1)∵,
∴,
∴,
∵,
∴.
(2),理由如下:
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
12.如图,点分别在上,连接,于点,.
(1)求的度数;
(2)若,求证:.
【答案】(1)
(2)见解析
【解析】本题考查了平行线的判定,垂直的定义,直角三角形特征,熟练掌握平行线的判定,同角的余角相等是解题的关键;
(1)根据垂直的定义和直角三角形特征可得,再通过等量代换即可求出;
(2)根据同角的余角相等可得,再通过等量代换可得,即可证明.
解:(1),
,
,
,
,
;
(2)证明:,
,
,
,
,
,
,
.
21世纪教育网(www.21cnjy.com)
同课章节目录
