2025年苏教版五年级下册数学暑假必刷专题:解决问题的策略(含解析)
文档属性
| 名称 | 2025年苏教版五年级下册数学暑假必刷专题:解决问题的策略(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 705.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 09:52:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年苏教版五年级下册数学暑假必刷专题:解决问题的策略
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一条毛毛虫从幼虫长到成虫,每天长大一倍,28天能长到20cm。当长到5cm时,需要( )天。
A.27 B.26 C.25 D.20
2.10+11+12+13+14+15=( )。
A.76 B.75 C.65
3.下面各图形中,与其它两个图形周长不一样的是( )。
A. B. C.
4.数学学习中,经常会用到一种思想“转化”。下面运用了“转化”思想的有( )。
A.②③ B.①②③ C.①③④ D.①②③④
5.如图运用了“转化”思想方法的有( )个。
A.1 B.2 C.3 D.4
6.下列选项中,用到转化策略的有( )个。
①将平行四边形的面积转化为长方形的面积。
②计算小数乘法时,把小数乘法转化为整数乘法。
③把异分母分数转化为同分母分数进行计算。
④推导圆的面积时,把圆剪成一个近似的长方形。
⑤推导乘法交换律。
A.5 B.4 C.3 D.2
7.下图是由一个大正方形与一个小正方形拼成的,已知小正方形的边长为4cm,阴影部分的面积为28cm2。那么空白部分的面积为( )cm2。
A.20 B.24 C.28 D.32
8.4张扑克牌排成一排,先将第1张和第2张交换位置,再将最后一张移到最前面,翻开后是4、7、8、2.原来的4张牌按顺序是( )
A.2、4、7、8 B.4、2、7、8 C.8、7、2、4 D.7、2、8、4
二、填空题
9.计算异分母分数加、减法时,把异分母分数转化成大小不变的( )分数进行计算。
10.数学思想方法是数学的灵魂,“转化”思想作为重要的数学思想方法之一,在我们的学习生活中无处不在。下面运用了“转化”思想的有( )。(填序号)
① 求内角和 ② 分数加法 ③ 求面积
11.求下面涂色图形的面积,可以把它转化成规则图形,将上面的半圆向( )平移( )格,就转化成一个长方形。这个长方形的面积是( )。(每小格边长是1厘米)
12.小红买了2支钢笔和3支毛笔,君君买了7支同样的毛笔,两人用去的钱一样多。一枝钢笔的价钱等于( )支毛笔的价钱。
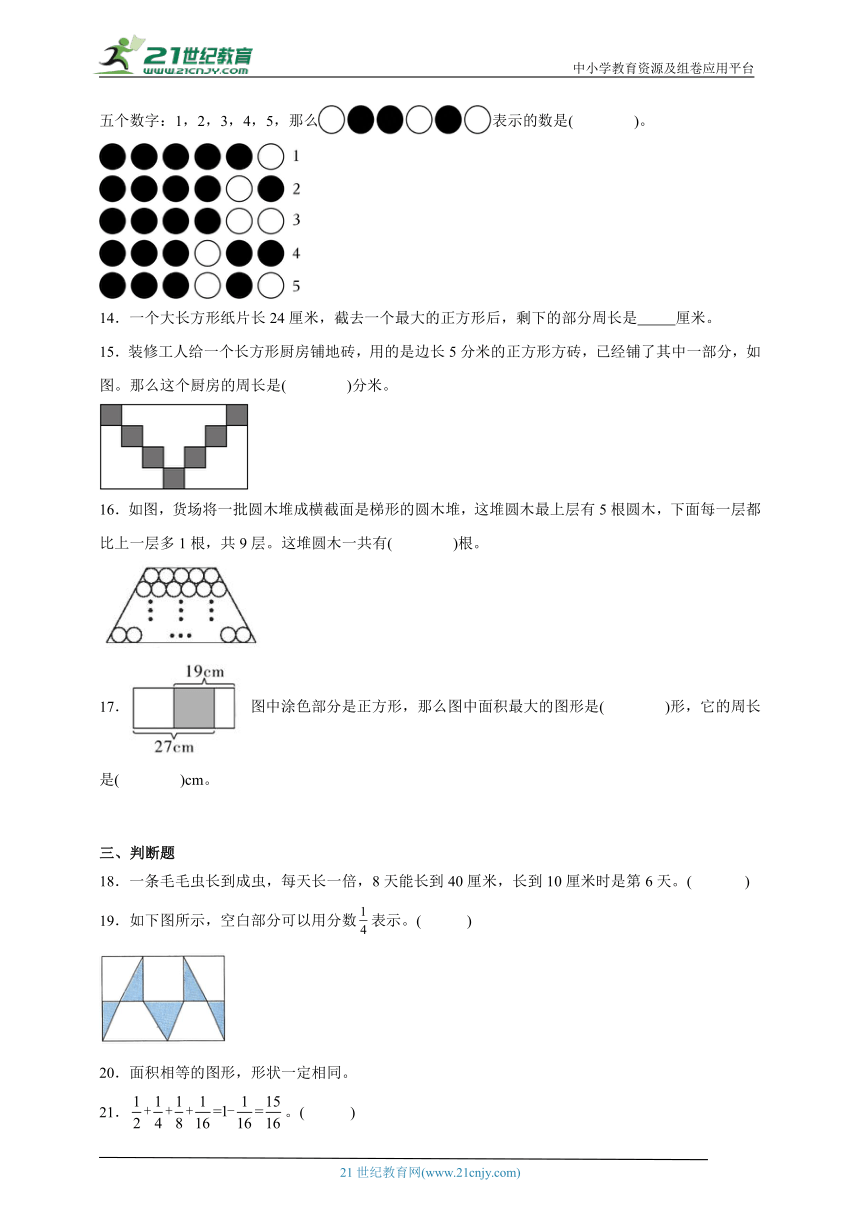
13.将6个灯泡排成一行,用和表示灯亮和灯不亮,如图是这一行灯的五种情况,分别表示五个数字:1,2,3,4,5,那么表示的数是( )。
14.一个大长方形纸片长24厘米,截去一个最大的正方形后,剩下的部分周长是 厘米。
15.装修工人给一个长方形厨房铺地砖,用的是边长5分米的正方形方砖,已经铺了其中一部分,如图。那么这个厨房的周长是( )分米。
16.如图,货场将一批圆木堆成横截面是梯形的圆木堆,这堆圆木最上层有5根圆木,下面每一层都比上一层多1根,共9层。这堆圆木一共有( )根。
17.图中涂色部分是正方形,那么图中面积最大的图形是( )形,它的周长是( )cm。
三、判断题
18.一条毛毛虫长到成虫,每天长一倍,8天能长到40厘米,长到10厘米时是第6天。( )
19.如下图所示,空白部分可以用分数表示。( )
20.面积相等的图形,形状一定相同。
21.。( )
四、计算题
22.能用简便算法的用简便算法计算。
23.计算下面各题,能简算的要简算。
+(+) -+
-+- ++++++
五、作图题
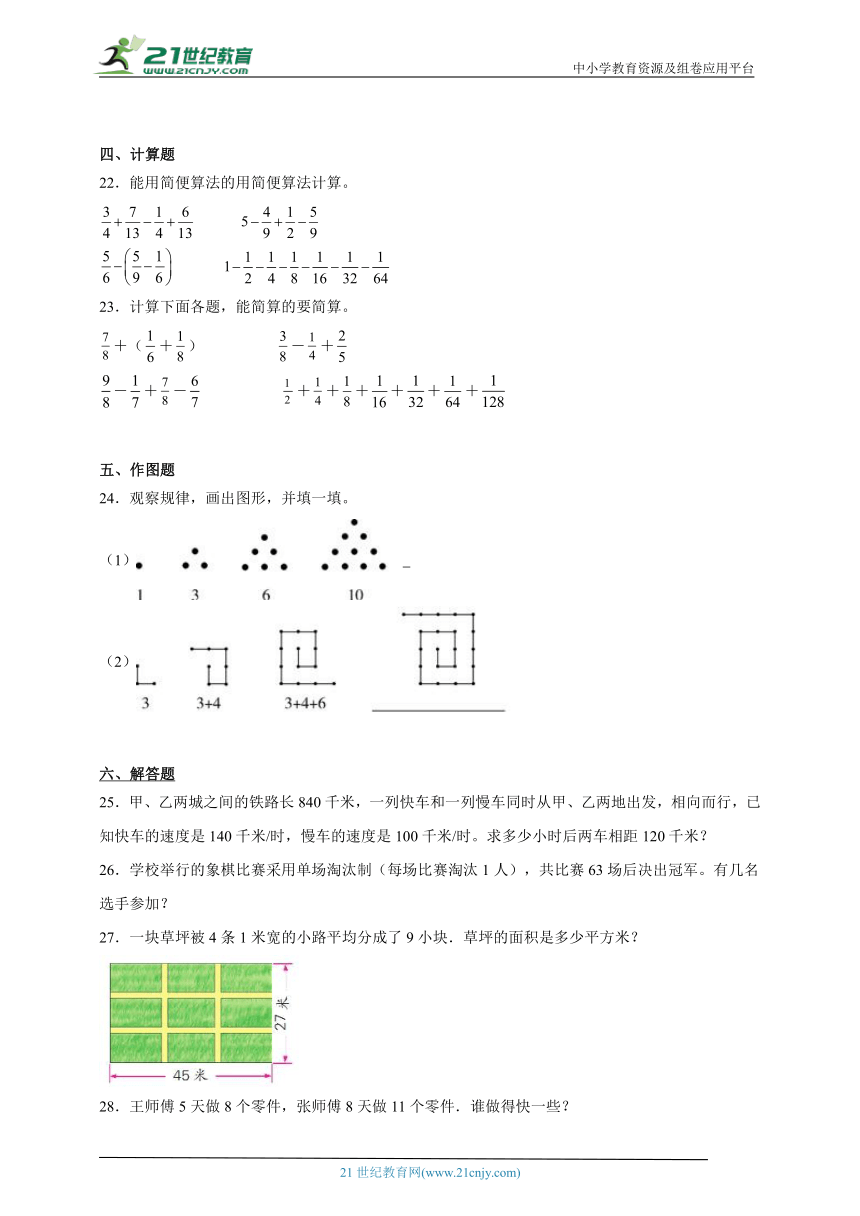
24.观察规律,画出图形,并填一填。
(1)
(2)
六、解答题
25.甲、乙两城之间的铁路长840千米,一列快车和一列慢车同时从甲、乙两地出发,相向而行,已知快车的速度是140千米/时,慢车的速度是100千米/时。求多少小时后两车相距120千米?
26.学校举行的象棋比赛采用单场淘汰制(每场比赛淘汰1人),共比赛63场后决出冠军。有几名选手参加?
27.一块草坪被4条1米宽的小路平均分成了9小块.草坪的面积是多少平方米?
28.王师傅5天做8个零件,张师傅8天做11个零件.谁做得快一些?
29.五金市场堆放了一堆钢管,横截面近似梯形。爸爸让华华去数一数钢管的数量,华华发现钢管的最上层放了4根,最下层放了10根,每一层都比上一层多1根。华华一下子就算出了钢管的数量,你知道华华是怎么算的吗?
《2025年苏教版五年级下册数学暑假必刷专题:解决问题的策略》参考答案
题号 1 2 3 4 5 6 7 8
答案 B B A D D B B C
1.B
【分析】根据题意,我们可以用倒推法,已知28天能长到20cm,那么27天就能长到20÷2=10cm,26天就能长到10÷2=5cm,据此解答即可。
【详解】由分析可知:
一条毛毛虫从幼虫长到成虫,每天长大一倍,28天能长到20cm。当长到5cm时,需要26天。
故答案为:B
2.B
【分析】根据数据特点,10+15=11+14=12+13,据此计算即可。
【详解】10+11+12+13+14+15
=(10+15)+(11+14)+(12+13)
=25×3
=75
故答案为:B
【点睛】本题也可以直接计算得出答案。
3.A
【分析】通过平移法,将不规则图形变换成规则图形即可解答。
【详解】B项把两边的横线上下平移、竖线左右平移,C项通过把短横线向上平移、短竖线向右平移,都可以填补成一个长是5cm,宽是2cm的长方形。而A项把中间的短横线向上平移后即可填补成长是5cm,宽是2cm的长方形,多了两条短竖线,所以周长比其他两个选项长。
故答案为:A。
【点睛】本题主要考查在遇到不规则图形求周长时,要学会利用平移法对图形进行变换解题的方法。
4.D
【分析】转化思想是数学中的重要方法,核心是将复杂、未知或抽象的问题转化为简单、已知或具体的形式。逐项判断四个数学问题中哪些运用了转化思想。
【详解】①把三角形转化成长方形,利用长方形的面积公式推导出三角形的面积公式,用到了转化思想。
②把异分母分数的加法转化成同分母分数相加,用到了转化思想。
③把的计算问题转化为图形面积求和,用到了转化思想。
④把圆转化成梯形,利用梯形的面积公式推导出圆的面积公式,用到了转化思想。
综上所述,运用了“转化”思想的有①②③④。
故答案为:D
5.D
【分析】①探究多边形的内角和,从多边形的一个顶点出发,向和它不相邻的顶点连线,把这个多边形变成若干个三角形,也就是把多边形的内角和转化成若干个三角形的内角和,这是运用了“转化”的思想;
②小数乘法的计算时,先不看小数点,按照整数乘法的计算方法求出结果,再根据小数的位数点上小数点,这是把小数乘法转化成了整数乘法,是运用了“转化”的思想;
③探究平行四边形的面积公式时,先把平行四边形沿着高剪开,然后平拼成一个长方形,拼成的长方形和平行四边形面积不变,而且长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高,根据长方形的面积=长×宽,得出平行四边形的面积=底×高;是运用了“转化”的思想;
④组合图形周长计算时,先把多边形的边通过平移转化成一个长方形,再根据长方形周长=(长×宽)×2,求出多边形周长,是运用了“转化”的思想。
据此即可选择。
【详解】由分析可知:
①②③④运用了“转化”的思想,则运用了“转化”思想方法的有4个。
故答案为:D
6.B
【分析】在小学数学里,经常将某一问题转化为另一问题,将某些已知条件或数量关系转化为另外的条件或关系,化生为熟、化难为易、化繁为简、化高为低、化曲为直,这就是转化的思想方法。例如:平行四边形的面积公式可以转化为长方形而求得;三角形的面积公式可以转化为平行四边形而求得;圆的面积公式可以转化为长方形而求得;小数乘法、小数除法转化为整数乘法、整数除法;异分母分数加减法转化为同分母分数加减法等都运用了转化的思想方法,据此解答。
【详解】
①
推导平行四边形的面积公式时,把平行四边形转化为长方形,利用“长方形的面积=长×宽”得出“平行四边形的面积=底×高”。
②
计算小数乘法时,把小数乘法转化为整数乘法计算出积,再点小数点,看因数中一共有几位小数就从积的右边起数出几位点上小数点,位数不够时用0补足,小数部分末尾的0要去掉。
③异分母分数的分数单位不相同,不能直接相加减,计算异分母分数加减法时,先把异分母分数转化为同分母分数,再按照同分母分数加减法计算。
④
推导圆的面积计算公式时,把圆剪拼成一个近似的长方形,把圆的面积转化为长方形的面积,长方形的长相当于圆周长的一半,长方形的宽相当于圆的半径,从而推导出“”。
⑤推导乘法交换律通常通过举例或直接逻辑推理,属于规律总结而非转化策略。
由上可知,用到转化策略的有①②③④,一共4个。
故答案为:B
7.B
【分析】阴影部分是由一个三角形和小正方形组成的。正方形的面积=边长×边长,据此可以求出小正方形的面积。用阴影部分的面积减去小正方形的面积即是三角形的面积,三角形的高是4厘米,根据三角形的面积=底×高÷2,可以求出三角形的底,即是大正方形的边长。求出大正方形的面积,再减去三角形的面积就是空白部分的面积。
【详解】28-4×4=12(平方厘米)
12×2÷4=6(厘米)
6×6-12=24(平方厘米)
故答案为:B
【点睛】用阴影部分的面积减去小正方形的面积求出三角形的面积,继而求出三角形的底是解题的关键。
8.C
【分析】根据“将最后一张移到最前面,翻开后第一张是4,”知道原来的最后一张是4,又因为“先将第1张和第2张交换位置,又将最后一张移到最前面”,那么原来的第二张还是后来的第二张,原来的第一张是后来的第三张,由此即可得出答案。
【详解】因为,最后一张移到最前面,翻开后第一张是4,7,8,2,
所以,移动前为:7,8,2,4;
则先将第1张和第2张交换位置前为:8,7,2,4.
故答案为:C
【点睛】解答此题的关键是,根据题意,运用逆推的方法,逐步找出扑克牌在移动前后的关系,即可做出选择。
9.同分母
【详解】计算异分母分数加、减法时,把异分母分数转化成大小不变的同分母分数后再进行计算。
例:
10.①②③
【分析】①把正六边形转化为三角形,再根据三角形内角和,求出六边形的内角和;
②把异分母分数相加转化为同分母分数相加,再按照同分母分数相加的方法计算异分母分数的加法;
③把平行四边形转化为长方形,利用长方形面积求出平行四边形的面积。
【详解】根据分析可知:①②③都运用了“转化”思想。
11. 下 2 8平方厘米
【分析】涂色不规则图形面积转化成规则图形的面积,也就是长方形的面积,长方形的面积=长×宽。因为每小格边长是1厘米,长是4个格子,则长是4厘米,宽是2个格子,则宽是2厘米。则面积是4平方厘米。
【详解】4×2=8(平方厘米)
将上面的半圆向下平移2格,就转化成一个长方形。这个长方形的面积是8平方厘米。
12.2
【分析】根据小红买了2支钢笔和3支毛笔,君君买了7支同样的毛笔,两人用去的钱同样多,7-3=4(支),可知2支钢笔的价格和4支毛笔的价格相同,进而求出一支钢笔的价钱等于几支毛笔的价钱。
【详解】7-3=4(支)
4÷2=2(支)
【点睛】此题主要考查了根据简单的等量代换解题的能力。
13.37
【分析】根据给出的这五种情况对应的数字可知:○在个位上表示1,在十位上表示2,在百位上表示4,在千位上表示8,依此类推,●表示0。
【详解】
中○在十万位上表示32。
1+0+4+0+0+32=37
因此表示的数是37。
14.48
【分析】设原长方形的宽为x厘米,根据题意可知,长方形中截去一个最大的正方形,剩下的图形是一个长x厘米、宽(24-x)厘米的长方形,根据长方形周长=(长+宽)×2,列式解题即可。
【详解】假设原长方形的宽为x厘米,可得:
(x+24-x)×2
=24×2
=48(厘米)
所以,剩下的部分周长是48厘米。
【点睛】明确长方形中截去一个最大的正方形,剩下的图形是一个长等于原长方形的宽、宽等于原长方形长与宽的差,是解答此题的关键。
15.110
【分析】利用平移的方法将地砖平移到上边可得到一个长方形,求出小长方形的长(房间的长)和宽,再用宽乘4,求出房间的宽,根据长方形周长=(长+宽)×2,代入数值进行计算即可求出这个房间地面的周长。
【详解】根据分析可知,这个厨房的长是:5×7=35(分米),宽是:5×4=20(分米);
(35+20)×2
=55×2
=110(分米)
则这个厨房的周长是110分米。
16.81
【分析】已知堆成梯形的圆木堆的最上层有5根圆木,下面每一层都比上一层多1根,共9层,那么下层就有(5+1×8)根圆木;再根据梯形的面积=(上底+下底)×高÷2,求出这堆圆木的总根数。
【详解】下层有:
5+1×8
=5+8
=13(根)
一共有:
(5+13)×9÷2
=18×9÷2
=81(根)
这堆圆木一共有81根。
17. 长方 92
【分析】观察图形可得:上面的19厘米加下面的27厘米,正好比最大的长方形的长多了一条中间小正方形边长,小正方形的边长与大长方形的宽相等,由此可得:19+27=46厘米就是这个大长方形的一条长与一条宽的和,根据长方形的周长=(长+宽) ×2即可解决问题。
【详解】(19+27)×2
=46×2
=92(厘米)
图中面积最大的图形是长方形,它的周长是92厘米。
【点睛】此题的图形是一个典型的题目,中间的正方形的边长是一个中间等量,正好等于大长方形的一条宽的长度;由此得出题干中19+27的和就是大长方形的长与宽的和。
18.√
【分析】根据题意知道,一条毛毛虫由幼虫长成成虫,每天长大一倍,8天能长到40厘米,逆推知道7天就长到20厘米,6天就长到10厘米,由此得出答案。
【详解】第8天能长到40厘米,
第7天能长到:40÷2=20(厘米)
第6天能长到:20÷2=10(厘米)
所以原题说法正确.
故答案为:√
【点睛】解答此题的关键是,根据题意,运用逆推的方法,不难得出答案。
19.×
【分析】将单位“1”平均分成若干份,表示这样一份或几份的数为分数。把长方形的面积看成单位“1”,以此计算出阴影部分面积解答。
【详解】图中的几个阴影部分三角形的高都是长方形宽的一半,并且底之和是长方形的长,所以阴影部分面积之和是× 长×(×宽)= ×长×宽,长方形面积=长×宽,所以阴影部分面积是长方形面积的。所以原题说法错误。
【点睛】解答此题我们可以整体考虑阴影部分的面积,找出阴影部分和长方形之间的联系是解题关键。
20.×
【详解】如果两个图形的面积相等,那么它们的形状不一定相同,所以本题说法错误;
故答案为:×
21.√
【分析】每相邻的两个分数拆项后,都有相同的数,故把每个分数拆成分数相减的形式:;;…然后相加即可判断。
【详解】
所以原题说法正确。
【点睛】此题考查了学生对分数的拆项的掌握情况,以及简算能力。
22.;;
;
【分析】第一题利用加法交换律和结合律即可简便计算;
第二题利用加法交换律和减法的性质即可简便计算;
第三题利用减法的性质即可简便计算;
第四题利用减法的性质即可简便计算。
【详解】
=
=
=
=
=
=
=
=
=
=
=
=
=
23.;
1;
【分析】(1)根据加法交换律a+b=b+a进行简算;
(2)从左到右依次计算;
(3)根据加法交换律a+b=b+a,加法结合律(a+b)+c=a+(b+c),减法的性质a-b-c=a-(b+c)进行简算;
(4)观察发现:=1-,=-,=-…,按此规律计算。
【详解】(1)+(+)
=++
=1+
=
(2)-+
=-+
=+
=+
=
(3)-+-
=+--
=(+)-(+)
=2-1
=1
(4)++++++
=1-+-+-+-+-+-+-
=1-
=
24.(1)15;21;
(2)3+4+6+8;3+4+6+8+10
【分析】(1)观察图形可知,图形变化规律:图形由上而下,下一行都比上一行多1个点数;数字规律:1=3=6=10,从首项开始,每次加的数值都会多1,首尾连加,以此规律解答。
(2)观察图形可知,图形变化规律:图形由内而外,逆时针旋转排列,每次以一条横线段和一条竖线段为一组增加,而且增加的每组线段的点数除去首尾点,中间的点数会逐次比上一组多1;数字规律:3、3+4、3+4+6,每次多加一个数,这个数比前一个数多2,以此解答。
【详解】(1)15;21;
(2)3+4+6+8;3+4+6+8+10
【点睛】此题关键在于学生对“找规律”题型的掌握和应用,平时要多注意观察前数与后数之间的差额,通过差额寻找规律变化,积累经验。
25.3小时或4小时
【分析】根据题意可知,分为两种情况:第一种情况未相遇两车相距120千米,两车行驶的总路程为(840-120)千米,再除以两车的速度和即可;第二种情况相遇后两车相距120千米,两车行驶的总路程为(840+120)千米,再除以两车的速度和即可;
【详解】未相遇:(840-120)÷(140+100)
=720÷240
=3(小时);
相遇后:(840+120)÷(140+100)
=960÷240
=4(小时);
答:3小时或4小时后两车都会相距120千米。
【点睛】解答本题时要考虑全面,分未相遇和相遇后两种情况分析。
26.64名
【分析】在单场淘汰制中,每场比赛淘汰1人。要决出冠军,需淘汰所有其他选手,即淘汰总人数为参赛人数减1(仅冠军不淘汰)。题目中共比赛63场,因此淘汰了63人。由此可得参赛人数为被淘汰人数加1,据此解答即可。
【详解】63十1=64(名)
答:有64名选手参加。
27.1075平方米
【详解】(45-1-1)×(27-1-1)
=43×25
=1075(平方米)
答:草坪的面积是1075平方米.
28.王师傅快
【详解】王师傅:8÷5= (个)
张师傅:11÷8= (个)
> 所以王师傅快.
29.49根
【分析】通过最上层有4根钢管,最下层有10根钢管,每一层都比上一层多1根,层数=(最下层根数-最上层根数)÷每相邻两层相差的根数+1,即可得出层数,然后根据高斯求和公式:(首项+末项)×项数÷2,即可解答。
【详解】层数:(10-4)÷1+1=7(层)
总数:(4+10)×7÷2=49(根)
答:一共有49根钢管。
【点睛】此题考查学生灵活运用梯形的面积公式,关键是求出一共有多少层。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025年苏教版五年级下册数学暑假必刷专题:解决问题的策略
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一条毛毛虫从幼虫长到成虫,每天长大一倍,28天能长到20cm。当长到5cm时,需要( )天。
A.27 B.26 C.25 D.20
2.10+11+12+13+14+15=( )。
A.76 B.75 C.65
3.下面各图形中,与其它两个图形周长不一样的是( )。
A. B. C.
4.数学学习中,经常会用到一种思想“转化”。下面运用了“转化”思想的有( )。
A.②③ B.①②③ C.①③④ D.①②③④
5.如图运用了“转化”思想方法的有( )个。
A.1 B.2 C.3 D.4
6.下列选项中,用到转化策略的有( )个。
①将平行四边形的面积转化为长方形的面积。
②计算小数乘法时,把小数乘法转化为整数乘法。
③把异分母分数转化为同分母分数进行计算。
④推导圆的面积时,把圆剪成一个近似的长方形。
⑤推导乘法交换律。
A.5 B.4 C.3 D.2
7.下图是由一个大正方形与一个小正方形拼成的,已知小正方形的边长为4cm,阴影部分的面积为28cm2。那么空白部分的面积为( )cm2。
A.20 B.24 C.28 D.32
8.4张扑克牌排成一排,先将第1张和第2张交换位置,再将最后一张移到最前面,翻开后是4、7、8、2.原来的4张牌按顺序是( )
A.2、4、7、8 B.4、2、7、8 C.8、7、2、4 D.7、2、8、4
二、填空题
9.计算异分母分数加、减法时,把异分母分数转化成大小不变的( )分数进行计算。
10.数学思想方法是数学的灵魂,“转化”思想作为重要的数学思想方法之一,在我们的学习生活中无处不在。下面运用了“转化”思想的有( )。(填序号)
① 求内角和 ② 分数加法 ③ 求面积
11.求下面涂色图形的面积,可以把它转化成规则图形,将上面的半圆向( )平移( )格,就转化成一个长方形。这个长方形的面积是( )。(每小格边长是1厘米)
12.小红买了2支钢笔和3支毛笔,君君买了7支同样的毛笔,两人用去的钱一样多。一枝钢笔的价钱等于( )支毛笔的价钱。
13.将6个灯泡排成一行,用和表示灯亮和灯不亮,如图是这一行灯的五种情况,分别表示五个数字:1,2,3,4,5,那么表示的数是( )。
14.一个大长方形纸片长24厘米,截去一个最大的正方形后,剩下的部分周长是 厘米。
15.装修工人给一个长方形厨房铺地砖,用的是边长5分米的正方形方砖,已经铺了其中一部分,如图。那么这个厨房的周长是( )分米。
16.如图,货场将一批圆木堆成横截面是梯形的圆木堆,这堆圆木最上层有5根圆木,下面每一层都比上一层多1根,共9层。这堆圆木一共有( )根。
17.图中涂色部分是正方形,那么图中面积最大的图形是( )形,它的周长是( )cm。
三、判断题
18.一条毛毛虫长到成虫,每天长一倍,8天能长到40厘米,长到10厘米时是第6天。( )
19.如下图所示,空白部分可以用分数表示。( )
20.面积相等的图形,形状一定相同。
21.。( )
四、计算题
22.能用简便算法的用简便算法计算。
23.计算下面各题,能简算的要简算。
+(+) -+
-+- ++++++
五、作图题
24.观察规律,画出图形,并填一填。
(1)
(2)
六、解答题
25.甲、乙两城之间的铁路长840千米,一列快车和一列慢车同时从甲、乙两地出发,相向而行,已知快车的速度是140千米/时,慢车的速度是100千米/时。求多少小时后两车相距120千米?
26.学校举行的象棋比赛采用单场淘汰制(每场比赛淘汰1人),共比赛63场后决出冠军。有几名选手参加?
27.一块草坪被4条1米宽的小路平均分成了9小块.草坪的面积是多少平方米?
28.王师傅5天做8个零件,张师傅8天做11个零件.谁做得快一些?
29.五金市场堆放了一堆钢管,横截面近似梯形。爸爸让华华去数一数钢管的数量,华华发现钢管的最上层放了4根,最下层放了10根,每一层都比上一层多1根。华华一下子就算出了钢管的数量,你知道华华是怎么算的吗?
《2025年苏教版五年级下册数学暑假必刷专题:解决问题的策略》参考答案
题号 1 2 3 4 5 6 7 8
答案 B B A D D B B C
1.B
【分析】根据题意,我们可以用倒推法,已知28天能长到20cm,那么27天就能长到20÷2=10cm,26天就能长到10÷2=5cm,据此解答即可。
【详解】由分析可知:
一条毛毛虫从幼虫长到成虫,每天长大一倍,28天能长到20cm。当长到5cm时,需要26天。
故答案为:B
2.B
【分析】根据数据特点,10+15=11+14=12+13,据此计算即可。
【详解】10+11+12+13+14+15
=(10+15)+(11+14)+(12+13)
=25×3
=75
故答案为:B
【点睛】本题也可以直接计算得出答案。
3.A
【分析】通过平移法,将不规则图形变换成规则图形即可解答。
【详解】B项把两边的横线上下平移、竖线左右平移,C项通过把短横线向上平移、短竖线向右平移,都可以填补成一个长是5cm,宽是2cm的长方形。而A项把中间的短横线向上平移后即可填补成长是5cm,宽是2cm的长方形,多了两条短竖线,所以周长比其他两个选项长。
故答案为:A。
【点睛】本题主要考查在遇到不规则图形求周长时,要学会利用平移法对图形进行变换解题的方法。
4.D
【分析】转化思想是数学中的重要方法,核心是将复杂、未知或抽象的问题转化为简单、已知或具体的形式。逐项判断四个数学问题中哪些运用了转化思想。
【详解】①把三角形转化成长方形,利用长方形的面积公式推导出三角形的面积公式,用到了转化思想。
②把异分母分数的加法转化成同分母分数相加,用到了转化思想。
③把的计算问题转化为图形面积求和,用到了转化思想。
④把圆转化成梯形,利用梯形的面积公式推导出圆的面积公式,用到了转化思想。
综上所述,运用了“转化”思想的有①②③④。
故答案为:D
5.D
【分析】①探究多边形的内角和,从多边形的一个顶点出发,向和它不相邻的顶点连线,把这个多边形变成若干个三角形,也就是把多边形的内角和转化成若干个三角形的内角和,这是运用了“转化”的思想;
②小数乘法的计算时,先不看小数点,按照整数乘法的计算方法求出结果,再根据小数的位数点上小数点,这是把小数乘法转化成了整数乘法,是运用了“转化”的思想;
③探究平行四边形的面积公式时,先把平行四边形沿着高剪开,然后平拼成一个长方形,拼成的长方形和平行四边形面积不变,而且长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高,根据长方形的面积=长×宽,得出平行四边形的面积=底×高;是运用了“转化”的思想;
④组合图形周长计算时,先把多边形的边通过平移转化成一个长方形,再根据长方形周长=(长×宽)×2,求出多边形周长,是运用了“转化”的思想。
据此即可选择。
【详解】由分析可知:
①②③④运用了“转化”的思想,则运用了“转化”思想方法的有4个。
故答案为:D
6.B
【分析】在小学数学里,经常将某一问题转化为另一问题,将某些已知条件或数量关系转化为另外的条件或关系,化生为熟、化难为易、化繁为简、化高为低、化曲为直,这就是转化的思想方法。例如:平行四边形的面积公式可以转化为长方形而求得;三角形的面积公式可以转化为平行四边形而求得;圆的面积公式可以转化为长方形而求得;小数乘法、小数除法转化为整数乘法、整数除法;异分母分数加减法转化为同分母分数加减法等都运用了转化的思想方法,据此解答。
【详解】
①
推导平行四边形的面积公式时,把平行四边形转化为长方形,利用“长方形的面积=长×宽”得出“平行四边形的面积=底×高”。
②
计算小数乘法时,把小数乘法转化为整数乘法计算出积,再点小数点,看因数中一共有几位小数就从积的右边起数出几位点上小数点,位数不够时用0补足,小数部分末尾的0要去掉。
③异分母分数的分数单位不相同,不能直接相加减,计算异分母分数加减法时,先把异分母分数转化为同分母分数,再按照同分母分数加减法计算。
④
推导圆的面积计算公式时,把圆剪拼成一个近似的长方形,把圆的面积转化为长方形的面积,长方形的长相当于圆周长的一半,长方形的宽相当于圆的半径,从而推导出“”。
⑤推导乘法交换律通常通过举例或直接逻辑推理,属于规律总结而非转化策略。
由上可知,用到转化策略的有①②③④,一共4个。
故答案为:B
7.B
【分析】阴影部分是由一个三角形和小正方形组成的。正方形的面积=边长×边长,据此可以求出小正方形的面积。用阴影部分的面积减去小正方形的面积即是三角形的面积,三角形的高是4厘米,根据三角形的面积=底×高÷2,可以求出三角形的底,即是大正方形的边长。求出大正方形的面积,再减去三角形的面积就是空白部分的面积。
【详解】28-4×4=12(平方厘米)
12×2÷4=6(厘米)
6×6-12=24(平方厘米)
故答案为:B
【点睛】用阴影部分的面积减去小正方形的面积求出三角形的面积,继而求出三角形的底是解题的关键。
8.C
【分析】根据“将最后一张移到最前面,翻开后第一张是4,”知道原来的最后一张是4,又因为“先将第1张和第2张交换位置,又将最后一张移到最前面”,那么原来的第二张还是后来的第二张,原来的第一张是后来的第三张,由此即可得出答案。
【详解】因为,最后一张移到最前面,翻开后第一张是4,7,8,2,
所以,移动前为:7,8,2,4;
则先将第1张和第2张交换位置前为:8,7,2,4.
故答案为:C
【点睛】解答此题的关键是,根据题意,运用逆推的方法,逐步找出扑克牌在移动前后的关系,即可做出选择。
9.同分母
【详解】计算异分母分数加、减法时,把异分母分数转化成大小不变的同分母分数后再进行计算。
例:
10.①②③
【分析】①把正六边形转化为三角形,再根据三角形内角和,求出六边形的内角和;
②把异分母分数相加转化为同分母分数相加,再按照同分母分数相加的方法计算异分母分数的加法;
③把平行四边形转化为长方形,利用长方形面积求出平行四边形的面积。
【详解】根据分析可知:①②③都运用了“转化”思想。
11. 下 2 8平方厘米
【分析】涂色不规则图形面积转化成规则图形的面积,也就是长方形的面积,长方形的面积=长×宽。因为每小格边长是1厘米,长是4个格子,则长是4厘米,宽是2个格子,则宽是2厘米。则面积是4平方厘米。
【详解】4×2=8(平方厘米)
将上面的半圆向下平移2格,就转化成一个长方形。这个长方形的面积是8平方厘米。
12.2
【分析】根据小红买了2支钢笔和3支毛笔,君君买了7支同样的毛笔,两人用去的钱同样多,7-3=4(支),可知2支钢笔的价格和4支毛笔的价格相同,进而求出一支钢笔的价钱等于几支毛笔的价钱。
【详解】7-3=4(支)
4÷2=2(支)
【点睛】此题主要考查了根据简单的等量代换解题的能力。
13.37
【分析】根据给出的这五种情况对应的数字可知:○在个位上表示1,在十位上表示2,在百位上表示4,在千位上表示8,依此类推,●表示0。
【详解】
中○在十万位上表示32。
1+0+4+0+0+32=37
因此表示的数是37。
14.48
【分析】设原长方形的宽为x厘米,根据题意可知,长方形中截去一个最大的正方形,剩下的图形是一个长x厘米、宽(24-x)厘米的长方形,根据长方形周长=(长+宽)×2,列式解题即可。
【详解】假设原长方形的宽为x厘米,可得:
(x+24-x)×2
=24×2
=48(厘米)
所以,剩下的部分周长是48厘米。
【点睛】明确长方形中截去一个最大的正方形,剩下的图形是一个长等于原长方形的宽、宽等于原长方形长与宽的差,是解答此题的关键。
15.110
【分析】利用平移的方法将地砖平移到上边可得到一个长方形,求出小长方形的长(房间的长)和宽,再用宽乘4,求出房间的宽,根据长方形周长=(长+宽)×2,代入数值进行计算即可求出这个房间地面的周长。
【详解】根据分析可知,这个厨房的长是:5×7=35(分米),宽是:5×4=20(分米);
(35+20)×2
=55×2
=110(分米)
则这个厨房的周长是110分米。
16.81
【分析】已知堆成梯形的圆木堆的最上层有5根圆木,下面每一层都比上一层多1根,共9层,那么下层就有(5+1×8)根圆木;再根据梯形的面积=(上底+下底)×高÷2,求出这堆圆木的总根数。
【详解】下层有:
5+1×8
=5+8
=13(根)
一共有:
(5+13)×9÷2
=18×9÷2
=81(根)
这堆圆木一共有81根。
17. 长方 92
【分析】观察图形可得:上面的19厘米加下面的27厘米,正好比最大的长方形的长多了一条中间小正方形边长,小正方形的边长与大长方形的宽相等,由此可得:19+27=46厘米就是这个大长方形的一条长与一条宽的和,根据长方形的周长=(长+宽) ×2即可解决问题。
【详解】(19+27)×2
=46×2
=92(厘米)
图中面积最大的图形是长方形,它的周长是92厘米。
【点睛】此题的图形是一个典型的题目,中间的正方形的边长是一个中间等量,正好等于大长方形的一条宽的长度;由此得出题干中19+27的和就是大长方形的长与宽的和。
18.√
【分析】根据题意知道,一条毛毛虫由幼虫长成成虫,每天长大一倍,8天能长到40厘米,逆推知道7天就长到20厘米,6天就长到10厘米,由此得出答案。
【详解】第8天能长到40厘米,
第7天能长到:40÷2=20(厘米)
第6天能长到:20÷2=10(厘米)
所以原题说法正确.
故答案为:√
【点睛】解答此题的关键是,根据题意,运用逆推的方法,不难得出答案。
19.×
【分析】将单位“1”平均分成若干份,表示这样一份或几份的数为分数。把长方形的面积看成单位“1”,以此计算出阴影部分面积解答。
【详解】图中的几个阴影部分三角形的高都是长方形宽的一半,并且底之和是长方形的长,所以阴影部分面积之和是× 长×(×宽)= ×长×宽,长方形面积=长×宽,所以阴影部分面积是长方形面积的。所以原题说法错误。
【点睛】解答此题我们可以整体考虑阴影部分的面积,找出阴影部分和长方形之间的联系是解题关键。
20.×
【详解】如果两个图形的面积相等,那么它们的形状不一定相同,所以本题说法错误;
故答案为:×
21.√
【分析】每相邻的两个分数拆项后,都有相同的数,故把每个分数拆成分数相减的形式:;;…然后相加即可判断。
【详解】
所以原题说法正确。
【点睛】此题考查了学生对分数的拆项的掌握情况,以及简算能力。
22.;;
;
【分析】第一题利用加法交换律和结合律即可简便计算;
第二题利用加法交换律和减法的性质即可简便计算;
第三题利用减法的性质即可简便计算;
第四题利用减法的性质即可简便计算。
【详解】
=
=
=
=
=
=
=
=
=
=
=
=
=
23.;
1;
【分析】(1)根据加法交换律a+b=b+a进行简算;
(2)从左到右依次计算;
(3)根据加法交换律a+b=b+a,加法结合律(a+b)+c=a+(b+c),减法的性质a-b-c=a-(b+c)进行简算;
(4)观察发现:=1-,=-,=-…,按此规律计算。
【详解】(1)+(+)
=++
=1+
=
(2)-+
=-+
=+
=+
=
(3)-+-
=+--
=(+)-(+)
=2-1
=1
(4)++++++
=1-+-+-+-+-+-+-
=1-
=
24.(1)15;21;
(2)3+4+6+8;3+4+6+8+10
【分析】(1)观察图形可知,图形变化规律:图形由上而下,下一行都比上一行多1个点数;数字规律:1=3=6=10,从首项开始,每次加的数值都会多1,首尾连加,以此规律解答。
(2)观察图形可知,图形变化规律:图形由内而外,逆时针旋转排列,每次以一条横线段和一条竖线段为一组增加,而且增加的每组线段的点数除去首尾点,中间的点数会逐次比上一组多1;数字规律:3、3+4、3+4+6,每次多加一个数,这个数比前一个数多2,以此解答。
【详解】(1)15;21;
(2)3+4+6+8;3+4+6+8+10
【点睛】此题关键在于学生对“找规律”题型的掌握和应用,平时要多注意观察前数与后数之间的差额,通过差额寻找规律变化,积累经验。
25.3小时或4小时
【分析】根据题意可知,分为两种情况:第一种情况未相遇两车相距120千米,两车行驶的总路程为(840-120)千米,再除以两车的速度和即可;第二种情况相遇后两车相距120千米,两车行驶的总路程为(840+120)千米,再除以两车的速度和即可;
【详解】未相遇:(840-120)÷(140+100)
=720÷240
=3(小时);
相遇后:(840+120)÷(140+100)
=960÷240
=4(小时);
答:3小时或4小时后两车都会相距120千米。
【点睛】解答本题时要考虑全面,分未相遇和相遇后两种情况分析。
26.64名
【分析】在单场淘汰制中,每场比赛淘汰1人。要决出冠军,需淘汰所有其他选手,即淘汰总人数为参赛人数减1(仅冠军不淘汰)。题目中共比赛63场,因此淘汰了63人。由此可得参赛人数为被淘汰人数加1,据此解答即可。
【详解】63十1=64(名)
答:有64名选手参加。
27.1075平方米
【详解】(45-1-1)×(27-1-1)
=43×25
=1075(平方米)
答:草坪的面积是1075平方米.
28.王师傅快
【详解】王师傅:8÷5= (个)
张师傅:11÷8= (个)
> 所以王师傅快.
29.49根
【分析】通过最上层有4根钢管,最下层有10根钢管,每一层都比上一层多1根,层数=(最下层根数-最上层根数)÷每相邻两层相差的根数+1,即可得出层数,然后根据高斯求和公式:(首项+末项)×项数÷2,即可解答。
【详解】层数:(10-4)÷1+1=7(层)
总数:(4+10)×7÷2=49(根)
答:一共有49根钢管。
【点睛】此题考查学生灵活运用梯形的面积公式,关键是求出一共有多少层。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
