2024-2025学年四年级下册数学期末全真模拟检测卷(人教版)(含解析)
文档属性
| 名称 | 2024-2025学年四年级下册数学期末全真模拟检测卷(人教版)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 495.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 00:00:00 | ||
图片预览




文档简介
2024-2025学年四年级下册数学期末全真模拟检测卷(人教版)
一、填空题
1.如图中小三角形的边长都相等,那么小蚂蚁从A点沿三角形的边爬到B点的最短路线有 条。
2.如图,有两个装有棋子的盒子,每次从甲盒中拿5个棋子放入乙盒,( )次之后,两盒的棋子数量相等。
3.小华有15本书,小玲有11本书,小华给小玲( )本书,两人的书就一样多。
4.一个六位数221110,将它的各个数位上的数字任意调换顺序,能组成( )个新的六位数。
5.停车场停放了一些小汽车和三轮车,从上面数共有67辆,从下面数共有261个车轮。停车场停放了( )辆小汽车和( )辆三轮车。
6.台湾自古以来就是我国神圣不可侵犯的领土,它的面积为三万六千一百九十二点八一五平方千米,写作( )km2,改写成用“万”作单位并保留两位小数是( )万km2。
7.一场足球赛的门票有两种,一种每张售价30元,另一种每张售价50元,李强购买10张票,一共用去420元,30元的门票买了( )张。
8.小华量得一个等腰三角形的一条边长为2cm,另一条边长为4.5cm。这个三角形的周长是( )cm。
9.参加某会议的30个人被安排在同一个宾馆里,11个房间(3人间和2人间)刚好住满。他们住了( )个3人间,有( )人住在2人间。
10.三根小棒首尾相连围成一个三角形,已知其中两根小棒分别长5cm和11cm,那么还有一根小棒最短可能是( )cm,最长可能是( )cm。(都取整厘米数)
11.如图,一个五边形的内角和是540°,试一试,推导出∠1+∠2+∠3+∠4+∠5=( )°。
12.某旅游团共有37人,一共租用了11艘游艇,正好坐满,其中快艇可以坐5人,摩托艇可以坐2人,租用的快艇有( )艘,摩托艇有( )艘。
二、判断题
13.在6.25的末尾添上两个0,这个数就扩大到原来的100倍。( )
14.4.36在自然数4和5之间,它约等于4。( )
15.已知为非零的数,和的结果都是0。( )
16.计算时,应先算减法。( )
17.从前面、上面、左面观察一个正方体,看到的形状都相同。( )
18.把1.2的小数点去掉,这个数就扩大到原来的10倍。( )
19.所有的四边形都是轴对称图形。( )
三、选择题
20.有2分和5分的硬币共100枚,一共3.2元钱。5分的硬币有( )枚。
A.40 B.100 C.60 D.30
21.你认识下面的徽章吗?( )徽章是轴对称图形。
A. B. C. D.
22.一款床单的标签如图所示,显示的规格为230×245,“245”和“230”分别表示这款床单的长和宽,结合生活实际判断这两个数的单位是( )
A.毫米 B.厘米 C.分米 D.米
23.如图,能围成三角形的一组线段是( )(单位:cm)。
A.①②③ B.①②④ C.①③④ D.②③④
24.电影票有10元、15元、20元三种票价,班长用500元买了30张电影票,其中票价为20元的比票价为10元的多( )张。
A.9 B.10 C.11 D.12
25.洋洋用三根小棒围成了一个三角形,其中两根小棒的长度分别是5cm、7cm。第三根小棒的长度可能是( )。
A.1cm B.11cm C.12cm D.13cm
26.6位中国象棋选手进行比赛,每两人之间比赛一局,如果是平局,参赛选手各得1分;否则赢者得3分,输者得0分。最后六位选手的得分之和为39分,则平了( )局。
A.3 B.4 C.5 D.6
27.霞霞用如图表示某运算定律,她表示的定律是( )。
A.加法结合律 B.乘法结合律 C.乘法交换律 D.乘法分配律
28.我国古代曾用算筹表示数。为了表示小数,就把小数点后面的数放低一行。如图1表示的数是3.12,那么图2表示的数是( )。
A.2.32 B.2.23 C.3.22
29.“0.5”这个数,在下面生活场景中使用最合适的是( )。
A.一袋食盐的质量 B.一个书包的价钱
C.一本数学书封面的大小 D.珠穆朗玛峰的高度
四、计算题
30.直接写出得数。
8×5÷8×5= 25×9×4= 32+68×0= 0×250÷5=
141-77-23= 0.78×100= 4.56÷10= 26×101=
31.竖式计算。(带★验算)
15.8+7.95= ★10-3.67= 25×104=
32.先想好运算顺序,再脱式计算。
235-(456-304)÷4 216÷[(32-18)×3]
209+102÷(52-35) 93×[138-(151-27)]
33.计算图中阴影部分的面积。(单位:米)
五、作图题
34.画出下面三角形指定底上的高。
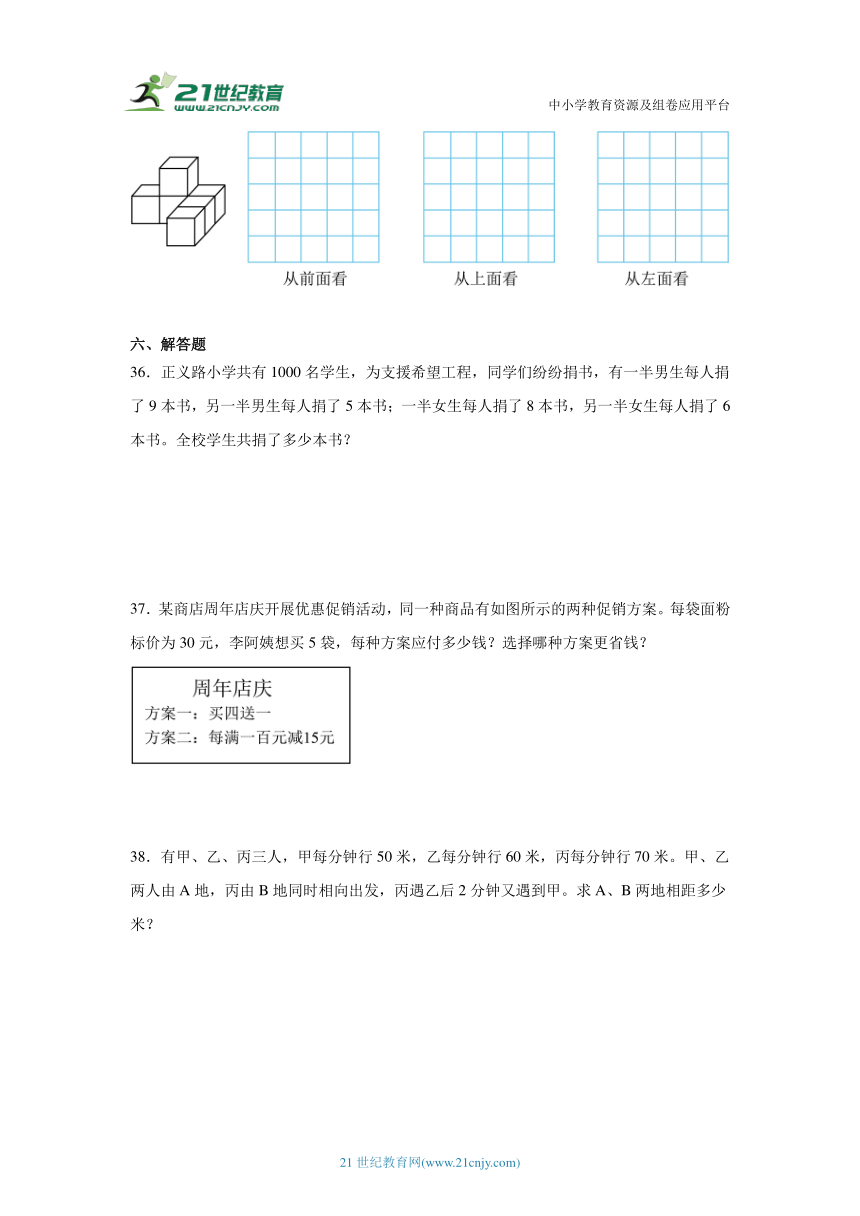
35.画出从前面 上面和左面看到的图形。
六、解答题
36.正义路小学共有1000名学生,为支援希望工程,同学们纷纷捐书,有一半男生每人捐了9本书,另一半男生每人捐了5本书;一半女生每人捐了8本书,另一半女生每人捐了6本书。全校学生共捐了多少本书?
37.某商店周年店庆开展优惠促销活动,同一种商品有如图所示的两种促销方案。每袋面粉标价为30元,李阿姨想买5袋,每种方案应付多少钱?选择哪种方案更省钱?
38.有甲、乙、丙三人,甲每分钟行50米,乙每分钟行60米,丙每分钟行70米。甲、乙两人由A地,丙由B地同时相向出发,丙遇乙后2分钟又遇到甲。求A、B两地相距多少米?
39.实验小学要买60个篮球,现在有甲、乙两个商店可以选择,两个商店的价格都是每个篮球40元,但两个商店的优惠方式不同,甲店:每买5个篮球送1个,乙店:每个篮球优惠5元,如果只能在一个商店购买,为了节约费用,实验小学应该在哪一个商店购买?购买的总价格为多少?
40.某停车场实施分段计费:不超过10个小时的部分每小时5元;超过10的小时不超过24小时的部分每小时4元;超过24小时的部分每小时3元(按整数小时计时收费,不足1小时的部分按1时间计算)。李老师两次在停车场停车共计40小时,停车费共交了176元。求两次停车各多长时间?
41.某景区门票价格为:成人票每张8元,儿童票每张5元。五一节当天该景区共售出门票3500张,总收入23500元。这天两种门票各售出多少张?
42.甲、乙两车同时从A、B两地相向开出,甲车每小时行驶80千米,乙车每小时行驶70千米,两车在距离中点15千米处相遇,相遇时,甲、乙两车经过了多少小时?
43.五一节淘气爸爸、妈妈带着淘气和5岁妹妹一起去丹霞山玩。
丹霞山售票处写着:成人票:100元,免费票:6岁以下儿童,优惠票:(6岁~18岁)50元。
(1)淘气全家去丹霞山的往返车费多少元?
(2)淘气一家去丹霞山的往返车票和门票一共多少元?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.5
【分析】小蚂蚁从A点到B点,最短路线,只能是从左向右,或从左上斜向右上爬,不能从右向左,也不能从右下向左上爬,根据标数法解答即可。
【解析】标数如下所示:
小蚂蚁从A点沿三角形的边爬到B点的最短路线有5条。
2.3
【分析】先看两盒棋子总数:甲盒有80个,乙盒有50个,把两盒棋子合起来,总数是固定不变的。
求平均数量:因为最后要让两盒数量相等,那这个相等的数量就是两盒棋子总数的平均数。也就是把总数平均分,分成两份一样多的,这两份就是最后甲、乙两盒各自的棋子数。
算甲要拿出的棋子数:知道了甲盒原来的棋子数和最后应有的棋子数(平均数),用原来的数量减去最后应有的数量,就能得到甲需要拿给乙的棋子总数。
求拿的次数:每次从甲盒拿5个棋子放到乙盒,用甲需要拿出的棋子总数除以每次拿的个数,得到的就是拿的次数。
【解析】[80-(80+50)÷2]÷5
=[80-130÷2]÷5
=[80-65]÷5
=15÷5
=3(次)
3次之后,两盒的棋子数量相等。
3.2
【分析】用15减去11求出小华比小玲多的本数,然后再把多的本数平均分成2份,其中的一份给小玲,两人的本数就一样多了。
【解析】(15-11)÷2
=4÷2
=2(本)
所以小华给小玲2本书,两人的书就一样多。
4.49
【分析】若这个六位数是由6个不同数字组成,那么十万位有6种选择,万位有5种选择,千位有4种选择,百位有3种选择,十位有2种选择,个位有1种选择,则一共可以组成6×5×4×3×2×1=720个数。对于六位数221110,其6个数字中:2有两个,1有三个。两个2可以交换位置,有2×1=2种方式;三个1可以交换位置,有3×2×1=6种方式。但交换后排列看起来相同,因此实际组成的数有720÷(2×6)=720÷12=60个数。这60个数中包括以0开头的排列(如011122, 011212等),这些不是六位数。以0开头的排列相当于固定第一位为0,剩下数字为2、2、1、1、1。5个数一共可以组成5×4×3×2×1=120个数,同理:在120个数中,两个2可以交换位置,三个1可以交换位置,那么以0开头的数字排列数为120÷(2×6)=120÷12=10个。有效的六位数排列数=60-10=50个。原始数字是221110,因此新的六位数是除了221110之外的其他排列,即50-1=49个。
【解析】
=
=
=60(个)
=
=
=10(个)
60-10-1=49(个)
一个六位数221110,将它的各个数位上的数字任意调换顺序,能组成49个新的六位数。
【点评】消除由于重复数字而产生的重复排列是解此题的关键。
5.60 7
【分析】假设全是三轮车,那么可以轮胎有:3×67=201(个),再计算出少算的轮胎数:261-201=60(个);因为把小汽车看作了三轮车,每辆车少算了轮胎数:4-3=1(个),然后用除法计算出小汽车有:60÷1=60(辆);再用停车场的车辆总数减去小汽车的数量,求出三轮车的数量,据此解答。
【解析】假设全是三轮车
小汽车:(261-3×67)÷(4-3)
=(261-201)÷1
=60÷1
=60(辆)
三轮车:67-60=7(辆)
停车场停放60辆小汽车和7辆三轮车。
6.36192.815 3.62
【分析】小数的写法,写小数的时候,整数部分仍按照整数的写法来写,如果整数部分是零就写0,小数点写在个位的右下角,要写成小圆点,小数部分按顺序写出每一个数位上的数;数的改写就是直接在原数的万位后面点上小数点,保留两位小数就是在小数点后看到第三位小数,采用“四舍五入法”保留两位小数,同时要在改写的小数后面写上“万”字。
【解析】三万六千一百九十二点八一五写作:36192.815
36192.815≈3.62万
台湾自古以来就是我国神圣不可侵犯的领土,它的面积为三万六千一百九十二点八一五平方千米,写作36192.815km2,改写成用“万”作单位并保留两位小数是3.62万km2。
7.4
【分析】若10张票全是30元的,根据“总价=单价×数量”,总花费是30×10=300元;实际花费420元,所以假设的花费比实际少了420-300=120元;每张50元的门票比每张30元的门票贵50-30=20元;把50元的门票当成30元来计算导致总花费减少,总共少了120元,每张少算20元,所以50元门票的张数为120÷20=6张;总共10张票,50元门票有6张,那么30元门票的张数是10-6=4张。
【解析】30×10=300(元)
420-300=120(元)
120÷(50-30)
=120÷20
=6(张)
10-6=4(张)
所以30元的门票买了4张。
8.11
【分析】等腰三角形的腰长相等,即等腰三角形有两条边相等,三角形的两边之和大于第三边,假设三角形的另一边是2cm,看是否能构成三角形,再假设三角形的另一边是4.5cm,看能否构成三角形,能构成三角形的第三边符合要求,据此求出第三边的长,再把三边的和相加求出三角形的周长即可。
【解析】因为2+2=4(cm)
4cm<4.4cm
所以2cm的边是底。
4.5+4.5+2
=9+2
=11(cm)
所以这个三角形的周长是11cm。
9.8 6
【分析】假设全是3人间,则应有(11×3)人,比实际人数30人多了(11×3-30)人;因为1间3人间比1间2人间多(3-2)人,那么(11×3-30)里有几个(3-2),就有几个2人间,再用房间总数减去2人间的数量,即是3人间的数量;然后用2人间的数量乘2,求出住2人间的人数。
【解析】假设全住3人间,则2人间有:
(11×3-30)÷(3-2)
=(33-30)÷1
=3÷1
=3(个)
3人间有:11-3=8(个)
住2人间的有:2×3=6(人)
他们住了8个3人间,有6人住在2人间。
10.7 15
【分析】根据三角形的特征,任意两边之和大于第三边,任意两边之差小于第三边,结合边长取整厘米数进行解答。
【解析】5+11=16(厘米)
11-5=6(厘米)
所以另一根小棒的长度要大于6厘米,小于16厘米,最短7厘米,最长15厘米。
11.360
【分析】从图中可知,∠1和∠6、∠2和∠7、∠3和∠8、∠4和∠9、∠5和∠10都组成平角180°,且五边形的内角和是540°,即∠6+∠7+∠8+∠9+∠10=540°,据此求出∠1+∠2+∠3+∠4+∠5的度数之和。
【解析】因为∠1+∠6=180°,∠2+∠7=180°,∠3+∠8=180°,∠4+∠9=180°,∠5+∠10=180°,则:
∠1+∠2+∠3+∠4+∠5
=(180°-∠6)+(180°-∠7)+(180°-∠8)+(180°-∠9)+(180°-∠10)
=180°+180°+180°+180°+180°-∠6-∠7-∠8-∠9-∠10
=180°×5-(∠6+∠7+∠8+∠9+∠10)
=900°-540°
=360°
所以,∠1+∠2+∠3+∠4+∠5=360°。
12.5 6
【分析】假设全是摩托艇,那么只能乘坐11×2=22(人),那么实际多坐了37-22=15(人),一艘快艇比一艘摩托艇多坐5-2=3(人),用实际多坐的人数除以一艘快艇比一艘摩托艇多坐的人数,求出快艇的艘数,再用游艇的总数减去快艇的数量即可求出摩托艇的艘数。
【解析】(37-11×2)÷(5-2)
=(37-22)÷3
=15÷3
=5(艘)
11-5=6(艘)
所以租用的快艇有5艘,摩托艇有6艘。
13.×
【分析】根据小数的基本性质,在小数的末尾添上0或去掉0,小数的大小不变。因此,在6.25的末尾添上两个0后,数值不会改变。
【解析】在6.25的末尾添上两个0,得到的新数是6.2500。根据小数的性质,6.25与6.2500的大小相等,因此这个数并未扩大到原来的100倍。原题说法错误。
故答案为:×
14.√
【分析】根据小数的大小比较方法比较4.36、4、5的大小,从而确定4.36是否在4和5之间。根据小数近似数的求法,将4.36保留整数部分,需观察十分位上的数字是否小于5;若小于5,则舍去小数部分,保留整数部分为4。
【解析】根据分析:
4<4.36<5,所以4.36在自然数4和5之间。
4.36十分位上的数字是3,3<5,舍去,所以 4.36保留整数部分的近似数为4。原题干说法正确。
故答案为:√
15.×
【分析】任何数加0等于原数,因此Δ+0=Δ≠0(Δ为非零数);任何数乘0等于0,因此Δ×0=0;0除以任何非零数等于0,因此0÷Δ=0。
【解析】已知为非零的数,和的结果都是0。说法错误,Δ+0结果不为0。
故答案为:×
16.√
【分析】计算时,应先算小括号内的减法,再算中括号内的乘法,最后算中括号外的除法。据此判断。
【解析】由分析可知,计算时,应先算减法。原题说法正确。
故答案为:√
17.√
【解析】正方体的6个面都是大小相等的正方形。从前面观察时,看到的是前面的正方形;从上面观察时,看到的是上面的正方形;从左面观察时,看到的是左面的正方形。由于所有面的大小和形状相同,因此从这三个方向观察到的形状均为正方形,且完全相同。据此判断。
【分析】正方体的每个面都是完全相同的正方形。从前面、上面、左面观察时,视线均垂直于对应面,看到的形状均为正方形,且大小和形状完全相同。原说法正确。
故答案为:√
18.√
【分析】将1.2的小数点去掉后得到12,从1.2变为12,小数点向右移动一位,小数扩大到原来的10倍。据此解答。
【解析】1.2×10=12
把1.2的小数点去掉,这个数就扩大到原来的10倍。题目说法正确。
故答案为:√
19.×
【分析】依据轴对称图形的定义解答,即:一个图形沿一条直线对折,对折后的两部分都能完全重合,则这个图形关于这条直线对称,这条直线就是这个图形的对称轴。
【解析】长方形和正方形都是轴对称图形,但不规则的四边形不一定是轴对称图形。
比如:
故答案为:×
20.A
【分析】假设都是2分的硬币,则一共2×100=200分,而实际一共有3.2元=320分,原因是硬币中有5分的,1个5分硬币比1个2分硬币多3分,现在多出320-200=120分需要多少个5分硬币呢?用120除以3,即可得解。
【解析】3.2元=320分
假设全是2分的硬币,5分的硬币有:
(320-100×2)÷(5-2)
=(320-200)÷3
=120÷3
=40(枚)
有2分和5分的硬币共100枚,一共3.2元钱。5分的硬币有40枚。
故答案为:A
21.A
【分析】把一个图形沿着某一条直线对折,左右两边能够完全重合的图形叫作轴对称图形,据此进行解答即可。
【解析】A.是轴对称图形;
B.不是轴对称图形;
C.不是轴对称图形;
D.不是轴对称图形。
故答案为:A
22.B
【分析】先把“230×245”用各选项的单位表示,根据进率“1米=10分米=100厘米=1000毫米”,把各选项中的单位换算成用“米”作单位的数,再结合生活实际可知,一般床单的长、宽在2米左右,据此判断这两个数的单位。
【解析】A.230毫米=0.23米,245毫米=0.245米,0.23米和0.245米表示床单的长、宽,太小了,所以“230×245”的单位不是“毫米”;
B.230厘米=2.3米,245厘米=2.45米,2.3米和2.45米表示床单的长、宽,符合生活实际,所以 “230×245”的单位是“厘米”;
C.230分米=23米,245分米=24.5米,23米和24.5米表示床单的长、宽,太大了,所以“230×245”的单位不是“分米”;
D.230米和245米表示床单的长、宽,太大了,所以“230×245”的单位不是“米”。
故答案为:B
23.D
【分析】根据三角形的三边关系,两边之和大于第三边,两边之差小于第三边,据此判断即可。
【解析】A.①②③:2+4=6;6=6,所以2,4,6即①②③不能组成三角形;
B.①②④:2+4=6;6<9,所以2,4,9即①②④不能组成三角形;
C.①③④:2+6=8,8<9,所以2,6,9即①②④不能组成三角形;
D.②③④:4+6=10;10>9,所以4,6,10即②③④能组成三角形。
能围成三角形的一组线段是②③④。
故答案为:D
24.B
【分析】总花费500元,30张票,假设30张票全是15元,则15元票的总花费是15×30=450元,多出来的50元,是因为20元票比10元票多;把一张15元票换成10元票会少花15-10=5元,把一张15元票换成20元票会多花20-15=5元。为了达到500元的花费,设把m张15元票换成10元票,n张15元票换成20元票,则有5n-5m=50,即5(n-m)=50,计算出n-m=10,也就是20元票比10元票多10张。
【解析】15×30=450(元)
500-450=50(元)
20-15=5(元)
15-10=5(元)
50÷5=10(张)
所以票价为20元的比票价为10元的多10张。
故答案为:B
25.B
【分析】根据三角形三边关系可知,另两边长度的差<第三边长度<另两边长度的和,据此解答。
【解析】5+7=12(cm)
7-5=2(cm)
因此第三边要大于2cm小于12cm,11cm符合题意。
故答案为:B
26.D
【分析】6位中国象棋选手进行比赛,每两人之间比赛一局:第1位选手,要和其余5位选手各赛1局,所以赛5局;第2位选手,已经和第1位比过了,只需和剩下4位赛,赛4局;第3位选手,和前两位都比过,还剩3位没比,赛3局;第4位选手,赛2局 ;第5位选手,赛1局 ;第6位选手,前面都比过啦,不用再赛;所以总共比赛5+4+3+2+1=15局。
把每一局比赛看作一个“头” ,把比赛的得分看作“脚”;假设所有比赛都“分出胜负”(类比鸡兔同笼里假设全是兔 ),此时每局比赛(每个“头”)对应的得分(“脚数”)是3分(胜者3分、负者0分,共3分 );若比赛是“平局”(类比鸡兔同笼里的鸡 ),每局比赛对应的得分是2分(双方各得1分,共2分 );比赛总场数15局,相当于“头数”;实际总得分39分,相当于“总脚数”;假设15局比赛全部分出胜负,那么按照每局3分计算,总得分应为:15×3=45分;但实际总得分是39分,比假设的全部分出胜负的情况少了45-39=6分,这是因为把平局的局数也按照分出胜负的3分来计算了,每把一局平局当成分出胜负,就多算了3-2=1分,少的这6分,就是因为有平局局数多算导致的,每一局平局多算1分,所以平局的局数为6÷1=6局。
【解析】5+4+3+2+1
=3×5
=15(局)
15×3-39
=45-39
=6(分)
6÷(3-2)
=6÷1
=6(局)
所以平了6局。
故答案为:D
27.D
【分析】第一个长方形中小正方形有6行,每行3个,小正方形的个数就是6×3个;第二个长方形中小正方形有3行,每行4个,小正方形的个数4×3个;把第一个长方形旋转90°,看成有3行,每行6个,和第二个长方形拼在一起,小正方形就变成了3行,每行(6+4)个,小正方形的总数就是(6+4)×3个这与6×3+4×3相等,即6×3+4×3=(6+4)×3,与乘法分配律a×c+b×c=(a+b)×c相符,由此求解。
【解析】由图可得算式:6×3+4×3=(6+4)×3,表示的定律是(乘法分配律)。
故答案为:D
28.B
【分析】根据图1表示的数3.12,可以看出整数部分需要用竖着的小棒来表示,是几就是几根小棒,小数后面的数放低一行,十分位上的数用横向的小棒表示,是几就是几根小棒,百分位上的数字用竖着的小棒来表示,是几就是几根小棒,据此解答。
【解析】我国古代曾用算筹表示数。为了表示小数,就把小数点后面的数放低一行。如图1表示的数是3.12,那么图2表示的数是2.23。
故答案为:B
29.A
【分析】由小数的意义可知,0.5表示把整体平均分成10份,取出其中的5份,根据生活经验以及对质量单位、面积单位、长度单位、人民币单位和数据大小的认识,结合实际情况进行选择,据此解答。
【解析】A.一袋食盐的质量大约是0.5千克;
B.一个书包的价钱不可能是0.5元;
C.一本数学书封面的大小不可能是0.5平方分米或者0.5平方米;
D.珠穆朗玛峰的高度不可能是0.5米或者0.5千米。
故答案为:A
30.25;900;32;0;
41;78;0.456;2626
【解析】略
31.23.75;6.33;2600
【分析】小数之间的加法计算:将两个小数的小数点及相同数位对齐,从最低位加起,满十进一……结果点上小数点并化简。
小数之间的减法计算:将两个小数的小数点及相同数位对齐,从最低位减起,不够减就从前一位“退一当十”再减……结果点上小数点。减法的验算方法是:被减数=差+减数。
三位数乘两位数的计算方法:先是用两位数的个位上的数与三位数相乘,所得的积末尾与个位对齐;接着用两位数的十位上的数与三位数相乘,所得的积末尾与十位对齐,最后把两次乘得的积相加;依此计算。
【解析】15.8+7.95=23.75 ★10-3.67=6.33 25×104=2600
验算:
32.
197;5……6;
215;1302
【分析】(1)先算括号里的减法,再算括号外的除法,最后括号外的减法。
(2)先算小括号里的减法,再算中括号里的乘法,最后中括号外的除法。
(3)先算括号里的减法,再算括号外的除法,最后算括号外的加法。
(4)先算小括号里的减法,再算中括号里的减法,最后中括号外的乘法。
【解析】(1)235-(456-304)÷4
=235-152÷4
=235-38
=197
(2)216÷[(32-18)×3]
=216÷[14×3]
=216÷42
=5……6
(3)209+102÷(52-35)
=209+102÷17
=209+6
=215
(4)93×[138-(151-27)]
=93×[138-124]
=93×14
=1302
33.84平方米
【分析】观察图形,图中的空白部分是十字形道路,我们可以把横向和纵向的空白道路分别平移到边缘,这样阴影部分就可以拼成一个新的长方形;原来长方形的长是16米,由于纵向道路宽2米,平移后新长方形的长为16-2=14米,原来长方形的宽是8米,由于横向道路宽2米,平移后新长方形的宽为8-2=6米;最后根据“长方形面积=长×宽” 计算出阴影部分的面积。
【解析】(16-2)×(8-2)
=14×6
=84(平方米)
所以阴影部分的面积是84平方米。
34.见详解
【分析】经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高,据此画图即可。
【解析】如图:
35.见详解
【分析】从前面看,共有2行,上面1行1个小正方形居中,下面1行3个小正方形;从上面看,共有3行,上面1行3个小正方形,下面1行1个小正方形,中间1行1个小正方形,右对齐;从左面看,共有2行,上面1行1个小正方形,下面1行3个小正方形,左对齐,据此解答即可。
【解析】
36.7000本
【分析】由“一半男生每人捐了9本书,另一半男生每人捐了5本”,可求出男生平均每人捐了(9+5)÷2=7(本);然后由“一半女生每人捐了8本书,另一半女生每人捐了6本书”,可求出女生平均每人捐了(8+6)÷2=7(本);由此可知不管男女生的比例是多少,全校1000名学生平均每人捐了7本书,进而求得一共捐书的本数即可。
【解析】(9+5)÷2
=14÷2
=7(本)
(8+6)÷2
=14÷2
=7(本)
1000×7=7000(本)
答:全校学生共捐了7000本书。
37.方案一应付120元,方案二应付135元。选择方案一更省钱。
【分析】方案一买四送一,也就是李阿姨买5袋,只需要4袋面粉的钱,用每袋面粉的价格乘4计算出方案一所需钱;方案二:用面粉单价乘5求出5袋面粉的钱数,再减去满一百减的15元,求出方案二所需钱数,最后进行比较即可。
【解析】方案一:30×4=120(元)
方案二:30×5=150(元)
150-15=135(元)
120<135
答:方案一应付120元,方案二应付135元。选择方案一更省钱。
38.3120米
【分析】根据题意可知,丙遇乙后2分钟和甲相遇,甲和丙2分钟走的路程就是乙和丙相遇时比乙比甲多走的路程,乙比甲每分钟多走60-50=10米,可求得乙和丙的相遇时间,乙和丙的速度和乘他们相遇时行走的时间,即等于A、B两地的路程,据此解答。
【解析】(50+70)×2÷(60-50)
=120×2÷10
=240÷10
=24(分钟)
(60+70)×24
=130×24
=3120(米)
答:A、B两地相距3120米。
39.甲商店;2000元
【分析】甲:买5个送1个,也就是付5个的钱,可以得到6个篮球,把6个篮球看作一组,60÷6=10(组),即送了10个篮球,只需要买60-10=50个篮球,根据总价=单价×数量,求出在甲店所花的总钱数。
乙:每个篮球优惠5元,即每个的单价是40-5=35元,再乘60求出在乙店购所花的总钱数。
最后比较总钱数,即可判断应该在哪一个商店购买。
【解析】甲店:60÷(5+1)
=60÷6
=10(组)
40×(60-10)
=40×50
=2000(元)
乙店:60×(40-5)
=60×35
=2100(元)
2000<2100,甲商店便宜。
答:实验小学应该在甲商店购买,购买的总价格为2000元。
40.12小时;28小时
【分析】假设一次停10小时,另一次停30小时,则停车费为:(10+10)×5+(24-10)×4+(30-24)×3=174(元),小于176元,所以判断两次停车都会超过10小时;假设两次停车都是在10—24小时内,那么停车费为:5×(10+10)+4×(40-10-10)=180(元),180>176,所以两次停车,一次停车时间在10—24小时内,另一次停车时间超过24小时;设一次停车x小时,10<x<24小时,则另一次停车(40-x)小时;根据停车收费标准,不超过10是小时的部分每小时5元,超过10小时没超过24小时的部分每小时4元,超过24小时部分每小时3元,列方程:5×10+4×(x-10)+5×10+4×14+3×(40-x-24)=176,据此即可解答。
【解析】假设有一次停10小时,另一次停30小时。
(10+10)×5+(24-10)×4+(30-24)×3
=100+14×4+6×3
=100+56+18
=174(元)
174<176
所以两次停车都会超过10小时。
假设两次停车都是在10—24小时内。
5×(10+10)+4×(40-10-10)
=100+80
=180(元)
180>176,所以两次停车,一次停车时间在10—24小时内,另一次停车时间超过24小时。
解:设一次停车x小时(10<x<24),则另一次停车(40-x)小时。
5×10+4×(x-10)+5×10+4×14+3×(40-x-24)=176
50+4x-40+50+56+3×(16-x)=176
10+4x+50+56+3×16-3x=176
60+56+4x+48-3x=176
116+48+x=176
164+x=176
x=176-164
x=12
40-12=28(小时)
答:两次停车时间分别是12小时和28小时。
【点评】判断出两次停车时间在哪个时间段是解答本题的关键。
41.2000张;1500张
【分析】假设售出的都是成人票,用售出的张数乘8,求出总钱数,再减去实际收入的钱数,再除以成人票和儿童票的差,即可求出儿童票售出的张数,用售出的总张数减去售出儿童票的张数,即可求出售出成人票的张数。
【解析】假设售出的都是成人票,收入为:3500×8=28000(元)
儿童票:(28000-23500)÷(8-3)
=4500÷3
=1500(张)
成人票:3500-1500=2000(张)
答:这天售出成人票2000张,儿童票1500张。
42.3小时
【分析】由题可知,甲比乙多走了15×2=30(千米),用甲乙的路程差÷甲乙的速度差=甲乙行走的时间,带入数值计算即可。
【解析】15×2÷(80-70)
=15×2÷10
=3(小时)
答:甲、乙两车经过了3小时。
43.(1)180元;(2)430元
【分析】(1)淘气全家去丹霞山单程需要购买2张成人票,2张半价票,单程车费再乘2,即可计算出淘气全家去丹霞山的往返车费多少元;
(2)淘气全家去丹霞山玩需要购买2张成人门票和1张儿童票(妹妹免费),据此计算出门票款再加上往返车票的钱数之和即可解答。
【解析】(1)30÷2=15(元)
(30×2+15×2)×2
=(60+30)×2
=90×2
=180(元)
答:淘气全家去丹霞山的往返车费180元。
(2)100×2+50+180
=200+50+180
=430(元)
答:淘气一家去丹霞山的往返车票和门票一共430元。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
一、填空题
1.如图中小三角形的边长都相等,那么小蚂蚁从A点沿三角形的边爬到B点的最短路线有 条。
2.如图,有两个装有棋子的盒子,每次从甲盒中拿5个棋子放入乙盒,( )次之后,两盒的棋子数量相等。
3.小华有15本书,小玲有11本书,小华给小玲( )本书,两人的书就一样多。
4.一个六位数221110,将它的各个数位上的数字任意调换顺序,能组成( )个新的六位数。
5.停车场停放了一些小汽车和三轮车,从上面数共有67辆,从下面数共有261个车轮。停车场停放了( )辆小汽车和( )辆三轮车。
6.台湾自古以来就是我国神圣不可侵犯的领土,它的面积为三万六千一百九十二点八一五平方千米,写作( )km2,改写成用“万”作单位并保留两位小数是( )万km2。
7.一场足球赛的门票有两种,一种每张售价30元,另一种每张售价50元,李强购买10张票,一共用去420元,30元的门票买了( )张。
8.小华量得一个等腰三角形的一条边长为2cm,另一条边长为4.5cm。这个三角形的周长是( )cm。
9.参加某会议的30个人被安排在同一个宾馆里,11个房间(3人间和2人间)刚好住满。他们住了( )个3人间,有( )人住在2人间。
10.三根小棒首尾相连围成一个三角形,已知其中两根小棒分别长5cm和11cm,那么还有一根小棒最短可能是( )cm,最长可能是( )cm。(都取整厘米数)
11.如图,一个五边形的内角和是540°,试一试,推导出∠1+∠2+∠3+∠4+∠5=( )°。
12.某旅游团共有37人,一共租用了11艘游艇,正好坐满,其中快艇可以坐5人,摩托艇可以坐2人,租用的快艇有( )艘,摩托艇有( )艘。
二、判断题
13.在6.25的末尾添上两个0,这个数就扩大到原来的100倍。( )
14.4.36在自然数4和5之间,它约等于4。( )
15.已知为非零的数,和的结果都是0。( )
16.计算时,应先算减法。( )
17.从前面、上面、左面观察一个正方体,看到的形状都相同。( )
18.把1.2的小数点去掉,这个数就扩大到原来的10倍。( )
19.所有的四边形都是轴对称图形。( )
三、选择题
20.有2分和5分的硬币共100枚,一共3.2元钱。5分的硬币有( )枚。
A.40 B.100 C.60 D.30
21.你认识下面的徽章吗?( )徽章是轴对称图形。
A. B. C. D.
22.一款床单的标签如图所示,显示的规格为230×245,“245”和“230”分别表示这款床单的长和宽,结合生活实际判断这两个数的单位是( )
A.毫米 B.厘米 C.分米 D.米
23.如图,能围成三角形的一组线段是( )(单位:cm)。
A.①②③ B.①②④ C.①③④ D.②③④
24.电影票有10元、15元、20元三种票价,班长用500元买了30张电影票,其中票价为20元的比票价为10元的多( )张。
A.9 B.10 C.11 D.12
25.洋洋用三根小棒围成了一个三角形,其中两根小棒的长度分别是5cm、7cm。第三根小棒的长度可能是( )。
A.1cm B.11cm C.12cm D.13cm
26.6位中国象棋选手进行比赛,每两人之间比赛一局,如果是平局,参赛选手各得1分;否则赢者得3分,输者得0分。最后六位选手的得分之和为39分,则平了( )局。
A.3 B.4 C.5 D.6
27.霞霞用如图表示某运算定律,她表示的定律是( )。
A.加法结合律 B.乘法结合律 C.乘法交换律 D.乘法分配律
28.我国古代曾用算筹表示数。为了表示小数,就把小数点后面的数放低一行。如图1表示的数是3.12,那么图2表示的数是( )。
A.2.32 B.2.23 C.3.22
29.“0.5”这个数,在下面生活场景中使用最合适的是( )。
A.一袋食盐的质量 B.一个书包的价钱
C.一本数学书封面的大小 D.珠穆朗玛峰的高度
四、计算题
30.直接写出得数。
8×5÷8×5= 25×9×4= 32+68×0= 0×250÷5=
141-77-23= 0.78×100= 4.56÷10= 26×101=
31.竖式计算。(带★验算)
15.8+7.95= ★10-3.67= 25×104=
32.先想好运算顺序,再脱式计算。
235-(456-304)÷4 216÷[(32-18)×3]
209+102÷(52-35) 93×[138-(151-27)]
33.计算图中阴影部分的面积。(单位:米)
五、作图题
34.画出下面三角形指定底上的高。
35.画出从前面 上面和左面看到的图形。
六、解答题
36.正义路小学共有1000名学生,为支援希望工程,同学们纷纷捐书,有一半男生每人捐了9本书,另一半男生每人捐了5本书;一半女生每人捐了8本书,另一半女生每人捐了6本书。全校学生共捐了多少本书?
37.某商店周年店庆开展优惠促销活动,同一种商品有如图所示的两种促销方案。每袋面粉标价为30元,李阿姨想买5袋,每种方案应付多少钱?选择哪种方案更省钱?
38.有甲、乙、丙三人,甲每分钟行50米,乙每分钟行60米,丙每分钟行70米。甲、乙两人由A地,丙由B地同时相向出发,丙遇乙后2分钟又遇到甲。求A、B两地相距多少米?
39.实验小学要买60个篮球,现在有甲、乙两个商店可以选择,两个商店的价格都是每个篮球40元,但两个商店的优惠方式不同,甲店:每买5个篮球送1个,乙店:每个篮球优惠5元,如果只能在一个商店购买,为了节约费用,实验小学应该在哪一个商店购买?购买的总价格为多少?
40.某停车场实施分段计费:不超过10个小时的部分每小时5元;超过10的小时不超过24小时的部分每小时4元;超过24小时的部分每小时3元(按整数小时计时收费,不足1小时的部分按1时间计算)。李老师两次在停车场停车共计40小时,停车费共交了176元。求两次停车各多长时间?
41.某景区门票价格为:成人票每张8元,儿童票每张5元。五一节当天该景区共售出门票3500张,总收入23500元。这天两种门票各售出多少张?
42.甲、乙两车同时从A、B两地相向开出,甲车每小时行驶80千米,乙车每小时行驶70千米,两车在距离中点15千米处相遇,相遇时,甲、乙两车经过了多少小时?
43.五一节淘气爸爸、妈妈带着淘气和5岁妹妹一起去丹霞山玩。
丹霞山售票处写着:成人票:100元,免费票:6岁以下儿童,优惠票:(6岁~18岁)50元。
(1)淘气全家去丹霞山的往返车费多少元?
(2)淘气一家去丹霞山的往返车票和门票一共多少元?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.5
【分析】小蚂蚁从A点到B点,最短路线,只能是从左向右,或从左上斜向右上爬,不能从右向左,也不能从右下向左上爬,根据标数法解答即可。
【解析】标数如下所示:
小蚂蚁从A点沿三角形的边爬到B点的最短路线有5条。
2.3
【分析】先看两盒棋子总数:甲盒有80个,乙盒有50个,把两盒棋子合起来,总数是固定不变的。
求平均数量:因为最后要让两盒数量相等,那这个相等的数量就是两盒棋子总数的平均数。也就是把总数平均分,分成两份一样多的,这两份就是最后甲、乙两盒各自的棋子数。
算甲要拿出的棋子数:知道了甲盒原来的棋子数和最后应有的棋子数(平均数),用原来的数量减去最后应有的数量,就能得到甲需要拿给乙的棋子总数。
求拿的次数:每次从甲盒拿5个棋子放到乙盒,用甲需要拿出的棋子总数除以每次拿的个数,得到的就是拿的次数。
【解析】[80-(80+50)÷2]÷5
=[80-130÷2]÷5
=[80-65]÷5
=15÷5
=3(次)
3次之后,两盒的棋子数量相等。
3.2
【分析】用15减去11求出小华比小玲多的本数,然后再把多的本数平均分成2份,其中的一份给小玲,两人的本数就一样多了。
【解析】(15-11)÷2
=4÷2
=2(本)
所以小华给小玲2本书,两人的书就一样多。
4.49
【分析】若这个六位数是由6个不同数字组成,那么十万位有6种选择,万位有5种选择,千位有4种选择,百位有3种选择,十位有2种选择,个位有1种选择,则一共可以组成6×5×4×3×2×1=720个数。对于六位数221110,其6个数字中:2有两个,1有三个。两个2可以交换位置,有2×1=2种方式;三个1可以交换位置,有3×2×1=6种方式。但交换后排列看起来相同,因此实际组成的数有720÷(2×6)=720÷12=60个数。这60个数中包括以0开头的排列(如011122, 011212等),这些不是六位数。以0开头的排列相当于固定第一位为0,剩下数字为2、2、1、1、1。5个数一共可以组成5×4×3×2×1=120个数,同理:在120个数中,两个2可以交换位置,三个1可以交换位置,那么以0开头的数字排列数为120÷(2×6)=120÷12=10个。有效的六位数排列数=60-10=50个。原始数字是221110,因此新的六位数是除了221110之外的其他排列,即50-1=49个。
【解析】
=
=
=60(个)
=
=
=10(个)
60-10-1=49(个)
一个六位数221110,将它的各个数位上的数字任意调换顺序,能组成49个新的六位数。
【点评】消除由于重复数字而产生的重复排列是解此题的关键。
5.60 7
【分析】假设全是三轮车,那么可以轮胎有:3×67=201(个),再计算出少算的轮胎数:261-201=60(个);因为把小汽车看作了三轮车,每辆车少算了轮胎数:4-3=1(个),然后用除法计算出小汽车有:60÷1=60(辆);再用停车场的车辆总数减去小汽车的数量,求出三轮车的数量,据此解答。
【解析】假设全是三轮车
小汽车:(261-3×67)÷(4-3)
=(261-201)÷1
=60÷1
=60(辆)
三轮车:67-60=7(辆)
停车场停放60辆小汽车和7辆三轮车。
6.36192.815 3.62
【分析】小数的写法,写小数的时候,整数部分仍按照整数的写法来写,如果整数部分是零就写0,小数点写在个位的右下角,要写成小圆点,小数部分按顺序写出每一个数位上的数;数的改写就是直接在原数的万位后面点上小数点,保留两位小数就是在小数点后看到第三位小数,采用“四舍五入法”保留两位小数,同时要在改写的小数后面写上“万”字。
【解析】三万六千一百九十二点八一五写作:36192.815
36192.815≈3.62万
台湾自古以来就是我国神圣不可侵犯的领土,它的面积为三万六千一百九十二点八一五平方千米,写作36192.815km2,改写成用“万”作单位并保留两位小数是3.62万km2。
7.4
【分析】若10张票全是30元的,根据“总价=单价×数量”,总花费是30×10=300元;实际花费420元,所以假设的花费比实际少了420-300=120元;每张50元的门票比每张30元的门票贵50-30=20元;把50元的门票当成30元来计算导致总花费减少,总共少了120元,每张少算20元,所以50元门票的张数为120÷20=6张;总共10张票,50元门票有6张,那么30元门票的张数是10-6=4张。
【解析】30×10=300(元)
420-300=120(元)
120÷(50-30)
=120÷20
=6(张)
10-6=4(张)
所以30元的门票买了4张。
8.11
【分析】等腰三角形的腰长相等,即等腰三角形有两条边相等,三角形的两边之和大于第三边,假设三角形的另一边是2cm,看是否能构成三角形,再假设三角形的另一边是4.5cm,看能否构成三角形,能构成三角形的第三边符合要求,据此求出第三边的长,再把三边的和相加求出三角形的周长即可。
【解析】因为2+2=4(cm)
4cm<4.4cm
所以2cm的边是底。
4.5+4.5+2
=9+2
=11(cm)
所以这个三角形的周长是11cm。
9.8 6
【分析】假设全是3人间,则应有(11×3)人,比实际人数30人多了(11×3-30)人;因为1间3人间比1间2人间多(3-2)人,那么(11×3-30)里有几个(3-2),就有几个2人间,再用房间总数减去2人间的数量,即是3人间的数量;然后用2人间的数量乘2,求出住2人间的人数。
【解析】假设全住3人间,则2人间有:
(11×3-30)÷(3-2)
=(33-30)÷1
=3÷1
=3(个)
3人间有:11-3=8(个)
住2人间的有:2×3=6(人)
他们住了8个3人间,有6人住在2人间。
10.7 15
【分析】根据三角形的特征,任意两边之和大于第三边,任意两边之差小于第三边,结合边长取整厘米数进行解答。
【解析】5+11=16(厘米)
11-5=6(厘米)
所以另一根小棒的长度要大于6厘米,小于16厘米,最短7厘米,最长15厘米。
11.360
【分析】从图中可知,∠1和∠6、∠2和∠7、∠3和∠8、∠4和∠9、∠5和∠10都组成平角180°,且五边形的内角和是540°,即∠6+∠7+∠8+∠9+∠10=540°,据此求出∠1+∠2+∠3+∠4+∠5的度数之和。
【解析】因为∠1+∠6=180°,∠2+∠7=180°,∠3+∠8=180°,∠4+∠9=180°,∠5+∠10=180°,则:
∠1+∠2+∠3+∠4+∠5
=(180°-∠6)+(180°-∠7)+(180°-∠8)+(180°-∠9)+(180°-∠10)
=180°+180°+180°+180°+180°-∠6-∠7-∠8-∠9-∠10
=180°×5-(∠6+∠7+∠8+∠9+∠10)
=900°-540°
=360°
所以,∠1+∠2+∠3+∠4+∠5=360°。
12.5 6
【分析】假设全是摩托艇,那么只能乘坐11×2=22(人),那么实际多坐了37-22=15(人),一艘快艇比一艘摩托艇多坐5-2=3(人),用实际多坐的人数除以一艘快艇比一艘摩托艇多坐的人数,求出快艇的艘数,再用游艇的总数减去快艇的数量即可求出摩托艇的艘数。
【解析】(37-11×2)÷(5-2)
=(37-22)÷3
=15÷3
=5(艘)
11-5=6(艘)
所以租用的快艇有5艘,摩托艇有6艘。
13.×
【分析】根据小数的基本性质,在小数的末尾添上0或去掉0,小数的大小不变。因此,在6.25的末尾添上两个0后,数值不会改变。
【解析】在6.25的末尾添上两个0,得到的新数是6.2500。根据小数的性质,6.25与6.2500的大小相等,因此这个数并未扩大到原来的100倍。原题说法错误。
故答案为:×
14.√
【分析】根据小数的大小比较方法比较4.36、4、5的大小,从而确定4.36是否在4和5之间。根据小数近似数的求法,将4.36保留整数部分,需观察十分位上的数字是否小于5;若小于5,则舍去小数部分,保留整数部分为4。
【解析】根据分析:
4<4.36<5,所以4.36在自然数4和5之间。
4.36十分位上的数字是3,3<5,舍去,所以 4.36保留整数部分的近似数为4。原题干说法正确。
故答案为:√
15.×
【分析】任何数加0等于原数,因此Δ+0=Δ≠0(Δ为非零数);任何数乘0等于0,因此Δ×0=0;0除以任何非零数等于0,因此0÷Δ=0。
【解析】已知为非零的数,和的结果都是0。说法错误,Δ+0结果不为0。
故答案为:×
16.√
【分析】计算时,应先算小括号内的减法,再算中括号内的乘法,最后算中括号外的除法。据此判断。
【解析】由分析可知,计算时,应先算减法。原题说法正确。
故答案为:√
17.√
【解析】正方体的6个面都是大小相等的正方形。从前面观察时,看到的是前面的正方形;从上面观察时,看到的是上面的正方形;从左面观察时,看到的是左面的正方形。由于所有面的大小和形状相同,因此从这三个方向观察到的形状均为正方形,且完全相同。据此判断。
【分析】正方体的每个面都是完全相同的正方形。从前面、上面、左面观察时,视线均垂直于对应面,看到的形状均为正方形,且大小和形状完全相同。原说法正确。
故答案为:√
18.√
【分析】将1.2的小数点去掉后得到12,从1.2变为12,小数点向右移动一位,小数扩大到原来的10倍。据此解答。
【解析】1.2×10=12
把1.2的小数点去掉,这个数就扩大到原来的10倍。题目说法正确。
故答案为:√
19.×
【分析】依据轴对称图形的定义解答,即:一个图形沿一条直线对折,对折后的两部分都能完全重合,则这个图形关于这条直线对称,这条直线就是这个图形的对称轴。
【解析】长方形和正方形都是轴对称图形,但不规则的四边形不一定是轴对称图形。
比如:
故答案为:×
20.A
【分析】假设都是2分的硬币,则一共2×100=200分,而实际一共有3.2元=320分,原因是硬币中有5分的,1个5分硬币比1个2分硬币多3分,现在多出320-200=120分需要多少个5分硬币呢?用120除以3,即可得解。
【解析】3.2元=320分
假设全是2分的硬币,5分的硬币有:
(320-100×2)÷(5-2)
=(320-200)÷3
=120÷3
=40(枚)
有2分和5分的硬币共100枚,一共3.2元钱。5分的硬币有40枚。
故答案为:A
21.A
【分析】把一个图形沿着某一条直线对折,左右两边能够完全重合的图形叫作轴对称图形,据此进行解答即可。
【解析】A.是轴对称图形;
B.不是轴对称图形;
C.不是轴对称图形;
D.不是轴对称图形。
故答案为:A
22.B
【分析】先把“230×245”用各选项的单位表示,根据进率“1米=10分米=100厘米=1000毫米”,把各选项中的单位换算成用“米”作单位的数,再结合生活实际可知,一般床单的长、宽在2米左右,据此判断这两个数的单位。
【解析】A.230毫米=0.23米,245毫米=0.245米,0.23米和0.245米表示床单的长、宽,太小了,所以“230×245”的单位不是“毫米”;
B.230厘米=2.3米,245厘米=2.45米,2.3米和2.45米表示床单的长、宽,符合生活实际,所以 “230×245”的单位是“厘米”;
C.230分米=23米,245分米=24.5米,23米和24.5米表示床单的长、宽,太大了,所以“230×245”的单位不是“分米”;
D.230米和245米表示床单的长、宽,太大了,所以“230×245”的单位不是“米”。
故答案为:B
23.D
【分析】根据三角形的三边关系,两边之和大于第三边,两边之差小于第三边,据此判断即可。
【解析】A.①②③:2+4=6;6=6,所以2,4,6即①②③不能组成三角形;
B.①②④:2+4=6;6<9,所以2,4,9即①②④不能组成三角形;
C.①③④:2+6=8,8<9,所以2,6,9即①②④不能组成三角形;
D.②③④:4+6=10;10>9,所以4,6,10即②③④能组成三角形。
能围成三角形的一组线段是②③④。
故答案为:D
24.B
【分析】总花费500元,30张票,假设30张票全是15元,则15元票的总花费是15×30=450元,多出来的50元,是因为20元票比10元票多;把一张15元票换成10元票会少花15-10=5元,把一张15元票换成20元票会多花20-15=5元。为了达到500元的花费,设把m张15元票换成10元票,n张15元票换成20元票,则有5n-5m=50,即5(n-m)=50,计算出n-m=10,也就是20元票比10元票多10张。
【解析】15×30=450(元)
500-450=50(元)
20-15=5(元)
15-10=5(元)
50÷5=10(张)
所以票价为20元的比票价为10元的多10张。
故答案为:B
25.B
【分析】根据三角形三边关系可知,另两边长度的差<第三边长度<另两边长度的和,据此解答。
【解析】5+7=12(cm)
7-5=2(cm)
因此第三边要大于2cm小于12cm,11cm符合题意。
故答案为:B
26.D
【分析】6位中国象棋选手进行比赛,每两人之间比赛一局:第1位选手,要和其余5位选手各赛1局,所以赛5局;第2位选手,已经和第1位比过了,只需和剩下4位赛,赛4局;第3位选手,和前两位都比过,还剩3位没比,赛3局;第4位选手,赛2局 ;第5位选手,赛1局 ;第6位选手,前面都比过啦,不用再赛;所以总共比赛5+4+3+2+1=15局。
把每一局比赛看作一个“头” ,把比赛的得分看作“脚”;假设所有比赛都“分出胜负”(类比鸡兔同笼里假设全是兔 ),此时每局比赛(每个“头”)对应的得分(“脚数”)是3分(胜者3分、负者0分,共3分 );若比赛是“平局”(类比鸡兔同笼里的鸡 ),每局比赛对应的得分是2分(双方各得1分,共2分 );比赛总场数15局,相当于“头数”;实际总得分39分,相当于“总脚数”;假设15局比赛全部分出胜负,那么按照每局3分计算,总得分应为:15×3=45分;但实际总得分是39分,比假设的全部分出胜负的情况少了45-39=6分,这是因为把平局的局数也按照分出胜负的3分来计算了,每把一局平局当成分出胜负,就多算了3-2=1分,少的这6分,就是因为有平局局数多算导致的,每一局平局多算1分,所以平局的局数为6÷1=6局。
【解析】5+4+3+2+1
=3×5
=15(局)
15×3-39
=45-39
=6(分)
6÷(3-2)
=6÷1
=6(局)
所以平了6局。
故答案为:D
27.D
【分析】第一个长方形中小正方形有6行,每行3个,小正方形的个数就是6×3个;第二个长方形中小正方形有3行,每行4个,小正方形的个数4×3个;把第一个长方形旋转90°,看成有3行,每行6个,和第二个长方形拼在一起,小正方形就变成了3行,每行(6+4)个,小正方形的总数就是(6+4)×3个这与6×3+4×3相等,即6×3+4×3=(6+4)×3,与乘法分配律a×c+b×c=(a+b)×c相符,由此求解。
【解析】由图可得算式:6×3+4×3=(6+4)×3,表示的定律是(乘法分配律)。
故答案为:D
28.B
【分析】根据图1表示的数3.12,可以看出整数部分需要用竖着的小棒来表示,是几就是几根小棒,小数后面的数放低一行,十分位上的数用横向的小棒表示,是几就是几根小棒,百分位上的数字用竖着的小棒来表示,是几就是几根小棒,据此解答。
【解析】我国古代曾用算筹表示数。为了表示小数,就把小数点后面的数放低一行。如图1表示的数是3.12,那么图2表示的数是2.23。
故答案为:B
29.A
【分析】由小数的意义可知,0.5表示把整体平均分成10份,取出其中的5份,根据生活经验以及对质量单位、面积单位、长度单位、人民币单位和数据大小的认识,结合实际情况进行选择,据此解答。
【解析】A.一袋食盐的质量大约是0.5千克;
B.一个书包的价钱不可能是0.5元;
C.一本数学书封面的大小不可能是0.5平方分米或者0.5平方米;
D.珠穆朗玛峰的高度不可能是0.5米或者0.5千米。
故答案为:A
30.25;900;32;0;
41;78;0.456;2626
【解析】略
31.23.75;6.33;2600
【分析】小数之间的加法计算:将两个小数的小数点及相同数位对齐,从最低位加起,满十进一……结果点上小数点并化简。
小数之间的减法计算:将两个小数的小数点及相同数位对齐,从最低位减起,不够减就从前一位“退一当十”再减……结果点上小数点。减法的验算方法是:被减数=差+减数。
三位数乘两位数的计算方法:先是用两位数的个位上的数与三位数相乘,所得的积末尾与个位对齐;接着用两位数的十位上的数与三位数相乘,所得的积末尾与十位对齐,最后把两次乘得的积相加;依此计算。
【解析】15.8+7.95=23.75 ★10-3.67=6.33 25×104=2600
验算:
32.
197;5……6;
215;1302
【分析】(1)先算括号里的减法,再算括号外的除法,最后括号外的减法。
(2)先算小括号里的减法,再算中括号里的乘法,最后中括号外的除法。
(3)先算括号里的减法,再算括号外的除法,最后算括号外的加法。
(4)先算小括号里的减法,再算中括号里的减法,最后中括号外的乘法。
【解析】(1)235-(456-304)÷4
=235-152÷4
=235-38
=197
(2)216÷[(32-18)×3]
=216÷[14×3]
=216÷42
=5……6
(3)209+102÷(52-35)
=209+102÷17
=209+6
=215
(4)93×[138-(151-27)]
=93×[138-124]
=93×14
=1302
33.84平方米
【分析】观察图形,图中的空白部分是十字形道路,我们可以把横向和纵向的空白道路分别平移到边缘,这样阴影部分就可以拼成一个新的长方形;原来长方形的长是16米,由于纵向道路宽2米,平移后新长方形的长为16-2=14米,原来长方形的宽是8米,由于横向道路宽2米,平移后新长方形的宽为8-2=6米;最后根据“长方形面积=长×宽” 计算出阴影部分的面积。
【解析】(16-2)×(8-2)
=14×6
=84(平方米)
所以阴影部分的面积是84平方米。
34.见详解
【分析】经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高,据此画图即可。
【解析】如图:
35.见详解
【分析】从前面看,共有2行,上面1行1个小正方形居中,下面1行3个小正方形;从上面看,共有3行,上面1行3个小正方形,下面1行1个小正方形,中间1行1个小正方形,右对齐;从左面看,共有2行,上面1行1个小正方形,下面1行3个小正方形,左对齐,据此解答即可。
【解析】
36.7000本
【分析】由“一半男生每人捐了9本书,另一半男生每人捐了5本”,可求出男生平均每人捐了(9+5)÷2=7(本);然后由“一半女生每人捐了8本书,另一半女生每人捐了6本书”,可求出女生平均每人捐了(8+6)÷2=7(本);由此可知不管男女生的比例是多少,全校1000名学生平均每人捐了7本书,进而求得一共捐书的本数即可。
【解析】(9+5)÷2
=14÷2
=7(本)
(8+6)÷2
=14÷2
=7(本)
1000×7=7000(本)
答:全校学生共捐了7000本书。
37.方案一应付120元,方案二应付135元。选择方案一更省钱。
【分析】方案一买四送一,也就是李阿姨买5袋,只需要4袋面粉的钱,用每袋面粉的价格乘4计算出方案一所需钱;方案二:用面粉单价乘5求出5袋面粉的钱数,再减去满一百减的15元,求出方案二所需钱数,最后进行比较即可。
【解析】方案一:30×4=120(元)
方案二:30×5=150(元)
150-15=135(元)
120<135
答:方案一应付120元,方案二应付135元。选择方案一更省钱。
38.3120米
【分析】根据题意可知,丙遇乙后2分钟和甲相遇,甲和丙2分钟走的路程就是乙和丙相遇时比乙比甲多走的路程,乙比甲每分钟多走60-50=10米,可求得乙和丙的相遇时间,乙和丙的速度和乘他们相遇时行走的时间,即等于A、B两地的路程,据此解答。
【解析】(50+70)×2÷(60-50)
=120×2÷10
=240÷10
=24(分钟)
(60+70)×24
=130×24
=3120(米)
答:A、B两地相距3120米。
39.甲商店;2000元
【分析】甲:买5个送1个,也就是付5个的钱,可以得到6个篮球,把6个篮球看作一组,60÷6=10(组),即送了10个篮球,只需要买60-10=50个篮球,根据总价=单价×数量,求出在甲店所花的总钱数。
乙:每个篮球优惠5元,即每个的单价是40-5=35元,再乘60求出在乙店购所花的总钱数。
最后比较总钱数,即可判断应该在哪一个商店购买。
【解析】甲店:60÷(5+1)
=60÷6
=10(组)
40×(60-10)
=40×50
=2000(元)
乙店:60×(40-5)
=60×35
=2100(元)
2000<2100,甲商店便宜。
答:实验小学应该在甲商店购买,购买的总价格为2000元。
40.12小时;28小时
【分析】假设一次停10小时,另一次停30小时,则停车费为:(10+10)×5+(24-10)×4+(30-24)×3=174(元),小于176元,所以判断两次停车都会超过10小时;假设两次停车都是在10—24小时内,那么停车费为:5×(10+10)+4×(40-10-10)=180(元),180>176,所以两次停车,一次停车时间在10—24小时内,另一次停车时间超过24小时;设一次停车x小时,10<x<24小时,则另一次停车(40-x)小时;根据停车收费标准,不超过10是小时的部分每小时5元,超过10小时没超过24小时的部分每小时4元,超过24小时部分每小时3元,列方程:5×10+4×(x-10)+5×10+4×14+3×(40-x-24)=176,据此即可解答。
【解析】假设有一次停10小时,另一次停30小时。
(10+10)×5+(24-10)×4+(30-24)×3
=100+14×4+6×3
=100+56+18
=174(元)
174<176
所以两次停车都会超过10小时。
假设两次停车都是在10—24小时内。
5×(10+10)+4×(40-10-10)
=100+80
=180(元)
180>176,所以两次停车,一次停车时间在10—24小时内,另一次停车时间超过24小时。
解:设一次停车x小时(10<x<24),则另一次停车(40-x)小时。
5×10+4×(x-10)+5×10+4×14+3×(40-x-24)=176
50+4x-40+50+56+3×(16-x)=176
10+4x+50+56+3×16-3x=176
60+56+4x+48-3x=176
116+48+x=176
164+x=176
x=176-164
x=12
40-12=28(小时)
答:两次停车时间分别是12小时和28小时。
【点评】判断出两次停车时间在哪个时间段是解答本题的关键。
41.2000张;1500张
【分析】假设售出的都是成人票,用售出的张数乘8,求出总钱数,再减去实际收入的钱数,再除以成人票和儿童票的差,即可求出儿童票售出的张数,用售出的总张数减去售出儿童票的张数,即可求出售出成人票的张数。
【解析】假设售出的都是成人票,收入为:3500×8=28000(元)
儿童票:(28000-23500)÷(8-3)
=4500÷3
=1500(张)
成人票:3500-1500=2000(张)
答:这天售出成人票2000张,儿童票1500张。
42.3小时
【分析】由题可知,甲比乙多走了15×2=30(千米),用甲乙的路程差÷甲乙的速度差=甲乙行走的时间,带入数值计算即可。
【解析】15×2÷(80-70)
=15×2÷10
=3(小时)
答:甲、乙两车经过了3小时。
43.(1)180元;(2)430元
【分析】(1)淘气全家去丹霞山单程需要购买2张成人票,2张半价票,单程车费再乘2,即可计算出淘气全家去丹霞山的往返车费多少元;
(2)淘气全家去丹霞山玩需要购买2张成人门票和1张儿童票(妹妹免费),据此计算出门票款再加上往返车票的钱数之和即可解答。
【解析】(1)30÷2=15(元)
(30×2+15×2)×2
=(60+30)×2
=90×2
=180(元)
答:淘气全家去丹霞山的往返车费180元。
(2)100×2+50+180
=200+50+180
=430(元)
答:淘气一家去丹霞山的往返车票和门票一共430元。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
