北师大版数学小升初高频易错考点专题训练:作图题(含解析)
文档属性
| 名称 | 北师大版数学小升初高频易错考点专题训练:作图题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 10:57:37 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
北师大版数学小升初高频易错考点专题训练:作图题
学校:___________姓名:___________班级:___________考号:___________
一、作图题
1.先将下图向上平移4格后,再向右平移5格,画出两次平移后的图形。
2.(1)画出图形①关于直线l的轴对称图形。
(2)画出图形②先向右平移6个方格,再向上平移3个方格后的图形。
3.请画出三角形AOB绕O点顺时针旋转90°后的图形。
4.在方格纸上分别画出从不同方向看左边立体图形所看到的形状。
5.画出如图的另一半,使它成为一个轴对称图形。
6.把一个平行四边形剪一次,符合下面的要求(用虚线画出)。
(1)剪成两个相同的三角形。
(2)剪成两个相同的梯形。
7.请你依据如下动物园的导览提示,在下图中分别用★、▲标注出熊猫馆、美猴馆的位置。
走进动物园大门,正北面有纪念馆和企鹅馆。
企鹅馆的西面是美猴馆,东面是大象馆。
从企鹅馆向西南方向步行可以到达熊猫馆。
孔雀馆在动物园的东南角。
8.请你画出一个直径是3厘米的圆。
9.操作。
(1)画出三角形ABC绕A点逆时针旋转90°后的图形。
(2)画出三角形ABC以1∶2的比例缩小后的图形。
10.按要求画一画。
(1)画出将图形①先向右平移2格,再向下平移4格得到的图形④。
(2)画出轴对称图形②的另一半。
(3)画出将图形③按2∶1扩大后的图形⑤。
11.看立体图形,分别画出从正面、左面、上面看到的立体图形的形状。
12.画一画。(用直尺和铅笔作图)
(1)将图形A绕点O逆时针旋转90°,得到图形B。
(2)将图形B向右平移6格,得到图形C。
13.三角形ABC是将原图形向上平移2格,再向右平移8格后得到的。请画出平移前的图形,再画出将三角形ABC绕C点逆时针旋转180°后得到的图形。
14.按要求画一画。
(1)以虚线为对称轴,画出轴对称图形①的另一半。
(2)画出图形②绕点O顺时针旋转90°后的图形。
(3)将图形③缩小,使缩小后的图形与原图形对应线段长的比为1∶2。
15.下面是正方形点子图,请你在图中选一个点作为点,使四边形成为一个梯形,至少画出两种情况。
(1) (2)
16.全民健身是使人们增强体魄、健康生活的基础和保障,是每一个人成长和实现幸福生活的重要基础。幸福公园进行升级改造,留出了一块长80米、宽60米的长方形场地。
(1)请你按1∶2000的比例尺画出这块长方形场地的平面图。
(2)设计师计划在这块场地上建造一个最大的圆形健身场地。算一算,这个圆形健身场地的实际占地面积是 平方米;如果在该健身场地一周每隔2米插一面旗子,大约需要 面旗子。
17.按要求在下面的方格中画图。
(1)将图形A向右平移5格,得到图形B。
(2)将图形A绕点O逆时针旋转90°得到图形C。
(3)将图形A按1∶2缩小,得到图形D。
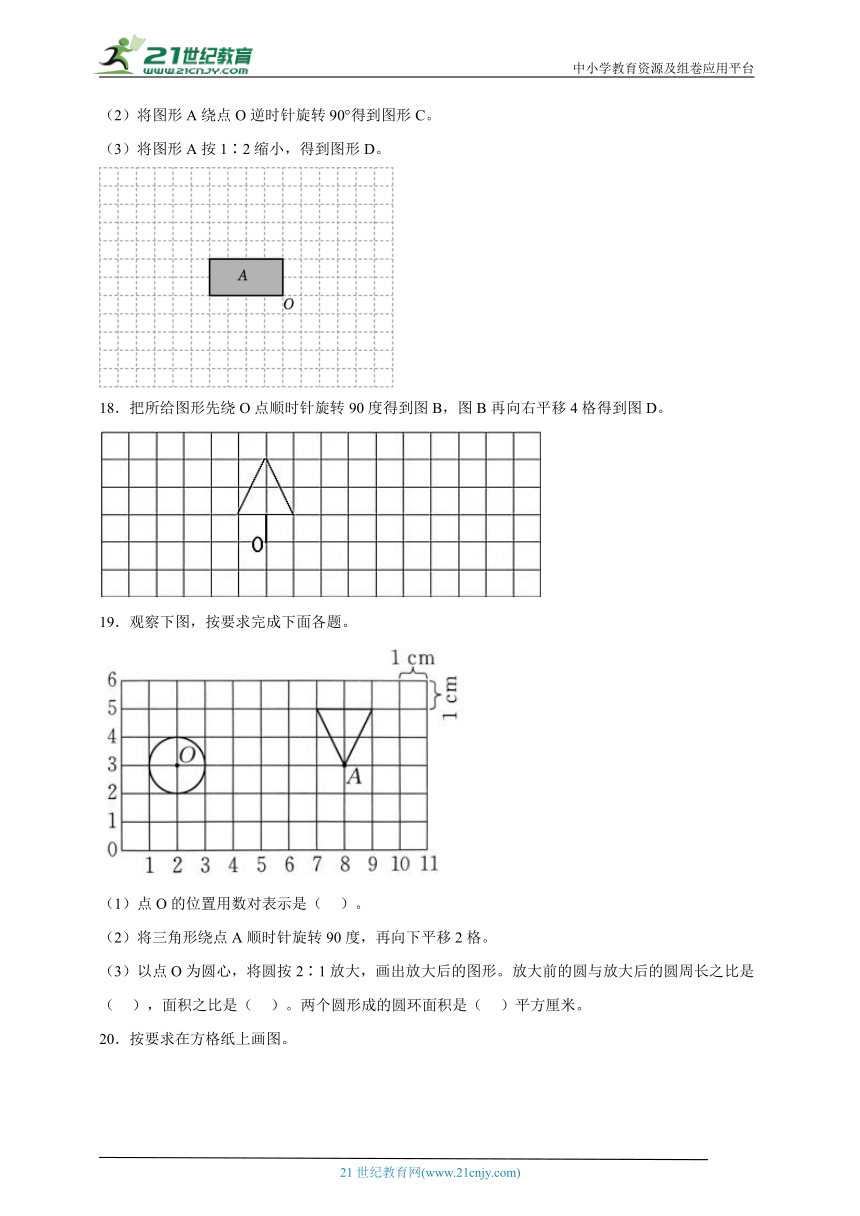
18.把所给图形先绕O点顺时针旋转90度得到图B,图B再向右平移4格得到图D。
19.观察下图,按要求完成下面各题。
(1)点O的位置用数对表示是( )。
(2)将三角形绕点A顺时针旋转90度,再向下平移2格。
(3)以点O为圆心,将圆按2∶1放大,画出放大后的图形。放大前的圆与放大后的圆周长之比是( ),面积之比是( )。两个圆形成的圆环面积是( )平方厘米。
20.按要求在方格纸上画图。
(1)将图形A绕O点逆时针旋转90°得到图形B。
(2)以直线L为对称轴作图形A的轴对称图形C,再将图形C向右平移4格得到图形D。
(3)画出图形E按2∶1放大后的图形F。
21.按要求画一画。
(1)将图形①绕点A逆时针旋转90°。
(2)将图形①先向上平移4格,再向右平移3格。
(3)画出图形②所有的对称轴。
(4)将图形③放大,使得放大后的图形与原图形对应线段长的比是2∶1。
22.操作题.
1.画一个面积是5平方厘米的三角形, 2.画一个只有2条对称轴的轴对称图形
23.画一画。
(1)在图中画出三角形的对称轴。
(2)画出把(1)中的三角形围绕右下方的顶点O顺时针旋转90°后的图形。
(3)画出把平行四边形向下平移2格后的图形。
(4)画出长方形按2∶1放大后的图形。
24.如下图,图形A绕点0顺时针旋转180°得到图形B,图形B向下平移4格得到图形C,把图形C按2∶1放大得到图形D。请画出图形B、图形C和图形D。
25.在由边长相等的小正方形组成的网格中,图中实线所围成的是一个梯形.请你在下图中用两种不同的方法将这个梯形分为3个三角形,使3个三角形的面积比是1:2:3.
26.过点A,画直线m的垂线和平行线。
27.按1∶3画出平行四边形缩小后的图形。
28.按要求画一画。
(1)以虚线MN为对称轴,画出图形甲的轴对称图形。
(2)将图形乙先向左平移3格,再向下平移6格。
(3)将图形乙绕点O顺时针旋转90°。
(4)将图形丙缩小,使缩小后的图形与原图形对应线段长的比为1∶2。
29.在方格纸上按要求画图。
(1)画出图形①向右平移5格后的图形。
(2)画出图形②绕点O顺时针旋转90°后的图形。
30.画一画。
(1)将图形A向右平移4格得到图形B。
(2)以直线l为对称轴,作图形B的对称图形,得到图形C。
31.按要求画图。
(1)将图①绕点O逆时针旋转90°,画出旋转后的图形。
(2)将图②向右平移2格,再向下平移3格,分别画出两次平移后的图形。
32.按要求画一画。
(1)以虚线MN为对称轴,画出轴对称图形①的另一半。
(2)画出图形②先向右平移7格,再向下平移2格后的图形。
(3)画出图形③绕点O按逆时针旋转90°后的图形。
(4)将图形④放大,使放大后的图形与原图形对应线段长的比为2∶1。
33.在下面的方格纸上按要求画长方形、正方形和平行四边形。
画一个长是10个格,宽是6个格的长方形。
画一个边长是4个格的正方形。
任意画一个平行四边形。
34.(1)画出长方形以O点为中心按顺时针方向旋转90度的图形。
(2)画出长方形的对称图形。
35.观察数轴,按要求完成:
(1)点A表示的数写成分数是。
(2)点C到O的距离和点B到O的距离相等,但方向相反,请标出C点,并将C点表示的数字写出来。
(3)在数轴上标出表示2.5和﹣的点。
36.如图的每个方格表示1cm2。将下面的长方形缩小,使缩小后的图形与原图形对应线段长的比为1∶2。
37.按要求在方格纸上画一画。
(1)将图①先向右平移8格,再向下平移3格
(2)以虚线MN为对称轴,画出图②的轴对称图形的另一半。
(3)将图③绕点O逆时针旋转
(4)将图③缩小,使得缩小后的图形与原图形对应线段长的比是1∶2。
《北师大版数学小升初高频易错考点专题训练:作图题》参考答案
1.
【分析】把此图的5个顶点先向上平移4格,再向右平移5格,描出这个五个点,然后将各点按原图顺次连接起来。
【详解】
【点睛】掌握平移的方法和平移图形的画法是解决此题的关键。把图形的各个顶点按照指定的方向和格数平移到新的位置,再把各点按原图连接起来。
2.(1)(2)见详解
【分析】(1)依据轴对称图形的画法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形,由此即可画图;
(2)根据平移的特征,把图形②各顶点分别向右平移6格,再向上平移3格,依次连结即可得到平移后图形。
【详解】(1)(2)如下图所示:
3.见详解
【分析】根据旋转的方法,将三角形与点O相连的两条边绕点O顺时针旋转90度,再将第三条边连起来即可。
【详解】
【点睛】做旋转的图形时,要注意旋转的方向和角度,旋转后图形的形状和大小不变,只是位置发生变化。
4.图见详解
【分析】根据从不同方向观察物体和几何图形的方法,分别画出从不同方向看立体图形所看到的形状即可。
【详解】如图:
5.见详解
【分析】平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形。根据轴对称图形的特征,对称点到对称轴的距离相等,找到图形的各顶点关于对称轴的对称点后,依次连接各点得到轴对称图形。
【详解】如图:
6.见详解
【分析】(1)根据三角形的特征,连接平行四边行两个相对的顶点,即可划分成两个相等的三角形。
(2)在平行四边形中,量出左上顶点向右和右下顶点向左相同的距离,连接两个点,即可划分成两个相等的梯形。
【详解】(1)
(答案不唯一)
(2)
(答案不唯一)
7.见详解
【分析】根据地图上方向的规定:上北下南,左西右东;以及方向具有相对性,即北与南相对、西与东相对、东北与西南相对、西北与东南相对,据此解答即可。
【详解】纪念馆正上方是企鹅馆;企鹅馆的左边是美猴王的位置;右边是大象馆的位置;大门的左侧是熊猫馆,大门的右侧是孔雀馆。
如图:
8.见详解
【分析】直径3厘米的圆,半径是1.5厘米,用圆规在直尺上量取1.5厘米,即两脚之间的距离,然后以一个脚放在圆心O,另一个脚画圆即可。
【详解】如图:
【点睛】此题主要考查学生对画圆方法的掌握与应用。
9.(1)(2)见详解
【分析】(1)绕A点逆时针旋转90°,需固定A点,将B、C两点绕A按逆时针转90°,依据网格确定旋转后坐标位置,再连线;
(2)按1∶2比例缩小,要先确定原三角形各边长度,再将边长除以2 ,以某顶点为参照确定新顶点位置,最后连接成缩小后的三角形。
【详解】(1)(2)作图如下:
10.见详解
【分析】(1)根据平移的特征,把图形①的各顶点分别向右平移2格,再向下平移4格,首尾连接即可得到平移后的图形④;
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出关键对称点,依次连接即可;
(3)根据图形放大知识,将图形③的三条边的长度扩大为原来的2倍,得到图形⑤。
【详解】根据要求,作图如下:
【点睛】图形平移、旋转、轴对称,只是位置、方向的变化,形状、大小不变;图形放大或缩小后大小变了,形状不变。作轴对称图形、作平移后的图形,关键是确定对称点(对应点)的位置;图形放大或缩小的倍数是指对应边放大或缩小的倍数。
11.见详解
【分析】观察图形可知,从正面看到的图形是2层:下层3个正方形,上层1个靠中间;从左面看到的图形是2层:下层2个正方形,上层1个靠左边;从上面看到的图形是两行,每行都是3个正方形,据此即可解答问题。
【详解】如图:
【点睛】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力。
12.(1)(2)见详解
【分析】(1)明确旋转中心为点O ,旋转方向是逆时针,角度为90°,通过直尺确定图形A各顶点绕点O逆时针旋转90°后的位置,再用铅笔连接各点得到图形B;
(2)确定平移方向为向右,距离是6格,用直尺将图形B的各顶点沿水平方向向右移动6格,最后用铅笔连接各平移后的顶点得到图形C。
【详解】(1)(2)作图如下:
13.见详解
【分析】把三角形ABC按原路返回,返回时平移的方向相反,距离不变。根据平移的特征把三角形ABC的各顶点分别向左平移8格,再向下平移2格,依次连接即可得到平移前的图形;根据旋转的特征,三角形ABC绕点C逆时针旋转180°,点C的位置不动,这个图形的各部分均绕此点按逆时针方向旋转180°即可画出旋转后的图形。
【详解】根据题意画图如下:
14.见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出关键对称点,依次连接即可;
(2)将图形②的两条直角边绕点O顺时针旋转90°后,再连接上两条边的顶点即可;
(3)根据图形缩小的知识,将图形③的四条边的长度缩小为原来的即可。
【详解】
【点睛】图形平移、旋转、轴对称,只是位置、方向的变化,形状、大小不变;图形放大或缩小后大小变了,形状不变。作轴对称图形、作平移后的图形、作旋转一定度数后的图形,关键是确定对称点(对应点)的位置;图形放大或缩小的倍数是指对应边放大或缩小的倍数。
15.见详解
【分析】只有一组对边平行的四边形是梯形,据此解答即可。
【详解】(1) (2)
【点睛】掌握梯形的特点是解答此题的关键,本题考查了梯形的特征以及画法。
16.(1)图见详解
(2)2826;94
【分析】(1)先根据进率“1米=100厘米”把长80米、宽60米换算成8000厘米、6000厘米,再根据“图上距离=实际距离×比例尺”求出图上的长、宽,据此画出这块长方形场地的平面图。
(2)根据题意,在这块长方形场地里建造一个最大的圆形健身场地,那么这个圆的直径等于长方形的宽,根据圆的面积公式S=πr2,求出这个圆形健身场地的实际占地面积。
如果在该健身场地一周每隔2米插一面旗子,先根据圆的周长公式C=2πr,求出该健身场地的周长,再根据封闭图形的植树问题“间隔数=棵数”,用周长除以间距,求出间隔数,也就是插旗子的数量。
【详解】(1)80米=8000厘米,60米=6000厘米
8000×=4(厘米)
6000×=3(厘米)
这块长方形场地的图上长4厘米、宽3厘米。
画图如下:
(2)3.14×(60÷2)2
=3.14×302
=3.14×900
=2826(平方米)
3.14×60=188.4(米)
188.4÷2≈94(面)
这个圆形健身场地的实际占地面积是2826平方米,大约需要94面旗子。
17.(1)(2)(3)图见详解
【分析】(1)找出构成图形的关键点,确定平移方向(向右)和平移距离(5格),由平移的距离确定关键点平移后的对应点的位置,依次连接各对应点。
(2)根据题目要求确定旋转中心(点O)、旋转方向(逆时针)、旋转角度(90°),分析所作图形,找出构成图形的关键边,按一定的方向和角度分别找出各关键边的对应边,最后依次连接组成封闭图形。
(3)把图形按照1∶n缩小,就是将图形的每一条边缩小到原来的,缩小后图形与原图形对应边长的比是1∶n。
【详解】(1)(2)(3)作图如下:
18.见详解
【分析】(1)根据旋转的意义,图形绕点O顺时针旋转90°后,点O的位置不动,其余各部分均绕点O按相同的方向旋转相同的度数,即可画出旋转后的图形B;
(2)根据图形平移的特征,把图形B的各顶点分别向右平移4格,再依次连接即可得到平移后的图形D。
【详解】
【点睛】本题考查了旋转和平移的意义,明确旋转和平移的定义是作图的关键。
19.(1)(2,3)
(2)图见详解
(3)1∶2;1∶4;9.42
【分析】(1)用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;据此用数对表示点O的位置。
(2)根据旋转的特征,将三角形绕点A顺时针旋转90度,点A位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形;
根据平移的特征,将旋转后的图形的各顶点分别向下平移2格,依次连接即可得到平移后的图形。
(3)原来圆的半径是1厘米,按2∶1放大,则放大后圆的半径是2,以点O为圆心,以2厘米为半径画出放大后的圆。
根据圆的周长公式C=2πr,分别求出放大前后两个圆的周长,进而得出两个圆的周长之比;
根据圆的面积公式S=πr2,分别求出放大前后两个圆的面积,进而得出两个圆的面积之比。
【详解】(1)点O的位置用数对表示是(2,3)。
(2)将三角形绕点A顺时针旋转90度,再向下平移2格后的图形,如下图。
(3)以点O为圆心,将圆按2∶1放大后的图形,如下图。
放大后圆的半径:1×2=2(厘米)
周长之比:(2π×1)∶(2π×2)=2π∶4π=1∶2
面积之比:(π×12)∶(π×22)=π∶4π=1∶4
圆环的面积:
3.14×(22-12)
=3.14×(4-1)
=3.14×3
=9.42(平方厘米)
放大前的圆与放大后的圆周长之比是(1∶2),面积之比是(1∶4)。两个圆形成的圆环面积是(9.42)平方厘米。
20.(1)(2)(3)见详解
【分析】(1)根据旋转的特征,图形A绕点O逆时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线L)的右边画出图形A的关键对称点,依次连接、涂色即可作图形A的轴对称图形C;根据平移的特征,把图形C的各顶点分别向右平移4格,依次连接、涂色即可得到平移后的图形D。
(3)根据图形放大的意义,把图形E的长、宽均放大到原来的2倍所得到的长方形就是原图形按2∶1放大后的图形F。
【详解】根据题意画图如下:
21.见详解
【分析】(1)确定图形①的各个顶点绕点O点逆时针旋转90°后的位置,再依次连接。
(2)确定图形①的各个顶点向上平移4格,再向右平移3格的位置,再依次连接。
(3)根据轴对称图形知识,画出图形②的所有对称轴即可。
(4)将图形③的底和高同时扩大到原来的2倍,画出放大后的图形即可。
【详解】根据要求,作图如下:
【点睛】本题考查了图形的平移、旋转、放大与缩小、轴对称图形画法,准确画图是关键。
22.
底:5厘米
高:2厘米
【详解】略
23.见详解
【分析】(1)根据画对称轴的方法:找出三角形的任意一组对称点,连结对称点,画出对称点所连线段的垂直平分线,就可以得到三角形的对称轴。
(2)根据旋转的特征,将三角形绕O点按顺时针方向旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(3)根据平移的特征,把平行四边形的各顶点分别先向下平移2格,依次连接各顶点,即可得到平移后的平行四边形。
(4)根据图形放大的方法,将长方形的长和宽按2∶1放大到原来的2倍,形状不变,画图即可。
【详解】根据分析,作图如下:
24.见详解
【分析】根据旋转的特征:图形A绕点O顺时针旋转180°,点O的位置不动,这个图形的各个部分关键点均绕此点按相同的方向旋转相同的度数,即可画出旋转后的图形B;
根据平移的特征,把图形B的各个顶点向下平移4格,依次连接,即可得到平移后的图形C。
分别计算出三角形扩大后的底和高的格数,然后画出三角形。
【详解】4×2=8(格);2×2=4(格)
【点睛】本题考查作旋转后的图形,作平移后的图形以及画放大后的图形。
25.
【详解】在五年级上册第五单元学习平行四边形的面积时,已经学会了用数方格的办法计算图形的面积.很容易可以看出,梯形的面积是6.因为我们要分的3个三角形的面积比是1:2:3,所以这3个三角形的面积是1、2、3.在此基础上,分的时候,可以利用三角形的面积公式.
26.见详解
【分析】用三角板的一条直角边与已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和A点重合,过A点沿直角边向已知直线画垂线即可;把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和A点重合,过A点沿三角板的直角边画平行线即可。
【详解】作图如下:
27.见详解
【分析】先数出原平行四边形各条边在方格中的长度(如水平、竖直或斜向格数)。按1∶3的比例,将每条边缩短到原长度的。在相同的方向上标出缩短后的长度并连接所得四个新顶点,便得到缩小后的平行四边形。
【详解】如图:
28.(1)(2)(3)(4)见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,找到图形甲的各顶点关于对称轴的对称点后,依次连接各点得到轴对称图形;
(2)根据平移的特征,把图形乙的各顶点分别向左平移3格,再向下平移6格,依次连接,即可得到平移后的图形;
(3)根据旋转的特征:图形乙绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同的方向旋转相同的度数,即可画出旋转后的图形;
(4)把图形丙按照1∶2缩小,就是将图形丙的底和高的缩小到原来的,底:4÷2=2,高:4÷2=2,画出缩小后的图形。
【详解】(1)见下图
(2)见下图
(3)见下图
(4)底:4÷2=2;高:4÷2=2;见下图
【点睛】本题考查了补全轴对称图形,作平移、旋转和缩小后的图形。掌握作图方法和步骤是解题的关键。
29.见详解
【分析】(1)根据平移的特征,将图形①的各顶点分别向右平移5格,依次连接即可得到平移后的图形。
(2)根据旋转的特征,将图形②绕点O顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
【详解】如图:
30.
【分析】先确定平移的方向,然后根据平移的格数确定对应点的位置,再画出平移后的图形;轴对称图形对应点到对称轴的距离是相等的,先描出对应点,再连点成图形即可。
【详解】
【点睛】掌握图形平移的方法和轴对称图形的特点是解决此题的关键。
31.(1)(2)见详解
【分析】(1)根据旋转的特征,图①绕点O逆时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(2)根据平移的特征,把图形②的各顶点分别向右平移2格,依次连接即可得到向右平移2格后的图形,同理可画出再向下平移3格后的图形。
【详解】(1)见下图
(2)见下图
【点睛】图形平移注意:原位置、平移方向、平移距离;图形旋转注意:原位置、旋转中心、旋转方向、旋转角。
32.见详解
【分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形步骤:(1)找点-找出构成图形的关键点。(2)定方向、距离-确定平移方向和平移距离。(3)画线-过关键点沿平移方向画出平行线。(4)定点-由平移的距离确定关键点平移后的对应点的位置。(5)连点-连接对应点。
(3)作旋转一定角度后的图形步骤:①根据题目要求,确定旋转中心、旋转方向和旋转角。②分析所作图形,找出构成图形的关键点。③找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点。④作出新图形,顺次连接作出的各点即可。
(4)把图形按照2∶1放大,就是将图形的每一条边放大到原来的2倍,放大后图形与原图形对应边长的比是2∶1,据此作图。
【详解】
【点睛】本题考查了补全轴对称图形,作平移、旋转和放大后的图形。掌握作图方法和步骤是解题的关键。
33.见详解
【分析】长方形、正方形、平行四边形都是由4条线段围成的图形,长方形、正方形四个角都是直角,由此根据长方形长和宽的格数画出长方形,根据正方形边长的格数画出正方形,再画出一个平行四边形即可。
【详解】如下图:
(答案不唯一)
34.见详解
【分析】(1)根据旋转的特征:长方形绕点O顺时针旋转90°后,点O的位置不动,其余各点均绕此点按照相同的方向旋转相同的度数即可画出旋转后的图形;
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的下边画出长方形的关键对称点,依次连接即可画出长方形的对称图形。
【详解】(1)(2)见详解:
【点睛】本题考查作旋转后的图形和补全轴对称图形。
35.(1)
(2)(3)见详解
【分析】(1)观察可知,1格平均分成4份,A所在位置是1格再多3份,根据分数的意义,平均分的份数作分母,所占的份数作分子,完整格可用整数表示,即A可表示为,再转化为假分数即可。
(2)B 表示的数是3,B 到 O 的距离是 3个单位,方向是O 的右边;则与其等距且方向相反的点 C 在O 的左边,根据正负数表示一组相反意义的量,O 的右边用正数表示,则O 的左边用负数表示,即C对应的数是 ﹣3。据此画图。
(3)正数在O 的右边,负数在O 的左边,根据小数的意义可知,2.5在2与3的中间,﹣可转化为﹣1.5,即在﹣1与﹣2的中间,据此画图。
【详解】(1)
点A表示的数写成分数是。
(2)见下图。
(3)﹣=﹣1.5
画图如下:
36.见详解
【分析】图中长方形的长是6格,宽是4格,根据图形放大或缩小的意义,按1∶2缩小后的长方形的长为3格,宽为2格,据此画图即可。
【详解】根据要求,作图如下:
【点睛】解答此题的关键是掌握图形放大或缩小的方法及比的意义。
37.见详解
【分析】(1)看清平移的方向和距离,画出平移后的图形即可;
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出原半图的关键对称点,依次连接即可;
(3)根据旋转的特征,三角形绕点O逆时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
(4)将图③的底和高同时缩小到原来的,画出缩小后的图形。
【详解】如图:
【点睛】本题考查了图形的平移、画轴对称图形、旋转、图形的放大与缩小,关键是能准确画图。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版数学小升初高频易错考点专题训练:作图题
学校:___________姓名:___________班级:___________考号:___________
一、作图题
1.先将下图向上平移4格后,再向右平移5格,画出两次平移后的图形。
2.(1)画出图形①关于直线l的轴对称图形。
(2)画出图形②先向右平移6个方格,再向上平移3个方格后的图形。
3.请画出三角形AOB绕O点顺时针旋转90°后的图形。
4.在方格纸上分别画出从不同方向看左边立体图形所看到的形状。
5.画出如图的另一半,使它成为一个轴对称图形。
6.把一个平行四边形剪一次,符合下面的要求(用虚线画出)。
(1)剪成两个相同的三角形。
(2)剪成两个相同的梯形。
7.请你依据如下动物园的导览提示,在下图中分别用★、▲标注出熊猫馆、美猴馆的位置。
走进动物园大门,正北面有纪念馆和企鹅馆。
企鹅馆的西面是美猴馆,东面是大象馆。
从企鹅馆向西南方向步行可以到达熊猫馆。
孔雀馆在动物园的东南角。
8.请你画出一个直径是3厘米的圆。
9.操作。
(1)画出三角形ABC绕A点逆时针旋转90°后的图形。
(2)画出三角形ABC以1∶2的比例缩小后的图形。
10.按要求画一画。
(1)画出将图形①先向右平移2格,再向下平移4格得到的图形④。
(2)画出轴对称图形②的另一半。
(3)画出将图形③按2∶1扩大后的图形⑤。
11.看立体图形,分别画出从正面、左面、上面看到的立体图形的形状。
12.画一画。(用直尺和铅笔作图)
(1)将图形A绕点O逆时针旋转90°,得到图形B。
(2)将图形B向右平移6格,得到图形C。
13.三角形ABC是将原图形向上平移2格,再向右平移8格后得到的。请画出平移前的图形,再画出将三角形ABC绕C点逆时针旋转180°后得到的图形。
14.按要求画一画。
(1)以虚线为对称轴,画出轴对称图形①的另一半。
(2)画出图形②绕点O顺时针旋转90°后的图形。
(3)将图形③缩小,使缩小后的图形与原图形对应线段长的比为1∶2。
15.下面是正方形点子图,请你在图中选一个点作为点,使四边形成为一个梯形,至少画出两种情况。
(1) (2)
16.全民健身是使人们增强体魄、健康生活的基础和保障,是每一个人成长和实现幸福生活的重要基础。幸福公园进行升级改造,留出了一块长80米、宽60米的长方形场地。
(1)请你按1∶2000的比例尺画出这块长方形场地的平面图。
(2)设计师计划在这块场地上建造一个最大的圆形健身场地。算一算,这个圆形健身场地的实际占地面积是 平方米;如果在该健身场地一周每隔2米插一面旗子,大约需要 面旗子。
17.按要求在下面的方格中画图。
(1)将图形A向右平移5格,得到图形B。
(2)将图形A绕点O逆时针旋转90°得到图形C。
(3)将图形A按1∶2缩小,得到图形D。
18.把所给图形先绕O点顺时针旋转90度得到图B,图B再向右平移4格得到图D。
19.观察下图,按要求完成下面各题。
(1)点O的位置用数对表示是( )。
(2)将三角形绕点A顺时针旋转90度,再向下平移2格。
(3)以点O为圆心,将圆按2∶1放大,画出放大后的图形。放大前的圆与放大后的圆周长之比是( ),面积之比是( )。两个圆形成的圆环面积是( )平方厘米。
20.按要求在方格纸上画图。
(1)将图形A绕O点逆时针旋转90°得到图形B。
(2)以直线L为对称轴作图形A的轴对称图形C,再将图形C向右平移4格得到图形D。
(3)画出图形E按2∶1放大后的图形F。
21.按要求画一画。
(1)将图形①绕点A逆时针旋转90°。
(2)将图形①先向上平移4格,再向右平移3格。
(3)画出图形②所有的对称轴。
(4)将图形③放大,使得放大后的图形与原图形对应线段长的比是2∶1。
22.操作题.
1.画一个面积是5平方厘米的三角形, 2.画一个只有2条对称轴的轴对称图形
23.画一画。
(1)在图中画出三角形的对称轴。
(2)画出把(1)中的三角形围绕右下方的顶点O顺时针旋转90°后的图形。
(3)画出把平行四边形向下平移2格后的图形。
(4)画出长方形按2∶1放大后的图形。
24.如下图,图形A绕点0顺时针旋转180°得到图形B,图形B向下平移4格得到图形C,把图形C按2∶1放大得到图形D。请画出图形B、图形C和图形D。
25.在由边长相等的小正方形组成的网格中,图中实线所围成的是一个梯形.请你在下图中用两种不同的方法将这个梯形分为3个三角形,使3个三角形的面积比是1:2:3.
26.过点A,画直线m的垂线和平行线。
27.按1∶3画出平行四边形缩小后的图形。
28.按要求画一画。
(1)以虚线MN为对称轴,画出图形甲的轴对称图形。
(2)将图形乙先向左平移3格,再向下平移6格。
(3)将图形乙绕点O顺时针旋转90°。
(4)将图形丙缩小,使缩小后的图形与原图形对应线段长的比为1∶2。
29.在方格纸上按要求画图。
(1)画出图形①向右平移5格后的图形。
(2)画出图形②绕点O顺时针旋转90°后的图形。
30.画一画。
(1)将图形A向右平移4格得到图形B。
(2)以直线l为对称轴,作图形B的对称图形,得到图形C。
31.按要求画图。
(1)将图①绕点O逆时针旋转90°,画出旋转后的图形。
(2)将图②向右平移2格,再向下平移3格,分别画出两次平移后的图形。
32.按要求画一画。
(1)以虚线MN为对称轴,画出轴对称图形①的另一半。
(2)画出图形②先向右平移7格,再向下平移2格后的图形。
(3)画出图形③绕点O按逆时针旋转90°后的图形。
(4)将图形④放大,使放大后的图形与原图形对应线段长的比为2∶1。
33.在下面的方格纸上按要求画长方形、正方形和平行四边形。
画一个长是10个格,宽是6个格的长方形。
画一个边长是4个格的正方形。
任意画一个平行四边形。
34.(1)画出长方形以O点为中心按顺时针方向旋转90度的图形。
(2)画出长方形的对称图形。
35.观察数轴,按要求完成:
(1)点A表示的数写成分数是。
(2)点C到O的距离和点B到O的距离相等,但方向相反,请标出C点,并将C点表示的数字写出来。
(3)在数轴上标出表示2.5和﹣的点。
36.如图的每个方格表示1cm2。将下面的长方形缩小,使缩小后的图形与原图形对应线段长的比为1∶2。
37.按要求在方格纸上画一画。
(1)将图①先向右平移8格,再向下平移3格
(2)以虚线MN为对称轴,画出图②的轴对称图形的另一半。
(3)将图③绕点O逆时针旋转
(4)将图③缩小,使得缩小后的图形与原图形对应线段长的比是1∶2。
《北师大版数学小升初高频易错考点专题训练:作图题》参考答案
1.
【分析】把此图的5个顶点先向上平移4格,再向右平移5格,描出这个五个点,然后将各点按原图顺次连接起来。
【详解】
【点睛】掌握平移的方法和平移图形的画法是解决此题的关键。把图形的各个顶点按照指定的方向和格数平移到新的位置,再把各点按原图连接起来。
2.(1)(2)见详解
【分析】(1)依据轴对称图形的画法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形,由此即可画图;
(2)根据平移的特征,把图形②各顶点分别向右平移6格,再向上平移3格,依次连结即可得到平移后图形。
【详解】(1)(2)如下图所示:
3.见详解
【分析】根据旋转的方法,将三角形与点O相连的两条边绕点O顺时针旋转90度,再将第三条边连起来即可。
【详解】
【点睛】做旋转的图形时,要注意旋转的方向和角度,旋转后图形的形状和大小不变,只是位置发生变化。
4.图见详解
【分析】根据从不同方向观察物体和几何图形的方法,分别画出从不同方向看立体图形所看到的形状即可。
【详解】如图:
5.见详解
【分析】平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形。根据轴对称图形的特征,对称点到对称轴的距离相等,找到图形的各顶点关于对称轴的对称点后,依次连接各点得到轴对称图形。
【详解】如图:
6.见详解
【分析】(1)根据三角形的特征,连接平行四边行两个相对的顶点,即可划分成两个相等的三角形。
(2)在平行四边形中,量出左上顶点向右和右下顶点向左相同的距离,连接两个点,即可划分成两个相等的梯形。
【详解】(1)
(答案不唯一)
(2)
(答案不唯一)
7.见详解
【分析】根据地图上方向的规定:上北下南,左西右东;以及方向具有相对性,即北与南相对、西与东相对、东北与西南相对、西北与东南相对,据此解答即可。
【详解】纪念馆正上方是企鹅馆;企鹅馆的左边是美猴王的位置;右边是大象馆的位置;大门的左侧是熊猫馆,大门的右侧是孔雀馆。
如图:
8.见详解
【分析】直径3厘米的圆,半径是1.5厘米,用圆规在直尺上量取1.5厘米,即两脚之间的距离,然后以一个脚放在圆心O,另一个脚画圆即可。
【详解】如图:
【点睛】此题主要考查学生对画圆方法的掌握与应用。
9.(1)(2)见详解
【分析】(1)绕A点逆时针旋转90°,需固定A点,将B、C两点绕A按逆时针转90°,依据网格确定旋转后坐标位置,再连线;
(2)按1∶2比例缩小,要先确定原三角形各边长度,再将边长除以2 ,以某顶点为参照确定新顶点位置,最后连接成缩小后的三角形。
【详解】(1)(2)作图如下:
10.见详解
【分析】(1)根据平移的特征,把图形①的各顶点分别向右平移2格,再向下平移4格,首尾连接即可得到平移后的图形④;
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出关键对称点,依次连接即可;
(3)根据图形放大知识,将图形③的三条边的长度扩大为原来的2倍,得到图形⑤。
【详解】根据要求,作图如下:
【点睛】图形平移、旋转、轴对称,只是位置、方向的变化,形状、大小不变;图形放大或缩小后大小变了,形状不变。作轴对称图形、作平移后的图形,关键是确定对称点(对应点)的位置;图形放大或缩小的倍数是指对应边放大或缩小的倍数。
11.见详解
【分析】观察图形可知,从正面看到的图形是2层:下层3个正方形,上层1个靠中间;从左面看到的图形是2层:下层2个正方形,上层1个靠左边;从上面看到的图形是两行,每行都是3个正方形,据此即可解答问题。
【详解】如图:
【点睛】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力。
12.(1)(2)见详解
【分析】(1)明确旋转中心为点O ,旋转方向是逆时针,角度为90°,通过直尺确定图形A各顶点绕点O逆时针旋转90°后的位置,再用铅笔连接各点得到图形B;
(2)确定平移方向为向右,距离是6格,用直尺将图形B的各顶点沿水平方向向右移动6格,最后用铅笔连接各平移后的顶点得到图形C。
【详解】(1)(2)作图如下:
13.见详解
【分析】把三角形ABC按原路返回,返回时平移的方向相反,距离不变。根据平移的特征把三角形ABC的各顶点分别向左平移8格,再向下平移2格,依次连接即可得到平移前的图形;根据旋转的特征,三角形ABC绕点C逆时针旋转180°,点C的位置不动,这个图形的各部分均绕此点按逆时针方向旋转180°即可画出旋转后的图形。
【详解】根据题意画图如下:
14.见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出关键对称点,依次连接即可;
(2)将图形②的两条直角边绕点O顺时针旋转90°后,再连接上两条边的顶点即可;
(3)根据图形缩小的知识,将图形③的四条边的长度缩小为原来的即可。
【详解】
【点睛】图形平移、旋转、轴对称,只是位置、方向的变化,形状、大小不变;图形放大或缩小后大小变了,形状不变。作轴对称图形、作平移后的图形、作旋转一定度数后的图形,关键是确定对称点(对应点)的位置;图形放大或缩小的倍数是指对应边放大或缩小的倍数。
15.见详解
【分析】只有一组对边平行的四边形是梯形,据此解答即可。
【详解】(1) (2)
【点睛】掌握梯形的特点是解答此题的关键,本题考查了梯形的特征以及画法。
16.(1)图见详解
(2)2826;94
【分析】(1)先根据进率“1米=100厘米”把长80米、宽60米换算成8000厘米、6000厘米,再根据“图上距离=实际距离×比例尺”求出图上的长、宽,据此画出这块长方形场地的平面图。
(2)根据题意,在这块长方形场地里建造一个最大的圆形健身场地,那么这个圆的直径等于长方形的宽,根据圆的面积公式S=πr2,求出这个圆形健身场地的实际占地面积。
如果在该健身场地一周每隔2米插一面旗子,先根据圆的周长公式C=2πr,求出该健身场地的周长,再根据封闭图形的植树问题“间隔数=棵数”,用周长除以间距,求出间隔数,也就是插旗子的数量。
【详解】(1)80米=8000厘米,60米=6000厘米
8000×=4(厘米)
6000×=3(厘米)
这块长方形场地的图上长4厘米、宽3厘米。
画图如下:
(2)3.14×(60÷2)2
=3.14×302
=3.14×900
=2826(平方米)
3.14×60=188.4(米)
188.4÷2≈94(面)
这个圆形健身场地的实际占地面积是2826平方米,大约需要94面旗子。
17.(1)(2)(3)图见详解
【分析】(1)找出构成图形的关键点,确定平移方向(向右)和平移距离(5格),由平移的距离确定关键点平移后的对应点的位置,依次连接各对应点。
(2)根据题目要求确定旋转中心(点O)、旋转方向(逆时针)、旋转角度(90°),分析所作图形,找出构成图形的关键边,按一定的方向和角度分别找出各关键边的对应边,最后依次连接组成封闭图形。
(3)把图形按照1∶n缩小,就是将图形的每一条边缩小到原来的,缩小后图形与原图形对应边长的比是1∶n。
【详解】(1)(2)(3)作图如下:
18.见详解
【分析】(1)根据旋转的意义,图形绕点O顺时针旋转90°后,点O的位置不动,其余各部分均绕点O按相同的方向旋转相同的度数,即可画出旋转后的图形B;
(2)根据图形平移的特征,把图形B的各顶点分别向右平移4格,再依次连接即可得到平移后的图形D。
【详解】
【点睛】本题考查了旋转和平移的意义,明确旋转和平移的定义是作图的关键。
19.(1)(2,3)
(2)图见详解
(3)1∶2;1∶4;9.42
【分析】(1)用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;据此用数对表示点O的位置。
(2)根据旋转的特征,将三角形绕点A顺时针旋转90度,点A位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形;
根据平移的特征,将旋转后的图形的各顶点分别向下平移2格,依次连接即可得到平移后的图形。
(3)原来圆的半径是1厘米,按2∶1放大,则放大后圆的半径是2,以点O为圆心,以2厘米为半径画出放大后的圆。
根据圆的周长公式C=2πr,分别求出放大前后两个圆的周长,进而得出两个圆的周长之比;
根据圆的面积公式S=πr2,分别求出放大前后两个圆的面积,进而得出两个圆的面积之比。
【详解】(1)点O的位置用数对表示是(2,3)。
(2)将三角形绕点A顺时针旋转90度,再向下平移2格后的图形,如下图。
(3)以点O为圆心,将圆按2∶1放大后的图形,如下图。
放大后圆的半径:1×2=2(厘米)
周长之比:(2π×1)∶(2π×2)=2π∶4π=1∶2
面积之比:(π×12)∶(π×22)=π∶4π=1∶4
圆环的面积:
3.14×(22-12)
=3.14×(4-1)
=3.14×3
=9.42(平方厘米)
放大前的圆与放大后的圆周长之比是(1∶2),面积之比是(1∶4)。两个圆形成的圆环面积是(9.42)平方厘米。
20.(1)(2)(3)见详解
【分析】(1)根据旋转的特征,图形A绕点O逆时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线L)的右边画出图形A的关键对称点,依次连接、涂色即可作图形A的轴对称图形C;根据平移的特征,把图形C的各顶点分别向右平移4格,依次连接、涂色即可得到平移后的图形D。
(3)根据图形放大的意义,把图形E的长、宽均放大到原来的2倍所得到的长方形就是原图形按2∶1放大后的图形F。
【详解】根据题意画图如下:
21.见详解
【分析】(1)确定图形①的各个顶点绕点O点逆时针旋转90°后的位置,再依次连接。
(2)确定图形①的各个顶点向上平移4格,再向右平移3格的位置,再依次连接。
(3)根据轴对称图形知识,画出图形②的所有对称轴即可。
(4)将图形③的底和高同时扩大到原来的2倍,画出放大后的图形即可。
【详解】根据要求,作图如下:
【点睛】本题考查了图形的平移、旋转、放大与缩小、轴对称图形画法,准确画图是关键。
22.
底:5厘米
高:2厘米
【详解】略
23.见详解
【分析】(1)根据画对称轴的方法:找出三角形的任意一组对称点,连结对称点,画出对称点所连线段的垂直平分线,就可以得到三角形的对称轴。
(2)根据旋转的特征,将三角形绕O点按顺时针方向旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(3)根据平移的特征,把平行四边形的各顶点分别先向下平移2格,依次连接各顶点,即可得到平移后的平行四边形。
(4)根据图形放大的方法,将长方形的长和宽按2∶1放大到原来的2倍,形状不变,画图即可。
【详解】根据分析,作图如下:
24.见详解
【分析】根据旋转的特征:图形A绕点O顺时针旋转180°,点O的位置不动,这个图形的各个部分关键点均绕此点按相同的方向旋转相同的度数,即可画出旋转后的图形B;
根据平移的特征,把图形B的各个顶点向下平移4格,依次连接,即可得到平移后的图形C。
分别计算出三角形扩大后的底和高的格数,然后画出三角形。
【详解】4×2=8(格);2×2=4(格)
【点睛】本题考查作旋转后的图形,作平移后的图形以及画放大后的图形。
25.
【详解】在五年级上册第五单元学习平行四边形的面积时,已经学会了用数方格的办法计算图形的面积.很容易可以看出,梯形的面积是6.因为我们要分的3个三角形的面积比是1:2:3,所以这3个三角形的面积是1、2、3.在此基础上,分的时候,可以利用三角形的面积公式.
26.见详解
【分析】用三角板的一条直角边与已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和A点重合,过A点沿直角边向已知直线画垂线即可;把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和A点重合,过A点沿三角板的直角边画平行线即可。
【详解】作图如下:
27.见详解
【分析】先数出原平行四边形各条边在方格中的长度(如水平、竖直或斜向格数)。按1∶3的比例,将每条边缩短到原长度的。在相同的方向上标出缩短后的长度并连接所得四个新顶点,便得到缩小后的平行四边形。
【详解】如图:
28.(1)(2)(3)(4)见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,找到图形甲的各顶点关于对称轴的对称点后,依次连接各点得到轴对称图形;
(2)根据平移的特征,把图形乙的各顶点分别向左平移3格,再向下平移6格,依次连接,即可得到平移后的图形;
(3)根据旋转的特征:图形乙绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同的方向旋转相同的度数,即可画出旋转后的图形;
(4)把图形丙按照1∶2缩小,就是将图形丙的底和高的缩小到原来的,底:4÷2=2,高:4÷2=2,画出缩小后的图形。
【详解】(1)见下图
(2)见下图
(3)见下图
(4)底:4÷2=2;高:4÷2=2;见下图
【点睛】本题考查了补全轴对称图形,作平移、旋转和缩小后的图形。掌握作图方法和步骤是解题的关键。
29.见详解
【分析】(1)根据平移的特征,将图形①的各顶点分别向右平移5格,依次连接即可得到平移后的图形。
(2)根据旋转的特征,将图形②绕点O顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
【详解】如图:
30.
【分析】先确定平移的方向,然后根据平移的格数确定对应点的位置,再画出平移后的图形;轴对称图形对应点到对称轴的距离是相等的,先描出对应点,再连点成图形即可。
【详解】
【点睛】掌握图形平移的方法和轴对称图形的特点是解决此题的关键。
31.(1)(2)见详解
【分析】(1)根据旋转的特征,图①绕点O逆时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(2)根据平移的特征,把图形②的各顶点分别向右平移2格,依次连接即可得到向右平移2格后的图形,同理可画出再向下平移3格后的图形。
【详解】(1)见下图
(2)见下图
【点睛】图形平移注意:原位置、平移方向、平移距离;图形旋转注意:原位置、旋转中心、旋转方向、旋转角。
32.见详解
【分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形步骤:(1)找点-找出构成图形的关键点。(2)定方向、距离-确定平移方向和平移距离。(3)画线-过关键点沿平移方向画出平行线。(4)定点-由平移的距离确定关键点平移后的对应点的位置。(5)连点-连接对应点。
(3)作旋转一定角度后的图形步骤:①根据题目要求,确定旋转中心、旋转方向和旋转角。②分析所作图形,找出构成图形的关键点。③找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点。④作出新图形,顺次连接作出的各点即可。
(4)把图形按照2∶1放大,就是将图形的每一条边放大到原来的2倍,放大后图形与原图形对应边长的比是2∶1,据此作图。
【详解】
【点睛】本题考查了补全轴对称图形,作平移、旋转和放大后的图形。掌握作图方法和步骤是解题的关键。
33.见详解
【分析】长方形、正方形、平行四边形都是由4条线段围成的图形,长方形、正方形四个角都是直角,由此根据长方形长和宽的格数画出长方形,根据正方形边长的格数画出正方形,再画出一个平行四边形即可。
【详解】如下图:
(答案不唯一)
34.见详解
【分析】(1)根据旋转的特征:长方形绕点O顺时针旋转90°后,点O的位置不动,其余各点均绕此点按照相同的方向旋转相同的度数即可画出旋转后的图形;
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的下边画出长方形的关键对称点,依次连接即可画出长方形的对称图形。
【详解】(1)(2)见详解:
【点睛】本题考查作旋转后的图形和补全轴对称图形。
35.(1)
(2)(3)见详解
【分析】(1)观察可知,1格平均分成4份,A所在位置是1格再多3份,根据分数的意义,平均分的份数作分母,所占的份数作分子,完整格可用整数表示,即A可表示为,再转化为假分数即可。
(2)B 表示的数是3,B 到 O 的距离是 3个单位,方向是O 的右边;则与其等距且方向相反的点 C 在O 的左边,根据正负数表示一组相反意义的量,O 的右边用正数表示,则O 的左边用负数表示,即C对应的数是 ﹣3。据此画图。
(3)正数在O 的右边,负数在O 的左边,根据小数的意义可知,2.5在2与3的中间,﹣可转化为﹣1.5,即在﹣1与﹣2的中间,据此画图。
【详解】(1)
点A表示的数写成分数是。
(2)见下图。
(3)﹣=﹣1.5
画图如下:
36.见详解
【分析】图中长方形的长是6格,宽是4格,根据图形放大或缩小的意义,按1∶2缩小后的长方形的长为3格,宽为2格,据此画图即可。
【详解】根据要求,作图如下:
【点睛】解答此题的关键是掌握图形放大或缩小的方法及比的意义。
37.见详解
【分析】(1)看清平移的方向和距离,画出平移后的图形即可;
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出原半图的关键对称点,依次连接即可;
(3)根据旋转的特征,三角形绕点O逆时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
(4)将图③的底和高同时缩小到原来的,画出缩小后的图形。
【详解】如图:
【点睛】本题考查了图形的平移、画轴对称图形、旋转、图形的放大与缩小,关键是能准确画图。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
