人教版数学小升初高频易错考点专题训练:单选题(含解析)
文档属性
| 名称 | 人教版数学小升初高频易错考点专题训练:单选题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 359.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版数学小升初高频易错考点专题训练:单选题
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.大约一千五百年前,我国古代有一本数学名著中记载了一道数学趣题——“鸡兔同笼”问题。请问这本名著是( )。
A. B.
C. D.
2.甲数比乙数少,乙数比甲数多( )%。
A.20 B.25 C.40
3.需要清楚地表示每个项目的具体数目应选择( )。
A.折线统计图 B.扇形统计图 C.条形统计图 D.以上三者均可以
4.在0.5的末尾添上一个零后,它的计数单位是( )。
A.0.1 B.百分位 C.十分位 D.0.01
5.与的分数单位相同的数是________,与它大小相等的数是________。( )
① ② ③
A.①② B.②③ C.①③
6.一个三角形的两条边分别是10cm和3cm,第三条边可能是( )cm。
A.7 B.13 C.9 D.15
7.从正面看到的形状是的立体图形是( ).
A. B. C.
8.比例尺是( )。
A.一把尺 B.一个比例 C.一个比 D.一个分数
9.利率是表示( )的百分比。
A.本金和利息 B.利息与本金 C.利息和时间
10.如下图所示, 韩梅家的左右两侧各摆了2盆花.每次, 韩梅按照以下规则往家中搬一盆花: 先选择左侧还是右侧, 然后搬该侧离家最近的.要把所有的花搬到家里,共有( )种不同的搬花顺序.
A.4 B.6 C.8 D.10
11.a÷b=8(a和b都是自然数),a和b的最小公倍数是( )。
A.a B.b C.8 D.ab
12.圆锥的侧面展开是一个( )。
A.长方形 B.正方形 C.扇形
13.在计算0.8÷0.24时,被除数和除数都要同时( )。
A.不扩大 B.扩大到原来的10倍 C.扩大到原来的100倍
14.下面成反比例的是( )。
A.看一本书,已看页数和未看页数。 B.长方形的周长一定,它的长和宽。
C.总价一定,商品的数量和单价。 D.圆柱的底面积和体积。
15.一个三角形三个内角的度数比是1:5:2,这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形
16.一种面粉的质量标识为“25±0.25千克”,则下列面粉中质量合格的是( )。
A.25.38千克 B.25.18千克 C.24.69千克 D.26.25千克
17.一个分数的分子缩小为原来的,分母扩大为原来的3倍,分数值就( )。
A.扩大为原来的3倍 B.扩大为原来的6倍
C.缩小到原来的 D.不变
18.以下几种情况最适合用折线统计图统计的是( )。
A.某公司销售业绩增减变化情况 B.描述六(2)班同学身高分组的分布情况
C.各类支出占家庭支出的百分比 D.希望小学图书角不同种类图书数量的多少
19.为了分析王玲从0岁到12岁的身高变化情况,采用( )比较合适。
A.统计表 B.折线统计图 C.条形统计图 D.扇形统计图
20.一种袋装食品标准净重为200g,质监工作人员为了解该种食品袋净重与标准的误差,把食品净重205g记为﹢5g,那么食品净重196g就记作( )g。
A.﹢196 B.﹣196 C.﹢4 D.﹣4
21.与数对(3,5)在同一行的是( )。
A.(5,3) B.(3,4) C.(4,5) D.(5,6)
22.用3个0和3个2组成六位数,读这个六位数时只要读一个0的是( )
A.202020 B.200202 C.222000 D.202000
23.下列图案中,是轴对称图形的是图( )。
A. B. C. D.
24.学校在小强家的东南面450米处,小强每分走50米,向东走了9分,小强能走到学校吗?( ).
A.能 B.不能 C.不能确定
25.从、、、四张卡片中任选两张组成一个两位数,组成的两位数中可能性最大的是( )。
A.合数 B.质数 C.偶数 D.奇数
26.几个小朋友分一箱水果,如果每人分8个,还剩1个;如果每人分10个,也剩1个。那么,这箱水果至少有( )个。
A.41 B.81 C.20
27.x、y、z是三个非零自然数,且,那么x、y、z按照从大到小的顺序排列应是( )。
A.z>y>x B.y>x>z C.y>z>x
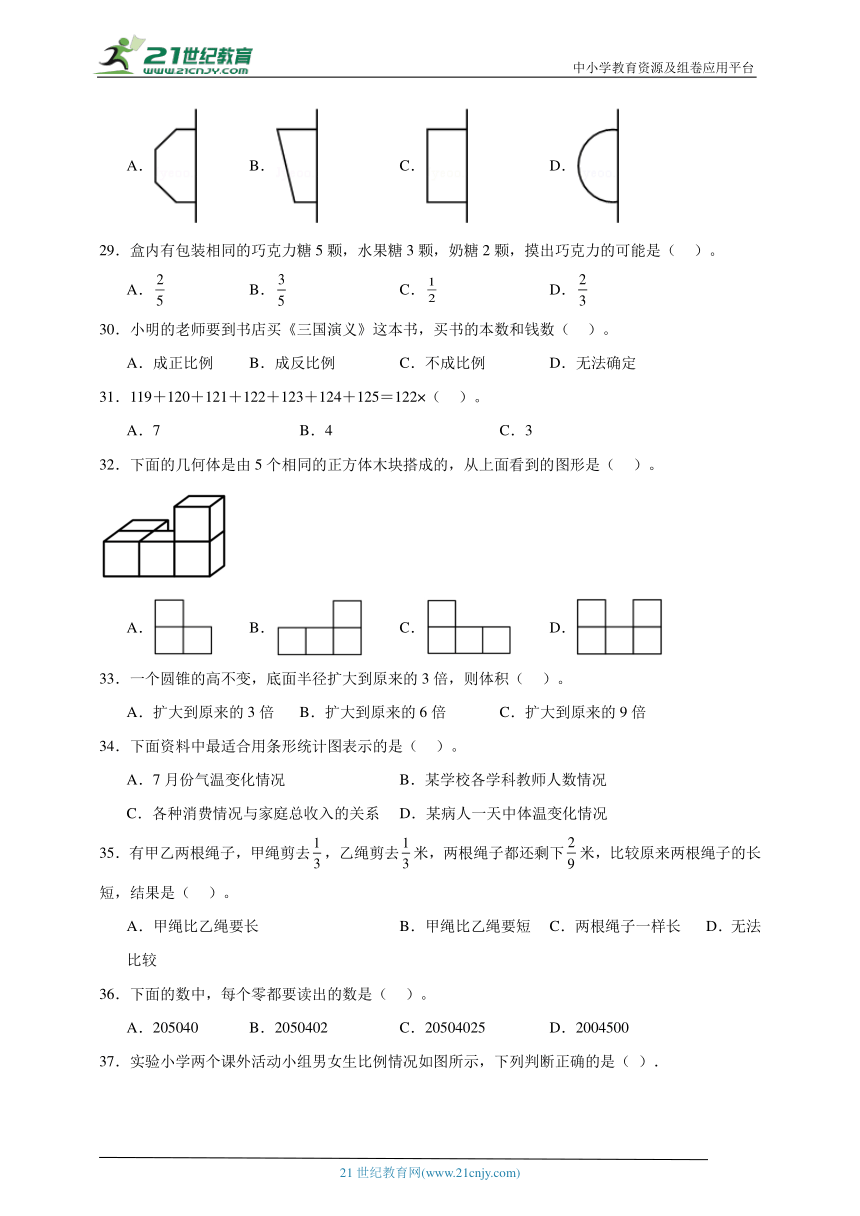
28.下图中,以直线为轴旋转一周,可以形成圆柱的是( )。
A. B. C. D.
29.盒内有包装相同的巧克力糖5颗,水果糖3颗,奶糖2颗,摸出巧克力的可能是( )。
A. B. C. D.
30.小明的老师要到书店买《三国演义》这本书,买书的本数和钱数( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
31.119+120+121+122+123+124+125=122×( )。
A.7 B.4 C.3
32.下面的几何体是由5个相同的正方体木块搭成的,从上面看到的图形是( )。
A. B. C. D.
33.一个圆锥的高不变,底面半径扩大到原来的3倍,则体积( )。
A.扩大到原来的3倍 B.扩大到原来的6倍 C.扩大到原来的9倍
34.下面资料中最适合用条形统计图表示的是( )。
A.7月份气温变化情况 B.某学校各学科教师人数情况
C.各种消费情况与家庭总收入的关系 D.某病人一天中体温变化情况
35.有甲乙两根绳子,甲绳剪去,乙绳剪去米,两根绳子都还剩下米,比较原来两根绳子的长短,结果是( )。
A.甲绳比乙绳要长 B.甲绳比乙绳要短 C.两根绳子一样长 D.无法比较
36.下面的数中,每个零都要读出的数是( )。
A.205040 B.2050402 C.20504025 D.2004500
37.实验小学两个课外活动小组男女生比例情况如图所示,下列判断正确的是( ).
A.两个小组的人数同样多
B.音乐组的女生和美术组的男生同样多
C.美术组的男生比音乐组的男生多
D.美术组男生多,音乐组女生多
38.下面几组相关联的量中,成反比例的是( )。
A.单价一定,总价和数量
B.速度一定,路程和时间
C.圆柱体的体积一定,它的底面积和高
39.左下图是水滴进玻璃容器的示意图(滴水速度相同),右下图表示的是容器中水的高度随滴水时间变化的情况(图中刻度、单位都相同)。下列选项中对应关系正确的是( )。
A.(1)—(a) B.(2)—(b) C.(3)—(c) D.(4)—(d)
40.把一个图形按1∶3的比缩小,再把缩小后的图形按2∶1的比放大,最后得到的图形与原图形相比,结果是( )。
A.缩小了 B.放大了 C.大小不变 D.不确定
41.观察如图的示意图,图中各场所的方位描述正确的是( )。
A.医院在学校北偏西20°方向100m处
B.邮局在学校西偏南20°方向300m处
C.公园在学校北偏东45°方向100m处
D.学校在广场南偏东45°方向100m处
42.综合实践课,小明制作了一顶帽子(如图),上面是圆柱形;帽檐部分是一个圆环,做这顶帽子一共用布( )平方厘米。
A.628 B.1256 C.1884 D.2198
43.已知一天有86400秒。“中国飞人”苏炳添经过五年(约157680000秒),从里约到东京,以9秒83创亚洲记录的成绩,成为首位闯进奥运会男子百米决赛的中国人。根据以上资料,如果计算一年共有多少秒(一年按365天计算),列式正确的是( )。
A.86400×30×365 B.86400×365 C.157680000÷9.83
44.下图的标志中,是轴对称图形的有( )个.
A.3 B.2 C.1 D.0
45.甲数是乙数的,乙数是丙数的甲、乙、丙三个数的比是( )。
A.45∶20∶6 B.6∶20∶45 C.20∶6∶45 D.6∶45∶20
46.用三根同样长的铁丝,分别围成长方形、正方形和圆(接口处长度忽略不计),关于三个图形周长和面积的大小关系,下面图中描述正确的是( )。
A. B.
C. D.
47.一个公司有50名员工,今天有2人请假未到。这个公司今天的出勤率是( )。
A.2% B.96% C.48% D.4%
48.一个三角形中,最大的一个角一定不小于( )。
A.50° B.60° C.70° D.90°
49.56人参加户外拓展训练,将22人安排在A营地,34人安排在B营地。从12:01开始,每逢整点A营地派出12人前往B营地,B营地派出8人前往A营地。已知两个营地之间的单程用时为30分钟,问以下哪个时间点,位于B营地的人数正好是A营地的3倍?( )
A.13:20 B.13:40 C.14:20 D.14:40
50.教室里有若干学生,走了10名女生后,男生是女生人数的2倍,又走了9名男生后,女生是男生人数的5倍。问:最初有多少名女生?( )。
A.15 B.12 C.10 D.9
《人教版数学小升初高频易错考点专题训练:单选题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C D A C A C B B
题号 11 12 13 14 15 16 17 18 19 20
答案 A C C C C B C A B D
题号 21 22 23 24 25 26 27 28 29 30
答案 C A D B A A A C C A
题号 31 32 33 34 35 36 37 38 39 40
答案 A C C B B B D C D A
题号 41 42 43 44 45 46 47 48 49 50
答案 C C B C B D B B D A
1.B
【详解】大约一千五百年前,我国古代数学名著《孙子算经》中记载了一道数学趣题——“鸡兔同笼”问题。
故答案为:B
2.B
【详解】略
3.C
【分析】条形统计图能直观地表示出每个项目的具体数目;折线统计图能直观地反映事物变化情况;扇形统计图能直观地表示出各部分在总体中所占的百分比。
【详解】需要清楚地表示每个项目的具体数目应选择条形统计图。
故答案为:C。
【点睛】明确不同统计图的特点是解答本题的关键。
4.D
【分析】考查计数单位与数位的知识,以及在小数的末尾添上0,小数的大小不变,但是计数单位会改变。
【详解】0.5的末尾添上一个零,得0.50,它的计数单位是0.01,即百分之一。
故答案为:D
5.A
【分析】把单位“1”平均分成若干份,取其中的一份的数,叫做分数单位,所以分母相同的两个分数的分数单位才相同;根据分数的基本性质,把分数约分成最简分数后就能判断出相等的分数。
【详解】与这个分数单位相同的数是,分数单位都是;
,,所以与它大小相等的数是。
故答案为:A。
【点睛】本题考查分数单位和分数的约分,明确分数单位的概念是解答此题的关键。
6.C
【分析】三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边。
【详解】三角形的两条边分别是10cm和3cm,则第三条边的长度大于7厘米,小于13厘米。
故答案为:C
【点睛】熟记三角形的三边关系是解答此题的关键。
7.A
【解析】略
8.C
【详解】比例尺是图上距离和实际距离的比。它是一个比;
故答案为:C
9.B
【分析】利率是指单位时间内,利息与本金的比率;据此解答。
【详解】利率是表示利息与本金的百分比。
故答案为B。
【点睛】此题考查了利率概念的理解,关键是熟记知识点。
10.B
【详解】略
11.A
【分析】根据题意,a÷b=8,即a是b的8倍;根据两个数是倍数关系时,最大公因数是较小数,最小公倍数是较大数;据此解答。
【详解】a÷b=8(a和b都是自然数),a与b是倍数关系,且a>b;
a和b的最小公倍数是a。
故答案为:A
【点睛】掌握两个数是倍数关系时,它们的最小公倍数的求法是解题的关键。
12.C
【分析】根据圆锥的特征,直接选出圆锥的侧面展开图即可。
【详解】圆锥的侧面展开是一个扇形。
故答案为:C
【点睛】本题考查了圆锥,圆锥的底面是圆,侧面是曲面,展开为扇形。
13.C
【分析】小数除法法则:先移动除数的小数点,使它变成整数。除数的小数点向右移动几位,被除数的小数点也向右移动相同的位数(位数不够的补“0”),然后按照除数是整数的除法进行计算。据此解答。
【详解】除数0.24要变成整数,小数点向右移动两位,相当于除数扩大到原来的100倍,根据商不变的性质可知,被除数也要扩大到原来的100倍。
故答案为:C
【点睛】此题的解题关键是利用小数除法的计算法则和商的变化规律来求解。
14.C
【详解】反比例公式为xy=k(积一定)
15.C
【详解】试题分析:根据三角形按角分类的方法可知,三角形中的最大角决定了三角形的类别,因此只要求出最大角的度数即可判断.依据三角形的内角和为180°,利用按比例分配的方法即可求得对应的份数最大的角(即最大角)的度数.
解:180°×=112.5(度),
因为112.5度角为钝角,
所以此三角形是钝角三角形.
故选C.
【点评】此题主要利用三角形的内角和与按比例分配的知识进行解答,也要明确三角形按角分类的方法.
16.B
【分析】正数、负数表示两种相反意义的量。“25±0.25千克”的含义是,25千克是这种面粉的标准净重,实际每袋最多不超过(25+0.25)千克,最少不低于(25-0.25)千克,据此解答。
【详解】最少不低于:25-0.25=24.75(千克)
最多不超过:25+0.25=25.25(千克)
A.25.38>25.25,不符合题意;
B.24.75<25.18<25.25,符合题意;
C.24.69<24.75,不符合题意;
D.26.25>25.25,不符合题意;
所以,面粉中质量合格的是25.18千克。
故答案为:B
17.C
【分析】分数与除法的关系:分子相当于被除数,分母相当于除数,分数线相当于除号。
商的变化规律:除数不变,被除数乘几,商就乘几;被除数除以几,商就除以几;
被除数不变,除数乘几,商反而除以几;除数除以几,商反而乘几。
【详解】一个分数的分子缩小为原来的,相当于被除数缩小为原来的,商(分数值)也缩小为原来的;分母扩大为原来的3倍,相当于除数扩大为原来的3倍,商(分数值)反而缩小到原来的;最终商(分数值)缩小到原来的×=。
故答案为:C
18.A
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;根据统计图的特点依次分析即可。
【详解】A.某公司销售业绩增减变化情况应该用折线统计图,故符合题意;
B.描述六(2)班同学身高分组的分布情况应该用条形统计图,故不符合题意;
C.各类支出占家庭支出的百分比应该用扇形统计图,故不符合题意;
D.希望小学图书角不同种类图书数量的多少应该用条形统计图,故不符合题意。
故答案为:A
【点睛】本题主要考查了统计图的选择,掌握各种统计图的特点是解题的关键。
19.B
【分析】折线统计图的特点,不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;
条形统计图用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;
扇形统计图清楚地看出各部分数量与总数量之间,部分与部分之间的关系。
【详解】为了分析王玲从0岁到12岁的身高变化情况,采用折线统计图比较合适;
故答案为:B
【点睛】明确各种统计图的特点是解答本题的关键。
20.D
【分析】通常把高于标准质量的质量用“﹢”表示,低于标准质量的质量用“﹣”表示。据此解答。
【详解】196<200
200-196=4(g)
即低于标准4克,用负数表示为﹣4g。
故答案为:D
【点睛】掌握正负数的意义,看清规定哪一个为正,则和它意义相反的就为负。
21.C
【分析】数对表示位置时,第一个数表示列数,第二个数表示行数;所以(3,5)表示第3列第5行;依次分析各选项表示的位置做出判断。
【详解】A.(5,3)表示第5列第3行,不合题意;
B.(3,4)表示第3列第4行,不合题意;
C.(4,5)表示第4列第5行,符合题意;
D.(5,6)表示第5列第6行,不合题意。
故答案为:C
【点睛】数对表示位置的方法是:先列后行。
22.A
【详解】解:用3个0和3个2组成六位数,且只读一个0,这个数是220002、220200、202020等.
故选A.
23.D
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,由此解答即可。
【详解】
A. 不是轴对称图形;
B. 不是轴对称图形;
C. 不是轴对称图形;
D. 是轴对称图形;
故答案为:D
【点睛】明确轴对称图形的特点是解答本题的关键。
24.B
【详解】略
25.A
【分析】将可以组成的两位数都写出来,看看质数、合数、偶数、奇数各有多少个,再根据“数量越多,可能性越大”进行判断即可。
【详解】组成的两位数有:12、13、14、21、23、24、31、32、34、41、42、43;
合数有:12、14、21、24、32、34、42;
质数有:13、23、31、41、43;
偶数有:12、14、24、32、34、42;
奇数有:13、21、23、31、41、43;
合数最多,所以组成合数的可能性最大;
故答案为:A。
【点睛】解答本题的关键是将可以组成的两位数都写出来,再根据合数与质数、偶数与奇数的定义进行判断。
26.A
【分析】求出8和10的最小公倍数,再加上1,即可求出这箱水果至少有多少个。
【详解】8=2×2×2
10=2×5
2×2×2×5
=4×2×5
=8×5
=40
8和10的最小公倍数是:40。
40+1=41(个)
所以,这箱水果至少有41个。
故答案为:A
【点睛】本题考查公倍数的计算及应用。理解题意,找出最小公倍数是解决本题的关键。
27.A
【分析】当乘法算式的乘积一定时,如果已知因数越小,那么与它相乘的另一个因数越大;相反地,已知因数越大,与它相乘的另一个因数就越小;据此解答。
【详解】
因为>>,所以z>y>x。
故答案为:A
【点睛】掌握乘法算式的乘积一定时两个因数的大小关系是解答题目的关键。
28.C
【分析】对于圆柱、圆锥、球以及由它们组成的几何体,都可以看做是由一个平面图形绕着一条直线旋转得到的,而圆柱是由一个长方形绕着一条边旋转得到的,得出结论。
【详解】因为圆柱从正面看到的是一个长方形。所以以直线为轴旋转一周,可以形成圆柱的是长方形。
故答案为:C
29.C
【分析】由题意可知,盒内共有5+3+2=10颗糖,用巧克力的颗数除以糖的总个数,再进行化简即可。
【详解】5÷(5+3+2)
=5÷10
=
则摸出巧克力的可能是。
故答案为:C
【点睛】本题考查求一个数是另一个数的几分之几,明确用除法是解题的关键。
30.A
【分析】根据x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,进行分析。
【详解】买书的钱数÷本数=单价(一定),买书的本数和钱数成正比例。
故答案为:A
【点睛】关键是理解正比例和反比例的意义,商一定是正比例关系,积一定是反比例关系。
31.A
【分析】可以将119拆成(122-3),120拆成(122-2),121拆成(122-1),123拆成(122+1),124拆成(122+2),125拆成(122+3),再进行计算;据此解答。
【详解】根据分析:
119+120+121+122+123+124+125
=(122-3)+(122-2)+(122-1)+122+(122+1)+(122+2)+(122+3)
=122-3+122-2+122-1+122+122+1+122+2+122+3
=122+122+122+122+122+122+122
=122×7
=854
所以119+120+121+122+123+124+125=122×7。
故答案为:A
【点睛】将每个加数都拆出122是解答本题的关键。
32.C
【分析】观察图形可知,从正面看到的图形是2层,下层是3个正方形,上层是1个正方形,靠右边;从上面看到的图形是2层,下层是3个正方形,上层是1个正方形,靠左边;从右面看到的图形是2层,下层2个正方形,上层1个正方形,靠左边。
【详解】
根据分析可知,从上面看到的是。
故答案为:C
33.C
【分析】圆锥体积=πr2h,那么可以假设原来圆锥的底面半径和高均是1,先求出原来的体积。再将底面半径乘3,求出变化后的半径,高不变,再求出后来的体积。利用除法,求出体积扩大到原来的几倍。
【详解】假设圆锥的高是1,底面半径也是1,那么体积为:
×π×12×1=
后来的底面半径是1×3=3,后来的体积为:
×π×32×1
=×π×9×1
=3π
3π÷=3π×=9
所以,一个圆锥的高不变,底面半径扩大到原来的3倍,则体积扩大到原来的9倍。
故答案为:C
34.B
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。若有两组及以上数据,应用复式统计图。
【详解】下面资料中最适合用条形统计图表示的是某学校各学科教师人数情况;
故答案为:B
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
35.B
【分析】理解题意,甲绳剪去,还剩下(1-),还剩下米,根据分数除法的意义,利用“量÷对应的分率”,求出甲绳的长度;乙绳是用剩下的长度加上剪去的长度即可求出;分别求出两根绳子的长度,再做比较即可。
【详解】甲绳长:÷(1-)
=÷
=×
=(米)
乙绳长:+
=+
=(米)
米<米
所以甲绳比乙绳要短。
故答案为:B
【点睛】本题考查了分数加法和分数除法的应用,需熟练分析数量关系列出算式并计算。
36.B
【分析】整数的读法:从高位到低位,一级一级地读,每一级末尾的0都不读出来,其他数位连续几个0都只读一个零,据此读出各数,然后分析选择即可。
【详解】A.205040读作:二十万五千零四十;3个0读出1个0。
B.2050402读作:两百零五万零四百零二;3个0读出3个0。
C.20504025读作:两千零五十万四千零二十五,3个0读出2个0。
D.2004500读作:两百万四千五百;1个0也不读出。
故答案为:B
【点睛】本题主要考查整数的读法,注意0的读法:每一级末尾的0都不读出来,其他数位连续几个0都只读一个零。
37.D
【详解】因为两个课外活动小组男女生比例情况如图所示,不能确定两个小组的人数,所以A、B、C都不对,在美术组中,男生占的百分数女生大,所以美术组男生比女生多,在音乐组中,女生占的百分数男生大,所以音乐组女生比男生多,即D正确.
38.C
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量叫作成正比例的量,它们的关系叫作正比例关系。两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量叫作成反比例的量,它们的关系叫作反比例关系。
【详解】A.总价÷数量=单价(一定),所以总价和数量成正比例;
B.路程÷时间=速度(一定),所以路程和时间成正比例;
C.圆柱的底面积×高=圆柱的体积(一定),所以它的底面积和高成反比例。
故答案为:C
39.D
【分析】根据四个容器的特征,一一分析各个图像和哪个容器相匹配即可。
【详解】由图(1)知(为常数,),与(b)(c)图象相符,由图(2)知,与图(1)比较底面积较大,即与(c)相符。图(1)与(b)相符。图(3)液面面积逐渐减小,增高速度加快,图(4)液面面积逐渐增大,增高速度减慢,综上,(1)—(b);(2)—(c);(3)—(a);(4)—(d)。
故答案为:D
【点睛】本题考查了学生的读图能力和解决实际问题的能力,对圆柱、圆锥等几何体有清晰认识,能从图中数据分析问题是解题的关键。
40.A
【分析】设原图纸上的一条线段长为6厘米,按1∶3的比缩小就是6÷3=2(厘米),再把缩小后的图形按2∶1的比放大就是2×2=4(厘米),4厘米<6厘米,即最后得到的图形与原图形相比缩小了。
【详解】由分析可知:
最后得到的图形与原图形相比,结果是缩小了。
故答案为:A
【点睛】此题很容易看出,放大的倍数不如缩小的倍数大,因此,最后得到的图形比原图形缩小了。
41.C
【分析】在地图上按照“上北下南,左西右东”确定方向,注意观测点是学校。根据图上距离和比例尺的关系确定实际距离。
【详解】A.50×2=100(米)
医院在学校西偏北20°方向100m处。所以原说法错误。
B.50×3=150(米)
邮局在学校西偏南20°方向150m处。所以原说法错误。
C.50×2=100(米)
公园在学校北偏东45°方向100m处。所以原说法正确。
D.50×2=100(米)
广场在学校南偏东45°方向100m处,则学校在广场北偏西45°方向100m处。所以原说法错误。
故答案为:C
【点睛】本题主要考查图上距离、实际距离与比例尺之间的关系,并会根据物体的位置描述方向。
42.C
【分析】帽子顶和帽檐合在一起就是一个大圆,先求出大圆的半径,然后根据圆的面积公式:S=πr2,圆柱的侧面积公式:S侧=Ch,分别计算大圆的面积和帽顶部分的侧面积,最后将两者相加就是所用布的总面积。
【详解】20÷2=10(厘米)
10+10=20(厘米)
3.14×20
=3.14×400
=1256(平方厘米)
3.14×20×10=628(平方厘米)
628+1256=1884(平方厘米)
即这顶帽子一共用布1884平方厘米。
故答案为:C
43.B
【分析】用每天的秒数乘一年的天数,可以求出一年有多少秒。或者,用五年的秒数除以5,也可以求出一年的秒数。据此解题。
【详解】如果计算一年共有多少秒(一年按365天计算),列式正确的是86400×365或157680000÷5。
故答案为:B
【点睛】本题考查了整数乘法,掌握乘法的意义,能正确列式是解题的关键。
44.C
【详解】略
45.B
【分析】观察分数,甲数是乙数的,即甲数∶乙数=3∶10;乙数是丙数的,即乙数∶丙数=4∶9。
两个比中都有乙数,但份数不相同,利用比的基本性质,甲数∶乙数的前项和后项同时乘2,乙数∶丙数的前项和后项同时乘5,乙数的份数相同,即可得出甲、乙、丙三个数的比。
【详解】甲数∶乙数=3∶10=(3×2)∶(10×2)=6∶20
乙数∶丙数=4∶9=(4×5)∶(9×5)=20∶45
甲∶乙∶丙=6∶20∶45
所以甲、乙、丙三个数的比是6∶20∶45。
故答案为:B
46.D
【分析】由题意可知,长方形、正方形和圆的周长都是铁丝的长度,所以三个图形周长相等。
①当周长一定时,长方形的长和宽相等时面积最大,所以在周长相等的长方形和正方形中,正方形的面积最大。
②根据题意可设铁丝的长为12.56米,根据正方形、圆形的周长公式分别计算出它们的边长、半径,然后再利用它们的面积公式分别计算出各自的面积,比较即可得到答案。
【详解】很容易知道长方形、正方形和圆的周长相等。
①当周长一定时,长方形的长和宽相等时面积最大,所以在周长相等的长方形和正方形中,正方形的面积最大。
②设铁丝的长为12.56米,
正方形的边长是:12.56÷4=3.14(米)
正方形的面积是:3.14×3.14=9.8596(平方米)
圆的半径是:12.56÷2÷3.14
=6.28÷3.14
=2(米)
圆的面积是:2×2×3.14
=4×3.14
=12.56(平方米)
9.8596<12.56;
所以围成的圆的面积最大。
故答案为:D
【点睛】本题考查了圆,正方形以及长方形的周长与面积公式的灵活应用。结论:当长方形、正方形、圆的周长相等时,圆的面积最大。
47.B
【分析】根据题意,先用员工总人数减去今天请假的人数,求出今天出勤的人数;再根据“出勤率=出勤人数÷总人数×100%”,求出今天的出勤率。
【详解】(50-2)÷50×100%
=48÷50×100%
=0.96×100%
=96%
这个公司今天的出勤率是96%。
故答案为:B
48.B
【分析】最大的一个角一定不小于多少度,实际上求的是最大的内角的最小值,由于3个内角的总和一定,始终是180度,当三个内角相等的时候,最大的内角最小。
【详解】当三个内角相等的时候,最大的内角最小,此时每个角都是60°;
所以最大的一个角一定不小于60°;
故答案选:B。
【点睛】本题考查的是三角形的内角和,三角形的内角和是180°,其它任意多边形的内角和都可以根据三角形内角和进行推导。
49.D
【分析】根据题意,整点时,本营地人数派出人到对方营地,人数相对减少,但半点时,对方营地的人到达本营地,人数又相对增加,据此解答。
【详解】A.13:20时,A营地派出12人前往B营地,B营地派出8人前往A营地,而对方营地派出的人还没有到达,这时A营地剩余22-12=10人,B营地剩余34-8=26人,不符合题意;
B.13:40时,两个营地各派出1次,且对方派出的人到达本营地,这时A营地有22-12+8=18人,B营地有34-8+12=38人,不符合题意;
C.14:20时,两个营地各派出两次,而第二次对方营地派出的人还没有到达,这时A营地有22-12+8-12=6人,B营地有34-8+12-8=30人,不符合题意;
D.14:40时,两个营地各派出两次,且对方派出的人到达本营地,这时A营地有22-12+8-12+8=14人,B营地有34-8+12-8+12=42人,42÷14=3,符合题意。
故答案为:D
【点睛】整点到半点之前,对方派出的人未到达本营地,本营地人数相对减少;半点到下一个整点之前,对方营地派出的人到达本营地,本营地人数相对增加。
50.A
【解析】设最初有x名女生,则男生有(x-10)×2人,根据(男生人数-9)×5=现在女生人数,列出方程解答即可
【详解】解:设最初有x名女生,男生有(x-10)×2人。
[(x-10)×2-9]×5=x-10
(x-10)×10-45= x-10
(x-10)×10=x+35
10x-100= x+35
9x=135
x=15
故答案为:A
【点睛】本题考查了列方程解决问题,关键是找到等量关系。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版数学小升初高频易错考点专题训练:单选题
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.大约一千五百年前,我国古代有一本数学名著中记载了一道数学趣题——“鸡兔同笼”问题。请问这本名著是( )。
A. B.
C. D.
2.甲数比乙数少,乙数比甲数多( )%。
A.20 B.25 C.40
3.需要清楚地表示每个项目的具体数目应选择( )。
A.折线统计图 B.扇形统计图 C.条形统计图 D.以上三者均可以
4.在0.5的末尾添上一个零后,它的计数单位是( )。
A.0.1 B.百分位 C.十分位 D.0.01
5.与的分数单位相同的数是________,与它大小相等的数是________。( )
① ② ③
A.①② B.②③ C.①③
6.一个三角形的两条边分别是10cm和3cm,第三条边可能是( )cm。
A.7 B.13 C.9 D.15
7.从正面看到的形状是的立体图形是( ).
A. B. C.
8.比例尺是( )。
A.一把尺 B.一个比例 C.一个比 D.一个分数
9.利率是表示( )的百分比。
A.本金和利息 B.利息与本金 C.利息和时间
10.如下图所示, 韩梅家的左右两侧各摆了2盆花.每次, 韩梅按照以下规则往家中搬一盆花: 先选择左侧还是右侧, 然后搬该侧离家最近的.要把所有的花搬到家里,共有( )种不同的搬花顺序.
A.4 B.6 C.8 D.10
11.a÷b=8(a和b都是自然数),a和b的最小公倍数是( )。
A.a B.b C.8 D.ab
12.圆锥的侧面展开是一个( )。
A.长方形 B.正方形 C.扇形
13.在计算0.8÷0.24时,被除数和除数都要同时( )。
A.不扩大 B.扩大到原来的10倍 C.扩大到原来的100倍
14.下面成反比例的是( )。
A.看一本书,已看页数和未看页数。 B.长方形的周长一定,它的长和宽。
C.总价一定,商品的数量和单价。 D.圆柱的底面积和体积。
15.一个三角形三个内角的度数比是1:5:2,这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形
16.一种面粉的质量标识为“25±0.25千克”,则下列面粉中质量合格的是( )。
A.25.38千克 B.25.18千克 C.24.69千克 D.26.25千克
17.一个分数的分子缩小为原来的,分母扩大为原来的3倍,分数值就( )。
A.扩大为原来的3倍 B.扩大为原来的6倍
C.缩小到原来的 D.不变
18.以下几种情况最适合用折线统计图统计的是( )。
A.某公司销售业绩增减变化情况 B.描述六(2)班同学身高分组的分布情况
C.各类支出占家庭支出的百分比 D.希望小学图书角不同种类图书数量的多少
19.为了分析王玲从0岁到12岁的身高变化情况,采用( )比较合适。
A.统计表 B.折线统计图 C.条形统计图 D.扇形统计图
20.一种袋装食品标准净重为200g,质监工作人员为了解该种食品袋净重与标准的误差,把食品净重205g记为﹢5g,那么食品净重196g就记作( )g。
A.﹢196 B.﹣196 C.﹢4 D.﹣4
21.与数对(3,5)在同一行的是( )。
A.(5,3) B.(3,4) C.(4,5) D.(5,6)
22.用3个0和3个2组成六位数,读这个六位数时只要读一个0的是( )
A.202020 B.200202 C.222000 D.202000
23.下列图案中,是轴对称图形的是图( )。
A. B. C. D.
24.学校在小强家的东南面450米处,小强每分走50米,向东走了9分,小强能走到学校吗?( ).
A.能 B.不能 C.不能确定
25.从、、、四张卡片中任选两张组成一个两位数,组成的两位数中可能性最大的是( )。
A.合数 B.质数 C.偶数 D.奇数
26.几个小朋友分一箱水果,如果每人分8个,还剩1个;如果每人分10个,也剩1个。那么,这箱水果至少有( )个。
A.41 B.81 C.20
27.x、y、z是三个非零自然数,且,那么x、y、z按照从大到小的顺序排列应是( )。
A.z>y>x B.y>x>z C.y>z>x
28.下图中,以直线为轴旋转一周,可以形成圆柱的是( )。
A. B. C. D.
29.盒内有包装相同的巧克力糖5颗,水果糖3颗,奶糖2颗,摸出巧克力的可能是( )。
A. B. C. D.
30.小明的老师要到书店买《三国演义》这本书,买书的本数和钱数( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
31.119+120+121+122+123+124+125=122×( )。
A.7 B.4 C.3
32.下面的几何体是由5个相同的正方体木块搭成的,从上面看到的图形是( )。
A. B. C. D.
33.一个圆锥的高不变,底面半径扩大到原来的3倍,则体积( )。
A.扩大到原来的3倍 B.扩大到原来的6倍 C.扩大到原来的9倍
34.下面资料中最适合用条形统计图表示的是( )。
A.7月份气温变化情况 B.某学校各学科教师人数情况
C.各种消费情况与家庭总收入的关系 D.某病人一天中体温变化情况
35.有甲乙两根绳子,甲绳剪去,乙绳剪去米,两根绳子都还剩下米,比较原来两根绳子的长短,结果是( )。
A.甲绳比乙绳要长 B.甲绳比乙绳要短 C.两根绳子一样长 D.无法比较
36.下面的数中,每个零都要读出的数是( )。
A.205040 B.2050402 C.20504025 D.2004500
37.实验小学两个课外活动小组男女生比例情况如图所示,下列判断正确的是( ).
A.两个小组的人数同样多
B.音乐组的女生和美术组的男生同样多
C.美术组的男生比音乐组的男生多
D.美术组男生多,音乐组女生多
38.下面几组相关联的量中,成反比例的是( )。
A.单价一定,总价和数量
B.速度一定,路程和时间
C.圆柱体的体积一定,它的底面积和高
39.左下图是水滴进玻璃容器的示意图(滴水速度相同),右下图表示的是容器中水的高度随滴水时间变化的情况(图中刻度、单位都相同)。下列选项中对应关系正确的是( )。
A.(1)—(a) B.(2)—(b) C.(3)—(c) D.(4)—(d)
40.把一个图形按1∶3的比缩小,再把缩小后的图形按2∶1的比放大,最后得到的图形与原图形相比,结果是( )。
A.缩小了 B.放大了 C.大小不变 D.不确定
41.观察如图的示意图,图中各场所的方位描述正确的是( )。
A.医院在学校北偏西20°方向100m处
B.邮局在学校西偏南20°方向300m处
C.公园在学校北偏东45°方向100m处
D.学校在广场南偏东45°方向100m处
42.综合实践课,小明制作了一顶帽子(如图),上面是圆柱形;帽檐部分是一个圆环,做这顶帽子一共用布( )平方厘米。
A.628 B.1256 C.1884 D.2198
43.已知一天有86400秒。“中国飞人”苏炳添经过五年(约157680000秒),从里约到东京,以9秒83创亚洲记录的成绩,成为首位闯进奥运会男子百米决赛的中国人。根据以上资料,如果计算一年共有多少秒(一年按365天计算),列式正确的是( )。
A.86400×30×365 B.86400×365 C.157680000÷9.83
44.下图的标志中,是轴对称图形的有( )个.
A.3 B.2 C.1 D.0
45.甲数是乙数的,乙数是丙数的甲、乙、丙三个数的比是( )。
A.45∶20∶6 B.6∶20∶45 C.20∶6∶45 D.6∶45∶20
46.用三根同样长的铁丝,分别围成长方形、正方形和圆(接口处长度忽略不计),关于三个图形周长和面积的大小关系,下面图中描述正确的是( )。
A. B.
C. D.
47.一个公司有50名员工,今天有2人请假未到。这个公司今天的出勤率是( )。
A.2% B.96% C.48% D.4%
48.一个三角形中,最大的一个角一定不小于( )。
A.50° B.60° C.70° D.90°
49.56人参加户外拓展训练,将22人安排在A营地,34人安排在B营地。从12:01开始,每逢整点A营地派出12人前往B营地,B营地派出8人前往A营地。已知两个营地之间的单程用时为30分钟,问以下哪个时间点,位于B营地的人数正好是A营地的3倍?( )
A.13:20 B.13:40 C.14:20 D.14:40
50.教室里有若干学生,走了10名女生后,男生是女生人数的2倍,又走了9名男生后,女生是男生人数的5倍。问:最初有多少名女生?( )。
A.15 B.12 C.10 D.9
《人教版数学小升初高频易错考点专题训练:单选题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C D A C A C B B
题号 11 12 13 14 15 16 17 18 19 20
答案 A C C C C B C A B D
题号 21 22 23 24 25 26 27 28 29 30
答案 C A D B A A A C C A
题号 31 32 33 34 35 36 37 38 39 40
答案 A C C B B B D C D A
题号 41 42 43 44 45 46 47 48 49 50
答案 C C B C B D B B D A
1.B
【详解】大约一千五百年前,我国古代数学名著《孙子算经》中记载了一道数学趣题——“鸡兔同笼”问题。
故答案为:B
2.B
【详解】略
3.C
【分析】条形统计图能直观地表示出每个项目的具体数目;折线统计图能直观地反映事物变化情况;扇形统计图能直观地表示出各部分在总体中所占的百分比。
【详解】需要清楚地表示每个项目的具体数目应选择条形统计图。
故答案为:C。
【点睛】明确不同统计图的特点是解答本题的关键。
4.D
【分析】考查计数单位与数位的知识,以及在小数的末尾添上0,小数的大小不变,但是计数单位会改变。
【详解】0.5的末尾添上一个零,得0.50,它的计数单位是0.01,即百分之一。
故答案为:D
5.A
【分析】把单位“1”平均分成若干份,取其中的一份的数,叫做分数单位,所以分母相同的两个分数的分数单位才相同;根据分数的基本性质,把分数约分成最简分数后就能判断出相等的分数。
【详解】与这个分数单位相同的数是,分数单位都是;
,,所以与它大小相等的数是。
故答案为:A。
【点睛】本题考查分数单位和分数的约分,明确分数单位的概念是解答此题的关键。
6.C
【分析】三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边。
【详解】三角形的两条边分别是10cm和3cm,则第三条边的长度大于7厘米,小于13厘米。
故答案为:C
【点睛】熟记三角形的三边关系是解答此题的关键。
7.A
【解析】略
8.C
【详解】比例尺是图上距离和实际距离的比。它是一个比;
故答案为:C
9.B
【分析】利率是指单位时间内,利息与本金的比率;据此解答。
【详解】利率是表示利息与本金的百分比。
故答案为B。
【点睛】此题考查了利率概念的理解,关键是熟记知识点。
10.B
【详解】略
11.A
【分析】根据题意,a÷b=8,即a是b的8倍;根据两个数是倍数关系时,最大公因数是较小数,最小公倍数是较大数;据此解答。
【详解】a÷b=8(a和b都是自然数),a与b是倍数关系,且a>b;
a和b的最小公倍数是a。
故答案为:A
【点睛】掌握两个数是倍数关系时,它们的最小公倍数的求法是解题的关键。
12.C
【分析】根据圆锥的特征,直接选出圆锥的侧面展开图即可。
【详解】圆锥的侧面展开是一个扇形。
故答案为:C
【点睛】本题考查了圆锥,圆锥的底面是圆,侧面是曲面,展开为扇形。
13.C
【分析】小数除法法则:先移动除数的小数点,使它变成整数。除数的小数点向右移动几位,被除数的小数点也向右移动相同的位数(位数不够的补“0”),然后按照除数是整数的除法进行计算。据此解答。
【详解】除数0.24要变成整数,小数点向右移动两位,相当于除数扩大到原来的100倍,根据商不变的性质可知,被除数也要扩大到原来的100倍。
故答案为:C
【点睛】此题的解题关键是利用小数除法的计算法则和商的变化规律来求解。
14.C
【详解】反比例公式为xy=k(积一定)
15.C
【详解】试题分析:根据三角形按角分类的方法可知,三角形中的最大角决定了三角形的类别,因此只要求出最大角的度数即可判断.依据三角形的内角和为180°,利用按比例分配的方法即可求得对应的份数最大的角(即最大角)的度数.
解:180°×=112.5(度),
因为112.5度角为钝角,
所以此三角形是钝角三角形.
故选C.
【点评】此题主要利用三角形的内角和与按比例分配的知识进行解答,也要明确三角形按角分类的方法.
16.B
【分析】正数、负数表示两种相反意义的量。“25±0.25千克”的含义是,25千克是这种面粉的标准净重,实际每袋最多不超过(25+0.25)千克,最少不低于(25-0.25)千克,据此解答。
【详解】最少不低于:25-0.25=24.75(千克)
最多不超过:25+0.25=25.25(千克)
A.25.38>25.25,不符合题意;
B.24.75<25.18<25.25,符合题意;
C.24.69<24.75,不符合题意;
D.26.25>25.25,不符合题意;
所以,面粉中质量合格的是25.18千克。
故答案为:B
17.C
【分析】分数与除法的关系:分子相当于被除数,分母相当于除数,分数线相当于除号。
商的变化规律:除数不变,被除数乘几,商就乘几;被除数除以几,商就除以几;
被除数不变,除数乘几,商反而除以几;除数除以几,商反而乘几。
【详解】一个分数的分子缩小为原来的,相当于被除数缩小为原来的,商(分数值)也缩小为原来的;分母扩大为原来的3倍,相当于除数扩大为原来的3倍,商(分数值)反而缩小到原来的;最终商(分数值)缩小到原来的×=。
故答案为:C
18.A
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;根据统计图的特点依次分析即可。
【详解】A.某公司销售业绩增减变化情况应该用折线统计图,故符合题意;
B.描述六(2)班同学身高分组的分布情况应该用条形统计图,故不符合题意;
C.各类支出占家庭支出的百分比应该用扇形统计图,故不符合题意;
D.希望小学图书角不同种类图书数量的多少应该用条形统计图,故不符合题意。
故答案为:A
【点睛】本题主要考查了统计图的选择,掌握各种统计图的特点是解题的关键。
19.B
【分析】折线统计图的特点,不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;
条形统计图用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;
扇形统计图清楚地看出各部分数量与总数量之间,部分与部分之间的关系。
【详解】为了分析王玲从0岁到12岁的身高变化情况,采用折线统计图比较合适;
故答案为:B
【点睛】明确各种统计图的特点是解答本题的关键。
20.D
【分析】通常把高于标准质量的质量用“﹢”表示,低于标准质量的质量用“﹣”表示。据此解答。
【详解】196<200
200-196=4(g)
即低于标准4克,用负数表示为﹣4g。
故答案为:D
【点睛】掌握正负数的意义,看清规定哪一个为正,则和它意义相反的就为负。
21.C
【分析】数对表示位置时,第一个数表示列数,第二个数表示行数;所以(3,5)表示第3列第5行;依次分析各选项表示的位置做出判断。
【详解】A.(5,3)表示第5列第3行,不合题意;
B.(3,4)表示第3列第4行,不合题意;
C.(4,5)表示第4列第5行,符合题意;
D.(5,6)表示第5列第6行,不合题意。
故答案为:C
【点睛】数对表示位置的方法是:先列后行。
22.A
【详解】解:用3个0和3个2组成六位数,且只读一个0,这个数是220002、220200、202020等.
故选A.
23.D
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,由此解答即可。
【详解】
A. 不是轴对称图形;
B. 不是轴对称图形;
C. 不是轴对称图形;
D. 是轴对称图形;
故答案为:D
【点睛】明确轴对称图形的特点是解答本题的关键。
24.B
【详解】略
25.A
【分析】将可以组成的两位数都写出来,看看质数、合数、偶数、奇数各有多少个,再根据“数量越多,可能性越大”进行判断即可。
【详解】组成的两位数有:12、13、14、21、23、24、31、32、34、41、42、43;
合数有:12、14、21、24、32、34、42;
质数有:13、23、31、41、43;
偶数有:12、14、24、32、34、42;
奇数有:13、21、23、31、41、43;
合数最多,所以组成合数的可能性最大;
故答案为:A。
【点睛】解答本题的关键是将可以组成的两位数都写出来,再根据合数与质数、偶数与奇数的定义进行判断。
26.A
【分析】求出8和10的最小公倍数,再加上1,即可求出这箱水果至少有多少个。
【详解】8=2×2×2
10=2×5
2×2×2×5
=4×2×5
=8×5
=40
8和10的最小公倍数是:40。
40+1=41(个)
所以,这箱水果至少有41个。
故答案为:A
【点睛】本题考查公倍数的计算及应用。理解题意,找出最小公倍数是解决本题的关键。
27.A
【分析】当乘法算式的乘积一定时,如果已知因数越小,那么与它相乘的另一个因数越大;相反地,已知因数越大,与它相乘的另一个因数就越小;据此解答。
【详解】
因为>>,所以z>y>x。
故答案为:A
【点睛】掌握乘法算式的乘积一定时两个因数的大小关系是解答题目的关键。
28.C
【分析】对于圆柱、圆锥、球以及由它们组成的几何体,都可以看做是由一个平面图形绕着一条直线旋转得到的,而圆柱是由一个长方形绕着一条边旋转得到的,得出结论。
【详解】因为圆柱从正面看到的是一个长方形。所以以直线为轴旋转一周,可以形成圆柱的是长方形。
故答案为:C
29.C
【分析】由题意可知,盒内共有5+3+2=10颗糖,用巧克力的颗数除以糖的总个数,再进行化简即可。
【详解】5÷(5+3+2)
=5÷10
=
则摸出巧克力的可能是。
故答案为:C
【点睛】本题考查求一个数是另一个数的几分之几,明确用除法是解题的关键。
30.A
【分析】根据x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,进行分析。
【详解】买书的钱数÷本数=单价(一定),买书的本数和钱数成正比例。
故答案为:A
【点睛】关键是理解正比例和反比例的意义,商一定是正比例关系,积一定是反比例关系。
31.A
【分析】可以将119拆成(122-3),120拆成(122-2),121拆成(122-1),123拆成(122+1),124拆成(122+2),125拆成(122+3),再进行计算;据此解答。
【详解】根据分析:
119+120+121+122+123+124+125
=(122-3)+(122-2)+(122-1)+122+(122+1)+(122+2)+(122+3)
=122-3+122-2+122-1+122+122+1+122+2+122+3
=122+122+122+122+122+122+122
=122×7
=854
所以119+120+121+122+123+124+125=122×7。
故答案为:A
【点睛】将每个加数都拆出122是解答本题的关键。
32.C
【分析】观察图形可知,从正面看到的图形是2层,下层是3个正方形,上层是1个正方形,靠右边;从上面看到的图形是2层,下层是3个正方形,上层是1个正方形,靠左边;从右面看到的图形是2层,下层2个正方形,上层1个正方形,靠左边。
【详解】
根据分析可知,从上面看到的是。
故答案为:C
33.C
【分析】圆锥体积=πr2h,那么可以假设原来圆锥的底面半径和高均是1,先求出原来的体积。再将底面半径乘3,求出变化后的半径,高不变,再求出后来的体积。利用除法,求出体积扩大到原来的几倍。
【详解】假设圆锥的高是1,底面半径也是1,那么体积为:
×π×12×1=
后来的底面半径是1×3=3,后来的体积为:
×π×32×1
=×π×9×1
=3π
3π÷=3π×=9
所以,一个圆锥的高不变,底面半径扩大到原来的3倍,则体积扩大到原来的9倍。
故答案为:C
34.B
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。若有两组及以上数据,应用复式统计图。
【详解】下面资料中最适合用条形统计图表示的是某学校各学科教师人数情况;
故答案为:B
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
35.B
【分析】理解题意,甲绳剪去,还剩下(1-),还剩下米,根据分数除法的意义,利用“量÷对应的分率”,求出甲绳的长度;乙绳是用剩下的长度加上剪去的长度即可求出;分别求出两根绳子的长度,再做比较即可。
【详解】甲绳长:÷(1-)
=÷
=×
=(米)
乙绳长:+
=+
=(米)
米<米
所以甲绳比乙绳要短。
故答案为:B
【点睛】本题考查了分数加法和分数除法的应用,需熟练分析数量关系列出算式并计算。
36.B
【分析】整数的读法:从高位到低位,一级一级地读,每一级末尾的0都不读出来,其他数位连续几个0都只读一个零,据此读出各数,然后分析选择即可。
【详解】A.205040读作:二十万五千零四十;3个0读出1个0。
B.2050402读作:两百零五万零四百零二;3个0读出3个0。
C.20504025读作:两千零五十万四千零二十五,3个0读出2个0。
D.2004500读作:两百万四千五百;1个0也不读出。
故答案为:B
【点睛】本题主要考查整数的读法,注意0的读法:每一级末尾的0都不读出来,其他数位连续几个0都只读一个零。
37.D
【详解】因为两个课外活动小组男女生比例情况如图所示,不能确定两个小组的人数,所以A、B、C都不对,在美术组中,男生占的百分数女生大,所以美术组男生比女生多,在音乐组中,女生占的百分数男生大,所以音乐组女生比男生多,即D正确.
38.C
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量叫作成正比例的量,它们的关系叫作正比例关系。两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量叫作成反比例的量,它们的关系叫作反比例关系。
【详解】A.总价÷数量=单价(一定),所以总价和数量成正比例;
B.路程÷时间=速度(一定),所以路程和时间成正比例;
C.圆柱的底面积×高=圆柱的体积(一定),所以它的底面积和高成反比例。
故答案为:C
39.D
【分析】根据四个容器的特征,一一分析各个图像和哪个容器相匹配即可。
【详解】由图(1)知(为常数,),与(b)(c)图象相符,由图(2)知,与图(1)比较底面积较大,即与(c)相符。图(1)与(b)相符。图(3)液面面积逐渐减小,增高速度加快,图(4)液面面积逐渐增大,增高速度减慢,综上,(1)—(b);(2)—(c);(3)—(a);(4)—(d)。
故答案为:D
【点睛】本题考查了学生的读图能力和解决实际问题的能力,对圆柱、圆锥等几何体有清晰认识,能从图中数据分析问题是解题的关键。
40.A
【分析】设原图纸上的一条线段长为6厘米,按1∶3的比缩小就是6÷3=2(厘米),再把缩小后的图形按2∶1的比放大就是2×2=4(厘米),4厘米<6厘米,即最后得到的图形与原图形相比缩小了。
【详解】由分析可知:
最后得到的图形与原图形相比,结果是缩小了。
故答案为:A
【点睛】此题很容易看出,放大的倍数不如缩小的倍数大,因此,最后得到的图形比原图形缩小了。
41.C
【分析】在地图上按照“上北下南,左西右东”确定方向,注意观测点是学校。根据图上距离和比例尺的关系确定实际距离。
【详解】A.50×2=100(米)
医院在学校西偏北20°方向100m处。所以原说法错误。
B.50×3=150(米)
邮局在学校西偏南20°方向150m处。所以原说法错误。
C.50×2=100(米)
公园在学校北偏东45°方向100m处。所以原说法正确。
D.50×2=100(米)
广场在学校南偏东45°方向100m处,则学校在广场北偏西45°方向100m处。所以原说法错误。
故答案为:C
【点睛】本题主要考查图上距离、实际距离与比例尺之间的关系,并会根据物体的位置描述方向。
42.C
【分析】帽子顶和帽檐合在一起就是一个大圆,先求出大圆的半径,然后根据圆的面积公式:S=πr2,圆柱的侧面积公式:S侧=Ch,分别计算大圆的面积和帽顶部分的侧面积,最后将两者相加就是所用布的总面积。
【详解】20÷2=10(厘米)
10+10=20(厘米)
3.14×20
=3.14×400
=1256(平方厘米)
3.14×20×10=628(平方厘米)
628+1256=1884(平方厘米)
即这顶帽子一共用布1884平方厘米。
故答案为:C
43.B
【分析】用每天的秒数乘一年的天数,可以求出一年有多少秒。或者,用五年的秒数除以5,也可以求出一年的秒数。据此解题。
【详解】如果计算一年共有多少秒(一年按365天计算),列式正确的是86400×365或157680000÷5。
故答案为:B
【点睛】本题考查了整数乘法,掌握乘法的意义,能正确列式是解题的关键。
44.C
【详解】略
45.B
【分析】观察分数,甲数是乙数的,即甲数∶乙数=3∶10;乙数是丙数的,即乙数∶丙数=4∶9。
两个比中都有乙数,但份数不相同,利用比的基本性质,甲数∶乙数的前项和后项同时乘2,乙数∶丙数的前项和后项同时乘5,乙数的份数相同,即可得出甲、乙、丙三个数的比。
【详解】甲数∶乙数=3∶10=(3×2)∶(10×2)=6∶20
乙数∶丙数=4∶9=(4×5)∶(9×5)=20∶45
甲∶乙∶丙=6∶20∶45
所以甲、乙、丙三个数的比是6∶20∶45。
故答案为:B
46.D
【分析】由题意可知,长方形、正方形和圆的周长都是铁丝的长度,所以三个图形周长相等。
①当周长一定时,长方形的长和宽相等时面积最大,所以在周长相等的长方形和正方形中,正方形的面积最大。
②根据题意可设铁丝的长为12.56米,根据正方形、圆形的周长公式分别计算出它们的边长、半径,然后再利用它们的面积公式分别计算出各自的面积,比较即可得到答案。
【详解】很容易知道长方形、正方形和圆的周长相等。
①当周长一定时,长方形的长和宽相等时面积最大,所以在周长相等的长方形和正方形中,正方形的面积最大。
②设铁丝的长为12.56米,
正方形的边长是:12.56÷4=3.14(米)
正方形的面积是:3.14×3.14=9.8596(平方米)
圆的半径是:12.56÷2÷3.14
=6.28÷3.14
=2(米)
圆的面积是:2×2×3.14
=4×3.14
=12.56(平方米)
9.8596<12.56;
所以围成的圆的面积最大。
故答案为:D
【点睛】本题考查了圆,正方形以及长方形的周长与面积公式的灵活应用。结论:当长方形、正方形、圆的周长相等时,圆的面积最大。
47.B
【分析】根据题意,先用员工总人数减去今天请假的人数,求出今天出勤的人数;再根据“出勤率=出勤人数÷总人数×100%”,求出今天的出勤率。
【详解】(50-2)÷50×100%
=48÷50×100%
=0.96×100%
=96%
这个公司今天的出勤率是96%。
故答案为:B
48.B
【分析】最大的一个角一定不小于多少度,实际上求的是最大的内角的最小值,由于3个内角的总和一定,始终是180度,当三个内角相等的时候,最大的内角最小。
【详解】当三个内角相等的时候,最大的内角最小,此时每个角都是60°;
所以最大的一个角一定不小于60°;
故答案选:B。
【点睛】本题考查的是三角形的内角和,三角形的内角和是180°,其它任意多边形的内角和都可以根据三角形内角和进行推导。
49.D
【分析】根据题意,整点时,本营地人数派出人到对方营地,人数相对减少,但半点时,对方营地的人到达本营地,人数又相对增加,据此解答。
【详解】A.13:20时,A营地派出12人前往B营地,B营地派出8人前往A营地,而对方营地派出的人还没有到达,这时A营地剩余22-12=10人,B营地剩余34-8=26人,不符合题意;
B.13:40时,两个营地各派出1次,且对方派出的人到达本营地,这时A营地有22-12+8=18人,B营地有34-8+12=38人,不符合题意;
C.14:20时,两个营地各派出两次,而第二次对方营地派出的人还没有到达,这时A营地有22-12+8-12=6人,B营地有34-8+12-8=30人,不符合题意;
D.14:40时,两个营地各派出两次,且对方派出的人到达本营地,这时A营地有22-12+8-12+8=14人,B营地有34-8+12-8+12=42人,42÷14=3,符合题意。
故答案为:D
【点睛】整点到半点之前,对方派出的人未到达本营地,本营地人数相对减少;半点到下一个整点之前,对方营地派出的人到达本营地,本营地人数相对增加。
50.A
【解析】设最初有x名女生,则男生有(x-10)×2人,根据(男生人数-9)×5=现在女生人数,列出方程解答即可
【详解】解:设最初有x名女生,男生有(x-10)×2人。
[(x-10)×2-9]×5=x-10
(x-10)×10-45= x-10
(x-10)×10=x+35
10x-100= x+35
9x=135
x=15
故答案为:A
【点睛】本题考查了列方程解决问题,关键是找到等量关系。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
