人教版数学小升初高频易错考点专题训练:作图题(含解析)
文档属性
| 名称 | 人教版数学小升初高频易错考点专题训练:作图题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 10:58:57 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版数学小升初高频易错考点专题训练:作图题
学校:___________姓名:___________班级:___________考号:___________
一、作图题
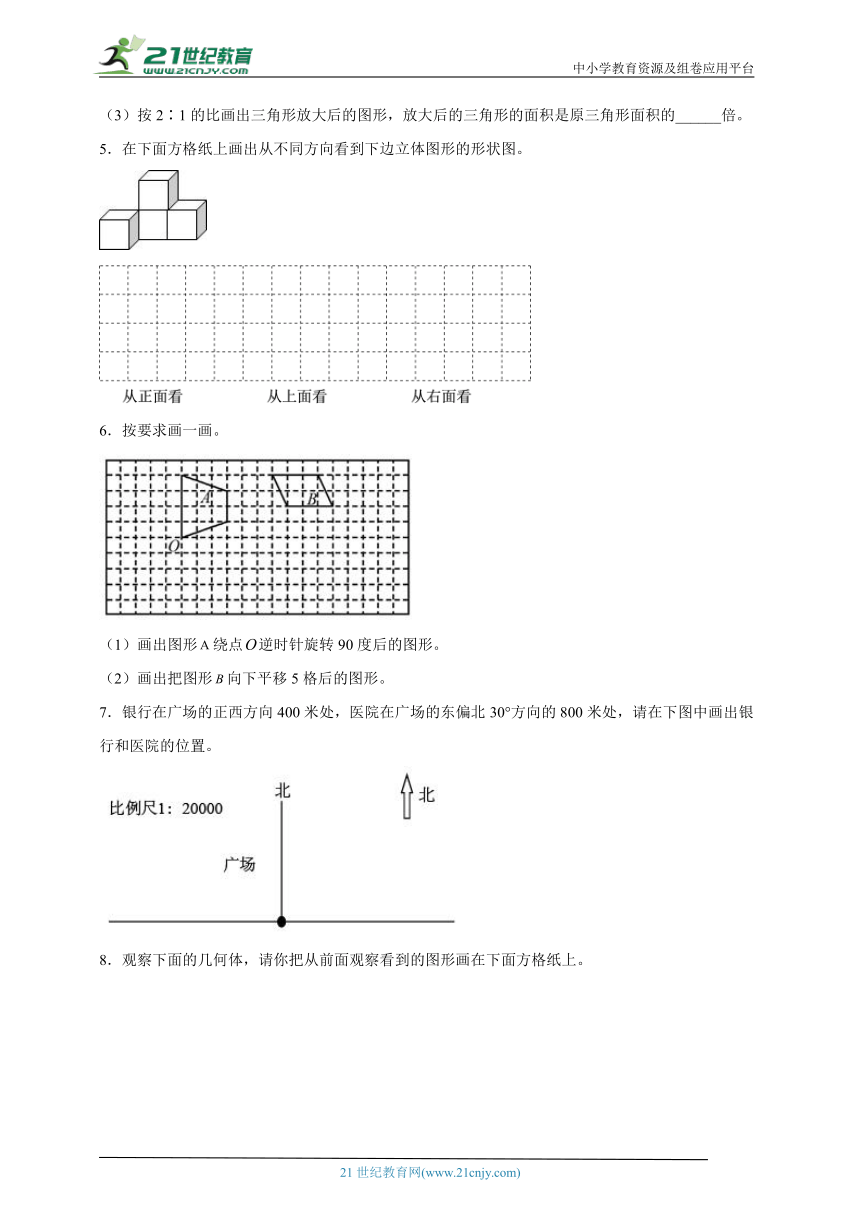
1.在平行四边形内画一条线段,把它分成两个面积相等的三角形。
2.画出下面三角形底边上的高。
3.将三角形ABC绕B点顺时针旋转90°;将三角形ABC按照2∶1放大。
4.动手操作。
(1)如图中的圆,圆心的位置用数对表示是 ,在这个圆中画一个圆心角是90°的扇形。
(2)将原来的三角形先向右平移5格,再向下平移4格,画出平移后的图形。
(3)按2∶1的比画出三角形放大后的图形,放大后的三角形的面积是原三角形面积的______倍。
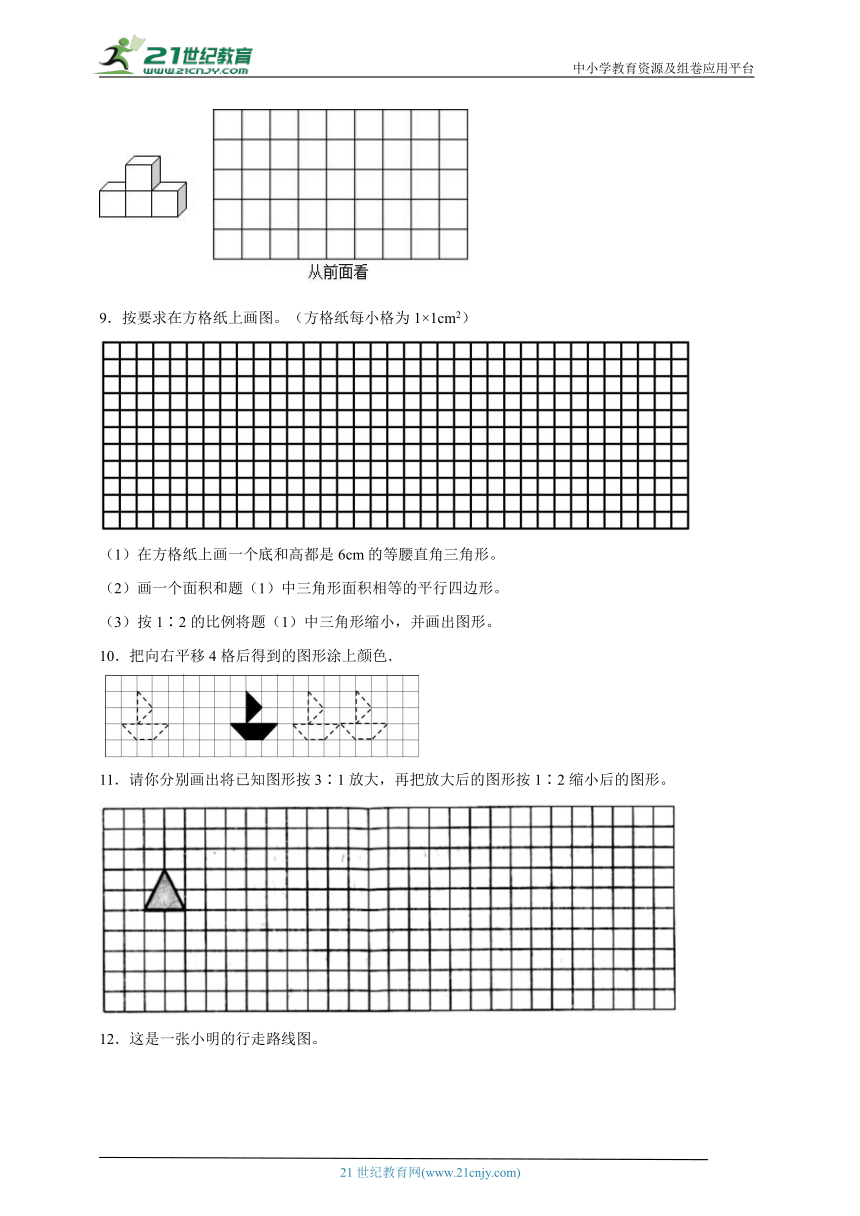
5.在下面方格纸上画出从不同方向看到下边立体图形的形状图。
6.按要求画一画。
(1)画出图形绕点逆时针旋转90度后的图形。
(2)画出把图形向下平移5格后的图形。
7.银行在广场的正西方向400米处,医院在广场的东偏北30°方向的800米处,请在下图中画出银行和医院的位置。
8.观察下面的几何体,请你把从前面观察看到的图形画在下面方格纸上。
9.按要求在方格纸上画图。(方格纸每小格为1×1cm2)
(1)在方格纸上画一个底和高都是6cm的等腰直角三角形。
(2)画一个面积和题(1)中三角形面积相等的平行四边形。
(3)按1∶2的比例将题(1)中三角形缩小,并画出图形。
10.把向右平移4格后得到的图形涂上颜色.
11.请你分别画出将已知图形按3∶1放大,再把放大后的图形按1∶2缩小后的图形。
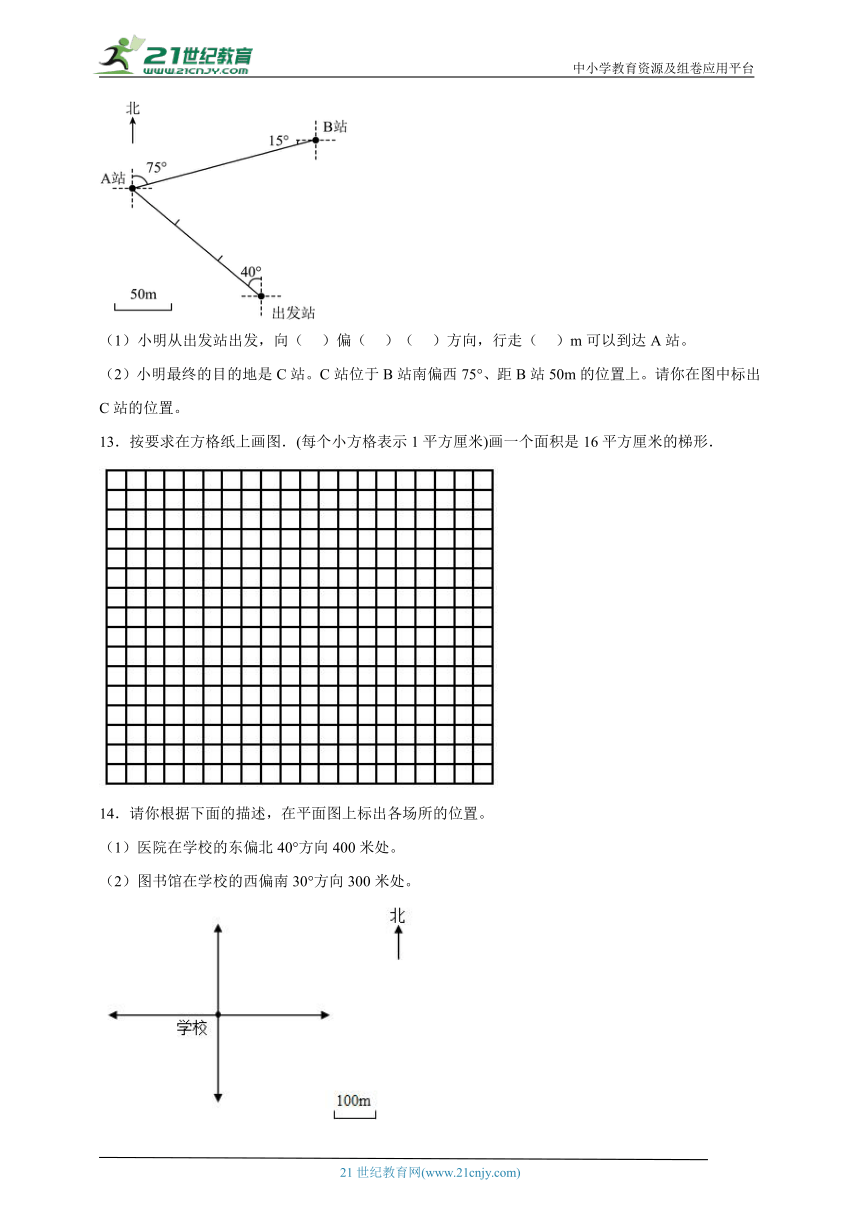
12.这是一张小明的行走路线图。
(1)小明从出发站出发,向( )偏( )( )方向,行走( )m可以到达A站。
(2)小明最终的目的地是C站。C站位于B站南偏西75°、距B站50m的位置上。请你在图中标出C站的位置。
13.按要求在方格纸上画图.(每个小方格表示1平方厘米)画一个面积是16平方厘米的梯形.
14.请你根据下面的描述,在平面图上标出各场所的位置。
(1)医院在学校的东偏北40°方向400米处。
(2)图书馆在学校的西偏南30°方向300米处。
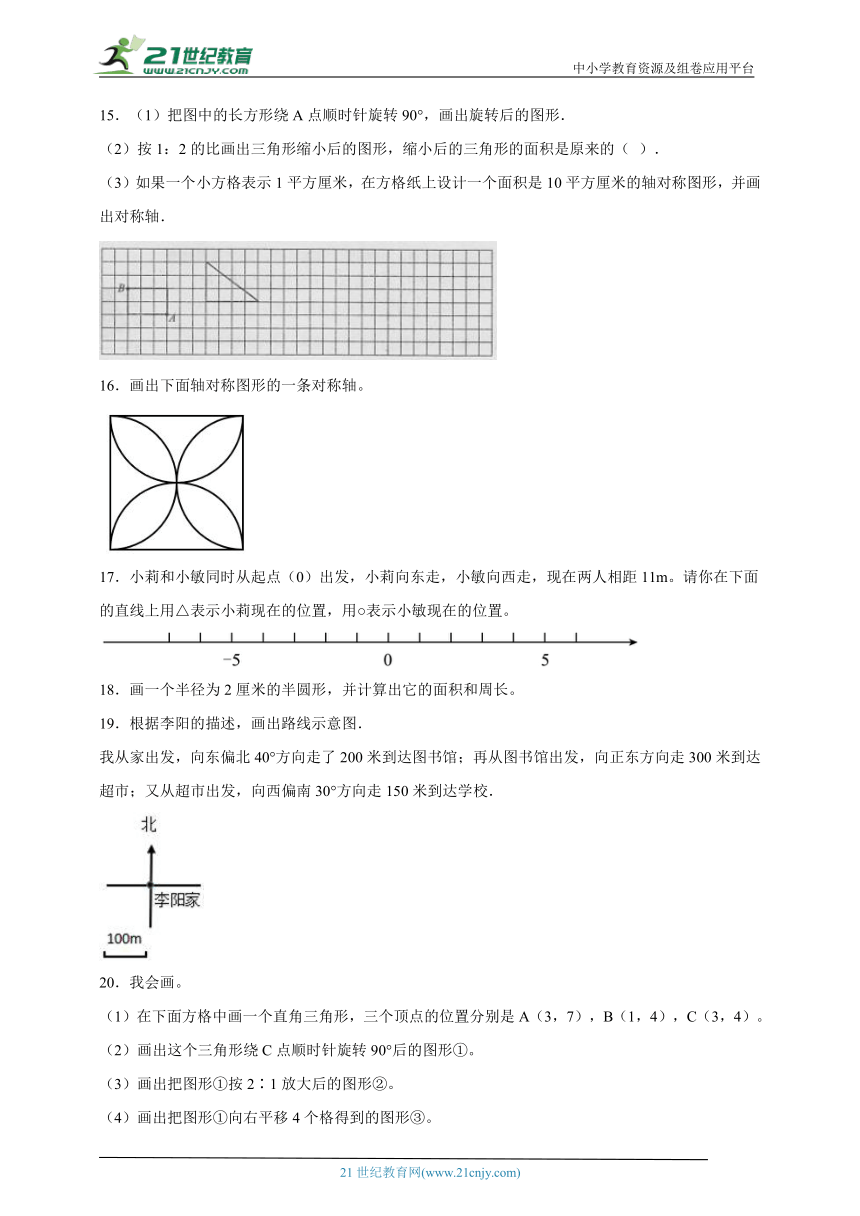
15.(1)把图中的长方形绕A点顺时针旋转90°,画出旋转后的图形.
(2)按1:2的比画出三角形缩小后的图形,缩小后的三角形的面积是原来的( ).
(3)如果一个小方格表示1平方厘米,在方格纸上设计一个面积是10平方厘米的轴对称图形,并画出对称轴.
16.画出下面轴对称图形的一条对称轴。
17.小莉和小敏同时从起点(0)出发,小莉向东走,小敏向西走,现在两人相距11m。请你在下面的直线上用△表示小莉现在的位置,用○表示小敏现在的位置。
18.画一个半径为2厘米的半圆形,并计算出它的面积和周长。
19.根据李阳的描述,画出路线示意图.
我从家出发,向东偏北40°方向走了200米到达图书馆;再从图书馆出发,向正东方向走300米到达超市;又从超市出发,向西偏南30°方向走150米到达学校.
20.我会画。
(1)在下面方格中画一个直角三角形,三个顶点的位置分别是A(3,7),B(1,4),C(3,4)。
(2)画出这个三角形绕C点顺时针旋转90°后的图形①。
(3)画出把图形①按2∶1放大后的图形②。
(4)画出把图形①向右平移4个格得到的图形③。
21.(1)画出三角形ABC绕A点逆时针旋转90°后的图形.
(2)画出三角形ABC以1:2的比例缩小后的图形.
22.下面是一个卧室的平面图。在卧室的西北角放一张长2米、宽1.5米的床,请你在平面图上画出床的示意图。
23.按照题目要求,完成下列各题。
(1)如图,将三角形OAB绕点O顺时针旋转90°后得到图形OA'B',请画出图形OA'B';
(2)请你在方格纸中画出一个与三角形OAB面积相等的长方形。
24.下面是电影院附近示意图。请根据示意图填一填,再根据描述在示意图上画一画。
(1)广场在电影院( )偏( )( )°方向( )米处。
(2)育才小学在电影院南偏东60°方向500米处。
(3)中山路在电影院的东面1000米处,并与鲈乡路平行。
25.在方格纸中画出下面图形从上面看到的形状.
26.(1)过顶点B作三角形的高,标出垂足O。
(2)若三角形的∠A=52°,则三角形的顶点A在顶点C的( )偏( )( )°方向上。
(3)画出三角形绕点B顺时针方向旋转90°后的图形;点C旋转后的位置可用数对( )表示。
27.按要求在方格图中作图。
(1)以钝角三角形的顶点A为端点画一条线段,将这个三角形分成面积相等的两部分。
(2)将直角三角形绕点O顺时针方向旋转90°,画出旋转后的图形。
(3)在方格图中画一个梯形,使它的面积是直角三角形面积的2倍。
28.下图中每个小方格表示边长l厘米的小正方形.
(1)请画出小旗向右平移8格的图形.
(2)画出小旗子绕O点按顺时针方向旋转90°后的图形
(3)画出小旗子按2:1扩大后的图形ABCO.
29.动手操作
画一画:(1)在下面的方格图(每个小方格的边长是1cm)中画一个半圆,半径是2cm;
(2)画出半圆的对称轴;
(3)画出半圆向右平移4格后的图形.
30.按要求在方格纸中作图。
①根据给定的对称轴画出图形A的另一半。
②画出图形B向右平移4格后的图形。
③画出将图形C按2∶1放大后的图形。
31.画一画,下面每个小方格的面积都是1cm2,请你按要求做图。
(1)画出面积是12cm2的平行四边形和三角形各一个。
(2)画一个面积是12cm2、高是3cm的梯形,并使下底长是上底的3倍。
32.李叔叔家位于镇政府正南方向1.2千米处,小林家位于镇政府南偏东30°方向,距离1.6千米处。请根据下面方框中的信息画出李叔叔家及小林家的位置。
33.用7个同样大的正方体摆成左边的物体,请在右边的方格纸上画出从前面,右面和上面看到的图形。
34.“狡兔三窟”指聪明的兔子会准备好几个藏身的窝。野外林区的摄像头拍下一只野兔的活动轨迹,如图所示。
(1)野兔从B窝出来,向西跑了4米,到达A窝。量一量:两个窝之间的图上距离是 厘米,轨迹图的比例尺是 ∶ 。
(2)野兔在A窝时,一只狐狸在距离A窝6米处出现,请在图中画出狐狸可能出现的所有位置。
(3)野兔从A窝向北偏西30°方向跑了8米到达C窝,请在如图中标出C窝的位置。
35.按要求画图。
(1)在格子图上画出轴对称图形的另一半。
(2)在格子图上画出一个平行四边形,使它的面积与轴对称图形的面积相等。
36.操作题.
画出三角形AOB绕O逆时针旋转90°,再向下平移2格后的图形.
37.(1)将图形A绕点O点顺时针旋转90°得到的图形B。
(2)将图形B向右平移4格得到图形C。
38.按要求在方格纸上图并完成填空。
(1)把图①绕M点逆时针旋转90°画出旋转后的图形,旋转后P点的位置用数对表示是( )。
(2)把图②按2∶1的比放大,画出放大后的图形,放大后的图形与原来图形的面积比是( )。
(3)图③中直角三角形ABC的斜边BC是圆的直径,O是圆心,AO=AC。如果每个小方格表示边长2厘米的小正方形,则点A在点O( )偏( )( )°方向( )厘米处。
39.请按要求在格子图中画一画。
(1)画出三角形ABC绕点C按顺时针方向旋转90°后的图形①。
(2)在格子图中画出将三角形ABC按2∶1放大后的图形②。
40.下面是仪征城区的平面图,请在图中画出有关街道和场所的位置。
(1)市政府东面300米的处有一条健康路,它与工农路平行。
(2)育才小学在市政府北偏西75°方向400米处。
41.按图形的变化规律,接着画。
42.在下面正方形中各画一个图形,使它的面积正好等于正方形的一半。(要求所画的图形各不相同,例如不同形状的三角形视为同一个图形)。
《人教版数学小升初高频易错考点专题训练:作图题》参考答案
1.见详解
【分析】平行四边形性质:平行四边形对边平行且相等,对角线将其分成两个三角形。面积相等依据:这两个三角形等底等高(底为平行四边形的边,高为平行四边形的高 ),根据三角形面积公式S=ah(a为底,h为高 ),等底等高的三角形面积相等。
【详解】
2.见详解
【分析】从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高;这条对边叫做三角形的底;依此画图即可。
【详解】
【点睛】熟练掌握三角形高的画法是解答此题的关键。
3.见详解
【分析】根据旋转的特征,把三角形各顶点绕B点顺时针旋转90°,再顺次连接即可;三角形ABC两条边AB和BC分别是3格、2格,按要求放大后分别是6格、4格,先画AB、BC两边,再连接第三条边;据此作图。
【详解】作图如下:
【点睛】解答本题的关键是掌握旋转和图形放大的作图能力,需注意的是旋转只改变图形的位置,不改变图形的形状和大小;图形的放大只改变图形的大小,不改变形状。
4.(1)(4,3);画图见详解
(2)画图见详解;
(3)画图见详解;4
【分析】(1)数对是一个表示位置的概念,先列后行。在图中找到圆心O,观察其所在的列数和行数。从左往右数,圆心在第4列,从下往上数,圆心在第3行,所以用数对表示为(4,3)。画扇形思路:以圆心O为顶点,利用直角工具(如三角板的直角),先画一条半径,再以圆心为端点,顺时针或逆时针旋转直角边,画出另一条半径,两条半径和它们所夹的圆弧就构成圆心角是90°的扇形。
(2)平移图形时,要根据平移的方向和格数移动图形的各个顶点。对于三角形,先找到它的三个顶点,将每个顶点都先向右平移5格,即列数增加5;再向下平移4格,即行数减少4。然后按照平移后顶点的位置,依次连接各顶点,画出平移后的三角形。
(3)按2∶1的比放大三角形,意味着三角形的底和高都变为原来的2倍。我们可以通过数方格的方式确定原三角形的底和高所占格数,进而得到放大后三角形的底和高所占格数,再根据三角形面积公式分别计算出原三角形和放大后三角形的面积,最后求出倍数关系。假设原三角形在方格图中底占2格,高占3格(可通过观察图形得出)。
【详解】(1)如图中的圆,圆心的位置用数对表示是(4,3)。
(2)(3)如图:
计算原三角形面积:根据三角形面积公式S=×底×高,原三角形底占2格,高占3格,那么原三角形面积
S1=×2×3
=1×3
=3
计算放大后三角形面积:按2∶1放大后,底变为2×2=4格,高变为3×2=6格,所以放大后三角形面积
S2=×4×6
=2×6
=12
计算倍数关系:用放大后的三角形面积除以原三角形面积可得倍数,即12÷3=4
5.见详解。
【分析】这个立体图形从正面能看到4个小正方形,分为两层,下层有3个小正方形,上层居中有1个小正方形;从上面看有3个小正方形,分为两层,下层靠左边有1个小正方形,上下两层未对齐,上层有2个小正方形;从右面看有3个小正方形,分为两层,下层有2个小正方形,上层靠右有1个小正方形;据此作图。
【详解】作图如下:
【点睛】本题考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形。
6.如图所示:
【分析】(1)旋转不改变图形的形状和大小。先画出图形A绕点O逆时针旋转90°后的下底,再画出与O点相邻的一条腰,然后再画出上底,最后再画出另一条腰。
(2)平移不改变图形的形状和大小。先确定图形B的每一条边平移后位置,再画出平移后的图形。
【详解】如图所示:
【点睛】本题考查图形的变换。掌握旋转和平移的要点是解答此题的关键。
7.
【分析】根据图上距离=实际距离×比例尺,求出银行和医院在图上的距离,结合方向标出相应的位置即可。
【详解】400米=40000厘米,800米=80000厘米
银行到广场的图上距离:40000×=2(厘米)
医院到广场的图上距离:80000×=4(厘米)
如图:
【点睛】本题考查比例尺和位置与方向,通过实际距离和比例尺求出图上距离是解题的关键。
8.见详解
【分析】从前面观察几何体,是2层3列,从左往右,每列分别有小正方形的个数:1个,2个,1个;据此画出平面图形。
【详解】
【点睛】掌握从不同的方向观察几何体,并能画出相应的平面图形是解题的关键。
9.见详解
【分析】(1)根据等腰直角三角形的特征,在方格纸上画一个底和高都是6cm的等腰直角三角形即可。
(2)题(1)中三角形面积是底×高÷2,算出三角形面积是18平方厘米,画一个面积是18平方厘米平行四边形即可。
(3)根据图形缩小的方法,按1∶2的比例将题(1)中三角形缩小,并画出图形即可。
【详解】(1)在方格纸上画一个底和高都是6cm的等腰直角三角形,如图:
(2)三角形面积是
=
=(平方厘米)
画一个面积是18平方厘米平行四边形,平行四边形可以底是6厘米,(答案不唯一)
(3)按1∶2的比例将题(1)中三角形缩小,如图:
(平行四边形画法不唯一)
【点睛】本题考查了等腰直角三角形、平行四边形的特征和画法以及图形的放大和缩小知识,结合题意分析解答即可。
10.
【分析】根据平移图形的特征,看哪个虚线图形与这个图形的各对应点相距4格,涂上颜色即可。
【详解】本题考查的知识点是利用对应法把一个图形平移,解答时要找到图形对应点平移的距离是不是4个格,平移的方向是不是向右。通过观察上图发现,只有黑色图形和它右边的图形是经历向右平移得到的。
【点睛】关键是看两图的对应点相距的格数。
11.见详解。
【分析】按3∶1的比例画出图形放大后的图形,就是把原图形的各边都扩大到原来3倍;再按1∶2缩小,就是把放大后的图形的各边再缩小到原来一半即可,依此画图。
【详解】作图如下:
【点睛】本题考查了图形的放大和缩小,能在方格纸上按一定的比例画出放大与缩小的图形。
12.(1)北;西;40°;150
(2)
【分析】(1)在地图上按照“上北下南,左西右东”确定方向,注意观测点是A站。根据图上距离和比例尺的关系确定实际距离。
(2)根据实际距离与比例尺的关系确定图上距离,再根据方位关系即可确定C站的位置。
【详解】(1)3×50=150(米)
小明从出发站出发,向北偏西40°方向,行走150m可以到达A站。
(2)90°-75°=15°
C站位于B站南偏西75°,即C站位于B站西偏南15°。
如图:
【点睛】本题考查根据方向和距离确定物体的位置,会根据位置描述方向以及会根据方向的描述确定物体的位置是解本题的关键。
13.如图:
(画法不唯一)
【详解】略
14.见详解
【分析】(1)以学校为观测点,在学校东偏北40°方向截取400÷100=4个单位长度,标出角度,终点处标注医院。
(2)以学校为观测点,在学校的西偏南30°方向截取300÷100=3个单位长度,标出角度,终点处标注图书馆。
【详解】(1)(2)作图如下:
【点睛】掌握根据方向、角度、距离确定物体位置的方法是解答题目的关键。
15.(1)
(2)如图,﹙2×1.5÷2﹚÷﹙4×3÷2﹚=
(3)如图,答案不唯一.
【详解】本题考查图形的变换、图形的缩放及轴对称图形.图形旋转注意三点:旋转点、方向和角度;图形放大和缩小关键点是对应边的放大和缩小;轴对称关键是找对称点.
(1)根据旋转的性质,先将长方形由点A引出的两条边顺时针旋转90度,由此即可确定旋转后的图形的位置与大小.(2)根据放大和缩小的性质,先把两条直角边分别缩小2倍,即可画出缩小后的三角形.(3)根据轴对称图形的定义和画指定面积的图形的方法,这里可以画一个长是10厘米、高是2厘米的等腰三角形,并画出它的对称轴.如图所示:
16.见详解
【分析】轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴。
【详解】作图如下:
(画法不唯一)。
【点睛】此题考查了轴对称的意义及在实际当中的运用。
17.见详解(答案不唯一)
【分析】向东走和向西走是两种具有相反意义的量,规定向东走为正,则向西走则为负,以0为界线,小莉向正数的位置方向走,小敏向负数的位置方向走,保证最后两人相距11格即可。
【详解】作图如下:
(答案不唯一)
【点睛】此题属于开放题,重在理解正负数在数轴上的表示方法。
18.图见详解;面积:6.26平方厘米;周长:10.28厘米
【分析】由题意可知:可以以任意一点为圆心,圆规两脚之间的距离是2厘米为半径,旋转半周即可画出符合要求的半圆弧,再把半圆弧的两端连接即可;半径已知,根据圆的面积公式:面积=π×半径2,代入数据,求出半径是2厘米的圆的面积,再除以2,即可求出半圆面积;根据半圆周长公式:周长=π×半径+半径×2,代入数据,即可解答。
【详解】如图:
半圆的面积:
3.14×22÷2
=3.14×4÷2
=12.56÷2
=6.28(平方厘米)
半圆的周长:
3.14×2+2×2
=6.28+4
=10.28(厘米)
半圆的面积是6.26平方厘米,周长是10.28厘米。
19.
【详解】200÷100=2(厘米)
300÷100=3(厘米)
150÷100=1.5(厘米)
20.见详解
【分析】(1)数对表示位置的方法是:第一个数字表示列,第二个数字表示行,由此在图中找出A、B、C三个点的位置顺次连接即可得出三角形ABC;
(2)根据图形旋转的方法,抓住三角形ABC的两条直角边绕点C顺时针旋转90°即可得出旋转后的三角形①;
(3)按照图形放大与缩小的方法,将三角形①的两条直角边按2∶1放大,即可得出放大后的三角形②;
(4)将三角形①的各个顶点向右移4格,再将各个顶点依次连接,据此即可得出答案。
【详解】(1)三角形ABC的位置如下图所示:
(2)三角形ABC绕C点顺时针旋转90°后的图形①如下图所示:
(3)图形①按2∶1放大后的图形如下图所示:
(4)图形①向右平移4个格得到的图形③如下图所示:
【点睛】此题主要考查了数对表示位置以及图形的旋转、平移和放大与缩小的方法。
21.
【详解】(1)画出三角形ABC绕A点逆时针旋转90°后的图形(图中红色部分).
(2)画出三角形ABC以1:2的比例缩小后的图形(图中绿色部分).
22.见详解
【分析】看图,比例尺是1∶100,将实际长度乘比例尺,求出床的长和宽的图上距离。西北角在卧室的右上角,据此结合数据画图即可。
【详解】2米=200厘米,1.5米=150厘米
长:200×=2(厘米)
宽:150×=1.5(厘米)
如图:
【点睛】本题考查应用比例尺画图,求出图上的长、宽值是解题的关键。
23.见详解
【分析】(1)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。
(2)三角形面积=底×高÷2,长方形面积=长×宽,据此先求出三角形面积,再确定长方形的长和宽,作图即可。
【详解】(1)作图如下:
(2)3×4÷2=6
6=3×2
画出的长方形长3格,宽2格即可,作图如下:
(长方形画法不唯一)
24.(1)( 南 )(西)(50)°(1500)
(2)(3)见图
【详解】(1)根据图可知,广场所在的位置应为南偏西50度方向,这50度,即为90-40=50。再测量出其图上距离为3厘米,由线段比例尺即可知道,图上3厘米就是实际1500米。
(2)见图
由线段比例尺可知,实际500米即图上1厘米。
(3)见图
实际1000米,即图上2厘米。其余见图。
25.解:在方格纸中画出下面图形从上面看到的形状:
【详解】左边的立体图形由5个相同的小正方体组成.从上面能看到4个正方形,分两列,左列3个,右列1个,上齐.
26.(1)图见详解
(2)南;西;38
(3)图见详解;(8,3)
【分析】(1)根据三角形高的意义,在三角形ABC中,从顶点B向它的对边AC画垂线,顶点到垂足之间的线段叫做三角形的高,由此作图即可;
(2)已知三角形的内角和是180°,那么直角三角形中两个锐角的度数之和是90°,减去已知的一个锐角,即可求出另一个锐角的度数;
以顶点C为观测点,以图上的“上北下南,左西右东”为准,结合方向、角度确定顶点A与顶点C的位置关系。
(3)根据旋转的特征,将三角形绕点B顺时针方向旋转90°,点B位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;据此用数对表示点C旋转后的位置。
【详解】(1)过顶点B作三角形的高,标出垂足O,如下图。
(2)∠C=90°-52°=38°
三角形的顶点A在顶点C的南偏西38°(或西偏南52°)方向上。
(3)画三角形绕点B顺时针方向旋转90°后的图形,如下图。
点C旋转后的位置可用数对(8,3)表示。
如下图所示:
27.见详解
【分析】(1)根据两个三角形等底等高时,面积相等,据此以钝角三角形的顶点A为端点画一条线段,把底边平分即可。
(2)根据旋转的特征,将直角三角形绕点O顺时针方向旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(3)已知直角三角形的底是3、高是4,根据三角形的面积=底×高÷2,求出直角三角形的面积;
要画的梯形的面积是直角三角形面积的2倍,用三角形的面积乘2,即是梯形的面积;根据梯形的面积=(上底+下底)×高÷2,据此确定所画梯形的上底、下底和高。
【详解】(1)以钝角三角形的顶点A为端点画一条线段,如下图。
(2)将直角三角形绕点O顺时针方向旋转90°,旋转后的图形如下图。
(3)三角形的面积:3×4÷2=6
梯形的面积:6×2=12
(2+4)×4÷2
=6×4÷2
=12
画一个上底为2、下底为4、高为4的梯形。
(梯形的画法不唯一)
28.作平移后的图形、旋转一定角度后的图形、放大后的图形如下:
【详解】(1)根据平移图形的特征,把小旗的各顶点分别向右平移8格,再依次连结,即可画出小旗向右平移8格的图形(图中红色小旗);
(2)根据旋转图形的特征,小旗绕O点顺时针旋转90°后,O点的位置不动,其余各部分均绕O点按相同方向旋转相同的度数即可画出小旗子绕O点按顺时针方向旋转90°后的图形(图中绿色小旗);
(3)根据图形放大与缩小的特征,把小旗的各部分均放大到原来的2倍即可画出小旗子按2:1扩大后的图形(图中蓝色小旗).
29.
【详解】略
30.见详解
【分析】①补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
②作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点。
③把图形按照n∶1放大,就是将图形的每一条边放大到原来的n倍,放大后图形与原图形对应边长的比是n∶1。
【详解】
【点睛】决定平移后图形的位置的要素:一是平移的方向,二是平移的距离。图形放大或缩小的倍数是指对应边放大或缩小的倍数。
31.见详解
【分析】(1)平行四边形面积=底×高,三角形面积=底×高÷2,分别确定平行四边形和三角形的底和高,作图即可;
(2)梯形上下底的和=面积×2÷高,先确定上下底的和,上下底的和÷总倍数,求出一倍数,是上底,上底×3=下底,作图即可。
【详解】(1)12=4×3,12×2=24=6×4,画出的平行四边形底是4厘米,高是3厘米即可;画出的三角形底是6厘米,高是4厘米即可;
(2)12×2÷3=8(厘米)
8÷(3+1)
=8÷4
=2(厘米)
2×3=6(厘米)
作图如下:
【点睛】关键是掌握平行四边形、三角形、梯形的面积公式。
32.见详解
【分析】根据“上北下南,左西右东”的方向以及比例尺确定物体的位置和行走路线,据此解答。
【详解】根据比例尺1∶40000得
1.2千米=120000厘米
120000÷40000=3(厘米)
1.6千米=160000厘米
1600÷40000=4(厘米)
画图如下:
【点睛】此题考查的是位置与方向,掌握“上北下南,左西右东”的方向以及比例尺确定物体的位置和行走路线是解题关键。
33.见详解
【分析】观察图形可知,从前面看到的图形是2层,下层是3个正方形,上层2个正方形,靠左边;从上面看到的图形是2层,下层是2个正方形,上层3个正方形,靠左边;从右面看到的图形是2层,下层2个正方形,上层1个正方形,靠右边;由此即可画图。
【详解】根据题意画图如下:
【点睛】本题是考查从不同方向观察物体和几何体以及三视图的画法,目的是训练学生的观察能力。
34.(1)1;1;400
(2)(3)见详解
【分析】(1)用直尺量出A、B两窝在图上的距离(实际操作测量,已知野兔从B窝向西跑4米(实际距离)到达A窝,因为4米=400厘米,根据“比例尺=图上距离∶实际距离”,将测量得到的图上距离与400厘米相比,即可得出比例尺;
(2)因为狐狸在距离A窝6米处,6米=600厘米,根据(1)中求出的比例尺,计算出狐狸位置的图上距离(图上距离=实际距离×比例尺),以A点为圆心,以计算得到的图上距离为半径画圆,圆上的所有点就是狐狸可能出现的位置;
(3)已知野兔从A窝向北偏西30°方向跑了8米(800厘米)到达C窝,根据比例尺算出A到C的图上距离(图上距离=实际距离×比例尺 ),用量角器以A为顶点,向北偏西30°方向画出射线,在射线上按照计算出的图上距离截取线段,端点即为C窝的位置。
【详解】(1)野兔从B窝出来,向西跑了4米,到达A窝。量一量可知,两个窝之间的图上距离是1厘米。
4米=400厘米
1厘米∶400厘米=1∶400
所以轨迹图的比例尺是1∶400。
(2)6米=600厘米
600×=1.5(厘米)
野兔在A窝时,一只狐狸在距离A窝6米处出现,在图中画出狐狸可能出现的所有位置。如下图:
(3)8米=800厘米
800×=2(厘米)
野兔从A窝向北偏西30°方向跑了8米到达C窝,在如图中标出C窝的位置。如图:
35.见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,找到图形的各顶点关于对称轴的对称点后,依次连接各点得到轴对称图形的另一半图形。
(2)从图中可知,轴对称图形是一个梯形,根据梯形的面积=(上底+下底)×高÷2,求出梯形的面积;
要画出一个平行四边形,使它的面积与轴对称图形的面积相等,根据平行的面积=底×高,确定所画平行四边形的底和高,据此画出这个平行四边形。
【详解】(1)在格子图上画出轴对称图形的另一半。如图:
(2)梯形的面积:
(8+4)×4÷2
=12×4÷2
=24
平行四边形的面积:6×4=24
画一个底为6、高为4的平行四边形,如下图。
(平行四边形画法不唯一)
36.如图中红色线所示△A1B1C1即是所求.
【详解】本题是旋转与平移的综合应用,作图时弄清楚图形的变换方式即可,特别注意旋转与平移过程不要混淆.
【考点点拨】本题主要考查旋转与平移的综合应用,是小升初的常见易考题型之一,难度系数 适中.
37.(1)、(2)如图:
【分析】(1)根据旋转的特征,图形A绕点O顺时针旋转90°后,点O位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(2)根据平移的特征,图形B向右平移4格,图形的大小、形状都不改变,整个图形向右平行移动4格。
【详解】(1)(2)如图:
【点睛】做旋转图形时,要注意旋转的方向与角度。做平移图形时,要注意平移的方向与距离。
38.(1)画图见详解;(4,2)
(2)画图见详解;4∶1
(3)东;北;60;6
【分析】(1)根据题意,以三角形其中一个顶点M,将图①逆时针旋转90°,大小保持不变,画出三角形即可。根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可用数对表示出旋转后P点的位置。
(2)把图②按2∶1的比放大,画出放大后的图形(图中绿色部分),放大后的图形与原来图形的面积比是(6×4)∶(3×2)=24∶6=4∶1。
(3)根据题意,A点在O点的右上方,依据上北下南左西右东,A点在O点的东偏北的位置,因为△AOC是等边三角形,依据三角形内角和180°,180°÷3=60°,因为O点距离A点3个小格,所以,距离为2×3即可。
【详解】(1)旋转后P点的位置用数对表示是(4,2)。
(2)放大后的图形与原来图形的面积比是4∶1。
(3)因为AO=AC,OA=OC,所以三角形AOC为等边三角形。
所以∠AOC=60°。
OA=OB=3格
2×3=6(厘米)
即点A在点O东偏北60°方向6厘米处。或点A在点O北偏东30°方向6厘米处。
39.(1)(2)见详解
【分析】(1)根据旋转的特征,三角形ABC绕点C顺时针旋转90°后,点C的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图形①,据此画图;
(2)先求出放大后三角形ABC的底和高各是多少,然后画出三角形ABC按2∶1放大后的图形②(位置不唯一)。
【详解】(1)如图:
(2)底:3×2=6(格);高:2×2=4(格)
如图:
40.
【分析】
方向和距离两个条件才能确定物体的位置,要画图首先要根据图形确定比例尺为1:10000,和方向上北下南左西右东。(1)健康路在市政府东面,可确定其方向,根据图上距=实际距离×比例尺,求出市政府到健康路图上距离。(2)育才小学在市政府北偏西75°,可确定其方向,再根据图上距离=实际距离×比例尺,可求出其图上距离,据此画图解答.本题的关键是确定比例尺和方向后,根据图上距离=实际距离×比例尺,求出图上距离,再画图解答。
【详解】(1)健康路到市政府的图上距离是:
300米=30000厘米
30000× =3(厘米)
(2)育才小学到市政府的图上距离是:
400米=40000厘米
40000× =4(厘米)
画图如下:
41.
【分析】观察题目给出的三幅图,发现每个小图形都是按照左上角→右上角→右下角→左下角这样的顺时针方向转动的,并且这里不用考虑转动引起的方向问题。
【详解】如图:
【点睛】本题较为简单,只需要考虑图形的转动,而不用考虑方向,相对是比较容易的。
42.
【分析】根据正方形、长方形、平行四边形等的面积间的相互关系,作图即可:如取对边中点连线,把正方形平均分成两个长方形;取一条边的中点,与对边的两个顶点连线的三角形;取四条边的中点连线的正方形;取一组对边中点,分别与对边的顶点连线组成的平行四边形等等。
【详解】根据分析,作图如下:
【点睛】理解掌握并能灵活运用长方形、正方形、三角形、平行四边形等的面积公式是解答此题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版数学小升初高频易错考点专题训练:作图题
学校:___________姓名:___________班级:___________考号:___________
一、作图题
1.在平行四边形内画一条线段,把它分成两个面积相等的三角形。
2.画出下面三角形底边上的高。
3.将三角形ABC绕B点顺时针旋转90°;将三角形ABC按照2∶1放大。
4.动手操作。
(1)如图中的圆,圆心的位置用数对表示是 ,在这个圆中画一个圆心角是90°的扇形。
(2)将原来的三角形先向右平移5格,再向下平移4格,画出平移后的图形。
(3)按2∶1的比画出三角形放大后的图形,放大后的三角形的面积是原三角形面积的______倍。
5.在下面方格纸上画出从不同方向看到下边立体图形的形状图。
6.按要求画一画。
(1)画出图形绕点逆时针旋转90度后的图形。
(2)画出把图形向下平移5格后的图形。
7.银行在广场的正西方向400米处,医院在广场的东偏北30°方向的800米处,请在下图中画出银行和医院的位置。
8.观察下面的几何体,请你把从前面观察看到的图形画在下面方格纸上。
9.按要求在方格纸上画图。(方格纸每小格为1×1cm2)
(1)在方格纸上画一个底和高都是6cm的等腰直角三角形。
(2)画一个面积和题(1)中三角形面积相等的平行四边形。
(3)按1∶2的比例将题(1)中三角形缩小,并画出图形。
10.把向右平移4格后得到的图形涂上颜色.
11.请你分别画出将已知图形按3∶1放大,再把放大后的图形按1∶2缩小后的图形。
12.这是一张小明的行走路线图。
(1)小明从出发站出发,向( )偏( )( )方向,行走( )m可以到达A站。
(2)小明最终的目的地是C站。C站位于B站南偏西75°、距B站50m的位置上。请你在图中标出C站的位置。
13.按要求在方格纸上画图.(每个小方格表示1平方厘米)画一个面积是16平方厘米的梯形.
14.请你根据下面的描述,在平面图上标出各场所的位置。
(1)医院在学校的东偏北40°方向400米处。
(2)图书馆在学校的西偏南30°方向300米处。
15.(1)把图中的长方形绕A点顺时针旋转90°,画出旋转后的图形.
(2)按1:2的比画出三角形缩小后的图形,缩小后的三角形的面积是原来的( ).
(3)如果一个小方格表示1平方厘米,在方格纸上设计一个面积是10平方厘米的轴对称图形,并画出对称轴.
16.画出下面轴对称图形的一条对称轴。
17.小莉和小敏同时从起点(0)出发,小莉向东走,小敏向西走,现在两人相距11m。请你在下面的直线上用△表示小莉现在的位置,用○表示小敏现在的位置。
18.画一个半径为2厘米的半圆形,并计算出它的面积和周长。
19.根据李阳的描述,画出路线示意图.
我从家出发,向东偏北40°方向走了200米到达图书馆;再从图书馆出发,向正东方向走300米到达超市;又从超市出发,向西偏南30°方向走150米到达学校.
20.我会画。
(1)在下面方格中画一个直角三角形,三个顶点的位置分别是A(3,7),B(1,4),C(3,4)。
(2)画出这个三角形绕C点顺时针旋转90°后的图形①。
(3)画出把图形①按2∶1放大后的图形②。
(4)画出把图形①向右平移4个格得到的图形③。
21.(1)画出三角形ABC绕A点逆时针旋转90°后的图形.
(2)画出三角形ABC以1:2的比例缩小后的图形.
22.下面是一个卧室的平面图。在卧室的西北角放一张长2米、宽1.5米的床,请你在平面图上画出床的示意图。
23.按照题目要求,完成下列各题。
(1)如图,将三角形OAB绕点O顺时针旋转90°后得到图形OA'B',请画出图形OA'B';
(2)请你在方格纸中画出一个与三角形OAB面积相等的长方形。
24.下面是电影院附近示意图。请根据示意图填一填,再根据描述在示意图上画一画。
(1)广场在电影院( )偏( )( )°方向( )米处。
(2)育才小学在电影院南偏东60°方向500米处。
(3)中山路在电影院的东面1000米处,并与鲈乡路平行。
25.在方格纸中画出下面图形从上面看到的形状.
26.(1)过顶点B作三角形的高,标出垂足O。
(2)若三角形的∠A=52°,则三角形的顶点A在顶点C的( )偏( )( )°方向上。
(3)画出三角形绕点B顺时针方向旋转90°后的图形;点C旋转后的位置可用数对( )表示。
27.按要求在方格图中作图。
(1)以钝角三角形的顶点A为端点画一条线段,将这个三角形分成面积相等的两部分。
(2)将直角三角形绕点O顺时针方向旋转90°,画出旋转后的图形。
(3)在方格图中画一个梯形,使它的面积是直角三角形面积的2倍。
28.下图中每个小方格表示边长l厘米的小正方形.
(1)请画出小旗向右平移8格的图形.
(2)画出小旗子绕O点按顺时针方向旋转90°后的图形
(3)画出小旗子按2:1扩大后的图形ABCO.
29.动手操作
画一画:(1)在下面的方格图(每个小方格的边长是1cm)中画一个半圆,半径是2cm;
(2)画出半圆的对称轴;
(3)画出半圆向右平移4格后的图形.
30.按要求在方格纸中作图。
①根据给定的对称轴画出图形A的另一半。
②画出图形B向右平移4格后的图形。
③画出将图形C按2∶1放大后的图形。
31.画一画,下面每个小方格的面积都是1cm2,请你按要求做图。
(1)画出面积是12cm2的平行四边形和三角形各一个。
(2)画一个面积是12cm2、高是3cm的梯形,并使下底长是上底的3倍。
32.李叔叔家位于镇政府正南方向1.2千米处,小林家位于镇政府南偏东30°方向,距离1.6千米处。请根据下面方框中的信息画出李叔叔家及小林家的位置。
33.用7个同样大的正方体摆成左边的物体,请在右边的方格纸上画出从前面,右面和上面看到的图形。
34.“狡兔三窟”指聪明的兔子会准备好几个藏身的窝。野外林区的摄像头拍下一只野兔的活动轨迹,如图所示。
(1)野兔从B窝出来,向西跑了4米,到达A窝。量一量:两个窝之间的图上距离是 厘米,轨迹图的比例尺是 ∶ 。
(2)野兔在A窝时,一只狐狸在距离A窝6米处出现,请在图中画出狐狸可能出现的所有位置。
(3)野兔从A窝向北偏西30°方向跑了8米到达C窝,请在如图中标出C窝的位置。
35.按要求画图。
(1)在格子图上画出轴对称图形的另一半。
(2)在格子图上画出一个平行四边形,使它的面积与轴对称图形的面积相等。
36.操作题.
画出三角形AOB绕O逆时针旋转90°,再向下平移2格后的图形.
37.(1)将图形A绕点O点顺时针旋转90°得到的图形B。
(2)将图形B向右平移4格得到图形C。
38.按要求在方格纸上图并完成填空。
(1)把图①绕M点逆时针旋转90°画出旋转后的图形,旋转后P点的位置用数对表示是( )。
(2)把图②按2∶1的比放大,画出放大后的图形,放大后的图形与原来图形的面积比是( )。
(3)图③中直角三角形ABC的斜边BC是圆的直径,O是圆心,AO=AC。如果每个小方格表示边长2厘米的小正方形,则点A在点O( )偏( )( )°方向( )厘米处。
39.请按要求在格子图中画一画。
(1)画出三角形ABC绕点C按顺时针方向旋转90°后的图形①。
(2)在格子图中画出将三角形ABC按2∶1放大后的图形②。
40.下面是仪征城区的平面图,请在图中画出有关街道和场所的位置。
(1)市政府东面300米的处有一条健康路,它与工农路平行。
(2)育才小学在市政府北偏西75°方向400米处。
41.按图形的变化规律,接着画。
42.在下面正方形中各画一个图形,使它的面积正好等于正方形的一半。(要求所画的图形各不相同,例如不同形状的三角形视为同一个图形)。
《人教版数学小升初高频易错考点专题训练:作图题》参考答案
1.见详解
【分析】平行四边形性质:平行四边形对边平行且相等,对角线将其分成两个三角形。面积相等依据:这两个三角形等底等高(底为平行四边形的边,高为平行四边形的高 ),根据三角形面积公式S=ah(a为底,h为高 ),等底等高的三角形面积相等。
【详解】
2.见详解
【分析】从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高;这条对边叫做三角形的底;依此画图即可。
【详解】
【点睛】熟练掌握三角形高的画法是解答此题的关键。
3.见详解
【分析】根据旋转的特征,把三角形各顶点绕B点顺时针旋转90°,再顺次连接即可;三角形ABC两条边AB和BC分别是3格、2格,按要求放大后分别是6格、4格,先画AB、BC两边,再连接第三条边;据此作图。
【详解】作图如下:
【点睛】解答本题的关键是掌握旋转和图形放大的作图能力,需注意的是旋转只改变图形的位置,不改变图形的形状和大小;图形的放大只改变图形的大小,不改变形状。
4.(1)(4,3);画图见详解
(2)画图见详解;
(3)画图见详解;4
【分析】(1)数对是一个表示位置的概念,先列后行。在图中找到圆心O,观察其所在的列数和行数。从左往右数,圆心在第4列,从下往上数,圆心在第3行,所以用数对表示为(4,3)。画扇形思路:以圆心O为顶点,利用直角工具(如三角板的直角),先画一条半径,再以圆心为端点,顺时针或逆时针旋转直角边,画出另一条半径,两条半径和它们所夹的圆弧就构成圆心角是90°的扇形。
(2)平移图形时,要根据平移的方向和格数移动图形的各个顶点。对于三角形,先找到它的三个顶点,将每个顶点都先向右平移5格,即列数增加5;再向下平移4格,即行数减少4。然后按照平移后顶点的位置,依次连接各顶点,画出平移后的三角形。
(3)按2∶1的比放大三角形,意味着三角形的底和高都变为原来的2倍。我们可以通过数方格的方式确定原三角形的底和高所占格数,进而得到放大后三角形的底和高所占格数,再根据三角形面积公式分别计算出原三角形和放大后三角形的面积,最后求出倍数关系。假设原三角形在方格图中底占2格,高占3格(可通过观察图形得出)。
【详解】(1)如图中的圆,圆心的位置用数对表示是(4,3)。
(2)(3)如图:
计算原三角形面积:根据三角形面积公式S=×底×高,原三角形底占2格,高占3格,那么原三角形面积
S1=×2×3
=1×3
=3
计算放大后三角形面积:按2∶1放大后,底变为2×2=4格,高变为3×2=6格,所以放大后三角形面积
S2=×4×6
=2×6
=12
计算倍数关系:用放大后的三角形面积除以原三角形面积可得倍数,即12÷3=4
5.见详解。
【分析】这个立体图形从正面能看到4个小正方形,分为两层,下层有3个小正方形,上层居中有1个小正方形;从上面看有3个小正方形,分为两层,下层靠左边有1个小正方形,上下两层未对齐,上层有2个小正方形;从右面看有3个小正方形,分为两层,下层有2个小正方形,上层靠右有1个小正方形;据此作图。
【详解】作图如下:
【点睛】本题考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形。
6.如图所示:
【分析】(1)旋转不改变图形的形状和大小。先画出图形A绕点O逆时针旋转90°后的下底,再画出与O点相邻的一条腰,然后再画出上底,最后再画出另一条腰。
(2)平移不改变图形的形状和大小。先确定图形B的每一条边平移后位置,再画出平移后的图形。
【详解】如图所示:
【点睛】本题考查图形的变换。掌握旋转和平移的要点是解答此题的关键。
7.
【分析】根据图上距离=实际距离×比例尺,求出银行和医院在图上的距离,结合方向标出相应的位置即可。
【详解】400米=40000厘米,800米=80000厘米
银行到广场的图上距离:40000×=2(厘米)
医院到广场的图上距离:80000×=4(厘米)
如图:
【点睛】本题考查比例尺和位置与方向,通过实际距离和比例尺求出图上距离是解题的关键。
8.见详解
【分析】从前面观察几何体,是2层3列,从左往右,每列分别有小正方形的个数:1个,2个,1个;据此画出平面图形。
【详解】
【点睛】掌握从不同的方向观察几何体,并能画出相应的平面图形是解题的关键。
9.见详解
【分析】(1)根据等腰直角三角形的特征,在方格纸上画一个底和高都是6cm的等腰直角三角形即可。
(2)题(1)中三角形面积是底×高÷2,算出三角形面积是18平方厘米,画一个面积是18平方厘米平行四边形即可。
(3)根据图形缩小的方法,按1∶2的比例将题(1)中三角形缩小,并画出图形即可。
【详解】(1)在方格纸上画一个底和高都是6cm的等腰直角三角形,如图:
(2)三角形面积是
=
=(平方厘米)
画一个面积是18平方厘米平行四边形,平行四边形可以底是6厘米,(答案不唯一)
(3)按1∶2的比例将题(1)中三角形缩小,如图:
(平行四边形画法不唯一)
【点睛】本题考查了等腰直角三角形、平行四边形的特征和画法以及图形的放大和缩小知识,结合题意分析解答即可。
10.
【分析】根据平移图形的特征,看哪个虚线图形与这个图形的各对应点相距4格,涂上颜色即可。
【详解】本题考查的知识点是利用对应法把一个图形平移,解答时要找到图形对应点平移的距离是不是4个格,平移的方向是不是向右。通过观察上图发现,只有黑色图形和它右边的图形是经历向右平移得到的。
【点睛】关键是看两图的对应点相距的格数。
11.见详解。
【分析】按3∶1的比例画出图形放大后的图形,就是把原图形的各边都扩大到原来3倍;再按1∶2缩小,就是把放大后的图形的各边再缩小到原来一半即可,依此画图。
【详解】作图如下:
【点睛】本题考查了图形的放大和缩小,能在方格纸上按一定的比例画出放大与缩小的图形。
12.(1)北;西;40°;150
(2)
【分析】(1)在地图上按照“上北下南,左西右东”确定方向,注意观测点是A站。根据图上距离和比例尺的关系确定实际距离。
(2)根据实际距离与比例尺的关系确定图上距离,再根据方位关系即可确定C站的位置。
【详解】(1)3×50=150(米)
小明从出发站出发,向北偏西40°方向,行走150m可以到达A站。
(2)90°-75°=15°
C站位于B站南偏西75°,即C站位于B站西偏南15°。
如图:
【点睛】本题考查根据方向和距离确定物体的位置,会根据位置描述方向以及会根据方向的描述确定物体的位置是解本题的关键。
13.如图:
(画法不唯一)
【详解】略
14.见详解
【分析】(1)以学校为观测点,在学校东偏北40°方向截取400÷100=4个单位长度,标出角度,终点处标注医院。
(2)以学校为观测点,在学校的西偏南30°方向截取300÷100=3个单位长度,标出角度,终点处标注图书馆。
【详解】(1)(2)作图如下:
【点睛】掌握根据方向、角度、距离确定物体位置的方法是解答题目的关键。
15.(1)
(2)如图,﹙2×1.5÷2﹚÷﹙4×3÷2﹚=
(3)如图,答案不唯一.
【详解】本题考查图形的变换、图形的缩放及轴对称图形.图形旋转注意三点:旋转点、方向和角度;图形放大和缩小关键点是对应边的放大和缩小;轴对称关键是找对称点.
(1)根据旋转的性质,先将长方形由点A引出的两条边顺时针旋转90度,由此即可确定旋转后的图形的位置与大小.(2)根据放大和缩小的性质,先把两条直角边分别缩小2倍,即可画出缩小后的三角形.(3)根据轴对称图形的定义和画指定面积的图形的方法,这里可以画一个长是10厘米、高是2厘米的等腰三角形,并画出它的对称轴.如图所示:
16.见详解
【分析】轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴。
【详解】作图如下:
(画法不唯一)。
【点睛】此题考查了轴对称的意义及在实际当中的运用。
17.见详解(答案不唯一)
【分析】向东走和向西走是两种具有相反意义的量,规定向东走为正,则向西走则为负,以0为界线,小莉向正数的位置方向走,小敏向负数的位置方向走,保证最后两人相距11格即可。
【详解】作图如下:
(答案不唯一)
【点睛】此题属于开放题,重在理解正负数在数轴上的表示方法。
18.图见详解;面积:6.26平方厘米;周长:10.28厘米
【分析】由题意可知:可以以任意一点为圆心,圆规两脚之间的距离是2厘米为半径,旋转半周即可画出符合要求的半圆弧,再把半圆弧的两端连接即可;半径已知,根据圆的面积公式:面积=π×半径2,代入数据,求出半径是2厘米的圆的面积,再除以2,即可求出半圆面积;根据半圆周长公式:周长=π×半径+半径×2,代入数据,即可解答。
【详解】如图:
半圆的面积:
3.14×22÷2
=3.14×4÷2
=12.56÷2
=6.28(平方厘米)
半圆的周长:
3.14×2+2×2
=6.28+4
=10.28(厘米)
半圆的面积是6.26平方厘米,周长是10.28厘米。
19.
【详解】200÷100=2(厘米)
300÷100=3(厘米)
150÷100=1.5(厘米)
20.见详解
【分析】(1)数对表示位置的方法是:第一个数字表示列,第二个数字表示行,由此在图中找出A、B、C三个点的位置顺次连接即可得出三角形ABC;
(2)根据图形旋转的方法,抓住三角形ABC的两条直角边绕点C顺时针旋转90°即可得出旋转后的三角形①;
(3)按照图形放大与缩小的方法,将三角形①的两条直角边按2∶1放大,即可得出放大后的三角形②;
(4)将三角形①的各个顶点向右移4格,再将各个顶点依次连接,据此即可得出答案。
【详解】(1)三角形ABC的位置如下图所示:
(2)三角形ABC绕C点顺时针旋转90°后的图形①如下图所示:
(3)图形①按2∶1放大后的图形如下图所示:
(4)图形①向右平移4个格得到的图形③如下图所示:
【点睛】此题主要考查了数对表示位置以及图形的旋转、平移和放大与缩小的方法。
21.
【详解】(1)画出三角形ABC绕A点逆时针旋转90°后的图形(图中红色部分).
(2)画出三角形ABC以1:2的比例缩小后的图形(图中绿色部分).
22.见详解
【分析】看图,比例尺是1∶100,将实际长度乘比例尺,求出床的长和宽的图上距离。西北角在卧室的右上角,据此结合数据画图即可。
【详解】2米=200厘米,1.5米=150厘米
长:200×=2(厘米)
宽:150×=1.5(厘米)
如图:
【点睛】本题考查应用比例尺画图,求出图上的长、宽值是解题的关键。
23.见详解
【分析】(1)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。
(2)三角形面积=底×高÷2,长方形面积=长×宽,据此先求出三角形面积,再确定长方形的长和宽,作图即可。
【详解】(1)作图如下:
(2)3×4÷2=6
6=3×2
画出的长方形长3格,宽2格即可,作图如下:
(长方形画法不唯一)
24.(1)( 南 )(西)(50)°(1500)
(2)(3)见图
【详解】(1)根据图可知,广场所在的位置应为南偏西50度方向,这50度,即为90-40=50。再测量出其图上距离为3厘米,由线段比例尺即可知道,图上3厘米就是实际1500米。
(2)见图
由线段比例尺可知,实际500米即图上1厘米。
(3)见图
实际1000米,即图上2厘米。其余见图。
25.解:在方格纸中画出下面图形从上面看到的形状:
【详解】左边的立体图形由5个相同的小正方体组成.从上面能看到4个正方形,分两列,左列3个,右列1个,上齐.
26.(1)图见详解
(2)南;西;38
(3)图见详解;(8,3)
【分析】(1)根据三角形高的意义,在三角形ABC中,从顶点B向它的对边AC画垂线,顶点到垂足之间的线段叫做三角形的高,由此作图即可;
(2)已知三角形的内角和是180°,那么直角三角形中两个锐角的度数之和是90°,减去已知的一个锐角,即可求出另一个锐角的度数;
以顶点C为观测点,以图上的“上北下南,左西右东”为准,结合方向、角度确定顶点A与顶点C的位置关系。
(3)根据旋转的特征,将三角形绕点B顺时针方向旋转90°,点B位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;据此用数对表示点C旋转后的位置。
【详解】(1)过顶点B作三角形的高,标出垂足O,如下图。
(2)∠C=90°-52°=38°
三角形的顶点A在顶点C的南偏西38°(或西偏南52°)方向上。
(3)画三角形绕点B顺时针方向旋转90°后的图形,如下图。
点C旋转后的位置可用数对(8,3)表示。
如下图所示:
27.见详解
【分析】(1)根据两个三角形等底等高时,面积相等,据此以钝角三角形的顶点A为端点画一条线段,把底边平分即可。
(2)根据旋转的特征,将直角三角形绕点O顺时针方向旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(3)已知直角三角形的底是3、高是4,根据三角形的面积=底×高÷2,求出直角三角形的面积;
要画的梯形的面积是直角三角形面积的2倍,用三角形的面积乘2,即是梯形的面积;根据梯形的面积=(上底+下底)×高÷2,据此确定所画梯形的上底、下底和高。
【详解】(1)以钝角三角形的顶点A为端点画一条线段,如下图。
(2)将直角三角形绕点O顺时针方向旋转90°,旋转后的图形如下图。
(3)三角形的面积:3×4÷2=6
梯形的面积:6×2=12
(2+4)×4÷2
=6×4÷2
=12
画一个上底为2、下底为4、高为4的梯形。
(梯形的画法不唯一)
28.作平移后的图形、旋转一定角度后的图形、放大后的图形如下:
【详解】(1)根据平移图形的特征,把小旗的各顶点分别向右平移8格,再依次连结,即可画出小旗向右平移8格的图形(图中红色小旗);
(2)根据旋转图形的特征,小旗绕O点顺时针旋转90°后,O点的位置不动,其余各部分均绕O点按相同方向旋转相同的度数即可画出小旗子绕O点按顺时针方向旋转90°后的图形(图中绿色小旗);
(3)根据图形放大与缩小的特征,把小旗的各部分均放大到原来的2倍即可画出小旗子按2:1扩大后的图形(图中蓝色小旗).
29.
【详解】略
30.见详解
【分析】①补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
②作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点。
③把图形按照n∶1放大,就是将图形的每一条边放大到原来的n倍,放大后图形与原图形对应边长的比是n∶1。
【详解】
【点睛】决定平移后图形的位置的要素:一是平移的方向,二是平移的距离。图形放大或缩小的倍数是指对应边放大或缩小的倍数。
31.见详解
【分析】(1)平行四边形面积=底×高,三角形面积=底×高÷2,分别确定平行四边形和三角形的底和高,作图即可;
(2)梯形上下底的和=面积×2÷高,先确定上下底的和,上下底的和÷总倍数,求出一倍数,是上底,上底×3=下底,作图即可。
【详解】(1)12=4×3,12×2=24=6×4,画出的平行四边形底是4厘米,高是3厘米即可;画出的三角形底是6厘米,高是4厘米即可;
(2)12×2÷3=8(厘米)
8÷(3+1)
=8÷4
=2(厘米)
2×3=6(厘米)
作图如下:
【点睛】关键是掌握平行四边形、三角形、梯形的面积公式。
32.见详解
【分析】根据“上北下南,左西右东”的方向以及比例尺确定物体的位置和行走路线,据此解答。
【详解】根据比例尺1∶40000得
1.2千米=120000厘米
120000÷40000=3(厘米)
1.6千米=160000厘米
1600÷40000=4(厘米)
画图如下:
【点睛】此题考查的是位置与方向,掌握“上北下南,左西右东”的方向以及比例尺确定物体的位置和行走路线是解题关键。
33.见详解
【分析】观察图形可知,从前面看到的图形是2层,下层是3个正方形,上层2个正方形,靠左边;从上面看到的图形是2层,下层是2个正方形,上层3个正方形,靠左边;从右面看到的图形是2层,下层2个正方形,上层1个正方形,靠右边;由此即可画图。
【详解】根据题意画图如下:
【点睛】本题是考查从不同方向观察物体和几何体以及三视图的画法,目的是训练学生的观察能力。
34.(1)1;1;400
(2)(3)见详解
【分析】(1)用直尺量出A、B两窝在图上的距离(实际操作测量,已知野兔从B窝向西跑4米(实际距离)到达A窝,因为4米=400厘米,根据“比例尺=图上距离∶实际距离”,将测量得到的图上距离与400厘米相比,即可得出比例尺;
(2)因为狐狸在距离A窝6米处,6米=600厘米,根据(1)中求出的比例尺,计算出狐狸位置的图上距离(图上距离=实际距离×比例尺),以A点为圆心,以计算得到的图上距离为半径画圆,圆上的所有点就是狐狸可能出现的位置;
(3)已知野兔从A窝向北偏西30°方向跑了8米(800厘米)到达C窝,根据比例尺算出A到C的图上距离(图上距离=实际距离×比例尺 ),用量角器以A为顶点,向北偏西30°方向画出射线,在射线上按照计算出的图上距离截取线段,端点即为C窝的位置。
【详解】(1)野兔从B窝出来,向西跑了4米,到达A窝。量一量可知,两个窝之间的图上距离是1厘米。
4米=400厘米
1厘米∶400厘米=1∶400
所以轨迹图的比例尺是1∶400。
(2)6米=600厘米
600×=1.5(厘米)
野兔在A窝时,一只狐狸在距离A窝6米处出现,在图中画出狐狸可能出现的所有位置。如下图:
(3)8米=800厘米
800×=2(厘米)
野兔从A窝向北偏西30°方向跑了8米到达C窝,在如图中标出C窝的位置。如图:
35.见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,找到图形的各顶点关于对称轴的对称点后,依次连接各点得到轴对称图形的另一半图形。
(2)从图中可知,轴对称图形是一个梯形,根据梯形的面积=(上底+下底)×高÷2,求出梯形的面积;
要画出一个平行四边形,使它的面积与轴对称图形的面积相等,根据平行的面积=底×高,确定所画平行四边形的底和高,据此画出这个平行四边形。
【详解】(1)在格子图上画出轴对称图形的另一半。如图:
(2)梯形的面积:
(8+4)×4÷2
=12×4÷2
=24
平行四边形的面积:6×4=24
画一个底为6、高为4的平行四边形,如下图。
(平行四边形画法不唯一)
36.如图中红色线所示△A1B1C1即是所求.
【详解】本题是旋转与平移的综合应用,作图时弄清楚图形的变换方式即可,特别注意旋转与平移过程不要混淆.
【考点点拨】本题主要考查旋转与平移的综合应用,是小升初的常见易考题型之一,难度系数 适中.
37.(1)、(2)如图:
【分析】(1)根据旋转的特征,图形A绕点O顺时针旋转90°后,点O位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(2)根据平移的特征,图形B向右平移4格,图形的大小、形状都不改变,整个图形向右平行移动4格。
【详解】(1)(2)如图:
【点睛】做旋转图形时,要注意旋转的方向与角度。做平移图形时,要注意平移的方向与距离。
38.(1)画图见详解;(4,2)
(2)画图见详解;4∶1
(3)东;北;60;6
【分析】(1)根据题意,以三角形其中一个顶点M,将图①逆时针旋转90°,大小保持不变,画出三角形即可。根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可用数对表示出旋转后P点的位置。
(2)把图②按2∶1的比放大,画出放大后的图形(图中绿色部分),放大后的图形与原来图形的面积比是(6×4)∶(3×2)=24∶6=4∶1。
(3)根据题意,A点在O点的右上方,依据上北下南左西右东,A点在O点的东偏北的位置,因为△AOC是等边三角形,依据三角形内角和180°,180°÷3=60°,因为O点距离A点3个小格,所以,距离为2×3即可。
【详解】(1)旋转后P点的位置用数对表示是(4,2)。
(2)放大后的图形与原来图形的面积比是4∶1。
(3)因为AO=AC,OA=OC,所以三角形AOC为等边三角形。
所以∠AOC=60°。
OA=OB=3格
2×3=6(厘米)
即点A在点O东偏北60°方向6厘米处。或点A在点O北偏东30°方向6厘米处。
39.(1)(2)见详解
【分析】(1)根据旋转的特征,三角形ABC绕点C顺时针旋转90°后,点C的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图形①,据此画图;
(2)先求出放大后三角形ABC的底和高各是多少,然后画出三角形ABC按2∶1放大后的图形②(位置不唯一)。
【详解】(1)如图:
(2)底:3×2=6(格);高:2×2=4(格)
如图:
40.
【分析】
方向和距离两个条件才能确定物体的位置,要画图首先要根据图形确定比例尺为1:10000,和方向上北下南左西右东。(1)健康路在市政府东面,可确定其方向,根据图上距=实际距离×比例尺,求出市政府到健康路图上距离。(2)育才小学在市政府北偏西75°,可确定其方向,再根据图上距离=实际距离×比例尺,可求出其图上距离,据此画图解答.本题的关键是确定比例尺和方向后,根据图上距离=实际距离×比例尺,求出图上距离,再画图解答。
【详解】(1)健康路到市政府的图上距离是:
300米=30000厘米
30000× =3(厘米)
(2)育才小学到市政府的图上距离是:
400米=40000厘米
40000× =4(厘米)
画图如下:
41.
【分析】观察题目给出的三幅图,发现每个小图形都是按照左上角→右上角→右下角→左下角这样的顺时针方向转动的,并且这里不用考虑转动引起的方向问题。
【详解】如图:
【点睛】本题较为简单,只需要考虑图形的转动,而不用考虑方向,相对是比较容易的。
42.
【分析】根据正方形、长方形、平行四边形等的面积间的相互关系,作图即可:如取对边中点连线,把正方形平均分成两个长方形;取一条边的中点,与对边的两个顶点连线的三角形;取四条边的中点连线的正方形;取一组对边中点,分别与对边的顶点连线组成的平行四边形等等。
【详解】根据分析,作图如下:
【点睛】理解掌握并能灵活运用长方形、正方形、三角形、平行四边形等的面积公式是解答此题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
