河南省驻马店实验中学2025届中考 数学五模试卷(含解析)
文档属性
| 名称 | 河南省驻马店实验中学2025届中考 数学五模试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 243.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 10:37:51 | ||
图片预览




文档简介
2025年河南省驻马店实验中学中考数学五模试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.2025的相反数是( )
A. B. 2025 C. D.
2.“陀螺”一词的正式出现是在明朝时期,打陀螺是一项深受各民族群众喜爱的体育运动.如图是一个水平放置的木陀螺上面是圆柱体,下面是圆锥体玩具,它的主视图是( )
A. B. C. D.
3.从河南省农业农村厅获悉,截至6月5日17时,我省已收获小麦7992万亩,约占全省种植面积的当日投入联合收割机万台,日收获小麦454万亩.“7992万”用科学记数法表示为( )
A. B. C. D.
4.如图,已知直线,BE平分,交CD于D,,则的度数是( )
A.
B.
C.
D.
5.下列计算正确的是( )
A. B.
C. D.
6.关于x的一元二次方程有两个不相等的实数根,则m的值可能是( )
A. 8 B. 9 C. 10 D. 11
7.如图,AB,BC为的两条弦,连接OA,OC,点D为AB的延长线上一点,若,则的度数为( )
A.
B.
C.
D.
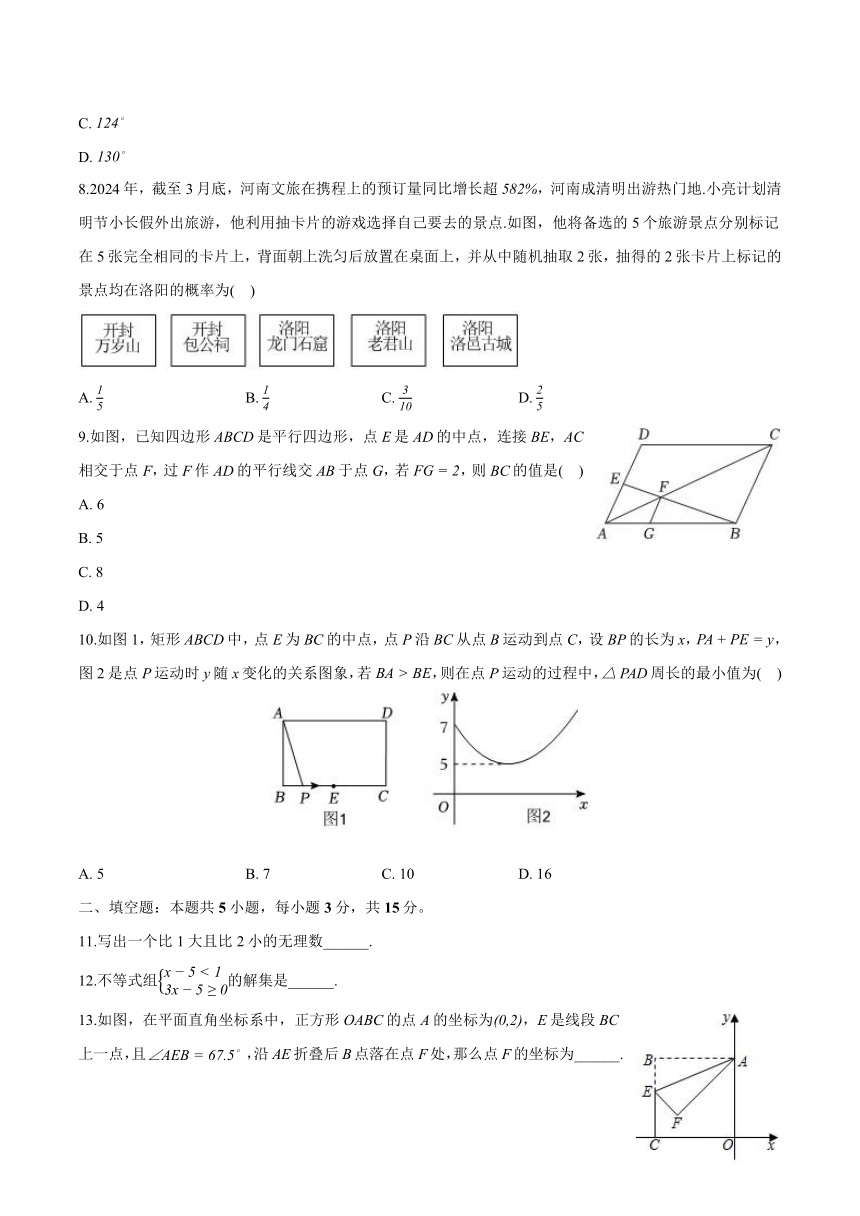
8.2024年,截至3月底,河南文旅在携程上的预订量同比增长超,河南成清明出游热门地.小亮计划清明节小长假外出旅游,他利用抽卡片的游戏选择自己要去的景点.如图,他将备选的5个旅游景点分别标记在5张完全相同的卡片上,背面朝上洗匀后放置在桌面上,并从中随机抽取2张,抽得的2张卡片上标记的景点均在洛阳的概率为( )
A. B. C. D.
9.如图,已知四边形ABCD是平行四边形,点E是AD的中点,连接BE,AC相交于点F,过F作AD的平行线交AB于点G,若,则BC的值是( )
A. 6
B. 5
C. 8
D. 4
10.如图1,矩形ABCD中,点E为BC的中点,点P沿BC从点B运动到点C,设BP的长为x,,图2是点P运动时y随x变化的关系图象,若,则在点P运动的过程中,周长的最小值为( )
A. 5 B. 7 C. 10 D. 16
二、填空题:本题共5小题,每小题3分,共15分。
11.写出一个比1大且比2小的无理数______.
12.不等式组的解集是______.
13.如图,在平面直角坐标系中,正方形OABC的点A的坐标为,E是线段BC上一点,且,沿AE折叠后B点落在点F处,那么点F的坐标为______.
14.如图,在的网格图中,每个小正方形的边长均为点A、B、C、D均在格点上.则图中阴影部分的面积为______结果保留
15.如图,在中,,,点D为AB的中点,点M,N分别是边AC,BC上的动点,且,点P是MN的中点,连接BP,DP,则:
①DP的最小值为______;
②当最大时,线段AM的长是______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题10分
;
17.本小题9分
随着自然语言处理、机器学习、深度学习等技术的不断进步,AI聊天机器人的智能化水平显著提高,能够更准确地理解用户意图并给出相应回答.预计2025年,我国对话机器人行业市场规模将达到亿元.有关人员开展了对A,B两款AI聊天机器人的使用满意度的评分调查,并从中各随机抽取20份数据,进行整理、描述和分析评分分数用x表示,满分100分,分为四个等级:不满意、比较满意、满意、非常满意,下面给出了部分信息.
抽取的对A款AI聊天机器人的评分数据中“满意”的数据:84,86,86,87,88,
抽取的对B款AI聊天机器人的评分数据:66,68,69,81,84,85,86,87,87,87,88,89,95,97,98,98,98,98,99,
抽取的对A,B两款AI聊天机器人的评分统计表
AI聊天机器人 平均数 中位数 众数 “非常满意”所占百分比
A 88 b 96
B 88 c
根据以上信息,解答下列问题.
上述图表中,______,______,______.
根据以上数据,你认为哪款AI聊天机器人更受用户喜爱?请说明理由写出一条理由即可
在此次调查中,有400人对A款AI聊天机器人进行评分,300人对B款AI聊天机器人进行评分.请通过计算,估计此次调查中对AI聊天机器人不满意的共有多少人.
18.本小题9分
如图,平行四边形ABCD中,,点M为AB的中点,连接
过点B作,交CD于点尺规作图,不写作法,保留作图痕迹;
求证:四边形DMBN为菱形;
若平行四边形ABCD的周长为18,,求四边形DMBN的面积.
19.本小题9分
停车楔如图①是一种固定汽车轮胎的装置,在大型货车于坡道停车时,放停车楔的作用尤为重要.如图②是轮胎和停车楔的示意图,当车停于水平地面上时,将停车楔置于轮胎后方即可防止车辆倒退,此时AC紧贴轮胎,边AB与地面重合且与轮胎相切于点为了更好地研究这个停车楔与轮胎的关系,小明在示意图②上,连接CO并延长交于点D,连接AD后发现
求证:;
小明通过查阅资料从停车楔的规格了解到,此停车楔的高度为点C到AB所在直线的距离,支撑边BC与底边AB的夹角,求轮胎的直径.
20.本小题9分
单摆是一种能够产生往复摆动的装置,某兴趣小组利用摆球和摆线进行与单摆相关的实验探究,并撰写实验报告如下.
实验主题 探究摆球运动过程中高度的变化
实验用具 摆球,摆线,支架,摄像机等
实验说明 如图1,在支架的横杆点O处用摆线悬挂一个摆球,将摆球拉高后松手,摆球开始往复运动摆线的长度变化忽略不计
如图2,摆球静止时的位置为点A,拉紧摆线将摆球拉至点B处,,,;当摆球运动至点C时,
,点O,A,B,C,D,E在同一平面内
实验图示
解决问题:根据以上信息,求DE的长.
参考数据:,,
21.本小题9分
《哪吒2魔童闹海》票房大卖,周边玩偶热销.小洋在网上开设相关周边专卖店,一次,小洋发现一张进货单上的一个信息是:A款哪吒玩偶的进货单价比B款哪吒玩偶少5元,花500元购进A款哪吒玩偶的数量与花750元购进B款哪吒玩偶的数量相同.
问:A、B两款的进货单价分别是多少元?
小洋决定将A款玩偶的销售单价定为12元,将B款玩偶的销售单价定为20元,小洋打算要花费1000元购进A、B两款玩偶若干个,且A款的数量不小于B款的一半,请你根据计算说明,当A、B两款各购进多少时,小洋获得的总利润最高,最高为多少?
22.本小题10分
一次足球训练中,小明从球门正前方8m的A处射门,球射向球门的路线呈抛物线.当球飞行的水平距离为6m时,球达到最高点,此时球离地面已知球门高OB为,现以O为原点建立如图所示直角坐标系.
求抛物线的函数表达式,并通过计算判断球能否射进球门忽略其他因素;
对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点O正上方处?
23.本小题10分
综合与实践
在数学学习中,我们发现除了已经学过的四边形外,还有很多比较特殊的四边形.请结合已有经验,对下列特殊四边过形的进行研究.
定义:如果四边形的一条对角线把该四边形分割成两个等腰三角形,且这条对角线是这两个等腰三角形的腰,那么我们称这个四边形为双等腰四边形.
【初步探究】
如图1,在四边形ABCD中,,连接BD,点E是BD的中点,连接AE,试判断在四边形ABCE是否是双等腰四边形:______;填“是”或“不是”
【问题解决】
在的条件下,若,求的度数;
【拓展应用】
如图2,点E是矩形ABCD内一点,点F是边CD上一点,四边形AEFD是双等腰四边形,且延长AE交BC于点G,连接若,,,求AB的长.
答案和解析
1.【答案】A
【解析】解:2025的相反数是
故选:
根据符号不同,绝对值相同的两个数互为相反数即可求得答案.
本题考查了相反数的概念,掌握只有符号不同的两个数叫做互为相反数是解答此题的关键.
2.【答案】A
【解析】解:从正面看易得,底层是一个三角形,上层是一个矩形,
故选:
找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中,看不到的棱需要用虚线来表示.
本题主要考查了三视图的知识,主视图是从物体的正面看得到的视图,掌握主视图的概念是解题的关键.
3.【答案】C
【解析】解:7992万
故选:
科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值时,n是正数;当原数的绝对值时,n是负数.
此题考查科学记数法的表示方法.科学记数法的表示形式为的形式,其中,n为整数,表示时关键要正确确定a的值以及n的值.
4.【答案】B
【解析】解:,
,
,
,
平分,
,
,
,
,
故选
求出,根据平行线的性质求出,根据角平分线的定义求出,再根据平行线的性质求出即可.
本题考查了邻补角,平行线的性质,角平分线定义的应用,解此题的关键是求出的度数和得出,注意:①两直线平行,同旁内角互补,②两直线平行,内错角相等.
5.【答案】B
【解析】解:不能合并,故选项A错误,不符合题意;
,故选项B正确,符合题意;
,故选项C错误,不符合题意;
,故选项D错误,不符合题意;
故选:
根据合并同类项的方法可以判断A;根据单项式除以单项式可以判断B;根据积的乘方可以判断C;根据完全平方公式可以判断
本题考查整式的混合运算,熟练掌握运算法则是解答本题的关键.
6.【答案】A
【解析】解:根据题意得,
解得
故选
根据判别式的意义得到,然后解关于m的不等式,最后对各选项进行判断即可.
本题考查了根的判别式.
7.【答案】C
【解析】解:如图,在优弧AC上取点P,连接PA,PC,
,
,
,
故选:
根据的度数可先求出弧AC所对应的圆周角的度数,进而可得答案.
本题考查圆内接四边形的性质与圆周角定理,熟练掌握圆周角定理是解题关键.
8.【答案】C
【解析】解:设用A表示开封万岁山,B表示开封包公祠,C表示洛阳龙门石窟,D表示洛阳老君山,E表示洛阳洛邑古城,并从中随机抽取2张,列树状图如下:
共有20种等可能的情况数,其中抽得的2张卡片上标记的景点均在洛阳的有6种情况,
抽得的2张卡片上标记的景点均在洛阳的概率为
故选:
利用画树状图或列表的方法,得出所有可能出现的结果总数,从中找到符合条件的结果数,进而求出概率即可.
本题主要考查了列表法与树状图法,概率公式,解答本题的关键是熟练掌握概率的求法.
9.【答案】A
【解析】解:是AD的中点,
,
四边形ABCD是平行四边形,
,,
,
,
∽,∽,
,,
,
解得,
故选:
由四边形ABCD是平行四边形,得,,在证明∽,∽,利用相似三角形的性质即可得解.
本题考查了平行四边形的性质,相似三角形的判定及性质,熟练掌握相似三角形的判定及性质即可得解.
10.【答案】D
【解析】解:由图象可知,,,
在中,,
令,则,
即,
解得:或4,
,
,,
点E为BC的中点,
,
作点A关于BC的对称点,连接,
,,
的最小值为,
,
周长的最小值为
故选:
由图象可知,,,根据勾股定理和已知条件得出,,作点A关于BC的对称点,连接,进而得出答案.
本题主要考查动点问题的函数图象,根据图象得出,是解题的关键.
11.【答案】 答案不唯一
【解析】【解答】
解:一个比1大且比2小的无理数有等,
故答案为:答案不唯一,
【分析】
根据无理数的大小比较和无理数的定义写出范围内的一个数即可.
本题考查了对估算无理数和无理数的定义的应用,注意:答案不唯一.
12.【答案】
【解析】解:解不等式,得:,
解不等式,得:,
则不等式组的解集为,
故答案为:
分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
13.【答案】
【解析】解:作于点D,于点G,
,
沿AE折叠后B点落在点F,
,,
,
,
,
点F的坐标为
故答案为:
由题意知,因为,所以,,作于点D,于点G,,所以,所以,所以点F的坐标为
本题考查了翻折问题、坐标与图形的性质及正方形的性质;翻折问题一定要找准相等的相等及相等的角,作出辅助线后利用勾股定理求解是解答本题的关键.
14.【答案】
【解析】解:取AB的中点O,连接CO,AC,如图:
根据勾股定理得:,,
,
,
为圆的直径,点O是AB的中点,
,,
,
故答案为:
先利用勾股定理求得,,再利用勾股定理的逆定理得,再根据即可求解,
本题考查了扇形的面积、勾股定理及逆定理,熟练掌握扇形的面积公式及勾股定理及逆定理是解题的关键.
15.【答案】
【解析】①解:连接CP,CD,如图所示:
在中,,,
,,
由勾股定理得:,
点D是斜边上的中线,
,
,点P是MN的中点,,
是斜边上的中线,
,
在点M,N的运动过程中,点P始终在以C为圆心,以为半径的圆上运动,
根据“两点之间线段最短”得:,
,
当C,P,D三点在同一条直线上时,DP最小,最小值为,
,,
的最小值为:,
故答案为:;
②解:当最大时,则点C到直线PB的距离最大,
由①可知:点P在C为圆心,以为半径的圆上,
当BP与圆C相切时,点C到直线PB的距离最大,即最大,
连接PC,过点点P作于点E,如图2所示:
与相切,
,
在中,,,
由勾股定理得:,
由三角形的面积公式得:,
,
,,
,
点P是MN的中点,
是的中位线,
,
,
当最大时,线段AM的长是
故答案为:
①连接CP,CD,先求出,则,再根据点P是MN的中点得,则点P始终在以C为圆心,以为半径的圆上运动,根据“两点之间线段最短”得,则,即当C,P,D三点在同一条直线上时,DP最小,最小值为,据此即可得出答案;
②当最大时,则点C到直线PB的距离最大,由①可知点P在C为圆心,以为半径的圆上,当BP与圆C相切时,点C到直线PB的距离最大,即最大,过点点P作于点E,先求出,再由三角形的面积公式得,证明PE是的中位线,则,然后根据即可得出线段AM的长.
此题主要考查了切线的性质,点到直线的距离,直角三角形斜边上的中线,三角形中位线定理,熟练掌握切线的性质,直角三角形斜边上的中线,三角形中位线定理是解决问题的关键,确定点P在以为圆心,以为半径的圆上是解决问题的难点.
16.【答案】;
【解析】解:
;
先化简各式,然后再进行计算即可解答;
先利用异分母分式加减法法则计算括号里,再算括号外,即可解答.
本题考查了分式的混合运算,实数的运算,负整数指数幂,特殊角的三角函数值,准确熟练地进行计算是解题的关键.
17.【答案】10,,98;
A款,因A款中位数大于B款的,所以A款好理由不唯一;
85人.
【解析】解:由题意得:A款“满意”所占百分比为,
“不满意”所占百分比为,
;
“满意”的数据:84,86,86,87,88,89;
把A款的评分数据从小到大排列,排在中间的两个数是88、89,
,
在B款的评分数据中,98出现的次数最多,
;
故答案为:10,,98;
款AI聊天机器人更受用户喜爱,理由如下:
因为A款评分数据的中位数比B款高,所以A款AI聊天机器人更受用户喜爱理由不唯一;
款中“不满意”的有3人,所占百分比为,
估计此次测验中对AI聊天机器人不满意的共有人
用1分别减去其他三个等级所占百分比可得a的值,根据中位数的定义可得b的值,根据众数的定义可得c的值;
通过比较A,B款的评分统计表的数据解答即可;
由A、B两款的不满意的人数之和即可得出答案.
本题考查了扇形统计图、中位数、众数以及样本估计总体等知识,正确理解中位数、众数的意义,熟练掌握中位数、众数的计算方法是解题的关键.
18.【答案】解:图形如图所示:
证明:,,
四边形DMBN是平行四边形,
,M是AB的中点,
,
四边形DMBN是菱形;
解:设,,则有,
解得,
,,
,,
四边形ADNM是平行四边形,
,
菱形DMBN的面积
【解析】作,BN交CD于点N
本题考查作图-复杂作图,平行四边形的判定和性质,菱形的判定和性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
19.【答案】解:如图1所示:
连接AC,OA,
根据题意可知,CD为的直径,是直径CD所对的圆周角,
,
,
与相切于点A,
,
即,
,
,
,
,
,
,
,
,
,
如图2所示:
过点C作于H点,
,
,
,
又点C到AB所在直线的距离为15,
,
,
,
,
又,
,
,
为等边三角形,
,
轮胎直径
【解析】连接AC,OA,根据圆周角定理的推论可得,由AB与相切可得到,从而得到,再由,得到,分别与,的关系而从推出结论;
过点C作于H点,得到为直角三角形,求出AC 的长,再由题的结论及条件得出为等边三角形即可得出结论.
本题了考查圆周角定理结论以及切线性质和等边三角形的判定,根据圆的切线垂直于过切点的半径,两直线平行,内错角相等,以及直角三角形的两个锐角互余,由此即可求解.
20.【答案】
【解析】解:,
,
,,
,
答:DE的长为
根据三角函数进行计算,求出,,,即可得到答案.
本题主要考查解直角三角形,熟练掌握三角函数是解题的关键.
21.【答案】A款的进货单价是10元,则B款的进货单价是15元;
购进A款25个,购进B款50个时,获得的总利润最高,最高为300元.
【解析】解:设A款的进货单价是x元,则B款的进货单价是元,
,
解得,
经检验,是该方程的解,
,
答:A单价是10元,则B单价是15元;
设购进B款n个,则购进A款个,
由题意可得:,
,
设总利润为w,则,
,
随n的增大而增大,
当n取得最大整数解50时,w取得最大值,最大值为,
此时,则,
答:购进A款25个,购进B款50个时,获得的总利润最高,最高为300元.
设A款的进货单价是x元,则B款的进货单价是元,根据题意列分式方程求解即可;
设购进B款n个,先根据“A款的数量不小于B款的一半”求得;再设总利润为w,则,然后利用一次函数的性质求解即可.
本题考查分式方程的应用、一元一次不等式的应用、一次函数的应用,理解题意是解答的关键.
22.【答案】解:,
抛物线的顶点坐标为,
设抛物线为,
把点代入得:,
解得,
抛物线的函数表达式为;
当时,,
球不能射进球门.
设小明带球向正后方移动m米,则移动后的抛物线为,
把点代入得:,
解得舍去或,
当时他应该带球向正后方移动1米射门,才能让足球经过点O正上方处.
【解析】求出抛物线的顶点坐标为,设抛物线为,用待定系数法可得;当时,,知球不能射进球门.
设小明带球向正后方移动m米,则移动后的抛物线为,把点代入得舍去或,即知当时他应该带球向正后方移动1米射门,才能让足球经过点O正上方处.
本题考查二次函数的应用,解题的关键是读懂题意,把实际问题转化为数学问题解决.
23.【答案】是;
;
或
【解析】解:,点E是BD的中点,
,
、是等腰三角形,且BE是腰,
四边形AECB是双等腰四边形;
故答案为:是;
如图,
,点E是BD的中点,
同理,
在四边形ABCE中,,
,
;
四边形AEFD是双等腰四边形,,
或
①如图,当时,过点E作于点H,延长HE交AB于点
,
,,
,
,
∽,
,
,
,,,
设,,则,,
,
∽,
,
解得,
;
②如图,当时,过点E作于点
由可知,,
,
,
是等腰直角三角形,
由①可知,,
又,
≌
,,
,
设,,则,,
在中,,
,
解得或不合题意,舍去,
;
综上所述,AB的长为或
根据双等腰四边形的定义即可判断;
根据等腰三角形的性质和四边形内角和求解即可;
依据题意可知或分类讨论,画出图形,然后根据一线三垂直证相似或全等,进而再根据建立关系求解.
本题主要考查了等腰三角形的判定和性质、矩形的性质、相似三角形的判定和性质、勾股定理、全等三角形的判定和性质等内容,熟练掌握相关知识是解题的关键.
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.2025的相反数是( )
A. B. 2025 C. D.
2.“陀螺”一词的正式出现是在明朝时期,打陀螺是一项深受各民族群众喜爱的体育运动.如图是一个水平放置的木陀螺上面是圆柱体,下面是圆锥体玩具,它的主视图是( )
A. B. C. D.
3.从河南省农业农村厅获悉,截至6月5日17时,我省已收获小麦7992万亩,约占全省种植面积的当日投入联合收割机万台,日收获小麦454万亩.“7992万”用科学记数法表示为( )
A. B. C. D.
4.如图,已知直线,BE平分,交CD于D,,则的度数是( )
A.
B.
C.
D.
5.下列计算正确的是( )
A. B.
C. D.
6.关于x的一元二次方程有两个不相等的实数根,则m的值可能是( )
A. 8 B. 9 C. 10 D. 11
7.如图,AB,BC为的两条弦,连接OA,OC,点D为AB的延长线上一点,若,则的度数为( )
A.
B.
C.
D.
8.2024年,截至3月底,河南文旅在携程上的预订量同比增长超,河南成清明出游热门地.小亮计划清明节小长假外出旅游,他利用抽卡片的游戏选择自己要去的景点.如图,他将备选的5个旅游景点分别标记在5张完全相同的卡片上,背面朝上洗匀后放置在桌面上,并从中随机抽取2张,抽得的2张卡片上标记的景点均在洛阳的概率为( )
A. B. C. D.
9.如图,已知四边形ABCD是平行四边形,点E是AD的中点,连接BE,AC相交于点F,过F作AD的平行线交AB于点G,若,则BC的值是( )
A. 6
B. 5
C. 8
D. 4
10.如图1,矩形ABCD中,点E为BC的中点,点P沿BC从点B运动到点C,设BP的长为x,,图2是点P运动时y随x变化的关系图象,若,则在点P运动的过程中,周长的最小值为( )
A. 5 B. 7 C. 10 D. 16
二、填空题:本题共5小题,每小题3分,共15分。
11.写出一个比1大且比2小的无理数______.
12.不等式组的解集是______.
13.如图,在平面直角坐标系中,正方形OABC的点A的坐标为,E是线段BC上一点,且,沿AE折叠后B点落在点F处,那么点F的坐标为______.
14.如图,在的网格图中,每个小正方形的边长均为点A、B、C、D均在格点上.则图中阴影部分的面积为______结果保留
15.如图,在中,,,点D为AB的中点,点M,N分别是边AC,BC上的动点,且,点P是MN的中点,连接BP,DP,则:
①DP的最小值为______;
②当最大时,线段AM的长是______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题10分
;
17.本小题9分
随着自然语言处理、机器学习、深度学习等技术的不断进步,AI聊天机器人的智能化水平显著提高,能够更准确地理解用户意图并给出相应回答.预计2025年,我国对话机器人行业市场规模将达到亿元.有关人员开展了对A,B两款AI聊天机器人的使用满意度的评分调查,并从中各随机抽取20份数据,进行整理、描述和分析评分分数用x表示,满分100分,分为四个等级:不满意、比较满意、满意、非常满意,下面给出了部分信息.
抽取的对A款AI聊天机器人的评分数据中“满意”的数据:84,86,86,87,88,
抽取的对B款AI聊天机器人的评分数据:66,68,69,81,84,85,86,87,87,87,88,89,95,97,98,98,98,98,99,
抽取的对A,B两款AI聊天机器人的评分统计表
AI聊天机器人 平均数 中位数 众数 “非常满意”所占百分比
A 88 b 96
B 88 c
根据以上信息,解答下列问题.
上述图表中,______,______,______.
根据以上数据,你认为哪款AI聊天机器人更受用户喜爱?请说明理由写出一条理由即可
在此次调查中,有400人对A款AI聊天机器人进行评分,300人对B款AI聊天机器人进行评分.请通过计算,估计此次调查中对AI聊天机器人不满意的共有多少人.
18.本小题9分
如图,平行四边形ABCD中,,点M为AB的中点,连接
过点B作,交CD于点尺规作图,不写作法,保留作图痕迹;
求证:四边形DMBN为菱形;
若平行四边形ABCD的周长为18,,求四边形DMBN的面积.
19.本小题9分
停车楔如图①是一种固定汽车轮胎的装置,在大型货车于坡道停车时,放停车楔的作用尤为重要.如图②是轮胎和停车楔的示意图,当车停于水平地面上时,将停车楔置于轮胎后方即可防止车辆倒退,此时AC紧贴轮胎,边AB与地面重合且与轮胎相切于点为了更好地研究这个停车楔与轮胎的关系,小明在示意图②上,连接CO并延长交于点D,连接AD后发现
求证:;
小明通过查阅资料从停车楔的规格了解到,此停车楔的高度为点C到AB所在直线的距离,支撑边BC与底边AB的夹角,求轮胎的直径.
20.本小题9分
单摆是一种能够产生往复摆动的装置,某兴趣小组利用摆球和摆线进行与单摆相关的实验探究,并撰写实验报告如下.
实验主题 探究摆球运动过程中高度的变化
实验用具 摆球,摆线,支架,摄像机等
实验说明 如图1,在支架的横杆点O处用摆线悬挂一个摆球,将摆球拉高后松手,摆球开始往复运动摆线的长度变化忽略不计
如图2,摆球静止时的位置为点A,拉紧摆线将摆球拉至点B处,,,;当摆球运动至点C时,
,点O,A,B,C,D,E在同一平面内
实验图示
解决问题:根据以上信息,求DE的长.
参考数据:,,
21.本小题9分
《哪吒2魔童闹海》票房大卖,周边玩偶热销.小洋在网上开设相关周边专卖店,一次,小洋发现一张进货单上的一个信息是:A款哪吒玩偶的进货单价比B款哪吒玩偶少5元,花500元购进A款哪吒玩偶的数量与花750元购进B款哪吒玩偶的数量相同.
问:A、B两款的进货单价分别是多少元?
小洋决定将A款玩偶的销售单价定为12元,将B款玩偶的销售单价定为20元,小洋打算要花费1000元购进A、B两款玩偶若干个,且A款的数量不小于B款的一半,请你根据计算说明,当A、B两款各购进多少时,小洋获得的总利润最高,最高为多少?
22.本小题10分
一次足球训练中,小明从球门正前方8m的A处射门,球射向球门的路线呈抛物线.当球飞行的水平距离为6m时,球达到最高点,此时球离地面已知球门高OB为,现以O为原点建立如图所示直角坐标系.
求抛物线的函数表达式,并通过计算判断球能否射进球门忽略其他因素;
对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点O正上方处?
23.本小题10分
综合与实践
在数学学习中,我们发现除了已经学过的四边形外,还有很多比较特殊的四边形.请结合已有经验,对下列特殊四边过形的进行研究.
定义:如果四边形的一条对角线把该四边形分割成两个等腰三角形,且这条对角线是这两个等腰三角形的腰,那么我们称这个四边形为双等腰四边形.
【初步探究】
如图1,在四边形ABCD中,,连接BD,点E是BD的中点,连接AE,试判断在四边形ABCE是否是双等腰四边形:______;填“是”或“不是”
【问题解决】
在的条件下,若,求的度数;
【拓展应用】
如图2,点E是矩形ABCD内一点,点F是边CD上一点,四边形AEFD是双等腰四边形,且延长AE交BC于点G,连接若,,,求AB的长.
答案和解析
1.【答案】A
【解析】解:2025的相反数是
故选:
根据符号不同,绝对值相同的两个数互为相反数即可求得答案.
本题考查了相反数的概念,掌握只有符号不同的两个数叫做互为相反数是解答此题的关键.
2.【答案】A
【解析】解:从正面看易得,底层是一个三角形,上层是一个矩形,
故选:
找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中,看不到的棱需要用虚线来表示.
本题主要考查了三视图的知识,主视图是从物体的正面看得到的视图,掌握主视图的概念是解题的关键.
3.【答案】C
【解析】解:7992万
故选:
科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值时,n是正数;当原数的绝对值时,n是负数.
此题考查科学记数法的表示方法.科学记数法的表示形式为的形式,其中,n为整数,表示时关键要正确确定a的值以及n的值.
4.【答案】B
【解析】解:,
,
,
,
平分,
,
,
,
,
故选
求出,根据平行线的性质求出,根据角平分线的定义求出,再根据平行线的性质求出即可.
本题考查了邻补角,平行线的性质,角平分线定义的应用,解此题的关键是求出的度数和得出,注意:①两直线平行,同旁内角互补,②两直线平行,内错角相等.
5.【答案】B
【解析】解:不能合并,故选项A错误,不符合题意;
,故选项B正确,符合题意;
,故选项C错误,不符合题意;
,故选项D错误,不符合题意;
故选:
根据合并同类项的方法可以判断A;根据单项式除以单项式可以判断B;根据积的乘方可以判断C;根据完全平方公式可以判断
本题考查整式的混合运算,熟练掌握运算法则是解答本题的关键.
6.【答案】A
【解析】解:根据题意得,
解得
故选
根据判别式的意义得到,然后解关于m的不等式,最后对各选项进行判断即可.
本题考查了根的判别式.
7.【答案】C
【解析】解:如图,在优弧AC上取点P,连接PA,PC,
,
,
,
故选:
根据的度数可先求出弧AC所对应的圆周角的度数,进而可得答案.
本题考查圆内接四边形的性质与圆周角定理,熟练掌握圆周角定理是解题关键.
8.【答案】C
【解析】解:设用A表示开封万岁山,B表示开封包公祠,C表示洛阳龙门石窟,D表示洛阳老君山,E表示洛阳洛邑古城,并从中随机抽取2张,列树状图如下:
共有20种等可能的情况数,其中抽得的2张卡片上标记的景点均在洛阳的有6种情况,
抽得的2张卡片上标记的景点均在洛阳的概率为
故选:
利用画树状图或列表的方法,得出所有可能出现的结果总数,从中找到符合条件的结果数,进而求出概率即可.
本题主要考查了列表法与树状图法,概率公式,解答本题的关键是熟练掌握概率的求法.
9.【答案】A
【解析】解:是AD的中点,
,
四边形ABCD是平行四边形,
,,
,
,
∽,∽,
,,
,
解得,
故选:
由四边形ABCD是平行四边形,得,,在证明∽,∽,利用相似三角形的性质即可得解.
本题考查了平行四边形的性质,相似三角形的判定及性质,熟练掌握相似三角形的判定及性质即可得解.
10.【答案】D
【解析】解:由图象可知,,,
在中,,
令,则,
即,
解得:或4,
,
,,
点E为BC的中点,
,
作点A关于BC的对称点,连接,
,,
的最小值为,
,
周长的最小值为
故选:
由图象可知,,,根据勾股定理和已知条件得出,,作点A关于BC的对称点,连接,进而得出答案.
本题主要考查动点问题的函数图象,根据图象得出,是解题的关键.
11.【答案】 答案不唯一
【解析】【解答】
解:一个比1大且比2小的无理数有等,
故答案为:答案不唯一,
【分析】
根据无理数的大小比较和无理数的定义写出范围内的一个数即可.
本题考查了对估算无理数和无理数的定义的应用,注意:答案不唯一.
12.【答案】
【解析】解:解不等式,得:,
解不等式,得:,
则不等式组的解集为,
故答案为:
分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
13.【答案】
【解析】解:作于点D,于点G,
,
沿AE折叠后B点落在点F,
,,
,
,
,
点F的坐标为
故答案为:
由题意知,因为,所以,,作于点D,于点G,,所以,所以,所以点F的坐标为
本题考查了翻折问题、坐标与图形的性质及正方形的性质;翻折问题一定要找准相等的相等及相等的角,作出辅助线后利用勾股定理求解是解答本题的关键.
14.【答案】
【解析】解:取AB的中点O,连接CO,AC,如图:
根据勾股定理得:,,
,
,
为圆的直径,点O是AB的中点,
,,
,
故答案为:
先利用勾股定理求得,,再利用勾股定理的逆定理得,再根据即可求解,
本题考查了扇形的面积、勾股定理及逆定理,熟练掌握扇形的面积公式及勾股定理及逆定理是解题的关键.
15.【答案】
【解析】①解:连接CP,CD,如图所示:
在中,,,
,,
由勾股定理得:,
点D是斜边上的中线,
,
,点P是MN的中点,,
是斜边上的中线,
,
在点M,N的运动过程中,点P始终在以C为圆心,以为半径的圆上运动,
根据“两点之间线段最短”得:,
,
当C,P,D三点在同一条直线上时,DP最小,最小值为,
,,
的最小值为:,
故答案为:;
②解:当最大时,则点C到直线PB的距离最大,
由①可知:点P在C为圆心,以为半径的圆上,
当BP与圆C相切时,点C到直线PB的距离最大,即最大,
连接PC,过点点P作于点E,如图2所示:
与相切,
,
在中,,,
由勾股定理得:,
由三角形的面积公式得:,
,
,,
,
点P是MN的中点,
是的中位线,
,
,
当最大时,线段AM的长是
故答案为:
①连接CP,CD,先求出,则,再根据点P是MN的中点得,则点P始终在以C为圆心,以为半径的圆上运动,根据“两点之间线段最短”得,则,即当C,P,D三点在同一条直线上时,DP最小,最小值为,据此即可得出答案;
②当最大时,则点C到直线PB的距离最大,由①可知点P在C为圆心,以为半径的圆上,当BP与圆C相切时,点C到直线PB的距离最大,即最大,过点点P作于点E,先求出,再由三角形的面积公式得,证明PE是的中位线,则,然后根据即可得出线段AM的长.
此题主要考查了切线的性质,点到直线的距离,直角三角形斜边上的中线,三角形中位线定理,熟练掌握切线的性质,直角三角形斜边上的中线,三角形中位线定理是解决问题的关键,确定点P在以为圆心,以为半径的圆上是解决问题的难点.
16.【答案】;
【解析】解:
;
先化简各式,然后再进行计算即可解答;
先利用异分母分式加减法法则计算括号里,再算括号外,即可解答.
本题考查了分式的混合运算,实数的运算,负整数指数幂,特殊角的三角函数值,准确熟练地进行计算是解题的关键.
17.【答案】10,,98;
A款,因A款中位数大于B款的,所以A款好理由不唯一;
85人.
【解析】解:由题意得:A款“满意”所占百分比为,
“不满意”所占百分比为,
;
“满意”的数据:84,86,86,87,88,89;
把A款的评分数据从小到大排列,排在中间的两个数是88、89,
,
在B款的评分数据中,98出现的次数最多,
;
故答案为:10,,98;
款AI聊天机器人更受用户喜爱,理由如下:
因为A款评分数据的中位数比B款高,所以A款AI聊天机器人更受用户喜爱理由不唯一;
款中“不满意”的有3人,所占百分比为,
估计此次测验中对AI聊天机器人不满意的共有人
用1分别减去其他三个等级所占百分比可得a的值,根据中位数的定义可得b的值,根据众数的定义可得c的值;
通过比较A,B款的评分统计表的数据解答即可;
由A、B两款的不满意的人数之和即可得出答案.
本题考查了扇形统计图、中位数、众数以及样本估计总体等知识,正确理解中位数、众数的意义,熟练掌握中位数、众数的计算方法是解题的关键.
18.【答案】解:图形如图所示:
证明:,,
四边形DMBN是平行四边形,
,M是AB的中点,
,
四边形DMBN是菱形;
解:设,,则有,
解得,
,,
,,
四边形ADNM是平行四边形,
,
菱形DMBN的面积
【解析】作,BN交CD于点N
本题考查作图-复杂作图,平行四边形的判定和性质,菱形的判定和性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
19.【答案】解:如图1所示:
连接AC,OA,
根据题意可知,CD为的直径,是直径CD所对的圆周角,
,
,
与相切于点A,
,
即,
,
,
,
,
,
,
,
,
,
如图2所示:
过点C作于H点,
,
,
,
又点C到AB所在直线的距离为15,
,
,
,
,
又,
,
,
为等边三角形,
,
轮胎直径
【解析】连接AC,OA,根据圆周角定理的推论可得,由AB与相切可得到,从而得到,再由,得到,分别与,的关系而从推出结论;
过点C作于H点,得到为直角三角形,求出AC 的长,再由题的结论及条件得出为等边三角形即可得出结论.
本题了考查圆周角定理结论以及切线性质和等边三角形的判定,根据圆的切线垂直于过切点的半径,两直线平行,内错角相等,以及直角三角形的两个锐角互余,由此即可求解.
20.【答案】
【解析】解:,
,
,,
,
答:DE的长为
根据三角函数进行计算,求出,,,即可得到答案.
本题主要考查解直角三角形,熟练掌握三角函数是解题的关键.
21.【答案】A款的进货单价是10元,则B款的进货单价是15元;
购进A款25个,购进B款50个时,获得的总利润最高,最高为300元.
【解析】解:设A款的进货单价是x元,则B款的进货单价是元,
,
解得,
经检验,是该方程的解,
,
答:A单价是10元,则B单价是15元;
设购进B款n个,则购进A款个,
由题意可得:,
,
设总利润为w,则,
,
随n的增大而增大,
当n取得最大整数解50时,w取得最大值,最大值为,
此时,则,
答:购进A款25个,购进B款50个时,获得的总利润最高,最高为300元.
设A款的进货单价是x元,则B款的进货单价是元,根据题意列分式方程求解即可;
设购进B款n个,先根据“A款的数量不小于B款的一半”求得;再设总利润为w,则,然后利用一次函数的性质求解即可.
本题考查分式方程的应用、一元一次不等式的应用、一次函数的应用,理解题意是解答的关键.
22.【答案】解:,
抛物线的顶点坐标为,
设抛物线为,
把点代入得:,
解得,
抛物线的函数表达式为;
当时,,
球不能射进球门.
设小明带球向正后方移动m米,则移动后的抛物线为,
把点代入得:,
解得舍去或,
当时他应该带球向正后方移动1米射门,才能让足球经过点O正上方处.
【解析】求出抛物线的顶点坐标为,设抛物线为,用待定系数法可得;当时,,知球不能射进球门.
设小明带球向正后方移动m米,则移动后的抛物线为,把点代入得舍去或,即知当时他应该带球向正后方移动1米射门,才能让足球经过点O正上方处.
本题考查二次函数的应用,解题的关键是读懂题意,把实际问题转化为数学问题解决.
23.【答案】是;
;
或
【解析】解:,点E是BD的中点,
,
、是等腰三角形,且BE是腰,
四边形AECB是双等腰四边形;
故答案为:是;
如图,
,点E是BD的中点,
同理,
在四边形ABCE中,,
,
;
四边形AEFD是双等腰四边形,,
或
①如图,当时,过点E作于点H,延长HE交AB于点
,
,,
,
,
∽,
,
,
,,,
设,,则,,
,
∽,
,
解得,
;
②如图,当时,过点E作于点
由可知,,
,
,
是等腰直角三角形,
由①可知,,
又,
≌
,,
,
设,,则,,
在中,,
,
解得或不合题意,舍去,
;
综上所述,AB的长为或
根据双等腰四边形的定义即可判断;
根据等腰三角形的性质和四边形内角和求解即可;
依据题意可知或分类讨论,画出图形,然后根据一线三垂直证相似或全等,进而再根据建立关系求解.
本题主要考查了等腰三角形的判定和性质、矩形的性质、相似三角形的判定和性质、勾股定理、全等三角形的判定和性质等内容,熟练掌握相关知识是解题的关键.
同课章节目录
