浙江省杭州市萧山区2025届中考模拟测试 数学练习卷(含答案)
文档属性
| 名称 | 浙江省杭州市萧山区2025届中考模拟测试 数学练习卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 578.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 00:00:00 | ||
图片预览



文档简介
2025年浙江省杭州市萧山区中考模拟测试数学练习卷
一、选择题:本题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.有理数的相反数是( )
A. B. C.5 D.
2.按照国家统计局的数据,2024年中国生产芯片在4300亿颗以上,数据4300亿用科学记数法表示为( )
A. B. C. D.
3.下列图形中,主视图和左视图一样的是( )
A. B.
C. D.
4.下列计算或变形正确的是( )
A. B. C. D.
5.如图是某地去年一至六月每月空气质量为优的天数的折线统计图,关于各月空气质量为优的天数,下列结论错误的是( )
A.五月份空气质量为优的天数是16天
B.这组数据的众数是15天
C.这组数据的中位数是15天
D.这组数据的平均数是15天
6.若xay,当x≥-1时,关于x的代数式ax-2恰好能取到两个非负整数值,则a的取值范围是( )
A.-47.如图,以为斜边的和位于直线的同侧,连接.若,则的长为( )
A.3 B.4 C. D.
8.如图,是的内接三角形,AD是的直径,若,则图中阴影部分的面积为( )
A. B. C. D.
9.关于x的二次函数y=-x2+2x-m(m≠0)与x轴有两个交点(x1,0),(x2,0)(x1<x2),关于x的方程x2-2x+m-1=0有两个非零实数根x3,x4(x3<x4),则下列关系式不成立的是( )
A.x3<x1<x2<x4 B.
C. D.x1-x3=x4-x2
10.如图,在矩形中,,,点E,F分别为的中点,相交于点G,过点E作,交于点H,则线段的长度是( )
A. B.1 C. D.
二、填空题:本题有6个小题,每小题3分,共18分.
11.因式分解: .
12.在一个不透明的袋子里装有红球和白球共若干个,它们除颜色外其余完全相同,每次搅匀后从中随机摸出一个球并记下颜色,再放回袋中,不断重复,统计汇总数据如下表:
摸球次数
摸到白球的频数
摸到白球的频率
已知袋子里白球有个,根据表格信息,可估计出红球的个数为 .
13.如图所示,已知,点E,F分别在直线上,点O在直线之间,.分别在和的平分线上取点M,N,连结,则 °, °.
14. 现有一张矩形纸片,其周长为36cm,将纸片的四个角各剪下一个边长为的正方形,然后沿虚线(如图所示)将纸片折成一个无盖的长方体.如果所得的长方体的底面积是,设原矩形纸片的长是,那么可列出方程为 .
15.已知抛物线(m为常数).若该抛物线与x轴只有一个交点,则 ;若该抛物线与直线有两个不同的交点,且这两个交点都在抛物线对称轴的同侧,则m的取值范围是 .
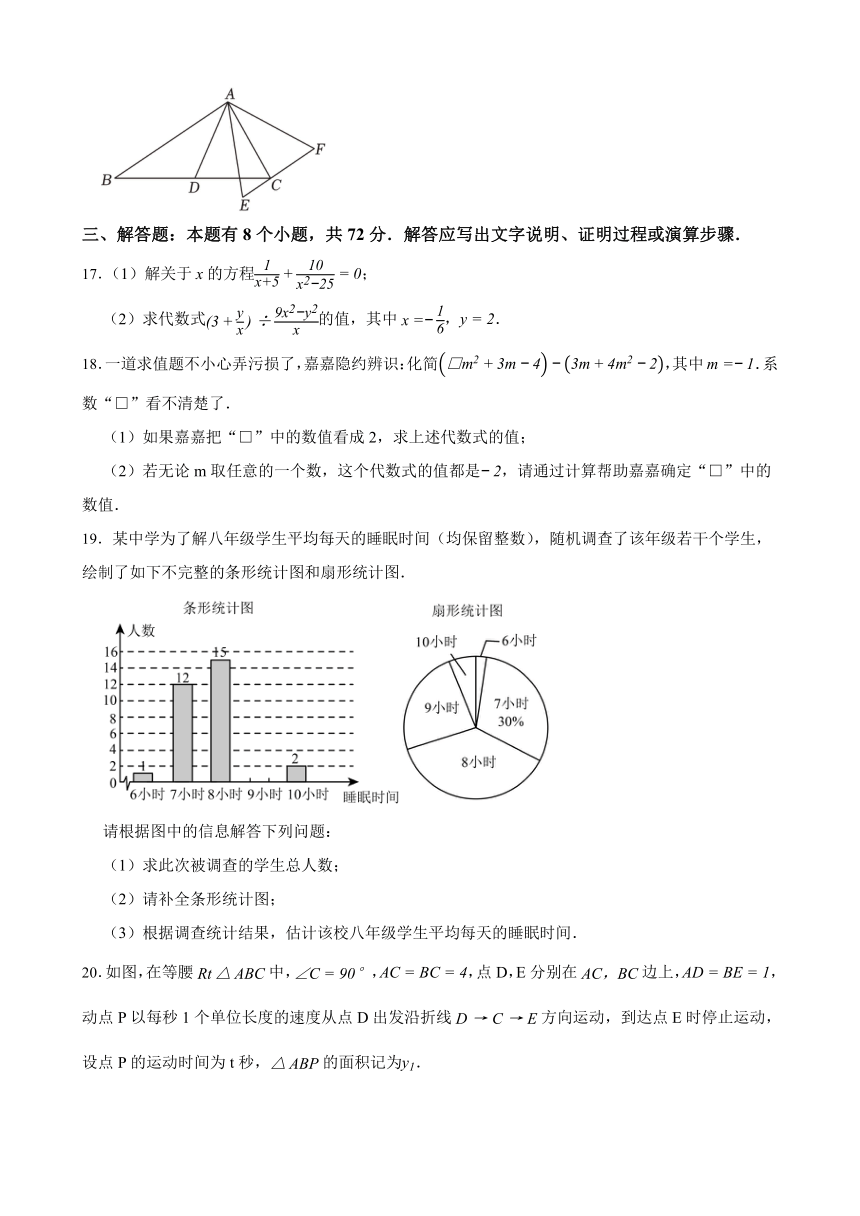
16.如图,在△ABC中,点D为BC的中点,△AEF的边EF过点C,且AE=EF,AB∥EF,AD平分∠BAE,CE=3,AB=12,则CF= .
三、解答题:本题有8个小题,共72分.解答应写出文字说明、证明过程或演算步骤.
17.(1)解关于的方程;
(2)求代数式的值,其中,.
18.一道求值题不小心弄污损了,嘉嘉隐约辨识:化简,其中.系数“□”看不清楚了.
(1)如果嘉嘉把“□”中的数值看成2,求上述代数式的值;
(2)若无论m取任意的一个数,这个代数式的值都是,请通过计算帮助嘉嘉确定“□”中的数值.
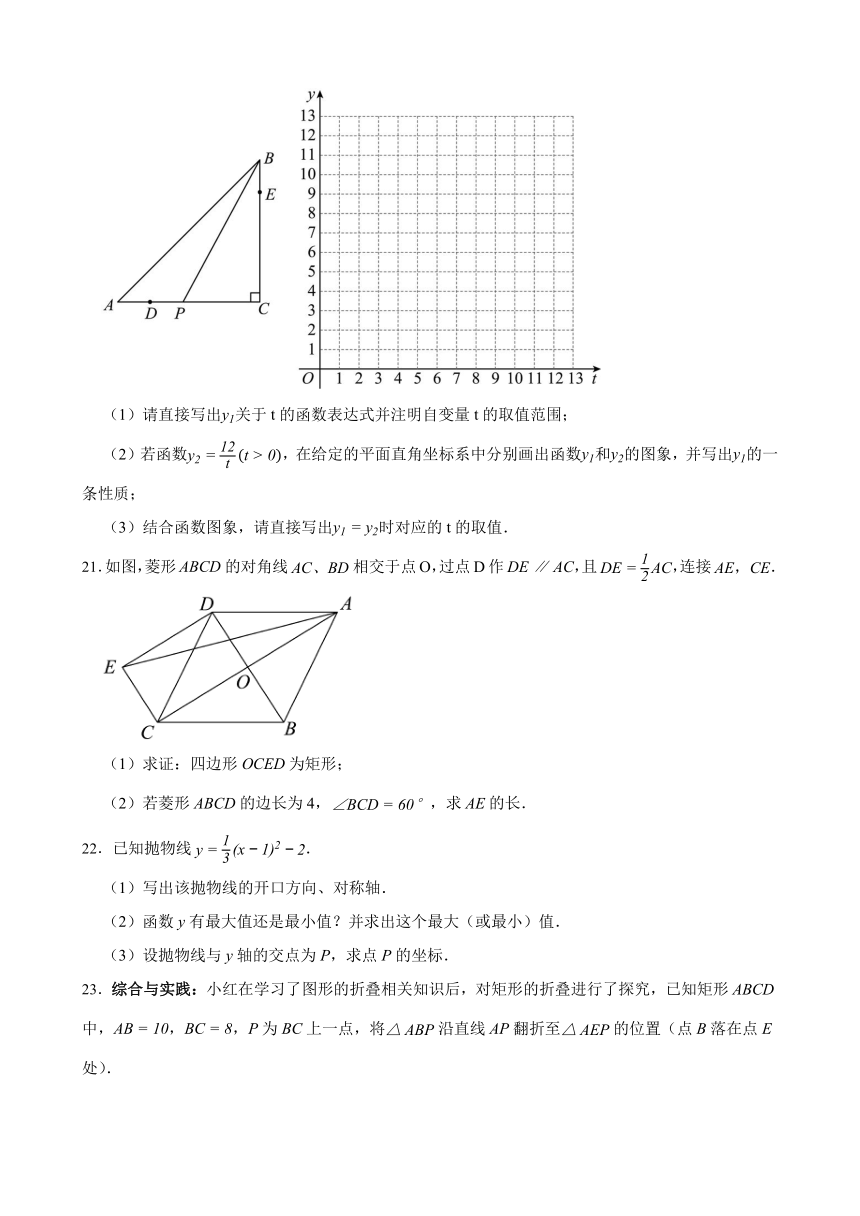
19.某中学为了解八年级学生平均每天的睡眠时间(均保留整数),随机调查了该年级若干个学生,绘制了如下不完整的条形统计图和扇形统计图.
请根据图中的信息解答下列问题:
(1)求此次被调查的学生总人数;
(2)请补全条形统计图;
(3)根据调查统计结果,估计该校八年级学生平均每天的睡眠时间.
20.如图,在等腰中,,,点D,E分别在边上,,动点P以每秒1个单位长度的速度从点D出发沿折线方向运动,到达点E时停止运动,设点P的运动时间为t秒,的面积记为.
(1)请直接写出关于t的函数表达式并注明自变量t的取值范围;
(2)若函数,在给定的平面直角坐标系中分别画出函数和的图象,并写出的一条性质;
(3)结合函数图象,请直接写出时对应的t的取值.
21.如图,菱形的对角线相交于点O,过点D作,且,连接.
(1)求证:四边形为矩形;
(2)若菱形的边长为4,,求的长.
22.已知抛物线.
(1)写出该抛物线的开口方向、对称轴.
(2)函数y有最大值还是最小值?并求出这个最大(或最小)值.
(3)设抛物线与y轴的交点为P,求点P的坐标.
23.综合与实践:小红在学习了图形的折叠相关知识后,对矩形的折叠进行了探究,已知矩形中,,,为上一点,将沿直线翻折至的位置(点落在点处).
(1)【动手操作】当点落在边上时,利用尺规作图,在图①中作出满足条件的图形(即的位置,不写作法,保留作图痕迹),此时________________;
(2)【问题探究】如图②,与相交于点,与相交于点,且,求证:;
(3)【拓展延伸】已知为射线上的一个动点,将沿翻折,点恰好落在直线上的点处,求的长.
24.如图,在中,,,,分别为上两动点,.
(1)如图1,若于交于,求证:;
(2)如图2,若交于,,,求证:;
(3)如图3,若,将绕点顺时针旋转得,为中点,当取得最小值时,请直接写出的面积.
参考答案
1.B
2.C
3.D
4.D
5.D
6.A
7.C
8.C
9.B
10.A
11.
12.
13.260;40
14.
15.;
16.3
17.(1)解:去分母,得,
解得,
检验:当时,,所以为原方程的增根,
所以原方程无解;
(2)解:原式
,
当,时,原式.
18.(1)解:原式.
当时,
原式;
(2)解:设“□”中的数值为,则原式.
无论取任意的一个数,这个代数式的值都是,
.
.
答:“□”中的数是4.
19.(1)解:被调查的学生总人数为:人,
答:被调查的学生总人数为人.
(2)解:人,
补图为:
(3)解:学生平均每天的睡眠时间为:小时,
答:该校八年级学生平均每天的睡眠时间为小时.
20.(1)
(2)解:y1,y2的函数图象,如图所示:
观察图象可得:当时,随t的增大而增大,当时,随t的增大而减小;
(3)或6
21.(1)证明:∵四边形是菱形,
∴,
∴,
∵,,
∴,
∴四边形是平行四边形,
又∵,
∴平行四边形是矩形;
(2)解:∵四边形是菱形,
∴,,,,
∵,
∴是等边三角形,
∴,
∴,
∴,
∴,
由(1)得:四边形为矩形,
∴,,
在中,由勾股定理得:.
22.(1)解:∵抛物线,
∴抛物线开口向上,对称轴为直线x=1;
(2)解:∵且顶点坐标为(1,-2)
∴函数y有最小值,最小值为-2.
(3)解:在 中,令x=0,则y=(0-1)2-2=-,
∴P(0,-).
23.(1)作图见解析,6;
(2)证明:由翻折的性质得,,,
,
设,则,
在和中,
,
,
,,
,
,,
在中,由勾股定理得,,
解得,即,
∴,
∴,
∴.
(3)解:分两种情况:
如解图所示,点在线段上时,
由翻折的性质得,,,,
,
,
四边形是矩形,
,
,
,
,
;
如解图所示,点在延长线上时,
由翻折的性质得,,,
,
设,则,,
,
,
在中,由勾股定理得,,
解得,即,
综上所述,的长为4或16.
24.(1)证明:,,
,
在和中,
,
,
,
又,于交于,
,,
,
;
(2)证明:如下图,过点作,则,
连接并延长交于,连接交于,
由(1)过程得,
,
,
,
,
,
,
在和中,
,
,
,
是等腰直角三角形,
,
又,,
、、三点共线,
设,则,
设,则,
,
,
,
,
(3)解:6
一、选择题:本题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.有理数的相反数是( )
A. B. C.5 D.
2.按照国家统计局的数据,2024年中国生产芯片在4300亿颗以上,数据4300亿用科学记数法表示为( )
A. B. C. D.
3.下列图形中,主视图和左视图一样的是( )
A. B.
C. D.
4.下列计算或变形正确的是( )
A. B. C. D.
5.如图是某地去年一至六月每月空气质量为优的天数的折线统计图,关于各月空气质量为优的天数,下列结论错误的是( )
A.五月份空气质量为优的天数是16天
B.这组数据的众数是15天
C.这组数据的中位数是15天
D.这组数据的平均数是15天
6.若x
A.-4
A.3 B.4 C. D.
8.如图,是的内接三角形,AD是的直径,若,则图中阴影部分的面积为( )
A. B. C. D.
9.关于x的二次函数y=-x2+2x-m(m≠0)与x轴有两个交点(x1,0),(x2,0)(x1<x2),关于x的方程x2-2x+m-1=0有两个非零实数根x3,x4(x3<x4),则下列关系式不成立的是( )
A.x3<x1<x2<x4 B.
C. D.x1-x3=x4-x2
10.如图,在矩形中,,,点E,F分别为的中点,相交于点G,过点E作,交于点H,则线段的长度是( )
A. B.1 C. D.
二、填空题:本题有6个小题,每小题3分,共18分.
11.因式分解: .
12.在一个不透明的袋子里装有红球和白球共若干个,它们除颜色外其余完全相同,每次搅匀后从中随机摸出一个球并记下颜色,再放回袋中,不断重复,统计汇总数据如下表:
摸球次数
摸到白球的频数
摸到白球的频率
已知袋子里白球有个,根据表格信息,可估计出红球的个数为 .
13.如图所示,已知,点E,F分别在直线上,点O在直线之间,.分别在和的平分线上取点M,N,连结,则 °, °.
14. 现有一张矩形纸片,其周长为36cm,将纸片的四个角各剪下一个边长为的正方形,然后沿虚线(如图所示)将纸片折成一个无盖的长方体.如果所得的长方体的底面积是,设原矩形纸片的长是,那么可列出方程为 .
15.已知抛物线(m为常数).若该抛物线与x轴只有一个交点,则 ;若该抛物线与直线有两个不同的交点,且这两个交点都在抛物线对称轴的同侧,则m的取值范围是 .
16.如图,在△ABC中,点D为BC的中点,△AEF的边EF过点C,且AE=EF,AB∥EF,AD平分∠BAE,CE=3,AB=12,则CF= .
三、解答题:本题有8个小题,共72分.解答应写出文字说明、证明过程或演算步骤.
17.(1)解关于的方程;
(2)求代数式的值,其中,.
18.一道求值题不小心弄污损了,嘉嘉隐约辨识:化简,其中.系数“□”看不清楚了.
(1)如果嘉嘉把“□”中的数值看成2,求上述代数式的值;
(2)若无论m取任意的一个数,这个代数式的值都是,请通过计算帮助嘉嘉确定“□”中的数值.
19.某中学为了解八年级学生平均每天的睡眠时间(均保留整数),随机调查了该年级若干个学生,绘制了如下不完整的条形统计图和扇形统计图.
请根据图中的信息解答下列问题:
(1)求此次被调查的学生总人数;
(2)请补全条形统计图;
(3)根据调查统计结果,估计该校八年级学生平均每天的睡眠时间.
20.如图,在等腰中,,,点D,E分别在边上,,动点P以每秒1个单位长度的速度从点D出发沿折线方向运动,到达点E时停止运动,设点P的运动时间为t秒,的面积记为.
(1)请直接写出关于t的函数表达式并注明自变量t的取值范围;
(2)若函数,在给定的平面直角坐标系中分别画出函数和的图象,并写出的一条性质;
(3)结合函数图象,请直接写出时对应的t的取值.
21.如图,菱形的对角线相交于点O,过点D作,且,连接.
(1)求证:四边形为矩形;
(2)若菱形的边长为4,,求的长.
22.已知抛物线.
(1)写出该抛物线的开口方向、对称轴.
(2)函数y有最大值还是最小值?并求出这个最大(或最小)值.
(3)设抛物线与y轴的交点为P,求点P的坐标.
23.综合与实践:小红在学习了图形的折叠相关知识后,对矩形的折叠进行了探究,已知矩形中,,,为上一点,将沿直线翻折至的位置(点落在点处).
(1)【动手操作】当点落在边上时,利用尺规作图,在图①中作出满足条件的图形(即的位置,不写作法,保留作图痕迹),此时________________;
(2)【问题探究】如图②,与相交于点,与相交于点,且,求证:;
(3)【拓展延伸】已知为射线上的一个动点,将沿翻折,点恰好落在直线上的点处,求的长.
24.如图,在中,,,,分别为上两动点,.
(1)如图1,若于交于,求证:;
(2)如图2,若交于,,,求证:;
(3)如图3,若,将绕点顺时针旋转得,为中点,当取得最小值时,请直接写出的面积.
参考答案
1.B
2.C
3.D
4.D
5.D
6.A
7.C
8.C
9.B
10.A
11.
12.
13.260;40
14.
15.;
16.3
17.(1)解:去分母,得,
解得,
检验:当时,,所以为原方程的增根,
所以原方程无解;
(2)解:原式
,
当,时,原式.
18.(1)解:原式.
当时,
原式;
(2)解:设“□”中的数值为,则原式.
无论取任意的一个数,这个代数式的值都是,
.
.
答:“□”中的数是4.
19.(1)解:被调查的学生总人数为:人,
答:被调查的学生总人数为人.
(2)解:人,
补图为:
(3)解:学生平均每天的睡眠时间为:小时,
答:该校八年级学生平均每天的睡眠时间为小时.
20.(1)
(2)解:y1,y2的函数图象,如图所示:
观察图象可得:当时,随t的增大而增大,当时,随t的增大而减小;
(3)或6
21.(1)证明:∵四边形是菱形,
∴,
∴,
∵,,
∴,
∴四边形是平行四边形,
又∵,
∴平行四边形是矩形;
(2)解:∵四边形是菱形,
∴,,,,
∵,
∴是等边三角形,
∴,
∴,
∴,
∴,
由(1)得:四边形为矩形,
∴,,
在中,由勾股定理得:.
22.(1)解:∵抛物线,
∴抛物线开口向上,对称轴为直线x=1;
(2)解:∵且顶点坐标为(1,-2)
∴函数y有最小值,最小值为-2.
(3)解:在 中,令x=0,则y=(0-1)2-2=-,
∴P(0,-).
23.(1)作图见解析,6;
(2)证明:由翻折的性质得,,,
,
设,则,
在和中,
,
,
,,
,
,,
在中,由勾股定理得,,
解得,即,
∴,
∴,
∴.
(3)解:分两种情况:
如解图所示,点在线段上时,
由翻折的性质得,,,,
,
,
四边形是矩形,
,
,
,
,
;
如解图所示,点在延长线上时,
由翻折的性质得,,,
,
设,则,,
,
,
在中,由勾股定理得,,
解得,即,
综上所述,的长为4或16.
24.(1)证明:,,
,
在和中,
,
,
,
又,于交于,
,,
,
;
(2)证明:如下图,过点作,则,
连接并延长交于,连接交于,
由(1)过程得,
,
,
,
,
,
,
在和中,
,
,
,
是等腰直角三角形,
,
又,,
、、三点共线,
设,则,
设,则,
,
,
,
,
(3)解:6
同课章节目录
