浙教版2024—2025学年八年级下学期数学期末考试押题冲刺卷(含答案)
文档属性
| 名称 | 浙教版2024—2025学年八年级下学期数学期末考试押题冲刺卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 549.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 07:09:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年八年级下学期数学期末考试押题冲刺卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列四个图形分别是绿色食品、节水、节能和回收标志,在这四个标志中,中心对称图形是( )
A. B. C. D.
2.甲、乙、丙、丁四名射击运动员进行射击测试,每人10次射击成绩的平均数(单位:环)及方差s2(单位:环2)如表所示:
甲 乙 丙 丁
9 8 9 9
s2 1.2 0.3 0.3 0.8
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A.甲 B.乙 C.丙 D.丁
3.下列二次根式是最简二次根式的是( )
A. B. C. D.
4.二次根式有意义的条件是( )
A.x>3 B.x>﹣3 C.x≥﹣3 D.x≥3
5.体育课上,体育老师记录了40位同学的实心球成绩,数据分别为x1,x2,……x40.但由于场地布置失误,导致每位同学的成绩都少记录了10cm,其实际数据分别为y1,y2,……y40,比较记录成绩和实际成绩这两组数据,统计量不会发生变化的是( )
A.方差 B.中位数 C.众数 D.平均数
6.在平面直角坐标系中,点A(1,4a),B(a,a+2)都在反比例函数的图象上,则k的值为( )
A.2 B.4 C.6 D.8
7.新能源汽车已逐渐成为人们的交通工具,据某品牌新能源汽车经销商1月至3月份统计,该品牌新能源汽车1月份销售1000辆,3月份销售1210辆.设月平均增长率为x,根据题意,下列方程正确的是( )
A.1210(1﹣x)2=1000 B.1000(1+x)2=1210
C.1000(1+2x)=1210 D.1210(1﹣2x)=1000
8.用反证法证明“在直角三角形中,至少有一个锐角不大于45°”时第一步应先假设( )
A.在直角三角形中,每一个锐角都大于45°
B.在直角三角形中,至多有一个锐角大于45°
C.在直角三角形中,每一个锐角都不大于45°
D.在直角三角形中,至多有一个锐角不大于45°
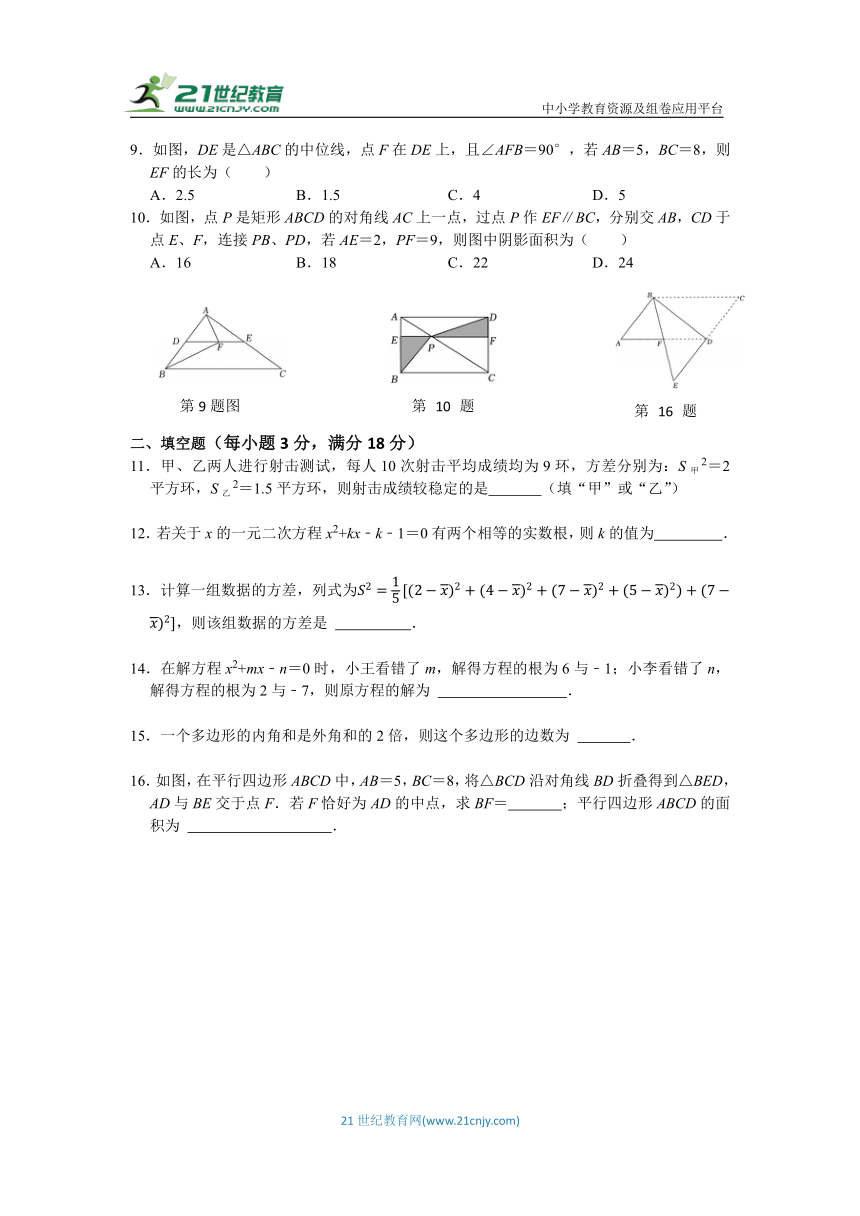
9.如图,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
A.2.5 B.1.5 C.4 D.5
10.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E、F,连接PB、PD,若AE=2,PF=9,则图中阴影面积为( )
A.16 B.18 C.22 D.24
二、填空题(每小题3分,满分18分)
11.甲、乙两人进行射击测试,每人10次射击平均成绩均为9环,方差分别为:S甲2=2平方环,S乙2=1.5平方环,则射击成绩较稳定的是 (填“甲”或“乙”)
12.若关于x的一元二次方程x2+kx﹣k﹣1=0有两个相等的实数根,则k的值为 .
13.计算一组数据的方差,列式为,则该组数据的方差是 .
14.在解方程x2+mx﹣n=0时,小王看错了m,解得方程的根为6与﹣1;小李看错了n,解得方程的根为2与﹣7,则原方程的解为 .
15.一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
16.如图,在平行四边形ABCD中,AB=5,BC=8,将△BCD沿对角线BD折叠得到△BED,AD与BE交于点F.若F恰好为AD的中点,求BF= ;平行四边形ABCD的面积为 .
浙教版2024—2025学年八年级下学期数学期末考试押题冲刺卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______ ______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2).
18.解方程:
(1)x2﹣6x=﹣9; (2)(x+1)(x﹣3)=6.
19.已知:,,求下列代数式的值:
(1)x2﹣y2;
(2)x2﹣3xy+y2.
20.如图,在菱形ABCD中,点P是BC边上的点,连结AP交对角线BD于点E,连结EC.
(1)求证:AE=CE.
(2)若∠ABC=45°,AE=PC,求∠BAP的度数.
21.为了进一步加强中小学生对于民族文化的认同感,某中学开展了形式多样的传统文化教育培训活动.为了解培训效果,该校组织全校学生参加了传统文化主题知识竞赛,为了解竞赛成绩,随机抽样调查了七、八年级各10名学生的成绩x(单位:分),分数如下:
七年级10名学生竞赛成绩:75,83,79,89,79,83,95,70,64,83;
八年级10名学生竞赛成绩中分布血80<x≤90的成绩如下:84,85,85,85,86.
【整理数据】:
年级 0<x≤70 70<x≤80 80<x≤90 90<x≤100
七年级 2 m 4 1
八年级 1 3 5 1
【分析数据】:
年级 平均数 众数 中位数 方差
七年级 80 a 81 71.6
八年级 80 85 b 59.8
根据以上提供的信息,回答下列问题:
(1)填空:m= ,a= ,b= ;
(2)若学生的竞赛成绩超过80分为“优秀”,请估计该校参加竞赛的八年级320名学生中,竞赛成绩为“优秀”的人数;
(3)根据以上统计结果,从不同角度说明七年级与八年级哪个年级成绩更优秀.
22.某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件.为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.
(1)降价前商场每月销售该商品的利润是多少元?
(2)要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?
(3)该商场1月份销售量为60件,2月和3月的月平均增长率为x,若前三个月的总销量为285件,求该季度的总利润.
23.如图,一次函数y=kx+b的图象与反比例函数y的图象交于A(1,3),B(﹣3,n)两点.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)根据图象直接写出一次函数值小于反比例函数值的x的取值范围;
(4)若点P在x轴上,点Q在反比例函数y的图象上,当以A、B、P、Q为顶点的四边形为平行四边形时,直接写出点Q的坐标: .
24.如图, ABCD中,E为BC边上的一个动点(不与B、C重合),过点E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G.
(1)若E为BC中点,求证:BF=CG;
(2)若AB=5,BC=10,∠B=60°,当点E在线段BC上运动时,FG的长度是否改变?若不变,求FG;若改变,请说明理由;
(3)在(2)的条件下,H为直线AD上的一点,设BE=x,若A、B、E、H四点构成一个平行四边形,请用含x的代数式表示BH.
25.如图,直线与反比例函数图象的交点分别为P,Q,且点P的坐标为(a,2),过点P作PB⊥x轴,垂足为B.直线与x轴交于点A,与y轴交于点C.
(1)求k的值;
(2)若点D是反比例函数图象上的一点,且在点P的右侧,连接PD,OP,OD,若S△POD=S四边形PBOC,求点D的坐标;
(3)若M为y轴上一个动点,N为平面内一点,当以M,N,P,Q为顶点的四边形为矩形时,请直接写出M的坐标.
参考答案
一、选择题
1—10:DCACA DBABB
二、填空题
11.【解答】解:∵S甲2=2>S乙2=1.5,方差小的为乙,
∴本题中成绩比较稳定的是乙.
故答案为:乙.
12.【解答】解:∵方程x2+kx﹣k﹣1=0有两个相等的实数根,
∴Δ=k2﹣4(﹣k﹣1)=k2+4k+4=(k+2)2=0,
解得:k=﹣2.
故答案为:﹣2.
13.【解答】解:由方差计算公式得这组数据为:2,4,7,5,7,
∴,
∴
=3.6;
故答案为:3.6.
14.【解答】解:根据根与系数关系得,
﹣n=6×(﹣1),﹣m=2﹣7,
解得:n=6,m=5,
∴原方程为x2+5x﹣6=0,
(x﹣1)(x+6)=0,
x﹣1=0或x+6=0,
∴x1=1,x2=﹣6,
故答案为:x1=1,x2=﹣6.
15.【解答】解:∵多边形的外角和是360度,多边形的内角和是外角和的2倍,
则内角和是720度,
720÷180+2=6,
∴这个多边形的边数为6.
故答案为:6.
16.【解答】解:如图,过点B作BN⊥AD于N,过点F作FM⊥AB于M,
∵ABCD是平行四边形,
∴∠A=∠C,
∵∠E=∠C,
∴∠A=∠E,
∵F为AD的中点,
∴AF=DF,
在△AFB和△EFD中,
,
∴△AFB≌△EFD(AAS),
将△BCD沿对角线BD折叠得到△BED,
∴∠BDC=∠BDE=90°,
∴△BCD为直角三角形,
∵AB=5,BC=8,
∴CD=5,
在Rt△BCD中,,
∴平行四边形ABCD的面积为.
故答案为:.
三、解答题
17.【解答】解:(1)原式
=0;
(2)
.
18.【解答】解:(1)x2﹣6x=﹣9,
x2﹣6x+9=0,
(x﹣3)2=0,
∴x1=x2=3;
(2)(x+1)(x﹣3)=6,
x2+x﹣3x﹣3=6,
x2﹣2x﹣3=6,
∴x2﹣2x=9,
∴(x﹣1)2=9+1,
∴x﹣1,
∴x1=1,x2=1.
19.【解答】解:(1)∵,,
∴,
∴x2﹣y2;
(2)∵,,
∴xy=2﹣9=﹣7,x﹣y=6,
∴x2﹣3xy+y2
=(x﹣y)2﹣xy
=36+7
=43.
20.【解答】(1)证明:∵四边形ABCD为菱形,
∴BA=BC,∠ABD=∠CBD,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE;
(2)解:设∠BAP=α,
∵△ABE≌△CBE,
∴∠BAP=∠BCE=α,
∵AE=PC,AE=CE,
∴PC=CE,
∴∠CPE=∠CEP(180°﹣∠BCE)=90°α,
∵∠CPE是△ABP的一个外角,∠ABC=45°,
∴∠CPE=∠ABC+∠BAP,
∴90°α=45°+α,
∴α=30°,
∴∠BAP=α=30°.
21.【解答】解:(1)m=10﹣2﹣4﹣1=3,
在75,83,79,89,79,83,95,70,64,83中,出现次数最多的是83,
∴众数a=83;
m=10﹣2﹣4﹣1=3,
八年级成绩中处于中间的两个数据为84和85,
∴中位数b84.5;
故答案为:3,83;84.5;
(2)320192(人),
∴估计该校参加竞赛的八年级320名学生中,竞赛成绩为“优秀”的人数192人;
(3)我认为八年级成绩更好,理由如下:
因为两个年级的平均数相同,而八年级的成绩的中位数和众数均都大于七年级.
22.【解答】解:(1)根据题意得:(360﹣280)×60
=80×60
=4800(元).
答:降价前商场每月销售该商品的利润是4800元;
(2)设每件商品降价m元,则每件的销售利润为(360﹣m﹣280)元,每月可售出(60+5m)件,
根据题意得:(360﹣m﹣280)(60+5m)=7200,
整理得:m2﹣68m+480=0,解得:m1=8,m2=60,
又∵要有利于减少库存,∴m=60.
答:每件商品应降价60元;
(3)根据题意得:60+60(1+x)+60(1+x)2=285,
整理得:4x2+12x﹣7=0,
解得:x1=0.5=50%,x2=﹣3.5(不符合题意,舍去),
∴60(1+x)=60×(1+50%)=90(件),60(1+x)2=60×(1+50%)2=135(件),
∴2月份这种商品的售价为360354(元),3月份这种商品的售价为360345(元),
∴该季度的总利润为(360﹣280)×60+(354﹣280)×90+(345﹣280)×135=20235(元).
答:该季度的总利润为20235元.
23.【解答】解:(1)∵反比例函数y的图象经过A(1,3),
∴m=1×3=3,∴反比例函数的表达式为y,
又∵点B(﹣3,n)在反比例函数y的图象上.
∴﹣3n=3,
∴n=﹣1,
∴B(﹣3,﹣1),
∵一次函数y=kx+b的图象经过A(1,3)、B(﹣3,﹣1)两点.
∴,
解得:,∴一次函数的表达式为y=x+2;
(2)如图1,设直线y=x+2与y轴交于点C,则C(0,2),
∴S△AOB=S△BOC+S△AOC2×32×1=4;
(3)由图象得:一次函数值小于反比例函数值的x的取值范围是:x<﹣3或0<x<1;
(4)分两种情况:
①如图2,四边形APBQ是平行四边形,
∵A(1,3),B(﹣3,﹣1),且点P的纵坐标为0,
∴点Q的纵坐标为2,
∴Q(,2);
②如图3,四边形AQPB是平行四边形,
∵A(1,3),B(﹣3,﹣1),且点P的纵坐标为0,
∴点Q的纵坐标为4,
∴Q(,4);
③如图4,四边形ABQP是平行四边形,同理得:Q(,﹣4);
综上所述,点Q的坐标为(,2)或(,4)或(,﹣4).
24.【解答】(1)证明:如图1中,
∵四边形ABCD是平行四边形,
∴BF∥CG,
∴∠BFE=∠G,
∵BE=CE,∠BEF=∠GEC,
∴△BEF≌△CEG(AAS),
∴BF=CG.
(2)解:结论:FG的长度不变.FG=5.
理由:如图2中,取BC的中点J,连接AC,AJ.
∵AB=BJ=5,∠B=60°,
∴△ABJ是等边三角形,
∴JA=JB=JC=5,
∴∠BAC=90°,ACAB=5,
∵EF⊥AB,
∴∠CAB=∠EFB=90°,
∴AC∥FG,
∵AF∥CG,
∴四边形AFCG是平行四边形,
∴FG=AC=5.
(3)解:如图3中,当点H在线段AD上时,作HM⊥BC于M.
在Rt△EHM中,∵∠HEM=∠ABC=60°,EH=AB=5,
∴EMHE,HMEM,
∴BH.
当点H′在DA的延长线上时,同法可得BH′,
综上所述,BH的长为或.
25.【解答】解:(1)直线与反比例函数图象的交点分别为P,Q,且点P的坐标为(a,2),将点P的坐标代入得:
,
解得:a=2,
∴P(2,2),
∵将点P的坐标代入反比例函数得:
2,
解得:k=4;
(2)过点D作DH⊥x轴,如图1,
在一次函数中令x=0,得y=1,
∴C(0,1),
∵P(2,2),PB⊥x轴,
∴S△POD=S四边形PBOC(1+2)×2=3,
∵点P、D在函数的图象上,PB⊥x轴,DH⊥x轴,
∴S△OPB=S△ODH,
∵S四边形OPDH=S△OPB+S梯形PBHD=S△ODH+S△OPD,
∴S梯形PBHD=S△OPD=3,
设,
则,
解得:t=4或t=﹣1,
∵点D在点P的右侧,
∴t=4,
∴D(4,1);
(3)M的坐标为(0,6)或(0,﹣9)或或;理由如下:
将与联立方程组得:
,
解得:或,
∴Q(﹣4,﹣1),
设M(0,m),
∴PQ2=(2+4)2+(2+1)2=45,PM2=22+(m﹣2)2=m2﹣4m+8,QM2=42+(m+1)2=m2+2m+17,
当以M,N,P,Q为顶点的四边形为矩形时,
如图2,当PQ是矩形的边时,
若∠QPM1=90°时,则PQ2,
∴45+m2﹣4m+8=m2+2m+17,
解得:m=6,
∴M1(0,6);
若∠PQM2=90°时,则,
∴45+m2+2m+17=m2﹣4m+8,
解得:m=﹣9,
∴M2(0,﹣9);
如图3,当PQ是矩形的对角线时,
则∠PMQ=90°时,则PQ2=QM2+PM2,
∴45=m2+2m+17+m2﹣4m+8,
解得:,
∴,,
综上所述,M的坐标为(0,6)或(0,﹣9)或或.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年八年级下学期数学期末考试押题冲刺卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列四个图形分别是绿色食品、节水、节能和回收标志,在这四个标志中,中心对称图形是( )
A. B. C. D.
2.甲、乙、丙、丁四名射击运动员进行射击测试,每人10次射击成绩的平均数(单位:环)及方差s2(单位:环2)如表所示:
甲 乙 丙 丁
9 8 9 9
s2 1.2 0.3 0.3 0.8
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A.甲 B.乙 C.丙 D.丁
3.下列二次根式是最简二次根式的是( )
A. B. C. D.
4.二次根式有意义的条件是( )
A.x>3 B.x>﹣3 C.x≥﹣3 D.x≥3
5.体育课上,体育老师记录了40位同学的实心球成绩,数据分别为x1,x2,……x40.但由于场地布置失误,导致每位同学的成绩都少记录了10cm,其实际数据分别为y1,y2,……y40,比较记录成绩和实际成绩这两组数据,统计量不会发生变化的是( )
A.方差 B.中位数 C.众数 D.平均数
6.在平面直角坐标系中,点A(1,4a),B(a,a+2)都在反比例函数的图象上,则k的值为( )
A.2 B.4 C.6 D.8
7.新能源汽车已逐渐成为人们的交通工具,据某品牌新能源汽车经销商1月至3月份统计,该品牌新能源汽车1月份销售1000辆,3月份销售1210辆.设月平均增长率为x,根据题意,下列方程正确的是( )
A.1210(1﹣x)2=1000 B.1000(1+x)2=1210
C.1000(1+2x)=1210 D.1210(1﹣2x)=1000
8.用反证法证明“在直角三角形中,至少有一个锐角不大于45°”时第一步应先假设( )
A.在直角三角形中,每一个锐角都大于45°
B.在直角三角形中,至多有一个锐角大于45°
C.在直角三角形中,每一个锐角都不大于45°
D.在直角三角形中,至多有一个锐角不大于45°
9.如图,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
A.2.5 B.1.5 C.4 D.5
10.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E、F,连接PB、PD,若AE=2,PF=9,则图中阴影面积为( )
A.16 B.18 C.22 D.24
二、填空题(每小题3分,满分18分)
11.甲、乙两人进行射击测试,每人10次射击平均成绩均为9环,方差分别为:S甲2=2平方环,S乙2=1.5平方环,则射击成绩较稳定的是 (填“甲”或“乙”)
12.若关于x的一元二次方程x2+kx﹣k﹣1=0有两个相等的实数根,则k的值为 .
13.计算一组数据的方差,列式为,则该组数据的方差是 .
14.在解方程x2+mx﹣n=0时,小王看错了m,解得方程的根为6与﹣1;小李看错了n,解得方程的根为2与﹣7,则原方程的解为 .
15.一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
16.如图,在平行四边形ABCD中,AB=5,BC=8,将△BCD沿对角线BD折叠得到△BED,AD与BE交于点F.若F恰好为AD的中点,求BF= ;平行四边形ABCD的面积为 .
浙教版2024—2025学年八年级下学期数学期末考试押题冲刺卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______ ______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2).
18.解方程:
(1)x2﹣6x=﹣9; (2)(x+1)(x﹣3)=6.
19.已知:,,求下列代数式的值:
(1)x2﹣y2;
(2)x2﹣3xy+y2.
20.如图,在菱形ABCD中,点P是BC边上的点,连结AP交对角线BD于点E,连结EC.
(1)求证:AE=CE.
(2)若∠ABC=45°,AE=PC,求∠BAP的度数.
21.为了进一步加强中小学生对于民族文化的认同感,某中学开展了形式多样的传统文化教育培训活动.为了解培训效果,该校组织全校学生参加了传统文化主题知识竞赛,为了解竞赛成绩,随机抽样调查了七、八年级各10名学生的成绩x(单位:分),分数如下:
七年级10名学生竞赛成绩:75,83,79,89,79,83,95,70,64,83;
八年级10名学生竞赛成绩中分布血80<x≤90的成绩如下:84,85,85,85,86.
【整理数据】:
年级 0<x≤70 70<x≤80 80<x≤90 90<x≤100
七年级 2 m 4 1
八年级 1 3 5 1
【分析数据】:
年级 平均数 众数 中位数 方差
七年级 80 a 81 71.6
八年级 80 85 b 59.8
根据以上提供的信息,回答下列问题:
(1)填空:m= ,a= ,b= ;
(2)若学生的竞赛成绩超过80分为“优秀”,请估计该校参加竞赛的八年级320名学生中,竞赛成绩为“优秀”的人数;
(3)根据以上统计结果,从不同角度说明七年级与八年级哪个年级成绩更优秀.
22.某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件.为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.
(1)降价前商场每月销售该商品的利润是多少元?
(2)要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?
(3)该商场1月份销售量为60件,2月和3月的月平均增长率为x,若前三个月的总销量为285件,求该季度的总利润.
23.如图,一次函数y=kx+b的图象与反比例函数y的图象交于A(1,3),B(﹣3,n)两点.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)根据图象直接写出一次函数值小于反比例函数值的x的取值范围;
(4)若点P在x轴上,点Q在反比例函数y的图象上,当以A、B、P、Q为顶点的四边形为平行四边形时,直接写出点Q的坐标: .
24.如图, ABCD中,E为BC边上的一个动点(不与B、C重合),过点E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G.
(1)若E为BC中点,求证:BF=CG;
(2)若AB=5,BC=10,∠B=60°,当点E在线段BC上运动时,FG的长度是否改变?若不变,求FG;若改变,请说明理由;
(3)在(2)的条件下,H为直线AD上的一点,设BE=x,若A、B、E、H四点构成一个平行四边形,请用含x的代数式表示BH.
25.如图,直线与反比例函数图象的交点分别为P,Q,且点P的坐标为(a,2),过点P作PB⊥x轴,垂足为B.直线与x轴交于点A,与y轴交于点C.
(1)求k的值;
(2)若点D是反比例函数图象上的一点,且在点P的右侧,连接PD,OP,OD,若S△POD=S四边形PBOC,求点D的坐标;
(3)若M为y轴上一个动点,N为平面内一点,当以M,N,P,Q为顶点的四边形为矩形时,请直接写出M的坐标.
参考答案
一、选择题
1—10:DCACA DBABB
二、填空题
11.【解答】解:∵S甲2=2>S乙2=1.5,方差小的为乙,
∴本题中成绩比较稳定的是乙.
故答案为:乙.
12.【解答】解:∵方程x2+kx﹣k﹣1=0有两个相等的实数根,
∴Δ=k2﹣4(﹣k﹣1)=k2+4k+4=(k+2)2=0,
解得:k=﹣2.
故答案为:﹣2.
13.【解答】解:由方差计算公式得这组数据为:2,4,7,5,7,
∴,
∴
=3.6;
故答案为:3.6.
14.【解答】解:根据根与系数关系得,
﹣n=6×(﹣1),﹣m=2﹣7,
解得:n=6,m=5,
∴原方程为x2+5x﹣6=0,
(x﹣1)(x+6)=0,
x﹣1=0或x+6=0,
∴x1=1,x2=﹣6,
故答案为:x1=1,x2=﹣6.
15.【解答】解:∵多边形的外角和是360度,多边形的内角和是外角和的2倍,
则内角和是720度,
720÷180+2=6,
∴这个多边形的边数为6.
故答案为:6.
16.【解答】解:如图,过点B作BN⊥AD于N,过点F作FM⊥AB于M,
∵ABCD是平行四边形,
∴∠A=∠C,
∵∠E=∠C,
∴∠A=∠E,
∵F为AD的中点,
∴AF=DF,
在△AFB和△EFD中,
,
∴△AFB≌△EFD(AAS),
将△BCD沿对角线BD折叠得到△BED,
∴∠BDC=∠BDE=90°,
∴△BCD为直角三角形,
∵AB=5,BC=8,
∴CD=5,
在Rt△BCD中,,
∴平行四边形ABCD的面积为.
故答案为:.
三、解答题
17.【解答】解:(1)原式
=0;
(2)
.
18.【解答】解:(1)x2﹣6x=﹣9,
x2﹣6x+9=0,
(x﹣3)2=0,
∴x1=x2=3;
(2)(x+1)(x﹣3)=6,
x2+x﹣3x﹣3=6,
x2﹣2x﹣3=6,
∴x2﹣2x=9,
∴(x﹣1)2=9+1,
∴x﹣1,
∴x1=1,x2=1.
19.【解答】解:(1)∵,,
∴,
∴x2﹣y2;
(2)∵,,
∴xy=2﹣9=﹣7,x﹣y=6,
∴x2﹣3xy+y2
=(x﹣y)2﹣xy
=36+7
=43.
20.【解答】(1)证明:∵四边形ABCD为菱形,
∴BA=BC,∠ABD=∠CBD,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE;
(2)解:设∠BAP=α,
∵△ABE≌△CBE,
∴∠BAP=∠BCE=α,
∵AE=PC,AE=CE,
∴PC=CE,
∴∠CPE=∠CEP(180°﹣∠BCE)=90°α,
∵∠CPE是△ABP的一个外角,∠ABC=45°,
∴∠CPE=∠ABC+∠BAP,
∴90°α=45°+α,
∴α=30°,
∴∠BAP=α=30°.
21.【解答】解:(1)m=10﹣2﹣4﹣1=3,
在75,83,79,89,79,83,95,70,64,83中,出现次数最多的是83,
∴众数a=83;
m=10﹣2﹣4﹣1=3,
八年级成绩中处于中间的两个数据为84和85,
∴中位数b84.5;
故答案为:3,83;84.5;
(2)320192(人),
∴估计该校参加竞赛的八年级320名学生中,竞赛成绩为“优秀”的人数192人;
(3)我认为八年级成绩更好,理由如下:
因为两个年级的平均数相同,而八年级的成绩的中位数和众数均都大于七年级.
22.【解答】解:(1)根据题意得:(360﹣280)×60
=80×60
=4800(元).
答:降价前商场每月销售该商品的利润是4800元;
(2)设每件商品降价m元,则每件的销售利润为(360﹣m﹣280)元,每月可售出(60+5m)件,
根据题意得:(360﹣m﹣280)(60+5m)=7200,
整理得:m2﹣68m+480=0,解得:m1=8,m2=60,
又∵要有利于减少库存,∴m=60.
答:每件商品应降价60元;
(3)根据题意得:60+60(1+x)+60(1+x)2=285,
整理得:4x2+12x﹣7=0,
解得:x1=0.5=50%,x2=﹣3.5(不符合题意,舍去),
∴60(1+x)=60×(1+50%)=90(件),60(1+x)2=60×(1+50%)2=135(件),
∴2月份这种商品的售价为360354(元),3月份这种商品的售价为360345(元),
∴该季度的总利润为(360﹣280)×60+(354﹣280)×90+(345﹣280)×135=20235(元).
答:该季度的总利润为20235元.
23.【解答】解:(1)∵反比例函数y的图象经过A(1,3),
∴m=1×3=3,∴反比例函数的表达式为y,
又∵点B(﹣3,n)在反比例函数y的图象上.
∴﹣3n=3,
∴n=﹣1,
∴B(﹣3,﹣1),
∵一次函数y=kx+b的图象经过A(1,3)、B(﹣3,﹣1)两点.
∴,
解得:,∴一次函数的表达式为y=x+2;
(2)如图1,设直线y=x+2与y轴交于点C,则C(0,2),
∴S△AOB=S△BOC+S△AOC2×32×1=4;
(3)由图象得:一次函数值小于反比例函数值的x的取值范围是:x<﹣3或0<x<1;
(4)分两种情况:
①如图2,四边形APBQ是平行四边形,
∵A(1,3),B(﹣3,﹣1),且点P的纵坐标为0,
∴点Q的纵坐标为2,
∴Q(,2);
②如图3,四边形AQPB是平行四边形,
∵A(1,3),B(﹣3,﹣1),且点P的纵坐标为0,
∴点Q的纵坐标为4,
∴Q(,4);
③如图4,四边形ABQP是平行四边形,同理得:Q(,﹣4);
综上所述,点Q的坐标为(,2)或(,4)或(,﹣4).
24.【解答】(1)证明:如图1中,
∵四边形ABCD是平行四边形,
∴BF∥CG,
∴∠BFE=∠G,
∵BE=CE,∠BEF=∠GEC,
∴△BEF≌△CEG(AAS),
∴BF=CG.
(2)解:结论:FG的长度不变.FG=5.
理由:如图2中,取BC的中点J,连接AC,AJ.
∵AB=BJ=5,∠B=60°,
∴△ABJ是等边三角形,
∴JA=JB=JC=5,
∴∠BAC=90°,ACAB=5,
∵EF⊥AB,
∴∠CAB=∠EFB=90°,
∴AC∥FG,
∵AF∥CG,
∴四边形AFCG是平行四边形,
∴FG=AC=5.
(3)解:如图3中,当点H在线段AD上时,作HM⊥BC于M.
在Rt△EHM中,∵∠HEM=∠ABC=60°,EH=AB=5,
∴EMHE,HMEM,
∴BH.
当点H′在DA的延长线上时,同法可得BH′,
综上所述,BH的长为或.
25.【解答】解:(1)直线与反比例函数图象的交点分别为P,Q,且点P的坐标为(a,2),将点P的坐标代入得:
,
解得:a=2,
∴P(2,2),
∵将点P的坐标代入反比例函数得:
2,
解得:k=4;
(2)过点D作DH⊥x轴,如图1,
在一次函数中令x=0,得y=1,
∴C(0,1),
∵P(2,2),PB⊥x轴,
∴S△POD=S四边形PBOC(1+2)×2=3,
∵点P、D在函数的图象上,PB⊥x轴,DH⊥x轴,
∴S△OPB=S△ODH,
∵S四边形OPDH=S△OPB+S梯形PBHD=S△ODH+S△OPD,
∴S梯形PBHD=S△OPD=3,
设,
则,
解得:t=4或t=﹣1,
∵点D在点P的右侧,
∴t=4,
∴D(4,1);
(3)M的坐标为(0,6)或(0,﹣9)或或;理由如下:
将与联立方程组得:
,
解得:或,
∴Q(﹣4,﹣1),
设M(0,m),
∴PQ2=(2+4)2+(2+1)2=45,PM2=22+(m﹣2)2=m2﹣4m+8,QM2=42+(m+1)2=m2+2m+17,
当以M,N,P,Q为顶点的四边形为矩形时,
如图2,当PQ是矩形的边时,
若∠QPM1=90°时,则PQ2,
∴45+m2﹣4m+8=m2+2m+17,
解得:m=6,
∴M1(0,6);
若∠PQM2=90°时,则,
∴45+m2+2m+17=m2﹣4m+8,
解得:m=﹣9,
∴M2(0,﹣9);
如图3,当PQ是矩形的对角线时,
则∠PMQ=90°时,则PQ2=QM2+PM2,
∴45=m2+2m+17+m2﹣4m+8,
解得:,
∴,,
综上所述,M的坐标为(0,6)或(0,﹣9)或或.
21世纪教育网(www.21cnjy.com)
同课章节目录
