湘教版2024—2025学年八年级下学期数学期末调研检测卷(含答案)
文档属性
| 名称 | 湘教版2024—2025学年八年级下学期数学期末调研检测卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
湘教版2024—2025学年八年级下学期数学期末调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2.在平面直角坐标系中,点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.若函数是正比例函数,则( )
A.1 B. C.0 D.2
4.如果在x轴上,那么m的值是( )
A. B.1 C.2 D.
5.凉山州某景区计划打造一个独具特色的多边形花坛.此花坛作为当地特色建筑风格的一部分,其内角和为,那么这个多边形花坛的边数是( )
A.8 B.9 C.10 D.11
6.三角形的三边长分别为,则它最大边上的中线长为( )
A. B. C.10 D.12
7.下列说法错误的是( )
A.平行四边形的对角线互相平分
B.矩形的对角线互相垂直且相等
C.菱形的对角线互相垂直平分
D.正方形的对角线互相垂直平分且相等
8.某学校组织科技知识测试,随机抽取50名学生的成绩,绘制成如图频数分布直方图,则样本中这一分数段的频率是( )
A.20 B. C. D.
9.若一次函数的图象不经过第二象限,则( )
A. B. C. D.
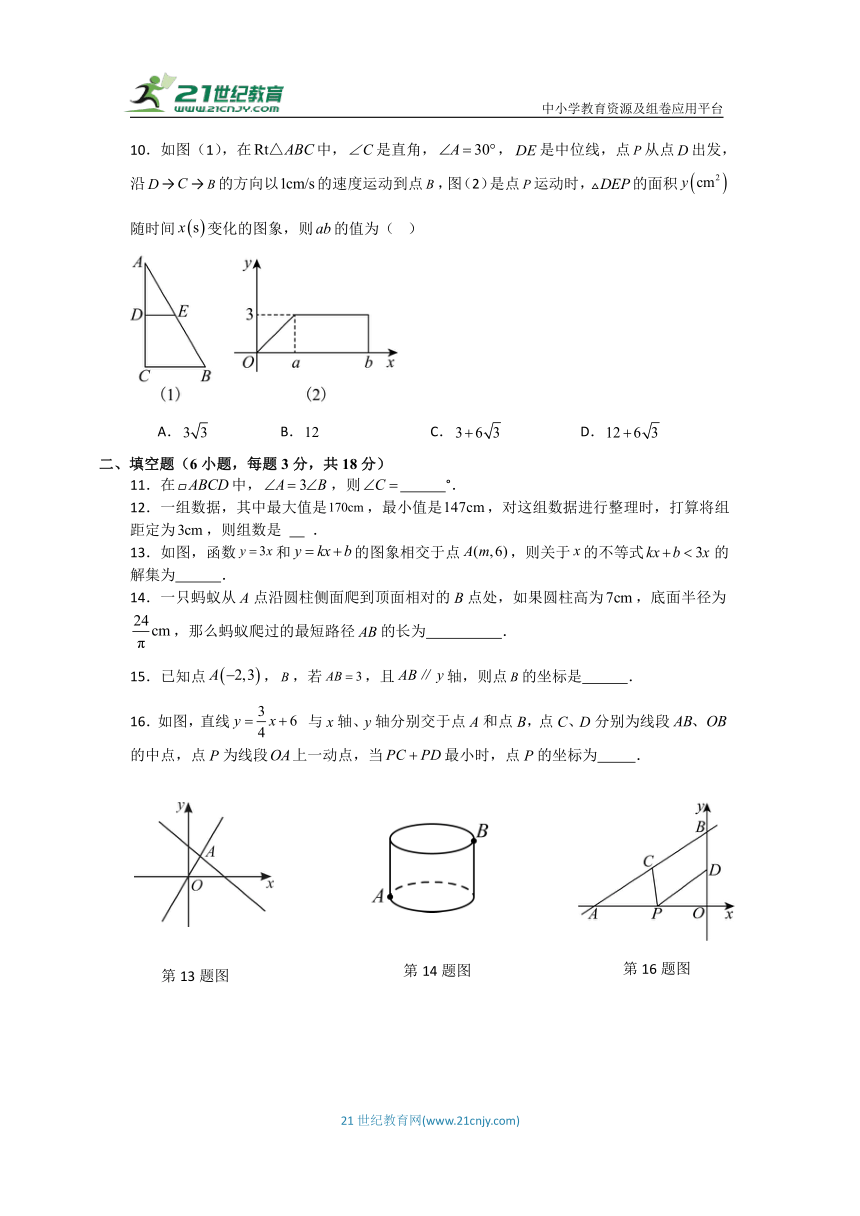
10.如图(1),在中,是直角,,是中位线,点从点出发,沿→→的方向以的速度运动到点,图(2)是点运动时,的面积随时间变化的图象,则的值为( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.在中,,则 °.
12.一组数据,其中最大值是,最小值是,对这组数据进行整理时,打算将组距定为,则组数是 .
13.如图,函数和的图象相交于点,则关于的不等式的解集为 .
14.一只蚂蚁从A点沿圆柱侧面爬到顶面相对的B点处,如果圆柱高为,底面半径为,那么蚂蚁爬过的最短路径的长为 .
15.已知点,,若,且轴,则点的坐标是 .
16.如图,直线 与x轴、y轴分别交于点A和点B,点C、D分别为线段的中点,点P为线段上一动点,当最小时,点P的坐标为 .
第II卷
湘教版2024—2025学年八年级下学期数学期末调研检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
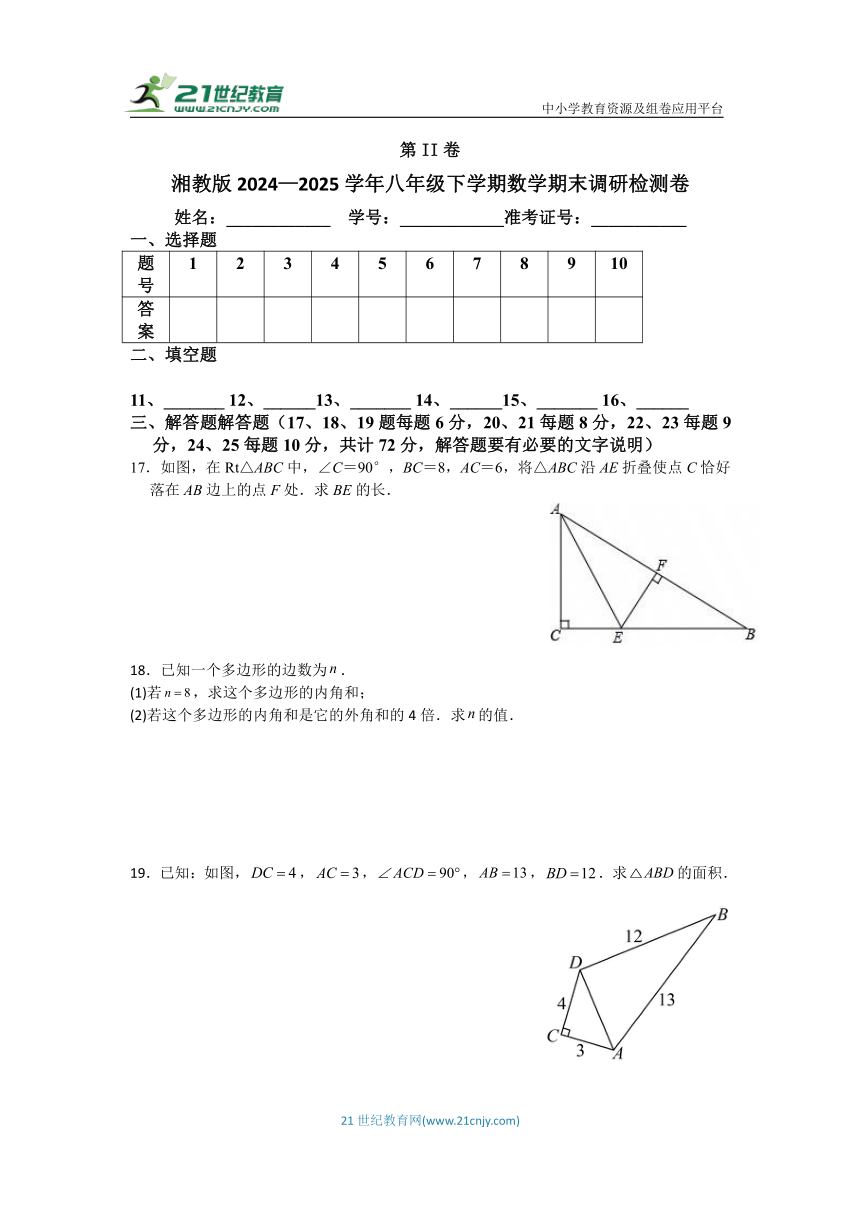
17.如图,在Rt△ABC中,∠C=90°,BC=8,AC=6,将△ABC沿AE折叠使点C恰好落在AB边上的点F处.求BE的长.
18.已知一个多边形的边数为.
(1)若,求这个多边形的内角和;
(2)若这个多边形的内角和是它的外角和的4倍.求的值.
19.已知:如图,,,,,.求的面积.
20.在2025年全国科技活动周期间,某校科技小组对甲、乙两个水产养殖基地水体的值进行了检测,并对一天(24小时)内每小时的值进行了整理、描述及分析.
【收集数据】
甲基地水体的值数据:
7.27,7.28,7.34,7.35,7.36,7.51,7.53,7.67,7.67,7.67,7.67,7.81,7.81,7.88,7.91,8.01,8.02,8.03,8.07,8.16,8.17,8.23,8.26,8.26.
乙基地水体的值数据:
7.11,7.12,7.14,7.25,7.36,7.52,7.63,7.67,7.69,7.75,7.77,7.77,7.81,7.84,7.89,8.01,8.12,8.13,8.14,8.16,8.17,8.18,8.20,8.21.
【整理数据】
甲 2 5 7 7 3
乙 4 2 9 a 2
【描述数据】
【分析数据】
平均数 众数 中位数 方差
甲 7.79 b 7.81 0.10
乙 7.78 7.77 c 0.13
根据以上信息解决下列问题:
(1)补全频数分布直方图;
(2)填空:______,______;
(3)请判断甲、乙哪个基地水体的值更稳定,并说明理由;
(4)已知两基地对水体值的日变化量(值最大值与最小值的差)要求为0.5~1,分别判断并说明该日两基地的值是否符合要求.
21.茂名地区的荔枝和三华李已入选广东非物质文化遗产名录.为满足消费者需求,某超市购进荔枝和三华李,已知荔枝比三华李每千克进价少2元,用900元购进荔枝与用1100元购进三华李的重量相同.
(1)求荔枝和三华李每千克进价分别是多少元;
(2)本次购进荔枝和三华李共800千克,均按每千克13元出售,购进荔枝的重量不超过三华李重量的3倍,且重量不少于400千克.若该批水果全部售完,则该超市应购进荔枝和三华李各多少千克才能获得最大利润?最大利润是多少?
22.如图,为斜边上的高,的平分线分别交,于点,,垂足为点.
(1)求证:;
(2)已知,,.求的面积.
23.在平面直角坐标系中,为坐标原点,将三角形进行平移,平移后点A,B,C的对应点分别是点,,.点,点,点,点.
(1)若,则的坐标为_____;(用含的式子表示)
(2)若,求的值;
(3)若点,其中.直线交轴于点,且三角形的面积为1,试探究和的数量关系,并说明理由.
24.如图1,将矩形放在直角坐标系中,O为原点,点C在x轴上,点A在y轴上,点B的坐标为,且a,b满足.把矩形沿对角线所在直线翻折,点C落到点D处,交于点E.
(1)求点B的坐标;
(2)求点E坐标;
(3)如图2,过点D作,交于点G,交于点H,连接.
①试判断四边形的形状,并说明理由;
②点M是坐标平面内一点,且使以A,E,D,M为顶点的四边形是平行四边形.请直接写出所有满足条件的M点的坐标.
25.如图,在平面直角坐标系中,直线与x轴、y轴分别交于点D、C,点A在x轴的正半轴上,若将沿直线折叠,点D恰好落在y轴正半轴上的点B处.
(1)求B点的坐标以及直线的解析式;
(2)点H是x轴上一动点,若,求出点H的坐标;
(3)在第一象限内是否存在点P,使为等腰直角三角形,若存在,直接写出点P的坐标;若不存在,请说明理由.
参考答案
一、选择题
1—10:BCBDC BBDBD
二、填空题
11.【解】:如图:∵四边形是平行四边形,
故答案为:135.
12.【解】:极差为,组距为,
,
则组数是8,
故答案为:8.
13.【解】:∵函数和的图象相交于点,
∴,
∴,
∴,
∴的解集为.
故答案为:.
14.【解】:连接,
圆柱的底面半径为,
,
在中,,
则,
即蚂蚁爬行的最短路径长为.
故答案为:
15.【解】:∵轴,
∴点的纵坐标与点的横坐标相同,
∵,
∴点的坐标是或,
故答案为:或.
16.【解】:作点关于轴的对称点,连接交轴于点,
此时值最小,如图所示.
在中,当,则,当时,
∴点的坐标为,点的坐标为,
∵点、分别为线段、的中点,
∴,点.
∵点和点关于轴对称,
∴点的坐标为.
设直线的解析式为,
∴,解得:
∴直线的解析式为.
在中,当,则,解得:,
∴点的坐标为.
故答案为:.
三、解答题
17.解:∵将△ABC沿AE折叠 使点C恰好落在AB边上的点F,
∴AC=AF=6,EF⊥AB,CE=EF,
∵在Rt△ABC中,∠C=90°,BC=8,AC=6,
∴AB10,
∴BF=AB﹣AF=10﹣6=4,
设BE=x,则EF=8﹣x,
∴x2=(x﹣8)2+42,
解方程得:x=5.
即BE=5.
18.(1)解:,
∴这个多边形的内角和为;
(2)解:由题意得,,
解得.
19.解:∵,,,
∴,
∵,,
∴,
∴,
∴的面积.
20.(1)解:根据题意得,
补全频数分布直方图如图;
;
(2)解:甲基地水体的值数据中,7.67出现了4次,出现次数最多,
则;
乙基地水体的值数据中,由小到大排列中间两个数为7.77和7.81:
则;
故答案为:;;
(3)解:∵甲的方差为0.10,乙的方差为0.13,,
∴甲基地水体的值更稳定;
(4)解:甲基地对水体值的日变化量:,
乙基地对水体值的日变化量:,
∴该日两基地的值甲符合要求,乙不符合要求.
21.(1)解:设荔枝每千克x元,则三华李每千克元,
由题意可得:,
解得.
经检验是原分式方程的解,
∴,
答:荔枝每千克9元,三华李每千克11元.
(2)解:设超市获得利润为y元,购进荔枝m千克,则购进三华李千克,
∵,
∴,
,
∵,
∴y随m的增大而增大,
∴当时,y的值最大,,
三华李数量千克.
答:当购进荔枝600千克,三华李200千克时获利最大,最大利润为2800元.
22.(1)证明:∵是的平分线,,,
∴,,
,,
∴,
∵,
∴,
∴,
∴.
(2)解:∵,
∴,
∵,
∴,
∵,
∴,
∴.
23.解:(1)已知平移后得到,的坐标的变化为,即向右平移个单位;纵坐标的变化为,即向下平移个单位,
同理,平移后得到,从到的坐标变化为,纵坐标变化为,结合到的平移规律,可知整体平移是向右个单位,向下个单位,
点,按照上述平移规律,向右平移个单位,的坐标变为;向下平移个单位,纵坐标变为,
∴点的坐标为;
(2)解:当时,
由三角形平移得到三角形,
的对应点分别为
,
可得,
解得.
∴的值为6;
(3)由三角形平移得到三角形,
,的对应点分别为
,.
可得,
由②得③,
把③代入①,得,
∴,
∴点与点的纵坐标相等,
∴轴,
∴点,
∴三角形的面积,
∵,
∴,.
∴,
∴,
∴,,.
又∵在平移中,点与点是对应点,
∴,
∴
,
∴.
24.(1)解:∵,
∴.
∴,,
∴B点坐标为.
(2)解:∵B点坐标为,
∴,.如图1.
∵四边形是矩形,
∴,,
∴.
由翻折可知,,
∴,
∴.
设,
则.
在中,
∵,
∴.
∴,
∴,
∴
(3)①解:如图2中,四边形是菱形.
∵,
∴.
由翻折的性质可知,,,
∴,
∴.
∵,
∴四边形是平行四边形.
∵,
∴四边形是菱形.
②由题意可得:,
由(1)可得:,,.
在中,可得:,
∴,
∴,
∴,
∴.
∵,,,设,
当为对角线时,由中点坐标公式得:
解得:,
∴;
当为对角线时,,,,设,
由中点坐标公式得:
解得:,
∴;
当为对角线时,,,,设,
由中点坐标公式得:
解得:,
∴.
综上所述,满足条件的点M的坐标为,,.
25.(1)解:当时,;
当时,,解得,
∴,,
∴,,
∵,
∴,
∵折叠,
∴,,
∴,
∴,
在中,,
∴
解得,
∴,
设直线解析式为,
∴
∴,
∴;
(2)解:联立方程组,
解得,
∴,
∵,
∴,
解得,
∵,
∴或,即或;
(3)解:①当,时,如图,过P作于H,
则,,
∴,
∴,,
∴,
∴;
②,,如图,过P作于H,
同理可证,
∴,,
∴,
∴;
③,,
设
如图,过P作于M,于N,
在四边形是矩形,
∴,
又,
∴,
又,,
∴,
∴,,
∴,
解得,
∴
综上,在第一象限内存在点P,使为等腰直角三角形,点P的坐标为或或.
21世纪教育网(www.21cnjy.com)
湘教版2024—2025学年八年级下学期数学期末调研检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2.在平面直角坐标系中,点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.若函数是正比例函数,则( )
A.1 B. C.0 D.2
4.如果在x轴上,那么m的值是( )
A. B.1 C.2 D.
5.凉山州某景区计划打造一个独具特色的多边形花坛.此花坛作为当地特色建筑风格的一部分,其内角和为,那么这个多边形花坛的边数是( )
A.8 B.9 C.10 D.11
6.三角形的三边长分别为,则它最大边上的中线长为( )
A. B. C.10 D.12
7.下列说法错误的是( )
A.平行四边形的对角线互相平分
B.矩形的对角线互相垂直且相等
C.菱形的对角线互相垂直平分
D.正方形的对角线互相垂直平分且相等
8.某学校组织科技知识测试,随机抽取50名学生的成绩,绘制成如图频数分布直方图,则样本中这一分数段的频率是( )
A.20 B. C. D.
9.若一次函数的图象不经过第二象限,则( )
A. B. C. D.
10.如图(1),在中,是直角,,是中位线,点从点出发,沿→→的方向以的速度运动到点,图(2)是点运动时,的面积随时间变化的图象,则的值为( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.在中,,则 °.
12.一组数据,其中最大值是,最小值是,对这组数据进行整理时,打算将组距定为,则组数是 .
13.如图,函数和的图象相交于点,则关于的不等式的解集为 .
14.一只蚂蚁从A点沿圆柱侧面爬到顶面相对的B点处,如果圆柱高为,底面半径为,那么蚂蚁爬过的最短路径的长为 .
15.已知点,,若,且轴,则点的坐标是 .
16.如图,直线 与x轴、y轴分别交于点A和点B,点C、D分别为线段的中点,点P为线段上一动点,当最小时,点P的坐标为 .
第II卷
湘教版2024—2025学年八年级下学期数学期末调研检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.如图,在Rt△ABC中,∠C=90°,BC=8,AC=6,将△ABC沿AE折叠使点C恰好落在AB边上的点F处.求BE的长.
18.已知一个多边形的边数为.
(1)若,求这个多边形的内角和;
(2)若这个多边形的内角和是它的外角和的4倍.求的值.
19.已知:如图,,,,,.求的面积.
20.在2025年全国科技活动周期间,某校科技小组对甲、乙两个水产养殖基地水体的值进行了检测,并对一天(24小时)内每小时的值进行了整理、描述及分析.
【收集数据】
甲基地水体的值数据:
7.27,7.28,7.34,7.35,7.36,7.51,7.53,7.67,7.67,7.67,7.67,7.81,7.81,7.88,7.91,8.01,8.02,8.03,8.07,8.16,8.17,8.23,8.26,8.26.
乙基地水体的值数据:
7.11,7.12,7.14,7.25,7.36,7.52,7.63,7.67,7.69,7.75,7.77,7.77,7.81,7.84,7.89,8.01,8.12,8.13,8.14,8.16,8.17,8.18,8.20,8.21.
【整理数据】
甲 2 5 7 7 3
乙 4 2 9 a 2
【描述数据】
【分析数据】
平均数 众数 中位数 方差
甲 7.79 b 7.81 0.10
乙 7.78 7.77 c 0.13
根据以上信息解决下列问题:
(1)补全频数分布直方图;
(2)填空:______,______;
(3)请判断甲、乙哪个基地水体的值更稳定,并说明理由;
(4)已知两基地对水体值的日变化量(值最大值与最小值的差)要求为0.5~1,分别判断并说明该日两基地的值是否符合要求.
21.茂名地区的荔枝和三华李已入选广东非物质文化遗产名录.为满足消费者需求,某超市购进荔枝和三华李,已知荔枝比三华李每千克进价少2元,用900元购进荔枝与用1100元购进三华李的重量相同.
(1)求荔枝和三华李每千克进价分别是多少元;
(2)本次购进荔枝和三华李共800千克,均按每千克13元出售,购进荔枝的重量不超过三华李重量的3倍,且重量不少于400千克.若该批水果全部售完,则该超市应购进荔枝和三华李各多少千克才能获得最大利润?最大利润是多少?
22.如图,为斜边上的高,的平分线分别交,于点,,垂足为点.
(1)求证:;
(2)已知,,.求的面积.
23.在平面直角坐标系中,为坐标原点,将三角形进行平移,平移后点A,B,C的对应点分别是点,,.点,点,点,点.
(1)若,则的坐标为_____;(用含的式子表示)
(2)若,求的值;
(3)若点,其中.直线交轴于点,且三角形的面积为1,试探究和的数量关系,并说明理由.
24.如图1,将矩形放在直角坐标系中,O为原点,点C在x轴上,点A在y轴上,点B的坐标为,且a,b满足.把矩形沿对角线所在直线翻折,点C落到点D处,交于点E.
(1)求点B的坐标;
(2)求点E坐标;
(3)如图2,过点D作,交于点G,交于点H,连接.
①试判断四边形的形状,并说明理由;
②点M是坐标平面内一点,且使以A,E,D,M为顶点的四边形是平行四边形.请直接写出所有满足条件的M点的坐标.
25.如图,在平面直角坐标系中,直线与x轴、y轴分别交于点D、C,点A在x轴的正半轴上,若将沿直线折叠,点D恰好落在y轴正半轴上的点B处.
(1)求B点的坐标以及直线的解析式;
(2)点H是x轴上一动点,若,求出点H的坐标;
(3)在第一象限内是否存在点P,使为等腰直角三角形,若存在,直接写出点P的坐标;若不存在,请说明理由.
参考答案
一、选择题
1—10:BCBDC BBDBD
二、填空题
11.【解】:如图:∵四边形是平行四边形,
故答案为:135.
12.【解】:极差为,组距为,
,
则组数是8,
故答案为:8.
13.【解】:∵函数和的图象相交于点,
∴,
∴,
∴,
∴的解集为.
故答案为:.
14.【解】:连接,
圆柱的底面半径为,
,
在中,,
则,
即蚂蚁爬行的最短路径长为.
故答案为:
15.【解】:∵轴,
∴点的纵坐标与点的横坐标相同,
∵,
∴点的坐标是或,
故答案为:或.
16.【解】:作点关于轴的对称点,连接交轴于点,
此时值最小,如图所示.
在中,当,则,当时,
∴点的坐标为,点的坐标为,
∵点、分别为线段、的中点,
∴,点.
∵点和点关于轴对称,
∴点的坐标为.
设直线的解析式为,
∴,解得:
∴直线的解析式为.
在中,当,则,解得:,
∴点的坐标为.
故答案为:.
三、解答题
17.解:∵将△ABC沿AE折叠 使点C恰好落在AB边上的点F,
∴AC=AF=6,EF⊥AB,CE=EF,
∵在Rt△ABC中,∠C=90°,BC=8,AC=6,
∴AB10,
∴BF=AB﹣AF=10﹣6=4,
设BE=x,则EF=8﹣x,
∴x2=(x﹣8)2+42,
解方程得:x=5.
即BE=5.
18.(1)解:,
∴这个多边形的内角和为;
(2)解:由题意得,,
解得.
19.解:∵,,,
∴,
∵,,
∴,
∴,
∴的面积.
20.(1)解:根据题意得,
补全频数分布直方图如图;
;
(2)解:甲基地水体的值数据中,7.67出现了4次,出现次数最多,
则;
乙基地水体的值数据中,由小到大排列中间两个数为7.77和7.81:
则;
故答案为:;;
(3)解:∵甲的方差为0.10,乙的方差为0.13,,
∴甲基地水体的值更稳定;
(4)解:甲基地对水体值的日变化量:,
乙基地对水体值的日变化量:,
∴该日两基地的值甲符合要求,乙不符合要求.
21.(1)解:设荔枝每千克x元,则三华李每千克元,
由题意可得:,
解得.
经检验是原分式方程的解,
∴,
答:荔枝每千克9元,三华李每千克11元.
(2)解:设超市获得利润为y元,购进荔枝m千克,则购进三华李千克,
∵,
∴,
,
∵,
∴y随m的增大而增大,
∴当时,y的值最大,,
三华李数量千克.
答:当购进荔枝600千克,三华李200千克时获利最大,最大利润为2800元.
22.(1)证明:∵是的平分线,,,
∴,,
,,
∴,
∵,
∴,
∴,
∴.
(2)解:∵,
∴,
∵,
∴,
∵,
∴,
∴.
23.解:(1)已知平移后得到,的坐标的变化为,即向右平移个单位;纵坐标的变化为,即向下平移个单位,
同理,平移后得到,从到的坐标变化为,纵坐标变化为,结合到的平移规律,可知整体平移是向右个单位,向下个单位,
点,按照上述平移规律,向右平移个单位,的坐标变为;向下平移个单位,纵坐标变为,
∴点的坐标为;
(2)解:当时,
由三角形平移得到三角形,
的对应点分别为
,
可得,
解得.
∴的值为6;
(3)由三角形平移得到三角形,
,的对应点分别为
,.
可得,
由②得③,
把③代入①,得,
∴,
∴点与点的纵坐标相等,
∴轴,
∴点,
∴三角形的面积,
∵,
∴,.
∴,
∴,
∴,,.
又∵在平移中,点与点是对应点,
∴,
∴
,
∴.
24.(1)解:∵,
∴.
∴,,
∴B点坐标为.
(2)解:∵B点坐标为,
∴,.如图1.
∵四边形是矩形,
∴,,
∴.
由翻折可知,,
∴,
∴.
设,
则.
在中,
∵,
∴.
∴,
∴,
∴
(3)①解:如图2中,四边形是菱形.
∵,
∴.
由翻折的性质可知,,,
∴,
∴.
∵,
∴四边形是平行四边形.
∵,
∴四边形是菱形.
②由题意可得:,
由(1)可得:,,.
在中,可得:,
∴,
∴,
∴,
∴.
∵,,,设,
当为对角线时,由中点坐标公式得:
解得:,
∴;
当为对角线时,,,,设,
由中点坐标公式得:
解得:,
∴;
当为对角线时,,,,设,
由中点坐标公式得:
解得:,
∴.
综上所述,满足条件的点M的坐标为,,.
25.(1)解:当时,;
当时,,解得,
∴,,
∴,,
∵,
∴,
∵折叠,
∴,,
∴,
∴,
在中,,
∴
解得,
∴,
设直线解析式为,
∴
∴,
∴;
(2)解:联立方程组,
解得,
∴,
∵,
∴,
解得,
∵,
∴或,即或;
(3)解:①当,时,如图,过P作于H,
则,,
∴,
∴,,
∴,
∴;
②,,如图,过P作于H,
同理可证,
∴,,
∴,
∴;
③,,
设
如图,过P作于M,于N,
在四边形是矩形,
∴,
又,
∴,
又,,
∴,
∴,,
∴,
解得,
∴
综上,在第一象限内存在点P,使为等腰直角三角形,点P的坐标为或或.
21世纪教育网(www.21cnjy.com)
同课章节目录
